Abstract
The experimentation is carried out to examine the influence of receiver aperture/opening ratio (receiver’s aperture diameter to the maximum diameter ratio, d/D), glass cover thickness and inclination angle of cavity receiver on its collection efficiency for various flow rates of ordinary water as a working fluid. Experimental tests have been conducted at lower incident energy, i.e., at lower cavity wall temperatures (less than 200 °C). The aperture ratio examined encompasses values as 0.46, 0.6, 0.7, and 0.93 for water flowing at flows of 0.8, 0.65, 0.5, and 0.4 LPM that corresponds to Reynolds numbers (Re) of 1880, 1525, 1175, and 938, respectively. The glazing thicknesses of 6, 4, and 2 mm were provided at an aperture. A modified cavity-type receiver is made inclined at angles 90°, 60°, 45°, and 30° (with 90° as down-facing receiver opening and 30° as close to sideway-facing of receiver opening). The tests have been conducted for cavity surface temperatures ranging from 90° to 180 °C. It is observed that an aperture ratio of 0.6 demonstrates maximum receiver performance for the values of Reynolds number studied, while the receiver performance exhibited reducing trend with reduction in receiver tilting angle from 90° to 30°.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
In solar-based power plant, the concentrated solar irradiation is transferred to a working fluid flowing through heat exchange element, called receiver situated at the focal location of a solar parabolic dish collector. This hot and pressurized working fluid (air or water) then energizes the prime movers (e.g., steam turbine or gas turbine). The receiver geometries of shapes, e.g., hemispherical, spherical, cylindrical, rectangular, dome-shaped, elliptical, etc., have been used so far for actual use and for investigation by Shuai et al. [1]. Investigating the effect of geometry shapes such as cylindrical, spherical, and conical cavity receiver, it is reported that a conical-shaped receiver captures maximum amount of energy among the three designs. The receiver optical efficiencies of 70%, 71%, and 75.3% are noticed for the examined cavity receiver geometries; spherical, cylindrical, and conical, respectively, at surface absorptivity value of 0.85. The optical efficiency of the receiver is also seen dependent on the radiative flux distribution inside the receiver [2].
The effect of receiver geometrical parameters; aperture diameter, inside diameter, and height of cylindrical cavity receiver, on the energy losses as well as collection efficiency has been examined by Chongzhe et al. [3]. The thermal losses are seen to be increasing with cavity length that is attributed to rise in surface area involved in energy transfer. The thermal efficiency exhibits a dropping trend with rise in aperture diameter. The optimum values of cylindrical cavity diameter, cavity length, and spiral tube number of turns, exhibiting efficiency of 71.41%, are 0.35 m, 0.403 m and five turns, respectively. An optimum value of aperture ratio for a cylindrical receiver cavity is 0.53 exhibiting better performance. The radiation loss from a cavity receiver increases with rise in opening diameter from 18.4 to 30 cm. However, with increase in opening diameter above 63%, convective as well as conductive losses decrease by less than 5%. As compared to percent reduction of conduction and convection losses due to rise of cavity aperture, percentage increase of radiation losses is very high [3].
The energy losses by all the three modes, from a semi-spherical cavity receiver have been examined for lower (75–150 °C) as well as higher temperature (150–300 °C) situations by Tan et al. [4], for various receiver inclination angles and aperture ratios. A receiver surface is heated up to a desired temperature by means of a hot working fluid circulated through it. In the present study, the radiative heat was supplied through the receiver aperture and the effects of receiver inclination angles, aperture ratios, and glazing thickness on the performance were examined.
The cavity receivers are told to be extra efficient compared to the external receivers due to reduced energy losses. The convective losses from the former ones are reported to be dependent on two aspects; mass transfer due to external wind as well as buoyancy effects and capability of receiver wall/surface to heat up an enclosed stagnant air. The cavity receivers involving larger expanse of hotter surface area may cause more amounts of convective losses. The radiative heat losses are reported to be dependent on the nature of radiative cavity surface, by Clausing [5]. In continuation to this research, Prakash et al. [6] have identified the zones of free convection and stagnant fluid in case of a cylindrical cavity for various inclination angles ranging from 0° to 90°. The stagnant fluid zone is seen at location where air temperature gradient ≤ 0.3 and naturally convected zone is depicted at zone where air temperature gradient > 0.3. It is represented as a ratio of ‘temperature variance between the temperature at the concerned location inside the receiver and inlet temperature of fluid’ to ‘distance between a particular location and top wall of receiver’. The stagnation zone is observed at the inside top end of a vertically downward inverted receiver and convective zone is seen at the bottom entry side of a receiver. The size of convective zone reduces with increased angle of receiver inclination from 0° (sideway opening) to 90° (down-facing receiver) [6].
According to Wu et al. [7], the heat exchange takes place mainly in the convection zone. An entire cavity of receiver is subjected to only stagnation zone, which results in minimum convective energy loss from receiver inclined at 90°. After all, it depends on the external wind velocity. In case the external wind velocity dominates over the naturally convected currents developed inside the cavity, the energy loss by means of combined free and forced-type convection loss takes over the free convection energy loss. As reported by Kaushika (1993), the modified cavity-type receiver having aperture plane at the opening of hemispherical cavity performs better than hemispherical or semi cavity receiver. The radiative energy loss dominates over the convective energy loss for receiver inclination angles greater than 45°, and hence, it should not be neglected while analysing performance of a receiver, as reported by Prakash et al. [6].
The provision of plate fins significantly reduces the convective heat losses by about 20% from the cavity receiver as well as it reduces the radiative energy losses by about 5% [8]. Radiation energy loss from a cavity receiver is seen to be unchanged for various receiver inclination angles (0°, 90°, and 180°).
The convective heat losses from the receiver are reported maximum for cavity aperture facing sideways and minimum when it is facing downwards. At sideways position, a receiver is dominated by the convective zone which diminishes for down-facing receiver due to stagnant fluid zone inside cavity. The provision of fins improves the receiver collection efficiency by about 2% [8]. Similarly, providing fins inside the conical receiver without glazing exhibited collection efficiency improvement of about 10% as compared to conical receiver with no fins [13]. The radiation heat transfer from receiver surface is reported independent of inclination angles by Cui et al. [40]. A radiation contribution of total heat loss increases with surface temperature and surface emissivity [40].
The convective losses from the cavity receiver can be reduced by controlling airflow by providing the air curtains. A CFD study has revealed that the optimized airflow control may reduce the energy losses by about 45% [9]. The external wind speed as well as its direction influences significantly the performance of a solar receiver. At lesser wind speeds, i.e., less than 2.5 m/s, the energy losses by forced convection are lesser than free convection. The losses by forced convection are dominant over free convection above 5 m/s wind velocity values [10]. Similar such observations have been noticed by Prakash et al. [11]. The convective losses induced by external wind are about 22–75% higher with no-wind case for wind speed of the tune of 1 m/s. The convective energy losses are seen to be increasing with average receiver wall/surface temperature and reduce with rise in receiver inclination angles [11]. The convection and radiative energy losses contribute about 52% and 71.34% of the total energy losses from the receivers, respectively, at 0° receiver inclination angle (i.e., receiver opening facing sideways). These values are 42.72% and 59.28% at 90° receiver inclination angle (i.e., receiver opening facing down) at about 400 °C as operating temperature. The radiation loss dominates the convection loss for receiver inclination angles above 45°. Radiative loss is dependent on the radiative surface area of a receiver and seen independent on its inclination/tilt angle [12].
Bakari et al. [14] have examined the ‘glazing thickness effect’ on the outcome of a solar flat plate collector system. An optimum glass thickness of 4 mm has demonstrated a better performance among the thicknesses of 3, 4, 5, and 6 mm. The maximum efficiency of 35.4% is reported in case of 4 mm glazing thickness as compared to 27.8% in case of 6 mm thickness. A 4 mm glazing thickness exhibits optimum transmittance and convective losses. The nature of cavity surface may also alter the receiver performance. In the study presented by Harraiz et al. [15], it is seen that a provision of absorptive coating over the receiver surface improved an overall outcome of a receiver. With rise in 2% absorptivity of a coating material, 4% increase in receiver collection efficiency is reported. However, the emissivity of surface has little effect on solar-thermal efficiency of a collection system [15].
Three different receiver geometries, spherical, hemispherical, and cubical, having equal heat transfer areas have been examined by Prakash et al. [16]. Losses by natural convection are observed reducing with rise in tilt angle of receiver from 0° to 90° (90° being receiver aperture facing vertically downwards). The hemispherical cavity exhibited maximum amount of energy losses as compared to spherical and cubical shaped receiver geometry. With reduced aperture ratio (d/D), the volume of stagnation zone increases that reduces the convection energy loss [16]. The combined convection–radiation energy losses vary in different proportions with tilting of the cavity receiver [17]. Xiao et al. [19, 20] have reported that the natural convective coefficient for heat transfer and Nu (Nusselt number) rises with opening ratio of a cylindrical cavity receiver. By considering physical property alteration of air due to receiver inclination, the convective heat transfer coefficient and Nu show an increasing and reducing trend with cavity surface temperature, respectively.
As reported earlier by Ngo et al. [8], radiation heat loss remains unaffected by change in inclination angle of a receiver. Therefore, according to them, receiver inclination influences the heat transfer (energy loss) by means of combined conduction and convection. The variation in receiver wall temperature has been noticed for change in receiver inclination angles, which is attributed to alteration of local convection and radiation energy losses. However, slight increase of radiative losses from the cylindrical cavity-type receiver is observed with increased receiver inclination (i.e., from 0° side facing to 90° down-facing) by Abbasi-Shavazi et al. [17]. Similar such observations have been seen by Taumoefolau et al. [18] and Reddy and Kumar [19].
Taumoefolau et al. [18] have stated that the radiative as well as conductive energy transfer from a cylindrical cavity-type receiver are independent of tilt angle ranging from + 90° to − 90°, operating at a temperature range of 450–650 °C. The energy loss by convection is maximum at receiver tilt angle of 45° and minimum (non-zero) at 90° (down-facing aperture). This overall convection loss increases with the aperture ratio (d/D) of the receiver, for the studied range of receiver inclination angles [18]. However, in case of modified cavity receiver, the contribution of heat lost by convection is seen minimum at inclination of 90° and reported extreme at inclination angle of 0° (sideway-facing of receiver opening), as described by Reddy and Kumar [19]. They have estimated conductive heat loss through the insulation, by completely closing the opening of receiver. According to their findings, the convective cum radiative energy losses take place from the receiver opening and conduction energy loss occurs through the lagging provided exterior of modified cavity receiver. In addition, they [20] have estimated contribution of heat loss by natural convection in case of modified cavity-type receiver with conical entry, compound parabolic concentrator (CPC) entry, and Trumpet reflectors’ entry to the concentrated radiation. The cone, CPC, and Trumpet reflector act as second-stage concentration. The provision of these second-stage reflectors reduce the contribution of natural convection loss by about 29.2% with cone, 19.81% with CPC, and 19.16% with Trumpet reflector at entry to modified cavity-type receiver. Among these three geometries examined, the Trumpet-shaped reflecting surface geometry exhibits better performance. The surface emissivity effect on the heat losses has also been examined.
Kumar and Reddy [21] have presented numerical examination of combined radiation and convection energy transfer from modified type cavity receiver using asymptotic CFD approach. The convection energy loss rises with increase in receiver surface temperature examined, 300 °C to 700 °C. The combined convection and radiation Nusselt number is reported to exhibit, a linearly increasing trend with receiver surface emissivity (0.05–1.0). This shows that the surface emissivity influences the receiver surface temperature, which ultimately influences the combined radiative and convective heat transfer from the concerned cavity. It is also seen that the energy loss through combined radiative and convective mode depicts a reducing trend with receiver inclination angle changing from 0° to 90°.
The effect of aperture ratio on energy loss by natural convection from the receiver cavity has been examined by Paitoonsurikarn et al. [22] for three values of aperture ratio, (d/D) of receiver 0.5, 0.7 and 1.0, surface temperature ranging from 800 to 900 K (527–627 °C) and for receiver inclination angle (0°–90°). It is found that energy loss by convection reduces with decrease in aperture ratio, exhibiting lowest contribution of natural convection loss at aperture ratio of 0.5. The corrugations provided inside the cavity hinder the building of expelling flow boundary layers. It reduces the convection energy loss from the cavity. The down-facing receivers depict a better performance on account of stagnant zone formation in the cavity. The stagnant zone formation inside the cavity suppresses heat losses from an aperture to occur.
The maximum concentration of solar radiation takes place at the receiver aperture for dish rim angle of about 45°. Compromising among the intercepted radiative heat and energy losses form a cavity-type receiver by various modes, the best aperture ratio suggested by Beltran et al. [23] is 0.130 m for intercepting factor of 0.980. For poor intercept factor, the value of receiver aperture may be larger. Very important and interesting observation presented by them is that the receiver efficiency depicts a reducing trend with rise in solar radiation intensity, owing to increased thermal losses. Hernandez et al. [24] have used conical receiver for a dish antenna having 90° rim angle. The rim angle of 90° dish antenna depicts the focus and the rim of a dish in one plane. The 45° rim angled dishes (focus outside of dish rim or away from the vertex) exhibit maximum performance on account of reduced optical and thermal energy losses. In case of 90° rim angled receiver, it omits considerable radiation reflected from mirrors located at the outer periphery of a dish. The instantaneous efficiency is seen to be decreasing with reduction in mass-flow rate of working fluid and with increase in its inlet temperature. The wind velocity also influences the performance of cavity receivers.
The overall heat loss from a trapezoidal-type cavity-type receiver increases linearly with wind velocity [25]. An increased wind velocity reduces the energy transfer (loss) by radiation and increases the loss by convective mode of heat transfer. The total energy loss depicts an increasing trend with the wind velocity and rises in receiver surface temperatures. The wind velocity also influences the energy losses from the glass cover acting as shield. With wind velocity, radiative energy loss and convection loss from the glass cover reduces, on account of drop of glass cover temperature due to wind velocity [25]. The increase of wind speed up to 3 m/s helps mitigating the energy lost by natural convection [26]. The losses by forced convection actually overcome the losses by free convection above a wind speed of 3 m/s. This phenomenon is observed at inclination angle of 30°. For higher receiver tilt angles, e.g., 60° and 90°, the convective energy losses rise monotonically [26]. A minimum value is observed for combined convective energy loss from a cavity receiver with increase in wind speed starting from zero m/s [27]. The contribution of combined convection loss drops up to 1.5–2.0 m/s of wind velocity, above which it increases with wind speed, for vertically upward facing cylindrical cavity receiver. The convective losses reported maximum value for receiver inclination angles between 30° and 45°, for the range of wind velocity (0–10 m/s) examined.
It is also seen that [28] with larger receiver opening sizes, the cavity surface temperature reduces by strengthening energy losses via convection and radiation. According to Shen et al. [28], the variation in trends of radiative and convective energy losses are not influenced by receiver aperture/opening ratio, tilt angles, and radiation heat fluxes.
In case of spherical cavity-type receiver made up of copper tubing, the total losses depict a decreasing trend for rise of inclination angle [29]. These losses increase with wind velocity currents. The energy losses are higher for head on wind direction as compared to side-on wind condition. The losses in case of side-on wind conditions are found even lesser as compared to no-wind condition [29].
Wu et al. [30] have investigated the influence of various parameters, e.g., tilt angle, heat (radiation) flux, and opening ratio on the energy losses for a situation when only bottom wall is subjected to uniform wall heat flux. The aperture ratio (d/D) for cylindrical cavity influences significantly the heat losses from a cavity-type receiver. Increase in aperture ratio increases almost linearly the radiative energy loss from the aperture and reduces both the conduction as well as convective energy loss. The magnitude/contribution of natural convective heat loss alters with an inclination angle of receiver. With reduced receiver inclination from 90° to 30°, the convection–contribution reduces. However, its effect on conduction and radiative heat losses is marginal.
Fewer contributions on cavity receivers operating at higher temperature ranges are reported. The receivers made up of ceramic have been generally used for high--temperature applications. Its performance may be enhanced by attaching fins on the surface of cavity receiver by improving working fluid side heat transfer coefficient, as reported by Strumpf et al. [31]. At higher operating temperatures, e.g., from 400 to 1000 K, the variation of convective energy loss with reference to receiver tilt angle is almost non-linear, while it is quite linear closer to 400 K, according to Ngo et al. [32]. The effect of receiver tilt angle on an energy loss by convection from a receiver is stronger at higher operating temperatures. Its contribution change is insignificant between receiver inclination angles of 75° and 90°. Its contribution increases with receiver aperture size [32].
A cylindrical cavity receiver with spirally wound coolant tube depicts maximum efficiency (about 74%) for aperture diameter of 180 mm and it reduces to 55% for larger aperture size of 300 mm [33]. This efficiency drop is attributed to increased energy losses by both convection and radiation modes. Smaller aperture size represents highly concentrated radiative heat flux, and makes hot zone that leads to failure of the parent metal. The increased aperture size reduces the thermal efficiency of a receiver on account of losses. The smaller aperture size may ask for highly concentrated radiation (with shrink-focus) or it may also obstruct the incoming concentrated radiation, which may otherwise drop the receiver collection efficiency. Gonzalez et al. [35] have presented numerical outcomes in the form of convective Nu and radiative Nu. The Convective Nusselt number is represented as a ratio of heat transfer at the hotter cavity surface due to free convection to the energy transfer by conduction only. Similarly, a radiative Nusselt number is dictated as a ratio of radiation heat transfer occurring from a heat transfer surface to the energy transfer by conduction mode. In case of larger temperature differences, radiative heat transfer is reported to be dominant over the other modes of heat transfer from the cavity.
Loni et al. [34] have investigated an influence of receiver shapes, e.g., hemispherical, cylindrical and cubical on the efficiency of concentrating solar collection systems using water as well as Behran oil, as working fluids. It is seen that the hemispherical receiver shows maximum collection efficiency among the three designs. The working fluid suggested for low-temperature applications is water since having better thermal properties as compared to oil. It also has portrayed lesser pumping power requirement that leads to better system efficiency.
In a similar fashion, two cavity receivers, the spiral tube and conical cavity, have been examined for various flow rates and working temperatures of oil as an operating fluid [36]. The collection efficiency of conical receiver is reported to be better than a spiral receiver. The enhancement in receiver thermal efficiency is reported to be 5.63% and 40.45% at 100 °C and 200 °C, respectively. The pumping power and receiver wall temperature have been reported to be higher in case of spiral receiver, which reduces its performance [36].
The effect of receiver tube diameter on the system’s thermal performance is examined by Caijun et al. [37]. It is seen that with reduction of tube diameter, the heat transfer coefficient shows improvement, while it added the pressure drop/pumping power. A tube of 38 mm diameter (wall thickness 3 mm) reported to exhibit better receiver overall performance.
Kumar and Bopche [38] have seen that the annular disc/plate at an opening of modified cavity-type receiver showed maximum unsafe temperature as compared to a hemispherical cavity surface temperature, which is in vicinity of a coolant. It is referred as spillage of aperture lip (plate), which occurs due to constant exposure of concentrated radiation. It may be attributed to the continuous exposure of incoming radiation concentrated by the concentrating collector, multiple internal re-radiative reflections, and unavailability of coolant in contact with the disc/plate at the opening of modified cavity receiver. These findings are supported by Jaffe [39]. The medium-grained extruded graphites (G-90 graphite & Grade CS graphite) and slip cast silica (with high purity) are the materials suggested for the receiver aperture plate. Its temperature can be kept within limits by adopting disc made up of reflective material instead of absorptive material. In this study, polished aluminium sheet is used as an annular disc at an opening of a modified cavity-type receiver.
The experimental studies found fewer, examining the influence of opening/aperture ratio on the receiver collection efficiency. In addition, the combined effect of aperture ratio (d/D), Reynolds number (Re), glass thickness (δ), and inclination (tilt) angle (θ) on the receiver performance, by experimental means, is very scarce in the literature. Investigating the combined effect of these parameters on the receiver collection efficiency and examining contribution of various modes of energy losses are the prime objective of this study.
In addition, the effect of glazing thickness (δ), on the performance through completely obstructing the convective energy losses and partly obstructing the re-radiative losses is also examined in present paper. The glazing thickness effect in case of flat plate collectors, examined by Bakri et al. [14], is available in the literature. Its effect on cavity receiver collection performance in the presence of concentrated heat irradiation is also presented in this paper.
Experimental program
It comprises manufacture of a modified cavity-type receiver and development of an experimental test facility.
Cavity receiver-modified type
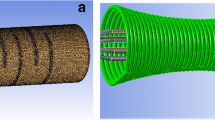
A schematic and photograph of modified cavity receiver fabricated for examination in the present study are as shown in Figs. 1 and 2, respectively. A copper tube is spirally wound round the exterior of hemispherical copper vessel. Tubes are brazed to the vessel ensuring the perfect contact in between. A spacing (pitch, p) of about 15 mm between the adjacent spiral coils is maintained constant, while brazing a tube with the vessel. The inner diameter of the vessel is 300 mm and maximum opening diameter is 280 mm. The inner diameter of copper tube is 8 mm. The cavity receiver was insulated properly by mineral wool of 25 mm thickness. The copper shell acts as an absorptive (selective) surface due to copper-oxide layer from inside. The opening plates are prepared of aluminium which acts as a reflective surface for preventing re-radiation loss from the receiver aperture.
Experimental setup
A line diagram of an experimental test facility is as shown in Fig. 3. An experimental apparatus includes following main elements: storage water tank, pump, regulating valve, cavity receiver, and infrared radiation heat source with CPC. A bypass valve cum pipe arrangement was used to adjust the flow through the tubing of cavity receiver. The receiver was supported on a structure with the help of steel wires, so that it can be tilted to any angle from 90° (receiver open end facing downward) to 30° (receiver open end facing close to sideway position).
The temperature of water as a working fluid flowing through the tube at entry and exit from the receiver and stored in the tank was measured with the help of resistance temperature detectors (RTDs).
The K-type thermocouples were used to detect a receiver wall temperature at various locations. The thermocouple response was detected by means of a digital micro-voltmeter of uncertainty ± 0.001 mV. All the thermocouples used in experimentation have been calibrated. The digital flow meter used for water flow measurement has an uncertainty of ± 0.25 L per minute (LPM) for 25 LPM flow measurement. The tests were conducted at constant concentrated infrared radiative heat flux (qr) at an opening of a cavity receiver of about 105.23 W/m2, which is obtained using radiation network analysis [45] inside the CPC.
Experimental procedure
The effect of four parameters have been examined that may influence the receiver thermal (collection) efficiency; receiver inclination angle, aperture (opening) ratio, flow Reynolds number, Re, and glazing thicknesses (δ). The performance were tested for four cavity receiver inclination angles 90°, 60°, 45°, and 30°; four values of aperture ratios (d/D) 0.93, 0.7, 0.6, and 0.46, four flow rates equivalent to Re; 938, 1175, 1525, and 1880, and for glazing thicknesses of 2, 4, and 6 mm.
The surrounding (ambience) temperatures were recorded at locations not influenced by the hot cavity temperature with the help of Mercury thermometers. The flow rates correspond to the flow Re of 938, 1175, 1525, and 1880, were 0.4, 0.5, 0.65, and 0.8 LPM, respectively. It took around 1–1.5 h to attain a steady state in case the values of parameters altered. If it was noticed that the temperature readings were not changing considerably for about 10–15 min, the whole system was assumed attaining steady state.
Data analysis
The receiver and CPC have been designed to capture and absorb the thermal energy of about 1000 W, to be utilized for household process heating applications. This energy may be captured by a parabolic dish collector having aperture diameter of 1.128 m or aperture area of 1 m2, from solar irradiation. The designed input details selected for the present experimentation work are presented in subsequent Sect. 3.1, along with the way that data reduced, from the recorded experimental data, in Sect. 4.1.
Data selection
The known variables, i.e., aperture ratio (d/D), Reynolds number (Re), glazing thicknesses, and receiver tilt angles, that were governed the experimental tests are depicted, as shown in Table 1.
The photographs showing modified cavity-type receiver with studied aperture ratios are as shown in Fig. 4.
Data reduction and mathematical formulation
This section expresses the mathematical equations used to reduce the collected data in terms of useful heat gain, receiver collection efficiency and energy losses.
Receiver collection efficiency
The heat gained by the water as a working fluid is obtained using Eq. (1):
The receiver performance parameter (\(\eta\)) of the modified receiver cavity is calculated using Eq. (2):
Uncertainty analysis
The uncertainty involved in temperature measurement is about ± 1.43% at 25 °C and ± 0.3% at 120 °C and in flow measurement is ± 2.5% and ± 1.25% for flow Reynolds numbers of 938 and 1880, respectively.
Energy loss analysis
In addition to evaluation of receiver collection efficiency, the energy losses from the cavity receiver by radiation, conduction, and convection modes are also obtained using expressions, as discussed ahead.
For estimating radiative energy loss, the configuration factor values have been calculated using configuration factor expression, Eq. (3), analytically obtained in the present study and using expressions available in Howell’s configuration factor catalogue [44].
Configuration factor To pursue ahead for an estimation of radiation heat loss, evaluation of configuration factor values is mandatory. An analytical problem has been formulated for configuration factor between an infinitesimal surface element ‘dA1’, located on inner surface of a cavity and an aperture/opening of a modified hemispherical cavity receiver. The geometrical situation is as shown in Fig. 5.
The analytical expression obtained for configuration factor is as given by Eq. (3):
Radiation heat loss The expressions used for estimating effective emissivity of a cavity surface and radiation heat loss are expressed by Eqs. (4) and (5), respectively [3]:
The equations referred for obtaining radiative energy loss due to reflection off the cavity surface are given as Eqs. (6) and (7) [3]:
Conduction and convection energy loss A conduction heat loss taking place from the receiver wall surface is obtained using Eq. (8), whereas for estimating heat transfer coefficient values of natural convection and forced convection, Eq. (9) [12] and Eq. (10) [3] have been used in an analysis, respectively:
Test situations
The experimental outcomes in the form of receiver collection efficiency are briefed for the test situations, as;
Test situation 1 Influence of glazing at 90° receiver inclination.
Test situation 2 Influence of aperture ratio at 90° receiver inclination.
Test situation 3 Influence of tilt angle of receiver.
Results and discussion
Influence of glass cover (glazing) with 90° receiver inclination
The influence of presence of gazing at an opening of modified cavity-type receiver is studied with use of transparent glass sheets of thicknesses 2.0, 4.0, and 6.0 mm. The variation of receiver collection efficiency with glazing thickness is plotted as shown in Fig. 6, for the aperture ratios of 0.6, 0.7, and 0.93 at two values of Reynolds number (Re) 938 and 1880. The zero glazing thickness represents the collection efficiency obtained without providing glass cover. Tests have been conducted for the entire studied coolant flow rates with receiver opening facing vertically downwards (i.e., 90° receiver inclination).
The glazing thickness of 4 mm exhibited better receiver collection efficiency of 88.4% compared to 87.9% and 86.4% for glass cover thicknesses of 6 mm and 2 mm, respectively, for an aperture ratio of 0.6. The presence of 4 mm glazing thickness improved the receiver collection efficiency by about 6.2% compared to with no glazing. The reason behind this improvement may be reduction of convective losses due to provision of glass covers. A change in glazing thickness may not alter the losses due to convection from the cavity. Increasing the glazing thickness reduces the steady radiative heat flux entering into the cavity through the glass cover. In short, increase in glazing thickness reduces the transmittance as well as convective losses and vice versa. A variation of glass thickness may also affect the losses due to re-radiative reflections from the cavity into the outer ambience. From the examination, the optimum glazing thickness was 4 mm, for giving optimal values of transmittance, and losses due to convection and re-radiative modes, in case of modified cavity receivers.
Influence of aperture ratio at 90° receiver inclination
One of the objectives of present work is to examine dimensions of modified cavity receiver affecting system performance. Tests have been pursued to examine the influence of receiver aperture/opening on its performance, at the flow Reynolds numbers studied without providing glass cover at receiver opening. The cover sheets used to vary an aperture size of a receiver were made of polished aluminium so as to re-reflect inside the internal re-radiative flux, which would have left out if it is absent. That way, it may contribute in enhancing the receiver collection efficiency.
The collection efficiency portrayed improvement with coolant flow rate and it showed decreasing trend with rise in aperture ratio, i.e., for 0.7 and 0.93. The aperture ratio of 0.6 exhibited maximum receiver performance, as depicted in Fig. 7. It may be attributed to the fact that increase in receiver opening size increases the heat losses due to convection as well as re-radiation; minimum may be the losses due to convection at 90° receiver inclination. Similar observations have been reported by Chongzhe et al. [3]. Too small the receiver aperture/opening, might have reduced the quantity of concentrated radiative flux entering into the cavity, i.e., at aperture ratio of 0.4, which exhibited poor performance in the present study.
In actual solar dish collector receiver system, with larger receiver aperture sizes, the cavity surface temperature reduces by strengthening energy losses through convection as well as radiation modes. It results into drop in efficiency at higher aperture ratio values. It is also reported in the literature [3] that in case of cylindrical cavity receiver, with increase in opening diameter above 63%, losses by means of convection decrease marginally. Above 63% opening, the percent reduction of convection losses due to rise of cavity aperture is lesser than percentage increase of radiation losses. In short, the percentage increase of radiative losses is higher as compared to percent reduction of convection loss. Moreover, with larger receiver opening sizes, the cavity surface temperature reduces by strengthening energy losses via radiation as well as convection. The radiation may be dominant over convection above aperture ratio of 0.6. These increased overall energy losses reduce the collection efficiency of the receiver above aperture ratio of 0.6.
The radiative loss depends on the receiver surface temperature and absorptivity of the receiver surface. The convective heat loss depends on the receiver geometry, ambient conditions, and receiver orientation.
With reduced aperture ratio, the intensity of solar radiation at the opening of modified cavity receiver increases due to higher value of concentration. The increased intensity of solar radiation and surface temperature of the cavity enhances the thermal losses by convection and radiation modes from the aperture. It may be the reason behind decreased receiver efficiency values for aperture ratio less than 0.6. Smaller aperture size represents highly concentrated incident radiation, with shrink-focus or it may obstruct the incoming reflected radiation in case of actual parabolic reflector-based collection systems, both of which may result into drop in receiver collection efficiency.
It is also found by Paitoonsurikarn et al. [22] that heat loss by convection reduces with decrease in aperture ratio, exhibiting lowest contribution at aperture ratio of 0.5. Referring to relevant literature studies and present study, it can be concluded that for lesser aperture values (< 0.6 in case of modified cavity receiver), the radiation heat loss is dominant over convection energy loss, which might result drop in receiver collection efficiency.
The radiation is dominant for lesser aperture ratio, on account of highly concentrated incident energy at the opening of modified cavity receiver, while it is dominant for larger aperture values due to increased view factor values. The change of view factor values for opening ratio less than 0.6 is negligible. However, the view factor and hence the radiation heat transfer enhance considerably for aperture ratio values more than 0.6. The variation of view factor (FA1–A3) values between finite hemispherical inside cavity surface, ‘A1’ and the opening ‘A3’ versus the opening ratio (d/D), for modified cavity receiver is as shown in Fig. 8. It is obtained using analytical expression given in view factor catalogue, by Howell [44].
View factor between finite area ‘A1’ and opening ‘A3’, ‘FA1–A3’ vs ‘d/D’ [44]
Influence of tilt angle of receiver
In a way to examine an effect of inclination/tilt angle of receiver on the system performance, a complete test facility including receiver, CPC, and heater assembly is inclined for 90° (down-facing receiver opening), 60°, 45°, and 30°. The photographs of the experimental test facility with inclination angles of 90°, 60°, and 45° in reference to horizontal axis are as shown in Fig. 9.
The variation of receiver collection efficiency for the studied receiver inclination angles and flow Reynolds numbers at aperture ratio values of 0.93, 0.7, 0.6, and 0.46, is depicted as shown in Figs. 10, 11, 12, and 13, respectively. The receiver collection efficiency displays a rising trend with the flow rates as well as with enhanced receiver inclination angle. The reason may be attributed to the increased contribution of energy losses for reduced inclination of receiver with respect to horizontal axis. The losses due to convection grow with decrease in inclination. It plays a leading role in dissipating energy from a receiver aperture, at lower temperature levels of cavity wall, i.e., less than 200 °C.
As discussed earlier, the aperture ratio of 0.6 exhibits maximum receiver performance as compared to other aperture ratios and inclination angles studied in this study. Two zones generally forms inside the modified type receiver, e.g., stagnant and convective. With increased receiver inclination angle from 0° to 90°, stagnant zone occupies more volume of the receiver cavity, which results in minimum losses through convection mode. However, with reduced receiver inclination angle, the convective zone captures more space as compared to stagnant zone that enhances the convective energy loss from the receiver.
The conduction and radiation losses are seen to be marginally dependent on receiver tilt angle. The variation in receiver wall temperature has been noticed for change in receiver inclination angles, which is attributed to alteration of local convection and radiation energy losses. However, slight decrease of radiative losses from the modified cavity-type receiver is observed with reduced receiver inclination (i.e., from 90°, down-facing to 0°, side facing receiver aperture), in the present study.
Heat loss analysis
The losses by means of conductive, convective (natural/forced), and radiative modes of heat transfer are obtained herewith, for the cases discussed earlier.
The energy losses involve conduction, convection, and radiation modes of transfer. It is reported in the literature [3] that an effect of shape of a cavity does not influence considerably the energy losses from the receiver. As discussed earlier, the loss of energy by conduction mode through the insulation is obtained using Eq. (8). During experimentation, it exhibited a rising trend with the surface temperature of cavity. A conduction loss contributes about 3.5–8.9% of total energy losses.
The contribution of energy loss by natural convection through a receiver aperture is obtained using correlation, as given by Eq. (9) proposed for Nusselt number, by Reddy and Kumar [12]. It is obtained for a constant aperture ratio of 0.6 (optimum value). A contribution of natural convection mode in total heat loss is about 28.64% for down-facing receiver (90°), 42.9% at 60°, 48.9% at 45°, and 53.45% at 30° receiver inclination angle, on an average, for cavity surface temperature ranging from 90° to 180 °C. The contribution of forced convection loss due to wind velocity (in a closed laboratory room) of about 0.3 m/s is found negligible, i.e., about 0.02 W, using Eq. (10) [3].
The configuration factor values obtained for a differential receiver surface element (dA1) with respect to various aperture sizes (A3) are plotted as depicted in Fig. 14. This analytical expression has been derived to see the influence of aperture size on the fraction of energy radiating by an individual surface element with an outer ambience through the receiver opening.
The configuration factor value shows an increasing trend with aperture size. It is obtained as zero for no/zero opening (closed receiver) and it is 0.5 for unity aperture ratio. This outcome is validated with the configuration factor value reported by Howell [44] for configuration factor between a finite area element on interior of hemisphere (area A1) to the entire base, i.e., area A3 and A2, as depicted in Fig. 5.
As reported [3], the contribution of radiative energy loss is about 60% of total losses from the receiver during morning and evening hours and approx. 75% at noon. It is due to the variation of convective losses throughout the day.
The radiation contribution in the overall energy losses is obtained using Eqs. (4) and (5) for the effective emissivity of cavity receiver and radiative energy transfer rate, respectively.
The surface emissivity of a receiver made of copper (oxidized surface) is 0.823. The radiative energy loss due to emission ranges within 11.1% and 41.8%, for cavity surface temperature varying from 90 to 180 °C. The radiative loss due to reflection off the cavity surface is obtained about 24.4% using Eqs. (6) and (7). Therefore, the maximum radiative energy loss (emission and re-reflection) from the cavity receiver is 66.2%. The effect of each 30° change (drop) in receiver inclination reduced the radiation loss by about 4.5%, i.e., from 90° to 60° receiver inclination values. It is attributed to the fact that heat loss by convection plays a dominant role with reduction of inclination (down-facing position to sideway receiver opening position), which ultimately reduced the cavity surface temperatures.
Similarly, the maximum contribution of convection and conduction mode in losing energy from the cavity receiver is estimated about 53.45% and 8.9% of the total energy loss, respectively, for the present case. The outcomes of the present investigation have been compared with literature findings, as portrayed in Table 2.
Correlations for receiver collection efficiency
The correlations for the ‘receiver collection efficiency’ are obtained by considering it a strong function of geometric as well as flow parameters of the receiver system, e.g., Reynolds number (Re), aperture/opening ratio (d/D), glazing sheet thickness (\(\delta\)) in ‘mm’, and receiver tilt/inclination angle (θ). The functional relationship is as given by Eq. \(\eta = f\left( {Re, \frac{d}{D}, \frac{\delta }{D}, \frac{\theta }{{\theta_{o} }}} \right)\).
The experimental data corresponding to 112 tests (data points) conducted were used for the regression analysis. Figure 15 exhibits performance parameter as a function of Reynolds number, depicting a relation as given in Eq. (11). The R2 value of this equation is obtained as 0.0163:
The constant ‘Ao’ will be a function of rest of the parameters, plotted as depicted in Fig. 16 versus aperture ratio (d/D). It gives relationship as Eq. (12), with value of R2 = 0.0551, with Bo as an average value of all constants:
The constant ‘Bo’ obtained, a function of glazing thickness ratio ‘δ/D’, is plotted as shown in Fig. 17.
It yields an expression as Eq. (13), with R2 value equal to 0.4646:
Finally, the constant ‘Co’ is plotted versus receiver inclination (tilt) angle ratio ‘θ/θo’, as depicted in Fig. 18.
The relationship is obtained out as Eq. (14), with R2 value of 0.3547:
where glass sheet thickness ‘δ’ in ‘mm’ and tilt angle, ‘θ’ in degree. Therefore, the correlation for receiver thermal collection efficiency is obtained as Eq. (15):
Figure 19 shows the variation of predicted values of receiver collection efficiency with respect to its experimentally obtained values. The R2 value of final Eq. (15) is 0.77 with approximately; 97.3% (109 out of 112) of the data points lie within the deviation of ± 15%.
Conclusions
The performance of a modified cavity-type receiver system has been studied in terms of collection efficiency. An influence of receiver aperture, transparent cover thickness, and inclination/tilt angle of receiver on the performance is presented in this paper. All the cases have been examined for flow Reynolds number of 938, 1175, 1525 ,and 1880 along with the energy losses (cond., conv., and rad.) from a cavity receiver, at lower temperature situations 90° to 180 °C. The outcomes of the work are elaborated as follows.
The wall temperature effect on the radiative as well as convective modes of energy losses is more noticeable as compared to in case of conductive mode of energy loss.
An aperture ratio of 0.6 demonstrates maximum receiver collection efficiency among the studied values of aperture ratio, e.g., 0.46, 0.6, 0.7, and 0.93, for all the values of mass-flow rates studied, which may be attributed to the reality that increase in receiver opening size increases the losses due to convection as well as re-radiation; minimum be the losses due to convection at 90° receiver inclination. This ratio needs to be utilized/maintained while erecting concentrating solar collector-based system with modified cavity receiver.
The system performance in the form of receiver collection efficiency has exhibited reducing trend with decrease in receiver inclination angle (from 90° down-facing receiver and 30° side way-facing of receiver). The contribution of convective losses from the receiver increases with reduction in inclination angle. The combined convection-radiation energy losses alter in different proportions with tilting of a cavity receiver. The maximum radiative loss (emission and re-reflection) from the cavity receiver is about 66.2%. The effect of each 30° change (drop) in receiver inclination reduced the radiation loss by about 4.5%, i.e., from 90° to 60° receiver inclination values. The contribution of energy losses due to natural convection is estimated within 28.64% to 53.45% for receiver inclinations varying from 90° to 30°. The contribution of conductive energy loss is about 3.5–8.9% for the studied range of receiver wall surface temperature.
An optimum glazing thickness observed was 4 mm, for giving optimal values of transmittance and losses due to convection cum re-radiative modes, in case of modified cavity receivers.
On carrying out the present study, for practical adoption, two suggestions are hereby given. A correct aperture ratio needs to be chosen for cavities to be applied in solar energy harnessing projects. The electronic components should be inclined at an angle of 30°–45° with respect to horizontal plane for enhanced cooling and better working life.
Abbreviations
- A :
-
Area or aperture area of smaller end of CPC (m2)
- A 2 :
-
Area of annular disc used to vary opening size
- A 3 :
-
Area of aperture (m2)
- A o, B o :
-
Constants
- C o :
-
Constants
- Cp:
-
Specific heat of fluid (J/kgK)
- d :
-
Aperture diameter (m)
- D :
-
Receiver diameter (m)
- Eff:
-
Effective
- F :
-
Configuration factor between the entire cavity surface and the aperture
- k :
-
Material/medium conductivity (W/mK)
- m :
-
Mass-flow rate (kg/s)
- Q :
-
Heat transfer/heat gain/heat loss (W)
- q :
-
Concentrated heat flux at entry to cavity receiver (W/m2)
- R :
-
Radius of modified cavity receiver (m)
- r :
-
Radius of receiver aperture/opening (m)
- T :
-
Temperature (K)
- w :
-
Cavity wall surface
- V :
-
Velocity (m/s)
- d/D :
-
Ratio of receiver’s aperture diameter to the receiver maximum diameter
- \(\delta /D\) :
-
Glazing thickness ratio
- Gr :
-
Grashof number
- Nu :
-
Nusselt number
- N RC :
-
Radiation-conduction number = \(\frac{{\sigma T_{\text{w}}^{4} \left( {\frac{D}{2}} \right)}}{{\left( {T_{\text{w}} - T_{\text{amb}} } \right)k_{\text{f}} }}\)
- Re :
-
Reynolds number
- T R :
-
Temperature ratio = \(\frac{{T_{\text{amb}} }}{{T_{\text{w}} }}\)
- \(\frac{\theta }{{\theta_{\text{o}} }}\) :
-
Angle ratio
- \(\alpha\) :
-
Surface absorptivity
- δ :
-
Thickness (m)
- \(\varepsilon\) :
-
Emissivity of the surface
- \(\eta\) :
-
Receiver collection efficiency or receiver performance parameter
- θ :
-
Inclination angle of cavity receiver with respect to horizontal axis (°)
- θ o :
-
Inclination angle of 90°
- \(\sigma\) :
-
Stefan–Boltzmann constant (W/m2K4)
- \(\varphi\) :
-
Angle formed by the aperture at the infinitesimal surface element
- Amb:
-
Ambient
- c :
-
Collector or CPC
- Cond:
-
Conduction
- Eff:
-
Effective
- f :
-
Fluid
- for.:
-
Forced convection
- i :
-
Inlet
- in:
-
Intercepted/incident by/at the receiver aperture
- Nat.:
-
Natural
- o :
-
Outlet
- o :
-
Receiver opening/aperture
- r :
-
Radiative
- Ref:
-
Reflection
- s :
-
Surface
- u :
-
Useful
- wi:
-
Wind
- w :
-
Wall surface
References
Shuai, Y., Xia, X.L., Tan, H.P.: Radiation performance of dish solar concentrator/cavity receiver systems. Sol. Energy 82(1), 13–21 (2008)
Daabo, A.M., Mahmoud, S., Al-Dadah, R.K.: The effect of receiver geometry on the optical performance of a small-scale solar cavity receiver for parabolic dish applications. Energy 114, 513–525 (2016)
Chongzhe, Z., Yanping, Z., Falcoz, Q., Neveu, P., Cheng, Z., Weicheng, S., Shuhong, H.: Design and optimization of a high-temperature cavity receiver for a solar energy cascade utilization system. Renew. Energy 103, 478–489 (2017)
Tan, Y., Zhao, L., Bao, J., Liu, Q.: Experimental investigation on heat loss of semi-spherical cavity receiver. Energy Convers. Manag. 87, 576–583 (2014)
Clausing, A.M.: Convective losses from cavity solar receivers comparisons between analytical predictions and experimental results. J. Sol. Energy Eng. 105(1), 29–33 (1983)
Prakash, M., Kedare, S.B., Nayak, J.K.: Determination of stagnation and convective zones in a solar cavity receiver. Int. J. Therm. Sci. 49, 680–691 (2010)
Wu, S.Y., Xiao, L., Cao, Y.R.: Convection heat loss from cavity receiver in parabolic dish solar thermal power system: a review. Sol. Energy 84, 1342–1355 (2010)
Ngo, L., Bello-Ochende, T., Meyer, J.P.: Three-dimensional analysis and numerical optimization of combined natural convection and radiation heat loss in solar cavity receiver with plate fins insert. Energy Convers. Manag. 101, 757–766 (2015)
Zhang, J.J., Pye, J.D., Hughes, G.O.: Active air flow control to reduce cavity receiver heat loss. In: ASME 2015 9th International Conference on Energy Sustainability Collocated with the ASME 2015 Power Conference and 13th International Conference on Fuel Cell Science Engineering Technology and the ASME 2015 Nuclear Forum, San Diego, California, June 28–July 2, pp. 1–10 (2015)
Reddy, K.S., Veershetty, G., Vikram, T.S.: Effect of wind speed and direction on convective heat losses from solar parabolic dish modified cavity receiver. Sol. Energy 131, 183–198 (2016)
Prakash, M., Kedare, S.B., Nayak, J.K.: Investigations on heat losses from a solar cavity receiver. Sol. Energy 83(2), 157–170 (2009)
Reddy, K.S., Kumar, N.S.: Combined laminar natural convection and surface radiation heat transfer in a modified cavity receiver of solar parabolic dish. Int. J. Therm. Sci. 47(12), 1647–1657 (2008)
Sauceda, D., Velazquez, N., Beltran, R., Quintero, M.: Thermal analysis of a conical receiver in a paraboloid dish to be used as generator in an advanced solar thermal cooling system. In: Proceedings of ANES/ASME Solar Joint 2006 XXXth Mexican National Solar Energy Week Conference, Veracruz, Mexico, 2–6 October, pp. 1–7 (2006)
Bakari, R., Minja, R.J.A., Njau, K.N.: Effect of glass thickness on performance of flat plate solar collectors for fruits drying. J. Energy 2014, 247287. https://doi.org/10.1155/2014/247287 (2014)
Lopez-Herraiz, M., Fernandez, A.B., Martinez, N., et al.: Effect of the optical properties of the coating of a concentrated solar power central receiver on its thermal efficiency. Sol. Energy Mater. Sol. Cells 159, 66–72 (2017)
Prakash, M., Kedare, S.B., Nayak, J.K.: Numerical study of natural convection loss from open cavities. Int. J. Therm. Sci. 51, 23–30 (2012)
Abbasi-Shavazi, E., Hughes, G.O., Pye, J.D.: Investigation of heat loss from a solar cavity receiver. Energy Procedia 69, 269–278 (2015)
Taumoefolau, T., Paitoonsurikarn, S., Hughes, G., Lovegrove, K.: Experimental investigation of natural convection heat loss from a model solar concentrator cavity receiver. ASME-J. Sol. Energy Eng. 126, 801–807 (2004)
Reddy, K.S., Kumar, N.S.: An improved model for natural convection heat loss from modified cavity receiver of solar dish concentrator. Sol. Energy 83, 1884–1892 (2009)
Reddy, K.S., Kumar, N.S.: Convection and surface radiation heat losses from modified cavity receiver of solar parabolic dish collector with two-stage concentration. Springer Heat Mass Transf. 45, 363–373 (2009)
Kumar, N.S., Reddy, K.S.: Investigation of convection and radiation heat losses from modified cavity receiver of solar parabolic dish using asymptotic computational fluid dynamics. Heat Transf. Eng. 31(7), 597–607 (2010)
Paitoonsurikarn, S., Lovegrove, K., Hughes, G., Pye, J.: Numerical investigation of natural convection loss from cavity receivers in solar dish applications. ASME J. Sol. Energy Eng. 133, 021004-1-10 (2011)
Beltran, R., Velazquez, N., Espericueta, A.C., Sauceda, D., Perez, G.: Mathematical model for the study and design of a solar dish collector with cavity receiver for its application in Stirling engines. J. Mech. Sci. Technol. 26(10), 3311–3321 (2012)
Hernandez, N., Riveros-Rosas, D., Venegas, E., Dorantes, R.J., Morin, A.R., Jaramillo, O.A., Arancibia-Bulnes, C.A.: Conical receiver for a paraboloidal concentrator with large rim angle. Sol. Energy 86, 1053–1062 (2012)
Reddy, K.S., Kumar, K.R.: Estimation of convective and radiative heat losses from an inverted trapezoidal cavity receiver of solar linear Fresnel reflector system. Int. J. Therm. Sci. 80, 48–57 (2014)
Flesch, R., Stadler, H., Uhlig, R., Hoffschmidt, B.: On the influence of wind on cavity receivers for solar power towers: An experimental analysis. Appl. Therm. Eng. 87, 724–735 (2015)
Shen, Z.G., Wu, S.Y., Xiao, L.: Numerical study of wind effects on combined convective heat loss from an upward-facing cylindrical cavity. Sol. Energy 132, 294–309 (2016)
Shen, Z.G., Wu, S.Y., Xiao, L., Qiu, Y., Wang, K.: Effect of aperture size on free convection and radiation heat transfer in isoflux upward facing cylindrical cavities. Exp. Therm. Fluid Sci. 87, 1–14 (2017)
Shewale, V.C., Dongarwar, P.R., Gawande, R.R.: Heat loss investigation from spherical cavity receiver of solar concentrator. J. Mech. Sci. Technol. 30(11), 5233–5238 (2016)
Wu, S.Y., Shen, Z.G., Xiao, L.: Experimental investigation and uncertainty analysis on combined heat losses characteristics of a cylindrical cavity with only bottom wall heated at constant heat flux. Heat Transf. Eng. 36, 539–552 (2015)
Strumpf, H.J., Kotchick, D.M., Coombs, M.G.: High temperature ceramic heat exchanger element for a solar thermal receiver. ASME Sol. Energy Eng. 104, 305–309 (1982)
Ngo, L.C., Ochende, T.B., Meyer, J.P.: Numerical investigation of natural convection of cavity receiver for low power application. Int. J. Green Energy 5, 6 (2016). https://doi.org/10.1080/15435075.2016.1161628
Feng, H., Zhang, Y., Zou, C.: A 3-D model simulation of high temperature solar cavity receiver. In: Proceedings of the ASME 2017 Power Conference Joint with ICOPE-17, Charlotte, North Carolina, USA, 26–30 June 2017, pp. 1–7. https://doi.org/10.1115/POWER-ICOPE2017-3307 (2017)
Loni, R., Askari Asli-Ardeh, E., Ghobadian, B., et al.: Numerical investigation of a solar dish concentrator with different cavity receivers and working fluids. J. Clean. Prod. 198, 1013–1030 (2018)
Gonzalez, M.M., Palafox, J.H., Estrada, C.A.: Numerical study of heat transfer by natural convection and surface thermal radiation in an open cavity receiver. Sol. Energy 86, 1118–1128 (2012)
Pavlovic, S., Loni, R., Bellos, E., et al.: Comparative study of spiral and conical cavity receivers for a solar dish collector. Energy Convers. Manag. 178, 111–122 (2018)
Caijun, S., Liping, P., Liwei, Z.: The effect of the tube diameter on the performance of the two stage receiver. In: International Conference on Renewable Power Generation (RPG 2015), Beijing, China,17–18 October 2015. https://doi.org/10.1049/cp.2015.0397. ISBN: 978-1-78561-040-0 (2015)
Kumar, S., Bopche, S.B.: Numerical investigation of the temperature distribution of a solar cavity receiver wall using finite element method. Applications of solar energy, pp. 57–78. Springer, New York (2017). (ISBN: 978-981-10-7205-5)
Jaffe, L.D.: Solar tests of aperture plate materials for solar thermal dish collectors. Trans. ASME J. Sol. Energy Eng. 106, 408–415 (1984)
Cui, F., He, Y., Cheng, Z., et al.: Study on combined heat loss of a dish receiver with quartz glass cover. Appl. Energy 112, 690–696 (2013)
Karimi, R., Gheinani, T.T., Avargani, V.M.: A detailed mathematical model for thermal performance analysis of a cylindrical cavity receiver in a solar parabolic dish collector system. Renew. Energy (2018). https://doi.org/10.1016/j.renene.2018.03.015
Fang, J., Tu, N., Wei, J., Fang, T., Du, X.: Numerical Investigation of the tube layout effects on the heat losses of solar cavity receiver. ASME J. Therm. Sci. Eng. Appl. 10, 011008-1-10 (2018)
Kribus, A., Doron, P., Rubin, R., Reuven, R., Taragan, E., Duchan, S.: Performance of the directly-irradiated annular pressurized receiver (DIAPR) operating at 20 bar and 1200°C. ASME J Sol. Energy Eng. 123, 10–17 (2001)
Howell, J.R.: A Catalogue of Radiation Configuration Factors, p. 208. McGraw Hill Book Company, New York (1982)
Modest, M.F.: Radiative heat transfer. Academic Press, New York (2003)
Acknowledgements
The authors of present study acknowledge financial support of Science and Engineering Research Board (DST, Govt. of INDIA) and administrative support of NIT Hamirpur, Govt. of INDIA, for carrying out present research work (Financial Grant Ref. No.: ECR/2017/000225).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
On behalf of all authors, the corresponding author states that there is no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Bopche, S.B., Kumar, S. Experimental investigations on thermal performance characteristics of a solar cavity receiver. Int J Energy Environ Eng 10, 463–481 (2019). https://doi.org/10.1007/s40095-019-00321-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40095-019-00321-4