Abstract
This paper examines the effect of building shape, zones, orientation and window to wall ratio (WWR) on the lighting energy requirement and the thermal comfort in the naturally ventilated houses in tropical climate. The lighting electricity and the adaptive thermal discomfort hours (ASHRAE 55 80% acceptability) of 300 different models of two-storey houses were obtained using Design Builder simulation software. The models were developed for three building shapes (square, rectangle and L-shaped) and the orientation of each model was changed for 24 orientations and four window to wall ratios. Results indicate that the rectangular shape with staircase positioned in the middle of the house will provide higher thermal comfort for WWR of 20 and for other WWRs the L-shaped models provide higher thermal comfort when the staircase is positioned at the short corner or middle. The square-shaped houses with staircase at the middle have the highest lighting electricity and the L shape has the lowest lighting electricity. Further, WWR changes the thermal comfort by 20–55% and the percentage change in lighting electricity due to WWR is only 1.5–9.5%. Therefore, thermal comfort should receive more attention in deciding the WWR. Moreover, the results show an effect when the zone sizes and location change.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
The issues related to indoor air quality, energy cost and other environmental issues associated with energy generation has created an interest in the natural ventilation in buildings in the recent literature. In the hot and humid region, the intensive solar radiation and the higher humidity level create the requirement of using mechanical cooling mechanisms which contribute substantially to energy consumption in buildings [1]. In most tropical countries, achieving thermal comfort without the use of air conditioning is becoming difficult due to poor building designs and global warming may make the issue worse. The thermal comfort of a poorly designed naturally ventilated building is difficult to control unlike in air-conditioned buildings, where thermal comfort can be achieved with the compensation of higher energy consumption.
Energy consumption in the household sector is governed by various factors including the building envelope characteristics and consumer behaviour [2]. In most of the tropical countries, the energy demand is heavily affected by the energy poverty, with lack of access to energy or energy security. While the usage of energy-consuming equipment such as air-conditioning units is restricted due to energy poverty, the only option to achieve the required thermal comfort will be the proper design of the building envelope. For low-income households, thermal renovation is difficult due to poor economic conditions [3,4,5,6]. Hence, considering the proper design aspects at the initial building design would avoid such costs and both thermal comfort and lower electricity requirement would be met. The effect of consumer behaviour on energy consumption has been widely discussed in various studies [7,8,9] and hence this paper will only focus on the aspects of building envelope which affect the energy consumption of residential buildings in tropical climate.
Globally, a significant proportion of the building energy is consumed for achieving the required thermal and optical comfort [10,11,12]. In addition to the building materials, the building form and the other associated factors heavily affect the indoor thermal comfort and the lighting energy of any air-conditioned or naturally ventilated building. The most important parameters affecting the thermal comfort and lighting energy requirement of the indoor environment are the building shape, orientation and the window to wall ratio (WWR) of the building [13,14,15,16,17,18,19,20]. These parameters are inter-related and a proper combination is required to achieve the optimal thermal comfort and energy efficiency.
Impact of building form on energy load of non-residential buildings
Several attempts have been made to identify the impact of the building form or building shape on the energy load of the building. Ourghi et al. [21] provided a simplified analysis method to predict the impact of the shape of an air-conditioned office building on its annual cooling and total energy use. The simulations were conducted for four locations including Rome, Tunis, Cairo and Gabes. The results indicated a strong interdependency between the annual building energy use and various basic building features such as building shape, window size and glazing type.
Caruso and Kampf [22] analysed the optimal three-dimensional form of buildings that minimise energy consumption (air-conditioning needs) due to solar irradiation using the evolutionary algorithm. The results indicate that the optimal forms are compact and oriented to a particular direction in the sky that depends on the site following a sort of self-shading concept. Further, Depecker et al. [23] suggested that in a cold climate, the heating load is directly proportional to the shape coefficient. Depecker et al. [23] defined the shape coefficient as follows.
where \(S_{\mathrm{e}}\) is the envelope surface area and V is the inner volume of the building. The study has focused only on the building shape and has ignored the parameters such as climate, orientation and WWR.
On the contrary, AlAnazi et al. [24] introduced an analysis method to estimate the impact of building shape on the energy efficiency of air-conditioned office buildings in Kuwait. The analysis has taken several building shapes and forms into account including rectangular, L shaped, U shaped, T shaped, cross shaped, H shaped and cut shaped. For buildings with low WWR, the total energy use is found to be inversely proportional to the relative compactness of the building, independent of its form.
On the effect of WWR and orientation on the energy consumption, Alwetaishi [25] conducted a research to identify the optimal WWR for educational buildings in various climatic regions and a WWR of 10% is recommended for a hot and humid climate region. A study in Teheran suggested that the orientation can save up to 105% of the annual energy of a building and the WWR has an important role in deciding the building orientation [26]. Hence, investigating the impact of orientation on energy efficiency is important while determining the effect of building shape on energy use.
Similar researches have been carried out for cold climates with the heating load. Oral and Yilmaz [27, 28] presented a methodology to determine the building form which provides minimum heat load. Further, Marks [29] studied the optimum proportions of wall lengths, their angles and glazing parameters for multistory office buildings in Australia. The study was further extended by Jedrzejuk and Marks [30] to present a multi-criteria optimisation method of the shape and structure of the buildings and optimisation of heat sources. For the buildings in tropical climate, Mangkuto et al. [31] conducted a simulation study to investigate the effect of WWR, window orientation and wall reflectance on lighting energy demand and daylight metrics. The optimum solution derived from Pareto optimisation indicated WWR 30%, wall reflectance of 0.8 and south orientation as the optimum design.
Impact of building form on energy load of residential buildings
The above-discussed studies are much focused on the non-residential buildings such as office buildings which heavily depend on heating and cooling. Residential buildings have a different occupancy pattern and the daytime energy consumption is lower compared to non-residential buildings. Several studies have been carried out to identify the effect of shape, WWR and orientation in residential buildings. Hachem et al. [32] demonstrated that the number of shading facades and the ratio between the shading to shaded facade significantly affect the solar radiation on non-convex shapes. The study was based on residential buildings in cold climate including seven different shapes (square, rectangle, trapezoid, L, U, H and T). Bichiou and Krarti [33] conducted a research on single-family homes in the USA including five different locations. This research considered the building shape, WWR and orientation as important parameters for the optimisation. Three optimisation algorithms were considered and the optimal design reduced the life-cycle cost by 10–25 % depending on the type of homes and climate.
For naturally ventilated residential buildings, Liping et al. [1] investigated the optimum thermal comfort by changing U values, WWR, orientations and lengths of the shading device. The research was conducted for a typical residential building in Singapore and the results indicated that the U value of facade materials for north and south should be less than \(2.5\,\mathrm{W}/\mathrm{m}^{2}\,K\) and for east and west U value should be less than \(2.5 \,\mathrm{W}/\mathrm{m}^{2}\,K\). Further, the optimum WWR was found to be 24%. However, this research has neglected the effect of shape and the lighting energy. In Mirrahimi et al. [11], the effect of building form was considered for the tropical climate in Malaysia and, in addition, other factors such as external walls, roofs, glazing area and natural ventilation were also evaluated. The research aimed mainly at the thermal performance and the total energy consumption of high-rise residential buildings and the lighting energy was not focused upon.
Most of the studies have been restricted to either air-conditioned buildings or buildings with one zone [34] and the knowledge of the impact of building form on energy consumption of the naturally ventilated buildings is rare, especially for residential buildings and in hot humid climate. Bre et al. [35] conducted a residential building design optimisation where some rooms are mechanically ventilated, while some are naturally ventilated. In their study, a typical residential building in Argentina was selected for the case study and, as per the overall results, solar absorptance of external walls, thermal transmittance of externals walls, orientation and window area fraction for natural ventilation were considered as the important factors for reducing the cooling demand.
However, in those previous works, the effect of building shape, WWR, orientation and the zones in residential buildings in hot and humid climate have not been sufficiently discussed. Further, the available studies on tropical residential buildings have not considered the effect of zone sizes or the locations. Furthermore, in most of the studies, the lighting energy demand of the residential buildings is neglected and the total energy demand is considered. Considering the effect of building envelope characteristics on the artificial lighting requirement, it is necessary to identify the effect on lighting energy separately. Given the lack of studies on the naturally ventilated residential buildings, our study aims to investigate the effect of shape, orientation and WWR on the lighting energy requirement and the thermal comfort of naturally ventilated houses, while giving a special emphasis on the zone sizes and the zone locations of the houses.
Hence this study is based on two research questions: (a) what is the effect of shape, zones, orientation and WWR on the lighting energy requirement of naturally ventilated residential buildings and (b) what is the effect of shape, zones, orientation and WWR on the thermal comfort of naturally ventilated residential buildings?
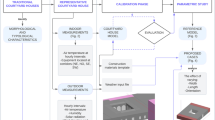
Methodology
Case study models
The model houses in the case study were two-storey houses with one living room, one kitchen, one bathroom and three bedrooms. The simulations were conducted in a hypothetical location at Katuanyake, Sri Lanka, which has a tropical hot humid climate (ASHRAE 1A climate zone). The family size was selected as four, being the average number of occupants per house in Sri Lanka [36]. Further, for permanent houses, the average living spaces per house is 4.4 [36] and therefore the model house was selected with three bedrooms, one kitchen and one living area (five living spaces). The selection of three-bedroom house was further verified using the pilot survey results (refer Table 1). Although the majority of the houses are single storey in Sri Lanka, two-storey houses (22.3% of the total houses in Colombo district [36]) were selected for the case study as two-storey houses are more available in the urban areas where the energy consumption is high. All the models were designed with flat roofs to avoid the impact of the roof shading and being the current trend in urban areas in Sri Lanka [37]. The total gross area of each house is \(68\,\mathrm{m}^2\) and the height of each floor is 3.01 m. The external dimensions of the model houses are illustrated in Fig. 1. The minimum dimensions for each zone were defined using Neufert guide [38] and listed in Table 2.
For the ease of zone arrangement and to maintain the same gross floor area, all the three bedrooms were placed on the first floor and other zones were moved to the ground floor. As all the bedrooms are arranged on the first floor the room arrangement allowed to have three different shapes as square, rectangle and L shape. For each different shape, the staircase location was changed and seven main cases were identified according to envelope shape and the staircase location as illustrated in Fig. 2. The location of the kitchen and bathroom of each case was changed relative to the staircase location ( refer Figs. 6, 7, 8). For each subcase, the zone sizes were started from the minimum size (as listed in Table 2) and increased later for space utilisation.
Simulation settings
Burnt brick (which is the walling material used by 53.2% of the households in Sri Lanka [36]) was selected for the envelope and the internal walls for the models as it provides better thermal comfort in tropical climate [39, 40]. The U values and thicknesses of external walls, internal walls, roof, floor and glazing are listed in Table 3. The entire house was set for natural ventilation (always on) and heating and cooling options were disabled. The outside air exchange rate was set to 5 \(\mathrm{ac}/\mathrm{h}\) to provide higher natural ventilation. The house models were designed for four occupants and the activities were set to a template with metabolic rate of 123 W per person and 0.5 Clo value. The occupancy was set as 5 pm to 7 am next day according to a result obtained from a pilot survey.
The lighting requirements for a residential building cannot be easily generalised as it heavily depends on the occupant behaviour and the specific requirements. The average illuminance levels for various spaces (living, kitchen, bedrooms and bathroom) of single-family houses varies from 100 to 200 lux [41], and except for the kitchen, all the other zones require 100–150 lux illuminance level. Since this study is a comparison of the building shapes and zone sizes and locations, the same level of illuminance needs to be maintained for all the models. For this case study, the target illuminance level for all the spaces was set as 150 lux as a reasonable estimate since high lighting levels are not often required. The LEED certification requires the single-family houses not to exceed the lighting power density (LPD) of \(7.7\,\mathrm{W}/\mathrm{m}^2\) to get at least 0.5 points for reducing the lighting power density [42]. Since there is a tendency to move to higher efficacy lighting to reduce the lighting energy consumption, the case study used LPD of \(7.7\,\mathrm{W}/\mathrm{m}^2\) as a reference and \(5\,\mathrm{W}/\mathrm{m}^{2}-100\) lux was used as the normalised power density. The interior walls were finished with cement/sand/limestone mortar and painted white. The lighting control option was set on to control the light according to daylighting illuminance. The lighting was scheduled from 5 am to 10 pm (according to the pilot survey results).
Design Builder V5 software (with Energy Plus simulation engine) was used for the optimisation. In total, 300 different models were developed and then they were simulated for optimisation using the objectives and design variables illustrated in Table 4. All the electricity loads except the lighting electricity were removed in the modelling and, therefore, minimising electricity was considered as the first objective function which reflects only the lighting electricity. Furthermore, the occupants of the naturally ventilated houses can accept higher indoor temperatures and wider temperature variations compared to the occupants of the air-conditioned houses [43]. Adaptive comfort models such as ASHRAE 55 can apply a wide range of temperatures than steady-state comfort models, as the occupants use various adaptive comfort measures to make the indoor environment more comfortable [44]. The thermal comfort conditions of the building can be maintained without using additional mechanical cooling if the temperature is within the adaptive comfort limits. In ASHRAE 55 standard, the comfort temperature is calculated using Eq. 2 (\(R^2 = 0.7\)), where \(t_\mathrm{c}\) is the comfort temperature and \(t_0\) is the prevailing mean outdoor air temperature PMOAT (10–33.5 \(\mathrm{C}^\circ\)) [45]:
To achieve the 80% adaptability comfort limits, \(\pm \,3.5\,\mathrm{C}^\circ\) is added to the comfort temperature. In this study, minimising the discomfort hours (ASHRAE 55 adaptive 80% acceptability) was selected as the second objective function, as in the hot humid climates the adaptive comfort model is more suitable for naturally ventilated houses.
Results and analysis
Effect of building shape, zone size and zone location
The optimisation solutions with the lowest discomfort hours and lowest lighting electricity of each model were identified and plotted against the model numbers in each case to compare the effect of shape and other factors. The effects of the shape and the zones on thermal comfort and lighting electricity are discussed separately under this section.
Effect of building shape on thermal comfort
As indicated in Fig. 3a, the discomfort hours do not show a clear difference with the change in the position of the staircase in square-shaped models. In S case 1, the staircase was placed at the corner of the house as in Fig. 2a, and in the S case 2 it was placed at the middle of the house as shown in Fig. 2b. In the rectangular shape, a clear difference in thermal comfortability can be observed in the cases where the staircase is in a corner (Fig. 2c) and the staircase is in middle (Fig. 2d). The discomfort hours of the rectangular-shaped model houses with respect to the position of the staircase is given in Fig. 3b. The results indicate that when the staircase is in the middle of the house, the thermal comfort is higher than it is in a corner. Also when the zone sizes change and the zones are moved while keeping the staircase at the same place, a difference in thermal comfort can be observed.
The staircase of the L-shaped model was positioned in the short corner (Fig. 2e), in the middle (Fig. 2f) and in the long corner (Fig. 2g). Similar to the square-shaped model, there is no clear difference between the cases in the L-shaped models when either the position of the staircase is changed or the position of the zones with respect to the staircase is changed as indicated in Fig. 3c. However, as per Fig. 3c, when the size of the zones changes, a clear difference can be observed in the L-shaped model. Figure 3d shows the overall results of the models based on the shape of the house. The overall results also cannot identify a clear difference or a pattern when the shape is changed. However as discussed in previous sections, the staircase location in rectangular-shaped houses and the zone sizes in houses of all the shapes affect the thermal comfortability of the houses.
Effect of building shape on lighting electricity
The lighting electricity also does not show a clear change with the building shape as shown in Fig. 4d except in the square-shaped models, where the staircase is placed at the middle (Fig. 4a). In the rectangular-shaped models (Fig. 4b) and in L-shaped models (Fig. 4c), there is only a marginal difference when the staircase position changes. Similar to the thermal comfort, variations can be observed within the cases when the zone sizes and zone location changes.
Effect of zone size and zone location
Sections 3.1.1 and 3.1.2 do not show a clear difference between the cases except in R case 2 for thermal comfort and S case 2 for lighting electricity. However, in all the cases, there is a variation in thermal comfort and lighting electricity when the size of the zones changes and the zone location relative to the staircases changes. Therefore, for each case, three size categories were identified and the floor areas of kitchen, bathroom and living room of each size category for each case are listed in Table 5. In size category 1, the floor area of the kitchen and bathroom are minimum and that of the living room is maximum for each case. In size category 2 and 3, the floor areas of the kitchen and bathroom are increased, while the floor area of the living room is decreased.
The variations in the discomfort hours and lighting electricity for three size categories for each case are presented in Fig. 5. When the zone sizes change, the discomfort hours change up to 4.15% and the lighting electricity changes up to 3.74%. However, a clear correlation cannot be observed for all the cases and there is no generalised correlation between thermal comfort and the lighting electricity. Further, the changing patterns of thermal comfort and the lighting electricity within the size categories cannot be generalised and is specific to each case.
Figures 6, 7 and 8 indicate the variation in discomfort hours and lighting electricity when the zone location (kitchen and bathroom) changes relative to the staircase location for square shape, rectangular shape and L shape, respectively. The zone locations are marked as A, B and C in the plan layout in each figure considering whether the zones are located by the side or away from the staircase. When the zone locations change, the thermal comfort can be changed up to 2.48% and the lighting electricity can be changed up to 9.24%. Similar to the previous case, there is no clear correlation between changing patterns of thermal comfort and lighting electricity and they are more case specific.
Effect of window to wall ratio and orientation
The effects of building shape and the zone sizes are analyzed in Sect. 3.1, using only the best thermal comfort or lighting energy requirement of each model. Therefore, the effect of WWR and the orientation was ignored in the analysis process. To identify the effect of those factors on thermal comfort and lighting electricity requirement, the models in the zone size category 1 (refer Table 5) in all the seven cases were selected for further analysis.
Effect of window to wall ratio
For the seven models representing the seven main cases, the discomfort hours and the lighting electricity results were obtained for 20, 40, 60 and 80 WWRs. The results indicate a positive correlation between WWR and discomfort hours as shown in Fig. 9. To be more precise, the percentage change in discomfort hours compared to the discomfort hours in the best WWR is listed in Table 6. As indicated in Table 6, WWR of 20 gives the best thermal comfort (minimum discomfort hours), and when WWR is increased to 40, the discomfort hours increase by more than 20% except in L case 2 where the increase is 17.8%. When the WWR is increased to 60, the thermal discomfort increases by 30–40% and in 80 WWR the percentage increase in discomfort hours is 45–55% except in L case 2 where the change is 41.48%. It is further evident that the difference in percentage change is only 10% between the 60 and 80 WWRs, where between other ratios the difference is more than 20%.
As illustrated in Fig. 10, the best lighting electricity (lowest value) occurs in 60 and 80 WWRs and the difference in lighting electricity between those WWRs is nearly zero. WWR of 20 has the highest lighting electricity value, and the percentage change in electricity compared to the best WWR is 1.5–3% in the square case and L case models, whereas the change is 8.5–9.5% in the rectangular case models.
Effect of orientation
For the same models discussed in Sect. 3.2.1, the best orientation with the lowest discomfort hours and the best orientation with the lowest lighting electricity were obtained separately for each case (refer Table 7). The best orientation was rotated by \(15^\circ\) and 24 different orientations were obtained for each case. The discomfort values and lighting electricity values for each orientation were obtained and the results are presented in Figs. 11 and 12. According to the Fig. 11, when the models are rotated \(90^\circ\) and \(270^\circ\) compared to the best orientation, the thermal discomfort will increase. However, the increase is marginal in square shape and L shapes where the difference is only 1.5–3%, and in rectangular case the percentage difference is 8.5–9.5%. In the case of lighting electricity, orientation does not indicate a clear effect as illustrated in Fig. 12 where the percentage increase compared to the best orientation is less than 0.25% in all the cases for all orientations.
Discussion
In the case development, the staircase location was considered as an important parameter mainly due to two reasons. Firstly, the staircase can be used as a reference for the zone location and, secondly, there can be several effects on the thermal comfort and the lighting energy requirement due to the location of the staircase. The thermal comfort of the models can be affected by the possible stack effect ventilation created by the staircase [46]. The stack effect ventilation occurs through vertical air movement. The cool air in the building warms up by human activities and the resulting warm air is discharged out through vertical elements such as air wells and ducts due to the difference in density [47]. Open staircases usually provide stack effect ventilation, and in historic buildings the stairways have been used as the exhaust stack [48].
Rectangular shape has the best thermal comfort when the staircase is in the middle for 20 WWR. Further, in rectangular shape when the staircase is moved to the middle of the house, the discomfort hours is reduced by 6%. The possible reason for having high thermal comfort can be the effective use of both stack ventilation effect and cross ventilation in that configuration. In WWR of 20, square shape and L shape do not show a clear difference. However, with the increase in WWR, the L case has the best thermal comfort which may be due to the self-shading effect. This further validates the findings of Liping [1], where the optimum WWR was found to be 24 for naturally ventilated residential buildings.
Square shape indicates the highest lighting electricity when the staircase is moved to the middle of the house. This is mainly due to the blocking of the light by the staircase. In this case study, lighting does not show a higher variation with WWR. This is mainly because of the occupancy schedule in the residential buildings. Artificial lights will be used only during the occupancy time, which is from evening to the next morning, where the lighting requirement will be compensated by daylight in a very short period of time. However, for that shorter duration, WWR can result in 1.2–2.2% energy consumption change.
The zone sizes change the thermal comfort up to 4.15% and lighting electricity up to 3.74%. Also the zone locations can change thermal comfort up to 3.48% and lighting electricity up to 9.24%. However, in both cases, the changing pattern cannot be generalised and the pattern is case specific. Therefore, to have a generalised correlation, a combination of multiple factors will need to be considered.
For naturally ventilated buildings, wind direction plays an important role in achieving the required thermal comfort. In square and L cases, the orientation change affects only 1.5–3% of the thermal comfort as the wall areas facing that direction will be same for all the orientations. However, in the rectangular case, the orientation can change the thermal comfort up to 8.5–9.5% as the area of the wind-facing wall varies with the orientation. Nevertheless, there is no clear effect of orientation on the lighting electricity, mainly due to the occupancy time and the placement of windows evenly in the envelope.
Conclusion
Given the lack of literature on the effect of building shape, zone sizes and zone locations on the thermal comfort and energy consumption of naturally ventilated houses, this study was conducted by analysing 300 different models. Four WWR ratios and 24 building orientations were considered for each model and the discomfort hours and lighting electricity were obtained through Design Builder simulations. According to the study results, building shape does not show a clear effect on either thermal comfort or lighting energy except in special cases. However, the results suggest that a rectangular shape with staircase positioned at the middle will provide higher thermal comfort for WWR of 20, and for other WWRs the L-shaped models, where the staircase is at the short corner and middle, provide higher thermal comfort. Square-shaped houses with staircase in the middle have the highest lighting electricity, while L shape has the lowest lighting electricity. Irrespective of the building shape, the zone sizes and the zone locations affect both the thermal comfort and lighting electricity. Further, WWR changes the thermal comfort by 20–55% and lower WWR provides higher thermal comfort and higher lighting electricity at the same time. However, the percentage change in lighting electricity due to WWR is only 1.5–9.5% and therefore thermal comfort should receive more attention in deciding the WWR. Further, in this case study, the building orientation does not have a clear contribution to the thermal comfort or the lighting electricity, mainly due to the occupancy schedules and placing the windows evenly. In future, a parametric analysis will be conducted by analysing the significance of building shape, zone sizes, zone location, WWR and the building orientation individually and collectively.
References
Wang, L., Nyuk, H.W., Li, S.: Facade design optimization for naturally ventilated residential buildings in singapore. Energy Build. 39(8), 954–961 (2007)
Besagni, G., Borgarello, M.: The determinants of residential energy expenditure in italy. Energy 165, 369–386 (2018)
Galvin, R., Sunikka-Blank, M.: Economic viability in thermal retrofit policies: learning from ten years of experience in germany. Energy Policy 54, 343–351 (2013)
Wolff, A., Schubert, J., Gill, B.: Risiko energetische Sanierung? In: Großmann, K., Schaffrin, A., Smigiel, C. (eds.) Energie und soziale Ungleichheit, pp 611–634. Springer VS, Wiesbaden (2017)
Großmann, K., Bierwirth, A., Bartke, S., Jensen, T., Kabisch, S., von Malottki, C., Mayer, I., Rügamer, J.: Energetische sanierung: Sozialräumliche strukturen von städten berücksichtigen. GAIA Ecol Perspect. Sci. Soc. 23(4), 309–312 (2014)
Michelsen, C., Müller-Michelsen, S.: Energieeffizienz im altbau: Werden die sanierungspotenziale überschätzt? ergebnisse auf grundlage des ista-iwh-energieeffizienzindex. Wirtschaft im Wandel 16(9), 447–455 (2010)
Brounen, D., Kok, N., Quigley, J.M.: Residential energy use and conservation: economics and demographics. Eur. Econ. Rev. 56(5), 931–945 (2012)
Longhi, S.: Residential energy expenditures and the relevance of changes in household circumstances. Energy Econ. 49, 440–450 (2015)
Filippini, M., Pachauri, S.: Elasticities of electricity demand in urban indian households. Energy Policy 32(3), 429–436 (2004)
Ahsan, T., Svane, O.: Energy efficient design features for residential buildings in tropical climates : the Context of Dhaka, Bangladesh. Sustain. Archit. Urvan Dev. 4, 183–202 (2010)
Mirrahimi, S., Mohamed, M.F., Haw, L.C., Ibrahim, N.L.N., Yusoff, W.F.M., Aflaki, A.: The effect of building envelope on the thermal comfort and energy saving for high-rise buildings in hot-humid climate. Renew. Sustain. Energy Rev. 53, 1508–1519 (2016)
Gago, E.J., Muneer, T., Knez, M., Köster, H.: Natural light controls and guides in buildings. Energy saving for electrical lighting, reduction of cooling load. Renew. Sustain. Energy Rev. 41, 1–13 (2015)
Tavares, PFdAF, Martins, AMdOG: Energy efficient building design using sensitivity analysisa case study. Energy Build. 39(1), 23–31 (2007)
Roetzel, A., Tsangrassoulis, A.: Impact of climate change on comfort and energy performance in offices. Build. Environ. 57, 349–361 (2012)
Yıldız, Y., Arsan, Z.D.: Identification of the building parameters that influence heating and cooling energy loads for apartment buildings in hot-humid climates. Energy 36(7), 4287–4296 (2011)
Cheung, C., Fuller, R., Luther, M.: Energy-efficient envelope design for high-rise apartments. Energy Build. 37(1), 37–48 (2005)
Ochoa, C.E., Capeluto, I.G.: Strategic decision-making for intelligent buildings: comparative impact of passive design strategies and active features in a hot climate. Build. Environ. 43(11), 1829–1839 (2008)
Porritt, S., Shao, L., Cropper, P., Goodier, C.: Adapting dwellings for heat waves. Sustain. Cities Soc. 1(2), 81–90 (2011)
Ihm, P., Krarti, M.: Design optimization of energy efficient residential buildings in tunisia. Build. Environ. 58, 81–90 (2012)
Florides, G., Tassou, S., Kalogirou, S., Wrobel, L.: Measures used to lower building energy consumption and their cost effectiveness. Appl. Energy 73(3), 299–328 (2002)
Ourghi, R., Al-Anzi, A., Krarti, M.: A simplified analysis method to predict the impact of shape on annual energy use for office buildings. Energy Convers. Manag. 48(1), 300–305 (2007)
Caruso, G., Kämpf, J.H.: Building shape optimisation to reduce air-conditioning needs using constrained evolutionary algorithms. Solar Energy 118, 186–196 (2015)
Depecker, P., Menezo, C., Virgone, J., Lepers, S.: Design of buildings shape and energetic consumption. Build. Environ. 36, 627–635 (2001)
AlAnzi, A., Seo, D., Krarti, M.: Impact of building shape on thermal performance of office buildings in Kuwait. Energy Convers. Manag. 50(3), 822–828 (2009)
Alwetaishi, M.: Impact of glazing to wall ratio in various climatic regions: a case study. J. King Saud Univ. Eng. Sci. (2017). https://doi.org/10.1016/j.jksues.2017.03.001 (in press)
Gomez-Mejia, D., Luis, Balkin, : Optimisation of building shape and orientation for better energy efficient architecture. J. Manag. Dev. 23(7), 635–648 (2007)
Oral, G.K., Yilmaz, Z.: The limit U values for building envelope related to building form in temperate and cold climatic zones. Build. Environ. 37(11), 1173–1180 (2002)
Oral, G.K., Yilmaz, Z.: Building form for cold climatic zones related to building envelope from heating energy conservation point of view. Energy Build. 35(4), 383–388 (2003)
Marks, W.: Multicriteria optimisation of shape of energy-saving buildings. Build. Environ. 32(4), 331–339 (1997)
Jedrzejuk, H., Marks, W.: Optimization of shape and functional structure of buildings as well as heat source utilization. Basic theory. Build. Environ. 37(12), 1379–1383 (2002)
Mangkuto, R.A., Rohmah, M., Asri, A.D.: Design optimisation for window size, orientation, and wall reflectance with regard to various daylight metrics and lighting energy demand: a case study of buildings in the tropics. Appl. Energy 164, 211–219 (2016)
Hachem, C., Athienitis, A., Fazio, P.: Parametric investigation of geometric form effects on solar potential of housing units. Sol. Energy 85(9), 1864–1877 (2011)
Bichiou, Y., Krarti, M.: Optimization of envelope and HVAC systems selection for residential buildings. Energy Build. 43(12), 3373–3382 (2011)
Bambrook, S.M., Sproul, A.B., Jacob, D.: Design optimisation for a low energy home in Sydney. Energy Build. 43(7), 1702–1711 (2011)
Bre, F., Silva, A.S., Ghisi, E., Fachinotti, V.D.: Residential building design optimisation using sensitivity analysis and genetic algorithm. Energy Build. 133, 853–866 (2016)
Department of Census and Statistics, “Census of Population and Housing,” tech. rep., (2012)
Halwatura, R.: Effect of turf roof slabs on indoor thermal performance in tropical climates: a life cycle cost approach. J. Constr. Eng. 2013, 1–10 (2013)
Neufert, E., Neufert, P.: Architects’ Data, 3rd edn. Blackwell Science Ltd, Oxford (2000)
Udawattha, C., Arooz, R., Halwatura, R.: Energy content of walling materials-a comparison of mud concrete blocks, bricks cabook and cement blocks in tropics. In: 7th International Conference on Sustainable Built Environment, vol. 7, pp. 30–42, (2016)
Jayasinghe, M., Attalage, R.: Passive techniques for residential buildings in low altitudes of Sri Lanka. Eng. J. Inst. Eng. Sri Lanka 29(2), 18–27 (1999)
CIBSE, Lighting Guide 9: Lighting for communal residential buildings. (2013)
U.S. Green Building Council, “LEED BD+C: Homes | v4 - LEED v4,” (2018)
ASHRAE, ANSI/ASHRAE Standard 55-2010, vol. 2010, p. 42 (2010)
Yao, R., Li, B., Liu, J.: A theoretical adaptive model of thermal comfort-adaptive predicted mean vote (apmv). Build. Environ. 44(10), 2089–2096 (2009)
Mishra, A.K., Ramgopal, M.: An adaptive thermal comfort model for the tropical climatic regions of India (Köppen climate type A). Build. Environ. 85, 134–143 (2015)
Edwards, C.: Design rules of thumb for naturally ventilated office buildings in Canada. PhD dissertation, University of British Columbia (2001)
Aflaki, A., Mahyuddin, N., Mahmoud, Z.Al-Cheikh, Baharum, M.R.: A review on natural ventilation applications through building facade components and ventilation openings in tropical climates. Energy Build. 101, 153–162 (2015)
Walker, A.: Natural Ventilation: Whole Building Design Guide. National Renewable Energy Laboratory, USA (2016)
Acknowledgements
The authors would like to acknowledge the financial support from the Senate Research Committee (SRC/ST/2017/42), University of Moratuwa.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflicts of interest
On behalf of all authors, the corresponding author states that there is no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Pathirana, S., Rodrigo, A. & Halwatura, R. Effect of building shape, orientation, window to wall ratios and zones on energy efficiency and thermal comfort of naturally ventilated houses in tropical climate. Int J Energy Environ Eng 10, 107–120 (2019). https://doi.org/10.1007/s40095-018-0295-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40095-018-0295-3