Abstract
This paper proposes a novel energy hub model for areas using both heat and cold demands that arise due to the major changes in environmental temperature in different periods of the year. The energy demand and the electrical price in a competitive electricity market are uncertain with stochastic values which are usually performed by a probability distribution function. Therefore, a stochastic mathematical model representing an optimal operation of energy hub is based on the objective function of minimization of energy costs (including electricity and gas). Several constraints such as energy balance, limited capacity of the transformer, air conditioners, gas boilers, absorption chillers, combined heat, and power and battery energy storage system are also incorporated into the model to guarantee the required specifications. The high-level algebraic modeling software, general algebraic modeling system has been employed to undertake calculations. Finally, numerical results have illustrated the efficiency and capability of the proposed models.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
The energy internet covering all popular forms of energy (electric, thermal and gas energy) is an indispensable model in future. The model has been studied significantly and continued to be developed, because it offers many benefits such as high-energy efficiency and lower energy supply costs. The concept of the Energy Hub (EH) has been introduced in this model [1]. The power center is derived by the connection between the source and the load through the mixture of inputs and outputs of energy. The types of energy sources and storage devices are described in the form of matrices. This concept has promoted many effects on the planning and optimization process of the operation of the energy system [2].
Studies on EH in the energy internet in recent years are quite abundant with particular attention to the optimal operation of the EH in the energy network [3]. The primary applications of the EH model are residential load [4] and industrial load [5]. The EH model is developed primarily by a Combined, Heat and Power (CHP) architecture. CHP uses primary energy as less polluting energy, providing high-efficiency electrical and thermal loads. The current CHP model has been developed strongly all around the world. It is predicted that by 2023, total capacity will reach 483.7 GW [6]. CHP with various technologies has been introduced such as diesel engine, natural gas engine, steam turbine, gas turbine, micro-turbine, and fuel cells with efficiency up to 90%. In particular, the gas turbine and micro-turbine have many advantages such as less space, low noise, flexibility in control, high efficiency, and reduced environmental pollution and it should be used widely [7, 8]. Consequently, more researches on CHP applications in energy systems have been conducted. CHP enables the energy systems to improve their efficiency such as reducing energy purchase costs, improving energy efficiency and reducing environmental pollution [9, 10]. At a higher level, the combined cooling, heat and power (CCHP) model was introduced in [11,12,13] with the aim of supplementing the additional cooling demand of the system air conditioner (AC) or absorption chiller (ACh).
Over the past decades, the electricity sector has made tremendous changes in business and administration. One of them is the process of restructuring the electricity market from the monopoly model to the competitive electricity market (CEM) model [14]. In CEM, customers can choose suppliers and prices which vary in terms of time and market rather than fixed price over time [15]. It has a great impact on the planning, design, and operation of power systems [16, 17]. Indeed, CEM has opened up the opportunity to introduce and adopt new approaches to increase the efficiency of energy systems. In particular, the energy price mechanism is one of the primary constraints in the optimal management of energy use [18]. In [19], a survey of 1000 households using a heat pump to optimize the demand for switching between electricity and heat, derived from fixed gas prices and electricity prices vary from time to time. The results show that in multi-energy systems, the household can be supplied without having to adjust the demand manually. Similarly, [19] establishes a mechanism for minimizing the cost of energy use based on the electricity price factor through the CCHP model, thereby optimizing the need for heating in winter and cooling in summer of the system. Power pricing uses the time of use (TOU) schedule and the typical load characteristics of the load in terms of time are used. The EH model with random wind, electricity, and power tariffs is also presented in [21, 22] with a minimal objective function of daytime running costs as well as technical constraints of the EH.
The load is a factor that is of a random nature, changes over time and the need to use it. Hence, there have been many studies on the random characteristic of loads through the Probability Distribution Functions (PDF) [23,24,25]. These studies mainly focus on solving the problem of operation and planning of the power grid considering the randomness of the load while assessing their impact on the economic and technical criteria of the power network. However, when considering the electrical power grid, especially the optimal operation problem, many studies have not mentioned this problem yet. A number of recent studies, such as [26], present a new perspective on the ability to exploit multi-energy systems through EH, and the paper also extends some concepts of the uncertainty of the load and electricity price thus helping to regulate available energy sources within the allowable limits. Reference [27] examines some uncertainties then proceeded to optimize the energy output of dispersed sources and storage systems with the smallest total cost of the objective function. Although these studies have mentioned in detail the randomness of the load, it only considers electricity and heat loads, there are no studies to solve the optimal operations of the EH model while considering the randomness of all three types of load (electricity, heat, and cold).
At present, optimizations and optimization methods are widely applied in many fields to effectively optimize the practical problems. Recent studies on the optimal operation of EH are approached in many directions with different objective and constraints. Tools used in computations are also varied, often using the advanced programming language like MATLAB, Fortran, Delphi, C++ [4]. In recent times, the General Algebraic Modeling System (GAMS) programming language has been developed and has widespread applications in the EH optimization problem. GAMS is capable of successfully solving optimal problems by solving algorithms built into the program [28]. Therefore, this study uses the GAMS programming language to solve the optimal operation problem of the proposed EH model.
From the above analysis, this study mainly solves the optimal operation problem of the EH model in the electricity market, taking into account the randomness of electricity and load factors to contribute to the improvement of the research perspective about the study on the optimal energy use problem in the energy grid, bringing the computational model closer to reality. In particular, the EH model is proposed with the ability to provide simultaneous electricity, heat, and cold for the loads. The model is capable of linking and exchanging between different forms of energy to select the optimum energy flow with minimum operating cost. The approach and problem solving are as follows: Firstly, the proposed EH model is based on the demand for electricity, heating, and cooling of the load. The structure and operational principles of the model will be introduced in Sect. 2. The randomness of the load, electricity price, and mathematical description will be introduced in Sect. 3. The optimal operation of the proposed EH model consists of the minimal objective function of the total energy cost of the system; the mathematical constraints which include input/output power balancing of the EH model, equipment conversion limits, power capacity limits of the system, and energy tariffs will be introduced in Sect. 4. The optimal operation problem using the GAMS programming languages solved in simulation result section. The optimal operation problem is considered in four specific cases to evaluate the random effect of the load and energy prices on the performance of the EH model. Finally, conclusions and future research directions are given in Sect. 6.
Modeling under energy hub approach
Introduction about EH model
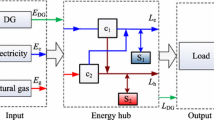
An integrated system, in which the energy can be converted, conditioned and stored, is referred to as the EH. Figure 1 illustrates different levels of a general EH. In an EH, different forms of energy are received at the input ports connected to the energy infrastructures and the energy services in the form of electricity, heating, and cooling is delivered at the output ports [29]. Within an EH, different forms of energy are converted and conditioned using converter technologies such as transformers, AC, CHP technology, heat exchangers, and absorption chillers.
The EH model is mathematically described in matrix—vector as follows:
where cij is the connecting factor that indicates the relationship between the input power at i button and output energy at the j button. P(1,…m) is the power input, and PL(1,…n) is the converted power output.
Proposed EH model
Today, the rapid pace of social development has led to a growing and varied demand for energy. A model that uses only one form of electrical energy is also less efficient. The demand for energy today is clearly different often designed in a systematic way and is mainly used which are in three forms: electricity, heating, and cooling. The demand for each type of energy varies widely during the day and is incidental. In addition, in the competitive electricity market, electricity prices often change over time, thus optimizing the energy purchase cost from the market by optimizing the energy flow supplied to the loads in EH. Therefore, this study calculates the optimum performance of the EH model, as shown in Fig. 2. Input energy includes natural gas and electricity, these two types of energy are converted through the devices in the model to supply for load including electricity, heating, and cooling. In particular, the electrical power has been supplied by the CHP and the electrical system via transformer (T), and heat supplied by CHP and GB; cold can be supplied by the AC with the electricity input or ACh with the heat input.
In addition, to improve the efficiency of the system, the model uses energy storage system battery (BESS). BESS is a fundamental solution to improve power supply reliability [30]. In fact, this storage system has been used extensively in operations and planning to reduce investment costs, and reduce the cost of purchasing power from the system with the goal of improving economic efficiency by adjusting the load graph (stored power during off-peak hours and release to the grid at peak hours [31]).
Uncertainty modeling of energy prices and demands
Electrical and gas prices
At present, electricity prices often use TOU prices to encourage electricity savings and reduce peak power, leading to reduced capital investment and transmission costs [31]. However, CEM in recent times has made significant changes, mainly aimed at ensuring energy supply and reducing costs. At that time, the electricity price was real-time price (RTP) depending on the market and the incidental [32]. Uncertainty in electricity prices is usually expressed by the normal PDF [33,34,35], as shown in Eq. (2) and Fig. 3:
where σ is the standard deviation and μ is the average value of the electricity variable x.
Because the PDF is the continuous function, the electricity prices are multi-state parameters. Therefore, the clustering technique is utilized to divide into states in each time segment. The different states of the electricity prices are determined for each time segment; thus, there is a specific value for the price at each state with the related probability.
A number of states in each PDF function are chosen in accordance with the methods and calculation algorithms. Because a small number of states affects accuracy, while a large number increase the complexity of computations. The natural gas price is constant as expressed by [4, 13, 24].
Electrical, heating, and cooling demands
In general, the demand for electricity in residential areas often changes drastically during the day and is incidental. Therefore, the system peak load will be assumed to follow the hourly load shape of the IEEE-RTS (reliability test system). Based on this assumption, the load will be divided into ten levels using a clustering technique, utilizing the centroid sorting process, developed in [37], which verifies that ten chosen equivalent load levels, with different probabilities, provides a reasonable trade-off between accuracy and fast numerical evaluation [38, 39]. In addition, recent studies demonstrate the characteristics of the load according to standard deviation function similar to electricity prices, with the advantages of being closer to the value of actual load when using previous survey data [40].
Similarly, the uncertainty of heating and cooling demand is also expressed in the normal PDF, as introduced in [21]. Therefore, this study uses the load model of electrical, heating, and cooling as a normal PDF as follows.
Combined model of price and demands of heating, cooling, and electrical
The stochastic of parameters leading to each state will have different values and probabilities. Therefore, assume that the state of the electricity price per time period (h) distributed as a function of the PDF is \( n_{s}^{\lambda e} \). Similarly, the number of states of electrical load, heating, and cooling is \( n_{s}^{e} ,n_{s}^{h} ,\,n_{s}^{c} \), respectively. In each state, the probabilities of loads and prices are determined from the PDF function with probability of the load, heating, cooling, and electricity prices in the states are denoted as \( \alpha_{s}^{e} \{P_{L}^{e}\} \),\( \alpha_{s}^{h} \{P_{L}^{h}\},\,\alpha_{s}^{c} \{P_{L}^{c} \} \), and \( \alpha_{s}^{\lambda e} \{\lambda^{e} \} \), respectively.
The concept of a hybrid model of different parameters was introduced in [37]. In particular, the parameters of the elements (electricity and gas price, the load factor of heating, cooling, and electrical) in each state are obtained by enumerating all combinations of their states according to the following matrix M:
where Cs is the matrix that enumerates the possible values of electricity prices and loads (heating, cooling, and electrical); \( \alpha_{s}^{{}} \{{ \text{C}}_{s} \} \) is a one-column matrix that represents the probability of any combination of loads and electricity prices determined by the mathematical formulas (4); and Ns is the sum of the individual states of the matrix M and is computed by the product of the possible states of the load components and the electricity price as expressed by the mathematical expression (5):
Parameters of the load, heating and cooling at time h are \( P_{L.h,s}^{e} \),\( P_{L.h,s}^{h} \), and \( P_{L.h,s}^{c} \), respectively, and expressed through parameters of the additional charge \( k_{s}^{e} \), \( k_{s}^{h} \), and \( k_{s}^{c} \) (these coefficients will receive values from 0 to 1) as represent in (6):
Similarly, electricity prices \( \lambda_{h,s}^{e} \) are also expressed by the coefficient \( k_{s}^{\lambda e} \) at hour h in equation (7):
Choosing the number of states is very important as it affects the accuracy of the results and the ability to calculate. If the number of states is too small, it will cause the large error. If the number of states is too large, the number of calculations is also very large. Therefore, a number of states in each time segment are chosen in accordance with the methods and calculation algorithms.
The researches [34, 37] utilized technique choosing number of states depending on maximum and minimum values of parameters. The minimum value is considered to be the first state and maximum value is considered to be the last state. In this study, the above method is also used and it is assumed that the coefficient of loads (heating, cooling, and electrical) varies from 0 to 1. The step is adjusted to be 0.1 for coefficient of loads. Similarly, 0.1 also is utilized to be the step adjusted for the factor of electricity price compared with maximum price. Therefore, a number of maximum states in each component (electrical, heat, cold and electricity price) are 10. Thus, the maximum number of computational states per hour h will be 104 states.
Mathematical model
The objective function
The goal of the problem is to optimize EH operating costs. Therefore, the minimum objective function of the cost of buying energy from the market each day consisting of electricity and gas as expressed in Eq. (8) with \( P_{h,s}^{e} ,\,P_{h,s}^{g} \) are the amount of electricity and natural gas purchased from the market in each state s at hour h being considered:
where \( \lambda_{h,s}^{e} \) is the electricity price at hour h at states; \( \lambda_{h}^{g} \) is the constant natural gas price; and Nh is the total number of hours a day (24 h).
The constraints
To ensure the ability to work and power the equipment in the EH model, the mathematical model should consider the following constraints:
Energy balance constraints of EH model
Based on the structure of the EH model presented in Fig. 2, and the matrix representing the energy balance relation of the model in Eq. (1), the energy balance constraint is defined according to the following expression:
where \( P_{{{\text{BE}} .h}}^{\text{ch}} \) and \( P_{{{\text{BE}} .h}}^{\text{dis}} \) are the charge and discharge power of BESS at hour h, respectively; \( \nu_{{{\text{AC}} .h,s}} \), \( \nu_{{{\text{CHP}}.h,s}}^{{}} \), and \( \nu_{{{\text{ACh}} .h,s}} \) are the dispatch ratios of electricity, natural gas, and heat conversion at hour h, respectively; \( \eta_{\text{CHP}}^{\text{ge}} \) and \( \eta_{\text{CHP}}^{\text{gh}} \) are the gas-to-electricity and heat conversion efficiency of the CHP; \( \eta_{\text{T}} \), \( \eta_{\text{GB}} \), and \( \eta_{\text{BE}} \) are efficiency of transformers, GB, and BESS, respectively. \( \eta_{\text{AC}}^{{}} \) and \( \eta_{\text{ACh}}^{{}} \) are efficiency of AC and Ach which usually are calculated based on coefficient of performance (COP) in the following equation [29]:
where \( COP_{AC} ,\,COP_{ACh} \) are the coefficient of performance for AC and Ach, respectively.
The energy balance, charging, and discharging constraints of BESS
The characteristics of electricity prices and electricity surcharge graphs vary with a 1-day, 24-h cycle. The electricity price is high at peak hours and vice versa. Therefore, the total energy stored and transmitted back to the system must be balanced by Eq. (11). The chosen calculation cycle is 24-h cycle to reduce investment costs of BESS. Hence, the constraint on energy balance in calculation cycle of BESS is expressed as such. In general, BESS can work in charge or discharge mode and can be charged from system depending on the model operation. The charge/discharge of BESS can be expressed through two binary variables \( \gamma_{{B{\text{E}} . {\text{h,s}}}}^{{d{\text{is}}}} \) and \( \gamma_{{B{\text{E}} . {\text{h,s}}}}^{\text{ch}} \):
The power and capacity constraints of BESS
The limits of BESS include maximum power and storage capacity. Therefore, the charge/discharge of BESS must ensure the limits as Eq. (12) with the maximum power of BESS, \( P_{{B{\text{E}}}}^{\hbox{max} } \):
Similarly, the total storage capacity of BESS must be less than the maximum capacity of BESS,\( E_{{B{\text{E}}}}^{\hbox{max} } \), with constraints as in (13):
The constraint of power purchased from market
The supply capacity of the system is limited by the capacity and energy stored. Consequently, the constraint is utilized as expression (14):
where \( P_{\text{e}}^{\hbox{max} } \) and \( P_{g}^{\hbox{max} } \) are the maximum allowable power of electrical energy and natural gas.
The total energy purchased from the electricity and natural gas system within a day of the EH is limited by the energy that can be supplied from the two systems above by the formula (15):
where \( E_{ \hbox{max} }^{e} ,\,E_{ \hbox{max} }^{g} \) are the limits of power that can be supplied from the electrical system and natural gas.
The constraints of power flow
The optimal operation of the EH model is based on the ability to control the power flow of AC, ACh, T, GB, BESS, and CHP devices. Therefore, the conversion limits of the above devices at time h and stage s are represent in Eq. (16):
They are considered as state variables that show converted energy values through the corresponding devices from time to time. The controllable flow devices are not allowed to operate over limited value.
The optimization problem with targeted function and binds was based on a programming language of GAMS/BONMIN solver [28].
Results and discussion
To clarify the advantages of residential EH in CEM with the mathematical model proposed in Sect. 4, the optimization of input power and energy costs of EH for each day is calculated. The effect of the uncertainties of loads, electricity prices, and the involvement of BESS is also compared in four computational cases, as shown in Table 1.
Assumptions and databases in analysis
Electrical, heating, and cooling demand
Energy loads in residential areas often change drastically during the day-to-day operations. Therefore, this research assumed that typical daily electrical, heating, and cooling load characteristic is shown in Fig. 4. Where, the maximum load power at 7PM with the power capacity of 5.5 MW and the minimum load power at 3AM with the power capacity of only 1.5 MW, corresponding to the proportion of 27% when reaching the max. Heating and cooling loads are relatively small with power capacities of 2.38 and 0.72 MW, respectively.
In each hour h, the uncertainty of energy demand is discussed in Sect. 2. From the energy demand survey, the power capacity of the loads corresponding to the probability of the normal PDF function is calculate. In every hour h, assume that the normal PDF function of the electricity price has five states (s) with an average load factor of μ = 0.8 and standard deviation of σ = 0.1, as shown in Table 2 [21, 34, 39]. Where, the power factor and the probability of the loads in state s are \( k_{L.s}^{e} \) and \( \alpha_{s}^{e} \), respectively. Similarly, the heating load, probability, and power factor for the heat demand are \( \alpha_{s}^{h} \) and \( k_{L.s}^{h} \), for cool demand, that are \( k_{L.s}^{c} \) and \( \alpha_{s}^{c} \).
The state with maximum probability, the state 2, is 52.5% corresponding to a power factor of 0.8. In contrast, states 1 and 5 have the minimum probability of 4.5%.
Electrical and gas energy price
Currently, gas prices changed a little in the short term, so in a typical day, it is an instant and is about 5.5¢/kWh [4, 40]. Electricity prices also vary widely over time and depend on the market. In this study, the largest electricity price per hour is shown in Fig. 5 [41,42,43]. The uncertainty of price is determined by the normal PDF from the hypothetical survey data which is similar to a part with the probability of \( \alpha_{s}^{\lambda e} \) corresponding to the max price of \( k_{L.s}^{\lambda e} \).
The equipment parameters and limits of system
The efficiency of energy conversion equipments is quite high, as shown in Table 3. The total conversion efficiency of CHP is 0.85 with 40% converted to electricity and 50% converted to heat [4, 13]. The efficiency of AC and Ach is calculated as Eq. (10) with coefficient of performance COPAC and COPACh, respectively. COPAC and COPAch are equal with value 1.5. Therefore, efficiency AC and Ach is the lowest and equals 60%; on the contrary, the highest efficiency is 95% of transformer.
The power limits of the equipment as well as the capacity of BESS and the system to ensure the proper operation of the equipment and its ability to supply the system is shown in Table 4.
Analysis results and discussion
The proposed model is calculated with the hypothetical parameters assumed above. The calculated results determine the energy flow in the devices in all operating states s and all hours of the day. Energy flow during minimum load is the 3rd hour (the electricity reaches 1.5 MW, the heat load is 1.13 MW and the cooling load 0.23 MW), and the maximum load is the 19th hour (the electricity load reaches 5.5 MW, the heat load is 2.0 MW, and the cooling load is 0.6 MW) in case 1 and case 2, as shown in Fig. 6.
The optimal energy flow was chosen when the load is minimum, CHP operating at 1.66 MW, and the power capacity of GB is 0.42 MW to supply for 1.13 MW heat load in case 1. Power bought from the electrical system is 1.12 MW along with the received power capacity from CHP to provide 1.5 MW for the electricity load. At the same time, all the cooling loads, supplied from AC due to very low price, are only 6.5 cent/kWh. Similarly, at the time of low electricity price, the amount of power received from the system increased by 0.15 MW corresponding to 13.39% to charge for BESS in case 2. The energy flow which through the remaining devices similar to case 1.
At the time of the peak load, CHP was chosen to operate with a high capacity of 4.0 MW in both cases to provide additional load, because the electricity price then reached 13 cent/kWh and the gas price was only 5.5 cent/kWh. Transmission capacity through GB also reached 1.0 MW. All the cooling loads are supplied from the ACh through the heat generated by CHP and GB due to the peak electricity price at this time. Power received from the system in case 2 decreased by 0.16 MW or 3.69% compared to case 1 due to the support of BESS during high electricity price hours.
Thus, in every operating state of EH, the energy flow in each electrical device to optimize the energy flow of EH always is determined. BESS storing electricity during low electricity price hours and transmitting at high electricity prices has reduced energy costs of EH. However, the above calculations with the load parameters and the electricity price assumed to be constant in each working hour have led to the errors, because loads are random quantities, as introduced in Sect. 3.
When the uncertainty of load and electricity price is considered in case 3 and case 4, the load capacity varies in each computing state; hence, the energy flow in each device also changes. The energy flow in the operating state with a minimum load is the state 1 in the 3rd hour when the maximum load is the state 256 in the 19th hour, as presented in Fig. 7. In state 1, the power consumed by the loads drops compared to the calculated maximum values in case 1, so the energy flow through the devices also decreases. The capacity of CHP is only 0.4 MW, the operating capacity of the GB is 0.11 MW, and the power purchased from the system reaches 0.86 MW. The entire demand for cooling is provided by AC due to low electricity price, which is similar to case 1. When considering the involvement of both BESS and the uncertainty of the demand and electricity prices in case 4, overall demand for cooling is still provided by AC, but the capacity received from the systems increases to charge BESS with the capacity of 0.15 MW in this period, corresponding to 17.44%.
At peak load, the state 256 at 7PM, electricity price reached the maximum, so all the cooling in case 3 and case 4 are both supplied by ACh through the heat with a capacity of 1.28 MW. The energy flow through CHP and GB is similar in both cases that are 4.0 MW 1.1 MW, respectively. Power capacity received from the system in case 4 decreases 0.15 MW due to the support of BESS.
The calculation results also determine the charge and discharge capacity of BESS in both cases in each operating hour, as shown in Fig. 8. During the lower electricity price hours (from 1AM to 3AM, from 10AM to 1PM, 3PM and 11PM, 12PM), BESS charges with a maximum power 0.15 MW corresponding to the maximum capacity. During the high electricity price hours (at 5 AM, 7 AM, 9 AM and from 5 PM to 10 PM), BESS discharges 0.15 MW back to the system. Due to the loss in BESS, the total power charged/discharged dropped by 0.15 MW, so the total power consumed in case 2 and case 4 increases compared to case 1 and case 3, respectively. The energy flow in GB, CHP also changes depending on the operating state as analyzed above.
The calculations in all states s, 24 h, in each day determine the energy required to purchase from the system in each hour for four cases, as shown in Fig. 9. In all four cases, the amount of gas purchased from the system increased during high electricity price hours such as from 7AM to 9AM and from 5PM to 10PM. Conversely, during the low electricity price hours, it can compete with gas, so the amount of gas purchased from the system is reduced and electricity increased.
Comparison of calculated results in Fig. 9a and c shows that energy purchased from the systems considering the uncertainties in case 3 always decreases compared to case 1, a minimum of 6.3% at the 6th hour and maximum of 11.3% at the 9th hour. In addition, the rate of electrical power in total energy input of case 3 always increases from 1.24 to 22% due to the impact of randomness of electricity prices.
When BESS used in case 2 and case 4, it changes the energy flow received from the system in each operating hour compared to case 1 and case 3, as shown in Fig. 9b, d. In both cases, with the involvement of BESS, the power capacity received from the system increases during the off-peak hours and decreases during the peak hours to reduce the costs of electricity prices purchased from the systems of the EH. In addition, the maximum transmission capacity in the distributed system decreases due to the ability to adjust the load graph of BESS which may lead to delay in upgrading electrical equipment. The efficiency of BESS in adjusting the energy flow in case 4 is smaller than case 2 when the minimum loading capacity is only 3.33% compared to 3.71%.
The total energy received from the system in all cases is also determined, as shown in Fig. 10. In case 1, it is 147.7 MW with the electrical power of 58.27% corresponding to 86.03 MW. When considering the uncertainty of the demand and the electricity price in case 3, the total energy received from the system is reduced to 133.4 MW due to the decrease in actual demand and the optimization of the power flow in all states. As a result, total energy has fallen by 14.3 MW (9.66%), with electricity falling by 23.2% and gas increasing by 9.0%. It shows that, given the uncertainty of the parameters, the total energy received from the system decreases compared between case 3 and case 1; this result is closer to the practical conditions.
When BESS participates in the optimal operation of EH, optimizing of the energy flow of CHP, AC, ACh, and BESS is achieved, the total energy purchased of the EH decreases. However, the performance of BESS gaining only 0.9, total energy consumption in both markets increased by 0.2%.
The calculation result of total operating costs of the EH shown in Fig. 11 implies that the randomness of parameters and BESS has a great influence on the performance of BESS. The EH optimizes the energy flow and energy types in all four cases. The operating costs in case 1 is 10492.6$. When considering the uncertainty of demand and energy prices in case 3, the total costs of energy purchased fell sharply to 1205.4$ or 11.5% compared to case 1.
The BESS stores electricity energy at low electricity price hours and generates back to the systems during high peak hours, thus reducing operating costs in both cases. The total EH operating costs fell 0.4% or 45.52$ compared to case 1. The effectiveness of BESS increased sharply when considering the effect of the randomness of parameters and fell 1251.6$ or 11.9% in case 4. Therefore, the total operating costs of the EH, in this case, is only 9241.0$ per calculation cycle, 24 h.
The test results show that the proposed model allows optimizing of energy flow in EH, thus reducing operating costs. Moreover, considering the uncertainty of the load and the electricity price, the net real demand of the system decreases, resulting in energy flow, the efficiency of the EH changes, and the response results are closer to the actual conditions.
Conclusions
This study addresses the following key issues:
-
1.
A more suitable model of EH with the diversity of the load is proposed. The model takes into account the BESS to increase operational flexibility and efficiency. Hence, the economic and technical aspects of the EH also are improved.
-
2.
The optimal operation schedules of the EH are calculated with the objective minimum of energy cost purchased from the system considering the uncertainties of the energy demand and electricity price. The mathematical model represents the uncertainties of three load types (electricity, heating, cooling) and electricity price. Two study scenarios have been proposed to specifically compare the differences considering the uncertainties in the model. The results obtained from hypothetical parameters show that the energy flow is optimized in all cases, states at the same time the technique requirements of the equipment also are ensured. The demand and total energy purchased from the system are reduced when uncertainties are considered. Therefore, the calculation error decreases and results are more suitable for real-world problems. The BESS incorporated in EH reduces the electrical energy purchased from the system and decreases operational costs of the EH.
In this research, the EH model with uncertainties of the loads (electricity, heating and cooling) and electricity price is introduced to optimize energy cost. However, the renewable sources with stochastic characteristics (photovoltaic and wind generators) and investment cost of equipments are not considered. Hence, the above aspects should be further investigated in problems optimal planning and operation for EH.
References
Favre-Perrod, P.: A vision of future energy networks. 2005 IEEE Power Engineering Society Inaugural Conference and Exposition in Africa Durban, pp 13–17 (2005)
Geidl, M., Koeppel, G., Favre-Perrod, P.: Energy Hubs for the future. IEEE Power Energy Mag 5(1), 24–30 (2007)
Moeini-Aghtaie, M., Abbaspour, A., Fotuhi-Firuzabad, M.: A decomposed solution to multiple-energy carriers optimal power flow. IEEE Trans Power Syst 29(2), 707–716 (2014)
Thanhtung, H., Yongjun, Z., Thang, V.V.: Energy hub modeling to minimize residential energy costs considering solar energy and BESS. J Modern Power Syst Clean Energy, 1–11 (2017)
Paudyal, S., Cañizares, C.A., Bhattacharya, K.: Optimal operation of industrial energy hubs in smart grids. IEEE Trans Smart Grid 2014; 6(2):1–10 (2014)
Darrow K., Tidball R., Wang J., Hampson A.: Combined heat and power partnership. U.S. Environmental Protection Agency (2015)
Review of Combined Heat and Power Technologies. Office of Energy Efficiency and Renewable Energy, U.S. Department of Energy, pp. 1–31 (1999)
Alanne, Kari, Saari, Arto: Sustainable small-scale CHP technologies for buildings: the basis for multi-perspective decision-making. Renew. Sustain. Energy Rev. 8, 401–431 (2004)
Xie D., Lu Y., Sun J.: Optimal operation of a combined heat and power system considering real-time energy prices. 2014 ACM CHI Workshop: Biological Rhythms and Technology, pp. 123–126 (2014)
Mohammadi-Ivatloo, B., Moradi-Dalvand, M., Rabiee, A.: Combined heat and power economic dispatch problem solution using particle swarm optimization with time varying acceleration coefficients. Electric Power Syst Res 95(1), 9–18 (2013)
Liu, M., Shi, Y., Fang, F.: Combined cooling, heating and power systems. Renew. Sustain. Energy Rev. 2014(35), 1–22 (2014)
Faeze, B., Masoud, H., Shahram, J.: Optimal electrical and thermal energy management of a residential energy hub, integrating demand response and energy storage system. Energy Build. 90(2015), 65–75 (2015)
Shahab, B., Farahbakhsh Safe, A.L.: Financial approach to evaluate an optimized combined cooling, heat and power system. Energy Power Eng 5, 352–362 (2015)
Harris, P.G.: Impacts of deregulation on the electric power industry. IEEE Power Eng Rev 20(10), 4–6 (2000)
Zareipour, H., Bhattacharya, K., Cañizares, C.A.: Electricity market price volatility: the case of Ontario. Energy Policy 35(9), 4739–4748 (2007)
Van Werven M.J.N., Scheepers M.J.J.: The changing role of distribution system operators in liberalised and decentralising electricity markets. 2005 International Conference on Future Power Systems. pp. 1–6 (2005)
Jiménez-Estévez, G.A., Palma-Behnke, R., Torres-Avila, R.: A competitive market integration model for distributed generation. IEEE Trans Power Syst 22(4), 2161–2169 (2007)
Siano, P.: Demand response and smart grids—a survey. Renew Sustain Energy Rev 30(2), 461–478 (2014)
Mancarella, P., Chicco, G.: Real-time demand response from energy shifting in distributed multi-generation. IEEE Trans Smart Grid 4(4), 1928–1938 (2013)
Best, R., Rivera, W.: A review of thermal cooling systems. Appl. Therm. Eng. 2015, 1162–1175 (2015)
Atwa, Y.M., El-Saadany, E.F.: Probabilistic approach for optimal allocation of wind based distributed generation in distribution systems. IET Renew. Power Gener. 5(1), 79–88 (2011)
Catalao, J.P.S., Pousinho, H.M.I., Mendes, V.M.F.: Optimal offering strategies for wind power producers considering uncertainty and risk. IEEE Syst. J. 6(2), 270–278 (2012)
Mostafa, F.S., El-Saadany, E.F.: Accommodating high penetrations of PEVs and renewable DG considering uncertainties in distribution systems. IEEE Trans Power Syst. 29(1), 259–271 (2014)
Reza, H., Rahmat-Allah, H., Taheri, Nabi: Distribution network expansion planning and DG placement in the presence of uncertainties. Electrical Power Energy Syst. 2015(73), 665–673 (2015)
Arash, Z., Younes, M., Mohammad, H.M.: Optimal multi objective placement and sizing of multiple DGs and shunt capacitor banks simultaneously considering load uncertainty via MOPSO approach. Electrical Power Energy Syst. 2015(67), 336–349 (2015)
Rastegar, M., Fotuhi-Firuzabad, M., Zareipour, H.: A probabilistic energy management scheme for renewable-based residential energy hubs. IEEE Trans. Smart Grid 8(5), 2217–2227 (2017)
Pazouki, S., Haghifam, M.R., Moser, A.: Uncertainty modeling in optimal operation of energy hub in presence of wind, storage and demand response. Int. J. Electr. Power Energy Syst. 2014(61), 335–345 (2014)
Richard E. Rosenthal. GAMS—a user’s guide. GAMS development corporation, Washington, USA (2010)
Barmayoon M.H., Firuzabad M.F., Ghahnavieh A.R., Aghtaie M.M.: Energy storage in renewable-based residential energy hubs, IET Generation Transmission &Distribution 2016; 10(13): 3127–3134 (2016)
Lu B., Shahidehpour M.: Short-term Scheduling of battery in a grid-connected PV/Battery system. IEEE Transactions on Power Systems 2015; 20(2): 1053–1061 (2015)
Leou R.C.: An economic analysis model for the energy storage systems in a deregulated market. 2008 IEEE International Conference on Sustainable Energy Technologies, pp. 744–749 (2008)
Neyestani, N., Yazdani-Damavandi, M., Shafie-Khah, M.: Stochastic modeling of multienergy carriers dependencies in smart local networks with distributed energy resources. IEEE Trans. Smart Grid 6(4), 1748–1762 (2015)
Liu, M., Shi, Y., Fang, F.: Combined cooling, heating and power systems: a survey. Renew. Sustain. Energy Rev. 2014(35), 1–22 (2014)
Soroudi, A., Mohammadi-Ivatloo, B., Rabiee, A.: Energy hub management with intermittent wind power. Green Energy Technol. 118(14), 413–438 (2014)
Liu, Z., Wen, F., Ledwich, G.: Optimal siting and sizing of distributed generators in distribution systems considering uncertainties. IEEE Trans. Power Delivery 26(4), 2541–2551 (2011)
Sheikhi, A., Ranjbar, A.M., Oraee, H., Moshari, A.: Optimal operation and size for an energy hub with CCHP. Energy Power Eng 2011(3), 641–649 (2011)
Atwa, Y.M., El-Saadany, E.F., Salama, M.M.A., Seethapathy, R.: Optimal renewable resources mix for distribution system energy loss minimization. IEEE Trans. Power Syst. 25(1), 360–370 (2010)
Pinheiro, J.M.S., Dornellas, C.R.R., Schilling, M.T., Melo, A.C.G., Mello, J.C.O.: Probing the new IEEE reliability test system (RTS-96): HL-II assessment. IEEE Trans. Power Syst. 1998(13), 171–176 (1998)
Thang, V.V., Minh, N.D.: Optimal allocation and sizing of capacitors for distribution systems reinforcement based on minimum life cycle cost and considering uncertainties. Open Electrical Electronic Eng. J. 2017(11), 165–176 (2017)
Rastegara, M., Firuzabada, M.F., Lehtonen, M.: Home load management in a residential energy hub. Electric Power Syst. Res. 119(119), 322–328 (2015)
Rafał, W.: Electricity price forecasting: a review of the state-of-the-ar with a look into the future. Int. J. Forecast. 30(4), 1030–1081 (2014)
Bozchalui M.C., Claudio A. Canizares and Kankar Bhattacharya: Optimal Energy Management of Greenhouses in Smart Grids. IEEE Transactions on Smart Grid 2015; 6(2): 827- 835 (2015)
Isha, S., Kankar, B., Claudio, C.: Smart distribution system operations with price-responsive and controllable loads. IEEE Trans Smart Grid 6(2), 795–807 (2015)
Acknowledgements
This work is supported by Thai Nguyen University of Technology (TNUT), Vietnam, as parts of a scientific project.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Thang, V.V., Zhang, Y., Ha, T. et al. Optimal operation of energy hub in competitive electricity market considering uncertainties. Int J Energy Environ Eng 9, 351–362 (2018). https://doi.org/10.1007/s40095-018-0274-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40095-018-0274-8