Introduction

Mauritius, a small island located in the tropical belt of the southwestern Indian Ocean basin, enjoys a tropical maritime climate that spans over two seasons: summer and winter. The population of the island in 2016 stood at 1,263,820, representing a growth of 0.1% as compared to the preceding year [1]. The increasing population dynamics fuels the need for increasing energy requirement. Consequently, this has led to an increase of 1% in total primary energy requirement during this 1 year interval to reach a value of 1550 ktoe [2]. Typical of small island developing states (SIDS), Mauritius relies heavily on imported fossil fuels (with a share of 85%), reflecting on the vulnerable and volatile economy of the country. The electricity generation for the year 2016 amounted to 3042 GWh, with a share of 78.2% attributed to imported fuel oil and coal and the remaining percentage (21.8%) coming from renewable energy sources comprising bagasse (16.3%), hydro (3.3%), photovoltaic (1%), wind (0.6%) and Landfill gas (0.6%) [2]. The huge renewable energy potential of the island for sustainable energy production has been recognized and bold measures are being taken by policy makers in the form of international partnerships and supportive regulatory frameworks to encourage independent power producers (IPPs) invest in the green sector. The long-term vision of the Government of Mauritius is to increase the percentage of electricity generation from renewable energy resources to 35% by 2025 [3].

Presently, the generation of electricity in Mauritius from wave resources is inexistent. Wave energy is acknowledged as being a reliable renewable energy source whose output can be predicted in both spatial and temporal scales [4]. In addition to displacing fossil fuels, which inadvertently help reduce greenhouse gas emissions and improve energy security, wave energy holds the benefit of being relatively less intermittent in nature than solar and wind. The heterogeneity associated with cloud systems and prevailing wind conditions results in fluctuations from solar and wind power generations. Consequently, the implementation of wave energy extraction devices in the near-shore and off-shore regions of the island would help reduce instabilities occurring in the national grid by conditioning power and smoothing fluctuations. The success of renewable energy lies in its diversification and the inclusion of wave energy can be a strong component in the renewable energy mix which would benefit to the local community at large. Moreover, the proximity of inland and coastal regions to the sea (typically less than 30 km radius) holds the benefit of electricity transmission and access even to remote locations on the island.

Conversion of wave resources can contribute substantially to the electricity demand of several islands. The Orkney archipelago, situated in the north of Scotland is estimated to have a mean wave power of 10–25 kW/m and has been earmarked to contribute 550 MW to the total 1.6 GW wave and tidal energy capacity from twelve leased sites by 2020 [5]. An assessment of the near-shore wave energy potential for the southern pacific islands of Fiji showed that mean wave power of 9.81 kW/m was detected at a depth of 15 m in the west of the main island while energy flux of around 28.78 kW/m was identified near Kadavu island at a depth of 18 m [6]. The Cape Verde Islands, located off the coast of West Africa in the central Atlantic Ocean, witnessed a wave power exceeding 7 kW/m in coastal areas neighboring the islands, with the summer season recording around half the wave potential of the winter season [7]. The island of El Hierro, situated south west of the Canary Islands in the Atlantic Ocean estimates its wave potential to be of the order of 25 kW/m, reflecting on the possibility of harnessing energy from waves [8].

The aim of the present study is to investigate the wave resource potential of open water sites, not too distant for electricity transmission inland and located outside of the coral reef platform of the island. Despite the fact that refracted ocean wave energies may be great at estuarine sites near wide entrances to the sea, significant energy loss occurs when entering estuaries, either by refraction around split platforms or through breaking on entrance shoals [9]. Waves entering basins may dominate the spectral estimates at sites close to the ocean [10]. Consequently, the complex wave climate imposed by estuarine environment on waves coming from deep water is worth exploring. The authors believe that information presented in this paper will be helpful to the Government or any relevant organization in making an informed decision with regard to major investments for harnessing the wave resource for domestic use at the investigated sites.

Material and methods

Geology and climatology

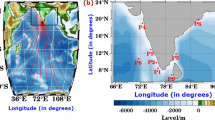
Mauritius (20\(^{\circ }\)10\({\prime }\)S, 57\(^{\circ }\) 30\({\prime }\)E), located in the south western Indian Ocean near the southern end of the Mascarene Ridge, has an approximated surface area of 1859 \(\mathrm{km}^2\) (Fig. 1). The island has an Exclusive Economic Zone (EEZ) of about 2.3 million \(\mathrm{km}^2\) (including approx. 400,000 \(\mathrm{km}^2\) jointly managed with the Seychelles) that extends over the islands of Rodrigues, Agalega, Cargados Carajos shoals, Chagos Archipelago and Tromelin. Of volcanic origin, starting with the Breccia Series 10–7.8 million years (my) B.P., the geomorphological features of the island comprise an elevated central plateau (about 500 m above sea level) surrounded by a chain of mountains and some isolated peaks. The elevation of the terrain decreases gently from the central plateau towards the coastal edge. The coastline measures about 200 km long and is composed of different shore types (categorized as sandy shores, rocky shores, muddy shores, mixed shores, calcareous limestone shores, cliffs and coastal wetlands) whose landforms are related to the coastal geomorphologic features. The shoreline is ringed by fringing coral reefs which enclose a lagoon having an approximated area of 243 \(\mathrm{km}^2\) [11]. With an annual growth rate of about 2 mm, living coral reef formations resist destruction from sea action by constantly growing due to the preference for light and sediment-free waters [11].

The climatological regime of the island, characterized as mild tropical maritime, is dictated by alterations of the two seasons: Summer (November–April) and winter (May–October). The summer season is distinguished as warm and humid while the winter season is generally cool and dry. Microclimatic conditions exist spatially in different localities attributed to the varying atmospheric conditions on the island. The wave patterns on the coast of Mauritius is influenced all year-round by the westerly and persistent southeasterly trade winds which is ensured by the geographical location of the island near to the Inter Tropical Convergence Zone (ITCZ).

Fig. 1
figure 1

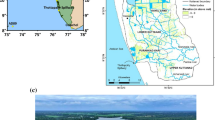
a Location of three earmarked sites considered in Mauritius for the assessment of wave potential. b Geographical location of the tropical island of Mauritius, southwest of Indian Ocean basin. c Magnified view of the two stations located just outside the coral reef platform on the western side of the island

Full size image

Coastal hydrodynamics

The geographical position of the island ensures that it benefits from the South Equatorial Current (SEC) flowing from west to east throughout the duration of the year. Additionally, the trade winds from anticyclones of the south Indian Ocean which moves from east to west influence the coastal hydrodynamics and offshore current systems of the island. These exhibit seasonal variations with the winter season experiencing relatively stronger currents in magnitude due to the strong prevailing South Easterly trade winds. The speeds of the current increase as it passes through the channels situated within the Mascarene Plateau resulting in the formation of strong gyres on the leeward side. When it reaches Madagascar, part of the current flows to the north to feed the Agulhas current in the Mozambique Channel and the East Africa current while the other part flows southwards along the Madagascan coast forming an anticyclone gyre further south [12]. During the South west monsoon, the SEC feeds into the Somali current along the East coast of Africa.

The west coast of the island is relatively more protected from wind and wave action than the east as the body of the island creates a lee whose effect is strengthened in the south west of the island by the presence of the mountains located in the south western region. Typically, wind waves in open sea are between 0.5 m during summer and 3 m during winter with a period of 3–11 s [12]. Significant wave heights in south, southwest (SSW) and southeast (SE) of the island are of the order of 1.5–2.5 m in summer and 2.5–3.5 m in winter [13]. High waves reaching 3–5 m with a wave period of 12–20 s traveling long distances, reaching the southern region of the island as swells with little loss in energy are generated by the deep low pressure systems in the high latitudes [12].

Site selection

Three study sites (Fig. 2) were selected based on diversified hydrologic and coastal environments, reflecting the distinct wave regimes prevailing at these localities. The impact of three different types of coastal hydrological environments (Sandy shore with reef, estuary and mixed shore with reef), geographical location in connection with the prevailing southeast trade winds and swells coming from the south west on the wave climate around the island are explored.

Flic en Flac is a sandy shore (with reef) composed essentially of sediments. The sediments, of carbonate origin are made up of coral fragments, crustaceans and molluscan shells among others. The sandy beach that it makes from the adjacent coral reefs constitutes one of the most economically important and environmentally sensitive coastal habitats of the Republic of Mauritius. Indeed, with the effect of climate change, this fragile ecosystem is at risk of damage due to the impacts of sea level rise, warming of air and sea, and increased storminess [14].

The wave characteristics on the estuarine environment of Tamarin is also studied. The influence of ocean waves may extend several kilometers into an estuary [15] but its effectiveness generally decreases with distance from the opening to the ocean [16]. The location of Tamarin bay on the southwest coast is angled so that the winds blow offshore such that incoming swells have to bend sharply around the coast before hitting the reef [17]. We choose to study the wave characteristics in the Tamarin estuary near the center of the wide entrance to the sea due to high refracted wave energies converging at this site.

Fig. 2
figure 2

Aerial view depicting the coastal environments of the three sites under investigation in this study. The exact location for the deployment of the Wave and Tide Recorder (WTR) on the western flanks of the island and the waverider buoy on the eastern side are presented in the figure

Full size image

Roches Noires is a mixed shore (reef) composed essentially of sediments and pebbles. It constitutes a fairly good balance of sands and rocks, generally interspersed. Located in the northeastern part of the island of Mauritius, Roches Noires is one region where the highest waves are usually observed off the reefs. This eastern region of the island is under the influence of the southeast trade winds throughout the year which provide the most substantial wave action that dominate the depositional dynamics [18].

The deployment of the instruments at those exact geographical coordinates was based on ease of access to the sites, human activity level near these regions and sensitivity of the apparatuses in the water depths placed. Other locations were also considered but dropped primarily due to safety issues arising from the fact that divers would not be able to access the devices easily. For the regions of Flic-en-Flac and Tamarin which have significant human activity levels, we chose to investigate sites relatively away from these influences for ease of deployment and to get minimum disturbance of wave records from anthropogenic activities. A description of the four wave measurement sites considered for deployment is provided in Table 1. More details on the regions of interest are provided in the following sub-section.

Table 1 Description of the four wave measurement sites in terms of period of deployment, radial distance from the shore \((d_\mathrm{shore})\), water depth (Dep) and human activity levels
Full size table

Materials and methods

The Seawatch mini II Waverider buoy, designed by Fugro Oceanor, is intended to follow the motion of the sea surface waves. This results in exact measurement of the water surface and can be employed to derive directional measurement of the surface wave field [19]. Solid-state accelerometers are used to represent accelerations on three orthogonal axes. Integration with simultaneous heading and tilt readings performed on-board using the ’wavesense’ computer unit installed in the buoy, results in accelerations being resolved to heave (vertical), east and north axes. The design ensures that it does not influence the active frequency range for surface waves, also minimizing any damping or phase shift on the signals. As stated by Joosten [20], the mooring design for floating wave buoys must make sure that they allow the latter to respond unimpeded to wave frequencies while providing the sufficient restoring force to resist tidal flow and drift forces. In this study, the buoy was moored using a 600 kg bottom weight attached to a 45 m polypropylene braided rope, having its end connected to a 15 m rubber cable. The waverider has a lead acid battery bank 12 V, 62 Ah \(\times \) 4 (248 Ah) coupled to an optional lithium battery bank rated 1088 Ah. Also included in the design are solar panels with a rating of 12 W \(\times \) 6 (72 W). The buoy was secured in water depth of 46.2 m at a distance of 1228 m from the shore of Roches Noires. Measurements started at this site on the 9th of February 2012 and lasted for 32 months. The buoy was retrieved on the 10th of November 2014. Cyclonic weather conditions resulting from the passage of cyclone ‘Imelda’ near the vicinity of the coast of Mauritius from the 6th to 16th of April 2013 resulted in extreme wave values recorded. Technical issue was encountered by the device in the period from 16th October 2013 to 7th November 2013.

A Valeport Wave and Tide recorder (WTR) was deployed in the month of April at two sites around the island: Flic-en-Flac and Tamarin. WTR sensor has a precision resonant quartz crystal and optional strain gauge with an accuracy of ± 0.01 m for water level measurements. Archived wave measurements taken for the month of April by the Mauritius Oceanography Institute has been chosen owing to important wave characteristics taking place in that specific month of the year. The selection of the years for analysis was primarily based on the fact that no missing wave records due to faulty apparatus were detected. Also, selection of years was based on a number of factors including the wave climate prevailing during the considered period. It was ensured that the selected years for which the WTR was deployed contained no data recorded in cyclonic weather conditions, which would inevitably lead to biased results when it comes to selecting the most energetic region for tapping in surface wave energy. The WTR and Waverider buoy were configured with a sampling frequency of 1 Hz to sample data for 1024 s. A 1 Hz frequency ensures that waves of up to 0.3 Hz (3.33 s) can be accurately recorded. Owing to the fact that waves resulting from meteorological events lie in the period range of 7–15 s, the selected sampling frequency would make optimum use of memory and batteries for such a long period deployment.

Theoretical background

Significant wave height \(H_{m0}\) and wave power \(P_\mathrm{w}\) are two important parameters when it comes to assessing the wave energy potential of a particular sea state. The significant wave height is defined as the average wave height of one-third of the highest waves in a wave record. For two regions: Flic-en-Flac and Tamarin, spectral data have been collected using the WTR. The spectral estimate of significant wave height can be estimated from the zeroth moment of variance spectrum \(m_{0}\) as follows:

$$\begin{aligned} H_{m0}=4\sqrt{m_{0}}. \end{aligned}$$
(1)

For the non-directional variance density spectrum, the spectral moment of \(n\mathrm{th}\) order, \(m_{n}\), is calculated using the following equation.

$$\begin{aligned} m_{n}=\sum _{i=1}^{n}{f_{i}}^n E_{i}\Delta f, \end{aligned}$$
(2)

where \({f_{i}}^n\) is the \(i\)th frequency corresponding to the \(n\)th order, \(\Delta f\) is the frequency increment and \(E_{i}\) is the sea surface variance density over a range of wave frequencies i.

The energy period \(T_\mathrm{e}\) which is the variance-weighted mean period of the non-directional variance density spectrum is calculated from the spectral moments as follows:

$$\begin{aligned} T_\mathrm{e}=\frac{m_{-1}}{m_{0}}. \end{aligned}$$
(3)

The wave power (kW/m) in deep water can be calculated using significant wave height and energy period as follows:

$$\begin{aligned} P_\mathrm{w}=\frac{\rho g^2}{64\pi } {H_{m0}}^2 \quad T_\mathrm{e} = 0.491 {H_{m0}}^2 T_\mathrm{e}. \end{aligned}$$
(4)

Since the points investigated lies outside the coral reef barrier in open water and are found in water depths exceeding 10 and 200 m from the shore, the use of Eq. 4 is justified.

For the Roches Noires dataset, information on spectral moments or spectral shape was not provided, and therefore, \(T_\mathrm{e}\) must be estimated from available dataset and one approach is to assume the following:

$$\begin{aligned} T_\mathrm{{e}} = \alpha T_\mathrm{{p}}, \end{aligned}$$
(5)

where \(\alpha \) is a coefficient whose value depends on the shape of the wave spectrum (0.86 for a Pierson–Moskowitz spectrum and increasing towards unity with decreasing spectral width) [21]. In the spectrum formulation, it is assumed that the wind is blowing steadily for a long time and over a large area such that the waves attain a point of equilibrium with the wind. The conversion from peak period (\(T_\mathrm{p}\)) to energy period (\(T_\mathrm{e}\)) was enable through the approximation:

$$\begin{aligned} T_\mathrm{{e}} \sim 0.86 T_\mathrm{{p}}. \end{aligned}$$
(6)

By combining Eqs. 4 and 6, the total wave energy resource at Roches Noires can be estimated. However, besides estimating the wave energy potential at the sites, it is of interest to analyze the temporal variability of the distributions. Steady wave energy flux are preferred to those having unsteady wave regimes due to the fact that they are more reliable and display greater efficiency [22].

Two coefficients that were proposed by Cornett [23] are employed to assess the temporal variability in wave power for selected sites around the island. They are: coefficient of variation (CV) and seasonal variability index (SV).

The CV is obtained through the ratio of standard deviation (\(\sigma \)) of the wave power time series [P(t)] and the mean power (\(\mu \)). A lower CV value is preferable to ease the sizing of a wave conversion system and to reduce the possible dumping of the converted wave energy system. The CV is given by:

$$\begin{aligned} \mathrm{{CV}}(P)=\frac{\sigma [f(t)]}{\mu [f(t)]}. \end{aligned}$$
(7)

The SV gives an indication of the seasonal variation that exists within the analysed time frame. It is obtained by subtracting the mean wave power for highest (\(P_{\mathrm{{s(max)}}}\)) and lowest (\(P_{\mathrm{{s(min)}}}\)) energy seasons and diving it by the annual mean wave power (\(P_\mathrm{year}\)). The equation describing SV is given by:

$$\begin{aligned} \mathrm{{SV}} = \frac{P_{\mathrm{{s(max)}}}-P_{\mathrm{{s(min)}}}}{P_\mathrm{year}}. \end{aligned}$$
(8)

Procedure adopted

Fig. 3
figure 3

Flowchart illustrating the main procedures adopted in the paper

Full size image

The flowchart portraying the adopted strategy in this paper is presented in Fig. 3. The intention of the current study involves assessing the wave potential at selected hydrology and coastal environments around Mauritius. Consequently, two sites having fairly distinct wave climate and located in the western part of the island have been selected. These include the sandy shore with reef region of Flic-en-Flac and the estuarine environment of Tamarin. Significant wave height (\(H_{m0}\)) and energy period (\(T_\mathrm{{e}}\)) measurements have been recorded at the two sites through the deployment of a Wave and Tide recorder for the time frames: 2 April–20 April 2007 (Flic-en-Flac) and 28 March 22 April 2014 (Tamarin). The selected time interval for the data as mentioned previously is based on suitability of data available (no missing wave records and no data selected in cyclonic weather conditions), safety issues for divers to access instrument, human activity level which may influence the wave measurements and important wave processes taking place in that specific month of the year. On the eastern region of the island, the mixed shore with reef site of Roches Noires has been chosen for further investigation. Significant wave height and peak period (\(T_\mathrm{{p}}\)) measurements have been acquired from the wave buoy for the time frame 9 February 2012–10 November 2014.

Due to the temporal variability of the phenomena under study, we attempt to compare the wave regimes of the three selected sites on the same time scale. Consequently, April datasets for the years 2012–2014 recorded at Roches Noires have been extracted and averaged (corresponding to day and time of record) to obtain a single ’significant wave height’ dataset from 1 April to 30 April for the region. Using the extracted and averaged dataset alongside with the ’significant wave height’ measurements conducted mostly for the month of April in the two western sites, statistical analysis is performed to probe on the differences among the wave regimes of the three sites investigated. We then proceed to investigate the dependence of western wave climate on Indian Ocean swells and the eastern wave climate on the trade winds in an attempt to characterize eastern and western wave regimes.

Next, we proceed in a case study to investigate the wave energy potential of the western sites of interest. Spectral wave measurements taken by the Wave and Tide recorder on the two western sites are used to produce a time series of the wave power flux prevailing for the month of April. Bivariate histograms showing the occurrence and energy distribution of the two sites are derived. Owing to the promising wave climate of the eastern site of Roches Noires, a long-term wave analysis (3 years) is performed which includes monthly, seasonal as well as wave energy potential computations. Wave power flux have been calculated using significant wave height measurements alongside with energy period computations, derived from peak period dataset and assuming Pierson–Moskowitz spectrum. The occurrence and wave energy power flux matrices are produced to portray the wave energy regimes of the region of Roches Noires. As a final step, we conduct an economical evaluation, technological assessment as well as devise maintenance operations for a proposed wave energy farm to be located at Roches Noires.

Results and discussions

Statistical differences among wave datasets

In view of determining whether significant differences exist among the significant wave height measurements recorded at the three regions, an ANalysis Of VAriance (ANOVA) test is performed for the selected month of April. Table 2 summarizes the main results of the analysis. Initially there are two hypotheses:

  • \(H_0\): No significant difference exists among the significant wave height datasets of spatially distant locations around the island.

  • \(H_1\): Significant differences exist among the significant wave height datasets of spatially distant locations around the island.

Results from Table 2 indicates the fact that the differences in significant wave height measurements taken at these three sites are highly significant (F = 19310.26, P value =0). This, therefore, leads to the rejection of the null hypothesis in favor of the alternative hypothesis.

Having detected significant differences among the datasets, a post-hoc analysis is performed in view of revealing those regions which differed significantly. Comparison tests are employed through the Tukey–Kramer method and the main results are highlighted in Table 3. Through this analysis it is revealed that all sites studied differ statistically in pair-wise comparison from one another. This demonstrates the fairly different wave regimes, attributed to the different hydrologic and coastal environments which have been chosen for investigation.

Table 2 Analysis of variance (ANOVA) of significant wave height measurements for Roches Noires, Tamarin and Flic-en-flac for the month of April
Full size table
Table 3 Post-hoc analysis through the Tukey–Kramer multiple comparisons test performed to reveal significant differences among the pair-wise combinations of regions investigated
Full size table

Since the ANOVA test cannot determine which particular pairs are ’significantly different’, a multiple comparisons of group means test is carried out to support the Tukey–Kramer test previously performed. The multiple comparisons of group means test is used to check for differences among the wave regimes prevailing at the three sites investigated as illustrated in Fig. 4. Also included are the lower and upper limits for the 95% confidence intervals for the true mean difference. The comparison intervals for the wave datasets corresponding to the three different sites do not intersect. This lack of intersection indicates that the means in significant wave height of the three regions investigated are significantly different from each other. However, as observed from Fig. 4, the significant difference is greater for the regions of Flic-en-Flac and Roches Noires or Tamarin and Roches Noires than for the regions of Flic-en-Flac and Tamarin. This reflects the difference in wave regimes that exists between eastern and western waters of Mauritius.

Fig. 4
figure 4

Multiple comparisons of group means test to check for differences among wave regimes of the three sites. Also included are the 95% confidence intervals

Full size image

Distributions of wave measurements

The main distributions of the significant wave height datasets are shown in the boxplots diagram of Fig. 5. It is evident from the figure that the region of Roches Noires witnesses a wave climate characterized by higher wave regimes with a mean value of 2.28 m and larger spread in the distribution than the other regions identified. The estuarine region of Tamarin records the lowest spread with a mean value of 0.34 m. This site detects a significant number of particularly high extreme values (outliers), reflecting on the unusually high occasional wave regimes of the estuarine structure. The region of Flic-en-flac observes a mean values of 0.49 m with occasionally high waves, inherent of its hydrologic and coastal structure.

Fig. 5
figure 5

Boxplot distributions of significant wave height records for three spatially distant sites around the coastal structure of Mauritius for the month of April. Also included is the presence of outliers, indicated by red crosses

Full size image

Variability and statistical interpretations of wave data

Table 4 gives a descriptive statistics of the main distributions for significant wave height (m) at the three sites of investigation. The region of Roches Noires portrays the best wave climate for surface wave energy extraction with high waves having a mean of 2.28 m that can reach a peak value of 3.42 m and the least variation as characterized by the lowest coefficient of variation (14.8%), indicative of the stability of the wave regime in the time frame considered. A low CV is preferable to facilitate the sizing of a wave conversion system and decrease the likelihood of possible dumping of converted wave energy system.

It can be noted from the significant wave height measurements of Fig. 6 that the swell signatures of the regions of Tamarin and Flic-en-Flac differ to some extent. This can be explained through the geographical location of the sites with respect to the incoming swells. The bathymetry of these regions also play a major role in the hydrodynamic processes taking place by surface waves.

The region of Tamarin offers the least likely environment to place a wave energy extraction due to its low wave regimes depicted by the low mean (0.34 m) and high coefficient of variation (79%), delineating the high variations in significant wave height throughout the temporal scale investigated. It can be observed from spectral time series of Fig. 6Ab that the occurrence of swells in the estuary of Tamarin is spasmodic in nature, characterized by sudden outbursts of energy which occurs infrequently. This characteristic is due to the relatively less exposed geographical location of the region pertaining to the incoming swells coming from south, southwest of the island.

The second western site of Flic-en-Flac (Fig. 6A) investigated demonstrated a higher mean in significant wave height (0.49 m) with higher quartiles than the region of Tamarin. Moreover, a lower coefficient of variation (53.1%) was registered at this site, indicating a lower variability and higher stability of the wave regimes for energy extraction as compared to Tamarin. On a comparative basis, the sandy shore with reef site of Flic-en-Flac has higher wave energy potential than the estuarine region of Tamarin despite the influence of both hydrological systems from the incoming swells on the western regions of the island.

Interpretation of the distributions of the significant wave height datasets of the three sites reveal that the western sites of Flic-en-Flac and Tamarin with kurtosis of 6.41 and 7.14, respectively, describe a sharper than normal distribution, characterizing them as leptokurtic. On the other hand, the eastern site of Roches Noires (kurtosis = 2.92) follow a platykurtic distribution with a flatter than normal distribution. All three sites demonstrate positively skewed distributions.

Table 4 Descriptive statistics which includes the mean, standard error mean (SE Mean), standard deviation (SD), coefficient of variation (CV) measured in percentage, minimum (Min.), lower quartile (Q1), median (Med.), upper quartile (Q3), maximum (Max.), skewness (Skew.) and kurtosis (Kurt.) of significant wave height measured in meters at the three sites of investigation for the month of April
Full size table
Fig. 6
figure 6

A Analysis of irregular offshore wave data at Flic-en-Flac for the month of April: a time series of significant wave height; b spectral time series of surface waves recorded; c zoomed images of energetic wave events occurring during the 18 days period at Flic-en-Flac. B Analysis of irregular offshore wave data at Tamarin for the month of April: a time series of significant wave height; b spectral time series of surface waves recorded; c zoomed images of energetic wave events occurring during the 26 days period at Tamarin

Full size image

Dependence of eastern wave climate on trade winds

The wave regime of Roches Noires (Fig. 7a) is dependent on the trade winds originating from the subtropical high-pressure zone and blowing in a southeasterly direction throughout the year. The predominance of the southeast trade winds influences mostly the eastern and southern coastal microclimate wave systems of the island. Fig. 7b shows the incoming wave direction at Roches Noires for the month of April, averaged over 3-years period (2012–2014). The directional rose shows that the incoming waves generally approach in an east, southeast direction with the higher occurrence in the southeast direction with significant wave height peaking at 4 m, supporting the idea that the wave conditions prevailing at this site is mostly due to the prevailing trade winds. It has been reported that these waves typically possess peak wave periods of less than 12 s [24].

Fig. 7
figure 7

Irregular offshore wave records at Roches Noires for the month of April which has been averaged over 3 years (2012–2014): a time series of significant wave height; b wave rose representing the significant wave height approaching in an ESE direction under the influence of trade winds

Full size image

Dependence of western wave climate on Indian Ocean swells

Figure 8 depicts the evolution of the eastward propagating swells from the Atlantic Ocean, after travelling beyond the coasts of South Africa towards the Indian Ocean. Since waves are very directional and tend to get shadowed by land masses, Mauritius situated in the line of sight from those sources end up in the shadow region due to the geographical location of Reunion island. This results in swell height peaking on average for the 3 days near the southern border of Mauritius at about 4.5 m and wave period of 18 s. Further movement of the swell eastwards caused the shadow zone area to reduce, thereby resulting in swells to be observed at higher latitudes on the western flank of the island. Also, upon hitting Reunion Island, much of the wave energy gets dissipated. It is of interest to note that the southern region will witness the first swells followed progressively by regions of higher latitudes.

Ocean swells are wind-waves generated by intense storms that journeys long distances as they propagate away from their generation zone. Unlike the Northern Hemisphere (Northern Atlantic and Pacific Ocean) where land masses provide a barrier which hinders the connection to other ocean basins, the Southern Hemisphere is open to the propagation of southern swell towards all ocean basins due to the fact that a circumpolar oceanic zone free of land barriers connects them together [25]. The wide connection existing among southern ocean basins permits extratropical south Indian Ocean swells originating from extratropical systems from adjacent extratropical areas to freely penetrate adjacent ocean basins. Storms within the extratropical south Atlantic, Indian and Pacific oceans generally propagate towards the east, below 40\(^{\circ }\)S, with maximum storm densities occurring on the western flanks of these ocean basins near 50\(^{\circ }\)S [25].

The geographic location of Reunion Island reduces the wave energy potential of the coasts of Mauritius. Swell heights of the order of 15.0 m, at the generation site is reduced to 6.0 m near Reunion Island [26]. It is revealed that the eastward propagating extratropical South Atlantic swell energy spreads through the entire Indian Ocean, attaining the coasts of Thailand, Indonesia and southwestern Australia and penetrating as far as the Tasman Sea [25]. Owing to the directional nature of waves, the wave climate of the south and southwestern region of Mauritius changes according to the variations in swell events due to being exposed to the incoming swells. Consequently, as revealed in this study, both western regions of Flic-en-Flac and Tamarin are influenced by swell events.

Fig. 8
figure 8

Swell charts delineating the evolution of swell height across the Indian Ocean in temporal scale with zoomed imagery for the scenario close to Mauritius occurring for three selected dates

Full size image

Wave energy case study

From the previous subsection, analysis led us to consider the regions of Roches Noires as potential site for harnessing wave energy. The higher waves and lower coefficient of variation of this site gives it an advantage on the other sites considered. It is of interest, however, to also probe into the wave energy potential of selected sites on the western part of the island, whose wave regimes are dictated by the incoming swells. Having compared the wave regimes of the two sites on the western flanks of the island, we provide a case study for the wave energy potential at the western sites of Flic-en-Flac and Tamarin during the same above-mentioned periods as recorded from spectral measurements of the WTR. These two sites provide contrasting wave regimes due to different coastal environments, bathymetry and geographical location to incoming swells.

The power flux for the region of Flic-en-Flac was computed and the time series presented in Fig. 9a delineates the variations in temporal scales. Statistical interpretation of the time series shows that the mean power flux at this site is 1.369 kW/m with a peak value of 33.7 kW/m recorded for the month of April. A high coefficient of variation (CV = 1.68) and standard deviation (SD = 2.30) indicates the highly variable wave energy regimes of this locality. The quartiles of distribution were calculated and results show that the lower quartile, median and upper quartiles are 0.206, 0.644 and 1.52 kW/m, respectively. The distribution itself is positively skewed (4.67) and leptokurtic (38.1).

The wave variability regimes of a particular sea state at a specific location is often conveyed on a histogram of wave height and energy period. Figure 9b gives the occurrence and wave energy scatters of significant wave height and energy period combinations for the 18 days records taken at Flic-en-Flac. The significant wave height is arranged in 0.05 m bins while energy period is organized in 0.5 s intervals. The color ramp represents the number of wave records falling within the bins, giving an indication on the occurrence of a particular wave state. That of Fig. 9c gives the total wave energy flux of the total number of points falling within the bins.

From Fig. 9b, c, it can be observed that the wave state of maximum occurrence does not coincide with the wave state of maximum total energy flux. The most commonly occurring wave state has significant wave height in the interval 0.25–0.45 m and energy period in the interval 11.2–12.2s while the most energetic wave state occurs for significant wave height in the interval of 0.58 and 0.75m and energy period in the interval 11.8 and 12.8s.

Fig. 9
figure 9

a Time series of wave power flux at Flic-en-Flac. Bivariate histograms showing the occurrence and energy distribution during the 18 days period. The contour colors of figure (b) indicate the frequency of wave records falling within a particular wave state while that of figure (c) represent the total wave energy flux of a particular wave state

Full size image

Variations in power flux for the region of Tamarin is presented in Fig. 10a and statistical analysis shows a mean power flux of around 0.484 kW/m with a peak value of 9.54 kW/m, indicative of the lower potential of this site as compared to that of Flic-en-Flac. The coefficient of variation (CV = 1.85) and standard deviation (SD = 0.894) reflects the relatively stable wave energy conditions prevailing at Tamarin as compared to that of Flic-en-Flac. The lower, median and upper quartiles of distribution was found to be 0.07, 0.133 and 0.426 kW/m, respectively, showing that the major portion of the distribution for wave energy computations at Tamarin lies significantly lower than that at Flic-en-Flac. Similar to the distribution observed at Flic-en-Flac, the region of Tamarin shows positively skewed distribution (3.86) and is characterized as leptokurtic (23.3).

For the case of Tamarin, the significant wave height is arranged in 0.05 m bins while energy period is organized in 0.1 s intervals. It can be observed again that the wave state of maximum occurrence does not coincide with the wave state of maximum total energy flux. The most commonly occurring wave state has significant wave height in the interval 0.15–0.25m and energy period in the interval 5.05–5.15s while the most energetic wave state occurs for significant wave height in the interval of 0.75–0.85m and energy period in the interval 5.25 and 5.30s.

An understanding of the performance of wave energy converters in different wave states is essential for the constructional details, cost and efficiency of the installed device. It would be preferable to install a wave energy converters in a wave state having a maximum total energy flux rather than in one having maximum occurrence.

Fig. 10
figure 10

a Time series of wave power flux at Tamarin. Bivariate histograms showing the occurrence and energy distribution during the 26 days period. The contour colors of figure b indicate the frequency of wave records falling within a particular wave state while that of figure (c) represent the total wave energy flux of a particular wave state

Full size image

Long-term analysis

Figure 11 shows the annual distributions of significant wave height on a monthly basis with standard deviation. It can be observed that the winter half extending from May through October experiences the higher average significant wave height, reflecting on the greater wave power flux as compared to the relatively calm summer half. The highest values of significant wave height were recorded from March to July with a bimodal peak in April (3.42 m) and in July (3.38 m). It is evident from the plot that the peak summer months of November and December record the lowest average significant wave height. The drop in significant wave height during the summer period is due to lower southeast trade wind speeds observed during that same time scale [13].

Fig. 11
figure 11

Average monthly significant wave height distributions for Roches Noires

Full size image

The wave roses showing the summer, winter and annual directional significant wave height measurements averaged over the years 2012–2014 is presented in Fig. 12. It can be observed that the southeast trade winds influences the significant wave height to a greater extent in the winter period with greater occurrence of southeasterly significant wave height measurements. However, on a comparative note, it can be observed that during summer, the magnitude of significant wave height measurements is greater with values peaking at 5–5.5 m as compared to the winter half where the magnitude attains a lower value of 3.5–4.0 m. This reflects on the higher intensity of trade winds in the summer period.

Fig. 12
figure 12

Wave rose showing the magnitude and direction in which the incoming significant wave height is approaching the region of Roches Noires during (a) summer (b) winter (c) annual, averaged over the years 2012–2014

Full size image

The boxplots representing the yearly mean evolution of significant wave height measurements are presented in Fig. 13. Data filtering processes have been performed, with the objective to remove missing data due to faulty instrument prior to boxplot representation. Of the 3 years investigated, the year 2013 records the larger spread in significant wave height measurements. This can be explained on the basis of the passage of cyclone ’Imelda’ within the vicinity of the island. Owing to relatively stable atmospheric conditions, the year 2014 recorded the lower spread of the distributions over the 3-year period. The greater number of high outliers is observed for the year 2012 while the median value over the 3-year period at Roches Noires seem to deviate not by much from the 2 m significant wave height mark.

Taking into consideration the temporal variability of significant wave height measurements, an average has been performed over the 3 years on the temporal basis (corresponding to timestamp records). Each of the yearly significant wave height dataset contained 15,948 records and when averaging the 3 years corresponding to the day and time of the year, results in the average 2012–2014 dataset also containing 15,948 records. From the ’average 2012–2014’ box plot, the median lies near the 2 m significant wave height mark, with upper and lower quartiles corresponding to 2.3 and 1.7 m, respectively.

Fig. 13
figure 13

Boxplots representing yearly distributions in significant wave height at Roches Noires

Full size image

Figure 14a represents a scatter table which displays a better characterization of the composition of the wave energy resource throughout the 3 years. Each power flux was calculated with intervals of \(\delta T_\mathrm{{p}}\) = 2 s and \(\delta H_{m0}\) = 0.5 m. From Fig. 14a, wave energy is mostly distributed between peak period \(T_\mathrm{{p}}\) = 6 s and \(T_\mathrm{{p}}\) = 26 s and significant wave height of \(H_{m0}\) = 1.5 m and \(H_{m0}\) = 5.5 m. From this distribution, the optimal energy is obtained at \(T_\mathrm{{p}}\) = 16 s and \(H_{m0}\) = 5.5 m. When further evaluating the total power flux distribution by including the occurrence for each wave, its optimal distribution shifts to the right as shown in Fig. 14b. This implies that the highest amount of waves which contribute to a maximum energy output lies at \(T_\mathrm{{p}}\) = 26 s and between \(H_{m0}\) = 1.5 m and \(H_{m0}\) = 4.0 m.

Fig. 14
figure 14

Scatter table representing 3 years (a) occurrence wave power matrix (kW/m) (b) total wave energy flux power matrix at Roches Noires from peak period \((T_p)\) and significant wave height \((H_{m0})\)

Full size image

Seasonal variation analysis at Roches Noires shows that the summer season with a SV index value of 34.3, is highly variable as compared to the winter season whose SV value approximates to 5.97. Moreover, the mean wave power observed in the summer season is 28.8 kW/m and is found to be lower as compared to the winter season (31.7 kW/m) averaged over 3 years interval. The winter season with higher observed wave power flux and lower variability demonstrates a higher potential for extracting wave energy for this site.

Feasibility of setting up a wave energy farm

Any area with yearly averages of 15 kW/m has the potential to generate wave energy [27]. As recognized, the yearly average wave resource potential of the region of Roches Noires found to be 29.7 kW/m is much higher than this threshold value and is characterized by low variations throughout the year due to persistent trade winds. A global technical potential of 500 GW is expected for offshore wave energy devices having an efficiency of 40% and installed near coastlines with wave climates of the order of 30 kW/m [28]. This highly encourages the placement of a wave energy converter at that location.

Maintenance operations on wave energy farm

Operation and maintenance are needed to maintain the optimum mechanical performance of the wave farm through an increase in productivity and reduction in running costs of wave energy converters [29]. The design for reliability and maintenance schedules need to be cautious due to the fact that system failures can be aggravated and there may be no appropriate weather window immediately available to retrieve the devices in case of failure [30]. Consequently, the plan to install a wave energy device in the offshore areas of Mauritius should come with an appropriate maintenance strategy. There exists several maintenance strategies for wave energy converters which includes corrective strategy performed after failure or preventive strategy done before a breakdown.

A systematic maintenance strategy exists which is based on systematic maintenance actions performed every 6 months combined with corrective maintenance action performed in case of breakdown. Despite the fact that systematic maintenance strategy presents a wide variety of maintenance actions, it is identified as the most costly strategy [31]. Nonetheless, it would suit the climate of Mauritius since as observed in the results section, the summer season experiences lower average significant wave height, reflecting a lower wave energy flux. Consequently, it would be appropriate to plan proper maintenance strategies in the summer half to be undertaken at intervals of 6 months.

Economic evaluation

Wave energy developers target high economic return with the intention to satisfy investor’s vested interests and generate profits. In addition to expected rate-of-return, investment risks that exist before and after project implementation is an important factor that cannot be neglected [32]. In the pre-construction stage, developers may experience friction with local inhabitants and marine conservation groups pertaining to the implementation of the project. On the other hand, in the post-construction stage, lower than expected energy output and high operations and maintenance costs may pose an economic risk for implementing the project in the waters of Mauritius. Besides, proper infrastructure costs need to be taken into consideration to build a rigid system capable of withstanding cyclonic weather conditions and storm surges to avoid excess expenditures for the repair of damaged systems.

For economic feasibility, wave power plants must be manufactured for an operating lifetime of at least 20 years [33]. The budget allocated to wave energy plant is spent as: pre-operating cost, capital expenditure, operational expenditure and decommissioning costs [34]. Pre-operating costs includes expenditures encountered in pre-construction stage, environmental impact assessment among others. Capital expenditure costs includes the main structure as well as installation expenses. The operational and maintenance costs are crucial for plant lifetime. The whole plant is supposed to be dismantled after 20 years and the decommissioning cost is estimated to be 0.5–1% of the initial investment [35]. According to a study, a 500 MW wave power plant set up in Oregon would entail a combined construction cost estimate of about $750,000/MW [36]. According to the same study, the implementation of such a project could produce over $90 million annually in new tax revenues on a statewide basis [36].

The introduction of a wave energy farm in the vicinity of the island would entail numerous economic benefits in the long run. Integrating wave energy resources in the energy mix of Mauritius would ensure security of energy supply and the transition to greener alternatives. Consequently, in the long run, the island may become less dependent on high costs fossil fuel imports. The higher wave energy potential site of Roches Noires identified, coupled to appropriate maintenance strategies planned are important aspects that contribute to the longevity and economic yield of a typical wave farm to be implemented in that region.

Technological assessment

Several technologies that are capable of absorbing energy from waves and converting it into electrical energy have been developed. However, the selection of appropriate wave device depends on the water depth and the location (shoreline, near-shore, offshore) considered for construction [37]. Classification of wave energy technologies is based on working principles and are mainly grouped into oscillating water column (with air turbine), oscillating bodies (with hydraulic motor, hydraulic turbine and linear electrical generator) and overtopping systems (with low-head hydraulic turbine) [37]. Each of them can be mounted on a fixed structure or placed on a floating platform. The Mutriku Breakwater Wave Plant located in Spain, having an installed capacity of 296 kW from 16 turbines and 16 oscillating water columns, produced and exported over 1.3 GWh of power to the Basque grid during its first 5 years [38]. Nevertheless, the efficiency of energy capture is a major limitation of wave energy converters. According to one study, out of 2700 GW power generated from waves, only about 500 GW can be captured using present technologies [39].

International standardization

For implementing the wave farm in the waters of Roches Noires, the IEC standard guideline (62600-101, 2015) which aims at defining good practices in the field of wave resource assessment needs to be taken into consideration. Having identified the region of Roches Noires as potentially suitable site for installing the wave energy converters, the next phase involves performing a spatial analysis of wave energy resources in that region. The IEC standard guideline establishes a system for estimating, analyzing and reporting the wave energy resource at sites identified having good wave energy resources [40]. The report provides methods regarding data collection and resolution alongside with the development of numerical model for wave energy resource estimation. In the data collection section, the need for preparation of a bathymetry contour map is highlighted and will be used to construct a Digital Elevation Model for the wave propagation model. Moreover, the section includes the fact that archived data may be used as primary data source while wave measurements can be used to validate the numerical model. Additional data which may be of use includes wind, tide, current and water density.

In the numerical model section, production of at least 10 years of sea state data, with wave resource taken as stationary, is required. The minimum frequency for sea state data is one dataset recorded at intervals of 3 h. Guidelines regarding the configuration of boundary conditions, data processing and validation of numerical modelling as well as dealing with missing data are mentioned. The practical implications of the report has been evaluated through comparison with the Biscay Marine Energy Platform (BiMEP) facility which is situated on the Basque coast. Consequently, the case study may be of relevance to the Government of Mauritius or any organizations considering the implementation of a wave farm in the identified site of Roches Noires.

Conclusions

This paper presents an assessment of the wave energy potential of three sites having distinct coastal environments and wave regimes. Two sites located on the western (leeward) side region of the island are observed to be influenced by episodic swell events originating from the Atlantic Ocean with the region of Flic-en-Flac more exposed and the estuarine environment of Tamarin less exposed to the SSW incoming swells. On the eastern side of the island, the region of Roches Noires is observed to have higher wave resource potential with lower variability and higher wave power flux. Wave rose plots depicted the fact that the incoming waves from Roches Noires are influenced by the prevailing southeast trade winds, with the winter season displaying a greater influence owing to the greater occurrence of incoming waves from the south east during that period. The mean high wave power flux registered at Roches Noires (28.8 kW/m in summer and 31.7 kW/m in winter) demonstrates the relatively higher potential of exploiting surface wave energy from this site as compared to the western regions of Flic-en-Flac and Tamarin. Consequently, for the tropical island of Mauritius, efficient harnessing of wave energy will be performed through the installation of wave energy converters around the eastern and southeastern coasts of the island, where the system is influenced by wind–wave generated system as compared to the western coast which is under the influence of extratropical South Indian Ocean swells. Having identified the eastern region of the island as most promising for harnessing energy from waves, further orientations of this research involve performing a spatial analysis of the wave resource potential of this study area through numerical modelling techniques. Numerical simulations coupled to a feasibility study on wave energy penetration in the eastern coasts of Roches Noires will be investigated in the next phase.

Data availability

The data that support the findings of this study are available from the Mauritius Oceanography Institute but restrictions apply to the availability of these data, which were used under approval for the current study, and so are not publicly available. Data are, however, available from the author upon reasonable request and with permission of the Mauritius Oceanography Institute.