Abstract
Electricity remains an essential commodity and is one of the most used forms of energy which can be generated from renewable and non-renewable (re)sources. Resource assessment has always constituted an initial first step in determining the potential of a resource to produce useful energy. In this work, two-dimensional aperiodic tidal series data are assessed using the continuous wavelet transform method (CWT). The data were obtained from the Hydrography Office of the Nigerian Navy (HONN) in Apapa, Lagos, for the period 2011–2015. The sites considered in this work are Apapa Lagos (latitude 6°27.0′N, longitude 3°23.0′E), Lagos Bar (latitude 6°24.0′N, longitude 3°23.9′E), and Bakana New Calabar River (latitude 4°44.0′N, longitude 6°58.0′E). The CWT method, more commonly used for periodic data, was modified and applied to the aperiodic tidal data. A fast and accurate computational MATLAB Toolbox/code [non-uniform continuous wavelet transform (NU-CWT)] was developed to characterize the data to precisely elucidate the results. Furthermore, because investors and developers require information on the economic feasibility of their investments, a levelized cost of energy (LCOE) analysis is also performed to understand the economic implications of the resource. The results indicate technically and economically significant resource potential.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
The oceans which cover more than 70% of the Earth’s surface and with 53% of its population living near a coast are receiving significant and growing attention as a potential source of energy that would contribute to increasing global demand sustainably. Theoretically, the oceans contain an energy source that is far larger than the human race could utilize, though, in practical terms, much of the resource remains inaccessible. Despite the difficulties, several governments and private institutions around the world are revisiting the idea of tidal power as a greener alternative to fossil fuel and nuclear power generation schemes.
Tidal stream energy continues to gain attention as a source of predictable and renewable energy. Tidal streams are very close in concept to traditional wind turbines; however, instead of operating with air currents, they draw energy from water currents/tidal waves. Tides are caused by the gravitational pull of the moon and the sun on the rotating earth. The associated motion of these bodies leads the surfaces of the oceans to be raised and lowered periodically, according to some interacting cycles. These cycles can be categorized as (1) half-day cycles, which are due to the rotation of the earth within the gravitational field; (2) 14-day cycles which are a combination of the gravitational field of the moon and the sun, yielding alternating spring (maximum) and neap (minimum) tides; (3) half-year cycles which are due to the inclination of the moon’s orbit relative to that of the earth, yielding, in general, maxima in the spring tides in March and September; and (4) other cycles such as those more than 19 years and 1600 years due to complex gravitational interactions [1].
Tidal stream energy works much like hydro-electric power (HEP) and wind turbine (WT) systems that use underwater devices that resemble wind turbines and are placed in fast tidal streams to extract energy. An array of these devices is often deployed to deliver significant amounts of energy to the electricity grid. The amount of energy obtainable from a tidal energy power system varies with location and time. A single tidal stream generator is, however, able to produce significantly more power than a wind turbine due to the higher density of water. The output changes as the tide ebb and flood are daily varying by a factor of four over a spring-neap cycle. Nonetheless, tidal energy is highly predictable in both magnitude and timing, more so than the wind and solar forms of energy. Tidal currents are the horizontal components of the flow of water that are associated with propagating waves. We note that in some regards, the velocities can be greatly enhanced and magnified in straits between islands or between islands and mainland [2]. The current in the water is, thus, much more reliable than the wind in the air.
The modern world as we know it today will grind to a halt without the necessary electrical energy infrastructure. Access to stable and secure energy is a key driver of today’s economic prosperity. Most nations today are taking an “all of the above” strategy towards energy security and sustainability; countries are developing every available energy resource within their terrain to meet the growing demand due to population pressures in a sustainable way. Evidently, fossil fuels and carbonaceous forms of energy are no longer the energy of the future. They are neither sustainable nor advantageous to the environment. Even with the price collapse of oil, renewable forms of energy continue to grow in capacity and remain very competitive with conventional forms of energy [3].
The electrical energy problem in Nigeria can be broadly categorized into three main pillars: (1) quantity; (2) reliability; and (3) efficiency. Quantity reflects the supply–demand imbalance, where what is generated and supplied is non-optimal. The supply–demand gap is believed to be the biggest in the world. Reliability pertains to the frequency or regularity of electrical energy supply, whereas efficiency stems from the overall effectiveness of the system to wheel power to the end-users from the source, and the quality of the supplied electricity to be effectively used. Nigeria continues to be ranked as a developing nation, on the whole, due to its poor electrical energy supply. Her generating capacity, which is less than 5000 MW, is much less than the energy produced by less-populous countries, e.g., South Africa, whose capacity is about 50,000 MW. Nigeria produces about 40 kW per thousand people, whereas South Africa produces 270 kW per thousand people. The several phases of electrical energy utilization, that is, generation, transmission, and distribution continue to account for about only 1% of Nigeria’s Gross Domestic Product (GDP). It has been estimated that GDP growth could be increased by as much as 11% if electrical energy supply was regular. Several reforms initiated by past and present government administrations are yet to be fully and more efficiently realized.
From a developer’s and an investor’s perspective, it is paramount to know the effectiveness and economics of utilizing an energy resource for electricity production. The associated costs of renewable energy technologies (RETs) continue to plummet due to improved technologies, regulatory incentives, increasing supply, and, demand for RETs, making them very competitive with conventional forms of energy. To evaluate the economics, the comparison is based on a levelized cost of energy (LCOE) analysis. The LCOE analysis is an approximation that yields a break-even sales price. It allows for the evaluation of any energy resource regarding its cost-effectiveness and goes further to evaluate upfront capital expenditures such as operating costs that need to be spent annually. We determine a price point for utilizing tidal energy in Nigeria and determine the variables that can contribute toward achieving and sustaining grid-parity with traditional grid power costs.
The objectives of concerned scientists, energy enthusiasts, environmentalists, and researchers are to continue to present the many alternatives that are available to alleviate the electrical power problem, which would lead to a more sustainable energy future. Resource characterization constitutes the first step in that approach. Thus, in this work, we perform resource characterization of Nigeria’s tidal energy resources, for selected sites, together with an LCOE analysis of the respective sites. Several studies have been reported on geographical sites in various parts of the world, to the assessment of the potential for tidal current energy utilization [4,5,6,7,8,9]. Tidal current technology continues to progress rapidly particularly in the United Kingdom.
As such, the aim of this work is for resource characterization, and we adopt/adapt a modified continuous wavelet transform method (CWT), applied to three selected sites. To the best of our knowledge, and together with our earlier work [10], it represents the first series of research work characterizing aperiodic tidal data. Most works in the literature are to periodic tidal data. As such analyzing aperiodic tidal data constitutes a knowledge gap and the significance of this work. The novelty/originality here compliments the existing body of knowledge from an international perspective while emphasizing the issues of Nigeria. The modified methodology used in this work was originally developed by Foster for application to astronomical data, and it is explained in detail through examples in Ref. [11]. Foster [11] modified the wavelet method, in particular, continuous wavelet transform, called the modified transform weighted wavelet Z-transform and applied for analyzing irregularly measured astronomical data. Here, we apply Foster’s modification to unevenly spaced or aperiodic tidal data and is discussed further later.
A brief on tidal energy technologies
The tidal technologies available today are (1) tidal range/barrage/reef technology (uses delta difference of low and high tides to generate energy), (2) tidal stream/current technologies (similar to horizontal/vertical axis turbines to generate energy), and (3) hybrid technology (combination use of (1) and (2)) for electricity generation. The reader is referred to [12] for more details on each of these technologies in greater detail. Furthermore, we note that the renewable energy industry employs more than 8.1 million people worldwide as of 2016, a 5% increase from 2015 [13]. As such, tidal energy continues to develop rapidly along with other forms of alternative and renewable energy. To estimate the resource, this work assumes the use of tidal stream technologies in the selected sites evaluated. Tidal stream/current technology works much in the same way as turbines extract energy from the wind. Despite the similarities, the dynamics of flow around wind turbines are significantly different due to the proximity of the free surface to tidal turbines.
Data source
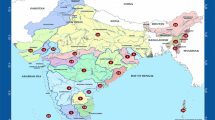
Nigeria is a tropical sub-Saharan West African country that lies between latitudes 4°N and 13°9′N of the equator and longitudes 2°2′ and 14°30′E having a standard atmospheric temperature of ~ 25 °C and P 0 = 1 bar for surrounding pressure, wet and dry seasons, and periodical rainfall throughout the year. The two-dimensional data used in this work were obtained from the Hydrographic Office of the Nigerian Navy (HONN) in Apapa, Lagos State [14]. The sampling period is years 2011–2015. The office maintains records for 19 sites in Nigeria and the data from the sites are unevenly/irregularly spaced (aperiodic) time series data. Observations and measurements were taken 3–4 times a day for each of the 19 locations. Only three of those sites (Apapa Lagos, Lagos Bar, and Bakana New Calabar River) are evaluated in this work for the sake of brevity, and other sites will be subsequently assessed. New Moon and Full Moon constraints were also taken into account in analyzing the data, and these will be elucidated later. Figure 1 shows a map with all the 19 sites.
Methodology
Suppose we have a collection of data f 1, f 2,…, f n at points in time t 1, t 2,…, t n we would like to have a function f(t) that fits the observed data, i.e., f(t 1) = f 1, f(t 2) = f 2, …, f(t n ) = f n . To do this, we will use the Lagrange Interpolation formula which is given by
with t 1 ≤ t ≤ t n and such that L j (t j ) = 1. Hence, the set of data can be represented by the function:
which means that, for every t j , the function corresponds to its data point f j since L j (t j ) = 1. We can then analyze the interpolated data even for points that are greater than the original collection of data sets as long as the time value is equally spaced. Now that we have a function that fits our data we can analyze it using a continuous wavelet transform.
We define the continuous wavelet transform on our function f(t) as:
with a positive σ often called the dilation which allows us to set the width of the wavelet, thus making it possible to focus on a part of the signal, the time shift, τ which allows us to search through the time points on the signal and the complex conjugate of the mother wavelet, ψ which is the envelope of which we enclose the signal. What the continuous wavelet transform (CWT) does is that it maps the function from the time domain onto the (τ, σ) domain which is essentially a time and frequency domain. This is similar to a Fourier transform, except that the Fourier transform only maps the function onto a frequency domain. This gives us a “breakdown” of the frequencies in the signal, but we lose the position of the frequencies, i.e., any information about when a particular frequency occurs is lost. And since most signals often have transient components, a Fourier transform would destroy the information about the position of the transient component. However, with the CWT, the location of all transient frequencies is preserved.
The most widely used mother wavelet is the Morlet wavelet represented by writing:
with frequency, w usually set to 2π and decay, α. The Morlet wavelet is frequently used for acoustic signal analysis.
In computational calculations, the integral of the wavelet transform is replaced by a finite sum:
However, for unequally spaced data this is a very rough approximation, making this approximation undesirable. So, the Morlet wavelet is modified into the abbreviated Morlet wavelet as:
In this case, we need to fit the function using a trial function, φ according to:
which fits the best data record. To compute the coefficients of φ, we need to define the inner product of two functions u and v as:
where w i is the weight assigned to φ given by
The best fit coefficients of the trial function can then be determined by multiplying the inverse of the S-matrix, \(S_{ij} = \langle \varphi_{i} |\varphi_{j} \rangle ,\) by the inner products of the trial function with the set of data collected, f, as:
\(\langle \varphi_{i} |f\rangle\) is just the projection of f on φ i , i.e., the part of f that is on φ i , where f is the function in Eq. (2). This turns out to be the best fit, in the sense that it minimizes the sum of the square of residuals just like the ordinary least square method in regression analysis. For an unevenly spaced data, Foster suggests using three trial functions:
Using the data, we construct the function f(t) according to Eq. (7) and analyze it with the wavelet transform (Eq. 5).
A note on the flow of the methodology
Essentially Foster’s approach is the introduction of a new trial function, \(\varphi_{1}\) in the foregoing equations, since other researchers use the ordinary wavelet transforms. The author [11] then multiplies the data \(f_{1j}\) with the new trial function, which is nothing else, but characteristic function of positive time, and represents the wavelet signal in terms of this product. In other words, to a signal Foster puts in correspondence a time-varying matrix, which is zero for negative time and is the matrix of an aperiodic data for positive time and further manipulates with this matrix. This then becomes the most important moment, whereby if you work in hourly scale (as is the case with the as-received data from HONN), one automatically ignores or loses some information from the data. We do not want to lose any information from the as-received data as that will compromise the effective characterization of the tidal resource. Thus, for convenience, hours within 1 day are converted into minutes, so if the tidal measurement is done at 16:43, in the converted version it is \(16 \times 60 + 43 = 1003.\) Furthermore, in the transformed scale one does not need φ 2 and φ 3 anymore, as shown in the equations, since, as we shall show later, the plots of the signal are already dense enough, and as such φ 1 is sufficient. One can argue at this point that we could reconstruct the signal also in seconds’ scale. We definitely could, but this would not improve the result any further.
Predicting future tidal data with wavelet transform method
Against the universally used harmonic method, and because of evident reasoning earlier explained in [10] it cannot be used for predicting unequally spaced time series. It turns out that Foster’s Z-transform allows for some periodicity analysis of unequally sampled time series [11]. After an average period is derived from given time series, it can be then periodically continued for t > t n and some future predictions can be made. The parameters of statistical weights w k defined in the previous subsection can be changed to make the predictions more accurate. Essentially, this indicates that the methodology discussed and used here can be employed for future tidal prediction where tidal data might be otherwise difficult to obtain. Nowadays, neural networks attract more attention, and some attempts are made to apply them to future prediction [10].
Energy and levelized cost of energy correlations
The kinetic energy of a fluid with mass, m and moving at velocity, v is given by
and power is the rate of change of the kinetic energy, which gives us:
with dm/dt the mass flux given by:
where ρ is the density of water and A is the turbine aperture. Therefore, given v(t) which is the instantaneous water velocity at time t, the power density has to be integrated over the desired time scale represented as:
And we can see that the power density is proportional to the cube of the velocity. The velocity is approximated via the time derivative of the signal from the data. Thus, the amount of electricity generated in a year, α t, can be written with the appropriate constants as:
where C i is the index of energy alterations due to device interactions and is usually set to 1 [15], and C p is the product of the turbine and power equipment efficiencies or the power coefficient of tidal stream turbines which is in the range of 0.35–0.50 [7, 16]. An operational year is considered to have 340 days [6, 17]. Such reductions correspond to downtime of the system due to operational and maintenance works. The prospect of tidal stream energy for large-scale commercial power production depends on cost as measured by the levelized cost of energy or LCOE. With this, we can calculate the cost of electricity, P E in a year as [15]:
where r is the discount rate, β t is the capital expenditure for year t, γ t is the operating and maintenance and operating cost for year t, and T is the lifespan of the tidal stream generator. For this study, T = 5 (2011–2015). The corresponding capital expenditure rate used in this study is approximately equal to β t = USD 5.6 m/MW, while operation and maintenance costs are taken equal to γ t = USD $0.08 m/MW. The discount rate most often used in LCOE assessments is 10% [15]. For further insight, we refer the reader to [18].
Results and discussion
In the following subsections, we present and discuss findings of the three sites studied in this work. The computations were carried out using MATLAB.
Apapa, Lagos (lat 6°27.0′N, long 3°23.0′E)
In measurements carried out in Apapa Lagos for the years 2011 and 2012, the tidal data exhibit a periodicity of ~ 15 days between the higher and lower variability, and there is a correspondence between the higher variability stages and both the new and full moon conditions. Until approximately the middle of the year, the full moon presents greater variability than the new moon while there is an inversion of the trend after mid-year where new moon days show higher variability than the full moon days.
For the year 2013, there appears to be an even trend between new moon and full moon days for the first ~ 150 days. The middle of the year, however, shows full moon days with higher variability than new moon days, albeit with lower tidal height measurements. For the year 2014, new moon days are more pronounced than full moon days in the early months of the year, with an inversion in the middle of the year, and then the trend evens out towards the end of the year. For the year 2015, new moon days show higher variability than full moon days in the early months of the year. An inversion occurs in the middle of the year, whereby full moon days show greater variability than new moon days until the end of the year. Lastly, there is a yearly trend that indicates that the lowest tidal records appear in the middle of the year, which coincides with the inversion of the variability pattern between New Moon and Full Moon (see Figs. 2, 3, 4, 5, 6). Furthermore, we consider the mean velocity profiles of the tides, as an economically viable tidal stream has a range of 2–3 m/s or a power density of 1 kW/m2 or above, with exceptionally strong sites exceeding 5 kW/m2 [19].
Figures 7, 8, 9, 10 and 11 show the mean velocity profiles for Apapa Lagos where we observe the positive velocity to be in the range of 0.5–10 m/s and the negative velocity to be in the range of 0.4–13 m/s. The positive velocity reflects the flood dominance, while the negative velocity reflects the ebb dominance. Given the observed velocity range, Apapa Lagos appears to offer a viable tidal stream.
Lagos Bar (lat 6°24.0′N, long 3°23.9′E)
For the year 2011, the first few months show similar variability between new moon and full moon days with new moon days being dominant until the middle of the year. The lowest tidal readings are shown to occur in the middle of the year whereas, toward the end of the year, an inversion occurs whereby full moon days are dominant on new moon days. For the year 2012, full moon days are dominant in the early months of the year. The middle part of the year also reflects lower tidal readings. Similar to the year 2011, an inversion occurs whereby new moon days show higher variability in the latter part of the year. In 2013, there is a relatively similar trend between full and new moon days in the early months of the year. The middle part of the year reflects the lowest tidal measurements, whereas, toward the end of the year, a similar trend is observed between new moon and full moon days. The year 2014 shows that new moon days have higher variability early in the year than full moon days. The middle of the year shows reductions in tidal readings whereas an inversion occurs later in the year, with full moon days showing greater variability than new moon days. It is observed that for the year 2015, new moon days show greater variability early in the year, depressed tidal readings in the middle of the year and an inversion that reflects full moon days with higher variability than new moon days in the later part of the year (see Figs. 12, 13, 14, 15, 16).
The mean velocity profiles for the period 2011–2015 for this site are shown in Figs. 17, 18, 19, 20 and 21. These patterns are essential for tidal stream energy and reflect the vast potential for tidal power in Nigeria. The negative velocity shows a range of 0.5–11 m/s, whereas the positive velocity shows a range of 0.5–10 m/s. Again, this represents a viable tidal stream.
Bakana New Calabar River (lat 4°44.0′N, long 6°58.0′E)
For this site, the year 2011 data show that full moon days show pronounced variability than new moon days in the first few months of the year. The middle part of the year shows slightly lower tidal readings. Towards the end of the year, there is an inversion that indicates that new moon days have a higher variability than full moon days. In the year 2012, however, full moon days appear to be dominant throughout the entire year. This is a notable difference for the year 2012 among the three sites considered in this work. The middle part of the year 2012 also shows slightly lower tidal measurements, which is consistent with other locations considered. The year 2013, similar to the year 2012, also shows full moon days to be dominant throughout the entire year with slightly lower tidal measurements in the middle of the year. This further demonstrates the aperiodic character of the tidal measurements of Nigeria. The year 2014 shows new moon days to be dominant than full moon days in the first few months, with lower tidal readings in the middle part of the year. An inversion then occurs, showing full moon days to be more dominant than new moon days toward the end of the year. The year 2015 also follows a similar pattern to the year 2014 (see Figs. 22, 23, 24, 25, 26). The extraordinarily low tidal height in Fig. 24 on day ~ 135 is simply an outlier from the obtained data.
The mean velocity profiles for the period 2011–2015 for this site are shown in Figs. 27, 28, 29, 30 and 31. The negative velocity shows a range of 0.5–18 m/s, whereas the positive velocity ranges between 0.5 and 10 m/s. As such the observations reported in this work bode well for the exploitation of tidal energy in Nigeria.
Levelized cost of energy (LCOE) estimations
As mentioned earlier, the associated costs of RETs continue to plummet, making them very competitive with conventional forms of energy. To evaluate the economics, we carry out an LCOE analysis. Table 1 shows the estimates for the three sites for the whole period of the functionality of the tidal sites, i.e., for 2011–2015. We note that due to the observed periodicity of data from all locations, LCOE will be the same for the next 5, 10, and 15 years in the ideal sense. The results of Table 1 show that these sites are efficient for energy production since they fall within the range (Table 2) of other forms of energy. Table 2 shows LCOE costs (average cost with no subsidies) developed by the US Energy Information Administration (EIA) in August 2016, over a 30-year period for energy sources that will be brought online in 2022 [20]. CCS in Table 2 implies Carbon Capture and Storage, otherwise referred to as sequestration of carbon in remote underground locations. The cost estimates are further buttressed in private communications with the Nigerian Electricity Regulatory Commission (NERC). Summarily, LCOE is computed for the whole period of the functionality of the tidal sites; that is 5 years. Due to the notable periodicity of data from all sites, in the ideal sense, LCOE will be the same for the next 5, 10, 15 years. An LCOE sensitivity study has been performed in the work of Ref. [15], and as such their findings would also apply to this work within reason.
Conclusions
Tidal power remains a yet to be fully exploited source of clean, renewable, and reliable energy, not just in Nigeria but also across many parts of the world where tidal energy potentials have been characterized to be significant. The UK-based Carbon Trust, for example, estimates that the global tidal energy market will be valued at about US $166 billion by 2050 [21, 22]. No one energy resource is a silver bullet; however, tidal energy can form a part of the repertoire of low-carbon impact, sustainable, and environmentally friendly power generation schemes. It is, indeed, an attractive option for a power-hungry world faced with numerous challenges of present-day power generating systems. The success of HEP and WT technologies establishes confidence for utilization of tidal energy technologies.
Our objective was to characterize the tidal energy resources of coastal sites in Nigeria. A novel methodology for aperiodic data was effectively applied to aperiodic tidal data series of Nigeria. Key findings in this work indicate that:
-
The tidal resource of the three sites assessed is recoverable in an economical way.
-
The tides in Nigeria are mixed semidiurnal tides, generally having two high and two low tides most of the year, with significant disparity between successive tides.
-
The LCOE estimates are favorable and comparable to estimates anywhere in the world and other energy technologies.
-
There is a notable yearly trend that shows that the lowest tidal records appear in the middle of the year (approximately between day 140 and 220), which coincides with the inversion of the variability trend between New Moon days and Full Moon days. These sites are summarily efficient for energy production.
-
Lastly, our findings offer developers and investors a way to better plan for exploitation of the resource through feasibility studies and site assessment plans.
We note that we do not discuss in detail the electrical energy generation variation of the tidal sites. This is deliberate to perform dense and high-order CFD analysis in the future to ascertain the resource potential fully. However, to establish some context, if we assume/consider the Atlantis AR1500 tidal turbine, for example, having a turbine rotor diameter of 18 m, and a swept area of 254.47 m2, a modest/conservative velocity estimate of 2 m/s, annual energy output would be 391 MW h. Further assuming a deployment of 40 tidal turbines at any of the respective sites, annual total tidal energy output by all turbines would be ~ 15.6 GW. These sites thus have the potential to deliver enormous amounts of energy.
Together with recommendations presented in our earlier work [10], it is further recommended that for an optimal approach, the developing nation of Nigeria should take measures to proactively balance and diversify her energy portfolio for economic and environmental sustainability and to increase usage efficiency. Utilization and deployment of tidal energy in Nigeria will constitute another component to the energy mix, one that is particularly more reliable than wind energy.
References
https://www.saylor.org/site/wp-content/uploads/2010/11/BIO308-Wiki-Tide.pdf. Last accessed 14 Jan 2017
https://core.ac.uk/download/pdf/280366.pdf. Last accessed 14 Jan 2017
http://www.renewableenergyworld.com/articles/2016/05/moving-offshore-the-future-of-tidal-energy.html. Last accessed 14 Jan 2017
Lewis, M., Neill, S.P., Robins, P.E., Hashemi, M.R.: Resource assessment for future generations of tidal-stream energy arrays. Energy 83, 403–415 (2015)
Gonzalez-Gorbena, E., Rosman, P.C.C., Qassim, R.Y.: Assessment of tidal current energy resources in Sao Marcos Bay, Brazil. J. Ocean Eng. Mar. Energy 1, 421–433 (2015)
Vazquez, A., Iglesias, G.: Capital costs in tidal stream energy projects—a spatial approach. Energy 107, 215–226 (2016)
Vazquez, A., Iglesias, G.: LCOE (levelised cost of energy) mapping: a new geospatial tool for tidal stream energy. Energy 91, 192–201 (2015)
Guillou, N., Chapalain, G.: Assessing the impact of tidal stream energy extraction on the Lagrangian circulation. Appl. Energy 203, 321–332 (2017)
Guillou, N., Chapalain, G., Neill, S.P.: The influence of waves on the tidal kinetic energy resource at a tidal stream energy site. Appl. Energy 180, 402–415 (2016)
Amoo, L.M., Layi Fagbenle, R.: On the application of continuous wavelet transform method for energy resource assessment of aperiodic time series tidal data and LCOE analysis in tropical Nigeria. Paper presented at the SOLARIS Conference 2017, Brunel University London, 27–28 July 2017
Foster, G.: Wavelets for period analysis of unevenly sampled time series. Astron. J. 112, 1709–1729 (1996)
International Renewable Energy Agency (IRENA). Tidal energy technology brief, June 2014. http://www.irena.org. Last accessed 2 Jul 2016
IRENA—Renewable Energy and Jobs—Annual Review 2016. http://www.irena.org/menu/index.aspx?mnu=Subcat&PriMenuID=36&CatID=141&SubcatID=2729. Last accessed 2 Jul 2016
Nigeria Navy Hydrographic Office. Apapa, Lagos, Nigeria
Vazquez, A., Iglesias, G.: Grid parity in tidal stream energy projects: an assessment of financial, technological and economic LCOE input parameters. Technol. Forecast. Soc. Chang. 104, 89–101 (2016)
Lim, Y.S., Koh, S.L.: Marine tidal current electric power generation: state of the art and current status, renewable energy. In: Hamons, T.J. (ed.) InTech (2009). ISBN 978-953-7619-52-7
Vazquez, A., Iglesias, G.: Device interactions in reducing the cost of tidal stream energy. Energy Convers. Manag. 97, 428–438 (2015)
Hearps, P.M.D.: Renewable energy technology cost review. Melbourne Energy Institute. Technical Paper Series (2011)
Hagerman, G., Polagye, B., Bedard, R., Previsic, M.: Methodology for estimating tidal current energy resources and power production by tidal in-stream energy conversion (TISEC) devices. Rev 2 DRAFT. 14 June 2016
US Energy Information Administration. https://www.eia.gov/outlooks/archive/aeo16/pdf/electricity_generation_2016.pdf. Last assessed 3 Aug 2017
[https://tethys.pnnl.gov/publications/methodology-estimating-tidal-current-energy-resources-and-power-production-tidal-stream]. Last assessed: 15 Oct 2016
https://www.asme.org/engineering-topics/articles/energy/scotland-gets-serious-tidal-energy. Last accessed: 30 Oct 2016
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to urisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Amoo, L.M. Techno-economic assessment of energy production potential from tidal streams in Nigeria. Int J Energy Environ Eng 9, 81–98 (2018). https://doi.org/10.1007/s40095-017-0256-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40095-017-0256-2