Abstract
Parabolic trough collector is an emerging solar technology for achieving the sustainability. Numerous studies have been focused on their performance evaluation and many techniques have been suggested for improving their thermal efficiency. The objective of this paper is to determine the impact of various thermal enhancement techniques on the thermal efficiency improvement of the PTC. The most usual techniques for increasing the thermal performance of parabolic trough collectors are the use of inserts, internal fins, metallic foams and the dimpled absorbers. A parametric analysis is conducted using different values of the thermal enhancement ratio (Nusselt number to the Nusselt number of the smooth absorber case). According to the final results, the thermal efficiency enhancement can reach up to 2% when the Nusselt number is about 2.5 times greater compared to the reference case and the inlet temperature is equal to 600 K. Moreover, in this case, the thermal losses are approximately 22% lower than in the respective reference case. For higher Nusselt number ratios, the thermal enhancement presents relatively small increase. This analysis is performed with a developed thermal model in Engineering Equation Solver (EES) which is validated with the literature results.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Renewable energy sources are promising solutions for facing the recent worldwide problems as the fossil fuel depletion [1], the climate change [2] and the increasing energy demand [3]. Solar energy is one of the most reliable choices among the renewable resources because this energy source can be converted into useful heat or electricity [4,5,6,7]. Numerous applications use solar energy for covering their energy needs. Solar energy is exploited for power production with photovoltaic panel and with concentrating solar collectors coupled with Rankine, Brayton or Stirling cycles. Moreover, solar energy is utilized for many other applications as hot water production, industrial heat production, desalination, cooling, space heating and methanol reforming [8, 9].
Solar collectors are the devices which are used for capturing the incident solar irradiation and to convert it to useful output. Parabolic trough collector (PTC) is the most mature solar technology for utilization in a great range of applications of temperatures up to 400 °C [10, 11]. The usual working fluids in PTC are water/steam, thermal oils and molten salts, as well as there are some applications with gas working fluids (air, nitrogen, helium and carbon dioxide) [12,13,14,15,16]. The cost of PTCs is reasonable and it is close to 200 €/m2 for great scale installations and thus PTCs are more competitive choices compared to other solar technologies. However, the sustainability of PTCs is depended on their thermal performance which directly indicates the useful energy production amount.
In this direction, numerous ways for enhancing their performance have been studied in the literature. Many ideas have been proposed and the main goal of them is to increase the heat transfer rate inside the absorber of the PTC in order more energy to be transferred to the heat transfer fluid [13, 17]. In other words, these ideas goal to increase the Nusselt number inside the flow and thus many ideas from the heat transfer science have been applied in PTCs. Furthermore, the heat transfer enhancement in PTC is able to reduce the temperature gradients in the circumferential temperature distribution of the absorber which leads to higher thermal stresses and to greater deformation problems [13, 18].
In the first category of literature studies, the use of internally fin absorbers is examined. Gong et al. [19] investigated the impact of pin fin arrays inside a PTC. They found small enhancements in Nusselt number up to 5%. Benabderrahmane et al. [20] examined a similar idea using to greater fins in the low part of the absorber. They found that the Nusselt number can be enhanced up to 80%. Bellos et al. [21, 22] investigated the use of internally finned absorbers operating with gas working fluids and they finally found 100% enhancement in heat transfer coefficient and consequently in the Nusselt number. According to their results, the thermal efficiency can be enhanced up to 3–4%.
The next category of studies examines modifications in the absorber surface. Wang et al. [23] studied the use of an asymmetric outward convex corrugated tube in PTC. The achieved Nusselt number was about 1.2 times greater than the smooth case. Bellos et al. [24] examined the use of converging–diverging absorber tube geometry for operation with thermal oil. They found 25% enhancement in the Nusselt number and thermal efficiency enhancement up to 4%. Huang et al. [25] examined a dimpled PTC and they found that the deeper dimples lead to 1.4 times greater Nusselt ratio compared to the respective smooth case.
The last category of literature studies examines the use of inserts inside the tube to the turbulence to be increased. Kumar and Reddy [26] examined the insert of porous discs vertical to flow and they proved 64% enhancement in Nusselt number. Mwesigye et al. [27] examined the use of wall-detached twisted tape inserts and they found that this method leads to 2.7 times greater Nusselt number and to 5% increase in thermal efficiency. Jaramillo et al. [28] found that the twisted tape inserts lead to 190% increase in the Nusselt number with 3% thermal efficiency enhancement. Too and Benito [29] conducted a comparative analysis of twisted tape insert, helical coil/wire insert, dimpled tube and porous foam inside a PTC operating with air, helium and carbon dioxide. According to their results, the Nusselt number enhancement is found 300, 200 and 100%, respectively. Using the thermal performance index criterion, they selected the dimpled tube as the best case and they found 0.8% thermal efficiency enhancement with this technology. Wang et al. [30] examined the use of metal foams in PTCs for steam generation. They proved that the Nusselt number can be about eight times greater than the empty tube, while huge pressure losses are found.
As it is obvious from the previous literature review, many thermal enhancement techniques have been evaluated in the literature. These studies present mainly results about the Nusselt number enhancement and they are not focused on the thermal efficiency enhancement of the PTC which is the main goal for the PTCs. In some cases, the Nusselt number enhancement is very small and in others has great values. This study comes to present with a clear and systematic way the relationship between the Nusselt number enhancement and the thermal efficiency enhancement. The results of this study indicate which Nusselt enhancements lead to adequate thermal efficiency enhancement. This knowledge makes easier the selection of thermal enhancement methods and clearly proves the need for Nusselt enhancement up to a limit. More specifically, this study makes clear the thermal efficiency enhancement margin for every thermal enhancement method if the increase in the Nusselt number is known. The module of the LS-2 PTC is used in this study which is a usual choice in similar studies about PTCs. The analysis is performed with a developed thermal model in Engineering Equation Solver (EES). This thermal model is validated with the literature results and it is can be assumed as reliable.
Materials and methods
The examined parabolic trough collector
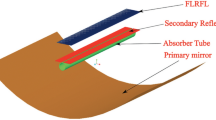
In this section, the examined PTC is presented. LS-2 PTC is selected to be examined as a usual PTC in similar studies. There is great knowledge about this module and the results can be easily compared with the literature. Moreover, there are adequate results for the validation of the developed model. Figure 1 presents the LS-2 designed in SolidWorks.
The receiver of this collector is an evacuated tube collector. The absorber of this collector is made of stainless steel and the cover is made of glass. There is vacuum (extremely pressure close to 0.01 Pa) between these materials to achieve approximately zero convection losses. Table 1 gives the main information about the examined PTC [31]. The concentration ratio of this collector is about 22.74, its aperture is 39 m2 and the optical efficiency is close to 75.7%. The reflectance has been selected close to 83% to take into account various errors about racking, clearness and manufacturing errors. The intercept factor is taken close to 1 because of the accurate design of the examined PTC [31].
Mathematical formulation
This section includes the developed mathematical modeling for the simulation of the PTC. Equations about the energy balances are given, as well as for the parameters which demanded in the present modeling. More information about the present mathematical modeling can be found in Refs. [14, 15].
The available solar energy on the collector aperture is the product of the direct beam solar irradiation (G b) and of the collector aperture (A a), according to Eq. 1 [14],
The absorbed energy from the absorber (Q abs) is given as [14]
The optical losses are calculated with the optical efficiency (η opt). This parameter is the product of various parameters, as they are given below [31]:
In the present study, zero incident angle is selected and thus the incident angle modifier K(θ) is taken equal to one. This assumption is made in order the emphasis to be given to the thermal behavior of the PTC.
The useful energy production (Q u) is calculated by the energy balance in the working fluid volume, as it presented by Eq. 4 [15]
The thermal efficiency (η th) of the solar collector is the ratio of the produced useful heat to the available solar energy (Q s) [15],
The useful heat can be also calculated by examining the heat transfer between the absorber tube and the working fluid. The mechanism of the heat transfer is the convection which is modeled using the heat transfer coefficient (h), as it is presented below [15]:
The mean fluid temperature (T fm) can be calculated as the mean value of the inlet (T in) and the outlet (T out) fluid temperatures [15],
The heat transfer coefficient can be estimated using the Nusselt number (Nu) which is defined as
For turbulent flow and smooth absorber (Re > 2300), the Nusselt number (Nu 0) can be calculated using the Dittus–Boelter equation [32]. In the present analysis, only turbulent conditions are examined and thus equation only for the turbulent region is given,
The Reynolds number (Re) and the Prandtl number (Pr) are defined according to the following equations. The Eq. 10 about Reynolds number corresponds to tubular absorbers,
The developed thermal model of this study is based on the energy balance on the absorber tube. The absorbed solar energy (Q abs) is separated into useful heat (Q u) and to thermal losses (Q loss), as Eq. 12 indicates
The thermal losses of the solar collector can be calculated as [15]
Equation 13 gives the thermal losses of the absorber to the cover in steady-state conditions [15]. This equation expresses the thermal losses of the absorber with mean temperature (T r) and the cover with mean temperature (T c). The absorber emittance (ε r) is taken as a function of its temperature level. For cermet coating, the following equation is selected is given below [33]:
The thermal losses of the cover to the ambient are calculated as [34]
These thermal losses have radiation and convection part. For the radiation part, the sky temperature (T sky) is estimated as [35]
The heat convection coefficient between cover and ambient (h out) is calculated according to Eq. 17 [34]. For wind velocity (V wind) close to 1 m/s, this equation indicated that the heat convection coefficient is close to 10 W/m2 K,
Moreover, it is useful to give the way that the volumetric flow rate (V) is calculated using the mass flow rate (m). The units are given in this formula to present it in a clear way,
At the end of this section, equations about the exergetic analysis of this collector are given. The exergy flow of the incident solar irradiation (E s) is calculated according to the Petela model [36]. This modeling is accurate for undiluted solar irradiation and it is ideal for the present case because the PTC utilizes only the solar beam irradiation. The sun temperature (T sun) is taken equal to 5770 K which is a representative value for the sun temperature in its outer layers,
The useful exergy output (E u) can be calculated as [15]
The exergetic efficiency of the solar collector (η ex) is the ratio of the useful exergy production to the exergy input [15],
Model validation
The developed thermal model of this study is validated using the literature data. These data are given in Ref. [33] and they have used for validation proposes in many studies as the Ref. [31]. The solar collector is tested under different operating conditions, as they are given in Table 2. The working fluid is Syltherm 800 and its properties are taken from Ref. [37].
Table 2 proves that the deviation in the outlet temperature calculation is 0.23% and in the thermal efficiency calculation is 2.12%. These small deviations prove the high accuracy of the developed thermal model. Moreover, it is important to state that this model has been used in many other studies as in Refs. [14, 15] where its validity has also proved.
Followed methodology
The objective of the present work is to determine the thermal efficiency enhancement of the PTC when there is an increase in the Nusselt number. The increase in the Nusselt number can be achieved using a thermal enhancement method, as the described methods in “Introduction”. For example, the use of internal fins, dimpled absorber, twisted tape inserts, helically fins and metal foam are usual techniques which can improve the Nusselt number many times. In the present study, the Nusselt number enhancement is approximated with a simple and direct way by inserting the Nusselt number ratio (R) in our study. This ratio is equal to the Nusselt number of the examined case with thermal enhancement method to the Nusselt number for the smooth case,
This ratio is equal the heat transfer coefficient ratios (see Eq. 8) approximately because the thermal properties are the same between the cases. The factor (R) takes values from 1 to 5 in this study, covering a great range of thermal enhancement cases as they are described in “Introduction”. The cases with smooth and empty absorbers as the module of LS-2 PTC are the reference cases and they are symbolized with the subscript “o”.
The thermal modeling has been developed in Engineering Equation Solver (EES) by F-Chart [38]. More information about this modeling, as well as a flow chart, can be found in Refs. [14, 15]. The developed model is based on the mathematical equations which have been presented in “Mathematical formulation”. It has been assumed that the absorber temperature is uniform (T r) in every case and the fluid properties have been calculated at the mean fluid temperature (T fm). These assumptions have been used in Refs. [14, 15], as well as in Refs. [39, 40]. The examined PTC is only a module and it is not very long, as the solar fields and thus these assumptions are reasonable and acceptable. Moreover, the fluid temperature variation from the inlet to the outlet is not very high (generally up to 10 K), the fact that proves that the selection of the thermal properties in the mean fluid temperature is acceptable. The working fluid is Syltherm 800 which can operate in liquid phase from − 40 to 400 °C under a low pressure of 15 bar [37]. It is important to state that this study does not examine the pressure losses because they are extremely low for operation with liquid working fluid [15].
The pressure losses can be increased by the use of the thermal enhancement methods but they are too low and they do not play an important role. The simultaneous evaluation of the Nusselt number increase and of the pressure losses increase has been evaluated from many other literature papers, as the majority of is described in “Introduction”, and it is not the objective of this work.
This work is focused on the thermal efficiency enhancement using different enhancements in the Nusselt number. Practically, the PTC is a special case for examining this phenomenon and it presents differences with the usual applications with heat transfer in usual heat exchangers. The amount of the heat transfer is depended on the heat transfer coefficient (~ Nusselt number) and of the tube temperature (receiver temperature—T r). Equation 23 gives the thermal efficiency enhancement using these parameters:
According to Eq. 23, higher (R) and higher (T r − T fm) increases the thermal efficiency enhancement. By assuming that the mean fluid temperature is approximately constant (a reasonable assumption for operation with high flow rates in the turbulent region), higher (T r) is needed for higher thermal efficiency enhancement according to Eq. 23. However, higher receiver temperature means higher thermal losses and lower useful heat amounts (see Eqs. 12 and 13, and assume constant T c). These reverse factors make the situation complicated and an analysis as the present is demanded. In every case, the receiver temperature is calculated using the equations of the “Mathematical formulation” and the thermal enhancement is calculated. Different Nusselt number ratios are used for flow rate equal to 100 L/min. This flow rate is adequate for achieving high performance, as it will be proved in “Results”.
In this study, the ambient conditions have been kept constant in order the emphasis to be given in the thermal enhancement method investigation. The solar collector is examined at the higher possible solar irradiation levels, a usual technique in similar studies. Table 3 includes the input values in the model.
At the end of this section, it is important to note which are the input and the output parameters of the developed model. The solar irradiation, the ambient temperature, the inlet fluid temperature, the flow rate and the parameter R are the inputs. The main outputs are the fluid outlet temperature, the thermal efficiency, the exergy efficiency, the thermal losses and the receiver mean temperature. The developed program in EES includes all the given equations of “Mathematical formulation”. These equations have been solved by the EES solver with a maximum relative error up to 10−6.
Results
Preliminary results of this analysis
This section is devoted to presenting the preliminary results of this paper. Figure 2 gives the collector thermal efficiency for various flow rates and inlet temperature levels. These results are obtained for the reference case which is the smooth absorber without any enhancement method or modification. In this case, the Nusselt number ratio (R) is equal to 1. The reason for including the Fig. 2 in this analysis is for determining an adequate flow rate for achieving high performance. The flow rate of 100 L/min is an adequate value which leads to high efficiency. Generally, higher flow rates are able to increase the pumping work and it is better not to be selected. Moreover, the literature data of Ref [33] indicates a relatively low flow rate of about 50–60 L/min. Thus, the selection of 100 L/min is a reasonable solution taking into account the previous statements.
The next part of this study is devoted to presenting results for various inlet temperatures and different Nusselt number ratios. In all the following cases, the flow rate is equal to 100 L/min, as it is stated before. Figure 3 gives the thermal efficiency curves for various cases with and without thermal enhancement. The curve with the blue color indicates the reference case, while the dotted black curves are the maximum possible achieved thermal efficiency. The maximum possible thermal efficiency is the case with infinite values of the Nusselt number ratio and in this case, the receiver temperature is approximately equal; to the mean fluid temperature. All the other cases represent cases with thermal enhancement methods and they are between the reference case and the maximum thermal efficiency case. Higher values of Nusselt number ratio lead to higher thermal efficiency, but after a limit (maybe R = 2–3) the curves are close to each other. This situation will be examined with more details in Figs. 7 and 8. Moreover, it is important to state that the thermal efficiency is getting lower with the increase of the inlet temperature and all the curves have similar trends. More specifically, these curves are approximately second-order polynomials.
Figure 4 exhibits the results of the thermal losses for all the respective cases of Fig. 3. It is obvious that higher thermal losses are associated with lower thermal efficiency, as the following equation indicates:
It is noticeable that the thermal efficiency presents a small variation with the inlet temperature (64–75%), while the thermal losses present from 10 W up to 4500 W. This result shows that an increase in the thermal losses leads to a relatively smaller reduction in the thermal efficiency.
The higher thermal losses are associated with higher receiver temperatures, as shown in Fig. 5. In Fig. 4, the thermal losses curves are second-order polynomials, while the curves of receiver temperature are approximately linear, according to Fig. 5. This figure indicates that the reference case presents the maximum receiver temperature and the cases with infinite Nusselt number ratio present the lowest receiver temperature close to the mean fluid temperature. For operation with Syltherm 800, the mean fluid temperature is close to the inlet temperature with a difference up to 5 K.
The exergetic efficiency is illustrated in Fig. 6. Practically, the cases with higher thermal efficiency are associated with higher exergetic efficiency. The exergetic efficiency of this collector has an increasing rate which is getting lower with the increase of inlet temperature. Practically, for inlet temperature close to 650 K, the exergetic efficiency is approximately maximized and it takes values close to 40%. More specifically, for the theoretical case with maximum performance (black dotted line), the exergetic efficiency is 38.73%, while for the reference case is 37.01%. The reason for the reducing rate of the exergetic efficiency increase is the reduction in the thermal efficiency, according to Fig. 2. At this point, it would be valuable to make a deeper analysis, using some extra equations. The useful exergetic efficiency can be written as Eq. 25 indicates, using the Eqs. (4, 19, 20, 21),
With the η pet to be the Petela factor for exergetic efficiency,
And the T m,ex to be the mean exergetic temperature,
The mean exergetic fluid temperature is close to the inlet temperature for the examined cases. This observation proves that the thermal efficiency is depended on the thermal efficiency (η th) and the exergetic factor (1 − T am/T m,ex), as Eq. 25 shows. Higher values of inlet temperature lead to lower thermal efficiency (see Fig. 2) and to higher values of the exergetic factor (1 − T am/T m,ex). These contrary factors make the exergetic efficiency to present approximately maximum point for inlet temperature close to 650 K.
Thermal enhancement analysis
In this section, results about the thermal performance and thermal enhancement of PTCs are given with more details. Figures 7 and 8 give results about the thermal efficiency of the examined PTC for various Nusselt number ratios and inlet temperatures equal to 300, 400, 500 and 600 K. Figure 7 proves that higher Nusselt ratio leads to higher thermal efficiency but after a limit, the increase is negligible. More specifically, for Nusselt ratios after 2.5, there is no practical increase in the thermal efficiency. Furthermore, Fig. 8 illustrates the thermal efficiency enhancement percentage for various Nusselt number ratios. It is again obvious that the Nusselt number ratio after the value of 2.5 does not create significant enhancement on the thermal performance. It is essential to state that the thermal enhancement is greater for operation at higher temperature levels. More specifically, for inlet temperatures 300, 400, 500 and 600 K, the maximum thermal enhancements are 0.6, 0.9, 1.5 and 2.7%, respectively. Higher inlet temperature levels create higher thermal losses and the enhancement margin is greater. This observation explains the higher thermal enhancements for operating at higher temperature levels.
Figures 9 and 10 depict the thermal losses of the examined cases. Figure 9 shows that higher Nusselt number ratio leads to lower thermal losses and Fig. 10 proves that the high thermal loss decreases can be achieved. It is important to state that the thermal loss decrease is up to 82% for operation with inlet temperature equal to 300 K, while for inlet temperatures 400, 500 and 600 K it reaches up to 46, 30 and 22%, respectively. The thermal loss decrease is many times greater than the thermal efficiency enhancement because the thermal losses are small compared to the useful energy production.
Figures 11 and 12 give results for the receiver temperature. It is obvious that receiver temperature is getting lower for higher Nusselt ratios, according to the results of Fig. 11. Figure 12 shows that the receiver temperature decrease for inlet temperatures 300, 400, 500 and 600 K are 18, 10, 6 and 5%, respectively. It is obvious that the receiver temperature reduction is higher than the thermal efficiency enhancement and lower than the thermal loss decrease.
Figures 13 and 14 exhibit results about the exergetic performance of the PTC. Figure 13 gives the exergetic efficiency for different inlet temperatures and Nusselt number ratios. It is obvious that higher inlet temperature leads to higher exergetic performance. Moreover, the impact of Nusselt number ratio is negligible after the value of 2.5. This result is also proved by Fig. 14. The thermal enhancements in the exergetic efficiency are similar with the thermal efficiency enhancements. This result can be explained by the Eq. 25.
Discussion
At this section, the main results about the thermal and exergetic enhancement, as well as about the thermal losses and receiver temperature decrease, are summarized in Table 4. These results are taken for inlet temperature equal to 600 K which is the most representative temperature for PTCs operation. According to the results in Table 4, and of the results of “Results”, it is obvious that thermal enhancement can be achieved with the increase of Nusselt number. Higher values of Nusselt number ratio lead to significant thermal loss decrease (up to 22%) and to lower decrease in receiver temperature up to 5% for inlet temperature equal to 600 K. The thermal efficiency enhancement and the exergetic efficiency enhancements are up to 3% for inlet temperature equal to 600 K.
It is important to state that the Nusselt number ratio increase leads to higher thermal efficiency enhancement for all the examined values from 1 to 5. However, after the limit of ~ 2.5, the thermal efficiency enhancement is not so intense. This observation makes clear the need for thermal enhancement techniques which leads to Nusselt number up to 2.5 times greater than the reference case. As reference case is the case of a smooth and empty tube of the LS-2 PTC module. Moreover, it is important to state that techniques which lead to greater Nusselt number ratios usually are associated with greater pressure losses and higher manufacturing difficulties-costs. Thus, it is important to select the proper technique which leads to the adequate Nusselt number enhancement.
According to the literature review, techniques as the use of internal fins and the use of twisted tape inserts lead to the proper Nusselt number ratios which make the thermal efficiency enhancement close to 2%. For example, the studies of Refs. [21, 22] indicate that the use of internal fins leads to thermal enhancements up to 3–4%. The Ref. [27] shows that the use of wall-detached twisted tape inserts lead to thermal efficiency enhancements up to 5% and the Ref. [28] indicates that the use of the twisted tape inserts leads to thermal efficiency enhancements up to 3%. Two recent studies [41, 42] about the use of internal fins lead up to 1% thermal efficiency enhancement. These literature findings indicate similar thermal enhancements with the present study. The results of this work can be used in real applications to know the maximum thermal efficiency enhancement using various techniques which aim to increase the Nusselt number.
At this point, it would be important to comment on the impact of the solar beam irradiation on the thermal efficient enhancement margin. Figure 15 depicts the thermal efficiency enhancement for various solar beam irradiation levels from 400 W/m2 up to 1000 W/m2. These results concern the case of Nusselt number ratio (R) equal to 2, which is a representative case. Figure 15 proves that the thermal efficiency enhancement is higher for higher solar beam irradiation levels. This result is observed for all the examined inlet temperature levels. Moreover, the thermal efficiency enhancement is higher at higher inlet temperatures. So, it can be said that in the most interesting cases with higher solar potential and higher inlet temperature, the thermal efficiency enhancement is higher. This result indicates the utilization of thermal enhancement methods in cases where the PTC operates generally under great solar beam irradiation levels.
At the end of the discussion section, important assumptions and limitations of the present work have to be given. The developed model assumes that the receiver has a uniform temperature level and there is no temperature variation on its length. This assumption is reasonable because in this study only a module of the collector is examined and not a great solar field. Moreover, the thermal properties of the fluid have been taken at the mean fluid temperature, something with very small impact on the results because of the small difference between outlet and inlet temperatures. Moreover, the present analysis has been conducted for specific solar irradiation level and solar angle and not for various combinations of these parameters. However, the selected values are typical for solar studies and they are acceptable.
Conclusions
This paper evaluates the thermal efficiency enhancement of parabolic trough collectors for various thermal enhancement cases. These thermal enhancements cases are examined parametrically by evaluating different Nusselt numbers via the Nusselt number ratio parameter. This parameter indicates how many times the Nusselt number is increased by the use of a thermal enhancement technique, compared to the reference case. The most usual and representative techniques are the use of internal fins, inserts, metal foams and dimpled absorbers. The module of LS-2 PTC is examined with a developed thermal model in EES. This model is validated with the literature results and it is proved that it is accurate.
According to the final results, it is found that the thermal losses can be decreased up to 22% for inlet temperature equal to 600 K, while the receiver temperature can be decreased up to 5%. In the respective cases, the thermal and exergetic efficiency enhancements reach up to 3%, small values which are based on the low thermal losses of PTC which let small enhancement margin. Moreover, it is found that Nusselt number ratios up to 2.5 have to be used because after this limit the thermal enhancement is extremely low. Thus, thermal enhancement techniques which are able to increase the Nusselt number up to 2.5 times compared to the respective smooth case can lead to 2% thermal efficiency enhancement. This small enhancement percentage is important in the long-term analysis for all the life of the PTCs and it is able to make them a more sustainable solution among the renewable energy technologies.
Abbreviations
- A :
-
Area, m2
- C :
-
Concentration ratio, –
- c p :
-
Specific heat capacity under constant pressure, J/kg K
- D :
-
Diameter, m
- E :
-
Exergy, W
- F :
-
Focal length, m
- G b :
-
Solar direct beam irradiation, W/m2
- h :
-
Heat transfer coefficient, W/m2 K
- h out :
-
Convection coefficient between cover and ambient, W/m2K
- k :
-
Thermal conductivity, W/mK
- K :
-
Incident angle modifier, –
- L :
-
Tube length, m
- m :
-
Mass flow rate, kg/s
- Nu :
-
Nusselt number, –
- Nu 0 :
-
Nusselt number of reference case, –
- Pr :
-
Prandtl number, –
- Q :
-
Heat flux, W
- R :
-
Nusselt number ratio, –
- Re :
-
Reynolds number, –
- r :
-
Concentrator reflectance, –
- T :
-
Temperature, K
- T sky :
-
Sky temperature, K
- V :
-
Volumetric flow rate, L/min
- V wind :
-
Ambient air velocity, m/s
- W :
-
Width, m
- α :
-
Absorber absorbance, –
- γ :
-
Intercept factor, –
- ε :
-
Emittance, –
- η ex :
-
Exergetic efficiency, –
- η opt :
-
Optical efficiency, –
- η th :
-
Thermal efficiency, –
- θ :
-
Solar beam incident angle, °
- μ :
-
Dynamic viscosity, Pa s
- τ :
-
Cover transmittance, –
- a:
-
Aperture
- abs:
-
Absorbed
- am:
-
Ambient
- c:
-
Cover
- ci:
-
Inner cover
- co:
-
Outer cover
- fm:
-
Mean fluid
- in:
-
Inlet
- loss:
-
Thermal loss
- m, ex:
-
Mean exergetic
- out:
-
Outlet
- pet:
-
Petela
- r:
-
Receiver
- ri:
-
Inner receiver
- ro:
-
Outer receiver
- s:
-
Solar
- u:
-
Useful
- 0:
-
Reference case
- EES:
-
Engineering Equation Solver
- PTC:
-
Parabolic trough collector
References
Zagba, L., Khennane, M., Mahamedi, I.H., Oudjana, H.S., Fezzari, A., Bouchakour, A., Terki, N.: A combined simulation and experimental analysis the dynamic performance of a 2 kW photovoltaic plant installed in the desert environment. Int. J. Energy Environ. Eng. 7, 249–260 (2016)
Al Mamum, S., Chowdhury, Z.I., Kaiser, M.S., Islam, M.S.: Techno-financial analysis and design of on-board intelligent-assisting system for a hybrid solar–DEG-powered boat. Int. J. Energy Environ. Eng. 7, 361–376 (2016)
Bellos, E., Tzivanidis, C.: Energetic and financial sustainability of solar assisted heat pump heating systems in Europe. Sustain. Cities Soc. 33, 70–84 (2017)
Jelley, S., Smith, T.: Concentrated solar power: recent developments and future challenges. J. Power Energy 229(7), 693–713 (2015)
Grosu, L., Marin, A., Dobrovicescu, A., Queiros-Conde, D.: Exergy analysis of a solar combined cycle: organic Rankine cycle and absorption cooling system. Int. J. Energy Environ. Eng. 7, 449–459 (2016)
Bellos, E., Tzivanidis, C., Antonopoulos, K.A.: Exergetic and energetic comparison of LiCl-HO and LiBr-HO working pairs in a solar absorption cooling system. Energy Convers. Manag. 123, 453–461 (2016)
Sabiha, M.A., Saidur, R., Mekhilef, S., Mahian, O.: Progress and latest developments of evacuated tube solar collectors. Renew. Sustain. Energy Rev. 51, 1038–1054 (2015)
Pintaldi, S., Sethuvenkatraman, S., White, S., Rosengarten, G.: Energetic evaluation of thermal energy storage options for high efficiency solar cooling systems. Appl. Energy 188, 160–177 (2017)
Tzivanidis, C., Bellos, E., Antonopoulos, K.A.: Energetic and financial investigation of a stand-alone solar-thermal Organic Rankine cycle power plant. Energy Convers. Manag. 126, 421–433 (2016)
Rovira, A., José Montes, R.B., Abbas, R., Varela, F.: Analysis and comparison of Integrated Solar Combined Cycles using parabolic troughs and linear Fresnel reflectors as concentrating systems. Appl. Energy 162, 990–1000 (2016)
Bellos, E., Tzivanidis, C.: Parametric analysis and optimization of an Organic Rankine Cycle with nanofluid based solar parabolic trough collectors. Renew. Energy 114B, 1376–1393 (2017)
Buehler, R., Yang, S., Ordonez, J.C.: Heat transfer fluids for parabolic trough solar collectors—a comparative study, In: Proceedings of “2016 IEEE Conference on Technologies for Sustainability—SusTech”, At Phoenix, Arizona (2016)
Fuqiang, W., Ziming, C., Jianyu, T., Yuan, Y., Yong, S., Linhua, L.: Progress in concentrated solar power technology with parabolic trough collector system: a comprehensive review. Renew. Sustain. Energy Rev. 79, 1314–1328 (2017)
Bellos, E., Tzivanidis, C., Antonopoulos, K.A., Daniil, I.: The use of gas working fluids in parabolic trough collectors—an energetic and exergetic analysis. Appl. Therm. Eng. 109, 1–14 (2016)
Bellos, E., Tzivanidis, C., Antonopoulos, K.A.: A detailed working fluid investigation for solar parabolic trough collectors. Appl. Therm. Eng. 114, 374–386 (2017)
Coventry, J., Andraka, C., Pye, J., Blanco, M., Fisher, J.: A review of sodium receiver technologies for central receiver solar power plants. Sol. Energy 122, 749–762 (2015)
Sandeep, H.M., Arunachala, U.C.: Solar parabolic trough collectors: a review on heat transfer augmentation techniques. Renew. Sustain. Energy Rev. 69, 1218–1231 (2017)
Price, H., Lüpfert, E., Kearney, D., Zarza, E.: Advances in parabolic trough solar power technology. J. Sol. Energy Eng. 124(2), 109–125 (2002)
Xiangtao, G., Fuqiang, W., Haiyan, W., Jianyu, T., Qingzhi, L., Huaizhi, H.: Heat transfer enhancement analysis of tube receiver for parabolic trough solar collector with pin fin arrays inserting. Sol. Energy 144, 185–202 (2017)
Benabderrahmane, A., Aminallah, M., Laouedj, S., Benazza, A., Solano, J.P.: Heat transfer enhancement in a parabolic trough solar receiver using longitudinal fins and nanofluids. J. Therm. Sci. 25, 410–417 (2016)
Bellos, E., Tzivanidis, C., Daniil, I.: Energetic and exergetic investigation of a parabolic trough collector with internal fins operating with carbon dioxide. Int. J. Energy Environ. Eng. 8(2), 109–122 (2017)
Bellos, E., Tzivanidis, C., Daniil, I., Antonopoulos, K.A.: The impact of internal longitudinal fins in parabolic trough collectors operating with gases. Energy Convers. Manag. 135, 35–54 (2017)
Wang, F., Tang, Z., Gong, X., Tan, J., Han, H., Li, B.: Heat transfer performance enhancement and thermal strain restrain of tube receiver for parabolic trough solar collector by using asymmetric outward convex corrugated tube. Energy 114, 275–292 (2016)
Bellos, E., Tzivanidis, C., Antonopoulos, K.A., Gkinis, G.: Thermal enhancement of solar parabolic trough collectors by using nanofluids and converging-diverging absorber tube. Renew. Energy 94, 213–222 (2016)
Huang, Z., Li, Z.-Y., Yu, G.-L., Tao, W.-Q.: Numerical investigations on fully-developed mixed turbulent convection in dimpled parabolic trough receiver tubes. Appl. Therm. Eng. 114, 1287–1299 (2017)
Kumar, K.R., Reddy, K.S.: Thermal analysis of solar parabolic trough with porous disc receiver. Appl. Energy 86, 1804–1812 (2009)
Mwesigye, A., Bello-Ochende, T., Meyer, J.P.: Heat transfer and entropy generation in a parabolic trough receiver with wall-detached twisted tape inserts. Int. J. Therm. Sci. 99, 238–257 (2016)
Jaramillo, O.A., Borunda, M., Velazquez-Lucho, K.M., Robles, M.: Parabolic trough solar collector for low enthalpy processes: an analysis of the efficiency enhancement by using twisted tape inserts. Renew. Energy 93, 125–141 (2016)
Too, Y.C.S., Benito, R.: Enhancing heat transfer in air tubular absorbers for concentrated solar thermal applications. Appl. Therm. Eng. 50(1), 1076–1083 (2013)
Wang, P., Liu, D.Y., Xu, C.: Numerical study of heat transfer enhancement in the receiver tube of direct steam generation with parabolic trough by inserting metal foams. Appl. Energy 102, 449–460 (2013)
Behar, O., Khellaf, A., Mohammedi, K.: A novel parabolic trough solar collector model—Validation with experimental data and comparison to Engineering Equation Solver (EES). Energy Convers. Manag. 106, 268–281 (2015)
Leinhard IV, J., Leinhard, V.J.: A Heat Transfer Textbook, 4th edn. Philogiston Press, Cambridge (2012)
Forristall, R.: Heat Transfer Analysis and Modeling of a Parabolic Trough Solar Receiver Implemented in Engineering Equation Solver. National Renewable Energy Laboratory—NREL, Colorado (2003)
Qiu, Y., Li, M.-J., He, Y.-L., Tao, W.-Q.: Thermal performance analysis of a parabolic trough solar collector using supercritical CO2 as heat transfer fluid under non-uniform solar flux. Appl. Therm. Eng. 115, 1255–1265 (2017)
Swinbank, W.C.: Long-wave radiation from clear skies. QJR Meteorol. Soc. 89, 339–340 (1963)
Petela, R.: Exergy of undiluted thermal radiation. Sol. Energy 74(6), 469–488 (2003)
http://www.loikitsdistribution.com/files/syltherm-800-technical-data-sheet.pdf. Accessed 15 May 2017
F-Chart Software, Engineering Equation Solver (EES). http://www.fchart.com/ees (2015). Accessed 15 May 2017
Bellos, E., Tzivanidis, C.: Parametric investigation of nanofluids utilization in parabolic trough collectors. Therm. Sci. Eng. Prog. 2, 71–79 (2017)
Bellos, E., Tzivanidis, C.: A detailed exergetic analysis of parabolic trough collectors. Energy Convers. Manag. 149, 275–292 (2017)
Bellos, E., Tzivanidis, C., Tsimpoukis, D.: Multi-criteria evaluation of parabolic trough collector with internally finned absorbers. Appl. Energy 205, 540–561 (2017)
Bellos, E., Tzivanidis, C., Tsimpoukis, D.: Thermal enhancement of parabolic trough collector with internally finned absorbers. Sol. Energy 157C, 514–531 (2017)
Acknowledgements
Dr. Evangelos Bellos would like to thank “Bodossaki Foundation” for its financial support.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Bellos, E., Tzivanidis, C. Assessment of the thermal enhancement methods in parabolic trough collectors. Int J Energy Environ Eng 9, 59–70 (2018). https://doi.org/10.1007/s40095-017-0255-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40095-017-0255-3