A biofilm model of microbial fuel cells for engineering applications

Abstract

A generalized low-order model of the biofilm in a microbial fuel cell (MFC), suitable for use in real-time engineering applications, is presented. It is based on the description of the charge transfer, diffusion process, and charge accumulation in the biofilm. Since the dynamic processes in an MFC are ruled mainly by the biofilm, it can be used for many different diffusion-based MFC types by just changing the boundary conditions. Different mode operations like batch, fed-batch, continuous, etc., are also possible. The time-responses of voltage, substrate concentration on the surface of the electrode, and Faradaic and capacitive currents have been tested under several experimental conditions.

Introduction

Microbial fuel cells (MFCs) are a promising sustainable technology, since they are able to produce electricity while reducing organic contaminants from wastewater. The MFCs consist of two electrodes, one is the anode, which is exposed to an electron donor (e.g., an organic pollutant), and the other is the cathode working as a terminal electron acceptor (e.g., oxygen). The bacteria responsible for the current generation in MFCs grow in a biofilm attached to the anode surface. These microbial cells release electrons to the anode. These electrons travel through the external load to the cathode, where the terminal electron acceptor is reduced [1].

Modeling MFCs is necessary for engineering applications like to plan optimization strategies, to decide control systems, and estimation or prediction strategies. System modeling is important not only for understanding and capturing the main phenomena that take place in the system but also for observing, predicting, and designing a suitable control law for the internal variables of the MFC. For example, a suitable model of an MFC should allow estimating the amount of biomass and substrate concentration by measuring only the current and potential of the cell. Also be able to predict what it will occur in a time $t+T$ having measurements only up to time t. It should also allow designing a control law on the amount of substrate to be supplied to maintain the cell at its optimum production point [2]. However, to be able to perform all these tasks, it is necessary that these models are simple, but that they adequately describe the most important processes of the MFC and that contain the most important variables. In this sense, some authors propose a simple alternative to model the MFC system. For example, the linearized first-order approximation reported by Boghani et al. [3] or the equivalent electrical circuit, composed of a capacitor in parallel with the electrode charge-transfer resistance, proposed by Ha et al. [4]. This kind of model is very simple to implement, since it does not require expert knowledge of the MFC internal processes or great computational cost. However, these models based on linearization work well for small variations of states around a fixed operational point of the MFC. For cases of large variations of the states, it is necessary to maintain the nonlinear characteristics of the cell without losing the simplicity.

An important group of models are based on fundamental biological, physical-chemical, and electrochemical principles, known as knowledge-based models (KBMs), that provide an accurate insight of the involved processes; see for example [5] for a recent review. To model the MFC, it is crucial to consider the most important processes that govern the dynamics of the cell. Some of the mechanisms controlling the behavior of the MFC are charge accumulation and electron transfer, which finally result in the power released.

The charge of the MFC is stored in two ways, either as biochemically bound or as immediately available, which are conditioned by the molecular diffusion in the biofilm and the double-layer capacity, respectively. Molecular diffusion is the net flux of substrate from the region of higher concentration to the lower one, which is located at the anode surface. Therefore, this mechanism defines the rate at which the substrate is degraded by microorganism and, consequently, the rate of the produced current. Several KBMs consider that the substrate concentration is a function of both time and location. For example, Sirinutsomboon [6] includes into the mass balance Fick’s second law to describe the substrate profile evolution into the biofilm in one dimension. Picioreanu et al. [7] propose spatial concentration gradients in one-, two-, or three-dimensional setups. Picioreanu et al. [8] consider that solutes move not only by diffusion, but also by convection and electromigration in a two-dimensional biofilm model. In [9, 10], a simplification is presented by assuming a steady-state profile for substrate concentrations.

The charge is also accumulated in the double layer, which provides an instantaneous current when changes are imposed on the external load. Then, the double-layer capacity is an important process involved in the MFC systems, which has already been studied and characterized by [11]. Moreover, the biofilm has a pronounced effect on the double-layer thickness at the electrode–electrolyte interface, increasing the capacitance of the system. To our knowledge, only Zeng et al. [12] modeled such an important process by including in the charge balances the capacitance of the anode and cathode.

The bacteria responsible for the current generation in MFCs may transfer electrons directly to the anode surface or using soluble mediators. Direct electron transfer involves either membrane-bound cytochromes or the proposed conducting structures termed nanowires [13]. Soluble mediators are chemicals that diffuse through the electrolyte and can shuttle electrons between microbial cells and the anode. Papers [14, 15] report that electrochemically active bacteria from a biofilm enriched in an MFC can produce mediator compounds in situ. Involvement of soluble mediators, which has already been modeled by [7, 8], justifies the existence of an oxidation and reduction reaction in the anode surface, which always occurs in any electrode–electrolyte interface [16].

As can be seen from the previous paragraphs, the biofilm growing on the anode is of great importance in the dynamic response of the MFC, since in this zone, substrate diffusion occurs, mediators participate in the electron transfer to the anode surface, and the biofilm modifies the double-layer capacity. Thus, the anode is often considered as the limiting factor of an MFC, which implies that the limiting processes for the electrochemical reactions take place at the anode.

All the KBMs described have complex approaches; their complexities are summarized in Table 1. It is obvious that the more the complexity of the model, the greater the number of parameters and variables considered. The problem with the high complex models is that they are difficult to use in real-time applications like control, prediction, and observation. Even more so if it is taken into account that some parameters are time-varying.

Table 1 Features of the MFC models

Basically, simple analogies are practical, but empirical and sometimes, they do not work properly. On the other extreme, there are electrochemical models with a great number of parameters and variables, which are very demanding to obtain. However, it is difficult to find simple models able to run in real time for engineering applications that interpret the processes involved using electrochemical states. A simple model should fulfill the following requirements: (1) low order with low computational needs, (2) identifiable with economic resources and based on simple measurements, and mainly (3) should be described by bioelectrochemical and physical variables and parameters.

Therefore, in this paper, a simple model is presented, considering mainly the dynamics of the biofilm at the anode. The model is not intended to interpret the intrinsic phenomena to a metabolic level; the aim is to interpret the global dynamics of the substrate consumption and the balance of electric charges. The proposed model can be used for many different diffusion-based MFCs by just changing the boundary conditions. Different mode operations like batch, fed-batch, continuous, etc., are also possible. Following electrochemical arguments, it is shown that the MFC dynamics can be characterized by a low-order model by considering (1) Fick’s laws to describe the substrate concentration profile due to the diffusion process in the biofilm in one dimension perpendicular to the anode surface, (2) the capacitance due to the biofilm at the anodic interface, and (3) a static nonlinearity due to the electrochemical reactions at the electrode interfaces, which is governed by a Butler–Volmer-type equation. Because of its simplicity, the model is suitable for digital real-time implementations.

Model formulation

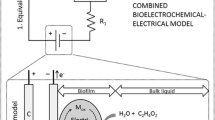
MFCs are basically a system conformed by two electrodes composed of conductive particles immersed in liquid media, generally water. Both electrodes are separated by a proton-conducting medium, for example a perfluoro-sulfonated cation-exchange membrane. In the case of a two-chamber MFC, the potential distribution is shown in Fig. 1. The negative electrode is the anode, covered by bacteria forming a biofilm, immersed in a solution at a given concentration of substrate. It is responsible to oxidize the organic matter—substrate—that arrives at the electrode surface by diffusion. The electrons are generated during oxidation of the organic substrate, by the bacteria. Considering acetate as the carbon source, the main reaction in the anode is as follows:

$$(\text{CH}_{2}\text{O})_{2} + 2\text{H}_{2}\text{O} \rightarrow 2\text{CO}_{2} + 8\text{H}^{+} + 8\text{e}^{-}.$$

(1)

The microbial cells are capable of transferring the electron to diffusible mediators. There are exogenous mediators naturally present or just added in the medium and there are also endogenous mediators produced by microbial cells. In this model, it is assumed that electron transfer between the electroactive bacteria and the anode surface occurs by exogenous mediators that are naturally present [20]. The anode transfers electrons to the cathode via the external circuit, which results in the production of electric energy under load. Simultaneously, protons are transferred via the membrane to the cathode to maintain charge balance. The cathode is the positive electrode where reduction is carried out given by the following reaction:

$$\text{O}_{2} + 4\text{H}^{+} + 4\text{e}^{-} \rightarrow 2\text{H}_{2}\text{O}.$$

(2)

In the energy-release processes, two main stages must be distinguished: one, corresponding to the charge-transfer process at the electrode–electrochemical interface, including electrochemical reactions and double-layer charging; another one, corresponding to substrate mass transfer to the anode. In the next subsections, both stages are described, which are the main part of the biofilm dynamical model where the following assumptions were made:

• The limiting processes for the electrochemical reactions take place at the anode. Several models [7,8,9, 17, 18, 21] consider the anode as the limiting factor of an MFC, which implies that all concentrations in the cathode are the maximum admissible and remain always almost constant.

• The anodic chamber has two parts, one corresponding to the bulk solution, which is considered homogeneous where pH, substrate concentration, pressure, and temperature inside are uniform and constant, and the other is the biofilm covering all the electrode surfaces. Uniform distribution and constant concentration of microbial population in the biofilm is assumed. The biofilm is considered as the unique power supply.

• The acetate is assumed to be the only carbon source in the anode and it is the only limiting substrate for microorganisms. Other nutrient concentrations like nitrogen or phosphorus are saturated.

• The carbon source diffuses in the biofilm towards the electrode surface where the redox reactions take place. Then, the modeled dynamic is governed by the diffusional and electron charge-transfer process inside the biofilm.

• The proton transport is not a limiting process.

• Carbon dioxide remains dissolved in the solution.

• Electrons are transferred from the cells to the anode by diffusible redox mediators. It is assumed that a certain concentration of these compounds exists from the beginning. Soluble mediators justify the existence of an oxidation and reduction reaction in the anode surface, which always occurs in any electrode–electrolyte interface [16].

• The diffusion is limiting in the transport of matter, such as in very thick biofilms. This occurs in processes that operate in batch, fed-batch, and continuous modes with slow flow rate.

• Saturation effects of the substrate concentration are not considered in this model.

Fig. 1

Two-chamber MFC with electroactive biofilm. Conceptual MFC scheme showing carbon source (acetate) conversion in the anodic compartment by anodophilic (attached) microorganisms with the mediator participation

Faradaic charge-transfer processes

With the acetate oxidation, reduction and oxidation reactions of the mediators occur simultaneously in the anode. The electrochemical oxidation is described by the following reaction [7]:

$$\begin{aligned} \text{M}_{\mathrm{red}} \leftrightarrow \text{M}_{\mathrm{ox}} + 2 \text{H}^{+} + 2 \text{e}^{-} \end{aligned}$$

(3)

where $\text{M}_{\mathrm{red}}$ and $\text{M}_{\mathrm{ox}}$ are the reduced and oxidized form of the mediator, respectively. The reduction reaction of $\text{M}_{\mathrm{ox}}$ is not a limiting step in the model; this implies that each electron provided by acetic biological oxidation is readily captured by a mediator molecule.

The electrochemical oxidation and reduction reactions taking place at the anode—and simultaneously at the cathode to keep the electrochemical balance—give rise to the Faradaic current, $I_{{\mathrm{f}}}(t)$. The Faradaic current may be described in terms of the Butler–Volmer equation, as follows [22, 23]:

$$I_{{\mathrm{f}}}=\tilde{k}^{\mathrm{r}} c^{{\mathrm{r}}} {\mathrm{e}}^{\alpha^{\mathrm{r}} \eta }- \tilde{k}^{\mathrm{o}} c^{\mathrm{o}} {\mathrm{e}}^{-\alpha^{\mathrm{o}} \eta },$$

(4)

where $c^{\mathrm{r}}$ and $c^{\mathrm{o}}$, $\tilde{k}^{\mathrm{r}}$ and $\tilde{k}^{\mathrm{o}}$ are the concentrations and constant rates of reduced and oxidized species at the electrochemical interface, respectively; $\alpha^{\mathrm{r}}=a^{\mathrm{r}} F/RT$ and $\alpha ^{\mathrm{o}}=a^{\mathrm{o}} F/RT$ are constants, where $a^{\mathrm{r}}$ with values in the interval (0, 1) and $a^{\mathrm{o}}=1-a^{\mathrm{r}}$ are symmetry factors; in this paper, it is assumed that the values $a_{\mathrm{r}}=a_{\mathrm{o}}=0.5$, which means $\alpha ^{\mathrm{r}}=\alpha ^0=\alpha$; F is the Faraday constant; R the universal gas constant; T is the temperature; and $\eta =E_{\mathrm{a}}-E_{\mathrm{a}}^{\mathrm{o}}$ is the anodic overpotential defined as the difference between the anode potential $E_{\mathrm{a}}$, see Fig. 1, and the reference potential $E_{\mathrm{a}}^{\mathrm{o}}$.

The importance of taking into account the oxidation reactions in the anode surface is clear when considering only the reduction term on the right-hand side of (4). Under zero current or equilibrium condition, $I_{\mathrm{f}}=0$, if the term corresponding to the oxidation reactions was missing, the overpotential should be $\eta =-\infty$, which is not possible.

Multiplying and dividing the first term on the right-hand side of Eq. (4) by the maximum acetate concentration, which is the reduced state of the active species ($\bar{c}^{\mathrm{r}}$) and, taking into account that the saturated concentration of the oxidized species ($c^{\mathrm{o}}$) remains almost constant—non limiting—, the following direct equation holds:

$$\begin{aligned} I_{\mathrm{f}}=k^{\mathrm{r}} S {\mathrm{e}}^{\alpha \eta }-k^{\mathrm{o}} {\mathrm{e}}^{-\alpha \eta }, \end{aligned}$$

(5)

where $k^{\mathrm{r}}=\tilde{k}^{\mathrm{r}}\bar{c}^{\mathrm{r}}$ and $k^{\mathrm{o}}=\tilde{k}^{\mathrm{o}} c^{\mathrm{o}}$, are both constants, and $S=c^{\mathrm{r}}/\bar{c}^{\mathrm{r}}$ is the fractional substrate or acetate concentration at the interface, which lies in the interval (0, 1). This is a Butler–Volmer equation expressing the functional relationship of current with respect to overpotential and concentration.

The MFC potential relationship is given by the following equation:

$$\begin{aligned} V = E_\mathrm{c} - E_{\mathrm{a}} - I R_\mathrm{i}= E_\mathrm{c} - E_{\mathrm{a}}^{\mathrm{o}}-\eta - I R_\mathrm{i}, \end{aligned}$$

(6)

where V is the potential between terminals of both electrodes, $E_\mathrm{c}$ is the constant potential between the cathode and the cathodic electrolyte in the surface of the electrode, I is the current that flows through the MFC, which is the difference between the Faradaic current $I_{\mathrm{f}}$ and the double-layer current $I_\mathrm{c}$ as will be described later, and $R_\mathrm{i}$ is the ohmic resistance including both the resistance to the flow of electrons through the electrodes and interconnections, and the resistance to the flow of ions through the proton-exchange membrane, the anodic, and cathodic electrolytes. Replacing (6) in (5), the following expression for the current is obtained:

$$\begin{aligned} I_{\mathrm{f}}= K^{\mathrm{r}} S {\mathrm{e}}^{-\alpha (V + I R_\mathrm{i})}-K^{\mathrm{o}} {\mathrm{e}}^{\alpha (V + I R_\mathrm{i})}, \end{aligned}$$

(7)

where $K^{\mathrm{r}}=k^{\mathrm{r}} {\mathrm{e}}^{\alpha (E_\mathrm{c}-E_{\mathrm{a}}^{\mathrm{o}})}$ and $K^{\mathrm{o}}=k^{\mathrm{o}} {\mathrm{e}}^{-\alpha (E_\mathrm{c}-E_{\mathrm{a}}^{\mathrm{o}})}$. From (7), it is possible to obtain the substrate concentration at the electrode surface S explicitly, as

$$\begin{aligned} S=\frac{K^{\mathrm{o}} {\mathrm{e}}^{\alpha (V + I R_\mathrm{i})}+I_{\mathrm{f}}}{K^{\mathrm{r}} {\mathrm{e}}^{-\alpha (V + I R_\mathrm{i})}}, \end{aligned}$$

(8)

which is a function of V, I, and $I_{\mathrm{f}}$.

Note that when the total current is zero, the open circuit voltage (OCV) can be explicitly written as follows:

$$\begin{aligned} \text{OCV}=A+B\log (S_{I=0}), \end{aligned}$$

(9)

where $A=B \log (K^{\mathrm{r}} /K^{\mathrm{o}})$ and $B=1/2\alpha =RT/F$ and $S_{I=0}$ is the substrate concentration at zero current. This relationship in steady state is called electromotive force (EMF) of the MFC [20]. The EMF represents the functional relationship between potential and concentration in an open circuit and in steady state. Therefore, keeping the bacterial concentration constant, the EMF increases as the concentration increases according to Eq. (9), up to substrate saturation.

The diffusion process

Equations describing the substrate diffusion transport constitute the second part of the model. This may be expressed by Fick’s first and second laws, which in the case of planar geometry corresponds to [24]:

$$\begin{aligned} J(z,t)= & {} -D\bar{c}_{\mathrm{r}}\frac{\partial S(z,t)}{\partial z}, \end{aligned}$$

(10)

$$\begin{aligned} \frac{\partial S(z,t)}{\partial t}\,=\, & {} D\frac{\partial ^2 S(z,t)}{\partial z^2} , \end{aligned}$$

(11)

where D is the effective diffusion coefficient, S(z, t) and J(z, t) are the substrate concentration and flux of the substrate in the biofilm at time t and spatial position z. Using Eq. (10) in (11), the following equation is obtained:

$$\begin{aligned} \frac{\partial S(z,t)}{\partial t}=-\frac{1}{\bar{c}_{\mathrm{r}}}\frac{\partial J(z,t)}{\partial z}. \end{aligned}$$

(12)

The analytical solution of Eq. (12) is complex. General solutions of the diffusion equation can be obtained for a variety of initial conditions and boundary conditions provided that the diffusion coefficient is constant, see [24]. However, when the boundary conditions are time-varying, such as a time-varying energy source as in our case, these solutions exist only for simple functions such as steps, ramps, or simple deterministic variations. In general, in these cases, numerical solutions are used. The numerical solution consists on approximating (12) into a set of ordinary differential equations using a spatial discretization. Spatial discretization is a very well-known method to approximate partial differential equations in ordinary differential equations; for details, see [25, 26]. Equation (12) can be discretized along the space variable z by considering N slices of the biofilm with thickness $\varDelta z$, as illustrated in Fig. 2. In this figure, the slice $N+1$ corresponds to the bulk solution and the slice 0 is the closest slice to the anode surface.

Fig. 2

Spatial discretization

If each slice is small enough, the concentration $S(z_\mathrm{i},t)$ in the ith slice, where ($0 \le i \le N$), can be considered constant with input and output substrate flux given by $J(z_{i+1},t)$ and $J(z_\mathrm{i},t)$, respectively. Using this approximation, Eqs. (10) and (12) can be written as follows:

$$\begin{aligned} J(z_\mathrm{i},t)= & {} \frac{D\bar{c}_{\mathrm{r}}}{\varDelta z}(S(z_{i},t)-S(z_{i-1},t)), \end{aligned}$$

(13)

$$\begin{aligned} \frac{\mathrm{d}S(z_\mathrm{i},t)}{\mathrm{d}t}= & {} -\frac{1}{\bar{c}_{\mathrm{r}} \varDelta z }(J(z_{i},t)-J(z_{i+1},t)). \end{aligned}$$

(14)

Replacing (13) in (14) and considering a boundary condition for the flux $J(z_{N+1},t)=0$, the following set of ordinary differential equations that describe the acetate concentration profile is fulfilled:

$$\begin{aligned} \begin{array}{ccc} \frac{\mathrm{d}S(z_0,t)}{\mathrm{d}t}&{}=&{}-a S(z_0,t)+a S(z_1,t)-J(z_0,t)/(\bar{c} \varDelta z), \\ \frac{\mathrm{d}S(z_1,t)}{\mathrm{d}t}&{}=&{}a S(z_0,t)-2a S(z_1,t)+a S(z_2,t),\\ \vdots &{}=&{} \vdots \\ \frac{\mathrm{d}S(z_\mathrm{i},t)}{\mathrm{d}t}&{}=&{}a S(z_{i-1},t)-2a S(z_\mathrm{i},t)+a S(z_{i+1},t),\\ \vdots &{}=&{} \vdots \\ \frac{\mathrm{d}S(z_{N-1},t)}{\mathrm{d}t}&{}=&{}a S(z_{N-2},t)-2 a S(z_{N-1},t)+a S(z_N,t), \end{array} \end{aligned}$$

(15)

where $a=D/\varDelta z^2$. Note that different boundary conditions can be used to model several operation modes. In this case, constant concentration at the bulk, $S(z_N,t)$, is considered, then

$$\begin{aligned} \frac{\mathrm{d}S(z_N,t)}{\mathrm{d}t}=0. \end{aligned}$$

(16)

The flux and the Faradaic current are given by the following relationship:

$$\begin{aligned} J(z_0,t)=\frac{I_{f}(t)}{\gamma F N_{\mathrm{e}}}, \end{aligned}$$

(17)

where $\gamma$ is the biofilm area and $N_{\mathrm{e}}$ is the electron-mol/acetate-mol ratio involved in the electrochemical reaction. Using (17) in (15), a set of ordinary differential equations is obtained, which can be written in a vector–matrix formulation as follows:

$$\begin{aligned}&{\dot{{\mathbf {S}}}}(t)={\varPhi } {\mathbf {S}}(t) +{\varGamma } I_{\mathrm{f}}(t)\nonumber \\&S(z_{0},t)= C \mathbf{S }, \end{aligned}$$

(18)

where $\mathbf{S }=[S(z_{0},t), S(z_{1},t), \ldots , S(z_{i},t), \ldots , S(z_{N-1},t), S(z_{N},t)]^\mathrm{T},$and

$$\begin{aligned} {\varPhi }=a \left[ \begin{array}{cccccc} -1 &{} 1 &{} 0 &{} 0 &{} \cdots &{} 0 \\ 1 &{} -2 &{} 1 &{} 0 &{} \cdots &{} 0 \\ 0 &{} 1 &{} -2 &{} 1 &{} \cdots &{} 0 \\ \vdots \\ 0 &{} 0 &{} \cdots &{} 1 &{} -2 &{} 1 \\ 0 &{} 0 &{} 0 &{} \cdots &{} 0 &{} 0 \\ \end{array}\right] ;\quad \varGamma = \left[ \begin{array}{c} -b \\ 0 \\ 0 \\ \vdots \\ 0 \end{array}\right] ;\quad C=\left[ \begin{array}{cccc} 1&0&\cdots&0 \end{array} \right] ; \end{aligned}$$

with

$$\begin{aligned} b=\frac{1}{F \gamma \bar{c} \varDelta z N_{\mathrm{e}}}. \end{aligned}$$

Fig. 3

MFC model scheme

The complete model

The formation of biofilm on the electrode surface can have a pronounced effect on the thickness of the double layer, which in turn influences the double-layer capacitance of the system [11, 27]. The value of double-layer capacitance depends on various factors such as electrode polarization, ionic concentration, temperature, type of ions, oxide layers, roughness of the electrode, etc. Thus, to build the complete model, the double-layer capacitive current $I_\mathrm{c}(t)$ is taken into account, according to the following dynamics:

$$\begin{aligned} I_\mathrm{c}(t)=C_{\mathrm{dl}} \frac{\mathrm{d}(E_\mathrm{c}-E_{\mathrm{a}})}{\mathrm{d}t}, \end{aligned}$$

(19)

where $C_{\mathrm{dl}}$ is the double-layer capacity. The capacitive current is modeled in parallel with the charge-transfer process. Then, the total measured current I(t) can be modeled as follows:

$$\begin{aligned} I_{\mathrm{f}}(t)= I(t) + I_\mathrm{c}(t). \end{aligned}$$

(20)

The complete model is then given by Eqs. (7) and (18)–(20). Considering S(t) in (7) is equal to $S(z_{0},t)$, and given initial conditions of V(0) and ${\mathbf {S}}(0)$, the complete model is given by the following equations:

$$\begin{aligned} I_{\mathrm{f}}(t)= & {} K^{\mathrm{r}} S(z_{0},t) {\mathrm{e}}^{-\alpha (V(t) + I(t) R_\mathrm{i})}-K^{\mathrm{o}} {\mathrm{e}}^{\alpha (V(t) + I(t) R_\mathrm{i})},\end{aligned}$$

(21)

$$\begin{aligned} \frac{\mathrm{d}{\mathbf {S}}(t)}{\mathrm{d}t}\,=\, & {} \varPhi {\mathbf {S}}(t) + \varGamma I_{\mathrm{f}}(t), \end{aligned}$$

(22)

$$\begin{aligned} S(z_{0},t)\,=\, & {} C \mathbf{S },\end{aligned}$$

(23)

$$\begin{aligned} \frac{\mathrm{d} (V(t) + I(t) R_\mathrm{i})}{\mathrm{d}t}= & {} \frac{I_{\mathrm{f}}(t)-I(t)}{C_{\mathrm{dl}}}. \end{aligned}$$

(24)

The schematic diagram is shown in Fig. 3. Proper simulation of the state variables can be done by solving numerically the set of model equations with given initial conditions. It is worth noting that although the constant bulk concentration case is considered, the model parameters remain the same for batch as well for feed-batch operation modes and changing only the boundary conditions of diffusion in matrix $\varPhi$ as it was described in the previous subsection.

Electrical analogy for small-signal operation

The output voltage V can be expressed as the sum of two components, one as a function of the substrate at zero current, $S_{I=0}$, according to the EMF in (9) and the other taking into account the contribution of the consumed current I. To obtain such a decomposition, Eq. (8) can be rewritten as follows:

$$\begin{aligned} S=\frac{K^{\mathrm{o}}}{K^{\mathrm{r}}} {\mathrm{e}}^{2\alpha (V+I R_x)}, \end{aligned}$$

(25)

where $R_x$ is a dummy resistance obtained by equating (8) and (25) and taking logarithms on both sides. After some algebra, the following relationship is obtained:

$$\begin{aligned} IR_x=IR_\mathrm{i}+I_{\mathrm{f}}R_z, \end{aligned}$$

(26)

where

$$\begin{aligned} R_z=\frac{1}{2I_{\mathrm{f}}\alpha } \ln \left( 1+\frac{I_{\mathrm{f}}}{K^{\mathrm{o}}} {\mathrm{e}}^{-\alpha (V+IR_\mathrm{i})}\right) . \end{aligned}$$

(27)

Note that resistances $R_x$ and $R_z$ are functions of the currents and the potential. Moreover, both $R_x$ and $R_z$ are positive-definite values, since the currents are always positive. Taking logarithm on both sides of (25), the following equality is obtained:

$$\begin{aligned} V=A+B \ln ( S)-IR_x. \end{aligned}$$

(28)

Then, it follows that the potential V, for arbitrary values of current I and substrate concentration S, is obtained by subtracting the factor $IR_x$ to the output of the EMF function, where $S=S(z_{0},t)$. The EMF function can be obtained experimentally for zero current and different values of substrate at the steady state.

Fig. 4

Equivalent circuit

Consider now the special case in which the substrate has small deviations from the constant bulk concentration $S=\bar{S}$ and the current has small variations around $I=\bar{I}=0$. Then, the potential can be well approximated by a pseudolinear function as follows:

$$\begin{aligned} V\approx & \, V(\bar{S},\bar{I})+\left. \frac{\partial V}{\partial S}\right| _{\bar{S},\bar{I}}(S-\bar{S})+\left. \frac{\partial V}{\partial I}\right| _{\bar{S},\bar{I}}(I-\bar{I})\nonumber \\ = & \, A+B\ln (\bar{S}) + \frac{B}{\bar{S}}(S-\bar{S})-IR_x-I^2\frac{\partial R_x}{\partial I}\nonumber \\ \approx & \, A+B\ln (\bar{S}) + \frac{B}{\bar{S}}(S-\bar{S})-IR_x. \end{aligned}$$

(29)

where the quadratic term was neglected.

Using a first-order approximation for the diffusion equations (22) and (23), the expression of the time derivative for substrate is

$$\begin{aligned} \frac{\mathrm{d}S(z_{0},t)}{\mathrm{d}t}=-\,aS(z_{0},t)+a{\bar{S}}+bI_{\mathrm{f}}(t). \end{aligned}$$

(30)

Thus, the complete linear model equations are given by (24), (26), (29), and (30), which can be rewritten in a compact form as follows:

$$\begin{aligned} \frac{\mathrm{d}X_1}{\mathrm{d}t}= -aX_1+\frac{bB}{\bar{S}} I_{\mathrm{f}},\end{aligned}$$

(31)

$$\begin{aligned} \frac{\mathrm{d}X_2}{\mathrm{d}t}= \frac{1}{C_{\mathrm{dl}}} I_\mathrm{c},\end{aligned}$$

(32)

$$\begin{aligned} V= & {} X_2-IR_\mathrm{i},\end{aligned}$$

(33)

$$\begin{aligned} \text{OCV}= & {} X_1+X_2+I_{\mathrm{f}} R_z, \end{aligned}$$

(34)

where

$$\begin{aligned} X_1=\frac{B}{\bar{S}}(\bar{S}-S);\quad X_2=V+I R_\mathrm{i};\quad \text{ and }\quad \text{OCV}=A+B\ln (\bar{S}), \end{aligned}$$

which has the electrical analogy shown in Fig. 4.

Materials and methods

Construction

The MFC used in this experimental test has two chambers: anodic and cathodic, with equal volume of 0.2 L. Both compartments are built of glass sheets with 0.005 m thickness. The anode consists of a network formed by a matrix of $4\times 4$ equally spaced electrodes of graphite blocks, each of 0.015 m $\times$ 0.008 m $\times$ 0.005 m, which is immersed in the anode chamber. The individual blocks are connected to a common terminal placed on a polypropylene cover. This scheme provides a total electrode area of 0.00688 $\text{m}^{2}$. For the cathodic chamber, an area of 0.0025 $\text{m}^2$ of carbon cloth incorporated with 0.5 $\text{mg}\,\text{cm}^{-2}$ Pt catalyst (E-Tek, NJ) is used. To allow proton conduction from the anode to cathode, a 0.0028 $\text{m}^{2}$ area of NAFION^® membrane is used. The cathodic chamber is continuously aerated and the MFC is maintained at a temperature of $25\pm 0.5\,^{\circ }\text{C}$ in a temperature-controlled room.

Medium and inoculum source

Sediment from the shore of the Río Negro river (Patagonia-Argentina) is used as inoculum. It is obtained at 0.2 m depth to assure anaerobic conditions [28]. A feed solution containing 0.5 $\text{g}\,\text{L}^{-1}$ of sodium acetate dissolved in 50 mM phosphorus buffer solution ($\text{Na}_{2}\text{HPO}_{4}$, 4.58 $\text{g}\,\text{L}^{-1}$; $\text{Na}_{2}\text{PO}_{4}\cdot \text{H}_{2}\text{O}$ 2.45 $\text{g}\,\text{L}^{-1}$; $\text{NH}_{4}\text{Cl}$ 0.31 $\text{g}\,\text{L}^{-1}$; KCl 0.13 $\text{g}\,\text{L}^{-1}$; trace minerals and vitamins) [29] is used in the anodic chamber. The cathodic chamber is filled with a phosphorus buffer solution following the procedure described in [30].

Start-up and operation

Fig. 5

Start-up of the MFC

By following the standard start-up procedure [29, 30], the MFC is filled with pure inoculum for the first cycle. It operates in a batch mode until the voltage decreases from the initial value in approximately 10 mV. Then, for the next two cycles, the liquid of anodic chamber is replaced with a mixture (50:50) of inoculum and feed solution. To force a current, an external resistance of $1000 \varOmega$ is connected to the electrical terminals of the MFC. In the next cycles, only the feed solution is used by replacing the liquid for fresh one every 3 days. At the beginning of each cycle, cathodic chamber liquid is replaced too. It is considered that the steady state is reached when repetitive values of voltage and bacterial concentration are obtained at each cycle. It was observed that repetitive data of OCV are obtained approximately after 60 days of operation. The evolution is depicted in Fig. 5.

Bacterial population is measured periodically. It is quantified by counting using a Bausch & Lomb Galen microscope with phase contrast and a Petroff Hausser camera. Bacteria growing over the anode are sampled from a face of graphite anode with an area of $3.2\times 10^{-5}\,\text{m}^2$, and this is resuspended in 20 mL of a phosphorus buffer solution. Each measurement consists on averaging three statistically independent counting. From the measurements, it is possible to ensure that the biomass in the steady state is kept constant within 5$\%$ of the measurement error. The mean value obtained is $2.15\times 10^6 (\text{cell}\,\text{mL}^{-1})$.

After the steady state is reached, several experiments are carried out to obtain data for model parameter identification and model validation, as is described in the next subsection. The experimental measurements are carried out immediately after the liquids of both chambers are replaced. Each experiment consists of connecting alternately different external resistors between the terminals of the cell voltage and measure the voltage. Each experiment lasts $5 \sim 6\,(\text{hs})$, approximately where the substrate concentration keeps constant at $c_{0}=0.5\,\text{g}\,\text{L}^{-1}$. Power density is calculated according to $P=1000VI/\gamma , (\text{mW}\,\text{m}^{-2})$, where $V\ (\text{V})$ is the measured potential, $I\ (\text{A})$ is the current density, and $\gamma \ (\text{m}^2)$ is the projected surface area of the anode. Sodium acetate concentration is determined by titration according to the method proposed by [31].

Parameter identification method

The unknown vector parameters are $\theta =[K^{{\mathrm{r}}}, R_\mathrm{i}, C_{\mathrm{dl}}, a, b]$. The symmetry factors are given by $\alpha ^{\mathrm{o}}=\alpha ^{\mathrm{r}}=1.97\,\,10^{-2}\,\text{mV}^{-1}$ [16], and $K^{\mathrm{o}}$ is obtained from (9), where $\log (S_{I=0}) =\log (\bar{S})=0,$ because $\bar{S}=1$ is the maximum constant concentration for current zero in steady state. Thus, $A=\text{OCV}$ and

$$\begin{aligned} K^{\mathrm{o}}=K^{{\mathrm{r}}}{\mathrm{e}}^{-A/B}=K^{{\mathrm{r}}}{\mathrm{e}}^{-\mathrm{OCV}/B}=K^{{\mathrm{r}}}{\mathrm{e}}^{-2 \; \mathrm{OCV}\alpha }. \end{aligned}$$

(35)

For a given number of slices N, the five remaining parameters in $\theta$ are obtained by numerically optimizing the following quadratic problem:

$$\begin{aligned} \arg \min _{\theta }\{Q(\theta )\}, \end{aligned}$$

(36)

where the quadratic cost function is given by the following:

$$\begin{aligned} Q(\theta )=\frac{1}{M}\sum _{i=1}^{M} \frac{(V(i)-\hat{V}(i,\theta ))^{2}}{ V^{2}(i)}, \end{aligned}$$

(37)

where V is the M-data record obtained by regularly sampling the MFC voltage every 10 s and $\hat{V}(i,\theta )$ is the voltage estimated by the model with parameter $\theta$ at the same sampling time. To cover 5 h of the experiment duration, $M=1800$ sampled data is required. The minimization is carried out using the SIMPLEX numerical optimization method running in MATLAB [32]. The value of the slices number N was chosen using the following strategy: starting with a few slices for the diffusional state-space discretization, the minimization procedure is repeated by increasing the number of slices until the cost does not vary significantly. To avoid local minima, several runs are carried out by starting from different initial values and verifying that the minimum is always the same in the constrained set of admissible values.

Results and discussion

Numerical parameter estimation

The initial substrate concentration on the anode surface is equal to 0.5 $\text{g}\,\text{L}^{-1}$, which corresponds to a fractional concentration of $S(Z_{0},0)=\bar{S}=1$. Eight experiments were carried out where the voltage between both electrodes was digitally recorded. Starting in an open circuit, for each experiment, different current amplitudes were obtained by connecting an external varying resistive load, $R_{{\mathrm{e}}}$, between the electrode terminals. The ohmic resistance ranges in the interval of $R_{\mathrm{e}}\in [50, 45000]\varOmega$.

A number of $N=7$ slices were used to represent the diffusional system. In Table 2, the parameter intervals obtained for the eight experiments are shown. The value of $R_{\mathrm{i}}$ coincides with those reported in [30] and the double-layer capacitance obtained per unit of area of the anode is similar to the values reported by [4].

Table 2 Parameter interval values obtained from model parameter estimation

Among the experimental set of data, Fig. 6 shows a representative one. Figure 6a shows the measured, V, and predicted, $\hat{V}(i,\theta )$, voltages. Figure 6b presents the predictions of acetate concentration at the anode surface $\hat{S}(z_0,t)$, Faradaic current $\hat{I}_{{\mathrm{f}}}(t)$ and capacitive current $\hat{I}_{\mathrm{c}}(t)$. It can be seen from the figures that model predictions are generally in good accordance with the measured data. The model satisfactorily predicts both the transient behavior and steady state at each step change in $R_{{\mathrm{e}}}$ and also at the OCV. It can be observed that at the beginning of the experiment, there is a net charge accumulation in the double layer, which is released when the external load is connected. The effect of the double-layer capacitance dominates the MFC dynamics during transient periods, while the Faradaic current increases gradually until reaching its steady-state value for the external load used. In Fig. 6b, after the system relaxes, the steady-state substrate concentration reaches the bulk concentration and the $\text{OCV}$ is the same as at the beginning of the experiment.

Fig. 6

Experiment 4. a Measured voltage: $V$ (dashed line), predicted voltage: $\hat{V}$ (solid line), b substrate concentration on the electrode surface: $\hat{S}(z_0,t)$ (dashed line), capacitive current: $\hat{I}_{c}$ (dashed dot line), Faradaic current: $\hat{I}_{f}$ (solid line)

Model validation

In Table 3, a cross-validation test is depicted. It consists of evaluating the cost of the ith record using the identified parameters, $\theta _j$, from the jth record. From the cross-validation test, it is observed that the relative error is always lesser than approximately $28\%$. In addition, the costs for all the experiments using the mean parameter values, $\bar{\theta }$, are shown. It can be seen that for the mean value parameters, the cost for all experiments is lower than approximately $13\%$.

Table 3 ${\bar{Q}}_{i}(\theta_j)$ obtained with the cross-validation test

To perform additional tests for model validation, the delivered power, $P=V^{2}/R_{\mathrm{e}}$, and the predicted power, $\hat{P}=\hat{V}^{2}(\bar{\theta })/R_{\mathrm{e}}$, versus the current I, at different steady states, both expressed as density, are compared and depicted in Fig. 7. The maximum value of power density obtained is 28.23 $\text{mW}\,\text{m}^{-2}$, with an $R_{\mathrm{e}} = 676\,\varOmega$. This power density is comparable with values reported by Inoue et al. [33] (36 $\text{mW}\,\text{m}^{-2}$) who employed a miniaturized MFC, and higher than the values reported by Ieropoulos et al. [34], (2.8 $\text{mW}\,\text{m}^{-2}$) who uses a two-chamber MFC. From the several experiments, it is concluded that the proposed model adequately represents the main processes involved in the dynamical behavior of the MFC.

Fig. 7

Measured, P (times symbol), and estimated, $\hat{P}$ (solid line), power density vs current density. a Predicted power density of Experiment 3 carried out with parameter values of Experiment 4, b predicted power density of Experiment 5 carried out with parameter values of Experiment 2

Conclusions

A simple model of the biofilm in an MFC is presented based on the electrochemical description of the transfer charge and diffusion processes. The model has only five parameters, which turns out to be easy for identification and to be used for real-time applications. The model also provides the Faradaic and capacitive current from which the important effect of the double-layer capacitance can be obtained during the transient. The state variables are the substrate concentration at different spatial positions in the biofilm and the potential at the biofilm, which is associated with the double-layer capacity. A simple second-order equivalent electrical circuit of the MFC is derived.

Tests using microbial cells from Río Negro river (Patagonia-Argentina) show that a low-order approximation of the diffusional process is, indeed, sufficient to obtain a good model fit. Voltage and power predictions are in good agreement with the experimental data, which were obtained using a wide range of external loads.

Glossary

$a=$

$D/\varDelta z^2$

$a^{\mathrm{r}}$ and $a^{\mathrm{o}}$

Symmetry factors

$\alpha^{\mathrm{r}}=$

$a^{\mathrm{r}} F/RT$

$\alpha ^{\mathrm{o}}=$

$a^{\mathrm{o}} F/RT$

$\alpha=$

$\alpha^{\mathrm{r}} = \alpha^{\mathrm{o}}$

$b=$

$-1/(F \gamma \bar{c} \varDelta z N_{\mathrm{e}})$

$c_{0}$

Initial substrate concentration

$c^{\mathrm{r}}$

Concentration of reduced species at the electrochemical interface

$\bar{c}^{\mathrm{r}}$

Maximum acetate concentration

$c^{\mathrm{o}}$

Concentration of oxidized species at the electrochemical interface

$C_{\mathrm{dl}}$

Double-layer capacity

D

Effective diffusion coefficient

$\varDelta z$

Thickness of the slice

$E_{\mathrm{c}}$

Constant cathode potential

$E_{\mathrm{a}}$

Anode potential

$E_{\mathrm{a}}^{\mathrm{o}}$

Anode reference potential

EMF

Electromotive force

F

Faraday constant

$\gamma$

Biofilm area

I

Total current

$I_{\mathrm{c}}$

Double-layer current

$I_{\mathrm{f}}$

Faradaic current.

J(z, t)

Flux of the substrate in the biofilm at time t and spatial position z

$K^{\mathrm{r}}$

Constant rate of reduced species

$K^{\mathrm{o}}$

Constant rate of oxidized species

$\text{M}_{\mathrm{ox}}$

Oxidized mediator

$\text{M}_{\mathrm{red}}$

Reduced mediator

$\eta$

Anodic overpotential

N

Number of slices

$N_{\mathrm{e}}$

Electron-mol/acetate-mol ratio

OCV

Open Circuit Voltage

R

Universal gas constant

$R_{\mathrm{e}}$

External load

$R_{\mathrm{i}}$

Ohmic resistance

$R_x$

Dummy resistance

$R_x$

Dummy resistance

S

Fractional substrate concentration at the interface

S(z, t)

Fractional substrate concentration in the biofilm at time t and spatial position z

$S(z_{0},t)$

Fractional substrate concentration in the biofilm at time t and spatial position $z=0$

$S_{I=0}$

Fractional substrate concentration at zero current

$\bar{S}$

Constant substrate concentration in the bulk

T

Temperature

V

Potential between the terminals of both electrodes