Introduction

By the end of 2016, cumulative global installed photovoltaic (PV) installations will outshine 310 gigawatts (GW), compared to just 40 GW at the end of 2010, and more than 69 GW in 2011 according to HIS [1]. The European Photovoltaic Industry Association (EPIA) reported that the production of solar energy is estimated to attain 1845 GW by 2030. Such potential will offer electricity to 4.5 billion people mostly in the developed countries [2].

In a short time, the world energy consumption would be 10 terawatts (TW) per year, and in less than 35 years, it is expected to reach 30 TW. The world would have need of utilizing around 20 TW of non-CO2 energy to reduce the amount of CO2 in the atmosphere by 2050 [3]. The easiest way to overcome such challenging goals is to get benefit from photovoltaics as well as from other renewable sources capable of producing these huge amounts in a timely manner.

In an attempt to enhance and increase the employment of PV systems, research activities are being piloted in an endeavor to gain further improvement in terms of cost, efficiency and reliability.

Unlike regular silicon cells, novel materials such as InGaN would be a reasonable choice to gain further reimbursements keeping in mind that, unfortunately, PV technology is still a costly and expensive solution as compared to fossils. Hence, III-nitrides are drawing more attention due to their high performance. Indium gallium nitride alloy exhibits excellent characteristics which makes it an ideal candidate to be used in solar cells. This system shows many interesting properties such as the important absorption coefficient, a tunable band gap which varies from 0.7 eV (InN) to 3.4 eV (GaN) covering almost the whole solar spectrum, a high carrier mobility, a large breakdown bias voltage, an effective electron transport and a strong spontaneous and piezoelectric polarization which improve the solar cell performance [1,2,3,4,5,6].

According to [7,8,9], it has been reported that the development of all-InGaN multi-junction solar cells with an overall effectiveness larger than 50% is theoretically feasible. However, practically, it is still doubtful to reach what has been estimated theoretically. This is due to numerous reasons such as the high indium (In) incorporation, the inadequate control during the epitaxial growth of thin films and the polarization effects [10,11,12].

For instance, and in an attempt to consider all physical and environmental impacts on the performance of the PV cell in terms of energy production, the previously mentioned polarization effects of the InGaN all along with the parasitic components such as the shunt and the series resistances would be taken into consideration when developing the Matlab/Simulink model. Obviously, the model, based on mathematical equations, is going to call for the effects of insolation and temperature changes on the extracted power.

This paper is organized as follows: Sect. 2 gives an overview of the electrical equivalent model of the InGaN solar cell along with the mathematical equations that describe the electrical behavior of the cell. Such an analysis has been implemented using a numerical model under the Matlab/Simulink environment in Sect. 3. Therefore, the effects of physical and environmental parameters’ variations on the performance of the InGaN solar cell have been highlighted. Finally, Sect. 4 has been allocated to construct a PV module starting from the PV cell model. The effects of the possible interconnections of the output voltage–current have been shown (Fig. 1).

Fig. 1
figure 1

Electrical equivalent circuit of a PV cell

Full size image

PV cell electrical model

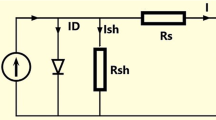
In terms of an electrical schematization, the PV cell can be modeled using an ideal current source corresponding to the photo-current (I ph), a diode that represents the semiconductor hetero-junctions (D), a shunt resistance aimed to account for the power losses around the junction (R sh), and a series resistance that devotes the losses through cells’ interconnections (R s). At the output terminals of the PV cell, the voltage and the current are denoted as V pv and I pv, respectively. For an opened cell, V pv becomes a potential difference at no-load and is known as the open-circuit voltage (V oc). The current reaches its maximum when the output terminals are short-circuited and, in such a case, it is called the short-circuit current (I sc). According to this electrical model, the current I pv is expressed as follows [13,14,15]:

$${\kern 1pt} I_{\text{pv}} = I_{\text{ph}} - I_{\text{s}} \left\{ {\exp \, \left( { \, q\frac{{(V_{\text{pv}} + R_{\text{s}} I_{\text{pv}} )}}{{AK_{\text{B}} T}} \, } \right) - 1} \right\} - \left( {\frac{{V_{\text{pv}} + R_{\text{s}} I_{\text{pv}} }}{{R_{\text{sh}} }}} \right),$$
(1)

where q is the free electron charge, A is the ideality factor, K B is the Boltzmann constant and T is the temperature.

There is no doubt that the photo-current produced by the solar cell differs from the current flowing through the external circuitry. In fact, the current I ph will split into three currents; the current that passes through the diode, the current that passes through the shunt resistance and the current I pv that will pass to the load. The voltage across the shunt resistance is normally the output voltage dropped by the voltage across the series resistance. The term I s represents the saturation current of the diode, in which are included the polarization effects. For photovoltaic cells to model, the discontinuity of the spontaneous polarization (P) between the GaN barrier and the InGaN quantum well leads to a formation of an interfacial charge density σ s such as σ s = P where P is given by:

$$P = \left[ {P_{{{\text{In}}_{x} {\text{Ga}}_{1 - x} {\text{N}}}}^{\text{sp}} - P_{{{\text{In}}_{x} {\text{Ga}}_{1 - x} {\text{N}}}}^{\text{pz}} } \right] - P_{\text{GaN}}^{\text{sp}} .$$
(2)

Here, P sp and P pz are the spontaneous and piezoelectric polarizations. It should be noted that the induced-polarization at the InGaN/GaN hetero-interface depends on the indium content in the InGaN epilayer and can be calculated using an ab initio model developed by Fiorentini et al. [11, 16]. Definitely, due to charge spreading at the vicinity of the interface, the polarization charges are distributed in a few atomic layers as thick as 1 nm [11, 12], called W pz. Hereafter; we assume that the polarization charges can be described by a bulk charge density ρ pz such as:

$$\rho_{\text{pz}} = \frac{P}{{W_{\text{pz}} }}.$$
(3)

In including the electron-sheet density and the spreading of piezoelectric polarization charges, the saturation current can be expressed by the following equation. Such a form of I s will be used as a basic equation in building our numerical model under Matlab/Simulink following Zhang et al. [17, 18] and Belghouthi et al. [11, 12]:

$$I_{\text{s}} = I_{0} \exp \left( {\frac{{q^{2} \rho_{\text{pz}} W_{\text{pz}}^{2} }}{KT}} \right).$$
(4)

When no-load is applied, the output voltage reduced to V oc and the cell’s current is null. Therefore, Eq. (1) is rewritten as:

$$0 = I_{\text{ph}} - I_{\text{s}} \left\{ {\exp \left( { \, q\frac{{(V_{\text{oc}} )}}{AKT} \, } \right) - 1} \right\} - \left( {\frac{{V_{\text{oc}} }}{{R_{\text{sh}} }}} \right).$$
(5)

Since, R sh is high enough so that \(\left( {\frac{{V_{\text{oc}} }}{{R_{\text{sh}} }}} \right) \cong 0\), then, the open-circuit voltage can be deduced as follows:

$$V_{\text{oc}} = \frac{AKT}{q}\ln \left( {\frac{{I_{\text{ph}} }}{{I_{\text{s}} }}} \right).$$
(6)

By substituting the saturation current I s by its expression into Eq. (6), the open-circuit voltage takes the following form:

$$V_{\text{oc}} = \frac{AKT}{q}\ln \left( {\frac{{I_{\text{ph}} }}{{I_{0} }}} \right) - \left( {\frac{{q^{2} \rho_{\text{pz}} W_{\text{pz}}^{2} }}{KT}} \right).$$
(7)

As shown from Eq. (7), the second term includes the piezoelectric polarization effects. When the potential difference between the two electrical terminals is null, the short-circuit current will be given by [23]:

$$I_{\text{sc}} = I_{\text{ph}} - I_{\text{s}} \left\{ {\exp \, \left( { \, q\frac{{\left( {R_{\text{s}} I_{\text{sc}} } \right)}}{AKT} \, } \right) - 1} \right\} - \left( {\frac{{R_{\text{s}} I_{\text{sc}} }}{{R_{\text{sh}} }}} \right).$$
(8)

On the other hand, the series resistance R s is as small as, then \(\exp \left( { \, q\frac{{\left( {R_{\text{s}} I_{\text{sc}} } \right)}}{AKT} \, } \right) \cong 1\) and thus, the short-circuit current can be approximated by the following expression:

$$I_{\text{sc}} = \frac{{I_{\text{ph}} }}{{1 + \frac{{R_{\text{s}} }}{{R_{\text{sh}} }}}}.$$
(9)

To achieve a better electric efficiency, many trends are focused on keeping the extracted power from the PV cell/module around the so-called maximum power point (MPP). In such a case, the current and voltage would be equal to I mpp and V mpp, respectively. In view of that and from Eq. (1), the following equation can be established [23]:

$$I_{\text{mpp}} = I_{\text{ph}} - I_{\text{s}} \left\{ {\exp \left( {q\frac{{(V_{\text{mpp}} + R_{\text{s}} I_{\text{mpp}} )}}{AKT}} \right) - 1} \right\} - \left( {\frac{{V_{\text{mpp}} + R_{\text{s}} I_{\text{mpp}} }}{{R_{\text{sh}} }}} \right).$$
(10)

Based on Refs. [19, 20], it is reported that the power delivered to the load as well as the quality factor of the diode that would be used to model a PV cell will be given according to:

$$P = IV$$
(11)

and

$$A = \frac{{_{{V_{\text{mpp}} + I_{\text{mpp}} R_{\text{s}} - V_{\text{oc}} }} }}{{V_{\text{T}} \left\{ {{\text{Ln}}\left( {I_{\text{sc}} - \frac{{V_{\text{mpp}} }}{{R_{\text{sh}} }} - I_{\text{mpp}} } \right) - {\text{Ln}}\left( {I_{\text{sc}} - \frac{{V_{\text{oc}} }}{R}} \right) + \frac{{I_{\text{mpp}} }}{{I_{\text{sc}} - \frac{{V_{\text{oc}} }}{{R_{\text{s}} }}}}} \right\}}}.$$
(12)

The short-circuit current given in a PV module datasheet is for standard test conditions of irradiance and air mass at a temperature of 25 °C, G 0 = 1000 W/m2, for AM1.5. Accordingly, for any given irradiance G, the PV cell current can be adjusted using the following law [19]:

$$I_{{{\text{sc}}/G}} = \, \left( {\frac{G}{{ \, G_{0} }}} \right)I_{{{\text{sc}}/G_{0} }} .$$
(13)

Matlab/Simulink based modeling of the InGaN solar cell

Upon the mathematical analysis of the PV cell in Sect. 2, the Matlab/Simulink model of Fig. 2 has been developed. As previously investigated, the polarization effects are described using Eq. (4). This later has been constructed under Matlab/Simulink as shown in Fig. 3.

Fig. 2
figure 2

InGaN double hetero-junction solar cell Matlab/Simulink model

Full size image
Fig. 3
figure 3

Implantation of polarization charges in Matlab/Simulink model

Full size image

Within this work, we would apply a numerical model to a p-i-n structure consisting of a stack of 150 nm thick n-GaN, 200 nm thick In0.12Ga0.88N/GaN and 100 nm thick p-GaN layers. The study has been conducted considering AM1.5 conditions and using material parameters provided by Brown et al. [21] and Rabeb et al. [11].

The preliminary simulation results of Fig. 4 have been obtained. In the same figure, the power and the cell’s current as function of the cell’s voltage has been plotted.

Fig. 4
figure 4

Current and power vs voltage characteristics for a In0.12Ga0.88N/GaN p-i-n solar cell

Full size image

To validate the Matlab/Simulink model, the obtained results have been compared to those previously found based on an analytical model developed by the same author [11]. Likewise, the same numerical results were matched to those experimentally obtained by [22]. Figure 5 shows an extremely good match of the experimental, analytical and numerical results.

Fig. 5
figure 5

Experimental current–voltage results (dots) and simulated ones obtained using the numerical and the analytical model for a p-i-(In0.12Ga0.88N)-n solar cell (dashes)

Full size image

The electrical specifications taken into consideration for the validation are listed below in Table 1.

Table 1 Photovoltaic parameters of In0.12Ga0.88N p-i-n hetero-junction solar cell structures under 1 sun illumination
Full size table

Nevertheless, and as shown by Fig. 5, the Matlab/Simulink simulation results seem to be closer to the experimental ones. This is owing to the fact that the numerical model is much more mature in terms of, and not limited to, the phenomena such as:

  1. 1.

    polarization effects,

  2. 2.

    shunt resistance,

  3. 3.

    series resistance.

Such promising results pushed strongly to go further towards the variation of the physical and environmental conditions in order to behaviorally investigate the InGaN solar cell. For the sake of a realistic and efficient description, the above listed parameters have been changed and their impacts on the cell’s efficiency have been shown next.

Effects of insolation on the PV cell

Obviously, when the solar irradiation increases, more electrons would be extracted from the solar cell. Hence, the current of the PV cell through the external circuitry increases significantly, so does the output voltage. Consequently, the extracted power increases exponentially with the insolation. Accordingly, Figs. 6 and 7 clearly show a significant shift of the maximum power point towards higher power levels as long as the insolation gets higher.

Fig. 6
figure 6

Effect of insolation on current–voltage characteristics of a In0.12Ga0.88N/GaN p-i-n solar cell

Full size image
Fig. 7
figure 7

Effect of insolation on power–voltage characteristics of a In0.12Ga0.88N/GaN p-i-n solar cell

Full size image

The above model calculates the PV cell photocurrent, which depends on the radiation and the temperature according to equation [20]:

$$I_{\text{ph}} = (I_{\text{cc}} + K_{\text{i}} (T - 298))\frac{G}{{G_{0} }},$$

where G is the solar radiation (W/m2), G 0 is the standard radiation (1000 W/m2), I cc is the short circuit current and K i = I cc/I 0 is the intrinsic relative constant of the material.

Thermal effects on the PV cell

Opposite to the insolation effects, the temperature has a drastic impact on the solar cell efficiency. Indeed, when photons hit the PV cell, they deliver their energies to the extracted electrons. These electrons would be, in principle, able to jump over the band gap and pass the photo-created electrons towards the external circuitry. However, some of them lack the required energy to do so. In such case, and due to the thermal agitation, the solar cell heats up and its photovoltaic conversion shows a drop.

The diode reverse saturation current varies as a cubic function of the temperature and it can be expressed as [23]:

$$I_{\text{s}} (T) = I_{\text{s}} \left( {\frac{T}{{T_{\text{nom}} }}} \right)^{3} \exp \left[ {\left( {\frac{T}{{T_{\text{nom}} }} - 1} \right)\frac{{E_{\text{g}} (T)}}{{N \cdot V_{\text{t}} }}} \right],$$

where I s is the diode reverse saturation current, T nom is the nominal temperature, E g(T) is the band energy of InGaN and V t is the thermal voltage.

The temperature-dependent band gap adopted for InGaN is [23]:

$$E_{\text{g}} (T) = E_{\text{g}} (T = 0\,{\text{K}}) - \frac{{\alpha T^{2} }}{\beta + T},$$

E g is the (T = 0 K) the band energy of InGaN at T = 0 K. α is the empirical constant eV. β is the constant associated with Debye temperature.

The photocurrent shows an increasing trend when temperature gets higher due to the diminution of the InGaN band gap, the output voltage, however, drops down significantly. This trend is basically caused by the reverse variation of the built-in electric field as a function of temperature. This leads to the conclusion that the electrostatic field would exhibit a decreasing tendency as temperature increases.

In summary, an increase in temperature can give rise to a slight increase of the current and to a significant drop of the voltage at output as well. This leads to a drop of the photovoltaic power as shown in Figs. 8 and 9. This has incited recent research works to try innovative cooling systems with the aim of improving solar cell efficiency [24].

Fig. 8
figure 8

Temperature dependence of the current–voltage characteristics of a In0.12Ga0.88N/GaN p-i-n solar cell

Full size image
Fig. 9
figure 9

Temperature dependence of the power–voltage characteristics of a In0.12Ga0.88N/GaN p-i-n solar cell

Full size image

Effects of the series resistance on the PV cell

The series resistance should be as small as it can be neglected. This still remains a critical issue of solar cells developers. However, in order to come up with a widespread numerical model, its effects have been extensively investigated. Now, it is well argued that the series resistances do not affect neither the short-circuit current, nor the open-circuit voltage of a PV cell [19, 20]. This means that, based on Kirchhoff’s voltage law, in the open-circuit situation, the series resistance is not flowed by any current so that its effects are systematically removed. This implies that the open-circuit voltage is not affected by R s. For the short-circuit, the current I sc that flows between the two terminals of the PV cell is the same current that flows through the series resistance, which means that the series resistance does not affect the short-circuit current of the PV cell.

Nevertheless, the series resistance consumes a fraction of the power, even a small amount by Joule effects. This leads to suggest that, as shown in Figs. 10 and 11, even though both the short-circuit current and the open-circuit voltage are affected, the maximum power point would shift towards lower energies as the series resistance increases.

Fig. 10
figure 10

Current–voltage characteristics of a In0.12Ga0.88N/GaN p-i-n solar cell for different series resistance values

Full size image
Fig. 11
figure 11

Power–voltage characteristics of a In0.12Ga0.88N/GaN p-i-n solar cell for different series resistance values

Full size image

Effects of the shunt resistance on the PV cell

As shown from the electrical equivalent model of the PV cell, the shunt resistance is connected in parallel to the junction diode. This resistance will form a node with the series resistance. According to Kirchhoff’s current law, the current through this resistance would be subtracted from the main current, I ph, and thus the resulting current, I pv, is the current that would pass to the external circuitry. In view of that, the higher the shunt resistance, the higher the current of the PV cell. This would mean that, when the shunt resistance increases, the efficiency of the PV cell gets better leading to power improvement. The relevant results are in agreement with such a prediction, as illustrated in Figs. 12 and 13.

Fig. 12
figure 12

Current–voltage characteristics of a In0.12Ga0.88N/GaN p-i-n solar cell for different values of shunt resistance

Full size image
Fig. 13
figure 13

Power–voltage characteristics of a In0.12Ga0.88N/GaN p-i-n solar cell for different values of shunt resistance

Full size image

Matlab/Simulink model for PV modules’ designs

Definitely, the output power of a single PV cell does not exceed few tenths of milliwatts. Such a small output power cannot be utilized in a real device. Therefore, the interconnection of few cells seems to be required in order to achieve a higher output power. PV cells could be interconnected either in series, in parallel or in series parallel. Each configuration has its own impact on the level of the current and/or voltage of the obtained module. In regular cells made up of silicon, the number of cells in a PV module could be 36 or 72 cells upon the required output current/voltage. However, because of the high performance of InGaN/GaN cells and regardless the cost of the material itself, the number of cells should be minimized. Hence, the modules’ size as well as losses could be reduced.

As has been previously claimed, the Matlab/Simulink reveals as a powerful computing tool to model the PV cells in a concordance with the users’ in terms of the voltage/current and power at output. In fact, within a PV module, when cells are associated in series, the current remains the same while the voltage is multiplied by the number of cells. In the case when the PV cells are connected in parallel, the module’s voltage is kept the same as the one of a single cell but the current is multiplied by the number of cells. The third possible configuration is the so-called mixed configuration. In this situation, firstly, cells are connected in series to form a branch, and then branches are connected in parallel. Accordingly, within a single branch, the voltage is multiplied by the number of cells that form the branch. We shall measure this voltage between the two terminals of the PV module. The module’s current is the one that flows through a branch multiplied by the number of branches connected in parallel. Obviously, within the same branch, all of the PV cells are traversed by the same current.

The above theoretical expectations seem to be of great interest to simulate numerically different architectures of PV cell devices. As an illustration, Fig. 14 presents the static waveforms of a PV module in which solar cells are connected in series Fig. 14a, in case cells are connected in parallel Fig. 14b, c when cells are connected in a mixed configuration.

Fig. 14
figure 14

From left to right current and power vs voltage characteristics for a In0.12Ga0.88N/GaN PV a module in series, b in parallel and in c series parallel

Full size image

Conclusion

This paper deals with the development of a numerical model of an InGaN p-i-n solar cell under Matlab/Simulink environment. It starts with an extensive outline of the electrical equivalent model based on mathematical equations. Thanks to its high performance on the cell output power, the InGaN physical proprieties have been considered. Moreover, for the sake of a widespread behavioral viewpoint, the environmental disturbances as well as the parasitic components have been taken into consideration. These are, respectively, the shunt and series resistances variations as well as the temperature and the insolation changes. To be aware of the impact of the previously listed parameters, the developed model has been firstly validated by means of a comparison to the experimental results, from one hand, and to the analytical results from the other hand. Such analytical and experimental results have been shown within the body of the paper. Besides, the spontaneous and the piezoelectric polarizations effects have been included within the Matlab/Simulink model. Once the model is validated, it has been extended to form a PV module. In fact, within a module, cells could be interconnected in three different configurations: series, parallel and mixed. The developed model has shown a mature flexibility in such a way, it could be an up-to-date solution in the field of solar photovoltaics modeling.