Introduction

Recently, a lot of research has taken place in the design and control of renewable energy systems such as solar, wind, hydraulic and biomass, because they are sustainable, cost-effective and alternatives for conventional energy sources.

For isolated and remote areas, it may not be practical or economically viable to provide a connection to the distribution grid system, where utility lines are uneconomical to install due to the terrain and geographical condition difficulties.

In the literature, regarding the efficient integration of renewable sources for supplying remote power systems, Sonia Leva [1, 2] presents a techno-economic analysis about the possible implementation of hybrid systems (photovoltaic and wind energy) on an existing plant for supplying isolated applications such as industrial applications related to telecommunications. In terms of the stability of an isolated system, the author [3] presents a theoretical approach for the dynamic stability analysis in case power-quality disturbances such as unbalances, harmonics, and inter harmonics take place. The pollution, resulting from the current and voltage the system acquires, may cause stability problems especially in isolated electric plants where small generators, supply motor drives, static converters, or nonlinear loads are involved. The present study constitutes a technical investigation, aiming at hardware implementation, to control small power generators, based on self-excited induction generators, and provides a versatile way to investigate different hybrid schemes of renewable energy generation fuel cell and PV.

Self-excited induction generators (SIEG) have been found to be very suitable for small power generation by small or micro-hydro as well as wind systems; they provide a promising solution for isolated areas to generate electrical energy because of the low price, mechanical simplicity and robust structure.

The use of cage induction machine connected to the fixed bank capacity has the advantage of simplicity in implementation and low cost due to the absence of a static converter. However, this configuration allows operating limits which must be taken into account, especially changes in amplitude and voltage frequency during load and speed variations [4]. In the literature, many authors [5–9] have discussed different criteria for selecting the limiting value of capacitance and speed for successful operation of SEIG under various conditions.

With regard to the drawback of this machine, the output voltage is affected by the load and speed condition. A number of schemes have been suggested for regulating the terminal voltage and have been reported in literature [10–16]. Since there is limited work published on the application of multilevel for the control of several SEIGs working in parallel and independent. Also, the literature is very limited on the application of H-bridge inverters in standalone systems, where they have several advantages, namely low distortion voltages and currents and low switching losses and the power can be efficiently transferred from different generators with better power quality.

The aim of this paper is to examine this technology for small power generation using self-excited induction generators. It is hoped that this will draw the attention of researchers toward its application, especially for remote and isolated locations. An attempt is made to control the terminal voltage and frequency from the number of SIEGs connected to multilevel converters.

Multilevel converters have been under research and development for more than three decades and have found successful industrial application. In recent years, many publications have addressed multilevel converter technology and stressed the growing importance of multilevel converters for high-power applications [17]. The most popular multilevel converter topologies are flying capacitor (FC), cascaded H-bridge (CHB) converters and neutral point clamped (NPC).

The cascaded H-bridge multilevel topology is the most convenient model compared to other topologies according to the required switching devices. This topology requires separate DC sources for each H-bridge which is an advantage for applications such as renewable or alternative energy sources, because it offers a modular solution by collecting large numbers of PV panels or generator as isolated DC sources, which allows generating a large number of voltage levels in the output. However, this advantage comes along with drawbacks, which are the inherent power imbalance between generators in each leg as well as a power imbalance among the different phases of the inverter [18, 19]; this condition will affect the performance of the CHB and load.

In this paper, the two types of imbalances will be addressed sequentially in the control strategy: first, the phase imbalanced is compensated through the modification of the phase references, and the amplitude imbalance is compensated by generating the same reference voltage, because the voltage generated by the SIEGs depends strongly on the variation of the prime mover.

A suitable topology has been proposed, through the design and control of an inverter for isolated load to efficiently make use of energy from the generators. The proposed inverter includes three H-bridges and four SPWM switching signals to control each bridge, respectively. The operating principle and design guidelines of the proposed scheme are presented along with the performance analysis and simulation using MATLAB Simulink with three self-excited induction generators operating at different variable speeds.

The experimental prototype has been developed for the validation of the proposed converter system. The Dspace controller is used to transfer the PWM signals and to feed back the voltage signals of each phase load voltage. The error between the reference RMS phase voltage and the feedback RMS phase voltages are used to effectively generate proper PWM signals to drive IGBTs of the controlled power converter.

The rest of this paper is organized as follows. The system configuration for small power generation is presented in “Configuration of the proposed standalone system”. The control scheme and hardware configuration are presented in “Configuration control algorithm”. The last section shows the simulation, experiment results and discussion.

Configuration of the proposed standalone system

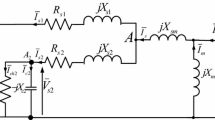
The system is designed for an isolated location. The complete configuration of the proposed generation system using an SEIG is shown in Fig. 1. The self-excited induction generator using three-phase AC capacitors can start its voltage buildup from a remnant magnetic flux in the core. This voltage buildup starts when the induction generators are driven at a given speed and an appropriate capacitance is connected at its terminals. The DC sources of each single-phase H-Bridge inverter are obtained from three-phase diode rectifiers powered by self-excited induction generators.

Fig. 1
figure 1

Configuration of the proposed standalone system

Full size image

The following sections present the modelling of all subsystems of the proposed system. The main components are SIEG, three-phase diode rectifier, three-level cascaded H-bridge inverter and AC load.

Self-excited induction generator

Including initial conditions, i.e. initial voltage in the capacitors and remnant magnetic flux in the core, one can obtain the following differential equation. The state-space form of the induction generator in the q–d synchronously rotating reference frame is given by [20]:

$$\begin{aligned} \frac{\text{d}}{{{\text{d}}t}}I = AI + B \hfill \\ I = \left[ {\begin{array}{*{20}c} {i_{\text{qs}} } \\ {i_{\text{ds}} } \\ {i_{\text{qr}} } \\ {i_{\text{dr}} } \\ \end{array} } \right],\quad B = \left[ {\begin{array}{*{20}c} {L_{\text{m}} K_{\text{q}} } & { - L_{\text{r}} V_{\text{cq}} } \\ {L_{\text{m}} K_{\text{d}} } & { - L_{\text{r}} V_{\text{cd}} } \\ {L_{\text{m}} V_{\text{cq}} } & { - L_{\text{s}} K_{\text{q}} } \\ {L_{\text{m}} V_{\text{cd}} } & { - L_{\text{s}} K_{\text{d}} } \\ \end{array} } \right],\;A = \frac{1}{L}\left[ {\begin{array}{*{20}c} { - L_{\text{r}} R_{\text{s}} } & { - L_{\text{m}}^{2} w_{\text{r}} L_{\text{m}} R_{\text{r}} } & { - L_{\text{m}} w_{\text{r}} L_{\text{r}} } \\ {L_{\text{m}}^{ 2} w_{\text{r}} } & { - L_{\text{s}} R_{\text{s}} L_{\text{m}} w_{\text{r}} } & {L_{\text{r}} L_{\text{m}} R_{\text{r}} } \\ {L_{\text{m}} R_{\text{s }} L_{\text{s}} w_{\text{r}} L_{\text{m}} } & { - L_{\text{s}} R_{\text{r }} } & { - L_{\text{s}} w_{\text{r}} L_{\text{r}} } \\ { - L_{\text{s}} w_{\text{r}} L_{\text{r}} L_{\text{m}} R_{\text{s}} } & { - L_{\text{s}} w_{\text{r}} L_{\text{r}} } & { - L_{\text{s}} R_{\text{r}} } \\ \end{array} } \right] \hfill \\ \end{aligned}$$
(1)

where \(L = L_{\text{r}} L_{\text{s}} - L_{\text{m}}^{2} .\)

The excitation system model is:

$$V_{\text{cq}} = 1/c(i_{\text{qs}} \_ i_{\text{rlq}} ) {\text{d}}t,$$
(2)
$$V_{\text{cd}} = 1/c(i_{\text{ds}} \_ i_{\text{rld}} ) {\text{d}}t,$$
(3)

where \(i_{\text{r}} d\) and \(i_{\text{r}} q\) are input currents of the three-phase diode bridge rectifier.

The instantaneous amplitude of the magnetizing current of the SEIG is computed as:

$$I_{m} = \sqrt {(i_{\text{qs}} + i_{\text{qr}} )^{2} + (i_{\text{ds}} + i_{\text{dr}} )^{2} } .$$
(4)

Three-phase diode rectifier

Three-phase diode bridge rectifier is used to convert the variable magnitude, variable frequency voltage at the induction generator terminal into DC voltage. The circuit consists of six diodes, a top group of three diodes and a bottom group of three diodes.

Three-level cascaded H-bridge inverter

Cascaded H-bridge inverter is seen as the most suitable topology for the integration of the renewable energy, since the separate DC sources that it requires can be directly fed by PV arrays, wind turbine or fuel cells. The three-level cascaded H-bridge inverter consists of three identical single-phase H-bridges in each phase (HB_A, HB_B and HB_C). Each HB is supplied by a separate DC source, where V is the unit voltage. Each HB generates three voltages at the output: +V, 0 and −V, Each H-bridge has three-switching states as defined in Table 1.

Table 1 Switching state definitions for phase R
Full size table

Configuration control algorithm

The control system permits the independent control for each H-bridge inverter; three PI controllers are necessary for independent control of each output of H-Bridge as shown in Fig. 2.

Fig. 2
figure 2

Control strategy of the proposed system

Full size image

The H-bridge topology has a left leg and a right leg. The phase shift between the upper H-bridge and the lower H-bridge is 90° and between each H-bridge 120°. The reference of each output voltage is the same for the three H-bridges. A two sinusoidal reference signal is compared to a triangular waveform to generate switching signals of inverter block in the SPWM modulation technique. The sinusoidal waveform is known as modulating signal and its frequency is 50 Hz. The triangular waveform is generated at a high frequency as carrier of modulation. The RMS output voltage of the H-bridge can be varied by changing the modulation index, M. The conventional PI controller is employed to adjust the equivalent modulation index.

$$M = \frac{{V_{\text{r}} }}{{ V_{\text{c}} }},$$
(5)

where, V r is the amplitude of the reference signal and V c is the amplitude of the control signal.

The RMS output voltage is defined as [21]:

$$V_{\text{rms}} = \left( {\mathop \sum \limits_{M = 1}^{2p} \frac{\sigma }{\pi }} \right)V_{\text{s}} ,$$
(6)

where V s is the input voltage, \(\sigma\) the width of the mth pulse and p the number of pulses per half-cycle.

Results and discussion

The feasibility of the proposed control method has been investigated and verified through computer simulations and experimental results.

Simulation results

MATLAB/Simulink® modelling is used to examine the effectiveness of the proposed control. The residual magnetism in the machine is taken into account in the simulation process, because it is not possible for the induction generator to be self-excited without it. The three induction generators are rated at 3.6 kW. The relationship between magnetizing inductance (L m) and phase voltage for induction machine was obtained experimentally by [22]: L m = 1.56e−11.\({v^{4}}\) + 2.44e−8.\(v^{3}\) − 1.19e−5.\(v^{2}\) + 1.42e−3.\({v^{{}}}\) + 0.245.

The proposed system starts excitation process from capacitors bank of 60 μF which are connected across the stator terminals of an induction machine. The global system is tested during 8 s, and the three generators are subjected to step change in the rotor speed as shown in Fig. 3 to give variable DC voltage to the input inverter. The reference RMS voltage of the three H-bridges is set at 230 V and later changed to 110 V after 6 s to show the effectiveness of the controller. The steady state and dynamic behaviour of the system under normal conditions are presented.

Fig. 3
figure 3

Variation rotor speed of the three generators: a SIEG 1, b SIEG 2, c SIEG 3

Full size image

Figures 4 and 5 show the effect of the stator terminal voltage and DC link voltage for three generators under variation of rotor speed, respectively.

Fig. 4
figure 4

Terminal stator voltage of the three generators: a SIEG 1, b SIEG 2, c SIEG 3

Full size image
Fig. 5
figure 5

DC link voltage of the three generators: blue (SIEG 1), red (SIEG 2), green (SIEG 3)

Full size image

Constant voltage control is effectively achieved by employing a cascaded three-level H-bridge inverter with controllable output voltage. Simulation results for control voltage are presented for the three induction generators subjected to step changes in the prime mover and reference setting to demonstrate the validity of the proposed control scheme. The simulation results of the proposed system based on three self-excited induction generators under variation of speed obtained from the downscaled prototype confirm the merits as show in Fig. 6.

Fig. 6
figure 6

RMS control voltages of the three-cascade H-bridge

Full size image

Experimental results

The experimental setup of the proposed system as shown in Fig. 7 comprises 1.1 kW induction generator driven by an induction motor (as prime mover). The generator stator phase output voltages with a capacitor bank for excitation are connected to three-phase diode rectifiers of an H-bridge inverter. Two other H-bridge inverters are connected with a separate isolation transformer. These isolation transformers are fed with an auto transformer to simulate the behaviour of output voltage of SIEG, such as variation of the prime mover. The three output voltages of each cascaded H-bridge inverter are connected to an isolated load. The output phase voltages are fed back through an analogue-to-digital converter (ADC) of the DSPACE. The error between the reference and the feedback signals are passed through PI controllers to generate the modulation indexes used for the PWM signals to switch 12 IGBTs of the cascaded H-bridge inverter.

Fig. 7
figure 7

Hardware used for experimental evaluation

Full size image

Performance of the proposed system with step change in DC and load

The system operates under standalone mode, and the output of the converter is connected with different conditions, no load, a three-phase resistive load and induction motor.

To validate the control scheme in the experiment, the reference voltage is fixed at 110 V and the experiment is done under variable and unequal DC voltage through changing of the speed of SIEG and the source voltages of the two isolated transformers with an autotransformer.

Measurements are made using the two digital oscilloscopes at the same time with capture screens, in which the first measures the three continuous voltages of the inverter input and the second measures the three simple voltages output of the inverter.

Figures 8d and 9d show the experimental performance of the control scheme for the output voltage under variable and unequal input DC voltage (Figs. 8a–c, 9a–c) with no load.

Fig. 8
figure 8

Performance of the proposed system under different DC input voltages. a DC link voltage of H-bridge 1. b DC link voltage of H-bridge 2. c DC link voltage of H-bridge 3. d AC output voltages of three H-bridges

Full size image
Fig. 9
figure 9

Performance of the proposed system under different DC input voltages. a DC link voltage of H-bridge 1. b DC link voltage of H-bridge 2. c DC link voltage of H-bridge 3. d AC output voltages of three H-bridges

Full size image

Figures 10d and 11d illustrate the experimental waveforms of the output voltage and line current under unequal DC voltage (Figs. 10a–c, 11a–c) due to variation of source and rotor speed of SIEG feeding resistive load and induction motor, respectively.

Fig. 10
figure 10

Performance of the proposed system under different DC input voltages. a DC link voltage of H-bridge 1. b DC link voltage of H-bridge 2. c DC link voltage of H-bridge 3. d AC output voltages of three H-bridges feeding resistive load blue (line current)

Full size image
Fig. 11
figure 11

Performance of the proposed system under different DC input voltages. a DC link voltage of H-bridge 1. b DC link voltage of H-bridge 2. c DC link voltage of H-bridge 3. d AC output voltages of three H-bridge feeding induction motor blue (line current)

Full size image

Figure 12d shows the line to line voltage of three-level cascade H-bridge feeding an induction motor.

Fig. 12
figure 12

Performance of the proposed system under different DC input voltages. a DC link voltage of H-bridge 1. b DC link voltage of H-bridge 2. c DC link voltage of H-bridge 3. d AC line to line output voltage of H-bridge and current feeding induction motor

Full size image

The test experiments are conducted to demonstrate the response of the close loop system; the modulation index is changed to achieve the desired RMS phase voltage with balanced operation of a three phase. The system behaves with variation in DC link voltage, while the RMS AC output voltage is maintained constant as evident from Table 2. It is worth mentioning that the inverter usually operates with effectiveness for all the five cases as shown from Figs. 8, 9, 10, 11 and 12.

Table 2 Results
Full size table

The performance of renewable energy system based on small power generation working independently and parallel through voltage regulation is investigated in experimental results for no load, resistive load and inductive load. It is shown that the output AC load voltage can be effectively kept at a fixed value of around 110 V for balanced operation of a three-phase isolated load regardless of perturbation of source and application of loads.

In both the simulation and experimental tests, the RMS voltage effectively tracks to their references even with the variation and inequality of the DC link. A robust performance is obtained. The proposed method can be easily extended to other renewable source such as the PV system to achieve optimal performance with good quality.

Conclusion

This study proposes an effective control voltage configuration for three SIEG-based renewable energy supplies (micro-hydraulic or wind). A comprehensive simulation study demonstrates the performance of the proposed system during variable speed conditions of the three generators. It has been observed that the controller is capable of regulating the output voltage.

The specific contribution of this paper is summarized as follows:

  • Suitable topology for application of small power generation using induction generator in isolated location by three-level cascade H-Bridge.

  • Proposed control scheme for the output voltage regulation of three cascades H-bridge inverter without DC bus voltage regulation with DC/DC converter in the input of the H-bridge.

  • The system is designed in a flexible and versatile way for the investigation of different hybrid schemes of renewable energy generation