Introduction

The process configuration of a regenerative gas cycle always consists of a heat exchanger circuit and a combination of cylinder piston assemblies. In the sealed machines the working gas is warmed up and cooled down alternating by the heat exchangers to generate the pulsating process pressure. The pistons are mechanically connected to a gear; during a power stroke they push the gas through the heat exchangers, and they generate mechanical work by changing the whole gas volume. A configuration therefore consists of the elementary components which the working gas flows through in a certain order:

  • cylinder space (displacement or working cylinder),

  • heat exchanger (cooler or heater for external heat transfer),

  • regenerator (internal heat transfer).

For the optimal design of these components different methods for modeling and simulation are used (cf. [4]). The differential equations for the conserved quantities: mass, energy, and momentum are usually not directly solvable, i.e., do not have closed form solutions. Instead, solutions must be approximated using numerical methods. For purposes of simplified calculations, one may assume that the process takes place from initiation to completion without a change in a special state quantity of the system. In this case also analytic solutions exist, such as the Schmidt model for Stirling engines [11]. One more model that has occasionally been used is the model for the regenerator due to Hausen [2].

For the symbolic mathematics-based simulation of the gas cycle the single components can be modeled separately, where every component has an independent solving method for itself. One advantage is that special boundary conditions for a component can simplify modeling to receive an efficient solution of the underlying differential equations. Another advantage is that it is possible to simulate a higher number of different process configurations (e.g. Stirling or Vuilleumier process [4]) with this modular construction. Thereby the components are arranged according to their number and location in the flow. The \( n_{\text{K}} \) components are coupled by the whole energy balance of the process:

$$ {\text{d}}U_{\text{ges}} = - p_{\text{ges}} {\text{d}}V_{\text{ges}} + \mathop \sum \limits_{i = 1}^{{n_{\text{K}} }} {\text{d}}Q_{i} = \frac{\kappa }{\kappa - 1} {\text{d}}\left( {pV} \right)_{\text{ges}} $$
(1)

The process pressure sets again a boundary condition for the single components. Furthermore the components are coupled by the energy flow of the involved masses as well as without mass via the surrounding.

Simulation models for the component of the cylinder space exist for regenerative gas cycles and also for reciprocating compressors or internal-combustion engines. Analytic solutions for the cylinder space may be obtained by assumption of an adiabatic-, polytropic-, or isothermal process (cf. [1]), as with the Schmidt model [11]. In contrast, the studies of multidimensional effects like heat transfer [13] or the pressure loss are solely based on numerical methods. Other models are also using numerical methods simulating the cylinder spaces for piston engines based on ordinary differential equations, like [5] for Vuilleumier engines, [8] for diesel engines, or [10] for Stirling engines.

The analytical or semi-analytical methods are only partially suitable for aims of simulation-based optimization because gross simplifications for the real situation must be superinduced. The numerical approximations do not deal with this problem but with an analytical model the solution is held in form of an equation. It will then be easier to handle and one can clearly recognize the characteristics of the physical process. Additionally, for the simulation of regenerative gas cycles it is possible to calculate directly the periodical-steady state of the system. This paper aims at exploiting the benefits of an analytical calculation method without using gross simplifications for the modeling.

To determine the change of the state quantities one has to solve the differential equations for the conserved quantities under respect of the boundary conditions. In this connection, the change of the cylinder volume and the gas density gives the required information for the bordering components, like the emitting and receiving gas mass flow. For the multidimensional problem numerical methods may approximate the solution of the differential equations and perhaps yield useful information on analytic solution. In this case the investigations of the structural intrinsic properties of the system may be used, to provide the information for

  • the determination of the influence parameters of the cylinder space,

  • their effects and especially the influence of individual parameters change,

  • the simplifications that result from fixing certain parameters for the simulation, and

  • the conditions for the isothermal process, which is widely accepted in the field.

Finally, for simulation purposes analytic solutions are generally considered superior to numerical approximations.

Energy equation

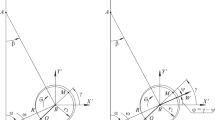
A single cylinder is connected with the remaining cylinder spaces of a process configuration by heat exchangers or by regenerators. The influencing quantities of the energy balance of a semi-open system are shown in Fig. 1. These are the transported heat and work via the surrounding and the enthalpy flow rate to connect the other modules by the interface \( x \):

Fig. 1
figure 1

Schematic view of a cylinder space with the influencing quantities of the energy balance

Full size image
$$ \dot{H} = \dot{m} c_{\text{p}} T_{\text{x}} $$
(2)

It has to be distinguished whether it concerns a gas taking or gas delivering cylinder space according to the temperature at the interface. In the first case, the temperature is a function of the bordering component: the heat exchanger. In case of the gas delivering cylinder the temperature at the interface corresponds to the temperature inside the cylinder space. Therefore:

  • \( T_{\text{x}} = T_{\text{in}} (\varphi ) \), a transient function for the gas taking up cylinder

  • \( T_{\text{x}} = T \), the temperature inside the cylinder space for the gas delivering cylinder

The working gas within the cylinder is considered as ideal mixed. The reason is that the gas streams alternately incoming and leaving the cylinder provide in each case an intense turbulence.

Furthermore, no basic differentiation of the energy balance is made between a displacement and working piston because that has only a constructive meaning. The appearing leaky mass flow about the piston seals (which can be predicted mathematically only inexactly) is extremely low at a displacement compressor due to the lower pressure differences, and the effects for the process can be neglected.

The energy equation for the semi-open system (cf. Figure 1) is expressed by:

$$ \frac{{{\text{d}}U}}{{{\text{d}}t}} = \dot{Q} + P + \dot{H} $$
(3)

With the thermodynamic work \( P{\text{d}}t = - p{\text{d}}V \) to change the cylinder volume, the internal energy \( U = m c_{\text{v}} T \) given by the total derivate and the enthalpy flow rate given by (2) Eq. (3) can be transformed into:

$$ m c_{\text{v}} \frac{{{\text{d}}T}}{{{\text{d}}t}} + T c_{\text{v}} \frac{{{\text{d}}m}}{{{\text{d}}t}} = \dot{Q} - p\frac{{{\text{d}}V}}{{{\text{d}}t}} + T_{\text{x}} c_{\text{p}} \frac{{{\text{d}}m}}{{{\text{d}}t}} $$
(4)

For regenerative gas cycles the working gas can be treated as an ideal gas, and with the differential form of the ideal gas law

$$ - p {\text{d}}V + T R {\text{d}}m = V {\text{d}}p - m R {\text{d}}T $$
(5)

the equation of energy (4) for the gas delivering cylinder gives

$$ m c_{\text{v}} \frac{{{\text{d}}T}}{{{\text{d}}t}} = \dot{Q} + V\frac{{{\text{d}}p}}{{{\text{d}}t}} - m R \frac{{{\text{d}}T}}{{{\text{d}}t}} $$
(6)
$$ m c_{\text{p}} \frac{{{\text{d}}T}}{{{\text{d}}\varphi }} = \frac{1}{\omega }\dot{Q} + V\frac{{{\text{d}}p}}{{{\text{d}}\varphi }} $$

where \( \varphi = \omega t \) is the phase and \( \Delta \varphi = 2\pi \) is the interval for a power stroke of the machine. Equation (6) indicates that the gas temperature within the cylinder space is depending on the change of the system pressure and the rate of heat flow.

Substituting (2) and (5) into (4) and applying the mass balance of the semi-open system \( {\text{d}}m = \dot{m} {\text{d}}t \), the differential equation for the gas taking up cylinder space becomes

$$ m c_{\text{p}} \frac{{{\text{d}}T}}{{{\text{d}}t}} + T c_{\text{p}} \frac{{{\text{d}}m}}{{{\text{d}}t}} = \dot{Q} + V\frac{{{\text{d}}p}}{{{\text{d}}t}} + T_{\text{in}} c_{\text{p}} \frac{{{\text{d}}m}}{{{\text{d}}t}} $$
(7)
$$ m c_{\text{p}} \frac{{{\text{d}}T}}{{{\text{d}}\varphi }} = \frac{1}{\omega }\dot{Q} + V\frac{{{\text{d}}p}}{{{\text{d}}\varphi }} + \frac{1}{\omega }\dot{m} c_{\text{p}} \left( {T_{\text{in}} - T} \right) $$

and towards (6) the temperature of the incoming gas flow \( T_{\text{in}} (\varphi ) \) is additionally available. Therefore, the temperature gradient within the cylinder space is a function of the rate of enthalpy flow difference with respect of the change of the system pressure and the rate of heat flow.

The observed rate of heat flow via the heat transfer surface of the cylinder \( A_{\text{q}} \) is determined by the overall heat transfer coefficient \( k(\varphi ) \) as well as by the temperature difference to the steady surrounding temperature \( T_{\text{U}} \). Inserting into (7) gives:

$$ V \varrho c_{\text{p}} \frac{{{\text{d}}T}}{{{\text{d}}\varphi }} = \frac{{k A_{\text{q}} }}{\omega }\left( {T_{\text{U}} - T} \right) + V\frac{{{\text{d}}p}}{{{\text{d}}\varphi }} + \frac{1}{\omega }\dot{V} \varrho c_{\text{p}} \left( {T_{\text{in}} - T} \right) $$
(8)

Correlations to the heat transfer of cylinder spaces are found in literature. In [12] different functions to calculate the inside heat transfer coefficient are delivered for steady-state conditions. Beyond that also transient functions for the cylinder space are available in case of internal combustion engines, but not for regenerative gas cycles. Therefore, in [4] the function

$$ Nu\left( \varphi \right) = {\text {0,15\, }Re}^{0,8} $$
(9)

is provided to calculate the Nusselt number of diesel engines, and the original terms giving the influence of combustion and angular momentum effects are not taken into account. As the characteristic length the piston diameter is used. Besides, for the regulation of the Reynolds number the piston speed is determinate.

To calculate the rate of heat transfer the temperature at the wall surface is accepted as steady, but in [5] a transient consideration was also implemented. Besides in the periodical-steady state, the gas temperature in the cylinder is characterized by a sine approximation that leads to the propagation of the penetration depth of the periodical temperature variation in the wall. The divergence of the heat transfer compared to a model with a steady inside temperature by metallic materials amounts to merely a few percent. Hence this approach is suggested, if necessary, in exclusively isolated cylinder rooms.

In the following the heat transfer surface of the cylinder consists only of the side area. The area of the top and bottom results in a thermally very well isolated piston for the avoidance of heat conduction loss. However, the crossing is already in the bordering heat exchanger, so these stationary heat loss terms can be regarded separately later in the whole energy balance of the process. In this case, the quotient of heat transfer surface and cylinder volume gives:

$$ \frac{{A_{\text{q}} (\varphi )}}{V(\varphi )} = \frac{d \pi 4}{{d^{2} \pi }} = \frac{4}{d} $$
(10)

Taking the ideal gas law and Eq. (10) into account, an equivalent form of (8) can be found:

$$ \frac{{{\text{d}}T}}{{{\text{d}}\varphi }} = \frac{{k A_{\text{q}} }}{{\omega V \varrho c_{\text{p}} }}\left( {T_{\text{U}} - T} \right) + \frac{1}{{\varrho c_{\text{p}} }} \frac{{{\text{d}}p}}{{{\text{d}}\varphi }} + \frac{{\dot{V}}}{\omega V}\left( {T_{\text{in}} - T} \right) $$
(11)
$$ \frac{{{\text{d}}T}}{{{\text{d}}\varphi }} = \frac{R}{{c_{\text{p}} }} \frac{4 k}{ p \omega d } T \left( {T_{\text{U}} - T} \right) + \frac{R}{{c_{\text{p}} }} \frac{T}{p} \frac{{{\text{d}}p}}{{{\text{d}}\varphi }} + \frac{{\dot{V}}}{\omega V}\left( {T_{\text{in}} - T} \right) $$

The differential equation depends upon three groups for heat transfer, pressure, and volume. They are:

$$ \mu = \frac{\kappa - 1}{\kappa } \frac{4 k}{p \omega d},\quad \varepsilon = \frac{\kappa - 1}{\kappa } \frac{{{\text{d}}p}}{{p {\text{d}}\varphi }},\quad \delta = \frac{{\dot{V}}}{\omega V} $$

Their meaning is as follows: \( \mu \) is a heat transfer parameter between gas and surrounding, similar to a gas temperature specific number of transfer units (NTU); \( \varepsilon \) is the gas-dependent ratio of the pressure gradient to the pressure; finally, \( \delta \) is the ratio of the volumetric flow rate to the present volume inside the cylinder space, which is usually not zero. Rewritten using the symbols \( \mu \), \( \varepsilon \) and \( \delta \), the Riccati equation for the gas taking up cylinder (11) becomes:

$$ \frac{{{\text{d}}T}}{{{\text{d}}\varphi }} = \delta T_{\text{in}} + \left( {\varepsilon + \mu T_{\text{U}} - \delta } \right) T - \mu T^{2} $$
(12)

So far, the model focused upon the gas taking up cylinder. For the gas delivering cylinder we received from the energy balance (6) the Bernoulli differential equation:

$$ \frac{{{\text{d}}T}}{{{\text{d}}\varphi }} = \left( {\varepsilon + \mu T_{\text{U}} } \right) T - \mu T^{2} $$
(13)

In comparison to this equation an additional term which arises from the temperature difference of the incoming gas flow is considered with the Riccati equation. Therefore:

  • \( \delta = f\left( \varphi \right) \) in case of the gas taking up cylinder space, and

  • \( \delta = 0 \) in case of the gas delivering cylinder space.

Solution of cylinder space temperature

A simplification of the solution to the underlying problem can be produced if special state changes are regarded. This is particularly the case if it acts around an adiabatic system (\( \mu = 0 \)) or acts around a stationary system pressure (\( \varepsilon = 0 \)). With the first-named boundary condition especially the square term is omitted, and by integrating the function of the incoming gas temperature elementary solutions of the Riccati Eq. (12) are received. Finally, the isentropic change in state (16) is a solution of (13) in the case of the adiabatic system.

Boundary conditions

General solution

\( \mu = 0 \)

\( T = p^{{\frac{\kappa - 1}{\kappa }}} V^{ - 1} \left( {c_{0} + \mathop \smallint \nolimits p^{{\frac{1 - \kappa }{\kappa }}} T_{\text{in}} {\text{d}}V} \right) \)

(14)

\( \mu = 0 \), \( \varepsilon = 0 \)

\( T = V^{ - 1} \left( {c_{0} + \mathop \smallint \nolimits T_{\text{in}} {\text{d}}V} \right) \)

(15)

\( \mu = 0 \), \( \delta = 0 \)

\( T = T_{0} \left( {\frac{p}{{p_{0} }}} \right)^{{\frac{\kappa - 1}{\kappa }}} \)

(16)

The difficulty still exists in the consideration of the usually transient pressure progression, because the functions to be integrated always contain exponents of non-natural numbers. With this consideration an analytical solution for (14) is limited, and whether it gives a suitable solution generally depends naively on the function of the pressure. Therefore, simplifications deliver only solutions for special boundary conditions, but not for the general case. In particular, the pressure progression is given during the simulation as a rule not as a function, and will be received first by the whole energy balance (1). Therefore, another procedure must be applied to get the solution.

The non-linear Riccati equation may be put in linear-form to be more suitable for calculation. If we write (cf. [3] )

$$ \mu T = \frac{{z^{\prime } }}{z} $$
(17)

the energy-balance (12) is given first by

$$ \frac{{{\text{d}}^{2} z}}{{{\text{d}}\varphi^{2} }} = \left( {\varepsilon + \mu T_{\text{U}} - \delta + \frac{{\mu^{\prime } }}{\mu }} \right)\frac{{{\text{d}}z}}{{{\text{d}}\varphi }} + \delta \mu T_{\text{in}} z $$
(18)

The square term for the temperature disappears, and the differential equation is compared with the original form out of higher order. Writing \( y_{1} = z \) and \( y_{2} = z' \) (18) gives a first order system of linear differential equation:

$$ \begin{gathered} \frac{\text{d}}{{{\text{d}}\varphi }}\left[ {\begin{array}{*{20}c} { y_{1} } \\ { y_{2} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} 0 & 1 \\ { \delta \mu T_{\text{in}} } & {\varepsilon + \mu T_{\text{U}} - \delta + \frac{{\mu^{'} }}{\mu }} \\ \end{array} } \right] \left[ {\begin{array}{*{20}c} { y_{1} } \\ { y_{2} } \\ \end{array} } \right] \hfill \\ \frac{\text{d}}{{{\text{d}}\varphi }}\,\,\,\,\,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{y} \,\,\,\,\, = \,\,\,\,\,\,\,\,\,\,\,\,\,\,\;\;\;\;\;\;\;\;\;\;\;\;\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{S} } \left( \varphi \right)\,\,\,\,\,\,\,\,\,\,\,\,\;\;\;\;\;\;\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{y} \hfill \\ \end{gathered} $$
(19)

Finally, the solution of the ordinary differential Eq. (17) gives (\( z_{0} \ne 0 \))

$$ \underline{y} = \left[ { \begin{array}{*{20}c} {y_{1} } \\ {y_{2} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} z \\ { z^{\prime } } \\ \end{array} } \right] = z_{0} \left[ {\begin{array}{*{20}c} {e^{{\mathop \smallint \nolimits \mu T {\text{d}}\varphi }} } \\ {\mu T e^{{\mathop \smallint \nolimits \mu T {\text{d}}\varphi }} } \\ \end{array} } \right] $$
(20)

and the initial condition:

$$ \underline{y}_{0} = \left[ {\begin{array}{*{20}c} 1 \\ {\mu_{0} T_{0} } \\ \end{array} } \right] \cdot {\mathbb{R}}^{*} $$
(21)

The initial value for the temperature at \( \varphi = 0 \) can be disregarded in case of the Riccati equation, because the cylinder space contains, on this occasion, still no volume. The intensive properties of the gas are not defined at that time. Only in the interval \( 0 < \varphi \le \pi \) of fluid flow does the cylinder space take up the working gas. For the initial value it is finally possible to chose any (numerically sensible) temperature

$$ T_{0} (\varphi \ne 0),\, \varphi \to 0 $$

with the appropriate low gas mass within the system without having influence on the result.

In general, and in particular for (19), there is no closed form solution for a system of linear differential equations, and an approximation method such as Magnus expansion [6] may have to be used. This first equation of the Magnus expansion or Magnus series coincides exactly with the solution in the scalar case

$$ \underline{y} (\varphi ) = \exp \left( {\mathop \smallint \limits_{{\varphi_{0} }}^{\varphi } \underline{\underline{S}} (\varphi )d\varphi } \right)\underline{y}_{0} $$
(22)

which is expressed by the exponent of a certain \( n \times n \) matrix \( X \) given by the Taylor series:

$$ \exp \left( {\underline{\underline{X}} } \right) = \mathop \sum \limits_{j = 0}^{\infty } \frac{{\underline{\underline{X}}^{j} }}{j!} $$
(23)

The Matrix \( \underline{\underline{S}} \) in (19) is not independent of \( \varphi \) and so (22) does not give the whole solution to solve the matrix initial value problem. If one insists on having an exponential representation, the exponent needs to be corrected with the rest of the Magnus series.

Another possibility to receive a correction is to regard the matrix \( \underline{\underline{S}} \) in segments as steady. With (22) for each of these \( n \) time steps \( \Delta\varphi = \varphi /n \) we get

$$ \underline{y}_{i} = \exp \left( {\underline{\underline{S}}_{ i} \Delta \varphi } \right)\underline{y}_{i - 1} \quad{i \in [1,n]} $$
(24)

with the arithmetic average of the matrix about the time step \( i \). Finally, the product

$$ \begin{aligned} y\left( \varphi \right) & = \exp \left( {\underline{\underline{S}}_{{ {{n}}}} \Delta \varphi } \right) \cdot \exp \left( {\underline{\underline{S}}_{{ {{n - 1}}}} \Delta\varphi } \right) \cdot \ldots \cdot \exp \left( {\underline{\underline{S}}_{ 1} \Delta\varphi } \right)\underline{y}_{0} \\ = \left[ {\mathop \prod \limits_{i = 1}^{n} \exp \left( {\underline{\underline{S}}_{{ 1 {{ + n - i}}}} \Delta \varphi } \right)} \right] \underline{y}_{0} \\ \end{aligned} $$
(25)

approximates the exact solution of (19) and therefore the primal Riccati Eq. (12) where \( n \) is present as a finite number of discrete time steps. The main advantage of this proposal is that the transient information can be provided to the cylinder space simulation continuously or discretely in every time step. However, with this method it is unfavorable to solve n-times the matrix exponential by the truncated series (23). In general, finding reliable and accurate methods to compute the matrix exponential is difficult (cf. [9]), but in case of a \( 2 \times 2 \)  matrix even an analytical solution occurs.

To compute the matrix exponential we have to diagonalise the matrix \( S \) by the eigenvalues and eigenvectors. The exponential can be obtained by just exponentiation every entry on the main diagonal. With the diagonal matrix \( D \) and eigenbasis \( V \) we get [6]:

$$ \exp \left( {\underline{\underline{S}}_{ i} \Delta \varphi } \right) = \underline{\underline{V}} \exp \left( {\underline{\underline{D}}_{ i} \Delta \varphi } \right) \underline{\underline{V}}^{ - 1} $$
(26)

The averaged components of \( S \) by (19) are

$$ \begin{gathered} s_{{\left\{ {1,1} \right\}}} = 0 \hfill \\ s_{{\left\{ {1,2} \right\}}} = 1 \hfill \\ s_{{\left\{ {2,1} \right\}}} = \frac{1}{2}\left\{ { \left( {\delta \mu T_{\text{in}} } \right)_{\text{i}} + \left( {\delta \mu T_{\text{in}} } \right)_{\text{i - 1}} } \right\} \hfill \\ s_{{\left\{ {2,2} \right\}}} = \frac{1}{2}\left\{ { \left( {\varepsilon + \mu T_{\text{U}} - \delta + \frac{{\mu^{'} }}{\mu }} \right)_{i} + \left( {\varepsilon + \mu T_{\text{U}} - \delta + \frac{{\mu^{'} }}{\mu }} \right)_{\text{i - 1}} } \right\} \hfill \\ \end{gathered} $$

and with the characteristic polynomial we get both eigenvalues

$$ \lambda_{1,2} = \frac{{s_{{\left\{ {2,2} \right\}}} }}{2} \pm \sqrt {\left( {\frac{{s_{{\left\{ {2,2} \right\}}} }}{2}} \right)^{2} + s_{{\left\{ {2,1} \right\}}} } $$
(27)

to fill the main diagonal of the diagonal matrix \( D \). The eigenvalues of \( S \) corresponding to the eigenvectors and the columns of the eigenbasis

$$ \underline{\underline{V}} = \left[ {\begin{array}{*{20}c} 1 & 1 \\ {\lambda_{1} } & {\lambda_{2} } \\ \end{array} } \right] $$
(28)

are those eigenvectors. Substitution (27) and (28) into (26) gives

$$ \exp \left( {\underline{\underline{S}}_{{ {\text{i}}}} \Delta\varphi } \right) = \frac{1}{{\lambda_{2} - \lambda_{1} }}\left[ {\begin{array}{*{20}c} {\lambda_{2} e^{{\lambda_{1} \Delta\varphi }} - \lambda_{1} e^{{\lambda_{2} \Delta\varphi }} } & {e^{{\lambda_{2} \Delta\varphi }} - e^{{\lambda_{1} \Delta\varphi }} } \\ {\lambda_{1} \lambda_{2} \left( {e^{{\lambda_{1} \Delta\varphi }} - e^{{\lambda_{2} \Delta\varphi }} } \right)} & {\lambda_{2} e^{{\lambda_{2} \Delta\varphi }} - \lambda_{1} e^{{\lambda_{1} \Delta\varphi }} } \\ \end{array} } \right] $$
(29)

as an analytical solution for the matrix exponential.

The symbolic solution for the Riccati equation is very efficient; particularly in comparison to a numerical approximation. Hence, it is applied in the following to solve the Bernoulli differential Eq. (13) for the gas delivering cylinder space. On this occasion, the matrix \( S \) is simplified first and all terms with the volume flow rate (the additional perturbation term of the non-linear Riccati equation \( \delta \)) are omitted. The components become:

$$ \begin{aligned} s_{{\left\{ {1,1} \right\}}} &= 0 \\ s_{{\left\{ {1,2} \right\}}} &= 1 \\ s_{{\left\{ {2,1} \right\}}} &= 0 \\ s_{{\left\{ {2,2} \right\}}} &= \frac{1}{2}\left\{ { \left( {\varepsilon + \mu T_{\text{U}} + \frac{{\mu^{'} }}{\mu }} \right)_{\text{i}} + \left( {\varepsilon + \mu T_{\text{U}} + \frac{{\mu^{'} }}{\mu }} \right)_{\text{i - 1}} } \right\} \end{aligned} $$

Apart from that the solution of the matrix exponential (29) coincides with the gas taking up cylinder space.

In this case the initial temperature \( T_{0} (\varphi = 0) \) is not discretionary anymore; it is a function of the cylinder space temperature at maximum gas capacity. This is received again from the solution of the Riccati equation with \( \varphi = \pi \) for the gas taking up cylinder.

Plot of Solution

We now evaluate the magnitudes of influence during a half power stroke with the help of the simulation. For the cylinder space the Riccati Eq. (12) based model is available. The equation depends on:

  • the heat transfer parameter \( \mu \),

  • the pressure parameter \( \varepsilon \),

  • the volume parameter \( \delta \),

  • the temperature of the surrounding area \( T_{\text{U}} \), and

  • the temperature of the incoming gas \( T_{\text{in}} \).

For the simulation of the gas delivering and the gas taking up cylinder, the proposed solution for the Riccati equation is used; the series expansion (25) and the analytic solution for the matrix exponential (29). The boundary conditions to calculate the progression of the temperature are presented in Table 1.

Table 1 List of boundary conditions for the temperature profile calculation of the cylinder spaces
Full size table

Figure 2 shows the solution for the temperature profiles over the course of a half power stroke (interval \( \Delta\varphi = \pi ) \) where the gas is delivered (\( \delta = 0 \)). It is evident that the pressure change, depending on the isentropic exponent, exerts the dominant influence on the cylinder space temperature. The contribution of the heat flow is lower even if the overall heat transfer coefficient is rising. If the regenerative gas cycle is well-designed, so that heat looses are small and the pressure changes are usually high (\( \varepsilon \gg \mu T \)), the adiabatic model for the gas delivering cylinder is fairly appropriate. In this case, the equation for an isentropic change in state (16) may be used.

Fig. 2
figure 2

Temperature for the gas delivering cylinder space over phase. Shown is the variation of the isentropic exponent (a) and the overall heat transfer coefficient (b)

Full size image

By contrast, at the gas taking up cylinder corresponding to Fig. 3, a significant influence of the supplied enthalpy flow is observed. Thereby the contribution of the temperature of the incoming gas depends on the ratio of volumetric flow to the volume of the cylinder space \( \delta \). In the simplest case, the volumetric flow rate is constant; for regenerative gas cycles the volumetric flow usually oscillates with a sinusoidal function. For both cases, the influence of the flow rate results in:

Incoming volumetric flow

Volume coefficient

\( \dot{V} = {\text{const}} . \)

\( \delta = \varphi^{ - 1} \)

(30)

\( \dot{V} = \dot{V}_{ \hbox{max} } \sin \left( \varphi \right) \)

\( \delta = \tan \left( {\frac{\varphi }{2}} \right)^{ - 1} \)

(31)

Fig. 3
figure 3

Temperature for the gas taking up cylinder space over phase. Shown is the variation of the pressure and of the temperature of the incoming gas

Full size image

The Eqs. (30) and (31) are a formal statement of the well-known fact that at \( \varphi = 0 \), there is no gas inside the cylinder (\( \delta = \infty \)). While the cylinder volume increases, the influence of the temperature of the incoming gas is reduced by decrease of the volume coefficient. Finally, the cylinder reaches the maximum gas capacity and the movement of the piston stops (\( \delta = 0 \)). In the following time interval the parameter for the volume stays at zero; the cylinder delivers the gas to the connected component.

Conclusion

The working gas inside a machine of a regenerative gas cycle is pushed through the heat exchangers and the regenerator by cylinder piston assemblies. For the optimal design of these components one requires the information of the gas mass flow emitting and receiving by the cylinder spaces. In that regard, account must be taken of the modeling of the mass change within any cylinder space, based on differential equations for the conserved quantities mass, energy, and momentum, which are theoretically as well as numerically difficult to treat.

The proposed model of the cylinder space describes the dynamic behavior already by an ordinary non-linear differential equation, in particular due to the assumption that the alternating incoming and outgoing gas mass flow ensures an intense turbulence. Depending on the selected boundary conditions analytical solutions can be obtained for some instances. In addition, by using a special mathematical transformation, the energy equation of the cylinder space could be obtained as a system of linear differential equations, where the general solution is based on the matrix exponential function. Of course, the energy equations could also be treated by any of the numerical algorithms to solve ordinary differential equations. The important point to be emphasized here is that the main reason for the usefulness of the exponential algorithms lies in the fact that it preserves structural intrinsic properties of the exact solution.

The approach is developed for simulating the dynamic behavior of the cylinder space, depending on:

  1. 1.

    the pulsating process pressure,

  2. 2.

    the heat transfer to the surrounding,

  3. 3.

    the temperature of the incoming gas flow, and

  4. 4.

    usually oscillatory volumetric flow from the gear in question.

For the temperature within the cylinder space the theoretical investigations showed an isentropic change in state for the influence of the process pressure depending on the isentropic exponent. To retain the isothermal state a heat transfer to the surrounding must be carried out, whereby the influence of the overall heat transfer coefficient would have to be very pronounced to compensate the pressure change. In addition, the temperature change by the pressure is pulsating. However, the heat flow has only one direction: cooling down or heating up. Finally, the temperature of the gas taking up cylinder depends on the temperature of the incoming volumetric flow, which is a function of the bordering component. Some people assume that the process takes place without an increase or decrease in a state quantity of the system like the temperature. The impact of the investigated parameters indicates this assumption is not always correct; the general solution appears indispensable for realistic simulation.

The information of the parameters can be provided to the featured cylinder space simulation continuously or discreetly, as this is present as a finite number of discrete time steps. The division of the time steps depending on required simulation accuracy is in this case virtually arbitrary since there is an analytical solution for the matrix exponential function. Thus an efficient symbolic solution, in comparison to the numerical approximation, of the underlying differential equation is obtained.

The presented model of the cylinder space can be used for design simulating software of regenerative gas cycles. By the modular construction of the simulation program the external boundary conditions of the cylinder space are provided via the coupling of the other modules. Number and arrangement of the individual modules of a regenerative gas cycle is determined by the process configuration and therefore the cylinder space module is suitable for simulating different machines. Furthermore, additional physical models such as for combustion or pressure loss may be integrated. Thus, the basic approach used for the symbolic mathematic based simulation of cylinder spaces opens up many fields of application like different regenerative gas cycles, reciprocating compressors or internal-combustion engines.