Abstract
In order to accomplish the objective of studying and optimizing the flow channel geometries and dimensions for high-temperature proton-exchange-membrane (PEM) fuel cells (with operating temperatures above 120 °C), a mathematical model has been developed in this work. As the major step of the modeling, the average concentrations of gas species in bulk flows as well as in the layers of electrodes are calculated through mass transfer analysis in one-dimensional direction normal to the membrane-electrodes layers. Therefore, the concentration and activation polarizations are simulated with much less computational work compared to a three-dimensional numerical model. The ohmic loss is taken into consideration through analysis of a representative network circuit simulating the electron and proton conduction in the elements of electrodes and electrolyte, respectively. The simulated results for high-temperature PEM fuel cells were compared with experimental results from literature. The results from the simulation and experimental tests showed good agreement, which validated the mathematical model. As the model requires less computational work, it was used to analyze a large number of cases with different gas flow channel dimensions and operating conditions, and optimization to the dimensions of channels and ribs was accomplished.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Highlights
-
A mathematical model for high-temperature PEM fuel cell was developed.
-
Modeling results were validated by experimental results from literature.
-
The cell performance V–I curves at different operating conditions were simulated.
-
The dimensions of gas flow channels/ribs for flow field were optimized.
Introduction
Recognized as clean power sources, proton-exchange membrane (PEM) fuel cells have a number of advantages, such as low emissions, high power density, and relatively fast start-up. Application of PEM fuel cells has become wider in recent years for power sources of cars, and portable or stationary backup power units at various power levels [1].
Based on operating temperatures, PEM fuel cells may be divided into two categories: low-temperature PEM fuel cells and high-temperature PEM fuel cells. Low-temperature PEM fuel cells have a low operating temperature below 100 °C, whereas high-temperature PEM fuel cells work at temperatures above 100 °C, typically in the range from 120 to 180 °C [2]. The heat and mass transport phenomena and material properties of low-temperature and high-temperature PEM fuel cells have some significant differences. A low-temperature PEM fuel cell typically needs and produces liquid water to keep the membrane hydrated, which incurs complicated heat and mass transport processes [3]. A high-temperature PEM fuel cell does not have liquid water in operation, which thus has different water transport mechanism compared to low-temperature PEM fuel cells.
Low temperature PEM fuel cells have been studied by many researchers during the past using various modeling and experimental approaches [4–13]; while high-temperature PEM fuel cells only have been studied in recent times due to the tough barrier of membrane development. One of the most outstanding characteristics of high-temperature PEM fuel cells is their tolerance for higher level of carbon monoxide than that of low-temperature PEM fuel cells [14]. High temperature PEM fuel cells also have improved water management and faster electrochemical kinetics [15]. When the fuel cell temperature is maintained above 100 °C, the produced water is in the form of vapor, which reduces the occurrence of flooding; however, this is the major problem for low temperature PEM fuel cells, in which the water flooding may block the flow of the reactant gasses and reduces the performance of the fuel cell. Nonetheless, high-temperature PEM fuel cells also have drawbacks. These include increased chances of membrane dehydration, decreased proton conduction, and cell degradation [16]. These drawbacks must be closely watched to ensure that a high temperature fuel cell does not have performance falling below acceptable levels. As high temperature proton conductive membranes, polybenzimidazole (PBI) membranes are doped with different acids [one of which is Phosphoric acid (PA)] to improve the proton conductivity. It was found that doping the PBI membrane with about 500 mol% of PA resulted in a better property [17].
Much effort has been devoted to improving high-temperature PEM fuel cells. For membrane materials, Ong et al. [18] experimentally studied the material compositions for MEA, which affects the proton conductivity and the polarization curves of a high-temperature PEM fuel cell. Mamlouk et al. [19] experimentally studied the effects of PBI loading and acid loading on anode and cathode layers and carbon supports, as well as the use of Pt alloy catalysts, on the performance of high-temperature PEM fuel cells. Harris et al. [20] developed a casting test bed for a polyphosphoric-acid (PPA)-based membrane material used in high-temperature PEM (HT-PEM) fuel cells with operating temperatures of up to 160 °C. Zhai et al. [21] studied the stability of Pt/C electrocatalysts in a PA-doped PBI-membrane-based HT-PEM fuel cell. For operation conditions, Zhang et al. [22] have studied the dependence of fuel cell performance on temperature and oxygen stoichiometry through experimental test. Li et al. [23] also studied the poisoning effect of carbon monoxide on a Pt/C catalyst in a high-temperature PEM fuel cell which used phosphoric-acid-doped PBI membrane at a temperature range from 125 to 200 °C. For numerical modeling, Shamardina et al. developed a simple model of a high-temperature PEM fuel cell. They validated the model against experimental test results [24]. Cheddie et al. [25] presented a one-dimensional mathematical model for high-temperature PEM fuel cells based on PBI membranes. They also developed an improved three-dimensional model of a high-temperature PEM fuel cell with polybenzimidazole (PBI) membrane [26]. Their model was used for a parametric study, and they concluded that the greatest potential for improving PBI PEM fuel cell performance was to increase the conductivity of membrane and also the performance of the catalyst [27]. Lobato et al. [28] implemented a three-dimensional half-cell model into a computational fluid dynamics (CFD) software. Their simulated cell has a high-temperature polyelectrolyte membrane (HT-PEMFC) in an area of 50 cm2. They also developed a neural network-based model and studied the effect of operating temperature on high-temperature PEM fuel cells [29]. Grigoriev et al. [30] reported a mathematical model of high-temperature PEM fuel cells, with H3PO4-doped polybenzimidazole (PBI) being used as the solid polymer electrolyte, and they conducted geometry optimization for important cell components.
The effect of flow field layout on high-temperature PEM fuel cell performance is another important issue, which aims at finding a uniform distribution of fuel and oxidizer. Efforts on this issue include some works that originated from Bejan’s constructal theory [31–36], as well as studies such as those by Taccani et al. [37], which reported that a serpentine flow field yields higher performance compared to a parallel flow field in their experimental tests. Through numerical analysis, Lobato et al. [28] also found that serpentine flow channels performed better than the flow field with pin arrays. Therefore, serpentine flow field was chosen in the present study for high-temperature PEM fuel cells.
It needs to be noted that the optimization of flow channel dimensions has not drawn sufficient attention, which is in fact a very important issue. Therefore, this paper focuses on developing a numerical model to not only study the effect of operating conditions of temperatures, pressures, and stoichiometry coefficients, but also the effect of flow channel dimensions (width of ribs and channels) on the cell performance. Consequently, both fuel cell design and operating parameters can be optimized for high power output. The mathematical model of high-temperature PEM fuel cells is for operating temperatures above 120 °C, which allows the authors to analyze the performance of fuel cells using flow channels in different dimensions (width of channels versus ribs) and thus optimize the gas channels. This is especially important because once all of the major designs have been decided, optimizing the flow channel dimensions will not change the overall layout, but will improve the performance of the fuel cell significantly. The general procedures of the present modeling of high-temperature PEM fuel cells stem from Ref. [1] for low-temperature fuel cells; however, details of mass transfer analysis, the activation polarizations, the membrane and its proton conductivities are different from that for low-temperature fuel cells. The effects of operating conditions on the high-temperature PEM fuel cell performance were also studied in this paper. The electrode activation polarizations and PBI membrane conductivities as functions of operating temperatures are also examined through comparison of modeling results and experimental data from literature.
Mathematical modeling
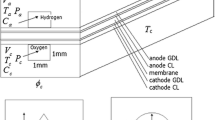
Figure 1 presents a view of the cross-section of a pair of flow channels (fuel and air) in a high-temperature PEM fuel cell. The PBI membrane is sandwiched by the two electrodes layers. Because the electromotive force and the irreversible losses due to activation polarization and concentration polarization are all related to the gas species concentrations and partial pressures at the reaction site (interface of electrolyte and electrode), mass transfer analysis is required in the model. Consequently, the electromotive force, the concentration and activation polarizations, and ohmic losses are all determined from the given conditions of fuel cell current density, operating temperature, and pressure.
In this model the average concentrations of gas species along the main flow direction are analyzed to decide the average partial pressures of gasses at the reaction site. Therefore, the model is one-dimensional in nature, in the direction perpendicular to the plane of the PBI membrane-electrode-assemble (MEA). The variation of concentrations of gas species from bulk flow to the surface of gas diffusion layer (GDL) and from across the GDL and the electrode layer needs to be determined. The advantage of the one-dimensional model is the simplicity but still with an acceptable accuracy [1]. It can be used to conduct parametric studies (of large number of cases) for optimization of design and operation, which a three-dimensional model is inconvenient to do due to a heavy load of computations. Some assumptions are made here for the modeling: (1) the operating temperature and pressure in both fuel flow and airflow are assumed to be maintained constant; (2) water in the fuel cell is in vapor state due to the high operating temperature well above 100 °C; (3) the reactant and product species in anode and cathode channels are all ideal gases; (4) the laminar flows of both air and fuel are incompressible.
Mass transfer analysis
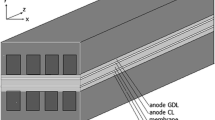
The mass transfer from bulk flow to PBI membrane experiences three processes—from bulk flow to the surface of gas diffusion layer (GDL), across the GDL, and across the electrode layer, as illustrated in Fig. 2. Humidified hydrogen and air are delivered to the anode and cathode gas channels, respectively. These gas species transfer through the GDL correspondingly to the electrode catalyst layers, where hydrogen molecules experience electrochemical reaction to become protons on the anode, and oxygen in cathode catalyst layer receives electrons from external loop to become anions. The released electrons on anode go through an externally closed loop (where a load is connected) to reach cathode where electrons are reused in the cathode electrochemical reaction.
Species mass transfer in flow channels
Analogous to the process of convective heat transfer and heat transfer coefficient h, a mass transfer process has a mass transfer coefficient hmass. The laminar convective mass transfer coefficient can be evaluated from a known Sherwood number as defined in Eq. (1). The Sherwood number for different flow channel geometries is listed in Table 1. The needed parameters in Eq. (1) are the hydraulic diameter of the flow channel and the diffusivity of the species of interest in the rest of the flow. The hydraulic diameter is the value of four times of the cross-sectional area divided by the perimeter of the cross section of the flow channel. The diffusivity between gas species in binary or more than binary mixture is a property to be discussed later.
The mass transfer rates of humidified hydrogen on the anode side at the surface of GDL can be obtained from Eqs. (3) and (4) [39]. As there is no water generation on anode side, the mass flux of water on the anode side is zero. It is also assumed that the water flux across the PBI membrane is zero.
where represents the bulk flow average mass concentration and it is determined as the average concentration of species in inlet and outlet flow. The difference of the concentration of species in the outlet flow from inlet flow is caused by the consumption or production of species resulting from the electrochemical reactions in fuel cells. The concentration represents the average mass concentration of a species on the surface of GDL.
On the cathode side, the convective mass transfer fluxes of species from bulk flow to the surface of GDL are given in Eqs. (5)–(7).
The mass consumption rates of hydrogen and oxygen, and , correlate with the operating current density in the form of Eqs. (8) and (9), where and represent the molecular weight of hydrogen and oxygen, respectively. The mass flux of water generated on cathode is calculated using Eq. (10). The direction of a positive mass flux is from wall toward the bulk flow. Therefore, a mass flux from the bulk flow to a wall due to mass consumption is negative.
Mass transfer in porous media
Three mechanisms contribute to mass transfer in the porous media in a fuel cell based on the Nernst–Planck equation [40], as shown in Eq. (11).
The first term of the equation is due to migration of the charged species which is caused by a potential gradient ΔΦ with associated charge number z i , concentration c i , and mobility u i . With no consideration of the potential gradient (Φ) effect (as it is usually small), the mass transfer only consists of mass diffusion due to concentration difference and the convection mass transfer due to the species’ motion from a surface to the bulk flow. Therefore, the Nernst–Planck equations for species’ mass transfer per unit area across the GDL can be simplified to:
where s are concentration gradients of species across the porous GDL. The terms, and are the anode and cathode diffusion velocities, respectively, due to the overall mass flux in the porous GDL, which are given as:
The effective diffusivity of the humidified hydrogen in the porous layers (GDL and catalyst layer) is related to binary ordinary diffusivity and porosity (ε g ). Detailed information of porosity is listed in Table 2. The effective diffusivity for hydrogen is calculated using Eq. (19) [25]. The ordinary diffusivity of two species is presented in Eq. (20), where = 7.07, = 17.9, = 16.6, = 12.7 [41].
Three species are involved in mass transfer on the cathode side. The effective diffusivity of humidified air components (oxygen, nitrogen, and water vapor) are presented in Eq. (21). Diffusivity of multiple species is obtained from Eq. (22), where x i is the molar fraction of species and it is obtained from Eq. (23).
Introducing the following effective diffusivities in gas diffusion layer and electrode:
We can obtain the mass flux equations in compact forms as:
Similar approach of analysis is applicable to the mass transfer flux and diffusivity in porous electrode layers. Therefore, the species’ mass concentration at the electrochemical reaction site—the interface between electrodes and PBI membrane, could be obtained at any given current density. Finally, partial pressures of each species are given as the product of the total pressure and the molar fraction of the interested species, as shown in Eqs. (34)–(36).
Over-potential due to activation polarization
The Butler–Volmer equation is commonly used to compute the activation polarization. For high-temperature PEM fuel cells, the simplified Butler–Volmer equations for the anode and cathode are given by Eqs. (37) and (38), respectively [43]:
The anode and cathode exchange current densities io,a and io,c are both temperature-dependent as given in Eqs. (39) and (40). T0 is a reference temperature chosen as 453 K (for 180 °C).
The anode and cathode reference exchange current densities and , the concentration exponentials and , the reference concentrations and , and the transfer coefficient are given in Table 3. The activation energy , as listed in Table 3, was obtained from analysis of the data given in Ref. [24].
Over-potential due to ohmic loss
The ohmic polarization of fuel cells is due to the electrical resistances, the contact resistances in the current collection process, and proton conduction resistance inside the membrane. Figure 3 presents a representative network circuit of the current flow path from an anode-side current collector to a cathode-side current collector. This path is discretized into multiple segments. The circuit includes electromotive forces and all discretized resistances. Given a current density for the fuel cell, one can analyze the mass transfer and find the electromotive force, and the over-potential due to activation polarization. Then, Kirchhoff’s current law can be applied for establishment of equations for the potentials at all the control nodes in the circuit. Solution to the equations will decide the potential difference between the two current collectors of the cathode and anode sides. This model for the ohmic losses analysis has been used successfully for analysis of low temperature PEM fuel cells [1, 44] and solid oxide fuel cells [45, 46].
The contact resistance is affected by the contacting of the pair of materials, which will cause a voltage drop across the contact surfaces. The contact surfaces roughness and contact pressure influence the contact area between the two materials. Yoon et al. [47] experimentally studied the effect of applied pressure on contact resistance of different materials. They reported that the contact resistance between two surfaces is on the order of 10−7 m2. They also found that the contact resistance decreases when the clamping force increases. However, it reached to a constant when the clamping force is above a certain value. For the present model, contact resistance is 1 × 10−7 m2. The resistivity of porous electrodes used in the numerical calculation is listed in Table 4. The resistivity of electrode and GDL may vary slightly with temperature, but is viewed as constant approximately. The resistance to proton migration in PBI membrane depends on the material and temperature of operation. At a temperature of 180 °C, the PBI membrane proton conductivity is 9.825 m [43]. Giving this temperature (T0 = 453 K or 180 °C) and the corresponding proton conductivity () as reference values, the proton conductivity of PBI membrane at other temperatures is calculated using the following equation:
where is activation energy, which is 20215.3 J/mol obtained from the work in Ref. [24]; R is universal gas constant, and the unit of T is K.
Procedures of computation to find I–V curves
The Nernst equation for electromotive force is calculated in the following form [48]:
The standard state electromotive force E0 is calculated from the systematic Gibbs free energy change, , of the global reaction based on low heating value for high-temperature PEM fuel cell. The equation of E0 given as a function of fuel cell operating temperature [49] is:
where temperature T is in K.
In the network circuit shown in Fig. 3, the electromotive force, , located inside the membrane, is the net value due to the electromotive force by Eq. (44) subtracting the activation polarizations from both anode and cathode. The electromotive force from Eq. (42) considers the partial pressures of species which thus considers the concentration polarization. The difference of E [from Eq. (42)] due to situations with no current output and with a current output, is the concentration polarization at the given current, which is obtained from Eqs. (45) and (46).
The output voltage of the high-temperature PEM fuel cell is the potential difference between the two current collectors on anode and cathode sides. This is obtained by calculating the network circuit potentials at every node, as seen in Fig. 3, using Kirchhoff’s first law while setting the potential of anode current collector as zero.
With all the above modeling work integrated, it is possible to predict the performance of a high-temperature PEM fuel cell at given operating parameters and conditions. The calculation process was programmed into Matlab code. Figure 4 shows a flow chart for the computation procedures, which includes the following steps. First, the mass concentrations of species at the interface between electrode and electrolyte are calculated based on given parameters and conditions. In this calculation, the reactant and product partial pressures at reaction site are calculated, which can be used to decide the concentration polarization. Second, activation polarizations are obtained based on species concentrations at reaction site for the given operating current density. Third, internal ohmic loss is accounted for by solving the representative electrical network circuit. Eventually, the potential difference between the two current collectors can be computed, which reflects the cell output voltage. These computation steps are conducted at all desired current densities to generate the polarization curves and power density curve.
It needs to be noted that in each computation at a given current density, the gas species concentrations have to be used to decide the gas diffusivity if a mixture has more than three species. Therefore, iteration of computation of the concentration is necessary until all results are converged.
Results and discussion
The mathematical model was used for the simulation of a high-temperature PEM fuel cell which has experimental results reported in literature. Comparison of the simulation results with reported experimental results was conducted to validate the modeling. The model was then applied for more simulation work with the objective of optimization for the dimensions of the gas flow channels and thus high power output under the same other conditions.
Validation to the mathematical model
As seen from the computational flow chart in Fig. 4, with given inlet flow rates, pressures, operating temperatures, membrane proton conductivities as function of temperatures, and current density of the fuel cell, the model can predict the fuel cell voltage. Carrying out this simulation for different current densities, one can predict the entire voltage–current (V–I) curve of the fuel cell.
The present validation work takes the fuel cell properties, operating conditions, and current density from experimental work in literature [50] as input for the modeling simulation. The voltage of the fuel cell is then predicted using the model. After simulations for different current densities, the cell voltages and thus the V–I curves were predicted for comparison with experimental data.
Yu et al. [50] reported the experimental results for a high temperature PEM fuel cell with a PA-doped PBI membrane under an operation condition of 1.0 atm (absolute) and a temperature of 180 °C with stoichiometric coefficients of hydrogen and oxygen of 1.2 and 2.0, respectively. They also reported experimental results which were tested using pure oxygen instead of air with the same stoichiometric coefficients of hydrogen and oxygen, respectively. The present simulation took the fuel cell properties and parameters from the work of Yu et al. [50] for simulation. The dimensions of anode flow channels are 1.0 mm in depth and 1.0 mm in width, and that for cathode channels are 1.5 mm in depth and 1.0 mm in width. The width of the current collection ribs is 1.0 mm. Figure 5 shows the simulated results in comparison with experimental results reported by Yu et al. [50]. The results in Fig. 5a were obtained based on air, while in Fig. 5b the results are based on pure oxygen. Obviously, the pure oxygen allowed the fuel cell to have high power output under the same other conditions. The simulated results and the experimental data agree with each other quite well, which confirms the validity of the modeling and the computational program developed in this work.
The three irreversible voltage losses
The mathematical model was able to predict the total and individual irreversible voltage losses so as to identify their contributions to the losses inside the fuel cell. For the above simulated fuel cell cases, the ohmic loss, activation polarization (total from both electrodes), and concentration polarizations are presented in Fig. 6. The results in Fig. 6a were obtained based on constant flow rates of hydrogen and airflow; while in Fig. 6b, the results are based on constant stoichiometric factors of hydrogen and oxygen (from airflow).
Cell output voltage and three types of voltage losses at operation temperature 180 °C and pressure 1.0 atm. a Constant flow rates of hydrogen and air corresponding to a limited current density of 1.2 A/cm2; b constant hydrogen stoichiometric coefficient of 1.2 and constant oxygen (from airflow) stoichiometric coefficient of 2.0
In both the cases, the activation polarization is the dominant loss, while concentration polarization and ohmic losses are about the same order. In Fig. 6b, as the hydrogen and oxygen stoichiometric coefficients are constant at all the current densities, the concentration polarization only has a slight increase with the increase of the current density. However, for the case with constant flow rates of hydrogen and airflow, the concentration polarizations are slightly higher than that in Fig. 6b at the same current densities; also, a sharp increase of the concentration polarization is seen at a high current density of 1.2 A/cm2, which incurs a significant cell voltage drop as seen in Fig. 6a. This is because the hydrogen and oxygen flow rates are completely used at a current density of 1.2 A/cm2 for this case. It is understandable that the ohmic loss increases with the current density in the same way for both the two cases in Fig. 6.
Effect of operating temperature on high temperature PEM fuel cells
High-temperature PEM fuel cells operate at temperatures in the range from 120 to 180 °C. The operation temperature influences the activation polarization as well as the proton conductivity of the membrane significantly. The anode and cathode exchange current densities and the proton conductivity of the membrane varying against temperatures are shown in Fig. 7 based on the calculated data from equations in the modeling for the case when air is used on the cathode.
The exchange current density of the cathode is much less than that of the anode, which is an indication that the cathode activation polarization is much higher than that of the anode. The exchange current densities increase with operating temperatures, which means that the activation polarization will decrease with the increase of temperatures. The proton conductivity of the membrane increases with the increase of the temperature as shown in Fig. 7c. Because the high operating temperature introduces lower activation polarization and higher proton conductivity, the fuel cell performance will increase with operating temperatures.
Figure 8a shows the simulation results of the fuel cell that has the same dimensions and operating parameters as presented above, except with different operating temperatures from 120 to 180 °C. Although the membrane must have a limit of operating temperature due to material safety, it is clear that high operating temperature allows for a higher voltage output under the same other conditions. Experimental tests conducted by Yu et al. [50] reported similar results on the effect of fuel cell temperatures on the voltage–current performance [51] as shown in Fig. 8b. Shamardina et al. [24] conducted both experimental tests and modeling analysis on high-temperature PEM fuel cells, and they reported a similar conclusion that cell output performance increases with operation temperature in the range from 127 to 180 °C.
High temperature PEM fuel cell polarization curves at different operating temperatures with constant hydrogen and oxygen (from airflow) stoichiometric coefficient of 1.2 and 2.0, respectively, and operating pressure of 1.0 atm. a Simulation results; b experimental results [50]
Effect of fuel and oxygen stoichiometry on fuel cell performance
Three different stoichiometric factors for hydrogen (1.0, 1.2 and 1.5) and oxygen (1.0, 1.5, 2.0) have been chosen to form operating conditions different in fuel and oxygen supplying. Air is fed for the needed oxygen. Figure 9 shows the fuel cell output voltage and power density at five combinations of hydrogen and oxygen stoichiometric coefficients. The baseline case has stoichiometry factors of both 1.0 for hydrogen and airflow. The best case has stoichiometric factors of 1.5 for hydrogen and 2.0 for oxygen. The maximum power densities from these two cases are quite different as seen in Fig. 9. The best case (with a hydrogen stoichiometric factor of 1.5 and an oxygen stoichiometric factor of 2.0) has maximum power density 25 % higher than that of the baseline case.
At the oxygen stoichiometric factor of 1.0, the increase of the hydrogen stoichiometric factor from 1.0 to 1.2 makes a slight increase in the maximum power density. However, compared to this case, the increase of the oxygen stoichiometric factor from 1.0 to 1.5 incurs a significant improvement of about 18.1 % of the maximum power density. When the stoichiometry of air increases from 1.5 to 2.0, the maximum power density still has a significant increase. Laboto et al. [18] reported a similar conclusion based on their simulation of high-temperature PEM fuel cells with a serpentine flow field [28]. They found that cell output voltage increased more significantly with the increase of the stoichiometric factor of cathode airflow than that of hydrogen flow. A similar conclusion has been reported from the experimental tests conducted by Shamardina et al. [24].
Effect of the operating pressure on cell performance
High-temperature PEM fuel cells may safely operate at pressures ranging from 1.0 to 5.0 atm. The effect of operating pressure on cell performance was studied using the present model. As shown in Fig. 10, the fuel cell V–I curve at an operating pressure of 2.0 atm is above that of the case of an operating pressure of 1.0 atm, and similarly V–I curve at 3.0 atm is above that of the case at 2.0 atm. Wang et al. have done experimental tests and modeling on pressure effect in low-temperature PEM fuel cells at an operation temperature of 70 °C, and obtained similar results [41]. Zhang et al. [42] also reported their experimental results on low-temperature PEM fuel cell operating at 23 °C, and they found that a decrease of backpressure causes a decrease of the power output. Ke et al. [43] conducted tests for high-temperature PEM fuel cells and studied the pressure effect at an operating temperature of 140 °C. Researchers also concluded that a high operating pressure improves the polarization curve [52, 53].
Figure 11 shows the activation polarizations and concentration polarizations of the fuel cells at different operating pressures. The influence of the operating pressure on the activation polarization is significant while the concentration polarization has no appreciable change. The higher operating pressure offers improved partial pressures for the reactants at the reaction site, which contributes to a lower activation polarization. Although higher operating pressures have positive effects on cell performance, increasing the back pressure for the entire fuel cell system will increase the load of the air and fuel pumps, causing a drop of the overall energy efficiency of the entire system. In addition, higher operating pressures also result in increased complexity of gasket design for leakage prevention.
Dimension optimization for gas flow channels
From previous work on low-temperature PEM fuel cells, it is known that the cell with different flow field design could perform significantly different. Due to better balance of pressure loss against water removal, the flow field with serpentine channels is considered the “industry standard” of PEM fuel cells, which showed better performance compared with many other designs [54, 55]. In the present study, serpentine flow channels were considered, and dimensions of channels and current collection ribs were optimized for obtaining high power density under the same other conditions.
In the analysis, the total width of the gas flow channel and one of the channel walls is defined as Lo. The width of the flow channel is Lc and that of the channel walls/ribs is Lr. The present simulation chose different combinations of Lo and the ratio of R = Lr/Lo. The range of Lo ranges from 1.5 to 6.0 mm with increment of 0.5 mm, and the rib ratio Lr/Lo ranges from 0.1 to 0.5 with an increment of 0.05.
The simulation considered a fuel cell operating temperature of 180 °C, a hydrogen stoichiometric factor of 1.2 and an oxygen (fed by airflow) stoichiometric factor of 2.0. For each case, the performance curve of current density versus power density was obtained. The maximum power densities on the curve for every case in different combinations of Lo and Lr/Lo are shown in Fig. 12 as a contour.
It is seen that at a given total width of Lo, the decrease of the ratio of Lr/Lo from 0.5 to 0.2 results in an increase of the maximum power density. At an optimized ratio of Lr/Lo between 0.1 to 0.2, the power density approaches maximum. For a given constant total width Lo, the decrease of Lr/Lo means that the width of the current collection rib decreases while the width of channel increases. This provides more area exposed to gas species for an electrochemical reaction, thus creating more power output from the fuel cell. However, when the rib ratio Lr/Lo is too small, the current collection from the reaction site to the ribs is under more resistance and thus the power output cannot increase anymore.
When keeping the rib ratio Lr/Lo constant, meaning both the rib width and the total width vary proportionally, the decrease of the total width results in higher power density as seen in Fig. 12. Finally, from the contour in the figure, one can see that the high power densities located at the corner of low total width of Lo and low ratio of Lr/Lo. The top maximum power density can be 43 % higher than the lowest power density, if the combinations of Lo and R (= Lr/Lo) are properly selected, or optimized.
Conclusion
A mathematical model has been developed in this study for high temperature proton-exchange-membrane fuel cells. The model calculates the average concentrations of gas species in bulk flow as well as in the layers of GDL and electrodes through mass transfer analysis in one-dimensional direction normal to the layers. The concentration and activation polarizations are simulated with much less computational work, and the ohmic loss is counted through analysis of a representative network circuit simulating the electron and proton conduction in elements of electrodes and electrolyte. The simulation results are compared with experimental results from literature. The simulation and experimental results agree very well. The analytical model was used to study the behavior of irreversible losses and the effects of operation parameters to the fuel cell polarization curves in high temperature PEM fuel cells. The effects of operating pressure, stoichiometric parameters of hydrogen and oxygen to the fuel cell performance are similar to what is known for low temperature PEM fuel cells. The extra supply of oxygen (at stoichiometric factor larger than 1.0) to the fuel cell is more significant for improving fuel cell performance than an extra supply of hydrogen. A higher operating temperature for a high-temperature PEM fuel cell results in better performance if the temperature is within the safety limit of the membrane.
The present model was also used to study and optimize the flow channel dimensions. The optimal total width of a flow channel and its wall/rib as well as the ratio of a rib against total width, were investigated for higher power density. It has been found that a relatively small total width and small rib-to-total width ratio are better for generating high power density in the fuel cell.
The current mathematical model is used as a convenient tool for the study of high temperature cell performance under different factors as well as a tool for fuel cell flow channel design.
Abbreviations
- A :
-
Interface area (m2)
- A channel :
-
The area of the cross-section of a channel (m2)
- C i :
-
Species mole concentration (mol/m3)
- D i :
-
Species diffusivity (m2/s)
- D hydro :
-
Hydraulic diameter (m)
- E :
-
Electromotive force (V)
- E A :
-
Activation energy (J/mol)
- F :
-
Faraday constant (96485 C/mol)
- h mass_i :
-
Mass transfer coefficient (m/s)
- I :
-
Current (A)
- i :
-
Current density (A/m2)
- J i :
-
Mass flux of species (kg/s)
- j i :
-
Mass flux of species per unit area (kg/s/m2)
- M i :
-
Species molecular weight (kg/mol)
- P :
-
Pressure (Pa)
- P channel :
-
Perimeter of channel (m)
- R :
-
Universal gas constant 8.314 (J/mol/K); ratio of Lr/Lo
- T :
-
Temperature (K)
- v :
-
Diffusion velocity (m/s)
- X i :
-
Mole fraction of species
- :
-
Porosity
- :
-
Transfer coefficient
- :
-
Concentration exponentials
- :
-
Species mass concentration (kg/m3)
- :
-
Activation polarization (V)
- :
-
Thickness of a porous layer
- :
-
PBI membrane conductivity S/m
- a:
-
Anode side
- c:
-
Cathode side
- :
-
Bulk flow
- s:
-
Surface of GDL facing bulk flow
- int:
-
Interface between GDL and an electrode layer
- ia:
-
Interface between anode catalyst layer and PBI membrane
- ic:
-
Interface between cathode catalyst layer and PBI membrane
- H2:
-
Hydrogen
- O2:
-
Oxygen
- H2O:
-
Water
References
Liu, H., Li, P., Wang, K.: Optimization of PEM fuel cell flow channel dimensions-Mathematic modeling analysis and experimental verification. Int. J. Hydrog. Energy 38, 9835–9846 (2013)
Ubong, E.U., Shi, Z., Wang, X.: Three-dimensional modeling and experimental study of a high temperature PBI-based PEM fuel cell. J. Electrochem. Soc. 156, B1276–B1282 (2009)
Lorenzini, G., Saro, O.: Thermal fluid dynamic modelling of a water droplet evaporating in air. Int. J. Heat Mass Transf. 62(C), 323–335 (2013)
Cao, T.-F., Lin, H., Chen, L., He, Y.-L., Tao, W.-Q.: Numerical investigation of the coupled water and thermal management in PEM fuel cell. Appl. Energy 112, 1115–1125 (2013)
Meidanshahi, V., Karimi, G.: Dynamic modeling, optimization and control of power density in a PEM fuel cell. Appl. Energy 93, 98–105 (2012)
Liu, H., Li, P., Jurez-Robles, D., Wang, K., Hernandez-Guerrero, A.: Experimental study and comparison of various designs of gas flow fields to PEM fuel cells and cell stack performance. Front. Energy Res. (2014). doi:10.3389/fenrg.2014.00002
Panha, K., Fowler, M., Yuan, X.-Z., Wang, H.: Accelerated durability testing via reactants relative humidity cycling on PEM fuel cells. Appl. Energy 93, 90–97 (2012)
Hao, W., Berg, P., Li, X.: Steady and unsteady 3D Non-isothermal modeling of PEM fuel cells with the effect of non-equilibrium phase transfer. Appl. Energy 87, 2778–2787 (2010)
Liu, H., Li, P.: Maintaining equal operating conditions for all cells in a fuel cell stack using an external flow distributor. Int. J. Hydrog. Energy 38, 3757–3766 (2013)
Perng, S.-W., Horng-Wen, W.: Non-isothermal transport phenomenon and cell performance of a cathodic PEM fuel cell with a baffle plate in a tapered channel. Appl. Energy 88, 52–67 (2011)
Liu, H., Li, P.: Optimization of PEM Fuel Cell Flow Channels: Modeling Analysis and Experimental Tests. In: ASME 2013 11th International Conference on Fuel Cell Science, Engineering and Technology Minneapolis, Minnesota, USA, July 14–19, (2013)
Qin, Y., Li, X., Jiao, K., Du, Q., Yin, Y.: Effective removal and transport of water in a PEM fuel cell flow channel having a hydrophilic plate. Appl. Energy 113, 116–126 (2013)
Liu, H., Li, P., Hartz, A.: A fuel cell stack architecture to make all cells have equal operational conditions and performance. In: ASME 2012 10th International Conference on Fuel Cell Science, Engineering and Technology San Diego, California, USA, July 23–26, (2012)
Kwon, K., Yoo, D.Y., Park, J.O.: Experimental factors that influence carbon monoxide tolerance of high-temperature proton-exchange membrane fuel cells. J. Power Sour. 185, 202–206 (2008)
Shao, Y., Yin, G., Wang, Z., Gao, Y.: Proton exchange membrane fuel cell from low temperature to high temperature: material challenges. J. Power Sour. 167, 235–242 (2007)
Zhang, J., Xie, Z., Zhang, J., Tanga, Y., Song, C., Navessin, T., Shi, Z., Song, D., Wang, H., Wilkinson, D.P., Liu, Z., Holdcroft, S.: Review high temperature PEM fuel cells. J. Power Sour. 160, 872–891 (2006)
Kwon, K., Kim, T.Y., Yoo, D.Y., Hong, S., Park, J.O.: Maximization of high-temperature proton exchange membrane fuel cell performance with the optimum distribution of phosphoric acid. J. Power Sour. 188, 463–467 (2009)
Ong, A.-L., Jung, G., Wu, C.-C., Yan, W.-M.: Single-step fabrication of ABPBI-based GDE and study of its MEA characteristics for high-temperature PEM fuel cells. Int. J. Hydrog. Energy 35, 7866–7873 (2010)
Mamlouk, M., Scott, K.: The effect of electrode parameters on performance of a phosphoric acid-doped PBI membrane fuel cell. Int. J. Hydrog. Energy 35, 784–793 (2010)
Harris, T.A.L., Walczyk, D.F.: Development of a casting technique for membrane material used in high-temperature PEM fuel cells. J. Manuf. Process. 8, 18–20 (2006)
Zhai, Y., Zhang, H., Xing, D., Shao, Z.: The stability of Pt/C catalyst in H3PO4/PBI PEMFC during high temperature life test. J. Power Sour. 164, 126–133 (2007)
Zhang, J., Tang, Y., Song, C., Zhang, J.: Polybenzimidazole membrane based PEM fuel cell in the temperature range of 120–200 °C. J. Power Sour. 172, 163–171 (2007)
Li, Q., He, R., Gao, J., Jensen, J.O., Bjerrum, N.J.: The CO poisoning effect in PEMFCs operational at temperatures up to 200 °C. J. Electrochem. Soc. 150, A1599–A1605 (2003)
Shamardina, O., Chertovich, A., Kulikovsky, A.A., Khokhlov, A.R.: A simple model of a high temperature PEM fuel cell. Int. J. Hydrog. Energy 35, 9954–9962 (2010)
Cheddie, D.F., Munroe, N.D.H.: Mathematical model of a PEMFC using a PBI membrane. Energy Convers. Manag. 47, 1490–1504 (2006)
Cheddie, D.F., Munroe, N.D.H.: Three dimensional modeling of high temperature PEM fuel cells. J. Power Sour. 160, 215–223 (2006)
Cheddie, D., Munroe, N.: Parametric model of an intermediate temperature PEMFC. J. Power Sour. 156, 414–423 (2006)
Lobato, J., Cañizares, P., Rodrigo, M.A., Javier Pinar, F., Mena, E., Úbeda, D.: Three-dimensional model of a 50 cm2 high temperature PEM fuel cell. Study of the flow channel geometry influence. Int. J. Hydrog. Energy 35, 5510–5520 (2010)
Lobato, J., Canizares, P., Rodrigo, M.A., Linares, J.J., Piuleac, C.-G., Curteanu, S.: The neural networks based modeling of a polybenzimidazole-based polymer electrolyte membrane fuel cell: Effect of temperature. J. Power Sour. 192, 190–194 (2009)
Grigoriev, S.A., Kalinnikov, A.A., Kuleshov, N.V., Millet, P.: Numerical optimization of bipolar plates and gas diffusion electrodes for PBI-based PEM fuel cells. Int. J. Hydrog. Energy 38, 8557–8567 (2013)
Lorenzini, G., Moretti, S.: Bejan’s Constructal theory analysis of gas-liquid cooled finned modules. ASME J. Heat Transf. 133(7): 071801-1–071801-10 (2011)
Liu, H., Li, P., Lew, J.V.: CFD study on flow distribution uniformity in fuel distributors having multiple structural bifurcations of flow channels. Int J Hyrog. Energy 35(9186), 98 (2010)
Ramos-Alvarado, B., Li, P., Liu, H., Hernandez-Guerrero, A.: CFD study of liquid-cooled heat sinks with microchannel flow field configurations for electronics, fuel cells, and concentrated solar cells. Appl. Therm. Eng. 31(14–15), 2494–2507 (2011)
Liu, H., Li, P.: Even distribution/dividing of single-phase fluids by symmetric bifurcation of flow channels. Int. J. Heat Fluid Flow 40, 165–179 (2013)
Ramos-Alvarado, B., Li, P., Liu, H., Hernandez-Guerrero, A.: CFD analysis of flow and heat transfer in a novel heat sink for electronic devices. In: ASME 2010 International Mechanical Engineering Congress and Exposition, pp. 1589–1596
Liu, H., Li, P.: CFD Assisted design optimization of a flow distributor for uniform fluid distribution. In: ASME 2011 International Mechanical Engineering Congress and Exposition, pp. 97–106
Taccani, R., Zuliani, N.: Effect of flow field design on performances of high temperature PEM fuel cells: experimental analysis. Int. J. Hydrog. Energy 36, 10282–10287 (2011)
O’Hayre, R., Cha, S.-W., Colella, W., Prinz, F.B.: Fuel cell fundamentals. Wiley, New Jersey (2006)
Ecker, E.R.G., Drake, R.M.: Heat and mass transfer, 2nd edn. Mc-Graw-Hill, New York (1956)
Weber, A.Z., Newman, J.: Macroscopic modeling of polymer-electrolyte membranes. In: T.S. Zhao, K.-D. Kreuer, T.V. Nguyen, (eds.) Advances in fuel cells, Charon Tec Ltd, pp. 60–124 (2007)
Fuller, E.N., Schettler, P.D., Giddings, J.C.: New methode for prediction of binary gas-phase diffusion coefficients. Ind. Eng. Chem. 58, 18–27 (1966)
Su, A., Ferng, Y.M., Shih, J.C.: Experimentally and numerically investigating cell performance and localized characteristics for a high-temperature proton exchange membrane fuel cell. Appl. Therm. Eng. 29, 3409–3417 (2009)
Sohn, Y.-J., Kim, M., Yang, T.-H., Kim, K.: Numerical analysis of convective and diffusive fuel transports in high-temperature proton-exchange membrane fuel cells. Int. J. Hydrog. Energy 36, 15273–15282 (2011)
Li, P., Ki, J.-P., Liu, H.: Analysis and optimization of current collecting systems in PEM fuel cells. Int. J. Energy Environ. Eng. 3, 2 (2012)
Liu, H., Akhtar, Z., Li, P., Wang, K.: Mathematical modeling analysis and optimizaiton of key design parameters of proton-conductive solid oxide fuel cell. Energies 7, 173–190 (2014)
Li, P., Tao, G., Liu, H.: Effect of the geometries of current collectors on the power density in a solid oxide fuel cell. Int. J. Energy Environ. Eng. 2, 1–11 (2011)
Yoon, Y.-G., Lee, W.-Y., Park, G.-G., Yang, T.-H., Kim, C.-S.: Effects of channel configurations of flow field plates on the performance of a PEMFC. Electrochim. Acta 50, 709–712 (2004)
Mench, M.M.: Fuel cell engines. Wiley, New Jersey (2008)
Perry, R.H., Green, D.W.: Perry’s chemical engineers’ handbook, 7th edn. McGraw-Hill, New York (1986)
Yu, S., Zhang, H., Xiao, L., Choe, E.-W., Benicewicz, B.C.: Synthesis of Poly(2,2′-(p-phenylene) 5,5′-bibenzimidazole) (para-PBI) and Phosphoric Acid Doped Membranes for Fuel Cells. Fuel Cells 4, 318–324 (2009)
Wang, L., Husar, A., Zhou, T., Liu, H.: A parametric study of PEM fuel cell performances. Int. J. Hydrog. Energy 28, 1263–1272 (2003)
Zhang, J., Tang, Y., Song, C., Cheng, X., Zhang, J., Wang, H.: PEM fuel cells operated at 0 % relative humidity in the temperature range of 23–120 °C. Electrochim. Acta 52, 5095–5101 (2007)
Ke, C., Li, J., Li, X., Shao, Z., Yi, B.: Protic ionic liquids: an alternative proton-conducting electrolyte for high temperature proton exchange membrane fuel cells. RSC Adv. 2, 8953–8956 (2012)
Aiyejina, A., Sastry, M.K.S.: PEMFC flow channel geometry optimization: a review. J. Fuel Cell Sci. Technol. 9, 011011–011024 (2012)
Li, X., Sbir, I., Park, J.: A flow channel design procedure for PEM fuel cells with effective water removal. J. Power Sour. 163, 933–942 (2007)
Acknowledgments
The authors appreciate the financial support from the Office of Naval Research of the USA and the University of Tennessee SimCenter under the contract of #8500011366.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
This article is published under license to BioMed Central Ltd. Open Access This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
About this article
Cite this article
Liu, H., Li, P., Hartz, A. et al. Effects of geometry/dimensions of gas flow channels and operating conditions on high-temperature PEM fuel cells. Int J Energy Environ Eng 6, 75–89 (2015). https://doi.org/10.1007/s40095-014-0153-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40095-014-0153-x