Abstract
Renewable energy is an inevitable choice to meet the demands of energy resource. In the 21st century, one of the serious problems facings us is the energy resources that restrict the social progress and sustainable development. Environmental pollution and fossil energy resources shortage force people to explore and use new energy resources. The aim of this paper is to study the effect of blade installation angle on power coefficient of a five-blade resistance type vertical axis wind turbine using CFD simulations. The computation is conducted for the turbine with the blade diameter of 0.76–0.86 m and the turbine radius R = 2 m. The results show that the maximum value of power efficiency of 28.48 % can be obtained when the installation angle is 19° for the five-blade resistance type vertical axis wind turbine with the blade diameter of 0.78 m and the turbine radius R = 2 m.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
In the 21st century, one of the serious problems facing us is the energy resources that restrict the social progress and sustainable development. Environmental pollution and fossil energy resources shortage force people to explore and use new energy resource. Renewable energy and sustainable development is a common concerned subject of the whole world. Wind energy is one of the most promising resources of renewable energy, many countries have grant plan to explore and use it due to its great advantage of pollution free, abundant availability and conversion locally, etc. It can thus help us to reduce environmental pollution and the dependency on fossil fuels [1].
The most application of wind energy is to generate electrical power through various types of wind turbines. Wind turbines can be classified into two families generally, i.e., the horizontal axial wind turbine (HAWT) and the vertical axial wind turbine (VAWT) [2]. A lot of study has been focused on HAWT till now, while the study of VAWT is relatively rare. However, VAWT has its greatest advantage of “omnidirection”. Although the propeller-type windmill could provide a larger power output, it needs greater wind velocity that is almost impossible in city. Besides, HAWT induces low frequency noise that is harmful to animals. It also has a weak response to temporal changes of wind velocity and direction. However, VAWT escapes these environmental problems, resulting in their use in urban environments.
Savonius type is one of the oldest types of the VAWT. It has been studied since the pioneer work of Savonius. Although the Darrieus type Vertical Axis Wind Turbine is more efficient than the Savonius type, the several advantages of Savonius type are still attractive, such as good starting torque, simple mechanism, lower rotation speed, and omnidirectional characteristics [3]. Unlike the Darrieus type of wind turbines, the Savonius type wind turbine is commonly considered as a drag-driven type of wind turbine. The general theory of the Savonius turbine is simple. The wind exerts a force on a surface and this surface is then moved around an axis.
Mahmoud et al. [4] studied the Savonius rotor performance experimentally, it was found that, the two-blade rotor is more efficient than three and four ones. The rotor with end plates gives higher efficiency than those of without end plates. Double stage rotors have higher performance compared to single stage rotors. The rotors without overlap ratio are better in operation than those with overlap. Zhao et al. [5] also studied the influence of blade number on power efficiency of Savonius turbine numerically, it was found that, the two-blade rotor is more efficient than three ones as well, and they clarified that the actual reason for the blade number influence is induced by the “shading effect”. From flowing field analysis, it is found that the effective concave winding area of the blade decreases due to the shading of the nearby blade for the three-blade Savonius turbine, while the effective convex winding area of the blade increases due to the addition of the other blade, which results in the lower power efficiency of three-blade Savonius turbine [5].
Kumbernuss et al. [6] investigated the relationship of the overlap ratio and phase shift angle (installation angle) of double stage three-bladed VAWT, they concluded that that larger phase shift angles produce better performance of the turbines at lower air velocities and smaller ones will increase the performance at higher air velocities.
Saha et al. [7] tested the performance of the twisted blade for a three-bladed rotor system in a low speed wind tunnel as compared with the conventional semicircular blades (with twist angle of 0°). The experimental results showed that larger twist angle is beneficial to produce maximum power and better starting characteristics under the condition of lower wind velocity. The optimized twist angle is α = 15° in terms of starting acceleration and maximum no load speed at low airspeeds of U = 6.5 m/s. In addition, the stalling angle of twisted blade is shifted by 25° with the increase in angle of twist from α = 0° to 12.5°, and the stalling angle shifts further with the increase of twist angle.
Wang et al. presented a way to improve the efficiency by increasing the number of blades of Savonius wind turbine and by covering the convex part of the blades behind a shield or vane. It showed that multi-bladed Savonius rotors have a more stable torque along the rotation and therefore present a better starting ability, their power coefficient can also be higher than the standard Savonius rotors if the right parameters are used. Design parameters such as blade number and dimensions have a strong influence on the aerodynamic efficiency [8].
Above studies indicate that both the shape and the relevant position affect the efficiency of VAWT obviously, multi-bladed Savonius rotors have a more stable torque along the rotation and therefore present a better starting ability, and the reason for the lower power efficiency of three-blade Savonius turbine than two-blade rotor is due to the “shading effect”.
The aim of this paper is to study the effect of blade installation angle on the power coefficient of a five-blade resistance type VAWT, so as to improve its performance. The “shading effect” is avoided by introducing the “blank space” among blades, which is adjusted by changing the blade size. The widely used Computational Fluid Dynamics (CFD) method [9–12] is employed to conduct the simulation.
Geometric distribution of five-blade VAWT
In accordance with the simulation of Savonius wind turbine [13–22], it could draw lessons from the effective digging to the “external potentiality” for improving the power efficiency. In fact, the “inner potential” for improving power efficiency is still need to dig.
In the present paper, a five-blade resistance VAWT turbine is studied by means of CFD simulation in the view point of “inner potential” by changing the installation angle of blades. The “shading effect” is avoided by introducing the “blank space” among blades, which is adjusted by changing the blade size.
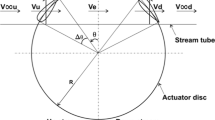
According to symmetry of the five-blade turbine, the 5 blades are distributed in plane of 360° homogenously, as shown in Fig. 1. The blade is semicylindrical shell of the diameter d (or radius r), the radius of the wind mill is R, θ is the installation angle of blade with respect to the radial direction from the origin of the turbine.
Mathematical model of flow field
Although the real flow field around wind turbine is three-dimensional one, the flow field along the blade height is nearly the same excluding at the blade ends, thus two-dimensional computation is commonly used to perform the simulation [23]. Figure 2 shows the two-dimensional computation model. In Fig. 2, there are three regions in this whole flow field. Z1 and Z3 are the stationary zones and Z2 is the rotating zone including blades. The width and the length of the computation region are represented by L and H, respectively. Let V and w represent the wind speed and the rotational rate of the turbine, respectively.
A grid independence model is employed to carry out the computation for a chosen configuration. The mesh chosen is structure quadrilateral cells; finer at the rotor and bigger as the distance from the rotor increases and the total number of grids can reach 3 × 105 cells. Figure 3 shows the details of the blade surface. The rotating zone and the stationary zone are separated by an interface which is two interfaces superposed [24–26].
The boundary condition of the computation flow field model is as follows: “velocity inlet” is imposed upstream of the rotor at a distance of 10R from the rotational axis of the turbine; the boundary condition of downstream of the rotor is imposed as “outflow” at 60R. The top and bottom of the flow field are taken at 17.5R from the rotational axis and is imposed as “symmetry” initially.
Numerical methods
The unsteady Reynolds-averaged Navier–Stokes equations are solved using the pressure-implicit with splitting of operators (PISO) pressure–velocity coupling scheme that is a part of the SIMPLE family of algorithms [26]. The model of turbulence is k–ω shear–stress transport (SST) which was developed by Menter to effectively blend the robust and accurate formulation of the k–ω model in the near wall region with the free-stream independence of the k–ε model in the far field and discretization scheme for momentum equation is the quadratic upwind interpolation of convective kinematics (QUICK) which may provide better accuracy than the second-order scheme for rotating or swirling flows and is applicable to quadrilateral or hexahedral meshes.
For the unsteady calculations, the flow is solved using the Sliding Mesh Model (SMM) and it depends on time: in the rotating zone, the grid and the geometry is moving [27]. Four complete revolutions are always computed, using a constant time step (0.02). The blades (walls) change position at every time step.
When the computation is finished, an output torque coefficient called Cm is obtained. Figure 4 illustrates the variation of the moment coefficient with respect to time. The average value in one or two cycle which is taken as the ultimate value, as the moment coefficient varies periodically with time.
Using Cm, the power of wind turbine can be calculated as,
In Eq. (1), C is a coefficient with the value of 0.6125, the power efficiency Cp, which represents the ratio of obtained power by the turbine and available power of the wind, is calculated by,
In Eq. (2), v is the inlet wind speed, ρ is air density, 1.225 kg/m3, S is the rotor swept area.
In the following paragraphs, the optimization process is conducted by taking the output power efficiency Cp as target function.
Numerical results
For fixed θ = 0
In this computation, the inlet wind speed v is taken as 8 m/s, the radius of the turbine is fixed at R = 2 m, the installation angle is fixed as θ = 0, i.e., the normal installation position, and the rotational rate of turbine vary. Blade diameter d = 2r is chosen to get optimizing value, such as 0.76, 0.80, 0.82 or 0.86 m, etc.
Figure 5 presents the variation of the power efficiency with respect to the blade diameter at different rotational rate w. The result in Fig. 5 shows that the performance of the turbine with the diameter of 0.80 m is the best for the rotational rate w = 17 rpm at θ = 0 and the power efficiency Cp reaches to 24.3 % by means of Eq. (2).
For varying θ
In this section, the inlet wind speed is still taken as 8 m/s, the radius of the turbine is fixed at R = 2 m too, let the installation angle θ vary, so as to obtain an optimized installation angle of the blade by means of Cp. As shown in Fig. 1, the way to change the installation angle is stated clearly. The blades are rotated at the outer vertices in clockwise direction with the angle θ.
Figures 6 through 9, give the variation of the power efficiency with respect to the installation angle θ and the turbine’s rotational rate w for different blade diameter d. The abscissa represents the value of θ and the ordinate represents the value of Cp. Each curve in these figures represents an individual rotational rate w.
From Fig. 6, the maximum power efficiency is 28.34 % at the installed angle θ of 20° and rotational rate w of 17 rpm for the blade diameter of 0.73 m. Figure 7 presents the result for the blade diameter 0.75 m, the maximum is 28.36 % at θ = 20°. Furthermore, the results for the blade diameter 0.78 and 0.80 m are expressed by Figs. 8 and 9, respectively. The results in Fig. 8 show that the maximum power efficiency appear at the θ = 19° for the blade diameter 0.78, and it reaches to 28.48 %, while the power efficiency maximum is 28.37 % for the blade diameter 0.80, which appears at θ = 19° as well.
In the viewpoint of highest power efficiency Cp, above results indicate that the optimized status for the five-blade turbine with the turbine radius R = 2 m is the installation angle θ being 19° and blade diameter 0.78.
In addition, some curves in Figs. 6 and 7 have a little oscillation, which results from the nonlinear property of the interaction between wind field and turbine.
Conclusion
This paper presents the results of a five-blade resistance type vertical axis wind turbine using numerical simulation. The computation shows that the maximum power efficiency for the blade diameter of 0.8 m and turbine radius R = 2 m in the normal installation angle (θ = 0) is 24.3 %; the maximum power efficiency for a turbine with the blade diameter of 0.78 m and turbine radius R = 2 m is at the installation angle of θ = 19°, which reaches to 28.48 %; optimizing installation angle is an effective method to improve power efficiency of resistance type VAWT.
Abbreviations
- R :
-
Wind turbine maximum radius (m)
- r :
-
Radius of the blade (m)
- d :
-
Diameter of blade (m)
- L :
-
The length of the computation region (m)
- H :
-
The width of the computation region (m)
- C :
-
Constant equal to 0.6125
- C p :
-
Power coefficient
- P :
-
Power produced by the turbine (w)
- C m :
-
Torque coefficient
- V :
-
Inlet wind speed (m/s)
- w :
-
Rotor rotational rate of turbine (rpm)
- S :
-
Rotor swept area (m2)
- ρ :
-
Air density (kg/m3)
- θ :
-
Installation angle of the blade (°)
References
Mohamed, M.H., Janiga, G., Pap, E.: Optimization of Savonius turbines using an obstacle shielding the returning blade. Renew. Energy 35, 2618–2626 (2010)
Dobrev, I., Massouh, F.: CFD and PIV investigation of unsteady flow through Savonius wind turbine. Energy Procedia 6, 711–720 (2011)
Gupta, R., Biswas, A., Sharma, K.K.: Comparative study of a three-bucket Savonius rotor with a combined three-bucket Savonius–three-bladed Darrieus rotor. Renew. Energy 33, 1974–1981 (2008)
Mahmoud, N.H., El-Haroun, A.A., Wahba, E., Nasef, M.H.: An experimental study on improvement of Savonius rotor performance. Alex. Eng. J. 51, 19–25 (2012)
Zhao, Z., Zheng, Y., Zhou, D., Liu, W., Xu, X., Hu, G.: Optimization of the performance of Savonius wind turbine based on numerical study. Acta Energiae Solar Sinica 31, 907–911 (2010)
Kumbernuss, J., Chen, J., Yang, H.X., Lu, L.: Investigation into the relationship of the overlap ratio and shift angle of double stage three bladed vertical axis wind turbine (VAWT). J. Wind. Eng. Ind. Aerodyn. 107–108, 57–75 (2012)
Saha, U.K., Rajkumar, M.J.: On the performance analysis of Savonius rotor with twisted blades. Renew. Energy 31, 1776–1788 (2006)
Wang, J., Emmanuel, B., Wang, X.: CFD Study of a new type of vertical axis wind turbine. J. Eng. Thermophys. 33, 63–65 (2012)
Fujisawa, N.: Velocity measurements and numerical calculations of flow fields in and around Savonius rotors. J. Wind Eng. Ind. Aerod. 59, 39–50 (1996)
Yaakob, O.B., Tawi, K.B., Sunanto, D.T.S.: Computer simulation studies on the effect overlap ratio for savonius type vertical axis marine current turbine. Int. J. Eng. Trans. A Basics 23, 79–88 (2010)
Simão Ferreira, C.J., Van Zuijlen, A., Bijl, H., Van Bussel, G., Van Kuik, G.: Simulating dynamic stall in a two-dimensional vertical-axis wind turbine: verification and validation with particle image velocimetry data. Wind Energy 13, 1–17 (2010)
Bedon, G., Castelli, M., Benini, E.: Numerical validation of a blade element—momentum algorithm based on hybrid airfoil polars for a 2-m Darrieus wind turbine. Int. J. Pure Appl. Sci. Tech. 12, 1–6 (2012)
Mohamed M.H., Janiga G., Pap E., Thevenin D.: Optimal blade shape of a modified Savonius turbine using an obstacle shielding the returning blade. Energy Conv. Manag. 52: 236–24 (2011)
Zullah, M.A., Prasad, D., Choi, Y.D., Lee, Y.H.: Study on the performance of helical savonius rotor for wave energy conversion. AIP Conf. Proc. 1225, 641–649 (2010)
Kamoji, M., Kedare, S., Prabhu, S.: Experimental investigations on single stage, two stage and three stage conventional Savonius rotor. Int. J. Energy Res. 32, 877–895 (2008)
Fernando, M.S.U.K., Modi, V.J.: A numerical analysis of the unsteady flow past a Savonius wind turbine. J. Wind Eng. Ind. Aerod. 32, 303–327 (1989)
Deglaire, P., Engblom, S., Ågren, O., Bernhoff, H.: Analytical solutions for a single blade in vertical axis turbine motion in two-dimensions. Eur. J. Mech. B Fluids 28, 506–520 (2009)
Tabrizi, A.S., Masoud, A., Xie, G., Lorenzini, G., Biserni, C.: Computational fluid—dynamics-based analysis of a ball valve performance in presence of cavitation. J. Eng. Thermophys. 23, 27–38 (2014)
Lorenzini, G., Moretti, S.: A CFD application to optimize T-shaped fins: comparisons to the Constructal theory’s results. ASME J Electr. Packag. 129, 324–327 (2007)
Lorenzini, G., Casalena, E.: CFD analysis of pulsatile blood flow in an atherosclerotic human artery with eccentric plaques. J. Biomech. 41, 1862–1870 (2008)
Lorenzini, G., Conti, A., De Wrachien, D.: Computational Fluid Dynamics (CFD) picture of water droplet evaporation in air. J. Irrig. Drain. Syst. Eng. 1, 1–12 (2012)
Wang, L.B., Zhang, L., Zeng, N.D.: A potential flow 2-D vortex panel model: applications to vertical axis straight blade tidal turbine. Energy Convers. Manag. 48, 454–461 (2007)
Zanon, A., Giannattasio, P., Simão Ferreira, C.: A vortex panel model for the simulation of the wake flow past a vertical axis wind turbine in dynamic stall. Wind Energy 16, 661–680 (2013)
Gormont R.E.: A mathematical model of unsteady aerodynamics and radial flow for application to helicopter rotors. Technical report. USAAV Labs TR72-67 (1973)
Goude A., Lundin S., Leijon M.: A parameter study of the influence of struts on the performance of a vertical-axis marine current turbine. In: Proceedings of the 8th European wave and tidal energy conference, EWTEC09, Uppsala, Sweden, 477–483 (2009)
Van den Braembussche R.A.: Numerical optimization for advanced turbo machinery design. Optimization and computational fluid dynamics, Heidelberg: Springer, Berlin, 147–188 (2008)
D’Alessandro, V., Montelpare, S., Ricci, R., Secchiaroli, A.: Unsteady Aerodynamics of a Savonius wind rotor, a new computational approach for the simulation of energy performance. Energy 35, 3349–3363 (2010)
Acknowledgments
This work was supported by the projects “13115 program” 2008 ZDKG-54 and “technological innovation program” 2011ZKC07-4 by Shaanxi Province, China.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
This article is published under license to BioMed Central Ltd. Open Access This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
About this article
Cite this article
Zheng, M., Li, Y., Tian, Y. et al. Effect of blade installation angle on power efficiency of resistance type VAWT by CFD study. Int J Energy Environ Eng 6, 1–7 (2015). https://doi.org/10.1007/s40095-014-0142-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40095-014-0142-0