Abstract
The uncertainty caused by the discontinuous nature of wind energy affects the power grid. Hence, forecasting the behavior of this renewable resource is important for energy managers and electricity traders to overcome the risk of unpredictability and to provide reliability for the grid. The objective of this paper is to employ and compare the potential of various artificial neural network structures of multi-layer perceptron (MLP) and radial basis function for prediction of the wind velocity time series in Tehran, Iran. Structure analysis and performance evaluations of the established networks indicate that the MLP network with a 4-7-13-1 architecture is superior to others. The best networks were deployed to unseen data and were capable of predicting the velocity time series via using the sliding window technique successfully. Applying the statistical indices with the predicted and the actual test data resulted in acceptable RMSE, MSE and R 2 values with 1.19, 1.43 and 0.85, respectively, for the best network.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
Introduction
Environmental effects of fossil resources combined with energy demand growth are important reasons for humanity’s recent desire for harnessing clean energy [1, 2]. High potential, sustainability and availability are factors supporting solar and wind energy, as potentially the most applicable renewable energy sources around the world [3, 4]. In this regard, Fig. 1 presents an illustrative comparison of the global average annual growth rate of renewable energy utilization in 2010 and 2005–2010 [5].
Average annual growth rate of renewable energy capacity [5]
To cover the uncertainty caused by the discontinuous nature of wind resources, a reliable energy system is required [6, 7]. Hence, forecasting the behavior of the wind resource can be a crucial role for energy managers, policy makers and electricity traders, to overcome the risk of unpredictability, and to provide energy security, for energy planning and handling energy storage policies including economic dispatch. Furthermore, such forecasting gives perspectives regarding time of operation, repair and replacement of wind generators and conversion lines and could help to shift towards optimum electrical networks.
Various approaches to forecast wind velocity and power have been reported. Examples include autoregressive integrated moving average (ARIMA) [8–10], nearest neighbor search, polynomial regression, Bayesian structural break [11], support vector machines (SVM) [12], Taylor Kriging [9], fuzzy logic and artificial neural network (ANN) [13, 14], ARIMA–Kalman [15], ARIMA–ANN [16] and wavelet derivatives such as wavelet-GP, wavelet-ANFIS, wavelet-ANN and wavelet packet [17–20]. These approaches are among the most utilized methods to predict wind resource components. The ANNs have resulted in acceptable performance compared to conventional methods due to their robustness and capability to address unpredictable complexities.
The objective of this paper is to utilize various ANN approaches to forecast the behavior of wind velocity time series in Tehran, Iran. For this purpose, measured wind velocity data of the region (at an altitude of 10 m) for 1 year (8,760 h) at 1-h intervals (averaged values of every 10 min) are provided by a meteorological ground station of the Iran National Meteorological Organization, to predict 1,314 test data points after training multiple networks. Regarding the sufficiency of the prediction size to be used for evaluation of the proposed networks, Table 1 compares the size of the predicted data of the present study to the data size related to prediction goals of recent similar studies. To check the accuracy of predictions, the output results are evaluated via applying common statistical error tests such as RMSE, MSE and R 2 using the predicted values and the actual data.
Sliding window technique, artificial neural networks
ANNs are of the most popular artificial intelligence techniques. They imitate the human brain systems and learn from examples. Applications of ANNs include but are not limited to clustering, regression analysis, estimating functions, fitness approximation, novelty detection, data processing as well as time series prediction. ANNs are capable of learning, memorizing and constructing relationships among data. An ANN consists of processing units, layers (input, output and hidden), neurons and transfer (activation) functions. ANN units are connected by weighted links that pass information and store the required knowledge in hidden layers. An input (x j ) of the network travels thorough the connection and the link multiplies its strength by a weight (w ij ) to generate x j w ij which is an argument of a transfer function (f). The transfer function produces an output as y i = f(x j w ij ), where i is an index of neurons in the hidden layer and j is an index of an input to the neural network [22]. During a training process, ANNs change weights to be trained for a minimum error and to achieve defined stopping criteria such as a considered error value, number of iterations, calculation time and validation limits. Multi-layer perceptron (MLP) networks are of the most common feed-forward estimator networks. These provide a robust architecture for learning nonlinear phenomenon. Feed-forward implies that neurons in continuous layers send their output (signals) forward and only forward connections exist [23]. MLP networks have been the most used architecture both in the renewable energy domain and in time series forecasting [24]. To predict values in MLP networks, a fixed number p of previous observed velocity values is considered as inputs of the network for each training process while the output is the forecasted values of the time series, which is the so-called the “sliding window technique” (see Fig. 2). The mathematical model for training the network can be expressed as:
where P and Q are the number of inputs and hidden nodes, respectively, and j is the transfer function. Respectively, “w j , j = 0, 1,…, Q” and “w i,j , i = 1, 2,…, P & j = 1, 2,…, Q” are the weight vectors from the hidden layer to the output and the weights from the input to the hidden nodes. Also, w 0j is the weight for each output between the input and the hidden layer [25]. For network consistency and reducing calculation time, input data should be normalized. Hence, the utilized data of the current study are normalized before processing. Normalization can be performed as follows:
Sliding window technique in ANN [22]
Network structures
The performance of trained networks depends on their architecture. The number of hidden layers, the number of neurons, the type of utilized transfer functions, the size of training and testing samples and the learning algorithms are effective training parameters in addition to the utilized stopping criteria. To find the best structure of the network in this study, various network structures are evaluated. Finding the best value/type for each network parameter involves finding a value/type for that parameter which minimizes the prediction error. In the same line, network parameters and their evaluated values/types in the study are given in Table 2. As noted earlier, a fixed number p of previous observed velocity values are considered as inputs to the network in each training process while the output is the forecasted velocity values of the time series. Data distribution for training, validation and test procedures is considered as 70, 15 and 15 % of the entire data set, respectively. The computation processes include training (via the Levenberg–Marquardt (LM) algorithm [26]) and evaluation of the results (via the statistical error indices), which are performed in the MATLAB® environment.
Also, the same data are provided to various radial basis function neural networks (RBFNNs) [27] for comparing their best outcome to the best performance yielded from the MLP networks trained by the LM algorithm. Regarding structure of the trained RBFNNs, a greater range of neuron numbers in the hidden layer is tested and compared to the MLP networks. To identify the best structure of the RBFNN, 0–25 neurons are examined in the hidden layer and the performances calculated for each structure are determined and compared in the results section.
Statistical indices for performance evaluation
The most common statistical indicators, including root mean square error (RMSE), absolute fraction of variance (R 2) and mean square error (MSE), are utilized with the forecasted data (v f) and the actual measured data (v m) to evaluate the performance of the proposed predictor systems. Table 3 shows the utilized statistical indicators accompanied by their relevant mathematical expressions.
Results and discussion
The results of training various networks with different structures are presented in this section.
For MLP networks, Table 4 shows a summary of trained structures with p = 4 input data and the related obtained errors (RMSE and MSE) and R 2 to find the best structure. Regarding the utilized statistical indices, RMSE provides information on the performance of the models, as it allows a term by term comparison of the actual deviation between the calculated and the measured values. The commonly used parameter, R 2, is a measure of the strength of the relationship between values. It is a function of RMSE and the standard deviation. Hence, to evaluate the performance of the established networks, low error values (nearer to 0) and high R 2 values (nearer to 1) are favorable for an efficient network.
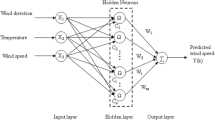
According to the results, a network with 4-7-13-1 structure is chosen as the best MLP network of this study. This network utilizes 4 input data in the input layer with 7 and 13 neurons in its first and second hidden layers to predict the output. The activation functions of the first and the second relevant hidden layers of this network are Tansigmoid and Logsigmoid, respectively. The network utilizes a linear function in its output layer to transfer the data to the output.
Similarly, various RBFNN structures are examined to find the related outperforming architecture. The performances obtained for RBFNN structures with p = 4 input and 0–25 examined neurons in the hidden layer are summarized in Fig. 3.
To test the best structures of the trained RBF and MLP networks, the identified structure from each approach is separately deployed to the same unknown test data, which were not utilized in the training process. Table 5 shows the performance results related to the outperformed structures of MLP (4-7-13-1) and RBFNN (4-25-1), considering the same test data.
Figure 4 illustrates the agreement of the actual target values and the predicted outputs for the outperformed structure of RBFNN (4-25-1) after de-normalization of the data. Along the same line, Fig. 5 illustrates the outperformed structure of MLP (4-7-13-1).
Evaluation of the statistical indices demonstrates acceptable predicted outputs and also the flexibility of both approaches when large changes occur. However, as shown in Table 5, the 4-7-13-1-MLP network performs better than the 4-25-1-RBFNN network, according to its higher R 2 value and lower MSE and RMSE values. Figure 6 illustrates a schematic structure of this selected network and its components.
For the outperformed structure of MLP network, applying the statistical indices with the predicted and the actual test data results in acceptable RMSE, MSE and R 2 values (considering similar previous studies, including Refs. [9, 14, 15]) of 1.19, 1.43 and 0.85, respectively. As can be seen in the error histogram of this network (Fig. 7), the largest error values range between −1 and 1, which indicates acceptable overestimation and underestimation values. Also, the standard deviation of error is 1.1951 and the symmetric shape of the error histogram around the zero point (following a normal distribution pattern) ensures low error values (near zero) for the sum of overestimated (positive values) and underestimated (negative values) data, when the sum of predicted velocities in a given period is desired.
Conclusions
Forecasting the behavior of the wind resource can provide valuable information for energy managers, energy policy makers and electricity traders, as well as times of operation, repair and replacement of wind generators and conversion lines. However, reliable power generation and effective integration of wind energy systems into the power distribution grid are affected by the intermittent and nonlinear nature of the wind resource. Accurate forecasting of wind velocities not only can address the challenges such as adverse shocks in conventional power units caused by excessive wind speed but also can provide useful information regarding voltage and frequency instabilities resulting from variation in wind power. ANNs are robust tools with advantageous capabilities for addressing the unpredictable complexities of nonlinear phenomena such as the stochastic behavior of the wind resource, which cannot be handled by conventional methods accurately. In this paper, wind velocity data for 1 year at 1-h intervals are utilized to train various artificial neural network (ANN) architectures for prediction of wind velocity data of Tehran, Iran. Structure analysis and performance evaluations of the established networks determine that the MLP network with a 4-7-13-1 architecture is superior to others. The best network was deployed to the unseen data and found to be capable of predicting velocity data via the sliding window technique successfully. Applying the statistical evaluation indices with the predicted and the actual test data results in acceptable RMSE, MSE and R 2 values of 1.19, 1.43 and 0.85, respectively. Predictions of wind power density or wind energy density, which are related to wind velocity, as well as comparing the performance of the ANN with other forecasting approaches, merit further investigation as an extension of the present study.
References
Fazelpour, F., Vafaeipour, M., Rahbari, O., Rosen, M.A.: Intelligent optimization of charge allocation for plug-in hybrid electric vehicles utilizing renewable energy considering grid characteristics. In: 2013 IEEE International Conference on Smart Energy Grid Engineering (SEGE), pp. 1–8. IEEE (2013)
Rahbari, O., Vafaeipour, M., Fazelpour, F., Feidt, M., Rosen, M.A.: Towards realistic designs of wind farm layouts: application of a novel placement selector approach. Energy Convers. Manag. 81, 242–254 (2014)
Fazelpourl, F., Vafaeipour, M., Rahbaril, O., Valizadehz, M.H.: Assessment of solar radiation potential for different cities in Iran using a temperature-based method. In: Proceedings of the 4th International Conference in Sustainability in Energy and Buildings (SEB12), vol. 22, pp. 199–208 (2013)
Vafaeipour, M., Valizadeh, M.H., Rahbari, O., Keshavarz Eshkalag, M.: Statistical analysis of wind and solar energy potential in Tehran. Int. J. Renew. Energy Res. 4(1), 233–239 (2014)
REN21: Renewables 2011 Global Status Report (2011)
Fazelpour, F., Vafaeipour, M., Rahbari, O., Rosen, M.A.: Intelligent optimization to integrate a plug-in hybrid electric vehicle smart parking lot with renewable energy resources and enhance grid characteristics. Energy Convers. Manag. 77, 250–261 (2014)
Fazelpour, F., Vafaeipour, M., Rahbari, O., Rosen, M.A.: Intelligent optimization of charge allocation for plug-in hybrid electric vehicles utilizing renewable energy considering grid characteristics. In: IEEE International Conference on Smart Energy Grid Engineering, Oshawa, Ontario, Canada, paper 39, pp. 1–8. IEEE (2013)
Kavasseri, R.G., Seetharaman, K.: Day-ahead wind speed forecasting using f-ARIMA models. Renew. Energy 34(5), 1388–1393 (2009). doi:10.1016/j.renene.2008.09.006
Liu, H., Shi, J., Erdem, E.: Prediction of wind speed time series using modified Taylor Kriging method. Energy 35(12), 4870–4879 (2010). doi:10.1016/j.energy.2010.09.001
Cadenas, E., Rivera, W.: Wind speed forecasting in the South Coast of Oaxaca, México. Renew. Energy 32(12), 2116–2128 (2007). doi:10.1016/j.renene.2006.10.005
Jiang, Y., Song, Z., Kusiak, A.: Very short-term wind speed forecasting with Bayesian structural break model. Renew. Energy 50, 637–647 (2013). doi:10.1016/j.renene.2012.07.041
Zhou, J., Shi, J., Li, G.: Fine tuning support vector machines for short-term wind speed forecasting. Energy Convers. Manag. 52(4), 1990–1998 (2011). doi:10.1016/j.enconman.2010.11.007
Celik, A.N., Kolhe, M.: Generalized feed-forward based method for wind energy prediction. Appl. Energy (2012). doi:10.1016/j.apenergy.2012.06.040
Li, G., Shi, J.: On comparing three artificial neural networks for wind speed forecasting. Appl. Energy 87(7), 2313–2320 (2010). doi:10.1016/j.apenergy.2009.12.013
Liu, H., Tian, H.-q., Li, Y.-f.: Comparison of two new ARIMA–ANN and ARIMA–Kalman hybrid methods for wind speed prediction. Appl. Energy 98, 415–424 (2012). doi:10.1016/j.apenergy.2012.04.001
Cadenas, E., Rivera, W.: Wind speed forecasting in three different regions of Mexico, using a hybrid ARIMA–ANN model. Renew. Energy 35(12), 2732–2738 (2010)
Kisi, O., Shiri, J., Makarynskyy, O.: Wind speed prediction by using different wavelet conjunction models. Int. J. Ocean Clim. Syst. 2(3), 189–208 (2011)
Catalão, J., Pousinho, H., Mendes, V.: Short-term wind power forecasting in Portugal by neural networks and wavelet transform. Renew. Energy 36(4), 1245–1251 (2011)
Lei, C., Ran, L.: Short-term wind speed forecasting model for wind farm based on wavelet decomposition. In: Third International Conference on Electric Utility Deregulation and Restructuring and Power Technologies, 2008. DRPT 2008, pp. 2525–2529. IEEE (2008)
Liu, H., Tian, H.-q., Pan, D.-f., Li, Y.-f.: Forecasting models for wind speed using wavelet, wavelet packet, time series and artificial neural networks. Appl. Energy 107, 191–208 (2013)
Zhang, W., Wang, J., Wang, J., Zhao, Z., Tian, M.: Short-term wind speed forecasting based on a hybrid model. Appl. Soft Comput. 13(7), 3225–3233 (2013). doi:10.1016/j.asoc.2013.02.016
Paoli, C., Voyant, C., Muselli, M., Nivet, M.-L.: Forecasting of preprocessed daily solar radiation time series using neural networks. Sol. Energy 84(12), 2146–2160 (2010). doi:10.1016/j.solener.2010.08.011
Vafaeipour, M.: An Artificial Intelligence Based Approach to Estimate Solar Irradiation in Tehran. South Tehran Branch, Islamic Azad University, Tehran (2012)
Voyant, C., Muselli, M., Paoli, C., Nivet, M.-L.: Hybrid methodology for hourly global radiation forecasting in Mediterranean area. Renew. Energy 53, 1–11 (2013). doi:10.1016/j.renene.2012.10.049
Shi, J., Guo, J., Zheng, S.: Evaluation of hybrid forecasting approaches for wind speed and power generation time series. Renew. Sustain. Energy Rev. 16, 3471–3480 (2012). doi:10.1016/j.rser.2012.02.044
Sftesos, A., Coonick, A.H.: Univariate and multivariate forecasting of hourly solar radiation with artificial intelligence techniques. Sol. Energy 68, 169–178 (2000)
Haykin, S.: Neural Networks: A Comprehensive Foundation. Prentice Hall PTR, New Jersey (1994)
Conflict of interest
The authors declare that they have no competing interests
Authors’ contributions
MV, OR, and PA have participated in implementation of the methods, computation process, validation of the results, and giving the study ideas. MV has also drafted the manuscript. As supervisor Profs., MR and FF have checked the study procedure and commented for qualification of the manuscript structure. All authors read and approved the final manuscript.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
This article is published under license to BioMed Central Ltd. Open Access This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
About this article
Cite this article
Vafaeipour, M., Rahbari, O., Rosen, M.A. et al. Application of sliding window technique for prediction of wind velocity time series. Int J Energy Environ Eng 5, 105 (2014). https://doi.org/10.1007/s40095-014-0105-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s40095-014-0105-5