Abstract
Using the first principle calculations, the structural, electronic and optical properties of the monolayer graphene-like MoX2 sheet are calculated. Our results show that the chalcogenide atoms in the stability and the lattice parameters of the MoX2 sheet have a key role, although it is known that the electronic properties are more dependent on the metal atoms in these sheets. Our data also confirm semiconductor behavior of the MoX2 monolayers with direct band gap for S, Se and Te chalcogenides. Compared with the bulk compounds, they have similar structural properties but represent unique electronic and optical properties that can be used in nano-devices, nano-electronics and so on. In this work, the investigation of the chalcogenide atoms role in modifying the optical properties of these single-layer sheets, such as absorption and refraction coefficients, is carried out; the dielectric constant plays an important role. We also try to study the possibility of using these compounds on the solar energy industries and optical devices.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Graphene is a 2D hexagonal carbon sheet [1]; its zero gap, Dirac-shaped energy levels along Γ paths and also the high electron transfer rate made it a suitable material for electronic conduction and mechanical strength [2]. Because of some restrictions as zero gap, the scientists’ attention has been attracted to graphene-like structures [3, 4] so that in the last few years, by reducing the graphite thickness, achievement of monolayer and multi-layer graphene sheets has been possible [5, 6]. Accordingly, the ability to develop its applied capacities has been provided such as chemical sensors [7, 8], nano-electronics [9] and hydrogen storage systems [10]. Besides carbon-based nanostructures [11], alternative extensively studied single-layer compositions are silicone [12], germanene [11], stanene [13], phosphorene [14] and single-layer transition metal dichalcogenides (MX2, M = Transition metal and X = Chalcogen) [15]. The 2D semiconducting sheets have the minimum possible thickness and wide band gaps; from the viewpoint of application, they can be used in photovoltaic, sensing, biomedicine, solar cells and catalysis [16,17,18]. The MX2 compounds including X-M-X sheets are loosely coupled by strong bonds within layers [19]. These compounds have attractive and diverse physical properties; for example, HfS2 is an insulator, MoS2 is a semiconductor, WTe2 and TcS2 have semimetal behavior, and all the NbCh2 and TaCh2 are superconductors. A new advantage in the nanoscale materials opened up a new window for two-dimensional dichalcogenides (TMDCs). MX2 such as MoS2, MoSe2 [20], WS2 and WSe2 [21, 22] has sizable bandgaps that change from indirect to direct in single layers, allowing applications such as transistors, photodetectors and electroluminescent devices. Transition metal dichalcogenide compounds also have a similar structure with graphite, which can be made by chemical vapor deposition such as MoS2 [23]; in addition, the 2D MoS2 sheets are made by micro-mechanical cleavage as old as grapheme [23]. The prior theoretical studies indicate that the MoS2 semiconductor bulk has an indirect band gap while the 2D MoS2 sheet has a direct band gap. Moreover, the MoS2 sheets can be piped into nanotubes, and the MoS2 monolayer and thin films can be extracted as ferromagnetic metals [24].
Recently, some applications have been reported for MoS2 compositions like the heterolayer structure [25, 26], FETs and memory devices with two-structure MoS2-Gr [27, 28]; photodetector devices include p–n junction [29] and MoS2–WS2 [30], in photovoltaic devices from Au–MoS2–Au [31] and other heterostructures [32,33,34]. The MoTe2 compositions have many applications, especially in optical devices, which one of them is in the novel heterolayer materials based on MoTe2-In [35]. Generally, the results indicate that quantum confinement of carriers within monolayers can be exploited in conjunction with chemical composition to tune the optoelectronic properties of layered transition metal dichalcogenides at the nanoscale [36].
In this paper, the electronic, optical and structural properties of the MoX2(X = S, Se, Te) sheets have been studied by first principle calculations. The electronic and structural properties including lattice parameters, band gap, cohesive energies, formation energies and density of states are in good agreement with previous research, so this study focuses more on optical parameters such as dielectric constant, the coefficients of reflection, refraction and absorption.
Methods
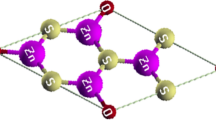
The calculations are based on the density functional theory using full potential linear augmented plane waves plus local orbital (FP-LAPW + lo) method with WIEN2K code [37]. The exchange–correlation (XC) energy calculations are used from the Perdew–Burke–Ernzerhof (PBE) functional form of the generalized gradient approximation (GGA) [37]. The separation energy used for both MoS2 and MoSe2 is -6 Ry while for MoTe2 is − 9 Ry. To avoid interaction between the mentioned sheets, the distance is considered more than 12A0, and also Kpoint, Rkmax, Lmax and Gmax, respectively, are chosen as 2000, 8.5, 10 and 12.5. In order to increase the calculations accuracy, the structures have been optimized by 1.0 a.u./dyne and the electrical charge convergence about 0.0001. Figure 1 is plotted by XCrysDen package, which after forming and relaxing the unit cell, we repeated it in directions x and y for better presentation. All of the other figures in this paper for greater clarity are plotted by the Sigma Plot software.
Results and discussions
Structural properties
The crystalline structure of the MoS2 sheet is shown as an example of MoX2 compounds in Fig. 1. The Mo atoms occupy a sub-lattice of a hexagonal sheet sandwiched between two layers of S atoms. In this work, the thickness of MoS2 is obtained 3.17 A0 after optimization which is compatible to value 3.13 A0 at previous works [38]. In addition, the optimized bond length for MoS2 is obtained 2.40 A0 that is in a good agreement with 2.42 A0 (2.39 A0) in PBE (LDA) calculations [38]. The different chalcogenides meaningfully change lattice parameters, listed in Table 1. The increase in chalcogenide atomic radius causes elevating the sheet thicknesses, bond length dMo-X and lattice constants as MoS2 < MoSe2 < MoTe2 that is in accordance with previous works using both XC approximations HSE (Heyed–Scuseri–Ernzerhof) and GW correction [38].
The difference in chalcogenides effects appears not only in lattice parameters but also in cohesive (EC) and formation (Eform) energies. In these calculations, cohesive energy is defined as:
where N is the number of atoms in a unit cell, EMoX2 is total energy of MoX2 sheet, EMo atom and EX atom are isolated atoms energy of metal and chalcogenide, respectively. The negative energy indicates more stability in compounds. Table 1 shows that EC(MoS2) < EC(MoSe2) < EC(MoTe2), and also, formation energy is defined as
where EMo bulk and EX dimer are atomic energies in their stabilities elemental structures in bulk states, respectively. All of the MoX2 sheets have negative values of EC and Eform indicating the thermodynamic stability.
Electronic properties
Figure 2 presents electronic band structure and DOS of MoX2 (X = S, Se, Te) sheets which have been affected by the change in chalcogenide atom. The initial DFT calculations generally underestimate the band gap of the material [39]. Therefore, the PBE method has been used for the XC functional to predict the band gap accurately. The MoS2 sheet is a semiconductor with a direct band gap at K symmetry point at 1.72 eV confirmed by the latest experimental works [40] and theoretical studies [18, 41]. As shown in Table 2, similar to the MoS2 sheet, the MoSe2 and MoTe2 sheets also have a direct band gap in K symmetry point, equal to 1.50 eV and 1.06 eV, respectively, which is validated by the previous work [38]. As a result, all compounds have similar semiconductor properties, so that their band gap is direct and around 1.5 eV, which can be used in solar energy, luminescence materials and so on. The electronic structures indicate the p-type semiconductor all of the mentioned cases by relatively high electron mobility in the conduction bands which is confirmed in the partial DOS at upper Fermi level; also, the Mo-4d and X-3p are the excited electron states based on their overlapping in this energy range. The electron states of the above-mentioned orbitals at conduction band are greater than their states at valance area which confirmed again high electron mobility for these compounds. The high electron states of the above-mentioned orbitals at conduction band than their states at valance band confirmed the high electron mobility these compounds again.
Optical properties
The optical properties of the graphene-like compounds discussed in the energy range of 0–30 eV are calculated. In a compound with hexagonal symmetry, there can be two types of electrical vector (E): parallel and perpendicular to the C axis, which can be written as ε┴(ω) = (εxx(ω) + εyy(ω)/2 and ε∥(ω) = εzz(ω) [42], where εxx(ω), εyy(ω) and εzz(ω) are the dielectric matrix elements εij(ω). In this case, the imaginary part of the dielectric function is calculated from the band structure and the real part from using the Kramers–Kronig relationship [39]. In Fig. 3, the imaginary and real parts of the dielectric function are shown in both perpendicular and parallel directions for MoS2, MoSe2 and MoTe2 sheets. In Fig. 3a, the MoS2 response to the incident light shows a high degree of anisotropic in the infrared regions up to the beginning of ultraviolet (E < 8 eV) and isotropic at higher energies, which are in a good agreement with previous studies [16, 43, 44].
It is important to mention that the peaks in the imaginary part of the dielectric function represent interband transitions. The imaginary part of the dielectric function, ε ∥2 (ω) and ε ┴2 (ω) for the MoS2 sheet, represents the optical transitions of filled levels to empty ones at points of A (2.8 eV), B (3.6 eV), C (4.3 eV) and D (5.3 eV). At A point, the transition of the interband (as shown in Fig. 3) occurs from valence band to conduction one along the Γ–M and K–Γ directions. At B point, the story is the same with this difference that it is along the Γ–M direction and vicinity of M point. The transitions at C and D points are occurred along K–Γ symmetry direction and at the M symmetry point, respectively. All the above interband transitions are essentially due to the p orbital of the S atoms to the d orbital of the Mo atoms, which are listed in Table 2. As seen, the structures move toward lower energies as we go from S to Se to Te.
It has been well established that the quantum confinement effects may change position and shape of bands [45]. According to Table 2, the calculated values of the real part of the dielectric function at the zero frequency (ε ∥1 (0), ε ┴1 (0)) for MoS2, MoSe2 and MoTe2 are (4.69, 8.33), (5.13, 9.30) and (11.63.5.98), respectively. The small case of ε1(0) is compatible with its relatively large gap in MoS2, and as expected, there is ε1(MoS2) < ε1(MoSe2) < ε1(MoTe2), which expresses the semiconductivity of these compounds, shown in Fig. 3. However, the largest response to the incident light occurs in parallel radiation for all compounds, indicating that these compounds may be suitable for optical industry or solar cells applications [25, 37, 46]. Furthermore, the negative sign of ε1(ω) has been seen in different regions above the UV for all cases representing the lack of light transmission. Completely anisotropy behaviors were occurred in the infrared (IR), visible area and ultraviolet (UV) edge for the light angle which were shown in the ε1(ω) curves. Since there is no optical transparency in the negative sign of ε1(ω) and in the energy interval of 4.5 eV to 18 eV, the sign ε1(ω) changes alternatively, so in this energy range, we see instability in the optical response. After 15 eV, the ε1(ω) and ε2(ω) have fully symmetric behavior for the two mentioned directions and their low amount implies the insulating treatment at higher energies for all cases. All three MoS2, MoSe2 and MoTe2 graphenes act like a transparent matter after 15 eV, and light could pass through them, completely.
As shown in Fig. 3, ε1(ω) becomes zero several times (listed in Table 2) which can be due to different reasons. The most important reason is the Plasmon oscillations that of course need the existence of a peak in the energy loss spectrum for confirmation. The Eloss curve shows the amount of reduction and drop in the light energy through the material which is shown in Fig. 4 for MoS2, MoSe2 and MoTe2 monolayers in both perpendicular and parallel polarization states. In the MoS2 composition, for perpendicular direction to the sheet, there are peaks at energies of 8.8 eV, 10.9 eV and 18.9 eV displaying surface Plasmon oscillations while there is a peak at the energy of 18 eV demonstrating volume Plasmon oscillations. For parallel direction, two peaks appear at energies of 8.1 eV and 7.1 eV corresponding to the surface Plasmon.
In the MoSe2, peaks at 17.9 eV and 17.5 eV represent volume Plasmon oscillations for perpendicular and parallel directions, respectively. Similarly, the sharp–large peaks in the MoTe2 single layer appear at 17.8 eV and 17.6 eV for perpendicular and parallel directions due to the absorption of Plasmon energy, respectively. Finally, yet importantly, the Eloss’s main peak experiences a shift toward lower energies for MoS2 to MoSe2 and MoTe2. The main losses of the optical curves in Fig. 4 have occurred in the two areas, 5–10 eV and 15–20 eV, which are resulted from the oscillation of electric dipoles and the environment ionizing. These compounds can have good optical efficiency at the IR and visible range based on zero amounts of Eloss curves in Fig. 4.
Figure 5 shows the absorption and reflection spectra for MoS2, MoSe2 and MoTe2 monolayers for both the mentioned directions. The absorption and reflection spectra of MoS2 monolayer can so forth be seen around 2.8 eV (442 nm), 5.6 eV (221 nm), 6.4 eV (193 nm) representing interband transition and returning to ground state, and also a minimum of the reflection and absorption is seen at 7.2 eV owing to volume Plasmon oscillations from 6.9 to 7.9 eV with a gap of 1 eV width.
Another important optical factor is the absorption coefficient calculated as A(ω) = 2ωK(ω)∕C, where K is the extinction coefficient. Accordingly, the maximum absorption occurs when there are a high extinction coefficient and a minimum wave transfer. As shown in Fig. 5a, the MoS2 combination has an upper absorption gap from around 2.4 eV (500 nm) to 22 eV (50 nm) and is a suitable absorber for electromagnetic waves. Moreover, it has several sharp peaks, ranged from 2.9 eV (500 nm) to 22 eV (50 nm), and it is also a good reflector from ultraviolet to infrared. Considering 5b, c diagrams, it can be found that by increasing the chalcogenide atomic number, the initiation of absorption and also reflection energies experience a redshift. In the infrared and visible areas, the MoSe2 also works better than the MoS2 while the MoTe2 is better than both of them. In Table 3, the extracted data from Fig. 5 which include the energies of absorption and reflection peaks in nanometer scale, as well as the static reflection coefficient R(0) of the MoX2 monolayers in two states of parallel and perpendicular (the important peaks are shown in full color), are listed. Based on the high absorption and continual diagrams of all the mentioned cases and low Eloss till 15 eV energy, these compositions are suitable optical absorber in the visible and UV edge. The reflection coefficients of all cases have the maximum amount in the 5 eV area, which was due to the electric charges oscillation and ionic behavior of these compounds.
The refraction coefficient is a complex function ň(ω) = n(ω) + ik(ω) related to the dielectric constant as [47]:
In Fig. 6, the refraction spectrum and the extinction coefficients are observed in both directions. The minimum static refraction coefficient (in zero energy) is n = 2.9 for MoS2 and then for MoSe2 is n = 3; the maximum value is n = 3.4 for MoTe2. Generally, n increases ascendingly from zero energy to the first peak (about 4 eV) and then decreases by a few oscillations down to a minimum value (approximately 16 eV energy). Accordingly, the notable point is that the first peaks of the real refraction coefficients from low to high energies are occurred for the above combinations as follows: MoTe2 at the energy of 1.6 eV (770 nm), MoSe2 at 2.4 eV (520 nm) and MoS2 at 2.5 eV (500 nm). The extinction coefficient diagram suggests that the non-penetration of electromagnetic waves for MoS2 is from about 2 eV (620 nm) to 16 eV (77 nm), for MoSe2 is from 1.5 eV (820 nm) to 16 eV (77 nm) and similarly for MoTe2 is from 1.1 eV (1120 nm) to 16 eV (77 nm). By comparing the extinction and corresponding reflection coefficients (Figs. 5, 6), it can be concluded that most of the peaks occur in the same level of energies for each composition as expected. The refraction and extinction diagrams have been increased and dropped rapidly, respectively, at 5 eV, and in the lower energies show the anisotropy. Also in the parallel mode, Fig. 6 curves have redshift. After 15 eV, the refraction is smaller than one and extinction rose to zero which implied to the superluminal phenomena (Table 4).
Another important note about refraction diagrams is a great peak for (< 4) MoS2, MoSe2 and MoTe2 graphenes in the visible area which can be used in the antireflection coatings for photonics and optoelectronics [48], high-performance substrates for advanced display devices [49] and optical encapsulants for the enhancement of photovoltaic cell response [50].
Conclusions
In summary, the structural, electronic and optical properties of the MoX2 graphene-like monolayers have been investigated using the first principle calculations. In this regard, it has been concluded that the stability level increases from MoTe2 to MoSe2 and also from MoSe2 to MoS2. Hence, the results show a good stability, and it is also possible to produce sheets from their stable elemental bulk structures applying chemical methods. The MoX2 sheets have similar lattice constants, increased by elevating the chalcogenide atomic number. All of three compounds are semiconductors with direct band gaps in the range of 1–1.7 eV, decreased by increasing the chalcogenide atomic number, and it is in a good agreement with previous experimental works. The density of states around Fermi energy depends on the d orbital of Mo atoms and the p orbital of chalcogenide atoms. In the dielectric function of MoX2 sheets, an asymmetric behavior is observed below the energy of 8 eV and a symmetric one at higher energies. These sheets are good absorbent of the electromagnetic waves, and the beginning of light absorption spectrum is encountered a redshift by increasing chalcogenide atomic number. In general, by increasing the chalcogenide atomic number, the threshold curve of optical functions includes the imaginary part of dielectric, absorption, reflection, refractive and extinction shifts toward less energy, and the altitude of these peaks decreases in the visible region by increasing their chalcogenide atomic number. In the UV region, these attitudes are in the order MoTe2 > MoS2 > MoSe2, respectively.
The data obtained in this study suggest that the MoX2 sheets have good potential in the field of nano-electronics and optical instruments such as solar cells, photodetectors, reflector layers and lenses.
References
Neto, A.C., Guinea, F., Peres, N.M., Novoselov, K.S., Geim, A.K.: The electronic properties of graphene. Rev. Mod. Phys. 81, 109 (2009)
Garcia, J.C., de Lima, D.B., Assali, L.V., Justo, J.F.: Group IV graphene- and graphane-like nanosheets. J. Phys. Chem. C 115, 13242–13246 (2011)
Boochani, A., Nowrozi, B., Khodadadi, J., Solaymani, S., Jalali-Asadabadi, S.: Novel graphene-like Co2VAl (111): case study on magnetoelectronic and optical properties by first-principles calculations. J. Phys. Chem. C 121, 3978–3986 (2017)
Soldano, C., Mahmood, A., Dujardin, E.: Production, properties and potential of graphene. Carbon 48, 2127–2150 (2010)
Novoselov, K.S., Geim, A.K., Morozov, S.V., Jiang, D., Katsnelson, M.I., Grigorieva, I.V., Dubonos, S.V., Firsov, A.A.: Two-dimensional gas of massless Dirac fermions in graphene. Nature 438, 197 (2005)
Wang, G., Yang, J., Park, J., Gou, X., Wang, B., Liu, H., Yao, J.: Facile synthesis and characterization of graphene nanosheets. J. Phys. Chem. C 112, 8192–8195 (2008)
Pumera, M.: Electrochemistry of graphene: new horizons for sensing and energy storage. Chem. Rec. 9, 211–223 (2009)
Casolo, S., Martinazzo, R., Tantardini, G.F.: Band engineering in graphene with superlattices of substitutional defects. J. Phys. Chem. C 115, 3250–3256 (2011)
Schwierz, F.: Graphene transistors. Nat. Nanotechnol. 5, 487 (2010)
Boukhvalov, D.W., Katsnelson, M.I., Lichtenstein, A.I.: Hydrogen on graphene: electronic structure, total energy, structural distortions and magnetism from first-principles calculations. Phys. Rev. B 77, 035427 (2008)
O’Hare, A., Kusmartsev, F.V., Kugel, K.I., Stable, A.: “Flat ″form of two-dimensional crystals: Could graphene, silicene, germanene be minigap semiconductors? Nano Lett. 12, 1045–1052 (2012)
Okamoto, H., Kumai, Y., Sugiyama, Y., Mitsuoka, T., Nakanishi, K., Ohta, T., Nozaki, H., Yamaguchi, S., Shirai, S., Nakano, H.: Silicon nanosheets and their self-assembled regular stacking structure. J. Am. Chem. Soc. 132, 2710–2718 (2010)
Rachel, S., Ezawa, M.: Giant magnetoresistance and perfect spin filter in silicene, germanene, and stanene. Phys. Rev. B 89, 195303 (2014)
Liu, H., Neal, A.T., Zhu, Z., Luo, Z., Xu, X., Tománek, D., Ye, P.D.: Phosphorene: an unexplored 2D semiconductor with a high hole mobility. ACS Nano 8, 4033–4041 (2014)
Ugeda, M.M., Bradley, A.J., Shi, S.-F., Felipe, H., Zhang, Y., Qiu, D.Y., Ruan, W., Mo, S.-K., Hussain, Z., Shen, Z.-X.: Giant bandgap renormalization and excitonic effects in a monolayer transition metal dichalcogenide semiconductor. Nat. Mater. 13, 1091 (2014)
Haldar, S., Vovusha, H., Yadav, M.K., Eriksson, O., Sanyal, B.: Systematic study of structural, electronic, and optical properties of atomic-scale defects in the two-dimensional transition metal dichalcogenides M X 2 (M = Mo, W; X = S, Se, Te). Phys. Rev. B 92, 235408 (2015)
Molina-Sanchez, A., Hummer, K., Wirtz, L.: Vibrational and optical properties of MoS2: from monolayer to bulk. Surf. Sci. Rep. 70, 554–586 (2015)
Tenne, R.: Advances in the synthesis of inorganic nanotubes and fullerene-like nanoparticles. Angew. Chem. Int. Ed. 42, 5124–5132 (2003)
Khan, F., Din, H.U., Khan, S.A., Rehman, G., Bilal, M., Nguyen, C.V., Ahmad, I., Gan, L.-Y., Amin, B.: Theoretical investigation of electronic structure and thermoelectric properties of MX2 (M = Zr, Hf; X = S, Se) van der Waals heterostructures. J. Phys. Chem. Solids 126, 304–309 (2019)
Ahmad, I., Khan, S.A., Idrees, M., Haneef, M., Shahid, I., Din, H.U., Khan, S.A., Amin, B.: Influence of strain on specific features of MoX2 (X = S, Se, Te) monolayers. Physica B 545, 113–118 (2018)
Muoi, D., Hieu, N.N., Phung, H.T., Phuc, H.V., Amin, B., Hoi, B.D., Hieu, N.V., Nhan, L.C., Nguyen, C.V., Le, P.T.T.: Electronic properties of WS2 and WSe2 monolayers with biaxial strain: a first-principles study. Chem. Phys. 519, 69–73 (2019)
Amin, B., Kaloni, T.P., Schwingenschlögl, U.: Strain engineering of WS 2, WSe 2, and WTe 2. Rsc Adv. 4, 34561–34565 (2014)
Garadkar, K.M., Patil, A.A., Hankare, P.P., Chate, P.A., Sathe, D.J., Delekar, S.D.: MoS2: preparation and their characterization. J. Alloys Compd. 487, 786–789 (2009)
Seifert, G., Terrones, H., Terrones, M., Jungnickel, G., Frauenheim, T.: Structure and electronic properties of MoS 2 nanotubes. Phys. Rev. Lett. 85, 146 (2000)
Li, X., Zhu, H.: Two-dimensional MoS2: properties, preparation, and applications. J. Materiomics 1, 33–44 (2015)
Amin, B., Singh, N., Schwingenschlögl, U.: Heterostructures of transition metal dichalcogenides. Phys. Rev. B 92, 075439 (2015)
Shih, C.-J., Wang, Q.H., Son, Y., Jin, Z., Blankschtein, D., Strano, M.S.: Tuning on–off current ratio and field-effect mobility in a MoS2–graphene heterostructure via Schottky barrier modulation. ACS Nano 8, 5790–5798 (2014)
Bertolazzi, S., Krasnozhon, D., Kis, A.: Nonvolatile memory cells based on MoS2/graphene heterostructures. ACS Nano 7, 3246–3252 (2013)
Choi, M.S., Qu, D., Lee, D., Liu, X., Watanabe, K., Taniguchi, T., Yoo, W.J.: Lateral MoS2 p–n junction formed by chemical doping for use in high-performance optoelectronics. ACS Nano 8, 9332–9340 (2014)
Huo, N., Kang, J., Wei, Z., Li, S.-S., Li, J., Wei, S.-H.: Novel and enhanced optoelectronic performances of multilayer MoS2–WS2 heterostructure transistors. Adv. Funct. Mater. 24, 7025–7031 (2014)
Fontana, M., Deppe, T., Boyd, A.K., Rinzan, M., Liu, A.Y., Paranjape, M., Barbara, P.: Electron-hole transport and photovoltaic effect in gated MoS 2 Schottky junctions. Sci. Rep. 3, 1634 (2013)
Deng, Y., Luo, Z., Conrad, N.J., Liu, H., Gong, Y., Najmaei, S., Ajayan, P.M., Lou, J., Xu, X., Ye, P.D.: Black phosphorus–monolayer MoS2 van der Waals heterojunction p–n diode. ACS Nano 8, 8292–8299 (2014)
Yu, W.J., Liu, Y., Zhou, H., Yin, A., Li, Z., Huang, Y., Duan, X.: Highly efficient gate-tunable photocurrent generation in vertical heterostructures of layered materials. Nat. Nanotechnol. 8, 952 (2013)
Lopez-Sanchez, O., Alarcon Llado, E., Koman, V., Fontcuberta i Morral, A., Radenovic, A., Kis, A.: Light generation and harvesting in a van der Waals heterostructure. ACS Nano 8, 3042–3048 (2014)
Villegas, C.E., Rocha, A.R.: Elucidating the optical properties of novel heterolayered materials based on MoTe2–InN for photovoltaic applications. J. Phys. Chem. C 119, 11886–11895 (2015)
Ramasubramaniam, A.: Large excitonic effects in monolayers of molybdenum and tungsten dichalcogenides. Phys. Rev. B 86, 115409 (2012)
P. Blaha, K. Schwarz, G.K. Madsen, D. Kvasnicka, J. Luitz.: wien2k. An augmented plane wave + local orbitals program for calculating crystal properties. Vienna University of Technology, Institute of Materials Chemistry, Vienna, Austria (2001)
Ding, Y., Wang, Y., Ni, J., Shi, L., Shi, S., Tang, W.: First principles study of structural, vibrational and electronic properties of graphene-like MX2 (M = Mo, Nb, W, Ta; X = S, Se, Te) monolayers. Physica B 406, 2254–2260 (2011)
Hafner, J.: Ab-initio simulations of materials using VASP: density-functional theory and beyond. J. Comput. Chem. 29, 2044–2078 (2008)
Splendiani, A., Sun, L., Zhang, Y., Li, T., Kim, J., Chim, C.-Y., Galli, G., Wang, F.: Emerging photoluminescence in monolayer MoS2. Nano Lett. 10, 1271–1275 (2010)
Lebegue, S., Eriksson, O.: Electronic structure of two-dimensional crystals from ab initio theory. Phys. Rev. B 79, 115409 (2009)
Reshak, A.H., Auluck, S.: Calculated optical properties of 2 H-MoS 2 intercalated with lithium. Phys. Rev. B 68, 125101 (2003)
Kumar, A., Ahluwalia, P.K.: A first principle comparative study of electronic and optical properties of 1H–MoS2 and 2H–MoS2. Mater. Chem. Phys. 135, 755–761 (2012)
Hieu, N.N., Ilyasov, V.V., Vu, T.V., Poklonski, N.A., Phuc, H.V., Phuong, L.T., Hoi, B.D., Nguyen, C.V.: First principles study of optical properties of molybdenum disulfide: from bulk to monolayer. Superlattices Microstruct. 115, 10–18 (2018)
Kuc, A., Zibouche, N., Heine, T.: Influence of quantum confinement on the electronic structure of the transition metal sulfide T S2. Phys. Rev. B 83, 245213 (2011)
Flöry, N., Jain, A., Bharadwaj, P., Parzefall, M., Taniguchi, T., Watanabe, K., Novotny, L.: A WSe2/MoSe2 heterostructure photovoltaic device. Appl. Phys. Lett. 107, 123106 (2015)
Zucca, R.R., Walter, J.P., Shen, Y.R., Cohen, M.L.: Wavelength modulation spectra of GaAs and silicon. Solid State Commun. 8, 627–632 (1970)
Bouhafs, D., Moussi, A., Chikouche, A., Ruiz, J.M.: Design and simulation of antireflection coating systems for optoelectronic devices: application to silicon solar cells. Sol. Energy Mater. Sol. Cells 52, 79–93 (1998)
Nakamura, T., Fujii, H., Juni, N., Tsutsumi, N.: Enhanced coupling of light from organic electroluminescent device using diffusive particle dispersed high refractive index resin substrate. Opt. Rev. 13, 104–110 (2006)
Ma, M., Mont, F.W., Poxson, D.J., Cho, J., Schubert, E.F., Welser, R.E., Sood, A.K.: Enhancement of photovoltaic cell response due to high-refractive-index encapsulants. J. Appl. Phys. 108, 043102 (2010)
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Lahourpour, F., Boochani, A., Parhizgar, S.S. et al. Structural, electronic and optical properties of graphene-like nano-layers MoX2(X:S,Se,Te): DFT study. J Theor Appl Phys 13, 191–201 (2019). https://doi.org/10.1007/s40094-019-0333-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40094-019-0333-4