Abstract
Different optical characterization techniques have been performed on a series of microcrystalline silicon thin films deposited using very high-frequency-assisted plasma-enhanced chemical vapor deposition process. The constant photocurrent method has been employed to study the defects states in density of states spectra of hydrogenated microcrystalline silicon thin films. The photocurrent measurements demonstrate anisotropy in the optoelectronic properties of the material. We have analyzed the optical absorption coefficient from UV spectroscopy and with the help of constant photocurrent method. The spectra have been analyzed in broad region and are presented for both the cases, i.e., surface and bulk light scatterings. The spectra were interpreted in terms of disorder, resulting defect density, crystalline/amorphous volume fractions and material morphology. The subgap-related parameters such as absorption coefficient, characteristic energy E0 of tail states and density of subgap defect states together with an estimate of the bandgap of silicon films prepared at various crystalline fractions have also been estimated. The density of localized tail states is found to fall exponentially toward the gap with band tail width of about 110 meV.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Recently, hydrogenated micro/nanocrystalline silicon thin films have attracted worldwide interest due to their diverse applications [1,2,3,4,5]. Microcrystalline silicon when combined with amorphous silicon in micromorph silicon tandem solar cell has the potential to reach 15% stable efficiency. Also compared to hydrogenated amorphous silicon (a-Si/H), it offers higher stability against light-induced degradation and wide absorption that extends to near infrared [6]. Higher efficiencies are achievable, which result from good passivation of defects by hydrogen in the plasma growth process of μc-Si/H and also due to enhanced optical absorption leading to efficient sunlight absorption in 1–4-μm-thick films and solar cells. The silicon dangling bond is the dominant defect (recombination center) in this material. The optical, electronic properties and the performance of the microcrystalline silicon films have been correlated with deposition parameters and structural properties [1]. It has complex heterogeneous structure comprising nano-sized crystallites, clustered into larger micrograins; all embedded in amorphous matrix. Due to heterogeneity, it leads to difficulties in explaining electronic transport and optical properties. Therefore, the detailed knowledge of the density of states (DOS) in μc-Si/H is of great importance to understand completely the transport mechanism. It is not surprising that still there is no conclusive DOS map. The absorption in the bandgap in hydrogenated amorphous silicon and related alloys is an important parameter to determine the suitability of material for device fabrication [7]. A number of techniques, such as constant photocurrent method (CPM), photothermal deflection spectroscopy (PDS), and dual-beam photoconductivity (DBP) have been used to determine the exact information about the sub-bandgap absorption [8, 9]. These spectroscopy techniques [10,11,12] have also been used to determine the DOS [3] in the lower energy range of the bandgap near the valence band, whereas transient photoconductivity (TPC) has been used to determine the DOS in the upper energy range of the gap, close to conduction band [6]. It is supposed that at low photon energies, an additional absorption appears involving states near the midgap, which could be silicon dangling bonds, forming a bump in the density of states. This subgap region is highly sensitive to deposition conditions. CPM has important advantages over PDS, such as it does not measure the absorption of the substrate. In the present investigation, we have used the constant photocurrent method in the ac mode to measure the absorption coefficient spectrum in microcrystalline silicon (µc-Si/H) films deposited using very high-frequency plasma-enhanced chemical vapor deposition system. Also, we have used derivative method to convert the measured data to DOS distribution curve.
Experimental details
Microcrystalline silicon films were deposited by the plasma-enhanced chemical vapor deposition (PECVD) technique. The silane was used as precursor gas (5% silane diluted in hydrogen). The excitation frequency used was 60 MHz (VHF). The films were deposited on corning 7059 glass at a substrate temperature of 270 °C. Before the deposition process, proper cleaning of the substrates was adopted using standard procedures [13]. Chamber cleaning was also carried out by Ar flushing and Ar plasma to make the chamber environment suitable for deposition process by making it free of residual contaminants. The power applied was varied in the range 10–50 W keeping other deposition parameters constant. The gaseous mixture within the chamber was maintained at a constant pressure of 0.18 Torr during deposition.
The thickness of films was measured using stylus profilometer (Ambios XP 200, USA). The structural properties were analyzed using Raman spectroscopy (LabRAM HR 800, Horiba JY) to estimate crystalline volume fraction (Xc) and the average crystallite size in the deposited films. The excitation of the samples was performed with an air-cooled Ar+ laser (Spectra physics) tuned at 488 nm. Measurements were carried out in the backscattered geometry using a 50-LWD microscope objective. The beam was focused at a spot size of 1.19 mm, and the power density was kept low to avoid laser-induced crystallization on the films or excessive heating on the probe region. With varied power range, the films with different crystalline volume fraction were obtained. A double-beam Hitachi UV–visible spectrophotometer was used to measure the optical absorption, and the optical bandgap (Eg) was estimated on the basis of Tauc’s plot. CPM measurements were done on the sample in the ac mode in a coplanar configuration made by evaporating aluminum electrodes with electrode spacing of 0.078 cm and a width of 1.0 cm. As the light source, we used a tungsten lamp of 250 W power and the focused light was allowed to pass through a high-intensity monochromator before falling on the sample detector. In order to keep the photocurrent constant at different energies, we varied the light intensity. Silicon detectors were used to detect the incident light intensity. The intensity was then converted to the number of photons. The field emission scanning electron microscopy (FESEM) images were obtained with a NOVA NANOSEM 450, FEI electron microscope [14].
Constant photocurrent method
The constant photocurrent method was used to measure the subgap absorption [7, 15]. The term constant photocurrent simply means the constant density of free electrons by assuming that electron mobility is not changed under light illumination. The photocurrent techniques importantly detect optically induced transitions between localized levels in the bandgap and extended levels in the bands, which generate free carriers. By appropriate spectroscopic methods, the density and energy position of defect states within the optical bandgap can be determined. A schematic of constant photocurrent measurement setup is given in Fig. 1.
The CPM uses the photocurrent, which is proportional to light absorbed in the film. Here, it is important that the photon flux is adjusted such that photoconductivity remains constant throughout the sample for all the incident photon energies. The CPM measures weak absorption corresponding to the defect states. It can be performed using ac or dc currents. So a low-intensity monochromatic beam is used to excite photoconductivity in the sample. In the present work, aluminum was deposited on silicon thin films in coplanar geometry mode and these coplanar aluminum electrodes were used to apply electric field and measure the generated photocurrent by the light beam. The system detects the transition of electrons from defect state (localized states) or from valance band state to conduction band (extended state). A light intensity is controlled by voltage regulation of halogen lamp in order to keep the photocurrent flowing through the sample constant. When the required photocurrent for each energy E is reached, the signals of both the detectors are measured using lock-in amplifiers. Typically, spectral response of photocurrent initially increases with the increase in photon energy and then attains maximum value at a particular energy which is according to the bandgap of the material. At higher values, the photocurrent starts to decrease. By doing this, one should ensure that the occupation of electronic states as well as the concentration of photogenerated carriers is constant. In addition, the mobility–lifetime product has to be constant. For constant photocurrent at all the wavelengths, the carrier lifetime can be taken constant. Under these conditions, resulting absorption coefficient is calculated as follows
From the above equation, we get relative values for the absorption coefficient. Absolute values can be obtained by matching the CPM curve with reflection/transmission measurements [16]. Absorption coefficients (α(hv)) were determined from CPM for wavelength ranging from 500 nm to 1400 nm. Excess absorption (αex) nearer to sub-bandgap states can be calculated from [4]
where E0 and α0 are Urbach energy and extrapolated values of absorption coefficient, respectively, and are determined by a fit to the exponential region. The density of defect states (Nd) can be calculated from the relation [17]
The density of states near Fermi energy level can be measured using SCLC method. The step-by-step method developed by DenBöer [18] can be used to calculate N(E) from the logJ versus logV characteristics in the SCLC region. The density of states near the Fermi level can be expressed as
where (J1, V1) and (J2,V2) are the points on the J–V curve in high electric field region, ϵ is the dielectric constant of the material, q is the electron charge, L is the thickness of the film, k is the Boltzmann constant and T is the temperature in Kelvin (K).
Results and discussion
As mentioned, microcrystalline silicon thin films were deposited on corning 7059 glass using very high-frequency PECVD process. Measurements were performed on coplanar geometry using aluminum electrodes of 0.08 cm spacing.
UV–VIS absorption spectroscopy
Figure 2 shows the variation in absorption spectrum of microcrystalline silicon films at different crystallinity. The optical bandgap (Eg) was extracted using Tauc’s equation by extrapolating tangent to the curve on the x-axis and the intercept which gives the value of bandgap of the material.
where α is the absorption coefficient, hν is the photon energy, Eg is optical bandgap and B is the constant defined as edge width parameter which is related to disorderness in the material. The bandgap values were found to vary from 1.9 to 2.1 eV.
A typical optical absorption spectrum measured by CPM is shown in Fig. 2 for 45% to 69% variation of the crystallinity. Figure 3 shows both the data, i.e., the absorption coefficient calculated from transmission measurements and the absorption coefficient obtained by the inverse of number of photons to keep photocurrent constant for the film deposited at Xc = 54%. Here, it is noted that there are two discontinuities in the figure and a smooth curve is obtained by a process of matching data points at 1.2 eV and 1.9 eV. The curve shows three regions:
-
1.
A saturation region corresponding to direct (extended states, i.e., valence band to conduction band) transition at higher energy (above about 1.9 eV) is realized.
-
2.
The second region is an exponential Urbach edge region where the absorption coefficient varies until it meets the low energy defect absorption shoulder. The exponential portion of the optical absorption is named as Urbach tail and E0 defines the characteristic energy of the band tail. This transition is due to a tail state to extended band transition.
-
3.
There is a third region where the sub-bandgap tail is superimposed on the Urbach edge. This is due to photon absorption by gap states. Here, the absorption is related to transition between localized states and extended states.
It is known that owing to the large density of states below the midgap the transition from occupied gap states below the Fermi level Ev to the conduction band contributes much more to the subgap absorption than transitions from the valence band to unoccupied localized states above Ev. The excess absorption due to subgap defect states is calculated from the subgap tail and Urbach edge. From Fig. 3, we observe an exponential tail around 1.1 eV. So this tail state can be interpreted as a disorder-induced broadening of the indirect absorption edge of c-Si. The defect associated with absorption largely below 1 eV is attributed to silicon dangling bonds mainly at the grain boundaries and in the amorphous tissue.
Raman spectroscopy
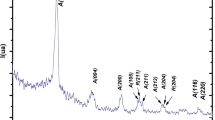
Raman spectroscopy is an effective and foremost sensitive technique in determining the crystalline as well as amorphous fraction in silicon-based thin films. The Raman spectra of deposited films were recorded in the wave number range 400–600 cm−1 and are shown in Fig. 4. It is observed that peak shifts from 480–519 cm−1 with the variation in crystalline volume fraction. The peak shifting clearly showed the transition from amorphous to highly microcrystalline growth. The shifting of Raman peak shows the phonon density of states and has been deconvoluted into three Gaussian or Lorentzian modes. The first one is centered at nearly 480 cm−1 representing the TO mode. The sharp peak Lorentzian distribution around 500–520 cm−1 can be divided into two TO vibrational modes depending on the crystal grains of different sizes named either nanocrystalline or microcrystalline silicon. The peak distribution around 500–510 cm−1 corresponds to TO vibrational mode of nanocrystalline silicon. The peak distribution at 510–520 cm−1 corresponds to TO vibrational mode of c-Si with size in the range few nm to microns [14]. The film deposited at crystalline fraction (Xc) of 31% can be identified as a mixed phase material consisting of broad characteristic hump at 480 cm−1 of amorphous silicon along with partial crystallization taking place where the TO mode shifts toward 515 cm−1; this is the clear evidence of origin of crystallization or transition from amorphous to nanocrystalline silicon. From the figure, it is clear that the crystalline fraction increases from 31 to 69% and the TO mode shifts to 519 cm−1.
The crystalline volume fraction (Xc) in the deposited films has been estimated with the help of Raman deconvoluted spectra using the following relation [19]
where I(C) is the intensity under crystalline peaks and I(T) is the total intensity of all the peaks. The average crystallite size (DR) of microcrystalline silicon can also be calculated using the relation [20]
Here, \(\Delta \omega\) represents the shift in phonon peak. Finally, the stress can also be calculated in the deposited films using
From Fig. 5, it is observed that with the variation in crystalline volume fraction, the crystallite size and grain boundary both vary in the deposited samples. Grain boundaries and crystallite size play an important role in microcrystalline silicon thin films. Increase in grain boundary is basically a crystallographic discontinuity where two dissimilar oriented grains meet. From Raman deconvolution, the spectra can be deconvoluted into three components, i.e., crystalline, amorphous and grain boundaries, respectively, at 520 cm−1, 480 cm−1 and 490 cm−1. In this case, the structure shifts to more relaxed structural configuration, i.e., at 519 cm−1. The film with low crystalline fraction has large contribution of grain boundaries, and 4 nm is the average crystallite size. The film deposited at crystalline fraction (Xc) of 54% has smaller grain boundary contribution and larger crystallite size (8.7 nm). There was less contribution of grain boundary region; moreover, crystalline component increases from 31% to 69% dominating grain boundaries. Similar increasing behavior in the crystallite size was also observed with variation in crystalline fraction. The grain boundaries are linked with the electrical properties of sample, i.e., larger the grain boundaries, worsen the electric properties. These grain boundaries result in the recombination and obstruct the flow of charge carriers.
The size of nanocrystals in silicon is important to understand quantum confinement of the electrons. Information related to crystalline fraction is important to monitor stability of films [14]. It is already reported that grain boundary component decreases with increasing crystalline volume fraction. The best sample results where the crystallite size is obtained at sample deposited at Xc of 54% along with lower fraction of grain boundaries. The films deposited above this crystalline fraction further results in reduced crystallite size with the increased grain boundaries. This can be explained based on nonuniform film deposition at higher powers. It might be assumed that at higher powers, etching process takes place and results in the increased crystalline fraction, but with the decreased crystallite size and increased grain boundaries. The samples with increased grain boundaries can be referred to as defective structures with poor optical and electrical properties. Further, these structural results are correlated with defect measurement techniques.
The stress can also be estimated using Raman spectroscopy in the deposited films. From Fig. 6, this is clear that the calculated value of stress decreases with the increase in crystalline volume fraction (Xc) and there is a large difference in the calculated value of stress. The calculated value varies nearly from about 1400 MPa to 250 MPa. With the increase in crystalline volume fraction, the stress in the deposited films is found to decrease and is well correlated with the other measurements. From Raman analysis, it was observed that the films deposited at higher crystalline fraction, bigger size of crystallites and lesser grain boundaries result in better silicon (Si–Si) network ordering. The improvement in the structure ordering and increase in crystalline fraction of these films result in the reduction of stress.
The Urbach energy and defect density were measured using constant photocurrent method and are shown in Fig. 7. This is observed from the figure that the defect density in the film decreases from 1019 to 1017 cm−3 with the increasing crystalline volume fraction. The Urbach energy also decreases from 200 meV to 115 meV. However, the defect density and Urbach energy are found to increase above Xc = 54%. The reason for this might be heterogeneity in the structure of microcrystalline silicon film. Moreover, the contribution of grain boundaries increases with the increasing crystallinity, as is clearly shown in Fig. 5. From all the results, it is clear that the film deposited above Xc = 54% resulted in increasing defects with reduced surface ordering in the structure.
I–V characteristics
The variation of the current density with respect to V for all the deposited films is shown in Fig. 8. The details of the samples A, B, C, D and E are given in Table 1.
The DOS profile of microcrystalline silicon films is an important study for defect analysis in silicon films. Although it is an estimate, it can help in visualizing the shape of localized band tail distribution near one of the band edges. It is already known that density of localized band tails is exponentially distributed in the conduction band region. In the calculation of DOS, it is generally assumed that the band tails extend to the mobility edge [21]. High-quality a-Si/H films have a somewhat lower deep defect density than μc-Si/H, suggesting that the amorphous tissue in mixed phase μc-Si/H is of poorer quality than homogeneous a-Si/H. This could be attributed to the passivating hydrogen locked into grain boundaries and being unavailable to terminate dangling bonds.
Conclusions
In the present work, the optoelectronic properties of microcrystalline silicon films have been studied by using ac-CPM. The CPM measured the (photocurrent) absorption spectrum directly in absolute units (cm−1) without influence of interference fringes. The defect density in the film was found to decrease from 1019 to 1017 cm−3 with the increasing crystalline volume fraction. The Urbach energy also decreased from 200 to 115 meV. However, the defect density and Urbach energy were found to increase above Xc = 54%. The disorder seemed to decrease with increasing crystallinity in the films. It was found that the light soaking enhances the value of the characteristic energy E0 and the defect density Ns in the material and this is accompanied by an increase in the subgap absorption related to an increase in the number of defects, probably dangling bonds. In view of their good optoelectronic properties, these films appear to be suitable for optoelectronics devices.
References
Klazes, R.H., van den Broek, M.H.L.M., Bezemer, J., Radelaar, S.: Determination of the optical bandgap of amorphous silicon. Philos. Mag. B 45, 377 (1982)
Aljishi, S., Cohen, J.D., Jin, S., Ley, L.: Band tails in hydrogenated amorphous silicon and silicon-germanium alloys. Phys. Rev. Lett. 64, 2811 (1990)
Larbi, F., Belfedal, A., Sib, J., et al.: Density of states in intrinsic and n/p-doped hydrogenated amorphous and microcrystalline silicon. J. Modern Phys. 2, 1030 (2011)
Kocka, J., Vanecek, M., Tfiska, A.: Energy and density of gap states in a-Si:H. Amorph. Silicon Relat. Mater. 1, 297 (1989)
Badran, R.I., et al.: A study of optical properties of hydrogenated microcrystalline silicon films prepared by plasma enhanced chemical vapor deposition technique at different conditions of excited power and pressure. Vacuum 83, 1023 (2009)
Tibermacine, T., Merazga, A., Ledra, M., Ouhabab, M.: Extraction of the defect density of states in microcrystalline silicon from experimental results and simulation studies. J. Semiconductors 36, 093001 (2015)
Tyagi, A., et al.: Studies of subgap absorption and related parameters by the constant photocurrent method of high rate deposited hydrogenated amorphous silicon films. Thin Solid Films 203, 251 (1991)
Vanecek, M., Kocka, J., Poruba, A., et al.: Direct measurement of the deep defect density in thin amorphous silicon films with the absolute constant photocurrent method. J. Appl. Phys. 78, 6203 (1995)
Fejfar, A., Poruba, A., Vanecek, M., et al.: Precise measurement of the deep defects and surface states in a-Si: H films by absolute CPM. J Non-Cryst. Solids 198, 304 (1996)
Wu, X.L., et al.: Raman scattering of alternating nanocrystalline silicon/amorphous silicon multilayers. Appl. Phys. Lett. 69, 523 (1996)
Bustarret, E., Hachicha, M.A., Brunel, M.: Experimental determination of the nanocrystalline volume fraction in silicon thin films from Raman spectroscopy. Appl. Phys. Lett. 52, 1675 (1988)
Veprek, S., Sarott, F.-A., Iqbal, Z.: Effect of grain boundaries on the Raman spectra, optical absorption, and elastic light scattering in nanometer-sized crystalline silicon. Phys. Rev. B 36, 3344 (1987)
Juneja, S., Sudhakar, S., Gope, J., Kumar, S.: Mixed phase silicon thin films grown at high rate using 60 MHz assisted VHF-PECVD technique. Mater. Sci. Semiconductor Process. 40, 11 (2015)
Juneja, S., Sudhakar, S., Srivastava, A.K., Kumar, S.: Morphology and micro-structural studies of distinct silicon thin films deposited using very high frequency plasma enhanced chemical vapor deposition process. Thin Solid Films 619, 272 (2016)
Wyrsch, N., Finger, F., McMahon, T., Vaněček, M.: How to reach more precise interpretation of subgap absorption spectra in terms of deep defect density in a-Si:H. J. Non-Cryst. Solids 137, 347 (1991)
Ritter, D., Weiser, K.: Suppression of interference fringes in absorption measurements on thin films. Opt. Commun. 57, 336 (1986)
Vaněček, M., et al.: Direct measurement of the gap states and band tail absorption by constant photocurrent method in amorphous silicon. Solid State Commun. 39, 1199 (1981)
DenBöer, W.: J. Phys. (Paris) Colloq. 42, 451 (1981)
Raha, D., Das, D.: Hydrogen induced promotion of nanocrystallization from He-diluted SiH4 plasma. J. Phys. D Appl. Phys. 41, 085303 (2008)
Richter, H., Wang, Z.P., Ley, L.: The one phonon Raman spectrum in microcrystalline silicon. Solid State Commun. 39, 625 (1981)
Reynolds, S.: Time resolved photoconductivity as a probe of carrier transport in microcrystalline silicon. MRS Symposium 910, A1-1 (2006)
Acknowledgements
One of the authors (SJ) thanks the Department of Science and Technology, Government of India for providing NPDF (Project No. MI01803G) at IIT Delhi.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Malik, H.K., Juneja, S. & Kumar, S. Employing constant photocurrent method for the study of defects in silicon thin films. J Theor Appl Phys 13, 107–113 (2019). https://doi.org/10.1007/s40094-019-0325-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40094-019-0325-4