Introduction

The synthesis of graphene [1] has created a new field in two-dimensional electronics which has been led to the fabrication of electronic devices based on single or few atom-thick layers. Graphene has the significant features such as quantum anomalous Hall effect [1, 2], high electron mobility [3,4,5] and long electron phase coherence length [6] which are technologically important. However, similar to three-dimensional electronics, in order to fabricate the various types of electronic devices require a group of conductive, semiconductor and insulating materials with tunable properties. A group of the two-dimensional semiconductors and semimetals is called transition metal dichalcogenides, and MoS2 is the most important member of this family with a direct band gap of Δ = 1.8 eV in its monolayer [7, 8]. The electron mobility of MoS2 on HfO2 substrate is about 200 cm2 V s−1 at room temperature which reduces to 0.1–10 cm2 V s−1 range on SiO2 substrate [9]. The various electronic devices such as transistors [10], logic circuits [11] and photodetectors [12] have been fabricated based on MoS2 monolayer whose properties can be easily tuned by adding external atoms, strain or structural and intrinsic defects. In one project, it has been showed that the presence of point defects in this structure can lead to a new photoemission peak and it increases the luminescence intensity of MoS2 monolayer [13].

The structural defects such as vacancies, grain boundaries and topological imperfections can be found in MoS2 structures which have been studied both theoretically and experimentally [14,15,16,17]. The recent experiments have shown that divacancies can be rarely found in this structure, whereas monovacancies have been often observed [18]. The intrinsic defects in this structure can be created without removing the atoms of the lattice. For instance, the Stone–Wales defect is formed by the rotation of atoms and the reconstruction of interlayer bonds [18]. Moreover, the line defects in MoS2 have attracted lots of attention. The line defects proposed by Enyashin et al. presented mirror plates around the defect in MoS2 monolayer. Hence, the inversion domains were formed which are important in electronics. They have reported the new states within the band gap of this semiconductor [19]. Although the electron transport in pristine MoS2 is isotropic, the strong anisotropy has been reported in the presence of line defects in this structure [20]. Also, it was showed that in the presence of a finite atomic line of sulfur vacancies, the structure can act as a pseudo-ballistic wire for the electron transport [21].

Among MoS2 nanoribbons, zigzag-edged types have attracted great attention due to their electronic and magnetic properties which are technologically significant [22, 23]. As we know, a MoS2 nanoribbon contains different atoms at its two edges, i.e., sulfur atoms are located at one edge of MoS2 nanoribbon while molybdenum atoms are observed at the opposite edge. Generally, the number of atoms in the width of zigzag nanoribbon can be even or odd so that the structures are symmetric or asymmetric. Note that the transport properties of graphene nanoribbons are strongly dependent on edge symmetry so that there is the spin-dependent transport only in the asymmetric zigzag graphene nanoribbons [24, 25]. Unlike graphene, the transport properties of zigzag MoS2 nanoribbons are independent of the number of atoms in the width of nanoribbon [26, 27].

In this research, we investigate the effect of line structural defects on the electron conductance of zigzag MoS2 nanoribbon and showed that these defects as scattering centers cannot create the effective transport channels, whereas the presence of them changes the electronic conductance of the zigzag MoS2 nanoribbon. From an empirical point of view, we studied the most stable non-stoichiometric defects such as the Mo–Mo bridge (metallic bond) and S bridge [19]. Recently, a group of researchers investigated the effect of these two defects on the spin-dependent transport of MoS2 nanoribbons. In order to increase the spin-dependent transport, they showed that the best position for defects is the middle part of nanoribbon [28]. However, the importance of edge effects in the presence of these types of defects has not been clearly investigated yet, so we calculated the density of energy states and found that the edge effects can play an important role in the electron transport of nanoribbon. Furthermore, we showed that the structure of edge bonds except zigzag-edged state is able to change the electron and spin-dependent properties. Also, using DFT calculations for the first time, we investigate the effect of Stone–Wales defect on the electron and spin conductance of zigzag MoS2 nanoribbon. Our results show that the electron and spin-dependent transport for zigzag MoS2 nanoribbon reduces in the presence of Stone–Wales defect.

Model and method

All computations which have been presented in this research are composed of two main parts: (a) the optimization of electron structure and (b) the computations concerned with electron transport properties. All of these computations have been performed using SIESTA and TranSIESTA softwares [29, 30].

The electron structure of monolayers, atomic positions and lattice vectors were completely optimized applying periodic boundary conditions with a vacuum separation of about 15 Å perpendiculars to monolayers and a vacuum region about 10 Å outside edge atomic sites of nanoribbon until the exerted forces on each atom become less than 0.003 eV/Å. The energy convergence limit 0.001 meV is considered.

The investigation of electron transport properties based on non-equilibrium Green’s function using DFT calculations has been vastly used in such studies. Here, the SZP basis sets were applied for all atoms. For describing exchange–correlation potential, LDA.PZ has been utilized [31, 32]. The kinetic energy cutoff was set to 100 Ry. Also, the Brillouin zone was sampled by using (1 \( \times \) 1 \( \times \) 100) k-points. Thus, the different electron properties such as conductance, density of states and local current have been calculated.

Using non-equilibrium Green′s function through Landauer–Buttiker formula, we calculate the electron conductance as follows [33, 34]:

$$ G(E) = \frac{{2e^{2} }}{h}Tr\left[ {\varGamma_{L} (E)G^{r} (E)\varGamma_{R} (E)G^{a} (E)} \right], $$
(1)

where E is energy, \( G^{r(a)} (E_{F} ) \) is the retarded (advanced) Green′s function and

$$ \varGamma_{L(R)} (E) = i\left\{ {\sum_{L(R)}^{r} (E) - \left[ {\sum_{L(R)}^{r} (E)} \right]^{\dag } } \right\}. $$
(2)

describes the broadening function of left (right) lead. Here, \( \sum_{L(R)}^{r} (E) \) is the self-energy function for left (right) lead which is calculated using iterative and recursive methods [35].

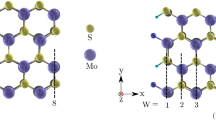
In this research, a two-electrode system consisting of a zigzag MoS2 nanoribbon as a central region and semi-infinite electrodes with similar size to the central region is considered (Fig. 1). Moreover, line structural defects containing S bridge, Mo–Mo bridge, non-zigzag edges (edges defect) and Stone–Wales defect are considered on the structure as shown in Fig. 2II–V, respectively.

Fig. 1
figure 1

Schematic structure of a two-electrode system including of a zigzag MoS2 nanoribbon. The left and right electrodes are MoS2 nanoribbon, and there are line defects on the central region

Full size image
Fig. 2
figure 2

Schematic view of considered structures for MoS2 nanoribbon: I without defect with zigzag edges, II in the presence of line defect including of S bridging atoms, III in the presence of line defect including of Mo–Mo metallic bonds, IV with non-zigzag edges and V with non-zigzag edges and Stone–Wales defect

Full size image

Results and discussion

Here, besides considering the structural defects on zigzag MoS2 nanoribbons, we study the electron transport properties of MoS2 nanoribbons in the presence of these defects in comparison with pristine nanoribbons. In Fig. 3, the electron conductance of MoS2 nanoribbon as a function of energy is displayed in presence of different structural defects.

Fig. 3
figure 3

Electron conductance as a function of energy for MoS2 nanoribbon: a without defect with zigzag edges, b in the presence of line defect including of S bridging atoms, c in the presence of line defect including of Mo–Mo metallic bonds, d with non-zigzag edges and e with non-zigzag edges and Stone–Wales defect

Full size image

The electron conductance as a function of energy for 5-MoS2 nanoribbon is shown in Fig. 3a. Number ‘5’ refers to the number of atoms along the width of nanoribbon. The 3p orbitals of sulfur valence shell and 4d orbitals of molybdenum valence shell concerned with the edge of the structure are responsible for effective electron conductance of this nanoribbon.

Here, the electron transport of nanoribbon depends on the presence and type of line defect. The conductance properties are determined by coupling between the electron transport states of optimized wave functions around Fermi energy when the structural defects act as the scattering centers for electrons. In this research, the Mo–Mo and S bridges are located in the middle of nanoribbon so that the mirror symmetry between upper and lower parts of nanoribbon can be preserved. For the S bridging atoms, the electron conductance exhibits a significant enhancement for negative values of energy (Fig. 3b), while in the presence of Mo–Mo metallic bonds, it is observed that the transmission spectrum covers both negative and positive values of energy (Fig. 3c). As a result, this property depends on the type of the defect, the distance of defect from the edges of MoS2 nanoribbon, the width of nanoribbon [29] and the edge type of structure. The structure (IV) in Fig. 2 has been shown as the elimination of Mo and S atoms at the upper and lower edges of the structure (I), respectively. It shows an effective increase in electron transport around Fermi energy (Fig. 3d), whereas in the structure in Fig. 3e which contains Stone–Wales point defect, the electron conductance decreases greatly. In fact, such defect in the narrow structure (V) breaks lattice symmetry and acts as a scattering center for electrons. Thus, the effect of electron scattering on the defect sites has created a wide transport for the positive values of energy in this structure. Indeed, the Stone–Wales defect which is created due to the rotation of Mo–S bond and the reconstruction of bonds in the hexagonal lattice is the simplest model of the structural defect in honeycomb lattices.

To study more detailed, the local current in these nanostructures has been investigated. In the non-defect structure (I) as shown in Fig. 4, edge atoms are responsible for the transmission of charge carriers so that the current flows through edge channels along the zigzag direction of the edges. Indeed, the 3p orbitals of sulfur valence shell and the 4d orbitals of molybdenum valence shell are responsible for this effect. As observed, the transport of charge carriers in MoS2 is performed through S–Mo–S bonds (in the case of S atoms edge) and Mo–Mo bond (in case of Mo atoms edge). As shown in Fig. 4, the current through S–Mo–S bonds is more than Mo–Mo bonds. In the structure (II) which contains the S bridging atoms, the S edge atoms (S–Mo–S bonds) and the Mo atoms at zigzag edges with line defect (Mo–Mo bonds) cause the middle part of nanoribbon to affect the electron transport. Being such a new transmission channel leads to an increase in the transmission spectrum. As shown in the structure (III), forming Mo–Mo strong metallic bonds in the middle of the bridge leads to creating 5-atom and 8-atom rings in this line defect when bonds forming the edges of the middle defect are S–Mo–S bonds. Although we expected that this line defect can create a new path for transmission, the charge carriers are transferred through the Mo atoms at the edge of nanoribbon and in the vicinity of the edge which have considerable effects on the transmission spectrum. In fact, in the case of being line defects in the middle of the nanoribbon, due to the presence of unsaturated S and Mo atoms at the edges of the line defect, new edge states are created in the vicinity of the defect so that they are new channels for the transmission of charge carriers. In the structure (III), the length of Mo–Mo bond in the middle of the bridge is short (the strength of Mo–Mo bond is strong). Thus, the density of electron charges is concentrated in those regions. Such bond and also the bond forming inner edge of defect (S–Mo–S) will be effective for the transmission of charge carriers when the distribution of electrons around S–Mo–S bond increases. We expect that with increasing the width of nanoribbon and the distance of Mo–Mo bond defect of nanoribbon edges, the electron distribution changes and the S–Mo–S edges of this defect can act as a transmission channel [28]. Generally, the effect of line defect on the transmission of electrons significantly depends on the electron distribution on the atoms in the vicinity of inner edges of line defect and the coupling between the electron transport states (which the electron distribution is displayed in Fig. 5). In structure IV, the free edges in this structure, especially in the direction of Mo atoms, lead to an increase in the electron conductance. In fact, the Mo–Mo bond is a more effective transmission channel than sulfur edge atoms (in the figure with non-zigzag edges). In structure (V), the local current is concentrated on the vicinity of the defect (red-colored regions) due to the electron scattering at the defect sites. In this structure, the ring-shaped channels have no the specified current direction and the path of electron movement is not appropriate for the electron transport. Also, the Mo–Mo bonds in the vicinity of the defect along the width of nanoribbon are ineffective channels for the transmission of charge carriers.

Fig. 4
figure 4

Local current in MoS2 nanoribbon: I without defect with zigzag edges, II in the presence of the line defect including of S bridging atoms, III in the presence of the line defect including of Mo–Mo metallic bonds, IV with non-zigzag edges and V with non-zigzag edges and the Stone–Wales defect

Full size image
Fig. 5
figure 5

Difference of electron density in MoS2 nanoribbon: I without defect with zigzag edges, II in the presence of the line defect including of S bridging atoms, III in the presence of the line defect including of Mo–Mo metallic bonds, IV with the non-zigzag edges and V with the non-zigzag edges and the Stone–Wales defect. The electron density in red-colored regions is larger

Full size image

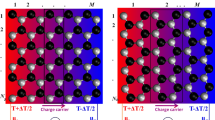
In Fig. 5, the electron difference density (EDD) has been displayed for the various structures. The EDD is the difference between the self-consistent valence electron density and the superposition of atomic valence electron densities. It shows clearly the charge carriers transfer between atoms forming the structure. The blue and red colors show the excess and shortage of electrons, respectively. As shown in this figure, the electron charge density decreases (increases) at the site of Mo (S) atoms. In the structures (III) and (V), the Mo–Mo metallic bond on the defect has stronger bond strength and the local concentration of electrons on them (red-colored regions) is obvious.

To continue, the density of states (DOS) as a function of energy is investigated in these structures. In this figure, we showed the total density of states (TDOS) and the partial density of states (PDOS) which are the contributions of the 3p orbitals and 4d orbitals for the S and Mo atoms, respectively. TDOS as a function of energy is shown in Fig. 6b for structure (II), and it has the highest values in Fig. 6c corresponding with structure (III) and shows a maximum peak around Fermi energy. In Fig. 6a for structure (I), the 3p orbitals of S atoms and the 4d orbitals of Mo atoms at the edge atoms of the structure have a great contribution in the density of states. In Fig. 6b, it can be seen that the value of the density of states for the 3p orbitals is greater than the 4d orbitals. This trend acts inversely in Fig. 6c. The DOS curve in Fig. 6c compared with Fig. 6b demonstrates peaks near deep valleys due to the resonance scattering in special energies. This occurrence causes the structure including of S bridging atoms can show the transmission spectrum better than the structure including Mo–Mo bond defects. In Fig. 6d and e for the structures (IV) and (V), there is similarly extensive and available density of energy states for the 3p and 4d orbitals around Fermi energy. Indeed, in structure 6e, the rotation of bonds also affects appearance of new states around Fermi energy. However, the occurrence of localized states and perfect electron scattering in the states with the Stone–Wales defect strongly decreases the electron conductance.

Fig. 6
figure 6

TDOS and PDOS of the 3p and 4d orbitals as a function of energy in MoS2 nanoribbon: a without defect with the zigzag edges, b in the presence of the line defect including of S bridging atoms, c in the presence of the line defect including of Mo–Mo metallic bonds, d with non-zigzag edges and e with non-zigzag edges and the Stone–Wales defect

Full size image

Then, spin conductance of zigzag 4-MoS2 (‘4’ refers to number of atoms across the nanoribbon width), non-zigzag nanoribbon (Fig. 2IV) and non-zigzag nanoribbon in the presence of Stone–Wales defect (Fig. 2V) is considered. As observed in Fig. 7, it has been shown that in all the structures, the conductance for spin-up and spin-down electrons is not equivalent, so it demonstrates the magnetic characteristic in these structures. Such magnetic characteristic is expectable for non-defect structure [24, 36], and it also is observed in the presence of Mo–Mo and S bridges [28]. In Fig. 7b in which the zigzag edges have been destroyed, this spin splitting can be observed more obvious in such a way that the dominant spin conductance can be seen in the positive and negative energies for spin-down and spin-up electrons, respectively. In Fig. 7c, we observe that the magnetic characteristic does not disappear even in the presence of Stone–Wales defect, so the spin-dependent transport has been strongly decreased.

Fig. 7
figure 7

Spin conductance as a function of energy in MoS2 nanoribbon: a without defect with zigzag edges, b with non-zigzag edges and c with non-zigzag edges and Stone–Wales defect

Full size image

Finally, in order to study the magnetic characteristics of the structures under consideration in Fig. 7 with more detailed, the spin-density space distribution (for spin-up and spin-down electrons) is displayed in Fig. 8; the positive (negative) values indicate domination of spin-up (down) electrons. According to this figure, the spin-density distribution is concentrated on the edges of nanoribbon and at each of the edges; the value of spin-density distribution for spin-up electrons is larger than spin-down electrons (which is in correspondence with positive value). Moreover, the value of spin-density distribution at Mo edge is more than S edge. Also, the non-zigzag edges displayed in figures II′ and III′ show stronger magnetic effects than figure I′. Moreover, after unsaturated Mo(S) atoms at the lower (upper) edge, the row of Mo atoms after them shows the negative (positive) spin-density distribution. These investigations show that bridging line defects induce a little magnetic effect on the defect [28] and our obtained results about figure III′ show that the presence of Stone–Wales defect decreases the magnetic effect in the middle of edges and it can be seen that the distribution of spin-down electrons in the row of Mo atoms for the atoms placed after the lower edge has little increased.

Fig. 8
figure 8

Spin-density space distribution (for spin-up and spin-down electrons) in MoS2 naoribbon: I without defect with zigzag edges, II with non-zigzag edges and III with non-zigzag edges and Stone–Wales defect. The red (blue) color describes positive (negative) values

Full size image

Conclusions

To summarize, in this project using non-equilibrium Green’s Function method based on DFT calculations, the effect of structural defects on the zigzag MoS2 nanoribbon was studied. The results show that electron transport in these structures depends on the type and position of the defect. Although these line defects are not channels for the transmission of charge carriers and act as the scattering regions, the presence of them can change the electron transport of the system and even make their around region participate in the electron transport more extensively. According to this, the configuration of S bridges and edge defects in the form of linear is more favorable for the electron transport. These properties are due to different couplings between the electron states of transport which leads to change in the local current in the vicinity of defect positions. Furthermore, in this paper, the contributions of 3p orbitals of S atoms and the 4d orbitals of Mo atoms have been considered which shows that edge atoms have the great effects on the electron properties of MoS2 nanoribbon. Moreover, the investigation of spin conductance in these structures shows that they have the magnetic characteristics and there is more the spin polarization for non-zigzag edges which is not destroyed even in the presence of the defect. Thus, applying the various structural defects in appropriate positions of MoS2 nanoribbon can be a favorable method for creating significant changes in the electron transport.