Abstract
The ZnS thin films have been deposited by radio frequency magnetron sputtering at room temperature. Post-deposition rapid thermal annealing treatment was done for the films deposited at different powers ranging from 70 to 100 W. One peak is observed for as-deposited and annealed thin films at around 28.48° corresponding to the (111) reflection plane indicating a zincblende structure. The overall intensity of the peaks and the FWHM values of as-deposited films increased after annealing corresponding to the increase in crystallinity. The optical energy bandgap is found in the range of 3.24–3.32 eV. With increasing annealing temperature, the decrease in the Urbach energy values indicating a decrease in localized states which is in good agreement with the XRD results where the crystallinity increased. The surface morphology of the films seems to be composed of Nano-granules with a compact arrangement. Apparently, the grain size increases in the deposited films as annealing temperature increases. The compositional ratio attained close to the stoichiometric ratio of 1:1 after annealing. From the Hall effect measurement, the carrier concentration and mobility are found to increase after annealing. The high carrier concentration and mobility also comply with structural and optical analysis. Best results are found for the film annealed at 400 °C deposited at 90 W.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
The II–VI semiconductor compound thin films have been investigated for many years because of the multiple applications of these materials, in the field of solar cells, photocatalysts, field-effect transistors, light-emitting devices, and optoelectronic devices [1,2,3,4,5,6,7,8,9,10]. As buffer layer in solar cell, II–VI compounds, such as CdS [7, 11,12,13], ZnS [9, 14, 15], CdZnS [16,17,18,19,20], CdSe [21, 22], CdSSe [23], etc., have been usually used. This binary/ternary compound thin film is reported to be synthesized by various techniques such as molecular beam epitaxy (MBE) [24], chemical bath deposition [5, 15, 25, 26], sputtering [9, 10, 14, 27, 28], atomic layer deposition [29], etc. Among these, radio frequency (RF) magnetron sputtering technique has sufficient control over the stoichiometry and uniformity to deposit ZnS thin films. Zinc sulfide (ZnS) has gained much more attention than any other II–VI semiconductor compounds due to its several advantages such as it is non-toxic, earth-abundant, has a wider bandgap around 3.6 eV, can transmit higher energy photons and better lattice-matching over CIGS thin-film absorber layer [5, 30]. For an antireflection coating [31], detection emission [32], and modulation of UV–visible light [33], ZnS thin film is potentially important material.
Pathak et al. [34] deposited ZnS thin films on different substrates, such as ordinary glass, indium tin oxide (ITO) coated glass, and Corning glass by RF magnetron sputtering, with a substrate temperature of 100 °C. They found good crystallinity and preferential orientation of the cubic structure. They also found the transmittance of the films was about 77% in the visible region. Kim et al. [1] prepared the ZnS thin films varying sputtering power from 85 to 115 W with a 10 W increment. The deposition was carried out with a substrate temperature at 200 °C. They achieved over 85% transmittance in the visible light, good crystallinity and the bandgap in the range of 3.3–3.4 eV for the films deposited at 85 and 95 W power. Gayou et al. [8] varied substrate temperature from 180 to 630 °C to deposit ZnS thin films on GaAs layer by RF planar magnetron sputtering system. The maximum grain size was found 34.95 nm by depositing with the substrate temperature of 270 °C. Shao et al. [27] deposited ZnS thin films of about 50 nm on glass substrates at a substrate temperature of 200 °C via RF reactive sputtering by using a zinc plate target and hydrogen sulfide (H2S) gas. They found a zinc blende (ZB) structure with 65% transmittance in the wavelength larger than 350 nm having 3.59–3.72 eV bandgap. All these works had been done with different substrate temperatures.
In this work, an attempt is taken to deposit earth-abundant ZnS thin film using controlled RF magnetron sputtering technique as well as to improve the quality of the films by controlled annealing treatment that can be implemented in thin-film solar cells specifically as a window layer. For controlled annealing treatment, rapid thermal annealing of the deposited films was carried out to investigate the effect of different annealing temperatures on the structural, morphological, optical, and electrical properties of the films.
Experimental details: preparation and characterization
The soda-lime glass (SLG), as the substrate, of size 30 × 30 mm thickness 1.5 mm, was cleaned in an ultrasonic bath, degreased by methanol-acetone-methanol solutions and deionized water for 10 min. The substrates were then dried with the blower of dry air and masked onto one side with Ketone tape. The substrates were then immediately placed in a top–down magnetron sputtering system manufactured by Nano-Master Inc. with Model NSC-4000. Figure 1 shows the schematic diagram of the system used to deposit ZnS thin films. For deposition material, ZnS sputtering target from Angstrom Sciences, Inc having purity 99.99% of two inches diameter was placed 95 mm above the substrate. The RF gun (maximum 300 W, frequency 12.56 MHz) was used to deposit the thin films. Before starting the sputtering, the chamber was pumped down to a base pressure below 5.33 mbar.
The deposition of ZnS onto cleaned SLG substrates were conducted at 6.67 mbar for 20 min under 70, 80, 90, and 100 W applied powers at 25 °C substrate temperature. After deposition, the films were annealed in N2 atmosphere at the pressure of 25 × 10−3 Torr with a rapid thermal annealer manufactured by Advance Riko with Model MILA-5000-P-N. Each set of deposited films were annealed at 350 °C, 400 °C, and 450 °C for 20 min with the ramp of 20 °C per minute. Annealed samples were then cooled down to 25 °C within 35 min.
After annealing, all the characterizations were performed at room temperature. The film thickness was measured with a surface profilometer manufactured by Bruker Corporation, USA, with Model DektaXT-A. The structural and crystallographic properties of the films were observed from X-ray diffractometer (XRD) (EMMA; GBC Scientific Equipment, Australia) using Cu_Kα radiation (I = 0.15406 nm) operated at 35.5 kV and 28 mA. The composition of the films was investigated by energy dispersive analysis of X-ray (TEAM EDS; EDAX, USA). The morphology of the films was measured by scanning electron microscopy (EVO18, Carl Zeiss AG, Germany). For optical properties, an ultraviolet–visible-near-infrared (UV–Vis-NIR) spectrometer (UH-4150; Hitachi High Technologies Corporation, Japan) with a wavelength range from 320 to 900 nm was used. The electrical parameters were determined by the Hall effect measurement system (HMS-3300; Ecopia Corporation, South Korea), using silver ohmic contacts on the surface of the films in a magnetic field of B = 0.55 T.
Result and discussion
Structural properties
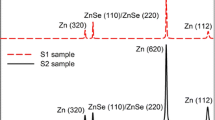
Figure 2 shows XRD patterns of as-deposited and annealed ZnS thin films deposited at different RF power ranging from 70 to 100 W. One peak was significantly observed for all of the films in the diffraction angle (2θ) ranging from 20° to 70°. Only one significant peak for the films indicating that the films are of a single crystalline structure and the planes are parallel to the substrate surface [9].
For as-deposited films, as shown in Fig. 2, the peak around 2θ = 28.48° is observed to appear corresponding to the (111) reflection plane occurring for a cubic or zincblende (JCPDS Card: 00-001-0792) structure. The overall intensity of the peaks of as-deposited films increased after annealing. From Fig. 2, the highest peak is found, for the film deposited with 90 W power, which indicates better crystallinity among the as-deposited films. The lattice parameter ‘a’ for cubic phase structure [hkl] for all of the films at different deposition powers is determined from the Brag’s law and Vegard’s law [35] as tabulated in Table 1.
The mean crystallite sizes (D) of the films are calculated using the Scherrer formula [35]:
where λ is the X-ray wavelength (0.15406 nm), and β is the full width at half maximum (FWHM) of the film diffraction peak at 2θ, where θ is the Bragg diffraction angle. The micro-strain (ε) developed in the thin films can be calculated from the relation [36]
where θ is Bragg’s angle, β is the width of the peak at half of the maximum peaks. The dislocation density for non-isotropic distribution of thin films are calculated by the Williamson and Smallman’s relation [4]
where n is a factor, which equals unity giving minimum dislocation density and Dhlk is the crystallite size along [hkl] direction. Different structural parameters of the as-deposited and annealed ZnS thin films having different growth at different powers are calculated by using relevant formulae and are systematically presented in Table 1.
From Table 1, the FWHM values are found to decrease from as-deposited to annealed samples and increase with the increase in thickness. Almost the same value of FWHM is found for the samples annealed at 400 °C and 450 °C. As, the FWHM of an XRD peak is reliant on the crystallite size and the lattice micro-strain caused by the defect and/or dislocations [37], the calculated value shows maximum crystallite size of 30.025 nm, corresponding minimum micro-strain of 4.90 × 10−3 for the sample deposited at 90 W power and annealed at 400 °C. Among the various deposition powers in conjunction with annealing temperature, the film deposited at 90 W power was found to possess the lowest micro-strain and dislocation density. It is possibly due to the collision rate between Ar atoms and ejected ZnS atoms; hence, the kinetic energy of these sputtered particles at 90 W power is sufficiently suitable to arrange them with minimal dislocation defects. Therefore, further analysis was carried out only for this set of samples.
Optical studies
Transmittance and absorption coefficient
Figure 3 illustrates the variation of transmittance spectra with wavelength for the films deposited at 90 W. It is found that the average transmittance percentage is about 83.77% in the visible region. It is seen that the optical transmittance of the films increases after annealing. The maximum average transmittance, 84.67%, is observed for the film deposited with 90 W sputtering power and annealed at 400 °C temperature. As the crystallinity was found highest in XRD peak analysis, the regular arrangement of ZnS atoms causes higher optical transmittance of the film. Pathak et al. [34] found about 77% transmittance in the visible region for sputtered ZnS thin film. Rahimzadeh et al. [30] found 84.1% transmittance for sulfur-rich sol–gel spin-coated films. Eventually, the buffer layer needs to be transparent enough to pass through the light to the absorber layer [38]. Therefore, in our case, this ZnS thin film is applicable as a buffer layer for thin-film solar cells.
The optical absorption coefficient [37] α was calculated from transmittance and reflectance data corresponding to different photon energies, using the equation:
where t is the film’s thickness, and T is the transmittance. It has been observed that the absorption coefficient has high values, in the order of 106 cm−1, for all ZnS thin films. Figure 4 shows that the value of the absorption coefficient decreases from as-deposited to annealed samples. A sudden decrease, in Fig. 4, from 320 to 390 nm, is observed in the absorption spectra, indicates the presence of the optical bandgap in the thin films and behavior as a semiconductor.
The absorption edge is determined for each thin film by extrapolating the steep portion of the absorption curve to intercept the photon wavelength axis. The effect of the annealing temperature on the onset of the absorption edge of ZnS thin films is clearly observed in Fig. 5 and recorded in Table 2. The absorption edge in the spectra is shifted toward the lower wavelength from as-deposited to annealed samples. This was probably due to the high degree of crystallinity of ZnS films for higher annealing temperatures. This shift is expected behavior [6] because it indicates the increase in the optical bandgap with increasing annealing temperature [9]. The linear nature of the plots at the absorption edge confirmed that ZnS is a semiconductor with the presence of a direct transition between the parabolic edges of the valance band and conduction bands.
Optical bandgap
Plotting (αhν)2 with respect to incident photon energy allows the calculation of semiconductor direct optical energy bandgap (Eg) using the Tauc [39] relation:
The optical energy bandgap is calculated from Fig. 6 by extrapolating the linear portion of the curve to (αhν)2= 0 for each thin film and found from 3.24 to 3.32 eV. Kim et al. [1] found the bandgap of 3.3–3.4 eV for sputtered ZnS thin film and got 2.11% conversion efficiency of glass/Mo/CZTS/ZnS/(i-ZnO/AZO) solar cell. Islam et al. [24] found a 5.34% conversion efficiency of MBE-grown ZnS of Al/n–ZnO/i–ZnO/ZnS/CIGS/Mo/SLG thin-film solar cell with 3.6 eV ZnS film bandgap. It is observed that the bandgap of the thin films increases from as-deposited to increasing annealing temperature. The increase in the bandgap of ZnS films with substrate temperature could be attributed to the Burstein–Moss effect [40], as the Fermi energy is strongly temperature-dependent. In general, the generation of a Burstein–Moss shift depends upon the creation of a very high density of electrons (holes) in the conduction (valence) band such that the energy levels near the bottom of the band fill up, and optical transitions thus have to involve higher empty band states, resulting in a blue shift of the fundamental absorption edge. This increasing phenomenon of the bandgap and its range is in good agreement with previous works of ZnS thin film [9, 10].
The skin
The absorption of the electromagnetic wave spectrum within thin films is dependent upon the material type, thickness, photo-conductivity, and extinction coefficient of the films [41]. Due to the surface morphology, the density of films, the refractive index, and the microstructure of samples, the photon current density decreases exponentially from the surface toward the midway of films. The depth at which the intensity of the radiation inside the medium becomes 1/e (about 37%) of the value at the surface is called skin depth (χ). The skin depth is calculated from the well-known equation [42]:
where α is the absorption coefficient.
Figure 7 shows the dependence of skin depth on the incident photon energy for the films of ZnS deposited at 90 W power. It is clear from the figure that the skin depth increased when the photon energy also increased up to the value of the highest absorption region then it decreased [37, 38]. It is also observed that skin depth increases from as-deposited to increasing annealing temperature. The highest skin depth is found for the film annealed at 400 °C, which can be correlated with the XRD result, as this sample is found to have the highest crystallinity and lower dislocation density.
Absorption band tail
Along the absorption coefficient curve and near the optical band edge, there is an exponential tail that appears for the low crystalline, disordered and amorphous materials. The exponential part called the Urbach tail appears because the materials have localized states extended in the bandgap [43,44,45]. The spectral dependence of the absorption coefficient (α) and photon energy (hν) in the low photon energy range,is known as Urbach empirical rule, which is given by the following equation [46]:
where α0 is a constant and EU denotes the energy of the band tail, Urbach energy. Taking the logarithm of both sides of the equation, hence one can get a straight-line equation. It is given as follows:
Therefore, the band tail energy or Urbach energy (EU) can be obtained from the reciprocal slope of the straight line of plotting ln (α) against the incident photon energy (hν). Figure 8 shows the dependence of ln (α) against the incident photon energy (hν).
The thin films of ZnS have low crystallinity nature as detected by X-ray diffractograms and have been confirmed from the spectral behavior of the transmittance. The calculated values of Urbach energy (EU) and the constant (α0) are tabulated in Table 2. It can be observed that the value of the band tail energy (EU) decreased with increasing annealing temperature.
Figure 9 illustrates the dependence of the optical bandgap and the band tail energy of the as-deposited and annealed thin films of different temperatures. The decrease in Urbach energy comes opposite to the behavior of the optical energy as shown in the figure. To get the interrelation between Eg and EU, as shown in Fig. 10, the plot of the values can be fitted. It can observe that the interrelation between Eg and the EU has a linear relationship. The empirical equation from this linear fitting is given as:
The average value of the constant (α0) of Eq. (7), which also can be obtained from the linear fitting of Fig. 10 is equal to 2.49 eV, which represents the bandgap energy in the case of the absence of tailing. The linear relation between bandgap energy and the width of the Urbach tail was observed for other semiconductors [44, 47, 48].
The steepness parameter, σ characterizing the broadening of the optical absorption edges due to electron–phonon interactions, was calculated by the following equation [49]:
where kB is the Boltzmann constant and T is the absolute temperature in Kelvin. Hence, the values of the strength of the electron–phonon interaction (Ee–p) can be estimated by the following relationship [46, 49]:
The estimated values of steepness parameters and the strength of the electron–phonon interaction are listed in Table 2. The decrease in the EU values with increasing annealing temperature is associated with the decrease in localized states originated from the non-radiative recombination [50]. As from XRD analysis, the crystallinity increases with increasing annealing temperature, minimize localized states which may be resulted either from a decrease in the vacancies or dislocation defects of the films.
Morphological and compositional study
The morphology of the deposited films with 90 W power is shown in Fig. 11. It is observed from the figure that the films seemed to be composed of nano-granules with a compact arrangement. Apparently, the grain size increases in the deposited films as annealing temperature increases.
The measurements of the atomic percentage of corresponding materials are performed only on the films which were deposited with 90 W power. The elemental composition is listed in Table 3. As the annealing temperature increases, the compositional ratio attained close to the stoichiometric ratio of 1:1. At higher temperature sulfur evaporation might have caused such a change; hence, XRD shows an increase in crystallinity and an increase in the bandgap.
Electrical properties
From Hall measurement, among all the as-deposited and annealed samples, a better result is found for the samples deposited with 90 W sputtering power. Figure 12 shows the carrier concentration, mobility, and resistivity against as-deposited to annealed films, deposited with 90 W power. As shown in Fig. 12, the negative value of carrier concentration implies the n-type conductivity of the films. The high carrier concentration of 7.18 × 1012 cm−3 and high mobility of 26.47 cm2/Vs are observed for the films annealed at 400 °C. Haque et al. [9] also found carrier concentration of the order of 1012 cm−3.
From Fig. 12, the lowest resistivity of 8.74 × 104 Ω-cm is found for the film deposited with 90 W power and annealed at 400 °C. The high carrier concentration and mobility also comply with structural and optical analysis.
Conclusions
In this experiment, the deposition conditions and annealing temperatures have been optimized to grow better-quality ZnS thin film for using it as a buffer layer in solar cells. ZnS thin films were deposited upon soda-lime glass substrate by the RF-sputtering method with 70, 80, 90, and 100 W powers. After that each film was annealed at 350 °C, 400 °C, and 450 °C temperature with 20 °C/min ramp rate for 20 min. Structural, electrical, and optical characterizations show better properties for the films deposited with 90 W power and annealed at 400 °C temperature. The XRD pattern indicates preferential orientation along (111) planes of the zincblende phase with a peak at around 28.48° for the films deposited with 90 W power. The lattice constant gradually decreases, and crystallite size gradually increases with the increase in annealing temperature. The wide direct bandgap is found in the range of 3.24–3.32 eV with above 84.67% transmittance. Urbach energy, or the band tail width (EU), steepness parameters and electron–phonon interactions were estimated. The relation between these parameters at different annealing temperatures was studied. The highest electron carrier concentration achieved was 1012 cm−3 with 26.47 cm2/Vs mobility. The result anticipates the wide range of potentiality of sputtered deposited ZnS thin films.
References
Kim, J., Park, C., Pawar, S.M., et al.: Optimization of sputtered ZnS buffer for Cu 2 ZnSnS 4 thin film solar cells. Thin Solid Films 566, 88–92 (2014). https://doi.org/10.1016/j.tsf.2014.07.024
Ubale, A.U., Kulkarni, D.K.: Preparation and study of thickness dependent electrical characteristics of zinc sulfide thin films. Bull. Mater. Sci. 28, 43–47 (2005). https://doi.org/10.1007/BF02711171
Lee, Y.L., Lo, Y.S.: Highly efficient quantum-dot-sensitized solar cell based on co-sensitization of CdS/CdSe. Adv. Funct. Mater. 19, 604–609 (2009). https://doi.org/10.1002/adfm.200800940
Padiyan, D.P., Marikani, A., Murali, K.R.: Influence of thickness and substrate temperature on electrical and photoelectrical properties of vacuum-deposited CdSe thin films. Mater. Chem. Phys. 78, 51–58 (2003). https://doi.org/10.1016/S0254-0584(02)00211-0
Goudarzi, A., Aval, G.M., Sahraei, R., Ahmadpoor, H.: Ammonia-free chemical bath deposition of nanocrystalline ZnS thin film buffer layer for solar cells. Thin Solid Films 516, 4953–4957 (2008). https://doi.org/10.1016/j.tsf.2007.09.051
Oladeji, I.O., Chow, L.: Synthesis and processing of CdS/ZnS multilayer films for solar cell application. Thin Solid Films 474, 77–83 (2005). https://doi.org/10.1016/j.tsf.2004.08.114
Matin, M.A., Amin, N., Zaharim, A., Sopian, K.: Ultra thin high efficiency CdS/CdTe thin film solar cells from numerical analysis. In: Proceedings of 8th WSEAS International Conference on Non-linear Analysis, Non-linear Systems CHAOS, 338–344 (2009)
Gayou, V.L., Salazar-Hernandez, B., Constantino, M.E., et al.: Structural studies of ZnS thin films grown on GaAs by RF magnetron sputtering. Vacuum 84, 1191–1194 (2010). https://doi.org/10.1016/j.vacuum.2009.10.023
Haque, F., Rahman, K.S., Islam, M.A., et al.: Growth optimization of ZnS thin films by RF magnetron sputtering as prospective buffer layer in thin film solar cells. Chalcogenide Lett 11, 189–197 (2014)
Hwang, D.H., Ahn, J.H., Hui, K.N., et al.: Structural and optical properties of ZnS thin films deposited by RF magnetron sputtering. Nanoscale Res. Lett. 7(1), 26 (2012)
Islam, M.A., et al.: Comparative study of ZnS thin films grown by chemical bath deposition and magnetron sputtering. In: 2012 7th international conference on electrical and computer engineering, Dhaka, pp. 86–89 (2012). https://doi.org/10.1109/ICECE.2012.6471491
Matin, R., Bashar, M.S., Sultana, M. et al.: Annealing effects on the structural, optical and electrical properties of chemically deposited CdS thin films using NH4Cl complexing agent. Int. J. Nanoelectron. Mater. 11, 221–232 (2018)
Rupom, R.H., Matin. R., Bashar, M.S. et al.: Fabrication and characterization of cadmium sulfide (CdS) buffer layer thin film by using chemical bath deposition method for solar cell. Am. Int. J. Res. Sci. 10–15 (2016)
Hwang, D.H., Ahn, J.H., Hui, K.N., Son, Y.G.: Structural and optical properties of gold-incorporated diamond-like carbon thin films deposited by RF magnetron sputtering. Mater. Res. Express 4, 076403 (2017). https://doi.org/10.1088/2053-1591/aa7430
Islam, M.A., Hossain, M.S., Aliyu, M.M. et al.: Comparative study of ZnS thin films grown by chemical bath deposition and magnetron sputtering. In: 2012 7th International Conference on Electrical and Computer Engineering ICECE, 86–89. (2012). https://doi.org/10.1109/ICECE.2012.6471491
Hossain, M.S., Rahman, K.S., Islam, M.A., et al.: Growth optimization of Zn x Cd 1-x S films on ITO and FTO coated glass for alternative buffer application in CdTe thin film solar cells. Opt. Mater. (Amst) 86, 270–277 (2018). https://doi.org/10.1016/j.optmat.2018.09.045
Hossain, M.S., Kabir, H., Rahman, M.M., et al.: Understanding the shrinkage of optical absorption edges of nanostructured Cd-Zn sulphide films for photothermal applications. Appl. Surf. Sci. (2017). https://doi.org/10.1016/j.apsusc.2016.09.095
Hossain, M.S., Kabir, H., Rahman, M.M., et al.: Understanding the shrinkage of optical absorption edges of nanostructured Cd-Zn sulphide films for photothermal applications. Appl. Surf. Sci. (2017). https://doi.org/10.1016/j.apsusc.2016.09.095
Karim, M.R., Dar, M.A., Shar, M.A., et al.: Impact of CdTe thin film thickness in ZnxCd1−xS/CdTe solar cell by RF sputtering. Sol. Energy 180, 559–566 (2019). https://doi.org/10.1016/j.solener.2019.01.019
Akhanda, S., Matin, R., Bashar, M.S., et al.: Experimental study on structural optical and electrical properties of chemical bath deposited CdZnS thin films. J. Fundam. Renew. Energy Appl. (2017). https://doi.org/10.4172/2090-4541.1000222
Zubair, M.A., Chowdhury, M.T., Bashar, M.S., et al.: Thickness dependent correlation between structural and optical properties of textured CdSe thin film. AIP Adv. 9, 045123 (2019). https://doi.org/10.1063/1.5096594
Pawar, S.M., Moholkar, A.V., Shinde, P.S., et al.: Room temperature electrocrystallization of CdSe thin films from ethylene glycol bath Room temperature electrocrystallization of CdSe thin films from ethylene glycol bath. J. Alloys Compd. (2008). https://doi.org/10.1016/j.jallcom.2007.05.015
Yadav, A.A., Masumdar, E.U.: Optical and electrical transport properties of spray deposited CdS 1–x Se x thin films. J. Alloys Compd. 505, 787–792 (2010). https://doi.org/10.1016/j.jallcom.2010.06.141
Islam, M.M., Ishizuka, S., Yamada, A., et al.: Solar energy materials & solar cells CIGS solar cell with MBE-grown ZnS buffer layer 93, 970–972 (2009). https://doi.org/10.1016/j.solmat.2008.11.047
Nakada, T., Mizutani, M., Hagiwara, Y., Kunioka, A.: High-efficiency Cu (In, Ga) Se thin-film solar cells with a CBD-ZnS buffer layer. Solar Energy Mater. Solar Cells 67, 255–260 (2001)
Search, H., Journals, C., Contact, A. et al.: 18% Efficiency Cd-free Cu (In, Ga) Se2 thin-film solar cells fabricated using chemical bath deposition (CBD) -ZnS buffer layers fabricated using chemical bath deposition (CBD) -ZnS buffer layers. 165:7–10 (2002). https://doi.org/10.1143/JJAP.41.L165
Shao, L.X., Chang, K.H., Hwang, H.L.: Zinc sulfide thin films deposited by RF reactive sputtering for photovoltaic applications. Appl. Surf. Sci. 212–213, 305–310 (2003). https://doi.org/10.1016/S0169-4332(03)00085-0
Zhang, M., Xia, Z., Zhou, W. et al.: RF Magnetron sputtered zinc sulfide thin films and their applications to thin film transistors
Kuk, S., Bang, S., Kim, I., et al.: Chemical and electrical properties of ZnS deposited with DEZ and H 2 S by atomic layer deposition method. Mater. Sci. Forum. 545, 689–692 (2007). https://doi.org/10.4028/www.scientific.net/MSF.544-545.689
Rahimzadeh, N., Ghodsi, F.E., Mazloom, J.: Effects of starting precursor ratio on optoelectrical properties and blue emission of nanostructured C-ZnS thin films prepared by spin coating. J. Electron. Mater. (2017). https://doi.org/10.1007/s11664-017-5874-1
Gangopadhyay, U., Kim, K., Mangalaraj, D., Yi, J.: Low cost CBD ZnS antireflection coating on large area commercial mono-crystalline silicon solar cells. Appl. Surf. Sci. 230, 364–370 (2004). https://doi.org/10.1016/j.apsusc.2004.02.059
Zhang, K., Yu, T., Liu, F., et al.: Selective fluorescence turn-on and ratiometric detection of organophosphate using dual-emitting Mn-doped ZnS nanocrystal probe. Anal. Chem. 86, 11727–11733 (2014). https://doi.org/10.1021/ac503134r
Rai, S.C., Wang, K., Ding, Y., et al.: Piezo-phototronic effect enhanced UV/visible photodetector based on fully wide band gap type-II ZnO/ZnS Core/shell nanowire array. ACS Nano 9, 6419–6427 (2015). https://doi.org/10.1021/acsnano.5b02081
Pathak, T.K., Kumar, V., Purohit, L.P., et al.: Substrate dependent structural, optical and electrical properties of ZnS thin films grown by RF sputtering. Phys. E Low-Dimens. Syst. Nanostruct. 84, 530–536 (2016). https://doi.org/10.1016/j.physe.2016.06.020
Warren, B.E.: X-Ray Diffraction. Dover Publications Inc, New York (1990)
Sen, S., Halder, S.K., Sen, Gupta S.P.: An X-ray line broadening analysis in the vacuum-evaporated silver films. J. Phys. Soc. Jpn. 38, 1641–1647 (1975)
Fewster, B.M.: Thin film analysis by X-ray (2006)
Grätzel, M.: Nanocrystalline injection solar cells (2006)
Pankove, J.I.: Optical Processes in Semiconductors, 2nd edn. Dover Publications Inc, New York (2010)
Burstein, E.: Anomalous optical absorption limit in InSb. Phys. Rev. 93, 632–633 (1954). https://doi.org/10.1103/PhysRev.93.632
Hassanien, A.S., Akl, A.A.: Influence of composition on optical and dispersion parameters of thermally evaporated non-crystalline Cd50S50-xSex thin films. J Alloys Compd. 648, 280–290 (2015). https://doi.org/10.1016/j.jallcom.2015.06.231
Eloy, J.F.: Power Lasers. National School of Physics, Grenoble, France. Wiley, Hoboken (1984)
Aly, K.A., Abd Elnaeim, A.M., Uosif, M.A.M., Abdel-Rahim, O.: Optical properties of Ge-As-Te thin films. Phys. B Condens. Matter. 406, 4227–4232 (2011). https://doi.org/10.1016/j.physb.2011.08.013
Ikhmayies, S.J., Ahmad-Bitar, R.N.: A study of the optical bandgap energy and Urbach tail of spray-deposited CdS: in thin films. J. Mater. Res. Technol. 2, 221–227 (2013). https://doi.org/10.1016/j.jmrt.2013.02.012
Melsheimer, J., Ziegler, D.: Band gap energy and Urbach tail studies of amorphous, partially crystalline and polycrystalline tin dioxide * the spraying method was used to prepare amorphous and partially crystalline tin dioxides at temperatures from 340 to 410 “c and polycrystalline. Thin Solid Films 129, 35–47 (1985)
Urbach, F.: The long-wavelength edge of photographic sensitivity and of the electronic Absorption of Solids [8]. Phys. Rev. 92, 1324 (1953). https://doi.org/10.1103/PhysRev.92.1324
Tonny, K.N., Rafique, R., Sharmin, A., et al.: Electrical, optical and structural properties of transparent conducting Al doped ZnO (AZO) deposited by sol-gel spin coating. AIP Adv. (2018). https://doi.org/10.1063/1.5023020
Wu, S., Yuan, S., Shi, L., et al.: Preparation, characterization and electrical properties of fluorine-doped tin dioxide nanocrystals. J. Colloid Interface Sci. 346, 12–16 (2010). https://doi.org/10.1016/j.jcis.2010.02.031
Hossain, M.S., Jiang, Z.-T., Kabir, H., et al.: Understanding the shrinkage of optical absorption edges of nanostructured Cd-Zn sulphide films for photothermal applications. Appl. Surf. Sci. 392, 854–862 (2016). https://doi.org/10.1016/j.apsusc.2016.09.095
Lim, W.F., Quah, H.J., Hassan, Z., et al.: Alteration of structural and optical properties in quaternary Al0.1In0.1Ga0.8 N films using ultraviolet assisted photo-electrochemical etching route. J. Alloys Compd. 649, 337–347 (2015). https://doi.org/10.1016/j.jallcom.2015.07.114
Acknowledgements
This study is supported by the Bangabandhu Science and Technology Fellowship Trust under the Ministry of Science and Technology, Peoples Republic of Bangladesh. This work is also supported by the Bangladesh Council of Scientific and Industrial Research (BCSIR), Dhaka-1205.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Bashar, M.S., Matin, R., Sultana, M. et al. Effect of rapid thermal annealing on structural and optical properties of ZnS thin films fabricated by RF magnetron sputtering technique. J Theor Appl Phys 14, 53–63 (2020). https://doi.org/10.1007/s40094-019-00361-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40094-019-00361-5