Abstract
The vortex gas injection into plasma torch is considered as a method for reducing electrodes erosion. In order to investigate the effects of vortex gas injection on plasma structure, as well as the effect of gas viscosity on the rate of rotation, a three-dimensional nonequilibrium and time-dependent non-transferred DC plasma torch model has been simulated. Viewing the general characteristics of the plasma shows that the model works well. The results have shown that if the components of the inlet gas velocity are not properly selected, it is possible that the rotary effects of the gas are greatly depleted even before the gas reaches the cathode tip and plasma formation. In this case, only the change in the axial component of the gas causes changes in the structure of the plasma. Vortex reduction is also observed during the movement of cold gases. It is observed that the change in viscosity of gas has significant effects on the rate of the vortex.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Plasma torch is widely used in many applications such as plasma spraying, plasma cutting, plasma welding, and plasma waste disposal [1]. This device is typically made up of two electrodes in which the plasma is formed by creating an arc between them. There are two types of direct current (DC) plasma torches: non-transferred and transferred arc torches. In non-transferred DC plasma torches, the electrodes are inside the body of the torch. Whereas in transferred, one electrode is outside [2]. Since the study of plasma behavior is costly and time consuming, the simulations are very cost effective [3]. Different simulations are performed in two-dimensional or three-dimensional, steady-state, or time-dependent models with different approximations.
Here, the goal is to simulate a relatively complete model for the study of the properties of the plasma. Therefore, the model is considered as three dimensional, nonequilibrium, and time dependent. Plasma is considered to be fluid, composed of heavy particles and electrons. In the local thermodynamic equilibrium approximation (LTE), the temperature of the electrons and the heavy particles is the same. This approximation is set for the plasma interior, but no longer exists in areas where the plasma interacts with the electrodes or with the cold gas [4, 5]. In the NLTE approximation, the electron temperature is no longer the same as heavy particles, and for each type, separate energy equations are solved. The use of NLTE models allows better investigation of plasma behavior, especially near the electrodes and regions with high-temperature gradients. So, a perfect plasma torch model should be three-dimensional, time-dependent and non-equilibrium [5].
Unfortunately, the erosion of electrodes is one of the most important problems in the design and construction of the plasma torch, which occurs due to the arc collision and the high temperature of the plasma. There are many ways to eliminate this problem. For example, an external magnetic field or swirl of the gas at the inlet is used to rotate the arc [6,7,8]. The plasma swirl causes a constant arc movement and thus reduces erosion of the electrodes [9]. In most of the researches on the gas rotation, the effect of the degree of gas spin on the plasma structure is usually studied. For example, the gas is introduced through a pipe and is rotated by changing the angle of the tube, and the effects of the gas rotation on the plasma structure are investigated [10]. However, the effects of the change in the velocity of each of the gas components are less considered.
In this paper, we try to examine this issue. The results indicate that gas rotation decreases gradually during the movement. So, if the components of the gas velocity are not properly selected, the rotation may be lost even before plasma formation. This is also evident in the rotation of cold gases. However, the rate of decrease of rotation inside the plasma torch is higher. Another goal of this paper is to study the effect of viscosity on the reduction of rotation in cold gases and to examine this dependence on the structure of the plasma torch. In “Model description” section, the description of the model is given. The boundary conditions are described in “Boundary conditions” section. The results and discussions are given in “Results and discussion” section, and finally, the conclusions are obtained in “Conclusion” section.
Model description
Model setup
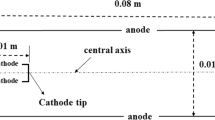
Figure 1 shows the simulation area, which includes the space between the electrodes, the gas inlet, and the outlet. In order to better understand the properties of the plasma, a part of the gas outlet area is also shown. The radius of the cathode is 1.5 mm and its length is 10 mm and the anode radius is 5 mm and its length is 25 mm. The simulation area is meshed to more than 106 cells. The gas enters the inlet region and after passing through the arc between the electrodes, the plasma goes out of the nozzle hole.
Assumptions
The model is considered based on the following main assumptions:
The plasma is in the nonequilibrium condition, and the temperature of the electrons and heavy particles are different.
The plasma is considered optically thin.
The gravitational effects are negligible.
Governing equations
In this paper, the plasma behaves like a fluid which contains electrons and argon particles such as argon atoms, electronically excited atoms \(({\text{Ar}}^{ *} )\), and atomic ions \(( {\text{Ar}}^{ + } )\). The role of \({\text{Ar}}^{ + 2}\) ions is very low and can be ignored.
The main reactions are presented in Table 1. These reactions include elastic, scattering, excitation, de-excitation, etc. These reactions include electron-induced reactions which depend on the temperature of the electrons and the reactions of heavy species which are dependent on the temperature of the gas.
The mass conservation equations are given as follows:
where \(\vec{V}\) is the particle velocity and \(\rho\) is total mass density, containing the mass of ions and electrons.
The Navier–Stokes equations can be written as
where \(u\), \(v\), and \(w\) are components of the velocity of particles along the coordinate axes. In these equations, the viscosity \(\mu\) is calculated from the mix kinetic theory of gases
where \(\Omega _{\mu }\) is the collision integral and is given by
and \(T^{*} = \frac{kT}{\varepsilon }\) is the dimensionless temperature. Using the Chapman–Enskog theory, the viscosity of a mixture of gases can be calculated as
where \(\phi_{\alpha \beta }\) is equal to
where \(N\) is the total number of particles in the gas mixture, \(x_{\alpha }\), \(\mu_{\alpha }\), and \(M_{\alpha }\) are the molar fraction, viscosity, and molecular mass of the particle \(\alpha .\)
Heavy particle conservation species equations are written as
In Eq. 7, the \(Y_{\alpha }\) is the mass fraction of species, \(V\) is the average particle velocity, \(S_{\alpha }\) is the production rate of the particle \(\alpha\), and \(\vec{J}_{\alpha }\) is defined as follows:
which is the same as diffusive flux. In Eq. 8\(D_{\alpha }\) is the diffusion coefficient and
where \(\mu_{\alpha \beta }\) is the mobility of ions and is calculated from the Langevin formula:
where \(\delta_{\alpha }\) is polarizability and \(m_{r}\) is the reduced mass of ions and neutral species.
The energy equations for electrons and heavy particles should be solved separately. The electron transport equation is written as
where \(\vec{\varGamma }_{e}\), the electron density flux, is equal to
where \(\mu_{e}\) is the mobility of electrons and \(D_{e}\) is the diffusion coefficient. The electron temperature is obtained using the energy equation:
where \(\chi = \left( {\frac{5}{2}} \right)n_{e} D_{e}\) and power density \(P\) is the total energy absorbed by electrons, such as Joule heating, inductive heating, and external heating.
In the plasma fluid model, the electron distribution function is assumed to be Maxwellian, and the electron transfer properties can be calculated as
A good approximation for electron collision frequency is [11]
The constant value \(v_{1}\) is specified as \(2 \times 10^{7}\). The energy equation for heavy particles is given by
Gas heating sources have been added to include the following phenomena: electron elastic and inelastic collisions, ion ohmic heating, ion-surface recombination, and kinetic impact.
Maxwell’s electromagnetic equations can be written for the magnetic vector potential as [6]
The standard \(K - \varepsilon\) model is introduced to turbulence. The effect of turbulence on heat transfer and mass diffusion is accomplished through the following relationships:
In these relations, the turbulent component of viscosity is defined as \(\mu_{t} = \rho C_{\mu } \frac{{K^{2} }}{ \in }\). The standard model uses the following transfer equations for \(K\) and \(\in\) [12]:
The constant values in the \(K - \in\) model, which are calculated using data fitting for a wide range of turbulent fluids, are given as [11]
Boundary conditions
Table 2 shows the details of the intended boundary conditions. In the plasma torch inlet, the gas temperature is 1000 K, and the gas enters with a total velocity of \(2\frac{m}{s}\). The gas flow rate in inlet is 8.5 slpm. At the outlet, a fixed pressure condition is applied. The cathode temperature is considered to be 1500 K. In the cathode and anode, no-slip condition is considered (\(u = v = w = 0\)) [8]. At the anode surface, a convective boundary condition with a heat transfer coefficient of \(10^{5} \,\frac{\text{W}}{{{\text{m}}^{2} }}\) and a cooling water temperature of 300 K is used [13]. The electron temperature in the electrodes is in the thermal flux balanced, in which the electron temperatures in the cells surrounding electrodes face are used to set their electron temperature.
The tangential components of the electric field and magnetic vector potential on the surface of the perfect conductor is considered zero. The total electrical current is 200 A. The cylindrical part of the cathode is thermally adiabatic, in this case, the wall temperature is floating and calculated by the solver.
Results and discussion
In order to investigate the effects of gas rotation on plasma structure, a three-dimensional, nonequilibrium, and time-dependent plasma torch model is simulated.
Examining the results, and comparing them with the work of other researches [10, 11, 14, 15], shows that the model works well (“General characteristics of the plasma” section). The purpose of “Rotational effects” section is to study the effect of gas rotation on the plasma structure, and for this purpose, the inlet gas enters the simulation zone with two general methods. In the first case, the gas is introduced at a constant total velocity and the effect of the inlet gas rotation is investigated. In this case, both tangential and axial velocity components are changed. In the second case, the aim is to observe the effect of the change in the tangential velocity component on the plasma structure. In this case, only the axial component of the gas velocity will be constant.
Finally, by simulating the movement of cold gases, their rotational motion, as well as the effect of changes of viscosity on the rate of rotation reduction, is also studied. The results indicate that the rotary motion of the gas is rapidly reduced by moving it to the front direction. Although increasing the viscosity of the gas will increase the rate of rotation reduction. The decrease and disappearance of gas rotation are also seen in the plasma torch, but due to the large change in the viscosity of the gas inside the plasma torch, the rate of rotational loss is much higher than that of cold gases. So, according to geometry, the axial velocity of the gas should be such that the rotary motion of the gas reaches the cathode tip.
General characteristics of the plasma
Figure 2a, b shows the plasma temperature and velocity profiles as a function of the time right in front of the cathode at the desired point at \(x = 15\,{\text{mm}}\), respectively. The total simulation time is \(0.04\,{\text{s}}\), and after about \(0.01\,{\text{s}}\), the plasma reaches a steady state and no further time is needed to extract data. This indicates simulation convergence.
The plot of the argon ions mole fractions as a function of the axial and radial distance is shown in Fig. 3. It is observed that the greatest amount of ionization of the gas in front of the cathode occurs. Approximately about 0.1 percent of the gas is ionized.
The temperature and velocity distributions profile are shown in Fig. 4a, b, respectively. As the gas approaches the cathode tip, it is ionized and accelerated, and therefore, its velocity increases sharply. The highest temperature of the plasma is observed in the front of the cathode.
Rotational effects
In this section, the effects of the vortex gas injection on plasma velocity and temperature are investigated. The effect of viscosity on the reduction in gas rotation is also studied. The inlet gas enters the simulated area with different values of rotation. Two general methods for studying the gas rotation on the plasma structure are considered:
- 1.
Changing the amount of gas rotation by changing the two components of the velocity vector, while the total velocity is constant.
- 2.
Changing the amount of gas rotation by changing the tangential velocity component, while the axial component is constant.
In the first case, both the axial and tangential components of the gas velocity will change. However, the total velocity of the inlet gas is constant. In the second case, the axial component of the gas velocity is constant and the effects of the tangential component on the plasma structure are investigated. In both cases, the gas velocity has no radial component.
Gas rotation with constant total velocity
The gas enters the simulation area with different values of the axial and tangential components of the velocity. Table 3 describes different modes of gas entry to the device. In all states, the total gas velocity is constant at \(2\frac{m}{s}\). The ratio \(S\) is defined as the ratio of the tangential component to the total velocity:
The increase in \(S\) represents an increase in the tangential component of the velocity and the reduction in its axial component. Figure 5 shows the changes in plasma velocity and temperature with radial changes in front of the cathode. These graphs are plotted along the desired probe line on the x–y plane and at x = 15 mm. As S increases, the total plasma velocity decreases which brings the temperature up. Therefore, the reduction in the axial component of the velocity, and increasing its tangential component, reduces the velocity of the entire plasma results in rising the temperature. It is not clear here that which component of the inlet gas velocity results in all these changes. In method 2 in order to reveal this issue, only, the tangential component of velocity has been changed.
The temperature and velocity changes in the plasma, along with the change in the axial distance from the cathode tip to the outlet, are shown in Fig. 6. However, in all states at almost one point, the plasma velocity is close to zero. As a result, it can be said that the flame length does not change for different values of the gas rotation (Fig. 6a). It is also observed that with increasing the degree of rotation of the gas, the peak of the graphs, i.e., the maximum plasma velocity, moves to the smaller \(x\), toward the tip of the cathode. By increasing the amount of S, the maximum plasma temperature will increase, while the plasma temperature decreases faster at the outlet (Fig. 6b). This can be justified by comparing the plasma velocity. The higher the degree of swirl gas, the less its velocity will be, and as a result, the temperature of the plasma will decrease faster. For different degrees of gas rotation, all plasmas reach the same temperature at one point. That is, at this point, the gas velocity is almost zero and the temperature reaches a constant value. This point can be considered as the end of the flame. The temperature of the plasma at this point is about 900 °C. The plasma temperature drop in the device is much lower than the outside of it. The point shown with the white vector, in Fig. 6b, is a good illustration of this change.
Although variations in the velocity vector components caused changes in the plasma properties, the results of the next section show that, with this input total velocity (\(2\frac{m}{s}\)), the rotational motion of the gas has become negligible before plasma formation. That is, only the change in the axial velocity component has transformed the plasma structure.
Rotation with constant axial component
Since in method 1, both the axial and tangential components of the velocity were changed when increasing the amount of gas rotation, it was not exactly known which of these components changed the properties of the plasma. So, here the simulation of the plasma was performed for different values of the rotational component of the inlet gas velocity. In this case, the constant axial component of the gas is considered to be \(2\frac{m}{s}\) (Table 4). This is while the total gas velocity is no longer constant. Figure 7 shows the velocity and temperature values of the plasmas right in front of the cathode at the desired point x = 15 mm.
It is observed that the change in the tangential component of the gas velocity does not have much effect on the plasma structure, but what changes the plasma is the change in the axial component of the inlet gas velocity. Because of the viscosity, the tangential gas velocity component decreases rapidly with the arrival and movement of gas in the region between the electrodes. As the gas approaches the tip of the cathode, the rotation of the gas almost disappears. This is consistent with the results of method 1; what caused the change in the plasma structure for different modes in Figs. 5 and 6 can be the change in the axial component of the incoming gas.
The value of \(w\) on the \(x - y\) plane represents the rotational component of the gas velocity. The \(w\) component changes with increasing \(x\) are shown in Fig. 8. The reduction in this velocity component is almost linear, and its amount is greatly reduced before the gas reaches the cathode tip and the formation of the plasma. Therefore, before the gas reaches the tip of the cathode, its rotational effects almost disappear, and as a result, the initial rotation of the gas does not have much effect on the plasma structure. The linear reduction in \(w\) indicates its uniformity during successive rotations and the upward movement of the gas. In Fig. 9, gas velocity vectors are shown on three levels perpendicular to the cathode. The reduction in gas rotational motion is also well visible in this figure.
The viscosity of gases varies with their temperature rise [16]. Surely, changes in viscosity will affect the rotation of the gas. In order to study how to reduce the rotation of gases, as well as the effect of viscosity on rotation, the motion of cold gases was also investigated. For this purpose, a hollow tube similar to the region between the anode and the cathode (Fig. 10) was considered, and the motion of cold gases was simulated. Cold gas enters the simulation zone with different viscosity values. Viscosity values are considered in the areas of the change in the viscosity of argon at various temperatures, as reported by Murphy [16]. Both the tangential and axial components of the inlet gas velocity are considered to be \(2\frac{m}{s}\). The diagram of the reduction in the tangential component of the velocity, with the motion of the gas inside the tube, is shown in Fig. 11 for different viscosity values.
Reduction in the \(w\) component of the gas velocity, along with the gas flow inside the pipe and the increase in \(x\), on a probe line shown in Fig. 10
By increasing the amount of viscosity, the rate of reduction in the rotating component of the gas velocity increases. Therefore, the rotary movement of the gas will be eliminated more quickly. An increase in viscosity increases the number of collisions between the gas molecules and thus changes the way they move. The comparison between Figs. 8 and 11 shows that although there is a loss of rotation for cold gases, this reduction rate for cold gases is much lower than the plasma. Therefore, the gas will travel longer until the spin disappears. One of the reasons for this is the high variation in viscosity during the gas movement in the plasma torch. However, the changes in other plasma properties may also affect this downturn.
Conclusion
Three-dimensional, time-dependent, and non-transferred plasma torch was simulated to investigate the plasma structure and the effects of inlet gas rotation. A review of the general characteristics of the plasma showed that the model works well. The velocity and temperature profiles are consistent with what was obtained by a similar model in [6]. Plasma properties were investigated by changing the amount of gas rotation in the inlet. The results show that by reducing the axial component and increasing the spin component, the temperature of the plasma can be increased and the total velocity can be reduced. By changing the degree of rotation of the gas, the maximum plasma velocity approaches the cathode tip. The reduction rate of the temperature inside the device is lower than the outside. For higher degrees of gas swirl, the plasma temperature reduction rate will be higher. Also, by changing the degree of rotation of gas, the flame length does not change. The study of gas rotation showed that the proper selection of the axial component of the inlet gas velocity is very important. Otherwise, the rotational component of the gas movement may be lost. Therefore, in order to use the gas spin in the plasma torch, the axial component of the inlet gas velocity must be determined so that the rotational effects of the gas do not disappear before the formation of the plasma. The loss of rotational effects in the movement of cold gases is also well visible. This reduction is due to the viscosity of the gas. The results showed that increasing the amount of viscosity of gas increases the rate of reduction in rotary effects. However, due to the change in gas structure during movement, the rate of this decrease for plasma torch is much higher. Other features of plasma may also have effects on this rate increase.
References
Chau, S.W., Hsu, K.L., Lin, D.L., Chen, J.S., Tzeng, C.C.: Modeling and experimental validation of a 1.2 MW DC transferred well-type plasma torch. Comput. Phys. Commun. 177(1), 114–117 (2007)
Liang, P., Groll, R.: Numerical study of plasma–electrode interaction during arc discharge in a DC plasma torch. IEEE Trans. Plasma Sci. 46(2), 363–372 (2018)
Guo, Z., Yin, S., Liao, H., Gu, S.: Three-dimensional simulation of an argon-hydrogen DC non-transferred arc plasma torch. Int. J. Heat Mass Transf. 80(September), 644–652 (2015)
Trelles, J.P., Chazelas, C., Vardelle, A., Heberlein, J.V.R.: Arc plasma torch modeling. J. Therm. Spray Technol. 18(5–6), 728–752 (2009)
Chazelas, C., Trelles, J.P., Choquet, I., Vardelle, A.: Main issues for a fully predictive plasma spray torch model and numerical considerations. Plasma Chem. Plasma Process. 37(3), 627–651 (2017)
Baeva, M., Uhrlandt, D.: Non-equilibrium simulation of the spatial and temporal behavior of a magnetically rotating arc in argon. Plasma Sourc. Sci. Technol. 20(3), 035008 (2011)
Lincun, L., Weidong, X., Science, P.: Time-dependent 2D modeling of magnetron plasma torch in turbulent flow. Plasma Sci. Technol 10(3), 328 (2008)
Felipini, C.L., Pimenta, M.M.: Some numerical simulation results of swirling flow in DC plasma torch. J. Phys: Conf. Ser. 591(1), 012038 (2015)
Sun, X., Heberlein, J.: Fluid dynamic effects on plasma torch anode erosion. J. Therm. Spray Technol. 14(1), 39–44 (2005)
Moon, J.H., Han, J.G., Kim, Y.J.: Performance of an atmospheric plasma torch with various inlet angles. Surf. Coat. Technol. 193(1–3), 94–100 (2005)
CFD-ACE+, ESI CFD Inc., Huntsville, Module Manual, Version 2014
Malalasekera, W., Versteeg, H.K.: An Introduction to Computational Fluid Dynamic: the Finite Volume Method. Pearson Prentice Hall (2007)
Guo, Z., Yin, S., Qian, Z., Liao, H., Gu, S.: Effect of the deviation of the current density profile center on the three-dimensional non-transferred arc plasma torch. Comput. Fluids 114, 163–171 (2015)
Baeva, M., Kozakov, R., Gorchakov, S., Uhrlandt, D.: Two-temperature chemically non-equilibrium modelling of transferred arcs. Plasma Sourc. Sci. Technol. 21(5), 055027 (2012)
Bird, R.B., Stewart, W.E., Lightfoot, E.N.: Transport phenomena. Appl. Mech. Rev. 55(1), R1–R4 (2002)
Murphy, A.B., Arundelli, C.J.: Transport coefficients of argon, nitrogen, oxygen, argon-nitrogen, and argon-oxygen plasmas. Plasma Chem. Plasma Process. 14(4), 451–490 (1994)
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Gharaeinia, M., Saviz, S. & Sari, A.H. Influence of the inlet gas velocity components on the survival of the vertex of gas in the plasma torch. J Theor Appl Phys 14, 1–10 (2020). https://doi.org/10.1007/s40094-019-00357-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40094-019-00357-1