Introduction

Two-dimensional (2D) carbon-based materials have attracted considerable attention in recent decades [1,2,3,4,5]. Examples of these 2D materials are graphene and graphyne sheets [1, 2]. Graphene is a 2D hexagonal network of sp2-bonded carbon atoms [3]. From the point of application, graphene is considered to be even more promising than other carbon-based nanostructures due to its extraordinary mechanical, thermal, electronic, and magnetic properties [3]. Like graphene, graphyne is a one-atom-thick layer of C atoms, but it contains both sp- and sp2-hybridized C atoms [4, 5]. There are several types of graphyne. The most known graphyne are α-, β-, γ- and 6,6,12-graphyne sheets [5]. Interestingly, it is reported that α-, β-, and 6,6,12-graphyne sheets posses amazing electronic properties similar to graphene because of their peculiar band structure featuring so-called Dirac points and cones [1, 4, 5]. At a Dirac point, the valence and conduction bands cross each other at a single point at the Fermi level. It means that these sheets are semiconductors with zero band gap, or, alternatively, as metals with zero density of states (DOS) at the Fermi level [3,4,5].

Although graphene and graphyne are promising materials for use in nanoelectronic, the absence of a band gap limits their applications. Many strategies such as applying external electric field, producing nanoribbons, adsorbing molecules, chemical doping, and functionalization have been proposed to introduce a band gap in graphene and graphyne [6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23]. In particular, many studies have been focused on the modulation of the electronic properties of these sheets by doping [8,9,10,11,12]. N and B atoms are considered as the typical electron (n-type) and hole (p-type) doping elements since they are located in the periodic table one position behind and before from C atom, respectively. B- and N-doped graphene and graphyne sheets are reported to be good semiconductors [8,9,10,11,12]. It is also found that BN co-doping is a process that opens a band gap in graphene and graphyne sheets, and changes the character of these sheets from a semimetal to a semiconductor [13,14,15,16]. Recently, graphene doped with BN nanodot has been realized experimentally [16, 18, 19]. Effects of geometric shape and size of embedded BN nanodot on the electronic properties of BN-doped graphene are studied theoretically [16, 18, 19]. It is found that the band gap of graphene increases with the size of the BN nanodot, regardless of the shape of BN nanodot. Motivated by these results, we have studied possibility of band gap opening in α- and β-graphyne sheets with BN nanodots doping based on density functional theory (DFT) in the present work.

Computational details

The calculations are carried out using DFT as implemented in OpenMX3.7 package [24]. The generalized gradient approximation (GGA) with Perdew–Burke–Ernzerhof (PBE) correction is employed for the exchange–correlation function [25]. The plane wave basis set is restricted by a cutoff energy of 100 Ry. All atomic structures are relaxed until the forces acting on each atom are smaller than 0.01 eV/Å. The k-point is set to be 41 along each high symmetry lines in the Brillouin zone. The charge transfer is calculated based on the Mulliken population analysis [26]. In order to have a better insight into the nature of bond characteristic, the charge density difference, \(\rho_{\text{diff}}\), is calculated by [27]:

$$\rho_{\text{diff}} = \rho_{\text{doped - sheet}} - \rho_{\text{pristine - sheet}}$$
(1)

where \(\rho_{\text{doped - sheet}}\) and \(\rho_{\text{pristine - sheet}}\) denote the electron charge density of BN-doped and pristine graphyne sheets, respectively.

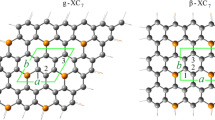
Two types of graphyne, namely α- and β-graphyne, are studied. The α-graphyne and β-graphyne sheets with 6 × 6 and 4 × 4 unit cells are considered (Fig. 1). The supercells of α- and β-graphyne sheets consist of 288 C atoms. The periodic boundary conditions are applied to the supercell. The sheets are separated by 20 Å to simulate an isolated graphyne sheet. It should be noted that we have calculated total energy to choose the size of the vacuum space. In Fig. 2, the total energy of α- and β-graphyne sheets as a function of the size of the vacuum space is shown. The minimum total energy is observed at the vacuum space of 20 Å. The BN nanodots with hexagonal shape and two different sizes are doped in the sheets. The sheets with BN nanodots are named Hn-(BN)m, where n is the number of BN hexagonal rings and m denotes the number of BN pairs doped in the graphyne sheets. For α-graphyne, two H1(BN)9 and H7(BN)42 structures are studied (Fig. 3). In the case of β-graphyne, two H1(BN)9 and H3(BN)27 structures are considered (Fig. 4).

Fig. 1
figure 1

Atomic structures of α- and β-graphyne sheets

Full size image
Fig. 2
figure 2

Total energy of a α- and b β-graphyne sheets versus size of vacuum space

Full size image
Fig. 3
figure 3

Atomic structures of H1-(BN)9 and H7-(BN)42 α-graphyne sheets

Full size image
Fig. 4
figure 4

Atomic structures of H1-(BN)9 and H3-(BN)27 β-graphyne sheets

Full size image

To discuss the stability of each structure, the cohesive energy is calculated. The cohesive energy per atom, Ecoh, is defined as the difference between the energy of the structure and sum of the energies of the isolated atoms [28,29,30,31]. The cohesive energy of pristine graphyne sheets is defined as:

$$E_{\text{coh}} = \frac{{E_{\text{pristine - sheet}} - n_{\text{C}} E_{C} }}{{n_{\text{C}} }}$$
(2)

For BN-doped graphyne sheets, it is given by:

$$E_{\text{coh}} = \frac{{E_{\text{doped - sheet}} - (n_{\text{C}} E_{\text{C}} + n_{\text{N}} E_{\text{N}} + n_{\text{B}} E_{B} )}}{{n_{\text{C}} + n_{\text{N}} + n_{\text{B}} }}$$
(3)

where \(E_{\text{pristine - sheet}}\) and \(E_{\text{doped - sheet}}\) are total energies of pristine and BN-doped graphyne sheets, respectively.\(E_{\text{C}}\), \(E_{\text{N}}\), and \(E_{\text{B}}\) denote energies of C, N, and B atoms, respectively. \(n_{\text{C}}\), \(n_{\text{N}}\), and \(n_{\text{B}}\) are the number of C, N, and B atoms present in the sheets, respectively.

Results and discussions

The atomic structures of pristine α- and β-graphyne sheets are shown in Fig. 1. The graphyne sheets consist of both sp- and sp2-hybridized C atoms. The C–C bond between two sp-hybridized C atoms is named t (Fig. 1). The C–C bond between sp2- and sp-hybridized C atoms is labeled by s1, and the C–C bond between two sp2-hybridized C atoms is shown by s2 (Fig. 1). In α-graphyne, the single C–C (s1) and triple C–C (t) bonds are 1.39 and 1.23 Å, respectively. For β-graphyne, the triple C–C (t) bond is 1.23 Å, and the single C–C (s1 and s2) bonds are 1.34 and 1.46 Å, respectively. These values are in good agreement with those reported in previous studies [5, 32]. Our calculated cohesive energies for α- and β-graphyne sheets are − 4.87 and − 5.84 eV/atom, respectively. Hence, β-graphyne with more negative cohesive energy is more stable than α-graphyne. It is in good agreement with previous results that report the cohesive energy of graphyne decreases systematically as the ratio of sp-bonded carbon atoms increases [32].

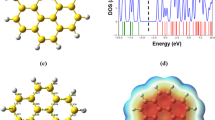
The charge density difference diagram for pristine α- and β-graphyne sheets is illustrated in Fig. 5. Here, charge density isosurface value of 0.012 e/Å3 is chosen for the given diagrams. Electron loss and gain are represented by cyan and yellow color isosurfaces, respectively. It is observed that electron accumulation is mainly located within the C bonds, while electron depletion occurs around C atoms. It means that the C–C bonds in pristine graphyne are covalent in nature.

Fig. 5
figure 5

Top view of charge density difference for pristine α- and β-graphyne sheets. (The yellow and cyan regions show the gain and loss of electron, respectively)

Full size image

To study the electronic properties of α- and β-graphyne sheets, their electronic band structures and DOS are calculated. As expected, the conduction and valence bands meet in a single point at the Fermi level (Fig. 6). The DOS is zero at the Fermi level. (The Fermi level is set at 0 eV.) These results mean α- and β-graphyne sheets have semimetallic properties as reported in the previous studies [4, 5, 8, 9].

Fig. 6
figure 6

Electronic band structures and DOS of a α- and b β-graphyne sheets

Full size image

The atomic structures of H1-(BN)9 and H7-(BN)42 α-graphyne sheets are shown in Fig. 3. When BN nanodots are embedded in the α-graphyne sheet, the B–C and N–C bonds are 1.51 and 1.34 Å, respectively. In both H1-(BN)9 and H7-(BN)42 α-graphyne sheets, the N–C bond lengths are shorter than the corresponding C–C bond of the pristine α-graphyne sheet (1.39 Å), while B–C bond lengths are found to be longer. It is in close agreement with the previous reported results [14, 32]. This is due to the fact that the higher electronegativity of N atoms attracts strongly the electron density compared with B atoms [14, 33]. The B–N (t) and B–N (s1) bonds are 1.27 and 1.40 Å, respectively. The cohesive energies of H1-(BN)9 and H7-(BN)42 α-graphyne sheets are calculated to understand the energetic stability of the sheets. The cohesive energies of H1-(BN)9 and H7-(BN)42 α-graphyne sheets are − 4.95 and − 5.25 eV/atom, respectively. The negative cohesive energies denote that BN doping in α-graphyne sheet is an exothermic process, and H1-(BN)9 and H7-(BN)42 α-graphyne sheets can be produced experimentally. Here, H7-(BN)42 with more negative cohesive energy is energetically more stable than H1-(BN)9.

For β-graphyne sheet, two structures named H1-(BN)9 and H3-(BN)27 are studied (Fig. 4). In the presence of BN nanodots, the B–C (s1), N–C (s1), B–N (t), and B–N (s1) bonds are 1.33, 1.54, 1.27, and 1.40 Å, respectively. Similar to α-graphyne, B–C (N–C) bond is longer (shorter) than the corresponding C–C bonds. This is due to the difference between atomic radius of B, C, and N atoms which follows trend of B < C < N. The cohesive energies of H1-(BN)9 and H3-(BN)27 β-graphyne sheets are − 5.26 and − 5.40 eV/atom, respectively. The negative cohesive energies indicate that BN doping in β-graphene is an exothermic process and the considered structures are energetically stable. It is also found that H3-(BN)27 is energetically more stable than H1-(BN)9.

As an example, the charge density difference diagrams for H7-(BN)42 α-graphyne and H3-(BN)27 β-graphyne sheets are shown in Fig. 7. A negative electron cloud around N atom resides as depicted by yellow isosurface, while electron deficiency takes place near B atom as depicted by cyan isosurface. The results of Mulliken charge analysis also support this finding. It is found that charge is transferred from B to N atom due to electronegativity difference of B and N atoms. It means N atoms gain and B atoms loss electrons. Thus, the B–N bond has some ionic character, while C–C bonds are covalent in BN-doped graphyne sheets. The presence of BN is also modified slightly the charge distribution near the C atoms adjacent to N and B atoms. The Mulliken charge analysis shows 0.70 and 0.14 e are transferred to N atom from B and adjacent C atoms; 0.06 e is moved from B atom to adjacent C atom.

Fig. 7
figure 7

Top view of charge density difference for H7-(BN)42 α-graphyne and H3-(BN)27 β-graphyne sheets. (The yellow and cyan regions show the gain and loss of electron, respectively)

Full size image

The electronic band structures and DOS of H1-(BN)9 and H7-(BN)42 α-graphyne sheets are also shown in Fig. 8. It is found that the electronic band structure of α-graphyne is effectively modulated by BN doping. The results show that H1-(BN)9 and H7-(BN)42 α-graphyne sheets are semiconductors with direct band gaps of 0.12 eV and 0.31 eV at the Γ point, respectively. It means that BN nanodots can effectively open a band gap in pristine α-graphyne.

Fig. 8
figure 8

Electronic band structures and DOS of a H1-(BN)9 and b H7-(BN)42 α-graphyne sheets

Full size image

The electronic band structures and DOS of H1-(BN)9 and H3-(BN)27 β-graphyne sheets are shown in Fig. 9. As seen, small band gaps of 0.02 eV and 0.05 eV are opened in H1-(BN)9 and H3-(BN)27 β-graphyne sheets, respectively. The opened band gap and consequently the changes in the electronic properties of β-graphyne sheet in the presence of BN nanodots are not considerable.

Fig. 9
figure 9

Electronic band structures and DOS of a H1-(BN)9 and b H3-(BN)27 β-graphyne sheets

Full size image

The atomic structures of α-graphyne- and β-graphyne-like BN sheets are illustrated in Fig. 10. In α-graphyne-like BN sheet and in β-graphyne-like BN sheet, the B–N bonds in the hexagons (s2) and at the middle of the chain (t) are found to be 1.41 and 1.27 Å, respectively. The B–N (s1) bond with B atom at hexagon and N atom at chain is 1.39 Å, while the B–N (s1) bond between N atom at hexagon and B atom at linear chain is 1.40 Å. This difference is due to the different neighboring environments of B and N atoms [32]. The cohesive energies of these BN graphyne sheets are − 6.23 and − 6.45 eV/atom. Hence, β-graphyne-like BN sheet is more favorable than α-graphyne-like BN sheet.

Fig. 10
figure 10

Atomic structures of α- and β-graphyne-like BN sheets

Full size image

In Fig. 11, charge density difference diagrams for α-graphyne- and β-graphyne-like BN sheets are shown. Here, B atoms loss electron and N atoms gain electron. The Mulliken charge analysis shows there are 0.71 e per BN pair transferring from B to N atoms. This is in good agreement with previous studies and confirms that the interaction between B and N atoms is ionic [36].

Fig. 11
figure 11

Top view of charge density difference for α- and β-graphyne-like BN sheets. (The yellow and cyan regions show the gain and loss of electron, respectively)

Full size image

Calculations of the electronic band structures and DOS of α-graphyne- and β-graphyne-like BN sheets (Fig. 12) show that these sheets are insulators with energy wide band gaps of 3.81 and 3.78 eV, respectively. The band gap of BN systems is attributed to the strong iconicity of B–N bonds [34,35,36].

Fig. 12
figure 12

Electronic band structures and DOS of a α- and b β-graphyne-like BN sheets

Full size image

Conclusions

It has been previously showed that α- and β-graphyne sheets have semimetallic properties. Here, the electronic properties of α- and β-graphyne sheets doped with hexagonal BN nanodots are investigated by using density functional theory calculations. For comparison, the electronic properties of graphyne-like BN sheets are also studied. The thermal stability of these sheets was confirmed by calculation of the cohesive energy. The negative cohesive energies confirm that the considered structures are thermodynamically stable. The stability of these systems is in the order of BN β-graphyne > BN α-graphyne > H3-(BN)27 β-graphyne > H1-(BN)9 β-graphyne > H7-(BN)42 α-graphyne > H1-(BN)9 α-graphyne > β-graphyne > α-graphyne. The results indicate that β-graphyne sheets are more stable than the α-graphyne sheets. In addition, the stability increases with the increase in the size of BN nanodots. To find the effect of BN nanodots on the electronic properties of the sheets, the electronic band structure and DOS of the sheets are calculated. As expected, α- and β-graphyne sheets show semimetallic behavior, while α- and β-graphyne-like BN sheets are insulator. The results reveal that BN nanodots could lead to a change in electron properties of α- and β-graphyne sheets. The BN nanodots open a band gap, and α- and β-graphyne sheets show semiconducting properties in the presence of the BN nanodots. In the studied sheets, increasing the size of the BN nanodots increases the energy band gaps. Hence, BN doping in α- and β-graphyne sheets could be utilized to open and control the band gap in graphyne sheets. Our results suggest that α- and β-graphyne sheets with BN nanodots are more proper than pristine α- and β-graphyne sheets and α- and β-graphyne-like BN sheets for use in nanoelectronic devices due to their semiconducting properties.