Abstract
A method for enhancing the resistance against corrosion of stainless steel 304L coated with 190 nm-thick manganese film and annealed with nitrogen flux at constant temperature (723 K) is reported. The variable quantity in this work is the temperature of the corroding solution (293 K and 333 K). X-ray diffraction analysis was employed to investigate the crystallographical changes of the annealed samples; atomic force microscope and scanning electron microscope were used for the morphology and studying the roughness of their surfaces; polarization analysis, electrochemical impedance spectroscopy, and phase and Bode diagrams, as well as the Kramers–Kronig transformation, were employed to study the susceptibility of the samples to corrosion, at temperatures 293 K and 333 K in 0.4 M H2SO4 solutions. Our results, from all the above analyses, unanimously point to the fact that in the process of enhancing resistance to corrosion, the annealing stage is the most crucial for improving the coating and the crystal structure of the samples and that the adsorption of Mn is not sufficient for the enhancement of the surface layer. Moreover, it was observed that increasing the temperature of the solution decreases the resistance of the samples owing to an increase in the rate of corrosion.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
There are several types of widely used stainless steel with different chemical compositions including austenitic, ferritic, martensitic, duplex, and precipitation-hardened stainless steel [1]. Austenitic stainless steels (with face-centered cubic structure) have been extensively employed in many industries such as food, pharmaceutical, and chemical industries due to their excellent corrosion resistance and good mechanical properties [2, 3]. The stability of the austenite phase at low temperatures is achieved with the addition of nickel. They can be divided into three groups: common chromium-nickel (300 series), manganese-chromium-nickel-nitrogen (200 series), and specialty alloys. The most widely used austenitic stainless steel is type 304 and 304L. The composition of the 304 stainless steel (also known as “18-8” stainless steel) includes 18 percent chromium and 8 percent nickel [4]. Type 304L stainless steel has lower carbon content (about 0.03%) than the 304 steel alloy (about 0.08%) which leads to decrease in deleterious or harmful carbide precipitation as a result of welding. It is well-known that a passive film formed from a mixture of iron and chromium oxides/hydroxide on the electrolyte/electrode interface leads to decrease in the electrode corrosion rate in corrosive media [5]. However, some techniques such as using from corrosion inhibitors [6,7,8,9,10], alloying elements [11,12,13], and organic [14,15,16] or inorganic [17,18,19,20] coatings have been proposed by many researchers to enhance the corrosion resistance in corrosive solutions.
Organic/inorganic coatings can decrease the rate of substrate metal corrosion by three basic protective mechanisms: (1) barrier protection, (2) inhibitive effect in active coatings, and (3) sacrificial protection by galvanic effect [21]. The barrier coatings postpone the corrosion process by acting as a barrier to penetration of water, oxygen, and corrosive ions from the environment. Although the high concentrations of Mn in the matrix of stainless steels may lead to increase in the susceptibility to localized corrosion due to the formation of MnS impurities on the passive layer [22, 23], Mn-based coatings can effectively improve the corrosion resistance of the steel substrate by the barrier and sacrificial mechanisms.
Grayeli-Korpi et al. [24] studied the effect of Mn coating and subsequent annealing with a flow of nitrogen on the corrosion behavior of stainless steel-type AISI 304 in 0.6 M NaCl solution. Their results showed that the Mn-nitride coating improved the corrosion resistance of the stainless steel substrate in the saline solution by forming an effective barrier between the substrate and the corroding medium. In another research, Savaloni et al. [25] investigated the corrosion resistance of AISI 316L-type stainless steel coated with a Mn-oxide coating with 300 nm thickness in 0.3, 0.5, and 0.6 M NaCl solutions. Their results showed that the corrosion resistance of coated samples in different saline solutions is improved relative to the bare samples. Münz et al. [26] reported an improvement in the anti-corrosion properties of Zn/Mn multilayer coatings and resulted that the formation of Zn–Mn and γ-Mn2O3 components suppressed oxygen reduction at the cathode, slowing the corrosion process. In another work by Wiman et al. [27], the effect of the current types (AC, DC, or AC + DC) on the phase structure, surface morphology, and anti-corrosion properties of electrodeposited Mn–Co coatings on AISI 430 was investigated. Their results indicated that the (MnxCo1−x)3O4 coating exhibited the protective effect against oxidation of the steel. However, to the best of our knowledge, there is no report on the use of Mn-based coating on the corrosion inhibition of 304L-type stainless steel in H2SO4 solution at the time of submission of this manuscript.
The influence of nitrogen dissolved in different types of stainless steel on the corrosion resistance of the systems in corrosive aqueous solutions is reported by few researchers. Lei et al. [28] reported that the thickness of passive film produced on a nitrogen-treated austenite stainless steel was significantly more than that of original stainless steel. Levey et al. [29] showed that nitrogen reduces the galvanic effects between the ferrite and austenite phases, hence reduces the general corrosion rate. Feng et al. [30] investigated the effect of nitrogen content on the corrosion behavior of martensitic stainless steel and showed that the nitrogen atoms can improve the corrosion resistance of the stainless steel by conversion of the main precipitates from M23C6 to M2N. Loable et al. [31] showed that there is a synergetic effect between molybdenum and nitrogen on the localized corrosion resistance of austenitic stainless in different pHs. Their electrochemical results proved that the potential of passive film breakdown increased upon the addition of nitrogen.
In this study, the effect of a 190 nm Mn-nitrogen layer on the corrosion protection performance of the 304L stainless steel is studied in 0.4 M H2SO4 solution at different temperatures (293 K and 333 K). X-ray diffraction (XRD), atomic force microscope (AFM) and scanning electron microscope tests are employed to analyze the crystallographic structure and surface roughness of the coated samples, respectively. Electrochemical measurements (polarization and impedance spectroscopy) were conducted to investigate the corrosion behavior of the bare and Mn-nitrogen-coated 304L stainless steel in 0.4 M H2SO4.
The results of EIS and polarization measurements showed a possible corrosion inhibition enhancement factor (η% = 98%) and a corrosion inhibition efficiency factor (PE%=97%), respectively, in the best sample. The surface morphology of the samples was measured using atomic force microscopy (AFM), while X-ray diffraction (XRD) study of the samples provided the crystal structure. Kramers–Kronig transformation analysis of the results confirmed the EIS data [24, 25].
Experimental conditions
Samples of (21 mm × 21 mm × 1 mm) stainless steel 304L were acquired to be used as the substrate. X-ray fluorescence (XRF) analysis was then used to determine the chemical composition of stainless steel 304L samples. The carbon content of which was determined by the CS-2000 device, Table 1.
In order to protect the sample surfaces from oxidation and mechanical damage, they were originally covered with a polyethylene foil which was carefully removed by immersing the samples in ethanol for several days. All the substrates were then treated ultrasonically in heated acetone (CH3COCH3) and heated ethanol (C2H5OH), for 15 min or more until the substrates were thoroughly cleaned, respectively. The deposition of Mn (97.99% purity) on 304L-type stainless steel substrates was performed using an electron gun at room temperature. Schematic diagram of the deposition operation is shown in Fig. 1.
The deposition operation was implemented using the (in-vacuum) vaporizing device (Model E19A3Edwards, England). The deposition rate was measured by the quartz crystal controller (Sigma Instruments, SQM-160, USA) which was situated near the substrate. In this deposition operation, the values obtained for pressure, thickness, and growth rate are presented in Table 2.
The annealing operation, on the samples Mn/SS304L, was carried out with a 300 sccm flow of nitrogen gas (99.999% purity) using a horizontal tube furnace (Exciton, 1200-30/6, T.H, Iran equipped with a Shinko temperature programmable controller PCD 33A) at a constant temperature (723 K).The annealing process was carried out in three stages: First, the samples were heated to a temperature of 723 K for 2 h. Then they were, together with the nitrogen flux, kept at this temperature for 6 h. Finally, they were allowed to cool down for 10–12 h until they reached room temperature. Figure 2 depicts the process of cooling of the sample as a function of time.
Temperature is the important quantity in this process, for it is at temperatures above 700 K that austenitic stainless steel samples decompose along grain boundaries and the carbon content of the steel reacts with chromium to form chromium carbide, thus decreasing the chromium content near the boundaries and increasing the likelihood of grain boundary corrosions. This process is referred to as the “sensitization of stainless steel.”
Each sample was studied and measured grain sizes were measured using crystallography—XRD analysis (X-Ray Diffractometer with STADI MP—STOE)—with Cukα source and step size of 0.02° and count time of 1.0 s per step. Also, AFM analysis (NT-MDT Scanning Probe Microscope, TS 150) and SEM (FEI NOVA NanoSEM450) were employed to investigate surface morphology and roughness of each sample.
EIS measurements were performed with a potentiostat coupled to a PC (Ivium, De Zaale 11, 5612 AJ Eindhoven, Netherlands) with reference to the open circuit potential (OCP) in the frequency range of 100 kHz to 0.01 Hz with a voltage amplitude of 10 mV. These measurements were performed on 1 cm2 surface area of the samples. The reference electrode in this analysis was an Ag/AgCl (saturated KCl, + 0.197 V vs. standard hydrogen electrode potential) electrode, while the auxiliary electrode was a Pt electrode. The test sample was used as the working electrode and was mounted in a polyamide (inert) fixture to enable the attachment of an electrical contact to the sample without undesirable effects. Prior to the EIS test, samples were immersed in the 0.4 M H2SO4 (corroding medium), and the OCP measurement was performed until it stabilized and continued to be stable for at least 50 min. Measurements were carried out at the desired temperatures (293 K and 333 K) and having achieved equilibrium at each of these temperatures, the main part of the experiment was performed. Throughout the polarization analysis and electrochemical impedance spectroscopy, the temperature of the corroding medium was kept constant. EIS data were fitted by equivalent electric circuits using ZView version 3.1 c software.
In order to apply the polarization potential to the sample, a copper wire was contacted to the back side of the sample which was mounted in the polyamide fixture. In this measurement setup, an Ag/AgCl electrode and a Pt electrode were also used as the reference and the counter electrodes. The potential was swept with a rate of 1 mV s−1 to cover a range of about 3 V (− 1.5 V to + 1.5 V) for each sample, starting from − 1.5 V versus OCP. In order to ascertain the validity of the results, the electrochemical tests of all samples were repeated three times.
The corrosion current density, icorr, and the corrosion potential, Ecorr, were calculated from the Stern–Geary equation: i = icorr[exp{ba(x − Ecorr)} − exp{bc(x − Ecorr)}] and fitting the polarization curve for each sample to the anodic and cathodic branches separately, using MATLAB, hence determining the rate of corrosion and the resistance to corrosion for each sample.
Results and inferences
AFM analysis
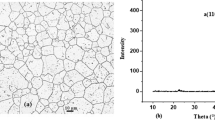
As shown in Fig. 3, surface morphology was conducted on 1 μm2 of each sample. The values obtained for grain size (DAFM), average surface roughness (Rave), and root-mean-square surface roughness (Rrms) of samples SS304L, Mn/SS304L, and MnNx/SS304L are presented in Table 3. Based on these experimental results, it can be inferred that in the deposition process, the average roughness of the surface and the grain sizes increase, whereas in the annealing process with nitrogen, the average roughness of the surface increases due to the increase in the solubility of nitrogen in the manganese coating, but the grain sizes decrease owing to the fact that at certain points in the annealing stage, the nitrogen flux can cause grain fracture, thus decreasing the grain size [32].
XRD analysis
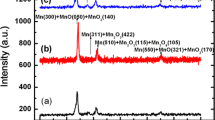
XRD diagrams of the samples, (a) SS304L, (b) Mn/SS304L, and (c) MnNx/SS304L, are illustrated in Fig. 4. Results from XRD analysis are presented separately in Table 4, in accord with the standard cards JCPDS.
The results for SS304L are the following peaks at angles 44.426°, 51.581°, 75.477°, and 91.432°, corresponding to γ-Fe(111), γ-Fe(200), γ-Fe(220), and γ-Fe(311), respectively, in accord with the JCPDS card (00-003-0397).
For the Mn/SS304L, the following peaks are observed: Mn(330) at angle 42.923° in accord with the JCPDS card (00-003-0992), MnO2(140) at angle 43.710° in accord with the JCPDS card (00-007-0222), Mn(222) at angle 50.722° in accord with the JCPDS card (00-003-1014-), MnO(222) at angle 74.690° in accord with the JCPDS card (00-003-1145), and Mn3O4 (433) at angle 90.788° in accord with the JCPDS card (00-016-0154).
The XRD pattern of MnNx/SS304L sample shows the following peaks: Mn3O4(103) at angle 32.263° in accord with the JCPDS card (00-016-0154), Mn3N2(105) at angle 43.424° in accord with the JCPDS card (01-081-0300), Mn(222) at angle 50.722° in accord with the JCPDS card (00-003-1014), Mn2N at angle 74.679° in accord with the JCPDS card (00-003-1163), and Mn3O4(433) at angle 90.717° in accord with the JCPDS card (00-016-0154). In the annealing process, the increase in the width of the peak of Mn(222) and the formation of Mn3O4(103) cause the Mn(222) peak intensity to reduce relative to its value before annealing.
FESEM analysis
Figure 5 shows the surface and cross-section images of the Mn/SS304L sample before annealing process. On the surface of this sample (large-scale image), some lined cracks can be seen, while finer valleys (cracks) also are visible on the small-scale image (inset). The cross section of this sample was prepared by careful scratching of the surface and seeking for undamaged parts as shown in Fig. 5b. The tapered (fine columns) can be observed on the wall of cross section (inset of Fig. 5b).
The FESEM images of the samples after corrosion test are given in Fig. 6. The un-annealed sample (Mn/SS304L) shows large cracks at grain boundaries which can be the result of possible defects in these sites. Hence, corrosion started from these defects and grew along the grain boundary. In addition, it can be seen that the surface of grains are showing hillocks pattern which can be as result of corrosion at the porous structure of the deposited film (referring to the tapered structure in Fig. 5). This can be seen on the inset image in Fig. 6a. When the sample annealed at 723 K and examined in 293 K, corroding medium, (MnNx293/SS304L) (Fig. 6b) almost no cracks (or cracks with much narrower width relative to the un-annealed sample (Fig. 6a), can be observed on the surface of the sample after corrosion test, while more uniform surface is also formed, hence showing improved corrosion inhibition. At 333 K corroding medium temperature (MnNx(333)/SS304L) (Fig. 6c), the cracks are again started to form and uniformity of the surface is decreased. The results obtained from the FESEM analysis are consistent with those obtained from electrochemical analysis discussed in the following sections.
The energy dispersive spectroscopy (EDS) spectrum of Mn/SS304L sample as a typical result is given in Fig. 7 and Table 5. This figure and the table clearly show the high intensity peaks for Mn and oxygen which confirm the formation of Mn-oxide result discussed in the XRD section (Fig. 4 and Table 4).
Polarization analysis
The polarization curves of the samples produced in this work and immersed in 0.4 M H2SO4 solution at different temperatures have been studied. Irregularities in the corrosion process may be attributed to the formation of oxide layers (such as manganese oxide), or certain reactions causing the generation of double layers, or such effects as might temporarily slow down the corrosion process [33].
As shown in Fig. 8, in the polarization curve of SS304L sample, there exist a passive potential EP = − 0.250 V and a passive current density iP = − 0.500 mA cm−2 which upon the application of an anodic polarization of − 0.08 V switches to the trans-passive regime and the surface of the layer becomes unstable. In Mn/SS304L, the layer’s passive potential and the trans-passive potential are 0.810 V and 1.342 V, respectively. Thus, comparing the passive intervals of the two samples, it is seen that the principal surface layer becomes more corrosion resistant after Mn is deposited on the substrate. The low resistance of this sample may be caused by the inhomogeneities and the absence of bonding at the boundary between the porous and the compressed layers. The heating operation gives rise to a passive layer potential range of 0.08–0.463 V for the MnNx(293)/SS304L, while the corresponding range for MnNx(333)/SS304L is negligible. The rise in temperature of the (ambient) corrosive solution has a marked impact on the cathodic reaction; it clearly increases the cathodic currents. Temperature is also directly correlated with corrosive reactions, increasing anodic disintegrations, since the intensity of anodic currents, too, increases at higher temperatures [34, 35]. The cathodic branch of MnNx(293)/SS304L is in a lower current density in comparison with other samples. Given the direct correlation between the current density and the rate of corrosion, it can be concluded that this sample has a lesser rate of corrosion and is accordingly more resistant to it.
Increasing the corrosion inhibitors, namely Mn, in the first stage and nitrogen, in the second stage, dramatically increase the resistive properties of the samples against corrosion, implying that nitrogen has formed a strong bonding with the Mn/SS304L substrate resulting in the enhancement of the samples after annealing. The contents of the solution, too, can play a major role in the interdependence of corrosion potential and the corrosion current density.
The Stern–Geary equation, i = icorr[exp{ba(E−Ecorr)} − exp{bc(E−Ecorr)}] was applied on the anodic and cathodic branches of the polarization curve of each sample [36].
The known quantities are E and i which are determined in each branch according to the fit interval. The other quantities, Ecorr, icorr, ba, and bc, are obtained from the best fitted curve. The evident similarity between curves for different coated samples can be attributed to the oxide nature of the coatings, but the discrepancy in the trial parameters, such as corrosion current density (icorr), corrosion potential (Ecorr), and anodic and cathodic Tafel slopes (ba, bc) may be due to differences in surface morphology and phase structure of the coatings.
Our methodology is as follows: First the value of Ecorr is deduced from the polarization curve for each sample. Then, using MATLAB, for the anodic branch, the interval from (Ecorr − 10 V) to (Ecorr + 50 V) and, for the cathodic branch, the interval from (Ecorr + 10 V) to (Ecorr − 50 V) was selected. Next, the resistance to corrosion efficiency (PE%) is calculated from anodic and cathodic branches using anodic and cathodic current densities in Eq. 1:
where \(i_{\text{corr}}^{0}\) is the corrosion current density (anodic or cathodic) for the substrate (stainless steel 304L) and \(i_{\text{corr}}^{\text{c}}\) is the corrosion current density (anodic or cathodic) for the coated samples.
Fits to the data of the polarization curves of the samples and the calculated values thereof, with the resistance to corrosion efficiency for each sample (as presented in Tables 6 and 7), for anodic and cathodic branches in the 0.4 M H2SO4 solution at different temperatures, are shown in Fig. 9.
In anodic and cathodic branches, the least current density, and greatest resistance to corrosion efficiency (PE%), is that of MnNx(293)/SS304L. Higher temperatures create holes and gaps on the surface and increase the grain boundaries. However, the corrosion resistance efficiency at higher temperatures is higher than in the state when the sample is not annealed. Therefore, annealing of the sample is the stage that increases the resistance of the sample, and one can conclude that the highest state of resistance to corrosion for the annealed sample occurs when the temperature of the corrosive solution is not raised.
EIS analysis
Electrochemical impedance spectroscopy is one of the standard means by which corrosion is studied. In this technique, a periodic potential with a small amplitude of a few mV is applied, over a wide spectrum of frequencies, in addition to a constant DC potential, and the system’s impedance and the phase angle of the impedance are examined. Electrical impedance is a measure of the resistance to a sinusoidally periodic current.
In an EIS analysis, the impedance, Z, and the phase angle between the impedance and the applied potential are determined as a function of the applied frequency. In general, impedance has two components: the real part which stems from the resistors in the circuit and can only affect the amplitude of the periodic wave; and an imaginary part due to capacitors and inductors present in the circuit. The imaginary part of impedance affects not only the amplitude but also the phase of the periodic wave.
EIS consists of the application of small time-varying potentials (with frequencies from 0.01 Hz to 100 kHz) around Ecorr (the corrosion potential), measurement of the net circuit current (i.e., the difference between the total currents due to oxidation and those due to reduction) Iex, determination of the system’s impedance, Z, and finally, the impedance phase, δ.
An electrochemical cell is modeled as an equivalent electric circuit each part of which is associated with a physical, chemical, or electrochemical process occurring in the cell. Capacitance corresponds to ions and polarized molecules in the electrolyte.
Hence, having applied time-varying potentials and generating an initial current, after a steady state is reached, no more currents are generated. The equivalent circuit is expressed in terms of the area of the working electrode. Impedance at maximum frequency indicates the resistance, RS, of the solution because if the sinusoidal frequency in the circuit is too large, the capacitor charges and discharges so fast that it acts as a short circuit; therefore, current flows through the branch associated with the capacitor and effectively sees no charge carrier resistance. Thus, the only resistance to the flow of current is that of the corrosive solution. Impedance at the lowest frequencies represents the sum of resistances of both the solution and the moving charges and since the resistance of the solution is very much less than that of the coating; this total resistance can be attributed to the coating alone, because provided the frequency is very small, the capacitor in the electrochemical circuit charges up fully within the very first microsecond and practically stops the current flow in its branch so that the current will flow through the solution resistor and the “charge transfer” resistor, in series, and therefore the two simply add up. Thus, the greater the diameter of the semicircle in the Nyquist plot, the greater the resistance to corrosion of the sample [21, 37].
The impedance graph in the complex plane (i.e., its imaginary part versus the real part) is exactly semicircular. However, most empirical impedance semicircles (obtained from experimental data) are “squeezed” semicircles which do not lend themselves to equivalent RC circuit description. In such cases, one usually invokes the constant phase element (CPE) technique. This electric object’s impedance with constant phase is defined according to Eq. 2.
where ω (in units of rad s−1) is the angular frequency, Y0 is the CPE admittance, j is the imaginary unit (square root of 1), and n is (in each case) a constant number having a value between − 1 to + 1, depending on the surface roughness. The numerical values 1, 0.5, 0, and − 1 for n correspond to pure resistance behavior, Warburg element behavior, pure capacitance behavior, and pure inductance behavior, respectively. Y0 and Cdl are related according to [38]:
where ωmax is the angular frequency at which the imaginary part of impedance is maximum.
The corrosion protection efficiency, η, in electrochemical impedance spectroscopy (EIS) is obtained from Eq. (4), where RP and RP(film) represent the charge transfer resistance before and after adding the inhibitors to the corrosive ambience:
Porosity, P, of the sample may be calculated from:
where RPS is the sample’s polarization resistance without the coating, RP is the coated sample’s polarization resistance, ∆Ecorr is the corrosion potential difference of the sample when it is coated and when it is not coated, and ba is the Tafel slope of the anodic branch for the uncoated sample. The impedance spectrum was modeled, using ZView, as a circuit comprising a resistor, a capacitor, and an inductor.
At low frequency, the impedance spectrum for the sample Mn/SS304L has an inductive loop and for SS304L, MnNx(293)/SS304L and MnNx(333)/SS304L, and it has a capacitive loops.
The sample MnNx(293)/SS304L in the 0.4 M sulfuric acid solution has the greatest resistance to corrosion but this resistance is greatly reduced at high temperatures, as shown in Fig. 10.
Figure 11 shows the equivalent circuit corresponding to SS304L, MnNx(293)/SS304L, and MnNx(333)/SS304L in the H2SO4 solution, with a single time constant. Here, there is only one contact between the sample and the solution, that is, the electrolyte is either in contact with the coating or with the metal. The time constant is interpreted as a type of relaxation time of the points near the surface. These may be the absorbed metal ions, dissolved metal sites, crystal lattice defects, or holes generated on the surface.
In this circuit, RS is the corrosive solution’s resistance; Cdl is the capacitance of the double layer (the solution–substrate interface); and Rct is the charge transfer resistance at the solution–substrate interface.
Figure 12 shows the equivalent circuit corresponding to Mn(293)/SS304L, comprising a time constant and an inductor. When an electrode is placed in an electrolyte, its surface is severely corroded and the absorption and re-absorption of the corrosion debris on the surface generate an effective inductance. Thus, corroded manganese ions enter the solution as manganese cations and the surface of the electrode becomes negatively charged.
Thence, the manganese ions become attracted to the metal surface and neutralize the latter’s negative charge, while the manganese ions themselves become neutral atoms again, and this process creates the inductive loop in the circuit. At low frequency, the Nyquist plot for Mn(293)/SS304L turns out to be a negative inductive loop corresponding to an inductor element L and an inductive resistance RL. Thus, this inductive loop may be attributed to metal dissolving reactions, formation of Mn(OH)2 (which is the product of manganese corrosion in sulfuric acid), and the absorption of the electrolyte’s ionic species.
These processes lead to local corrosion of the surface holes type. The impedance spectrum of each sample in the sulfuric acid solution may include several inductive loops where each inductive loop represents the substance adsorbed on the surface.
In this circuit, RS is the solution’s resistance; L is the inductive element; RL is the inductor’s resistance; Cdl is the capacitance of the double layer (the solution–substrate interface); and Rct is the charge transfer resistance at the solution–substrate interface. Cdl is employed, in lieu of the ideal capacitor, to treat the “depressing” of the capacitive loop. This phenomenon is usually related to the inhomogeneities (roughness, cracks, and pores) of the coating surface. When the sample is immersed in the corrosive solution, the defects in the coating provide paths of infiltration for the solution into the sample [39, 40].
High surface porosity and holes with relatively large diameters generate ways of infiltration of the electrolyte into the substrate’s metallic surface. Therefore, the less porous the surface, the higher its resistance to corrosion.
Thus, with the values obtained for the quantities in Table 8, minimum Cdl (a measure of surface porosity); minimum amount of porosity, P; maximum resistance (to corrosion) efficiency, η (%); and maximum resistance to corrosion, are those corresponding to MnNx(293)/SS304L. Raising the temperature, increases the rate of chemical reactions on the sample’s surface, thus raising the porosity of the sample and reducing the resistance and resistance efficiency.
Bode and phase diagrams
One of the essential parameters in the Bode diagram is that of the capacitive region and the resistive region. The resistance of a capacitor is a function of frequency. Therefore, the impedance versus frequency curve cannot be horizontal. However, the impedance of a resistor is not a function of frequency; it remains constant at all frequencies and so its curve is a horizontal line. The time constant for each such curve can be determined from the number of peaks of the graph of phase angle versus frequency [40, 41].
In general, the time “constant” at high frequency will be related to the resistive behavior of the defects (holes, pores) in the coating. At low frequency, the time constant is indicative of the behavior of the intersecting layers, while intermediate frequencies concern the inter-layers resistance. In fact, as we approach the 90° angle, we increasingly observe capacitor-like behavior and as the angle approaches 0°, the behavior becomes resistor-like. The decrease in the intensity peak of the phase diagram compared with other diagrams may be due to charge transfer and lesser absorption of water during immersion which would cause the system to deviate from capacitive behavior and tend, rather, to the resistive [42,43,44].
Figure 13 shows the analysis of the Bode diagram (for evaluating the resistance of each sample) and of the phase diagram (for evaluating the number of peaks) in the 0.4 M H2SO4 solution at different temperatures (Table 9).
It is to be noted that the resistance deduced from the results of the Bode diagram and that deduced from the Nyquist curve are entirely consistent. The Bode diagram too shows the sample MnNx(293)/SS304L to have the greatest resistance. Since at low frequency, the Bode diagram has not yet reached the resistive state, it differs from the Nyquist curve as regards the resistance of the samples.
Kramers–Kronig transformations
The impedance technique is frequently used in electrochemical systems in order to study the various aspects of corrosion in that system. However, before embarking upon the analysis and modeling the results of the experiments on this basis, it is necessary to ascertain the validity of the impedance data. A common mathematical procedure for achieving this goal was introduced by Kramers and Kronig [45, 46].
Thus, the calculated impedance values are acceptable if they satisfy the following fourfold conditions:Linearity if the impedance obtained does not change with half the applied AC signal amplitude, the system is considered to be linear. Causality the response of the system must be completely determined by the applied disturbance potential. Stability this is determined by the response of the system to its inputs. Finiteness the values of real and imaginary parts of impedance must be finite at all frequencies (0 < ω < ∞).In general, Eqs. 6 and 7 are used in the Kramers–Kronig transformation for calculating the real and imaginary parts of the empirical electrochemical impedance [47,48,49,50].
As is evident from Fig. 14, in both “real to imaginary” and “imaginary to real” parts, in 0.4 M H2SO4 solution at different temperatures, Kramers–Kronig fits on the Nyquist curve for each sample confirm the real value obtained for the impedance, and it is clearly seen that the obtained values in the given frequency range are real.
Summary and conclusion
In brief, it is observed that surface morphology changes with the type of coating employed. The Nyquist curves for coatings on the sample Mn(293)/SS304L, one semicircle in the frequency range 0.01 Hz–100 kHz indicate that corrosion of manganese nitride coatings involves a single time constant. Having studied the extent of corrosion at different temperatures of the solution, we infer that porosity is directly correlated with temperature, while resistance to corrosion decreases with it. Hence we conclude, according to the analyses carried out, that deposition of manganese on the surface of stainless steel SS304L does not significantly change the resistance of the layer. Therefore, pure manganese must not be considered suitable for the purpose of enhancing the surface and the resistance of stainless steel. However, since the resistance of the sample’s surface to corrosion in a 0.4 M H2SO4 solution at room temperature was substantially increased after being annealed in nitrogen flux, one may conclude that annealing must be regarded as a highly significant stage in the process. Grain boundaries are regions where the surface of the sample has pores, holes, and fractures; therefore, decreasing grain boundaries will help increase surface stability and inhibit the infiltration of electrolytes into the surface.
References
Lo, K.H., Shek, C.H., Lai, J.K.L.: Recent developments in stainless steels. Mater. Sci. Eng. 65, 39–104 (2009)
Davison, R.M., Laurin, T.R., Redmond, J.D., Watanabe, H., Semchyshen, M.: A review of worldwide developments in stainless steels. Mater. Des. 7, 111–119 (1986)
Saravanan, M., Devaraju, A., Venkateshwaran, N., Krishnakumari, A., Saarvesh, J.: A review on recent progress in coatings on AISI austenitic stainless steel. Mater. Today Proc. 5, 14392–14396 (2018)
Pardo, A., Merino, M.C., Coy, A.E., Viejo, F., Arrabal, R., Matykina, E.: Pitting corrosion behaviour of austenitic stainless steels: combining effects of Mn and Mo additions. Corros. Sci. 50, 1796–1806 (2008)
Marcus, P., Olefjord, I.: A round robin on combined electrochemical and AES/ESCA characterization of the passive films on Fe–Cr and Fe–Cr–Mo alloys. Corros. Sci. 28, 589–602 (1988)
Loto, R.T., Loto, C.A., Popoola, P.A., Fedotova, T.: Inhibition effect of N, Nʹ-dimethylaminoethanol on the pitting corrosion austenitic stainless steel type 304. Medziagotyra 21, 1–5 (2015)
Javidparvar, A.A., Naderi, R., Ramezanzadeh, B.: Designing a potent anti-corrosion system based on graphene oxide nanosheets non-covalently modified with cerium/benzimidazole for selective delivery of corrosion inhibitors on steel in NaCl media. J. Mol. Liq. 284, 415–430 (2019)
Javidparvar, A.A., Naderi, R., Ramezanzadeh, B., Bahlakeh, G.: Graphene oxide as a pH-sensitive carrier for targeted delivery of eco-friendly corrosion inhibitors in chloride solution: experimental and theoretical investigations. J. Ind. Eng. Chem. 72, 196–213 (2019)
Refaey, S.A., Taha, F., Abd El-Malak, A.: Inhibition of stainless steel pitting corrosion in acidic medium by 2-mercaptobenzoxazole. Appl. Surf. Sci. 236, 175–185 (2004)
Ait Albrimi, Y., Ait Addi, A., Douch, J., Souto, R.M., Hamdani, M.: Inhibition of the pitting corrosion of 304 stainless steel in 0.5 M hydrochloric acid solution by heptamolybdate ions. Corros. Sci. 90, 522–528 (2015)
Kamachi Mudali, U., Shankar, P., Ningshen, S., Dayal, R.K., Khatak, H.S., Raj, B.: On the pitting corrosion resistance of nitrogen alloyed cold worked austenitic stainless steels. Corros. Sci. 44, 2183–2198 (2002)
Ha, H.-Y., Lee, T.-H., Bae, J.-H., Chun, D., Ha, H.-Y., Lee, T.-H., et al.: Molybdenum effects on pitting corrosion resistance of FeCrMnMoNC austenitic stainless steels. Metals 8, 653 (2018)
Pardo, A., Merino, M.C., Coy, A.E., Viejo, F., Arrabal, R., Matykina, E.: Effect of Mo and Mn additions on the corrosion behaviour of AISI 304 and 316 stainless steels in H2SO4. Corros. Sci. 50, 780–794 (2008)
Mondal, J., Marandi, M., Kozlova, J., Merisalu, M., Niilisk, A., Sammelselg, V.: Protection and functionalizing of stainless steel surface by graphene oxide-polypyrrole composite coating. J. Chem. Chem. Eng. 8, 786–793 (2014)
Javidparvar, A.A., Naderi, R., Ramezanzadeh, B.: Epoxy-polyamide nanocomposite coating with graphene oxide as cerium nanocontainer generating effective dual active/barrier corrosion protection. Compos. B Eng. 172, 363–375 (2019)
Javidparvar, A.A., Ramezanzadeh, B., Ghasemi, E.: The effect of surface morphology and treatment of Fe3O4 nanoparticles on the corrosion resistance of epoxy coating. J. Taiwan Inst. Chem. Eng. 61, 356–366 (2015)
Wang, Y., Northwood, D.O.: An investigation into TiN-coated 316L stainless steel as a bipolar plate material for PEM fuel cells. J. Power Sourc. 165, 293–298 (2007)
Mondal, J., Marques, A., Aarik, L., Kozlova, J., Sammelselg, V.: Development of a thin ceramic-graphene nanolaminate coating for corrosion protection of stainless steel. Corros. Sci. 105, 161–169 (2015)
Krishna, D.S.R., Sun, Y.: Thermally oxidised rutile-TiO2 coating on stainless steel for tribological properties and corrosion resistance enhancement. Appl. Surf. Sci. 252, 1107–1116 (2005)
Doodman, P., Faghihi-Sani, M.A., Barati, N., Afshar, A.: Alumina nanostructured coating for corrosion protection of 316L stainless steel. Int. J. Nano Dimens. 5, 27–33 (2014)
Sørensen, P.A., Kiil, S., Dam-Johansen, K., Weinell, C.E.: Anticorrosive coatings: a review. J. Coat. Technol. Res. 6, 135–176 (2009)
Park, K.J., Kwon, H.S.: Effects of Mn on the localized corrosion behavior of Fe–18Cr alloys. Electrochimica Acta. 55, 3421–3427 (2010)
Merello, R., Botana, F.J., Botella, J., Matres, M.V., Marcos, M.: Influence of chemical composition on the pitting corrosion resistance of non-standard low-Ni high-Mn–N duplex stainless steels. Corros. Sci. 45, 909–921 (2003)
Grayeli-Korpi, A.R., Savaloni, H., Habibi, M.: Corrosion inhibition of stainless steel type AISI 304 by Mn coating and subsequent annealing with flow of nitrogen at different temperatures. Appl. Surf. Sci. 276, 269–275 (2013)
Savaloni, H., Agha-Taheri, E., Abdi, F.: On the corrosion resistance of AISI 316L-type stainless steel coated with manganese and annealed with flow of oxygen. J. Theor. Appl. Phys. 10, 149–156 (2016)
Münz, R., Wolf, G., Guzman, L., Adami, M.: Zinc/manganese multilayer coatings for corrosion protection. Thin Solid Films 459, 297–302 (2004)
Wiman, P., Thublaor, T., Witthayarungruengsri, O.: Fabrication of (Mnx Co1−x)3O4 Coated Stainless Steel AISI 430 by Electrodeposition with AC + DC Signals, vol. 728, pp. 117–122. Trans Tech Publications, Stafa-Zurich (2017)
Lei, M.K., Zhu, X.M.: Role of Nitrogen in Pitting Corrosion Resistance of a High-Nitrogen Face-Centered-Cubic Phase Formed on Austenitic Stainless Steel. J. Electrochem. Soc. 152, B291 (2005)
Levey, P.R., van Bennekom, A.: A mechanistic study of the effects of nitrogen on the corrosion properties of stainless steels. Corrosion 51, 911–921 (2010)
Feng, H., Jiang, Z., Li, H., Lu, P., Zhang, S., Zhu, H., et al.: Influence of nitrogen on corrosion behaviour of high nitrogen martensitic stainless steels manufactured by pressurized metallurgy. Corros. Sci. 144, 288–300 (2018)
Loable, C., Viçosa, I.N., Mesquita, T.J., Mantel, M., Nogueira, R.P., Berthomé, G., et al.: Synergy between molybdenum and nitrogen on the pitting corrosion and passive film resistance of austenitic stainless steels as a pH-dependent effect. Mater. Chem. Phys. 186, 237–245 (2017)
Khojier, K., Savaloni, H., Sadeghi, Z.: A comparative investigation on growth, nanostructure and electrical properties of copper oxide thin films as a function of annealing conditions. J. Theor. Appl. Phys. 8, 116 (2014)
Ballote, L.D., Ramanauskas, R., Bartolo-p, P.: Μn oxide film as corrosion inhibitor of Zn–Mn coatings. Corros. Rev. 18, 41–52 (2000)
Blasco-Tamarit, E., Igual-Muñoz, A., García, Antón J., García-García, D.: Effect of temperature on the corrosion resistance and pitting behaviour of Alloy 31 in LiBr solutions. Corros. Sci. 50, 1848–1857 (2008)
Escrivà-Cerdána, C., Blasco-Tamarita, E., García-Garcíaa, D.M., García-Antón, J., Guenbourb, A.: Temperature effect on the austenitic stainless steel UNS N08031 used in the wet method phosphoric acid production. Chem. Eng. Trans. 32, 1717–1722 (2013)
Rahmouni, K., Keddam, M., Srhiri, A., Takenouti, H.: Corrosion of copper in 3% NaCl solution polluted by sulphide ions. Corros. Sci. 47, 3249–3266 (2005)
Macdonald, J.R.: Impedance spectroscopy. Ann. Biomed. Eng. 20, 289–305 (1992)
Poorqasemi, E., Abootalebi, O., Peikari, M., Haqdar, F.: Investigating accuracy of the Tafel extrapolation method in HCl solutions. Corros. Sci. 51, 1043–1054 (2009)
Balaraju, J.N., Narayanan, T.S.N.S., Seshadri, S.K.: Evaluation of the corrosion resistance of electroless Ni-P and Ni-P composite coatings by electrochemical impedance spectroscopy. Solid State Electrochem. 5, 334–338 (2001)
Narayanan, T.S.N.S., Baskaran, I., Krishnaveni, K., Parthiban, S.: Deposition of electroless Ni-P graded coatings and evaluation of their corrosion resistance. Surf. Coat. Technol. 200, 3438–3445 (2006)
Mahdavian, M., Attar, M.M.: Another approach in analysis of paint coatings with EIS measurement: phase angle at high frequencies. Corros. Sci. 48, 4152–4157 (2006)
Yoganandan, G., Premkumar, K.P., Balaraju, J.: Evaluation of corrosion resistance and self-healing behavior of zirconium–cerium conversion coating developed on AA2024 alloy. Surf. Coat. Technol. 270, 249–258 (2015)
Gao, H., Li, Q., Dai, Y., Luo, F., Zhang, H.X.: High efficiency corrosion inhibitor 8-hydroxyquinoline and its synergistic effect with sodium dodecylbenzenesulphonate on AZ91D magnesium alloy. Corros. Sci. 52(5), 1603–1609 (2010)
Palomino, L.E.M., Aoki, I.V., de Melo, H.G.: Microstructural and electrochemical characterization of Ce conversion layers formed on Al alloy 2024-T3 covered with Cu-rich smut. Electrochim. Acta 51(26), 5943–5953 (2006)
Abdeli, M., Parvini Ahmadi, N., Azari Khosroshahi, R.: Influence of bis-(2-benzothiazolyl)-disulfide on corrosion inhibition of mild steel in hydrochloric acid media. J. Solid State Electrochem. 15, 1867–1873 (2011)
Hassanzadeh, A.: Validity of dynamic electrochemical impedance spectra of some amine corrosion inhibitors in petroleum/water corrosive mixtures by Kramers–Kronig transformation. Corros. Sci. 49, 1895–1906 (2007)
Popkirov, G., Schindler, R.N.: A new approach to the problem of “good” and “bad” impedance data in electrochemical impedance spectroscopy. Electrochimica Acta 39, 2025–2030 (1994)
Achatz, G., Herzog, G.W., Plot, W.H.: Kramers–Kronig transformation of double-layer capacitances. Surf. Technol. 11, 431–441 (1980)
Allen, J., Bard, L.R.F.: Electrochemical Methods, Fundamentals and Applications. Wiley, New York (2001)
Zhang, J., Monteiro, P.J.M.: Validation of resistivity spectra from reinforced concrete corrosion by Kramers–Kronig transformations. Cem. Concr. Res. 31, 603–607 (2001)
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Modiri, F., Savaloni, H. A study of the corrosion of stainless steel 304L coated with a 190 nm-thick manganese layer and annealed with nitrogen flux in a 0.4-mole solution of H2SO4 at different temperatures. J Theor Appl Phys 14, 21–35 (2020). https://doi.org/10.1007/s40094-019-00345-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40094-019-00345-5