Introduction

Recently, with the development of nanofabrication technology, plasmonics and optical metamaterials, which enable control over light at both the micro- and nanometer scale beyond the limits of conventional optics, have been attracting considerable attention [1, 2]. An enhanced effective nonlinear optical response could be attained through plasmonic effects. The surface plasmons (SPs) as collective excitations of the electron density control the high-frequency electromagnetic response of materials because of their affect on intrinsic dielectric and refractive properties, along with screening and amplifying external fields at surface boundaries.

Since nonlinear effects produce a lot of novel phenomena, such as optical bistability (OB), second-harmonic generation (SHG), optical rectification, absorption coefficient and refractive index in different low-dimensional nanomaterials, these surprising phenomena can be applied to control light with light. For this purpose, plenty of experimental and theoretical works have been undertaken, leading to the improvement of models and methods approving to link nanostructure and nonlinear optical response [3,4,5]. For instance, OB means using a control beam to induce a nonlinear change in the dielectric properties of the materials; therefore, adjusting the plasmonic resonances and the propagation of a signal beam would happen [6].

Besides, Kerr nonlinearity as one of the most important nonlinear phenomena begins to happen from the fact that the permittivity and refractive index of the structure depend on intensity [7]. The plasmonic nanostructures can help to enhance nonlinear effects; such structures afford field enhancement near the metal–dielectric interface, related to the localized surface plasmons (LSPs) excitations or surface plasmon polaritons (SPPs) excitations [7]. The local electric field enhancement in core–shell nanoparticles has an important role in diverse applications such as nonlinear optical effects [8], optical sensors [9] and quantum optomechanics [10].

The impact of plasmonic nanostructures in all-optical switching, or to achieve highly tunable photonic properties, based on enhancing Kerr-type nonlinearities has been comprehensively studied [11,12,13,14,15,16,17,18].

On the other hand, it has been found that the localized plasmon resonance peak magnitude and its spectral position are strongly dependent on the size, shape, orientation, optical permittivity and interparticle spacing of the nanoparticles as well as on their local environment and the surrounding dispersion medium [19, 20]. In spherical metal nanoparticles, the resonance magnitude tuning is weak and the redshift of plasmon resonance generally depends on the local dielectric environment [19]. Mostly, the plasmon resonance shift does not have high sensitivity to the dielectric environment fluctuations. However, nonspherical nanoparticles exhibit new possibilities for plasmon resonance frequency tuning [21, 22]. Plasmon resonances in nanoshells of prolate and oblate spheroidal shape have been investigated and showed that both longitudinal and transverse resonances are a function of aspect ratio and shell thickness [23]. Although the LSPRs of spherical nanoshells are studied comprehensively, spheroidal nanoshells have received less attention [22, 24]. Experimentally, spheroidal particles consisting of a dielectric core and a gold shell have been synthesized, a nanostructure known as the nanorice [25]. It has been proved that ellipsoidal geometry has better tunability, larger local field enhancement and greater LSPR sensitivity than other dielectric–metal nanostructures [25]. Nowadays, numerous technologies for nanorods and nanospheroids synthesis are investigated [26, 27].

On the other hand, modifying LSPs with a magnetic field gives rise to new techniques for designing active plasmonic apparatuses. By an adequate internal architecture of the constituting components, the magneto-optical activity of these systems can be greatly increased due to the electromagnetic field enhancement associated with the plasmon resonance [28]. Generally, in the presence of an applied external magnetic field, propagation constants of the magneto-optical (MO) materials would be different for circularly polarized waves with right- and left-handed circular polarizations (RCP and LCP), respectively. This new feature can be applied as an external controlling parameter to improve nonlinearity in the plasmonic structures. The active magneto-plasmonic nanostructures may find their applications in optical switching [13, 18]. Magnetic particles (MPs) in the nanoscales open a new route in modern biomedical methods and therapies, which can be applied in a variety of biological sensing applications [29].

In the present study, field enhancement factor in core–shell ellipsoidal nanoparticles containing a MO shell in the quasistatic limit is investigated. Also, we calculate the conditions for the existence of the optical bistability in a coated ellipsoidal particle with a nonlinear magneto-optical shell. The significant role of the size and shape distributions of nanoparticle is also demonstrated. Our numerical results show stronger field enhancement and optical bistability in a nonlinear ellipsoid rather than spherical nanoparticles.

Theoretical model and methods

We assume that the uniform electrostatic field \(E_{i}\) is directed to a coated ellipsoidal nanoparticle with inner radius \(R_{\rm c}\) and outer radius \(R_{\rm s}\), embedded in the host medium with relative permittivity \(\varepsilon _{\rm h}\) as shown in Fig. 1. The most common smooth particle without edges- or corners-off regular shape is an ellipsoid. The dielectric constants of the core and shell are given as \(\varepsilon _{\rm c}\) and \(\varepsilon _{\rm s}\), respectively.

Fig. 1
figure 1

Schematic of the core–shell nanoellipsoid nanoparticle

Full size image

The dipole approximation is at the basis of many effective medium models, which can be applied when the NPs are much smaller than the wavelength of the light. In this small-size limit, it is usually claimed that a heterogeneous nanocomposite material can be studied as a homogeneous medium whose macroscopic optical response is explained by an effective dielectric tensor. It is assumed that in the MO medium, magnetization vector is parallel to the z-axis. Therefore, the permittivity tensor of the MO shell would be in the form of [13]

$$\begin{aligned} \overleftrightarrow {\varepsilon _s} = \begin{pmatrix} \varepsilon &{} ig&{}0 \\ -ig &{} \varepsilon &{}0\\ 0&{}0&{}\varepsilon \end{pmatrix} \end{aligned}$$
(1)

The off-diagonal component \(G= i \textit{g}\) is considered as the strength of MO activity of the media which depends on applied magnetic field \({\mathbf{B}} \), vanishing in its absence. Therefore, the optical anisotropy and the MO effect of such a material are purely induced by the external magnetic field. In the noble metal, the enhancement of the MO response due to LSPR effects can be attained.

The diagonal component \(\varepsilon \) is defined as the dielectric constant of the shell. In this manuscript, the Maxwell’s equations are linear in the field variables. However, nonlinearity and consequently bistability occur due to nonlinear coated NPs in which the shell is nonlinear with the field-dependent permittivity as \( \varepsilon = \varepsilon + \chi | E_{\rm s}|^{2}\) with the third-order nonlinear susceptibility \(\chi = 3 \times 10^{-9}\,{\text {esu}}\) [30].

In order to solve this interaction, we should use the geometrical factors to shift spherical particles into ellipsoid shape particle. This process in the case under consideration can be done by solving the electrostatic boundary problem for the two interfaces: core–shell and shell–environment. The electric field in the core, shell and environment regions is correspondingly denoted by \(E_{\rm s}\), \(E_{\rm c}\) and \(E_{\rm h}\).

$$\begin{aligned} \left\{ \begin{array}{ll} \vec {E}_{\rm c} ={\hat{A}}\vec {E_i} &{}r< R_{\rm c}\\ \vec {E}_{\rm s} = {\hat{B}} \vec {E_i} + \frac{3({\hat{C}}\vec {E_i}.\vec {n})\vec {n}}{r^{3}}-\frac{{\hat{C}}\vec {E_i}}{r^{3}} &{}R_{\rm c}<r<R_{\rm s}\\ \vec {E}_{\rm h} = \vec {E}_{i} - \frac{{\hat{D}} \vec {E}_{i}}{r^{3}}+ \frac{(3{\hat{D}}\vec {E_i}.\vec {n})\vec {n}}{r^{3}}&{}r >R_{\rm s} \end{array}\right. \end{aligned}$$
(2)

Here, \(\vec {n}\) is the unit vector of normal directed from nanoparticles into the external medium. We come to the boundary conditions for the first and second interfaces at \(r = R_{\rm c}\) and \(r = R_{\rm s}\) in the following form

$$\begin{aligned} {\hat{n}}\times (\vec {E_{\rm s}}-\vec {E_{\rm c}})|_{r=R_{\rm c}}=0 \nonumber \\ {\hat{n}}\times (\vec {E_{\rm h}}-\vec {E_{\rm s}})|_{r=R_{\rm s}}=0 \nonumber \\ {\hat{n}}.(\vec {D_{\rm s}}-\vec {D_{\rm c}})|_{r=R_{\rm c}}=0 \nonumber \\ {\hat{n}}.(\vec {D_{\rm h}}-\vec {D_{\rm s}})|_{r=R_{\rm s}}=0 \end{aligned}$$
(3)

The following coupled equations for a core–shell ellipsoid are achieved

$$\begin{aligned} \left\{ \begin{array}{ll} {\hat{A}}={\hat{B}} - \frac{{\hat{C}}}{R_{\rm c}^{3}}\\ {\hat{I}} - \frac{{\hat{D}}}{R_{2}^{3}}= {\hat{B}} - \frac{{\hat{C}}}{R_{\rm s}^{3}}\\ L\varepsilon _{\rm c}{\hat{A}}= \varepsilon \left[ L{\hat{B}} +(1-L) \frac{{\hat{C}}}{R_{\rm c}^{3}}\right] + {\hat{G}}\left[ L{\hat{B}} - (1-L)\frac{{\hat{C}}}{R_{\rm c}^{3}}\right] \\ \varepsilon _{\rm h}\left[ L +(1-L)\frac{{\hat{D}}}{R_{\rm s}^{3}}\right] = \varepsilon \left[ L{\hat{B}} +(1-L)\frac{{\hat{C}}}{R_{\rm s}^{3}}\right] \\ \quad +{\hat{G}}\left[ L{\hat{B}} - (1-L)\frac{{\hat{C}}}{R_{\rm s}^{3}}\right] \\ \end{array}\right. \end{aligned}$$
(4)

To check these results, we note that a sphere is a special ellipsoid with \(L=\frac{1}{3}\). We introduce a new definition what we called volume fraction

$$\begin{aligned} \frac{R_{\rm c}}{R_{\rm s}} = 1-P \end{aligned}$$
(5)

For the sake of simplicity in calculations, these parameters are introduced

$$\begin{aligned} \left\{ \begin{array}{ll} {\hat{M}} = L\varepsilon _{\rm c}{\hat{I}} - L\varepsilon {\hat{I}}- L{\hat{G}}\\ {\hat{N}} = L\varepsilon _{\rm c}{\hat{I}} + (1-L)\varepsilon {\hat{I}}-(1-L){\hat{G}}\\ {\hat{P}} = L\varepsilon {\hat{I}} + L{\hat{G}} +\varepsilon _{\rm h} (1-L){\hat{I}}\\ {\hat{Q}} = -(1-L)\varepsilon {\hat{I}}+(1-L){\hat{G}}+(1-L)\varepsilon _{\rm h}{\hat{I}} \end{array}\right. \end{aligned}$$
(6)

Consequently, the coefficients of the electrical field in Eq. (2) can be obtained as follows

$$\begin{aligned} \left\{ \begin{array}{ll} {\hat{C}} = \frac{\varepsilon _{\rm h}{\hat{M}}R_{\rm c}^{3}R_{2}^{3}}{{\hat{P}}{\hat{N}}R_{2}^{3}-{\hat{Q}}{\hat{M}}R_{\rm c}^{3}}\\ {\hat{B}} = \frac{\varepsilon _{\rm h}{\hat{N}}R_{\rm s}^{3}}{{\hat{P}}{\hat{N}}R_{\rm s}^{3}-{\hat{Q}}{\hat{M}}R_{\rm c}^{3}}\\ {\hat{A}} = \frac{\varepsilon _{\rm h}R_{\rm s}^{3}[\varepsilon {\hat{I}}+(2L-{\hat{I}}){\hat{G}}]}{{\hat{P}}{\hat{N}}R_{\rm s}^{3}-{\hat{Q}}{\hat{M}}R_{\rm c}^{3}}\\ \end{array}\right. \end{aligned}$$
(7)

The polarization of the incident field [right circular polarization (RCP) and left circular polarization (LCP)] is considered as \(E_{i}=E_{0}e^{ikz}(1, \pm i,0)^{T}\).

By solving the system of equations, the unknown coefficients are calculated

$$\begin{aligned} {\hat{A}} = \begin{pmatrix} a_{11}&{}ia_{12}&{}0\\ -ia_{12}&{}a_{11}&{}0\\ 0&{}0&{}a_{33} \end{pmatrix} \end{aligned}$$
(8)

and

$$\begin{aligned} {\hat{A}} = \varepsilon _{\rm h}R_{\rm s}^{3} \begin{pmatrix} \frac{\varepsilon a +gb(2L-1)}{a^{2}-b^{2}}&{} i\left( \frac{\varepsilon b +ga(2L-1)}{a^{2}-b^{2}}\right) &{}0\\ -i\left( \frac{\varepsilon b +ga(2L-1)}{a^{2}-b^{2}}\right) &{}\frac{\varepsilon a +gb(2L-1)}{a^{2}-b^{2}} &{}0\\ 0&{}0&{}\frac{\varepsilon }{c} \end{pmatrix} \end{aligned}$$
(9)

where

$$\begin{aligned}\left\{ \begin{array}{l} a = (L\varepsilon +(1-L)\varepsilon _{\rm h})(L\varepsilon _{\rm h} + (1-L)\varepsilon )R_{\rm s}^{3} \\ \qquad -\, R_{\rm c}^{3}(\varepsilon (L-1)+\varepsilon _{\rm h}(1-L))L(\varepsilon _{\rm c}-\varepsilon )\\ \qquad +\, g^{2}L(1-L)(R_{\rm c}^{3}-R_{\rm s}^{3}),\\ b = -ig(R_{\rm s}^{3}(1-L)(L\varepsilon +(1-L)\varepsilon _{\rm h})\\ \qquad -\, LR_{\rm s}^{3}(L\varepsilon _{\rm c} +(1-L)\varepsilon )\\ \qquad -\, R_{\rm c}^{3}L(\varepsilon (L-1) + \varepsilon _{\rm h}(1-L))\\ \qquad +\, R_{\rm c}^{3}L(1-L)(\varepsilon _{\rm c}-\varepsilon ),\\ c =R_{\rm s}^{3}(L\varepsilon +(1-L)\varepsilon _{\rm h})(L\varepsilon _{\rm c} +(1-L)\varepsilon )\\ \qquad -\, R_{\rm c}^{3}L(\varepsilon (L-1)+\varepsilon _{\rm h}(1-L))(\varepsilon _{\rm c}-\varepsilon ). \end{array}\right. \ \end{aligned}$$

Therefore, the average electrical field in the core is calculated as

$$\begin{aligned} | E_{\rm c}|^{2}=2\left[ | a_{11}|^{2}+| a_{12}|^{2} \pm (a_{11}a_{12}^*+a_{12}a_{11}^*)\right] | E_{i}|^{2} \end{aligned}$$
(10)

The dielectric function of a plasmonic noble metal is described by the Drude model and given by \(\varepsilon (\omega ) = \varepsilon _{\infty }- \frac{\omega _p^2}{\omega (\omega +i\gamma _{\rm F})}\), where \( \omega _{\rm p} \), \(\gamma _{\rm F}\) and \(\varepsilon _{\infty }\) are the plasma frequency of the metal, the collision frequency of free electrons and the high-frequency part of the dielectric function [31]. In this study gold is used for the core and the relevant parameters of gold and silver are as follows: \( \omega _{\rm p}^\mathrm{Au} = 8.9\,{\text {eV}} \), \(\epsilon _{\infty }^\mathrm{Au} = 6.9\), and \( \gamma _{\rm F}^\mathrm{Au} = 0.072\,{\text {eV}}\), \( \omega _{\rm p}^\mathrm{Ag} = 9.2\,{\text {eV}} \), \(\epsilon _{\infty }^\mathrm{Ag} = 3.7\), and \( \gamma _{\rm F}^\mathrm{Ag} = 0.02\,{\text {eV}},\) respectively.

Results and discussion

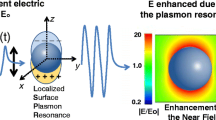
In this section, the field enhancement and OB behavior from the core–shell ellipsoidal nanoparticle are numerically investigated. As illustrated in Fig. 2, by increasing the volume fraction P, the field enhancement would be improved noticeably. As is well known, the metallic nanoshells evolution from spherical geometry to spheroidal geometry would improve field enhancement in various applications. Hence, the field enhancement depends largely on the aspect ratio of the outside dimensions of the shell particle. For higher P parameter, the volume fraction of magneto-optical shell is much more than that of the core. Consequently, we see better field enhancement. Interaction light with plasmons leads to large electromagnetic field enhancement. In the other words, the surface plasmon resonance could induce large local electromagnetic fields.

The most remarkable feature of these graphs is the presence of two peaks in the enhancement factor graph at two different frequencies. The positions and values of these maxima strongly depend on P. By increasing P, both maxima become higher and move closer to each other. It should be noted that another parameter that affects the enhancement factor in this nanostructure and causes the appearance of the second peak is nonlinearity of the metallic part of the nanoparticle [32].

Fig. 2
figure 2

Field enhancement factor for core–shell nanoparticle for different values of P, \(L = 0.37\), \(R_{\rm s} = 10\,{\text {nm}}\), \(g = (-1+ 0.15i)10^{-2}\), \(\varepsilon \) is for Au, \(\varepsilon _{\rm c}=2.25\), and \(\varepsilon _{\rm h}=1\)

Full size image

Figure 3 shows the effect of depolarization factor on the field enhancement. For spherical nanoparticles, the field enhancement is less than that for ellipsoidal nanoparticles under the same circumstances. This means that the enhancement factor increases for large depolarization factor; hence, the maximum enhancement factor is observed for prolate geometry which is four times more than that for spherical nanoparticle. It was shown that the enhanced optical properties originate from increased plasmon coupling between the inner and outer surface plasmons in the spheroidal nanoshell structure [33].

Fig. 3
figure 3

Enhancement factor for core–shell nanoparticle for different values of L, \(P = 0.6\), \(R_{\rm s} = 10\,{\text {nm}}\), \(\varepsilon \) is for Au, \(g = (-1+0.15i)10^{-2}\), \(\varepsilon _{\rm c}=2.25\), and \(\varepsilon _{\rm h}=1\)

Full size image

In Fig. 4 field enhancement for right circular polarization (RCP) and left circular polarization (LCP) of incident field is plotted. For these two different polarizations, frequency shifting does not happen. However, for LCP field enhancement is more than that for RCP.

Fig. 4
figure 4

Enhancement factor for core–shell nanoparticle for RCP and LCP of incident field, \(L = 0.37\), \(P = 0.6\), \(R_{\rm s} = 10\,{\text {nm}}\), \(\varepsilon \) is for Au, \(g = (-1+0.15i)10^{-2}\), \(\varepsilon _{\rm c}=2.25\), and \(\varepsilon _{\rm h}=1\)

Full size image
Fig. 5
figure 5

Enhancement factor for core–shell nanoparticle in the absence and presence of external magnetic field, \(L = 0.37\), \(P = 0.6\), \(R_{\rm s} = 10\,{\text {nm}}\), \(\varepsilon \) is for Au, \(g = (-1+0.15i)10^{-2}\), \(\varepsilon _{\rm c}=2.25\), and \(\varepsilon _{\rm h}=1\)

Full size image
Fig. 6
figure 6

Optical bistability curves \(|E_{\rm c}|\) as a function of the incident applied field \(|E_{0}|\) for a core–shell nanoparticle for different values of L, \(P = 0.6\), \(R_{\rm s} = 10\,{\text {nm}}\), \(\varepsilon \) is for Au, \(g = (-1+0.15i)10^{-2}\), \(\varepsilon _{\rm c}=2.25\), and \(\varepsilon _{\rm h}=1\)

Full size image
Fig. 7
figure 7

Optical bistability curves \(|E_{\rm c}|\) as a function of the incident applied field \(|E_{0}|\) for a core–shell nanoparticle for different values of P. \(L = 0.37\), \(R_{\rm s} = 10\,{\text {nm}}\), \(\varepsilon \) is for Au, \(g = (-1+0.15i)10^{-2}\), \(\varepsilon _{\rm c}=2.25\), and \(\varepsilon _{\rm h}=1\)

Full size image

Field enhancement for different values of g is investigated in Fig. 5. It can be easily seen that g could modify the surface conductivity and tunable surface plasmon resonance is achievable by adjusting the MO parameter of the shell as a consequence of external magnetic field.

For the comparison between the influences of depolarization factor on the OB of core–shell nanoparticles, the average local core field as a function of the applied electromagnetic field for different values of L is plotted in Fig. 6. It can be seen that under the same situation, the electromagnetic field does not show optical bistability in the small range of input field intensities for spherical core–shell nanoparticles, whereas, in ellipsoidal nanoparticles, OB is observed. Interestingly, OB behavior would be improved in the prolate geometry. By increasing L factor, the hysteresis loop of OB increases and one can see OB behavior for wider range of incident electromagnetic fields.

Figure 7 illustrates the impact of the parameter P on the OB response. When the shell is a MO plasmonic material, increasing P or the shell fraction leads to decreases in the threshold intensity obviously. It can be seen from the simulations that the position of the LSPR and consequently the nonlinearity for such core–shell NPs are effectively manipulated by the presence of the geometrical characteristics such as the thickness of the shell and the ratio between them.

It should be noted that in this manuscript, the Maxwell’s equations are treated as linear in the field variables. Therefore, we solved linear problems by definition. OB occurs then due to Kerr nonlinearity of the magneto-plasmonic shell. Since the small MNPs with size below 100 nm are the best candidate in in vivo biomedical imaging and drug delivery in order to ensure endocytosis in target organs and cells [34] and also coated MNPs with shell have a significant role in generating successful biomedical applications [35, 36], this model would offer a precise magneto-optics-based biological sensor.

Conclusion

In conclusion, field enhancement and OB behavior of an ellipsoidal magneto-optical core–shell nanoparticles is investigated theoretically. We demonstrated that the hysteresis responses strongly depend on parameters such as MO parameter and geometrical parameter of NP. In brief, they are the most important factors that restrict the further decrease in the switching intensities in OB. Due to considerable field enhancement, giant optical nonlinearities and tunable optical property, they could potentially open a new route for achieving all-optical switching, optical sensor and optical memory.