Abstract
Optical transfer function for add–drop resonator is derived in the presence of coupling loss using the scattering matrix method. A critical coupling condition for ADR is calculated. The response of the ADR under variation of coupling losses and coupling coefficients is studied. The number of allowed states under the critical condition is determined. The full width at half maximum as sharp as 0.17 nm is achieved. It is found that the relative phase shifts of through and drop ports show the same responses under the critical coupling condition. This response emerges in a butterfly-like phase shift, which can be considered as a new evaluating factor for checking the system in critical coupling condition.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Ring resonators have found versatile functionalities in optical switching [1, 2], optical filters, photonics sensors [3, 4] and optical communications [5, 6]. The superiorities of resonating systems rather than Fabry–Perot cavities, Bragg gratings and other integrated feedback waveguide devices are in automatic pumping system for the feedback process and the possibility of jointing several waveguides into the a ring. Resonators benefit from low photon loss rate and have ability to store energy in a microsized volume [7]. These features have made the ring resonators as multipurpose components for photonics and optoelectronics. Several methods have been used to check the quality and characteristics of output light from resonator systems. These methods include critical coupling condition, over coupling [8], multiple-stage ring resonator [9], parallel coupling [10], symmetric coupling [11] and asymmetric coupling [12]. The critical coupling condition in ring resonator has been a subject of interest due to its potential application in optical communication [13, 14] and photonics sensors [15]. The add–drop ring resonators have been used as an optical notch type filter in optical networks [16, 17]. Optical filters need to be tunable for using network system. Some parameters in ring resonators are effective factors in the quality of output signals. To evaluate the functionalities of resonator-based filters, the critical coupling condition and full width at half maximum (FWHM) are considered as the key parameters in checking the quality of output signals [18,19,20]. In this paper, a critical coupling condition of ADR system is determined by considering the coupling loss. The behavior of the silicon–ADR system is studied under the variation of coupling coefficients and coupling factors. A visual method for checking the quality of the output signals is introduced based on the relative phase shifts of through and drop ports from ADR filter. This proposed method is applicable in signal processing, optical filters and optical communication.
Theoretical background
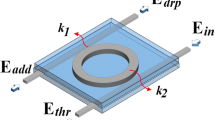
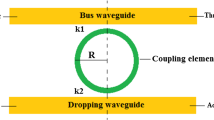
The input light undergoes some variations while passing through a resonator system. The light response versus spectrum can be investigated by the scattering matrix method [21, 22]. A layout of add–drop resonator (ADR) is illustrated in Fig. 1. Two light beams can simultaneously be coupled into the add–drop resonator via two couplers. Here, the ring waveguide manages the feedback mechanism. The wavelength selectivity is obtained based on the resonance condition inside the ring, \(mL = n_{\text{eff}} \lambda\) [23]; thus, only specific wavelengths can resonate inside the ring. A power coupling coefficient, k, is defined for each coupling region. A fraction of input light beam passing via direct path waveguide is shown by c (Fig. 1), which can be calculated by \(c_{1} = \sqrt {(1 - \gamma )(1 - k_{1} )}\) and \(c_{2} = \sqrt {(1 - \gamma )(1 - k_{2} )}\) for each coupler [24, 25]. A portion of input light crosses over the waveguides via evanescent fields. This evanescent portion can be calculated as \(is_{1} = \sqrt {(1 - \gamma )k_{1} }\) for the first coupler and \(is_{2} = \sqrt {(1 - \gamma )k_{2} }\) for the second coupler [26,27,28]. Based on the scattering matrix method, the relation between input and output signals in each coupler, k1 and k2, can be written by the following matrices:
and
where Ein and Eadd are input fields to the couplers and Eth and Edrop represent the output fields from couplers 1 and 2, respectively. As illustrated in Fig. 1, an input light with the electric field of Ein transmits across the waveguides and couples into the ring waveguide. A positive feedback emerges inside the ring, and the field E2 starts to build up. The pulse undergoes a phase shift of \(\xi = {\text{e}}^{ - \alpha L} {\text{e}}^{ - i\varphi }\) [29] via each round trip. Here, α is the waveguide loss, L is the ring’s circumference and \(\varphi = 2\pi Ln_{\text{eff}} /\lambda\) [30] denotes the phase delay inside the ring in which neff represents the effective index of the ring’s waveguide. The propagated light inside the ring’s waveguide undergoes a \(\xi^{{}}\) phase shift. Existing of m couplers within the perimeter of the ring can reduce this phase shift to \(\sqrt[m]{\xi }\). The following equations represent the relation between the fields traveling inside the ADR system:
According to Eqs. (1)–(4), the optical transfer function for the through and drop ports of add–drop resonators is calculated as:
The phase of the transmitted light at each coupler can be calculated by the argument of optical transfer function at that coupler [31]
and the normalized intensity for the through and drop ports of ADR can be calculated by
The full width at half maximum (FWHM) is an important parameter in determining the sharp signals. It shows the central section of the signal and has been used in determining the spectral band width of optical system [32]. For an ADR system, the FWHM is given by [33]
The critical coupling condition represents the situation that all of the input signals get coupled into the ring’s waveguide. In this case, the light transmission via through port reaches to zero value \(H_{\text{Thr}} (\varphi = 2m\pi ) = 0\). In contrast to the through port, almost all of the input light can be realized at the drop port \(E_{\text{in}} = E_{\text{drop}}\). The critical coupling condition can be calculated by considering the numerator of Eq. (5) equal to zero. For simplicity, we supposed that \(\xi \approx 1\) and the critical coupling coefficient (kc) for add–drop resonator in the presence of coupling loss is calculated to be
where k1 shows the value of coupling coefficient for the first coupler and γ1 and γ2 represent the coupling losses in each coupling region of the ADR system.
Results and discussion
The effect of equal coupling coefficients (k1 = k2) on FWHM of output signals from through and drop ports of ADR system is shown in Fig. 2. The results simulated for the ADR from silicon microring resonators with 1.5 μm radius and the group refractive index of 4.2 [34]. The intensity responses versus wavelength were simulated for equal coupling coefficients values less than 0.1 with reduction step of 0.02. The FWHM for 3 dB coupling coefficients of ADR (k1 = 0.5—black line) is added for comparison. It is observed that any decrease in the coupling coefficients leads to detection of sharper signals with narrower FWHM. Results of Fig. 2 reveal that decreasing the coupling coefficient from 0.1 to smaller values as small as 0.02 brings about the detection of signals with the FWHM from 2.1 to 0.4 nm, respectively. The free spectral range of 62.5 nm is achieved, which is concordant with reported experimental results in [34].
Based on Eq. (12) for lossless coupling areas, the critical coupling will be the same as symmetric coupling coefficients \(k_{1}^{{}} = k_{2} = 0.1\) and an increase in coupling loss will decrease the critical coupling to the values less than 0.1 (\(k_{2} < 0.1\)). Increasing the coupling loss with step size of 0.01 (\(0 \le \gamma \le 0.05\)) generates six allowed states for the ADR system with first coupling coefficient of \(k_{1} = 0.1\), three states admitted for \(k_{1} = 0.05\) and only one acceptable state available for \(k_{1} = 0.01\) as shown in Figs. 3, 4 and 5, respectively. The coupling coefficient is a number in range of \(0 \le k \le 1\) and shows the fraction of power divided between the waveguides. Here, based on Eq. (12) the states with positive values of critical coupling coefficients are considered as the allowed states. Some sets of critical coupling coefficients together with coupling losses were selected and are shown in Fig. 3a, b. Each set of critical coupling engenders unique signal with a specific intensity at the drop port. Since c1 and c2 become small values at critical coupling, the intensities at the through port, Eq. (9), are almost unchanged under the applied sets of critical coupling. However, all of these through port signals have almost the same FWHM as sharp as 2.1 nm.
Decreasing the value of the first coupling coefficient to \(k_{1} = 0.05\) brings about a reduction in the number of the allowed states to three states as shown in Fig. 4. All of these allowed states (at through and drop ports) have an equal FWHM as sharp as 0.96 nm. Based on the results of Figs. 4 and 5, set of equal coupling coefficients for lossless coupling provides a maximum cross talk. Here, increasing the loss in couplers leads to smaller values of critical coupling coefficients, which leads to advent of signals with a lower cross talk.
Based on the critical coupling condition, only one state will be allowed for a constant coupling coefficient of \(k_{1} = 0.01\) with the increment step size of 0.01 (\(0 \le \gamma \le 0.05\)). These allowed states, \((k_{1} ;k_{2} ;\gamma ) = (0.01;0.01;0)\), generate the FWHM as sharp as 0.17 nm as shown in Fig. 5. This achieved FWHM is exactly the same as the reported experimental data in [34]. Based on the simulated results in Figs. 3, 4 and 5, there exists a trade-off between coupling loss and coupling coefficient in each coupler. It means that the maximum intensity in resonant peaks belongs to lossless coupler and changing the coupling coefficient will change the FWHM of output signal. In order to achieve a signal with the same FWHM as that of from lossless case, the coupling loss and coupling coefficient should be balanced.
Relative phase shifts of through and drop ports for different coupling coefficients and coupling losses are demonstrated in Figs. 3c, 4c and 5c. Results show that relative phase shift in critical coupling condition is independent from optical parameters of couplers (coupling coefficients and coupling loss). The relative phase shifts of the through and drop ports can be considered as a new evaluating factor for checking the system on critical coupling condition. When an ADR system is in a critical coupling condition, the through and drop ports will have the butterfly-like relative phase shift as shown in parts c of Figs. 3, 4 and 5. The through gain shows the fraction of electric fields at the through port to the input port, while the drop gain is given by Edrop/Ein. The effect of critical coupling variations in the response of the through port gain versus drop port gain is shown in Figs. 3d, 4d and 5d. Based on the simulated results, the behavior of gains at the drop and through ports remains the same for lossless coupling. It seems that the coupling coefficient is not a determinative factor in the output gains of ADR. Change in coupling losses and coupling coefficients is quite effective in the through port gain. As shown in Figs. 3e, 4e and 5e, increasing the coupler loss can decrease the through port gain. This treat can be observed in intensity response on through port versus drop port, too. The transmission characteristics of light via through and drop ports of ADR are totally dependent on the critical condition parameters, especially coupler’s parameters. As shown in Fig. 3f, the 50 dB transmission at the through port of ADR corresponds to the 42 dB transmission at the drop port for k1 = 0.1, k2 = 0.1 with lossless coupling. An increase in coupler loss will reduce the drop port transmission to a value less than 25 dB. In this case, the through port transmission holds its 50 dB value. Changing the coupling coefficient to k1 = 0.05; k2 = 0.05 with \(\gamma = 0\) will change the through and drop ports transmissions to 45 and 39 dB, respectively. Here, increment of coupler loss solely effects on the drop port transmission.
Results of Figs. 3c, 4c and 5c reveal that the phase-shift responses at the through and drop ports follow a unique trend under the critical coupling condition. This butterfly-like shape remains its shape, provided that the ADR system’s parameters fulfill the critical coupling condition. This butterfly phase shift can be considered as a new gauge for quick inspection of ADR systems, which are in the critical coupling condition.
Conclusion
The behavior of light via add–drop ring resonator from silicon waveguide is studied. A critical coupling condition is calculated in the presence of coupling loss for coupling regions in ADR system. Some limited states with the same FWHM were determined based on the critical coupling condition. The critical coupling condition is quantified by butterfly-like relative phase shift. A pictorial method for checking the system under the critical condition was introduced based on the relative phase shifts of through and drop ports from filters. It provides an easy approach for checking the quality of the output signals for optical sensors and notch ring-based filters.
References
Nawi, I., Bahadoran, M., Ali, J., Yupapin, P.: A theoretical model of all-optical switching induced by a soliton pulse in nano-waveguide ring resonator. J. Phys. Conf. Ser. 431, 012029 (2013)
Stern, L., Zektzer, R., Mazurski, N., Levy, U.: Enhanced light-vapor interactions and all optical switching in a chip scale micro-ring resonator coupled with atomic vapor. Laser Photonics Rev. 10, 1016–1022 (2016)
Bahadoran, M., Noorden, A.F.A., Mohajer, F.S., Abd Mubin, M.H., Chaudhary, K., Jalil, M.A., Ali, J., Yupapin, P.: Detection of Salmonella bacterium in drinking water using microring resonator. Artif. Cells Nanomed. Biotechnol. 44, 315–321 (2016)
Wu, T., Liu, Y., Yu, Z., Peng, Y., Shu, C., Ye, H.: The sensing characteristics of plasmonic waveguide with a ring resonator. Opt. Express 22, 7669–7677 (2014)
Amiri, I.S., Alavi, S.E., Idrus, S., Afroozeh, A., Ali, J.: Soliton Generation by Ring Resonator for Optical Communication Application, vol. 11788. Nova Science Publishers, Hauppauge (2014)
Rafizadeh, D., Zhang, J., Hagness, S., Taflove, A., Stair, K., Ho, S., Tiberio, R.: Waveguide-coupled AlGaAs/GaAs microcavity ring and disk resonators with high finesse and 21.6-nm free spectral range. Opt. Lett. 22, 1244–1246 (1997)
Wang, X., Wang, P., Chen, C., Chen, J., Lu, Y., Ming, H., Zhan, Q.: Plasmonic racetrack resonator with high extinction ratio under critical coupling condition. J. Appl. Phys. 107, 124517 (2010)
Mansoor, R.D., Sasse, H., Al Asadi, M., Ison, S.J., Duffy, A.P.: Over coupled ring resonator-based add/drop filters. IEEE J. Quantum Electron. 50, 598–604 (2014)
Romero-García, S., Moscoso-Mártir, A., Müller, J., Shen, B., Merget, F., Witzens, J.: Wideband multi-stage CROW filters with relaxed fabrication tolerances. Opt. Express 26, 4723–4737 (2018)
Mansoor, R.D., Sasse, H., Al-Asadi, M., Ison, S.J., Duffy, A.P.: Estimation of the bandwidth of acceptable crosstalk of parallel coupled ring resonator add/drop filters. IEEE Trans. Electromagn. Compat. 57, 1005–1012 (2015)
Yupapin, P., Saeung, P., Li, C.: Characteristics of complementary ring-resonator add/drop filters modeling by using graphical approach. Opt. Commun. 272, 81–86 (2007)
Vorckel, A., Monster, M., Henschel, W., Bolivar, P.H., Kurz, H.: Asymmetrically coupled silicon-on-insulator microring resonators for compact add-drop multiplexers. IEEE Photonics Technol. Lett. 15, 921–923 (2003)
Yariv, A.: Universal relations for coupling of optical power between microresonators and dielectric waveguides. Electron. Lett. 36, 321–322 (2000)
Zhang, W., Serna, S., Le Roux, X., Vivien, L., Cassan, E.: Highly sensitive refractive index sensing by fast detuning the critical coupling condition of slot waveguide ring resonators. Opt. Lett. 41, 532–535 (2016)
Chandran, S., Gupta, R.K., Das, B.K.: Dispersion enhanced critically coupled ring resonator for wide range refractive index sensing. IEEE J. Sel. Top. Quantum Electron. 23, 424–432 (2017)
Palací, J., Villanueva, G.E., Galán, J.V., Martí, J., Vidal, B.: Single bandpass photonic microwave filter based on a notch ring resonator. IEEE Photonics Technol. Lett. 22, 1276–1278 (2010)
Absil, P., Hryniewicz, J., Little, B., Wilson, R., Joneckis, L., Ho, P.-T.: Compact microring notch filters. IEEE Photonics Technol. Lett. 12, 398–400 (2000)
Dey, S., Mandal, S.: Modeling and analysis of quadruple optical ring resonator performance as optical filter using Vernier principle. Opt. Commun. 285, 439–446 (2012)
Mandal, S., Dasgupta, K., Basak, T., Ghosh, S.: A generalized approach for modeling and analysis of ring-resonator performance as optical filter. Opt. Commun. 264, 97–104 (2006)
Bahadoran, M., Noorden, A.F.A., Chaudhary, K., Aziz, M.S., Ali, J., Yupapin, P.: Nano force sensing using symmetric double stage micro resonator. Measurement 58, 215–220 (2014)
Poon, J., Scheuer, J., Mookherjea, S., Paloczi, G., Huang, Y., Yariv, A.: Matrix analysis of microring coupled-resonator optical waveguides. Opt. Express 12, 90–103 (2004)
Bahadoran, M., Noorden, A.F.A., Chaudhary, K., Mohajer, F.S., Aziz, M.S., Hashim, S., Ali, J., Yupapin, P.: Modeling and analysis of a microresonating biosensor for detection of Salmonella bacteria in human blood. Sensors 14, 12885–12899 (2014)
Bahadoran, M., Aziz, M., Noorden, A., Jalil, M., Ali, J., Yupapin, P.: Novel approach to determine the young’s modulus in silicon-on-insulator waveguide using microring resonator. Digest J. Nanomater. Biostruct. 9, 1095–1104 (2014)
Bahadoran, M., Ali, J., Yupapin, P.P.: Ultrafast all-optical switching using signal flow graph for PANDA resonator. Appl. Opt. 52, 2866–2873 (2013)
Bahadoran, M., Afroozeh, A., Ali, J., Yupapin, P.P.: Slow light generation using microring resonators for optical buffer application. Opt. Eng. 51, 044601-1–044601-8 (2012)
Bahadoran, M., Ali, J., Yupapin, P.P.: Graphical approach for nonlinear optical switching by PANDA vernier filter. IEEE Photonics Technol. Lett. 25, 1470–1473 (2013)
Aziz, M., Daud, S., Bahadoran, M., Ali, J., Yupapin, P.P.: Light pulse in a modified add-drop optical filter for optical tweezers generation. J. Nonlinear Opt. Phys. Mater. 21, 1250047 (2012)
Noorden, A.F.A., Chaudhary, K., Bahadoran, M., Aziz, M.S., Jalil, M.A., Tiong, O.C., Ali, J., Yupapin, P.: Rabi oscillation generation in the microring resonator system with double-series ring resonators. Optoelectron. Lett. 11, 342–347 (2015)
Rabus, D.G.: Ring resonators: theory and modeling. In: Integrated Ring Resonators: The Compendium, pp. 1–15. Springer, Berlin (2007).
Noordena, A.F.A., Bahadorana, M., Chaudharya, K., Aziza, M.S., Jalilb, M.A., Alia, J., Yupapin, P.: Optical bistability in all-pass Mobius configuration microring resonator. J. Teknol. 76, 101–108 (2015)
Heebner, J.E., Wong, V., Schweinsberg, A., Boyd, R.W., Jackson, D.J.: Optical transmission characteristics of fiber ring resonators. IEEE J. Quantum Electron. 40, 726–730 (2004)
Herbert Gross, B.D., Muller, H.: Handbook of Optical Systems, vol. 5. Wiley, London (2012)
Vorckel, A., Monster, M., Henschel, W., Bolivar, P.H., Kurz, H.: Asymmetrically coupled silicon-on-insulator microring resonators for compact add-drop multiplexers. IEEE Photonics Technol. Lett. 15, 921–923 (2003)
Xu, Q., Fattal, D., Beausoleil, R.G.: Silicon microring resonators with 1.5-μm radius. Opt. Express 16, 4309–4315 (2008)
Acknowledgements
We would like to acknowledge for the research facilities of Ton Duc Thang University, Vietnam, through GUP Tier 2 Project (15J57).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Bahadoran, M., Yupapin, P. Butterfly-like phase shift: a novel gauge for critical coupling of add–drop resonator. J Theor Appl Phys 12, 127–134 (2018). https://doi.org/10.1007/s40094-018-0291-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40094-018-0291-2