Abstract
Construction of the reduced spin and helicity density matrix for systems of two and three particles are described by a wave packet with sharp and Gaussian momentum distribution. The entropy for the spin and helicity part of the systems is calculated from the viewpoint of moving observers.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Special relativity effects on quantum entanglement and quantum information are investigated by many authors. Considerable efforts have also been expanded on the theoretical investigation of quantum information theory in relativistic framework, which has gone beyond from photons to electrons, and from explicit examples calculated in some specific cases to general framework formulated in relativistic quantum mechanics and even relativistic quantum field theory [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31]. In practice, Lorentz transformations in some special cases can change the entanglement of the spin and helicity of massive particles. Since the helicity has an advantage in providing a smooth transition to the massless case, it is the helicity rather than spin that is more often under both theoretical consideration and experimental detection in high energy physics. We know the helicity states and the spin states can be the basis of Hilbert space, they differ in the way of unitary transformation under the action of Lorentz group. As a result, the entanglement properties for helicity differs from spin after we trace out the momentum degree of freedom. Thus, for both theoretical completeness and possible implementation in high energy physics, it is intriguing and significant to investigate quantum entanglement between helicity and momentum in relativistic framework.
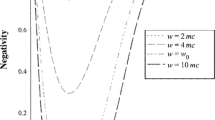
One of the early works in this area has considered a massive spin 1/2 field and by calculating reduced spin and helicity density matrix. It is shown that the resultant helicity entropy is different from spin in general [32]. According to [32], the helicity and spin entropy for one particle are \(S^{(h)}_{1}=0.4917\) and \(S^{(s)}_{1}=1,\) respectively. This paper is an effort for studying some special features of two and three particles, spin and helicity entanglement in inertial frames. We consider a quantum system of two and three massive spin 1/2 particles that is observed by inertial observers. The state of system for helicity state is supposed to have an appropriate sharp momentum distribution and for spin state the momentum distribution is supposed to be Gaussian. We use the entropy as a measure for the helicity entanglement as viewed in the boosted frame because the entropy is one of the most important measure for entanglement. At the end, we have very interesting results.
Our paper is organized as follows: in Sects. 2 and 3 we discuss entanglements for two and three particles' spin and helicity with momentum and calculating of spin and helicity reduced density matrix and finally we obtained the entropy of the states. In Sect. 4 we conclude our results.
Two-particle entanglement
The quantum state of the two particles of mass m and spin 1/2 is
where \(p_{i}\) is the four momentum of particle i, and \(\varrho _{i}\) represents the spin of particle i along the z-axis. It is a complete orthonormal basis for Hilbert space of two particles. Similarly, we can also choose the helicity state
It is also a complete orthonormal basis for the two-particle state where \(\kappa\) is the helicity. The former is usually called spin representation, and the latter is called helicity representation. Moreover, these spin states and helicity states are related by the representation transformation as
Here, R(p) is the rotation that carries the z-axis into the direction p, and D is the spin 1/2 irreducible unitary representation of the Lorentz group [33]
where
that \(\vartheta\) is speed of particle, \(\lambda\) is speed of the observer and \(\xi\) is the Wigner’s angle with \(p_{i}=(\sin \xi _{i} \cos \phi _{i} , \sin \xi _{i} \sin \phi _{i} , \cos \xi _{i} )\) and indices i denoted particle i and \(\phi _{i}\) is the angle of \(p_{i}\) with x-axis. Note that the spin states and helicity states considered here are observed within the same inertial reference frame. For a pure two-particle state, we can represent it as expansion of the spin states, i.e. ,
with the normalized condition
where we have
A more realistic situation involves the wave packet of the system with a momentum distribution function with finite width. In this approach, while the spin subsystem is discrete, the momentum subsystem is continuous and we cannot use the same method for studying the entanglement in these two subsystems. However, in our approach, we assume that the wave packet is sharply distributed around some given momenta. Then, the reduced spin density matrix associated with the above-normalized state is obtained by tracing the momentum degree, i.e.,
Note that we have used the orthonormal relation for the spin states. Then, as mentioned above, \(\mid \psi >\) can also be expanded by the helicity states as
According to the transformation relation between the spin states and helicity states Eq. (1) we have
which follows the reduced helicity density matrix as
Considering two particles with the spin in z-direction, i.e.,
which implies that the corresponding spin entropy is zero. However, it doesn’t mean that helicity entropy also vanishes for this state. By Eqs. (2) and (8), the reduced helicity density matrix can be explicitly written as
In the following to simplify the calculations, we suppose that the \(\psi \left(\frac{1}{2},\frac{1}{2};{\mathbf {p}} _{1},{\mathbf {p}} _{2}\right)\) is independent of the angle \(\xi.\) In this case, the reduced helicity density matrix is written as:
and its eigenvalues are given by \(\rho '_{1}=\frac{1}{4}\left(\frac{\pi ^{2}}{16}+\frac{\pi }{2}+1\right),\,\rho '_{2}=\frac{1}{4}\left(\frac{\pi ^{2}}{16}-\frac{\pi }{2}+1\right)\) and \(\rho '_{3}=\rho '_{4}=\frac{1}{4}\left(1-\frac{\pi ^{2}}{16}\right).\) In addition, the entropy which is one of the most important measures for entanglement is given by Von-Neumann relation i.e., \(S=- \sum _{i}\ {\rho '_{i} \log _{2} \rho '_{i}}\). Actually, this quantity measures the entanglement of the helicity or spin part relative to the momentum part. Here, the helicity entropy reads
According to [32] the entropy for one particle is \(S^{(h)}_{1}=0.4917\) and for two particles we obtained \(S^{(h)}_{2}=0.9834\approx 2S^{(h)}_{1}.\) Note that, in the case considered above, the helicity entropy doesn’t depend on the specific form of wave function but for spin state it is better to use Gaussian wave function for a minimum uncertainty state i.e.,
where
then we combine Eqs. (6, 7) with Eq. (5) to obtain the reduced spin density matrix as
Now consider instead particles in the eigenstate of spin with eigenvalues +1/2 and isotropic momenta distributions such as Gaussian. The reduced spin density matrix lead to
so
the eigenvalues are easy to obtain as \(\rho _{1}=\frac{1}{4}\left(1+\frac{\pi ^{2}}{16}\right),\,\rho _{2}=\frac{1}{4}\left(1-\frac{\pi ^{2}}{16}\right) \ {\text{and}}\ \rho _{3}=\rho _{4}=\frac{1}{4}.\) The spin entropy reads as \(S_{(2)}^{s}=-\frac{1}{4}[\left(1+\frac{\pi ^{2}}{16}\right)\log _{2}\left(\frac{1}{4} +\frac{\pi ^{2}}{64}\right)+\left(1-\frac{\pi ^{2}}{16}\right)\log _{2}\left(\frac{1}{4} -\frac{\pi ^{2}}{64}\right)-4]=1.8524 .\) This resultant spin entropy value implies that entropy of the spin state is more than entropy of the helicity state for two particles.
Three particle entanglement
Now for the three particles we have
where D is presented in Eq. (2) and for pure three particle state, we can write
where
and
The reduced spin density matrix associated with this state is
This state can also be expanded by the helicity states as
where
We obtain the reduced helicity density matrix as follows:
If three particles prepared in z-direction, i.e.,
we rewrite
By this equation and Eq. (2) we have
that helicity state \(\Phi\) is used as Eq. (24) and \(\otimes\) means direct product of the states. If \(\psi \left(\frac{1}{2},\frac{1}{2},\frac{1}{2};{\mathbf {p}} _{1},{\mathbf {p}} _{2},{\mathbf {p}} _{3}\right)\) be independent of the angle \(\xi\) (for simplicity without loss of generality), the reduced helicity density matrix can be calculated as
The corresponding eigenvalues are
and the helicity entropy reads
If we again suppose the wave packet to be Gaussian
where
One can write the reduced spin density matrix as
Now suppose three particles move in z-direction so \(\xi _{1}=\xi _{2}=\xi _{3}=\xi\) and \(\psi\) is independent of \(\xi\) then reduced spin density matrix become
The eigenvalues for the matrix above is \(\rho _{1}=\rho _{3}=\frac{1}{8}\left(\frac{\pi ^{2}}{8}+1\right), \rho _{2}=\rho _{4}=\frac{1}{8}\) and \(\rho _{5}=\rho _{6}=\rho _{7}=\rho _{8}=\frac{1}{8}\left(1-\frac{\pi ^{2}}{16}\right),\) so the spin entropy for these eigenvalues are \(S_{(3)}^{s}=2.3988\) that is more than two-particle spin entropy and similar to two-particle state, the spin entropy is more than helicity entropy for three particle state.
Conclusion and outlook
In this work, we investigated helicity and spin entropy of systems of two and three massive particles described by sharp and Gaussian momentum-distributed wave packet, also with calculating we obtained three interesting results: 1- We showed with increasing the number of particles that the helicity and spin entropy increases, 2- For one-, two- and three-particle systems, the spin entropy is more than helicity entropy, 3- For helicity entropy of two and three particles, we have approximately two and three times of one-particle helicity entropy (good approximation) and the relation seems to exist \(S_{n}^{(h)}\approx nS_{1}^{(h)}\) for helicity entropy of n particles that an interested reader can check the validity of this relationship.
References
Czachor, M.: Nonlocal looking equations can make nonlinear quantum dynamics local. Phys. Rev. A 55, 72 (1997)
Peres, A., Terno, D.R.: Two roles of relativistic spin operators. J. Mod. Opt. 49, 1255 (2002)
Peres, A., et al.: Relativistic spin operator and Lorentz transformation of spin state of a massive Dirac particle. Phys. Rev. Lett. 88, 230402 (2002)
Alsing, P. M., Milburn, G. J.: Speeding up entanglement degradation, arXiv:quant-ph/0203051 (2009)
Gingrich, R.M., Adami, C.: Quantum entanglement of moving bodies,. Phys. Rev. Lett. 89, 270402 (2002)
Peres, A., Terno, D.R.: Quantum information and special relativity. Mod. Opt. 50, 1165 (2003)
Peres, A., Terno, D.R.: Quantum helicity entropy of moving bodies. Int. J. Quant. Inf. 1, 225 (2003)
Pachos, J., Solano, E.: Entanglement entropy: helicity versus spin. Quant. Inf. Comput. 3, 115 (2003)
van Enk, S.J., Rudolph, T.: Local vs. joint measurements for the entanglement of assistance. Quant. Inf. Comput. 3, 423 (2003)
Czachor, M., Wilczewski, M.: Two-spinors, oscillator algebras, and qubits: aspects of manifestly covariant approach to relativistic quantum information. Phys. Rev. A 68, 010302 (2003)
Esfahani, B.N., Aghaee, M.: Tripartite entanglements seen from a relativistically moving frame. Int. J. Quant. Inf. 09, 1255 (2011)
Bergou, A.J., et al.: Maximum entanglement and its proper measure. Phys. Rev. A 68, 042102 (2003)
Alsing, P.M., Milburn, G.J.: Teleportation with a uniformly accelerated partner. Phys. Rev. Lett. 91, 180404 (2003)
Esfahani, B.N., Aghaee, M.: Spin fidelity for three qubit Greenberger-Horne-Zeilinger and W states under Lorentz transformations. Int J. Theor. Phys. 5, 1395 (2011)
Peres, A., Terno, D.R.: Quantum information and relativity theory. Rev. Mod. Phys. 76, 93 (2004)
Soo, C., Lin, C.C.Y.: Quantum helicity entropy of moving bodies. Int. J. Quant. Inf. 2, 183 (2004)
Moradi, S., Aghaee, M.: Frame independent nonlocality for three qubit state. Int. J. Theor. Phys. 49, 615 (2010)
Alsing, P.M., et al.: Teleportation in a non-inertial frame. J. Optics. B6, S834 (2004)
Shi, Y.: Entanglement in relativistic quantum field theory. Phys. Rev. D 70, 105001 (2004)
Kim, W.T., Son, E.J.: One- and two-spin-1/2 particle systems under the Lorentz transformations. Phys. Rev. A 71, o14102 (2005)
Czachor, M.: Relativistic spin operator and Lorentz transformation of the spin state of a massive Dirac particle. Phys. Rev. Lett. 94, 078901 (2005)
Fuentes-Schuller, I., Mann, R.B.: Alice falls into a black hole: entanglement in non-inertial frames. Phys. Rev. Lett. 95, 120404 (2005)
Caban, P., Rembielinski, J.: Unstable particles as open quantum systems. Phys. Rev. A 72, 012103 (2005)
Esfahani, B.N.: Relativistic entanglement for spins and momenta of a massive three-particle system. Quant. Inf. Process. 11, 529 (2011)
Kok, P., Braunstein, S.L.: Diversities in quantum computation and quantum information. Int. J. Quant. Inf. 4, 119 (2006)
Ball, J.L., et al.: Entanglement in an expanding spacetime. Phys. Lett. A 359, 550 (2006)
Lamata, L., et al.: Relativity and Lorentz invariance of entanglement distillability. Phys. Rev. Lett. 97, 250502 (2006)
Lamata, L., et al.: Dynamics of momentum entanglement in lowest-order QED. Phys. Rev. A 73, 012335 (2006)
Jordan, T.F., et al.: Einstein-Podolsky-Rosen correlations of Dirac particles: quantum field theory approach. Phys. Rev. A 73, 032104 (2006)
Alsing, P.M., et al.: Entanglement of Dirac fields in noninertial frames. Phys. Rev. A 74, 032326 (2006)
Shi, Y.: Charmed hadron spectroscopy from focus. Phys. Lett. B 641, 486 (2006)
He, S., et al.: Quantum helicity entropy of moving bodies, arXiv:quant-ph/0702028 (2007)
Weinberg, S.: The Quantum Theory of Fields. Cambridge University Press, Cambridge (1995)
Caban, P., Rembielinski, J.: Quantum state of a free spin-1/2 particle and the inextricable dependence of spin and momentum under Lorentz transformations. Phys. Rev. A 74, 042103 (2006)
Jordan, T.F., et al.: Entanglement entropy: helicity versus spin, arXiv:quant-ph/0608061 (2007)
Ling, Y., et al.: Quantum entanglement and teleportation in higher dimensional black hole spacetimes. J. Phys. A 40, 9025 (2007)
Adesso, G., et al.: Extremal entanglement and mixedness in continuous variable systems, arXiv:quant-ph/0701074 (2007)
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Aghaee, M., Rabeie, A. & Takook, M.V. Two and three particles entanglement; helicity and spin with momentum. J Theor Appl Phys 11, 263–268 (2017). https://doi.org/10.1007/s40094-017-0265-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40094-017-0265-9