Abstract
In the present paper, we have investigated a situation where a high intensity laser beam passes through a gas and ionizes this gas by tunnel ionization. Here the electric field of the laser provides a sufficient velocity to the electrons to surpass the Coulomb barrier of the atom. Owing to the ionization the plasma density enhances which affects the laser beam propagation. The use of paraxial ray approximation theory for the present case of super-Gaussian lasers reveals the self-focusing of the beams and frequency upshifting. The predicted self-focusing of the laser beams is contrary to the expected outcome of defocusing of these beams in the plasma, indicating that the paraxial theory may not be valid for the case of super-Gaussian lasers even for the inclusion of most of the near axis region in the theory.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
The interaction of high power laser pulse with gases and plasmas is a major field of research due to its applications in laser electron accelerator, laser driven fusion, and super-continuum generation [1,2,3,4]. For many of these applications, it is highly desirable that the laser pulse propagate extended distances (many Rayleigh lengths) at high intensity. The problem of spot size evolution, self-focusing and defocusing of the laser pulse in plasma are of great interest. Self-focusing is a non-linear optical process induced by a change in refractive index of material exposed to intense laser radiation. A medium whose refractive index increases with electric field intensity acts as focusing lens for a laser beam characterized by an initial transverse intensity gradient. There are studies where people have tried to enhance the Rayleigh length. Most of the studies have been conducted for the laser beams having Gaussian profile using paraxial ray approximation [5,6,7,8].
Sodha et al. [9] reviewed the self-focusing of electromagnetic beams in plasmas, referring primarily to steady state self-focusing. Esarey et al. [10] gave an extensive review of paraxial ray theory of self-focusing and self-guiding of short laser pulses in ionizing gases and plasmas. Fedosejevs et al. [11] reported experimental results on the competing processes of ionization-induced refraction and relativistic self-focusing. Liu and Tripathi [7] developed a theoretical framework to study the combined effects of the laser-frequency upshift, self-defocusing, and ring formation. The self-defocusing of the laser prepulse and laser guiding of the second laser pulse in an axially nonuniform plasma channel has also been studied by them [12]. The Ohmic and the ponderomotive nonlinearities at sub-picosecond pulse lengths are weak, as the time scale for ambipolar plasma diffusion is much longer. However, two other major nonlinearities are important. These arise due to tunnel ionization of atoms in the optical field of the laser and due to the relativistic dependence of electron mass on its velocity. The former nonlinearity is important when the laser field is comparable with the atomic Coulomb field.
However, the super-Gaussian lasers have recently attracted the researchers all over the world [13,10,11,12,17] for their better extraction from saturated laser amplifiers, better non-linear conversion for same peak intensity, and top-hat beams have a parabolic thermal lens which does not decrease beam quality. Due to this reason, it becomes vital to investigate the profile of super-Gaussian lasers when they tunnel ionize the gas and produce the plasma. Hence, in the present article, we have derived the coupled equations for the amplitude and phase of super-Gaussian laser beam and solve it numerically using initial conditions.
Coupled equations for amplitude and phase
Let us consider the propagation of a circularly polarized laser beam in a gas jet target. At z = 0, the laser field is given by
where \(E_{0} = E_{00} { \exp }\left( { - r^{ 4} / 2r_{0}^{ 4} } \right)\) for t > 0 and E 0 = 0 for t < 0.
The field of the laser ionizes the gas as it passes through it. The tunnel ionization of the gas gives rise to a changing plasma density n p and plasma frequency ω p, given by:
where
is the rate of tunnel ionization by the laser electric field E, \(\omega_{\text{N}}^{2} = 4\pi n_{\text{N}} e^{2} /m,\) n N is the initial density of neutral atoms, \(E_{\text{a}} = (4/3)\sqrt {2m} \left( {I_{0} } \right)^{3/2} /e\hbar\) is the characteristic atomic field, I 0 is the ionization potential, and h = 2π \(\hbar\) is the Planck’s constant.
Inside the ionizing gas (z > 0), \(\vec{E} = (\hat{x} + i\hat{y})A(t,z,r)\exp ( - i\varphi ),\) where A is the slowly varying complex amplitude and φ(t,z) is the fast phase of the wave. We define ω = ∂φ/∂t, k = − ∂φ/∂z, \(\omega_{\text{P0}}^{2} = \omega_{\text{P}}^{2} \left( {t,z,r = 0} \right).\) The wave equation for the laser pulse is written as:
Substituting for \(\vec{E}\) we obtain, to successive orders, in the WKB approximation,
Differentiating Eq. (5) w.r.t. t, using ∂k/∂t = − ∂ω/∂z, and defining \(v_{\text{g}} = c\left( { 1 - \omega_{{{\text{P}}0}}^{2} /\omega^{ 2} } \right)\), we obtain
Combining the first and fourth, and second and fifth terms of Eq. (6) and defining the action amplitude A F = (ω/ω 0)1/2 A, t′ = t − z/c, z′ = z, and assuming \(\omega_{\text{P}}^{2} /\omega^{ 2} \ll 1\), we can rewrite Eqs. (6) and (7) simply as
together with γ T0 = γ T(r = 0). We consider cylindrically symmetric propagation and write A F = A F0 exp (iQ), where A F0(t′, z′, r) and Q (t′, z′, r) are real. Separating the real and imaginary parts of Eq. (8), we obtain:
To solve these equations, we expand \(\omega_{\text{P}}^{2}\), Q, γ T in powers of r 2, as:
i.e., in the non paraxial approximation. Since the electric field profile of the super-Gaussian laser beam is flat over a certain region away from the axis, we have included higher order terms (up to r 6) so that most of the region can be included. Keeping the analysis up to r 4 order terms, a significant error shall occur. However, the higher order terms shall have negligible impact in the case of Gaussian laser beams.
In this approximation, we write the laser intensity as:
The coefficients involved in the expansion of γ T can be determined using Eq. (3). On comparing the successive powers of \(r^{2}\), we obtain the various equations:
The above coupled equations are written in the dimensionless quantities ς = z′/R d, τ = γ T00 t′, ω SF = ω/ω 0, and R d = (ω 0/c)\(r_{0}^{ 2}\) is Rayleigh length.
Results and discussion
The coupled equations are solved by applying boundary conditions for an initially plane wave front. The initial and boundary conditions are at \(\tau = 0, \omega_{\text{P0}}^{2} ,\omega_{\text{P2}}^{2} , \omega_{\text{P4}}^{2} ,\omega_{\text{P6}}^{2} = 0\) for all ς and at ς = 0, \(f_{\text{B}} = 1, \frac{{\partial f_{\text{B}} }}{\partial \varsigma }\) = 0, \(\omega_{\text{SF}} = 1, a_{2} , a_{4} , a_{6} = 0, Q_{4} ,Q_{6} = 0\) for all τ. Since the Keldysh parameter γ decides the nature of ionization and γ ≪ 1 for the tunnel ionization, we select the laser and plasma parameters such that this condition is satisfied. The Keldysh parameter is given by \(\gamma = \sqrt {\frac{{E_{\text{I}} }}{{2U_{\text{P}} }}} = \sqrt {\frac{{\varepsilon_{0} m_{\text{e}} cE_{\text{I}} \omega^{2} }}{{q^{2} I}}}\), where E I is the ionization potential of atom, q is charge on the electron, I is the intensity of the laser beam and other symbols have their usual meanings.
Figure 1 shows that the beam width parameter goes down with the distance travelled by the laser beam, indicating the self-focusing of the beams. The effect of self-focusing is found to be more for a laser beam of small spot size and smaller wavelength. On the other hand, self-focusing is found to be reduced as we increase the density of neutral atom in the gas.
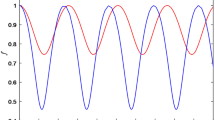
Figure 2 shows the variation of beam width parameter for three different gases, namely xenon, argon and neon. Here one finds that the self-focusing of the laser in the case of neon gas is more as compared to the argon and xenon gases. On the other hand, this is observed that the lasers of much higher intensities encounter less significant effect of the focusing (see Fig. 3).
Variation of beamwidth parameter f B for different intensities of the laser beams, when τ = 0.3, r 0/λ 0 = 4 and \(\omega_{\text{N}}^{2} /\omega_{0}^{ 2}\) = 0.008 and the other parameters are the same as in Fig. 2. The intensity I in the legends carries the units W/m2
We have plotted Fig. 4 for examining the change in intensity profile of the lasers when they propagate in the tunnel ionized plasma for different gases. The figure shows strong self-focusing of the lasers for all the gases. However, there is a significant change in the laser intensity profile when it ionizes the xenon gas and propagates in it. This effect is found to be prominent in the case of lasers carrying lower intensity (Fig. 5).
Normalized intensity (A/E 00)2 pattern of the lasers as a function of r/r 0 for different intensities. This figure corresponds to Fig. 4. The intensity I0 in the legends carries the units W/m2
The theory used in the present article also predicts the frequency shifting of the lasers when they tunnel ionize the gas and propagate in the formed plasma. The change in the frequency with various parameters is shown in the forthcoming figures.
Figures 6, 7 and 8 show the variation of frequency of the laser when it propagates in the plasma. This is evident from these figures that the frequency gets upshifted during the propagation of the laser beam in the plasma. The highest shifting takes place in the case of xenon gas, whereas this is the least in the case of neon gas. The significant upshifting of the laser frequency takes place when the laser carries higher intensity (Fig. 7). Under this situation, less significant change in the laser profiles was also noticed. This is observed that the lasers with higher spot size undergo much significant changes in the frequency (Fig. 8); similar is the effect when there is a gas with larger number of neutrals. Another observation is that the lasers of larger wavelength undergo with the larger upshifting in its frequency.
Dependence of frequency ω SF on the wavelength of the laser, spot size and density of neutrals, when intensity = 6.8 × 1019 W/m2 and the other parameters are the same as in Fig. 2
Conclusions
We have considered super-Gaussian beam profile having maximum intensity on the axis and minimum intensity away from the axis. As the laser beam propagates in the gas to form the plasma, the plasma density should stay maximum on the axis which should result in minimum refractive index on the axis. Since the phase velocity of the lasers depends inversely on the refractive index, the phase velocity becomes maximum on the axis and falls down sharply on the edges. This would lead to a diverging wavefront, causing the laser beam to defocus. Kumar and Tripathi [6] observed the self-defocusing of Gaussian laser pulse based on the paraxial ray theory in tunnel ionized helium plasma. Liu and Tripathi [7] also observed the self-defocusing of Gaussian beam based on the paraxial ray theory in tunnel ionized neon plasma. However, we point out that the use of this theory in the case of super-Gaussian lasers beams provides an unphysical result of self-focusing of these beams. Hence, the paraxial ray approximation theory does not seem to be authentic in the case of super-Gaussian laser beams.
References
Braun, A., Korn, G., Liu, X., Du, D., Squier, J., Mourou, G.: Self-channeling of high-peak-power femtosecond laser pulses in air. Opt. Lett. 20, 73–75 (1995)
Esarey, E., Sprangle, P.: Generation of stimulated back scattered harmonic generation from intense laser interactions with beams and plasmas. Phys. Rev. A 45, 5872–5882 (1992)
Malik, H.K.: Analytical calculation of wakefield generated by microwave pulses in a plasma filled waveguide for electron acceleration. J. Appl. Phys. 104, 053308(1–7) (2008)
Deutsch, G.C., Furukawa, H., Mima, K., Murakami, M., Nishihara, K.: Interaction physics of the fast ignitor concept. Phys. Rev. Lett. 77, 2483 (1996)
Faisal, M., Mishra, S.K., Verma, M.P., Sodha, M.S.: Ring formation in self-focusing of electromagnetic beams in plasmas. Phys. Plasmas 14, 103103 (2007)
Kumar, N., Tripathi, V.K.: Non-paraxial theory of self-defocusing/focusing of a laser pulse in a multiple-ionizing gas. Appl. Phys. B 82, 53–58 (2006)
Liu, C.S., Tripathi, V.K.: Laser frequency upshift, self defocusing, and ring formation in tunnel ionizing gases and plasmas. Phys. Plasmas 7, 4360 (2000)
Singh, A., Singh, N.: Guiding of a laser beam in a collisionless magnetoplasma channel. J. Opt. Soc. Am. B 28, 081844(1–7) (2011)
Sodha, M.S., Prasad, S., Tripathi, V.K.: Nonstationary self-focusing of a Gaussian pulse in a plasma. J. Appl. Phys. 46, 637 (1975)
Esarey, E., Sprangle, P., Krall, J., Ting, A.: Self-focusing and guiding of short laser pulses in ionizing gases and plasmas. IEEE J. Quantum Electron. 33, 1879 (1997)
Fedosejevs, R., Wang, X.F., Tsakiris, G.D.: Onset of relativistic self-focusing in high density gas jet targets. Phys. Rev. E 56, 4615 (1997)
Liu, C.S., Tripathi, V.K.: Laser guiding in an axially nonuniform plasma channel. Phys. Plasmas 1, 3100 (1994)
Singh, D., Malik, H.K.: THz generation by mixing of two super-Gaussian laser beams in collisional plasma. Phys. Plasmas 21, 083105(1–5) (2014)
Malik, A.K., Malik, H.K.: Tuning and focusing of terahertz radiation by DC magnetic field in a laser beating process. IEEE J. Quantum Electron. 49, 232–237 (2013)
Malik, H.K.: Terahertz radiation generation by lasers with remarkable efficiency in electron–positron plasma. Phys. Lett. A 379, 2826–2829 (2015)
Malik, H.K.: Density bunch formation by microwave in a plasma-filled cylindrical waveguide. Europhys. Lett. 106, 55002(1–5) (2014)
Malik, H.K., Malik, A.K.: Strong and collimated terahertz radiation by super-Gaussian lasers. Europhys. Lett. 100, 45001(1–5) (2012)
Acknowledgements
One of the authors, Lalita Devi, would like to thank CSIR, Govt. of India for providing the financial support for this work.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Devi, L., Malik, H.K. On validity of paraxial theory for super-Gaussian laser beams propagating in a plasma. J Theor Appl Phys 11, 165–170 (2017). https://doi.org/10.1007/s40094-017-0262-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40094-017-0262-z