Introduction

Graphene is a one-atom-thick crystal of sp2-bonded carbon atoms ordered in a two-dimensional (2D) hexagonal lattice [1]. Graphene and graphene nanoribbon (GNRs) have attracted much recent attention for their unique two-dimensional structures and physicochemical properties [2], as well as their wide potential applications in electronics [3, 4], photonics, and optoelectronics [5], energy storage and conversion [6], and chemical-bio sensing [7].

Regarding the broad usage of GNR in nano-electronics, physics and chemistry, this substance is under wide investigations at present. Most of these investigations are done using some software based on density functional theory (DFT), and they need structural relaxation of nanoribbons. It takes much time, especially if the length of nano-transistors being investigated is more than 10 nm. In this case, the number of atoms will increase. If the method for simulation of the structure is based on order-N3, the time it needs will be much more even for supercomputers. In the case of investigating multilayer graphene nanoribbon, the situation will deteriorate.

The idea is proposing a method having the dimer number of GNR and its length to acquire the structural relaxation and the exact position of atoms. In this case, either the general need for structural relaxation would be unnecessary or even by doing this, the time will be extremely decreased.

To use graphene nanoribbon as a channel, we should first determine the approximate position of atoms. Then these positions should be given to applications such as SIESTA, VASP and ATK [8,9,10] which change them using structural relaxation and spending a long time, until these atoms are placed in their precise positions. The running time for relaxation depends on several parameters: the accuracy of initial positions given to the software, the method used in the software for structural relaxation, the parameters that the user sets in the software, and the value of the requested accuracy to end run.

Except for the initial positions, the rest of the parameters are usually specified by the researcher at the beginning, and do not change [10,11,12]. Given that the initial position of the atoms is of paramount importance in comparison to the rest of the parameters, it is under way in the present study. It is natural that if we relax an atomic structure and set the obtained positions to the software as new initial positions and repeat the structural relaxation, the run time would be reduced several times. This time for very large structures, can be reduced from months to days. So acquiring a way to determine the precise initial atomic positions sounds completely logical.

Researchers obtain these initial positions from some specific ways: downloading from the Internet, using simple formulas available in books and articles [13, 14], and the use of applications that calculate these positions for a number of particular structures such as carbon nanotube [15]. It is natural that the atomic structures found on the Internet are limited. Using the simple formula readily accessible in the books and articles, we can calculate the positions with low accuracy, and so much time is required to run structural relaxation.

Applications that are available in this field are also very limited. For example, Nano Tube Modeler software, which is used for CNT [15, 16]. Such applications use simple and ideal formulas to calculate the atomic positions too, which make the run time very long. So by determining the exact formulas for the positions in GNRs in this paper, researchers can utilize these formulas.

In all applications and simple formulas, C–C bond lengths are considered constant for all GNRs in different directions [13, 14]. As we calculate the exact atomic position for all atoms, it will be obvious that the D cc (carbon-carbon bond length) is not equal for them. We consider the average value of middle atoms in all GNRs in two directions and compare them.

The paper is organized as follows: in Sect. 2, we present a basic formula for atomic positions for all carbon atoms in ideal (slab cut of graphene) and real (relaxed) AGNR. In Sect. 3, we derive all atomic positions in x and y directions and energy gap, and then present a generic formula for them and show the fact that the C–C bond lengths are different in two directions. Finally, Sect. 4 summarizes our findings.

Problem statement

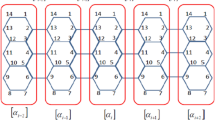
In this paper, we present two groups of AGNR slabs. For the first group, all edge carbon atoms saturate with hydrogen atoms and for second group, they are bare (without hydrogen). The width of AGNR is defined by the number of dimer lines (N y ) and that of length is defined by the number of atoms in slab direction, as illustrated in Fig. 1. Since the band gaps of AGNRs depend on its width and exhibit three distinct families, (3n + m) behavior [17, 18], we choose AGNRs with length N c = 6 (number of carbon atoms in X direction), and width N y  = 5–30, representing the family behavior with the n = 1–10 and m = 0, 1 and 2. In addition, wider AGNRs with N y  = 40–42, are also calculated to examine the size-dependent effects, and to see some especial effects better.

Fig. 1
figure 1

An AGNR slab with its whole details

Full size image

At first, we can consider an ideal graphene nanoribbon. The exact position of each atom is obtained by following equations [13, 14] (we show these positions in ideal states with capital letters):

$$Y(i,j) = C_{2} + (j - 1)\frac{\sqrt 3 }{2}D_{cc } : {\text{for all}}\; i \, \&\, j,$$
(3)
$$X(i = {\text{Odd}},\,j) = X(i = 1,\,j) + 3 \times N_{x} \times D_{\text{cc}}$$
(4)
$$X(i = {\text{Even}},\,j) = X(i = 2,\,j) + 3 \times N_{x} \times D_{\text{cc}} ,$$
(5)

where N x is the number of unit cells in X direction (every two adjacent columns of atoms in X direction, is a unit cell), C 1 and C 2 are arbitrary constant numbers, and D cc is C–C bond length. Now we are going to relax the various nanoribbons with different widths. The computed positions for these atoms are denoted by small letters. Let us call it the real value. In general, the positions in real and ideal states are not equal. We define this variation as:

$$x({\text{Real}}) = X({\text{Ideal}}) + \Delta x(i,j,N_{y} ),$$
(6)
$$y({\text{Real}}) = Y({\text{Ideal}}) + \Delta y(i,j,N_{y} ).$$
(7)

Now if we obtain the exact value of ∆x and ∆y, according to obtained ideal value of X and Y with formulas (1)–(5), we will have a general formula for the relaxed value of x and y, and the relaxation of nanoribbons will not be needed any more. Even if we need to relax the nanoribbons the time of relaxation will be decreased considerably.

Results and discussion

Electronic structures and geometry relaxations are calculated based on the DFT [19], using the Spanish initiative for electronic simulations with thousands of atoms package (SIESTA) [20, 21] with local-density approximation (LDA) [22]. A double-ζ plus polarization basis set is employed to describe the localized atomic orbitals and an energy cutoff for real-space mesh size is set to be 380 Ry. All nanostructure geometries are fully relaxed with a force tolerance, 0.01 eV/Å [11].

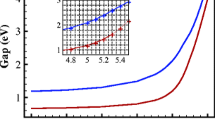
We do the structural relaxation using SIESTA for AGNRs with N y from 5 to 30 in two states, with and without hydrogen for carbon atoms in edges. Then we use the output files of these simulations as input files in MATLAB and process all the output data of SIESTA by several programs written in MATLAB. According to reports by other researchers, it is obvious that energy bandgap diagram vs the dimer number is divided into three categories. The dimer number is shown as:

$$N_{y} = 3n + m,$$
(8)

where n is a natural number and m is 0, 1 or 2, other studies have shown that energy bandgap diagram depends on the value of m [23]. We also obtain the same diagrams in this research. Figures 2, and 3, show this diagram in two states, with and without hydrogen. These diagrams indicate that each branch of these diagrams can be shown with a specific formula:

$$f(x) = A_{0} + \frac{{A_{1} }}{x},$$
(9)

where f = E g and x = N y . As a result, we fit these diagrams with the obtained data using nonlinear regression. We obtain the coefficient A 0, A 1 and the mean square error (MSE) for various three branches of diagrams and in two cases, with and without hydrogen by listing them in Table 1. The diagrams related to nonlinear regression (as fitted to) of the data together with the data itself obtained in simulations are shown in Figs. 2, and 3. It can be figured out from these diagrams that the obtained data in simulations is perfectly coinciding with the proposed formula so that five out of six branches coincide in a way that almost no difference can be observed between simulation and nonlinear regression.

Fig. 2
figure 2

Energy gap vs dimer number for AGNR with H

Full size image
Fig. 3
figure 3

Energy gap vs dimer number for AGNR without H

Full size image
Table 1 Energy gap in AGNRs vs m
Full size table

In Table 1, each column of data is related to a specific category of AGNRs, which has been shown by the value m = 0, 1, and 2. In MSE section of the table, it can be seen clearly that the value of error for m = 1, and for the case without hydrogen is more than the other considerably.

As a result, the diagram of simulation and nonlinear regression (for m = 1) in Fig. 3, are slightly different from each other. Although there exist some minor errors in one branch, simulation results show enough good matches with that of proposed formula.

Computing ∆x

We take the idea from last paragraph and extend this regression to all parameters of GNRs, including ∆x and ∆y. The diagram of ∆x based on the atom index in Y direction (j) is drawn in Figs. 4, and 5, for the two dimer numbers, 29 and 30 (odd and even). By looking over these figures it is observable that the diagram is odd for nanoribbons having even dimer number and vice versa. In addition, except for edge carbon atoms of nanoribbons (on both sides) which have the most variations, the diagram relating to the rest of atoms is zigzag shape. It means the amount of variations in X direction depends on atom index being odd or even, and this state looks normal considering the arrangement of atoms in graphene (or AGNR) unit cell which they are placed alternatively as atoms type 1 and 2.

Fig. 4
figure 4

Percentage of ∆x for N y  = 29 vs atom index in Y direction (j) for two atom index in x direction (i = 1, i = 2)

Full size image
Fig. 5
figure 5

Percentage of ∆x for N y  = 30 vs atom index in Y direction (j) for two atom index in x direction (i = 1, i = 2)

Full size image

Considering these points, we can write the ∆x formula according atoms’ index. It is enough to have the mean and peak to peak value of the zigzag. In this case the formulas can be written as:

$$\Delta x(i = {\text{Odd}},\;j = {\text{Odd}}) = {\text{Av}}(i = 1) - \frac{1}{2}{\text{P}}2{\text{P}}\,(i = 1) ,$$
(10)
$$\Delta x(i = {\text{Odd}},\;j = {\text{Even}}) = {\text{Av}}(i = 1) + \frac{1}{2}{\text{P}}2{\text{P}}\,(i = 1),$$
(11)
$$\Delta x(i = {\text{Even}} ,\;j = {\text{Odd}}) = {\text{Av}}(i = 2) + \frac{1}{2}{\text{P}}2{\text{P}}\,(i = 2) ,$$
(12)
$$\Delta x(i = {\text{Even}},\;j = {\text{Even}}) = {\text{Av}}(i = 2) - \frac{1}{2}{\text{P}}2{\text{P}}\,(i = 2),$$
(13)

where Av and P2P are the mean and peak to peak values of zigzags, respectively. The diagram relating to the mean value is depicted in Fig. 6. Moreover, that relating to the peak to peak is shown in Fig. 7, (both of them are plotted for nanoribbons without hydrogen). The same diagrams obtain for nanoribbons with hydrogen. Considering these diagrams, it can be seen that the hyperbolic formula (9) which is proposed for GNR’s bandgap energy is also valid here. In this formula f = Av or P2P and x = N y . In this case, each diagram alone is divided into three categories (for three different values of m) and the nonlinear regression for each category.

Fig. 6
figure 6

Average of differences in percentage in X direction for AGNRs without H for all first atoms (i = 1) and their fitted curves

Full size image
Fig. 7
figure 7

Peak to Peak percentage of ∆x for middle first atoms in Y direction (i = 1) for AGNRs without H vs dimer number

Full size image

The obtained coefficients and the MSE for each category are shown in Tables 2, and 3 for the mean and peak to peak of zigzag section, respectively, for two cases, with and without hydrogen.

Table 2 The average of ∆x in middle carbons
Full size table
Table 3 Peak to Peak of ∆x in middle carbons
Full size table

Now we have to obtain the value of ∆x of GNR for edge carbon atoms and atom near the edge. In addition, beside the edge carbon atom, the atoms near the edge are a little far from the ideal zigzag shape that we consider for central atoms. We have sketched the diagrams relating to ∆x for edge carbon atom (j = 1) in Fig. 8, and for the second atom from the edge (j = 2) in Fig. 9, according to the dimer number. Both of these figures are plotted for nanoribbons without hydrogen.

Fig. 8
figure 8

Percentage of ∆x for first carbon in Y direction (j = 1) for all AGNRs without H vs dimer number, and their fitted curves

Full size image
Fig. 9
figure 9

Percentage of ∆x for second carbon in Y direction (j = 2) for all AGNRs without H vs dimer number, and their fitted curves

Full size image

We have achieved all these diagrams for both cases, with and without hydrogen, and for four atoms near the edge (j = 1, 2, 3, 4), but considering the high number of figures, we do not draw them all. In all these diagrams, the general shape of hyperbolic can be seen. Thus, we use the formula (9). In this formula f = ∆x and x = N y .

In Fig. 8, it can be seen that the diagrams are coinciding for all three categories. It means this diagram does not depend on m value, but as we can see in Fig. 9, those three categories are unlike each other. This manner is extendable for other atoms in the same way. It means that the various categories of the diagram coincide for odd atoms but not for even atoms. We use the general formula (9) again. In this formula f = ∆x and x = N y . The various coefficients obtained from nonlinear regression for the first four atoms near the edge and for AGNRs with, and without hydrogen are listed in Tables 4 and 5, respectively. The points mentioned for odd and even edge atoms, are obvious in these tables.

Table 4 ∆x of four first carbons in AGNRs with H
Full size table
Table 5 ∆x of four first carbons in AGNRs without H
Full size table

Now by considering diagrams being odd or even, we have to write the formulas relating to second edge for first four atoms of the edge. These formulas are:

$$\Delta x\left( {i,N_{y} - j} \right) = \varvec{ }\Delta x(i,j):j = 1,2,3,4\; {\text{and}} \;N_{y} = {\text{Odd}},$$
(14)
$$\Delta x(i,N_{y} - j) = {\text{Av}}(i) - \varvec{ }\Delta x(i,j)\varvec{ }:j = 1,2,3,4\; {\text{and}}\; N_{y} = {\text{Even}} .$$
(15)

Therefore, using Tables 2, 3, 4 and 5 in Eqs. (10)–(15), we compute the exact value of \(\Delta x\) for all atoms and for each dimer number. By inserting this value in Eq. (7), we obtain the real value of x.

Computing ∆y

Figure 10, shows ∆ y diagram in two cases, with and without hydrogen, according to atom index in Y direction (j) for GNR with dimer number 29 as an example. The basic difference between diagrams related to ∆ x and ∆ y is that the coefficients relevant to various indices in X direction (i) are completely coinciding in ∆ y diagrams while these coefficients in ∆ x diagrams are different.

Fig. 10
figure 10

Percentage of ∆Y for N y  = 29 vs atom index in Y direction (j) with edge atoms

Full size image

Now to look at the inner atoms more carefully, we eliminate two atoms from the edges of the diagram and focus on central atoms. This diagram has shown as an example for dimer number 30 in Fig. 11. Now suppose we divide atom’s index in Y direction (j) into three categories means j = 3 × n + m j . Based on this figure it is obvious that the value of ∆ y depends on the categories (m j ). However, there is not much difference between categories (m j ) for the most dimer numbers. This point can be seen in Fig. 12, for dimer number 29. However, if we consider original figure in that two edge atoms are not eliminated (Fig. 10), the effect of m j can be ignored.

Fig. 11
figure 11

Percentage of ∆Y for N y  = 30 vs atom index in Y direction (j) without edge atoms

Full size image
Fig. 12
figure 12

Percentage of ∆Y for N y  = 29 vs atom index in Y direction (j) without edge atoms

Full size image

Another important point is that if we eliminate the edge atoms, a linear shape can be seen for other atoms. Thus, we can consider ∆ y formula for central atoms as linear. For doing it, we use the linear regression in MATLAB to obtain the slope and offset values for each AGNR with various dimer numbers. As an example, the slope diagram is depicted for AGNR without hydrogen in Fig. 13. As it can be seen easily, the diagram is hyperbolic and depends on m.

Fig. 13
figure 13

Slope in the curve of D cc difference in percentage in AGNRs without H in Y direction for middle atoms vs dimer number

Full size image

Considering this point, we use the general formula (9) and the linear regression. The obtained coefficients for the slopes and offsets of these lines have listed in Tables 6 and 7, respectively, in two cases, with and without hydrogen.

Table 6 The slope (S) in AGNRs in Y direction
Full size table
Table 7 The offset (O) in AGNRs in Y direction
Full size table

Thus, by having the values of the slope and offset, ∆ y formula can be written for central atoms as:

$$\Delta y(i,j) = S(N_{y} ) \times j + O(N_{y} ).$$
(16)

It can also be figured out from Figs. 11, and 12, that it is not only the edge atom is placed out of linear regression but also there are a couple of other atoms, which do the same slightly. As a result, the value of ∆ y for the first four edge atoms for AGNRs in two cases, without and with hydrogen, are listed in Tables 8 and 9, respectively. These values also follow the general hyperbolic shape. These values for ANGRs without hydrogen depend on m, but for AGNRs with hydrogen are independent of it.

Table 8 ∆Y of four first carbons in AGNRs without H
Full size table
Table 9 ∆Y of four first carbons in AGNRs with H
Full size table

As we have mentioned before, the diagram ∆Y based on j (compared to the central atom of ANGR) is an odd function, thus for atoms near the second edge the following formula can be written:

$$\Delta y(i,N_{y} - j) = - \Delta y(i,j):j \;= 1,2,3,4 .$$
(17)

Therefore, using Tables 6, 7, 8 and 9 in Eqs. (16) and (17), we compute the exact value of \(\Delta {\text{y}}\) for all atoms and for each dimer number. By inserting this value in Eq. (8), we obtain the real value of y. Using these equations, we repeat structural relaxations again. Comparing the calculation time required for new relaxations using the real positions and the ideal positions, we show that the calculation time is approximately reduced between 4 and 7 times. For example, this time for relaxation of AGNR with N y  = 42 reduced from 17 days to less than four days. This reduction is unbelievable when the channel length is more 10 nm or when the GNR is multilayer.

Difference between C–C bond length in two directions

If we look at the two Figs. 4, and 5 more carefully, we understand with a little change in D cc in X direction, the mean value of zigzag shape can be equal to zero in both cases, i = 1 and i = 2. By summing this change to the last value of D cc, we obtain its new value. Because this value is the mean value for all central atoms, we can name it the real value for D cc in x direction. By writing Eq. (3) in two states before and after the change of D cc, we can calculate the amount of change in D cc accurately:

$$\Delta D_{\text{ccx}} = - \frac{4}{3}{\text{Av}}1,$$
(18)
$${\text{P}}2{\text{P}}_{2} = {\text{P}}2{\text{P}}_{1} + \frac{2}{3}{\text{Av}}1,$$
(19)

where Av1 and P2P1 are mean value and peak to peak of the zigzag part of ∆X diagram in central atoms which their hyperbolic coefficients are listed in Tables 2 and 3, respectively. P2P2 is the amount of peak to peak after the changing of the D cc obtained from the formula (18). The figures obtained from MATLAB programs have proven the improvements which we refuse to draw these figures because of their numbers and being repetitious.

Now, we consider D cc in Y direction. If we look at the Figs. 10, 11, and 12, again, we can observe a slope in central atoms. This slope shows that the D cc we considered in this direction, is different than the last one, and we can remove the slope by improving it. Using the Eq. (3) and considering the fact that slope in this diagram means the change of ∆Y in two next atoms in Y direction, the following equation can be easily written as:

$$\Delta D_{\text{ccy}} = - \frac{2}{\sqrt 3 } S_{1} .$$
(20)

The parameter S 1 is the amount of obtained slope before applying the change in D cc in Y direction which its hyperbolic coefficients are shown in Table 6. We achieved other diagrams using MATLAB programs for this state, which confirms the validity of our sayings. However, we refuse to draw these figures because of their numbers and being repetitious.

Now that we can have an estimation from existing differences in D cc in two various directions, we compute both changes by using the formulas (18) and (20) for specific dimer number, for example, N y  = 29, for the state of AGNR without hydrogen. These values are approximately equal to:

$$\Delta D_{\text{ccx}} \approx \% 0.4,\quad \;\Delta D_{\text{ccy}} \approx \% 0.06.$$
(21)

We can see that the amount of change is different in two directions of AGNR. Regarding to the value of D cc for graphene (D cc ≈ 1.42 Å), the difference between C–C bond lengths is approximately 0.005 Å. As another example, the value for N y  = 5, it is nearly 0.017 Å, and it reduces to zero when the dimer number goes to infinity.

Conclusions

We proposed a general hyperbolic formula, and we proved that the way the AGNRs bandgap energy is relatable, there are lots of other parameters, which can be shown by this formula. In this way, we showed that the atomic positions of all carbon atoms in AGNRs can be calculated by the formula, and so we can perform the analysis without the need to its structural relaxations. Using obtained equations, we did the structural relaxations for AGNRs with different dimer numbers again, and could reduce the analysis times, 4–7 times. We also showed that the edge effect would not be only for the first edge atom, and this effect can be observed in the couple of atoms close the edges.

We also showed that the C–C bond length is slightly different for each various directions. This difference is about 0.017 Å for AGNRs with small dimer numbers and is reduced to zero for AGNRs with large width (graphene).