Introduction

Soliton is a localized structure which can propagate in medium without diffraction spreading. Ion acoustic soliton, electrostatic soliton and electromagnetic soliton (EM) are different types of solitons that could be created in plasma medium [1,2,3,4]. EM soliton is one of the spectacular phenomena due to the nonlinear interaction between high intensity laser pulse and plasma. The electromagnetic solitons have reach variety applications such as laser fusion, plasma-based particle accelerators and etc. [5, 6]. This type of soliton is a result of various physical effects that betide in the propagation of strong laser pulse through plasma, including relativistic mass change of electrons, alteration of plasma density due to ponderomotive force and dispersion effects. The electromagnetic solitons were investigated by Kozlov et al. [7]. In the theoretical aspects, EM solitons are assumed as coupling between modulated laser pulse and electron plasma wave that have been studied by many different researchers continuously [8, 9]. For discussion on the formation and features of EM soliton, the Maxwell and fluid equations should be solved. A multiple scales technique is used to solve the fluid-Maxwell equations in cold plasma [10,11,12,13,14]. Kuehl and Zhang [15] have expressed the creation of bright and dark EM soliton in weakly relativistic approximation. Also, Borhanian et al. [16] employed same technique for investigation of EM solitons in magnetized plasma.

The presence of energetic particles in plasma, is an inherent factor in many space and laboratory evidences [17, 18]. In this case, the distribution function of plasma’s particles don’t obey Maxwell–Boltzmann distribution function [19]. It is obvious, existence and feature of nonlinear phenomena in plasma tightly depend on properties of plasma and distribution function of particles.

Observations by Viking spacecraft [20] and Freja satellite [21] indicated on existence of electrostatic solitary structure in magnetosphere which couldn’t be expressed by Maxwell distribution function.

The nonthermal distribution function for plasma’s particles of was proposed by Cairns et al. This distribution function could express the presentation of rarefactive ion sound solitons very similar to those observed by Freja satellite and Viking spacecraft [22]. In the nonthermal distribution function, population of the nonthermal particles are shown by α which could vary between 0 and 1. In the case α → 0, the Maxwellian distribution function is recovered. Many researchers have assumed the Cairns distribution function in plasma’s model and investigated the phenomena in the presence of these particles [23,24,25]. In an attempt to generalize the Boltzmann–Gibbs (BG) entropy, Tsallis proposed the nonextensive statistical mechanic to describe the systems with long interaction [26, 27], as usually happen in astrophysics and plasma physics. Nonextensive statistic has been used for describing various phenomena in plasma such as dissipative optical lattices [28], plasma wave propagation [29, 30]. The foremost character of Tsallis distribution function, is q parameter which stands on the degree of nonextensivity. The nonextensive parameter has two separate states. For −1 < q < 1, particles cover all velocity. While in q > 1, the distribution function has a cutoff on the maximum permitted value for velocity of the particles, given by \( v_{\hbox{max} } = \sqrt {2 /\left( {q - 1} \right)} v_{T} \). In which, \( v_{T}^{2} = 2kT /m \) is thermal velocity of the plasma particle, T and m is the temperature and mass of the particle respectively. In the case q < −1, distribution function is unnormalized.

Comparison of Maxwellian and nonextensive distribution function demonstrate, for q > 1, high energy states are more likely in the Maxwellian distribution function. Although, for −1 < q < 1 high energy status are more probable in the nonextensive distribution function. In condition, q → 1, Tsallis distribution function converts to Maxwell–Boltzmann distribution function.

Ion acoustic solitary wave was investigated in a two component plasma with nonextensive electrons by Tribeche et al. [31]. They realized this model of plasma could explain both rarefactive and compressive solitons. A recent study by them has proposed a hybrid Cairns–Tsallis distribution function, which purports to offer enhanced parametric flexibility in modeling nonthermal plasmas. Whereas such a two-parameter demonstration of the distribution function could be useful in fitting to a wider range of experimental plasmas. Subsequently, Amour et al. [32] applied this distribution to the study of acoustic solitary. Motivated by these efforts to explain various phenomena in the presence of non-Maxwellian particles, we investigate the electromagnetic soliton in non-Maxwellian plasma.

In the present paper we analyze the circularly polarized intense EM wave propagating in a weakly relativistic plasma. The electrons of plasma obey the mixed Cairns–Tsallis distribution function. The ions of plasma are assumed to be stationary. The relevant nonlinear Schrödinger equation is introduced. Roles of mixed electrons on the existence of bright and dark solitons and amplitude of them were discussed in detail.

The layout of this article goes as follows; following the introduction in “Introduction” section, we present the basic equations describing the dynamics of the nonlinear interaction of laser and plasma. We use the reductive perturbation method to derive the nonlinear Schrödinger (NLS) equation. In “Results and discussion” section, numerical results and discussion are presented and finally “Conclusion” section is devoted to conclusion.

Model description

We start with description of the propagation of a circularly polarized electromagnetic pulse in a weakly relativistic plasma in x direction. In this paper, we consider collisionless, unmagnetized, two component plasma, and ion is assumed as immoble singly charged positive particle. Then, we employ the momentum and continuity equations for electrons as Eqs. (1)–(2) respectively. Equations (3) and (4) are giving an expressions for the Poisson’s equation and electromagnetic wave equation in the Coulomb gauge

$$ m_{e} N_{e} \left( {\frac{\partial }{\partial t} + v_{e} \cdot \nabla } \right)v_{e} = - eN_{e} E - \frac{e}{c}N_{e} v_{e} \times B - \nabla \cdot P_{e} $$
(1)
$$ \frac{{\partial N_{e} }}{\partial t} + \frac{\partial }{\partial x}\left( {N_{e} v_{e} } \right) = 0 $$
(2)
$$ \frac{{\partial^{2} \phi }}{{\partial x^{2} }} = 4\pi e\left( {N_{e} - N_{i} } \right) $$
(3)
$$ \frac{{\partial^{2} \varvec{A}}}{{\partial x^{2} }} - \frac{1}{{c^{2} }}\frac{{\partial^{2} \varvec{A}}}{{\partial t^{2} }} - \frac{1}{c}\frac{\partial }{\partial t}\nabla \phi = \frac{4\pi e}{c}\left( {N_{e} v_{e} - N_{i} v_{i} } \right) $$
(4)

with one-dimensional approximation in which ∂/∂y = ∂/∂z = 0, set of the normalized hydrodynamic equations (continuity and momentum) for electrons of plasma and Maxwell’s equations for the scalar and vector potentials, ϕ and A, can be written as

$$ n_{e} \left( {\frac{\partial }{\partial t} + u_{e} \frac{\partial }{\partial x}} \right)\left( {\gamma u_{e} } \right) = n_{e} \frac{\partial \phi }{\partial x} - \frac{{n_{e} }}{2\gamma }\frac{{\partial A_{ \bot }^{2} }}{\partial x} - \frac{1}{{m_{0} N_{0} c^{2} }}\frac{{\partial P_{e} }}{\partial x} $$
(5)
$$ u_{e \bot } = \frac{{A_{ \bot } }}{{\gamma_{e} }} $$
(6)
$$ \frac{{\partial n_{e} }}{\partial t} + \frac{\partial }{\partial x}\left( {n_{e} u_{e} } \right) = 0 $$
(7)
$$ \frac{{\partial^{2} \phi }}{{\partial x^{2} }} = n_{e} - 1 $$
(8)
$$ \frac{{\partial^{2} A_{ \bot } }}{{\partial x^{2} }} - \frac{{\partial^{2} A_{ \bot } }}{{\partial t^{2} }} = \frac{{n_{e} A_{ \bot } }}{\gamma }y $$
(9)

Here γ is the relativistic factor.

$$ \gamma = \sqrt { (1 + A_{ \bot }^{2} ) / (1 - u_{e}^{2} )} $$
(10)

In writing the above equations, length, time, velocity, scalar and vector potential and density are normalized over c/ω pe0, \( \omega_{pe0}^{ - 1} \), c, m 0 c 2/e and N 0, respectively; \( \omega_{pe0} = \sqrt {4\pi N_{0} e^{2} /m_{0} } \) is the electron plasma frequency. m 0 is the rest mass of electron and N 0 is the unperturbed electron background density.

We also rewrite momentum equation in parallel direction by using following expression

$$ \frac{{\partial P_{e} }}{\partial x} = \left( {\frac{{{\text{d}}P_{e} / {\text{d}}\phi }}{{{\text{d}}N_{e} / {\text{d}}\phi }}} \right)\frac{{\partial N_{e} }}{\partial x} \equiv \left( {\frac{{{\text{d}}P_{e} }}{{{\text{d}}N_{e} }}} \right)_{\phi = 0} \frac{{\partial N_{e} }}{\partial x} = m_{0} c_{se}^{2} \frac{{\partial N_{e} }}{\partial x} $$
(11)

where

$$ c_{se}^{2} = \left[ {\frac{1}{{m_{0} }}\left( {\frac{{{\text{d}}P_{e} }}{{{\text{d}}N_{e} }}} \right)_{\phi = 0} } \right] $$
(12)

As it is mentioned, in our plasma model, the electrons distribution function of plasma obey the Cairns–Tsallis distribution function as follow [31, 32]

$$ f_{e} \left( {v_{x} } \right) = C_{q,\alpha } \left( {1 + \alpha \frac{{v_{x}^{4} }}{{v_{te}^{4} }}} \right)\left\{ {1 - \left( {q - 1} \right)\frac{{v_{x}^{2} }}{{2v_{te}^{2} }}} \right\}^{{\frac{1}{q - 1}}} $$
(13)

where C q,α is the constant of normalization which depends on q and α

$$ C_{q,\alpha } = N_{0} \sqrt {\frac{{m_{e} }}{{2\pi T_{e} }} } \frac{{\Gamma \left( {\frac{1}{1 - q}} \right)\left( {1 - q} \right)^{5/2} }}{{\Gamma \left( {\frac{1}{1 - q} - \frac{5}{2}} \right)\left[ {3\alpha + \left( {\frac{1}{1 - q} - \frac{3}{2}} \right)\left( {\frac{1}{1 - q} - \frac{5}{2}} \right)\left( {1 - q} \right)^{2} } \right]}}\quad {\text{for}}\; - 1 < q < 1 $$

and

$$ C_{q,\alpha } = N_{0} \sqrt {\frac{{m_{e} }}{{2\pi T_{e} }} } \frac{{\Gamma \left( {\frac{1}{1 - q} + \frac{3}{2}} \right)\left( {q - 1} \right)^{5/2} \left( {\frac{1}{1 - q} + \frac{3}{2}} \right)\left( {\frac{1}{1 - q} + \frac{5}{2}} \right)}}{{\Gamma \left( {\frac{1}{1 - q} + 1} \right)\left[ {3\alpha + \left( {\frac{1}{1 - q} - \frac{3}{2}} \right)\left( {\frac{1}{1 - q} - \frac{5}{2}} \right)\left( {1 - q} \right)^{2} } \right]}}\quad {\text{for}}\;q > 1 $$
(14)

Here α is the parameter indicating the proportion of nonthermal electrons and q implicates nonextensive parameter, and Γ represents the standard Gamma function.

To derive the number density expression in the Cairns–Tsallis distribution function, Eqs. (13)–(14) are employed with replacing \( v_{x}^{2} \) by \( v_{x}^{2} - \left( {2e\varphi /m_{e} } \right) \) in two ranges, q > 1 and −1 < q < 1. Then

$$ \begin{aligned} N_{e} \left( \phi \right) & = \left\{ {\begin{array}{*{20}l} {\int_{{ - v_{\hbox{max} } }}^{{v_{\hbox{max} } }} {f_{e} \left( {v_{x} } \right){\text{d}}v_{x} } } \hfill & { q > 1} \hfill \\ {\int_{ - \infty }^{ + \infty } {f_{e} \left( {v_{x} } \right){\text{d}}v_{x} } } \hfill & { - 1 < q < 1} \hfill \\ \end{array} } \right. \\ & = N_{e0} \left\{ {1 + \left( {q - 1} \right)\frac{e\phi }{{kT_{e} }}} \right\}^{{\frac{1}{q - 1} + \frac{1}{2}}} \times \left\{ {1 + A\left( {\frac{e\phi }{{kT_{e} }}} \right) + B\left( {\frac{e\phi }{{kT_{e} }}} \right)^{2} } \right\} \\ \end{aligned} $$
(15)

where the confidences of A and B are expressed as

$$ A = - 16q\alpha /(3 - 14q + 15q^{2} + 12\alpha ) $$
(16)
$$ B = 16\,(2q - 1)q\alpha /(3 - 14q + 15q^{2} + 12\alpha ) $$
(17)

It is noted in the case q → 1, nonextensive density converts to pure Cairns et al. (nonthermal) as follow

$$ N_{e} \left( \phi \right) = N_{e0} \left\{ {1 + A\left( {\frac{e\phi }{{kT_{e} }}} \right) + B\left( {\frac{e\phi }{{kT_{e} }}} \right)^{2} } \right\}\exp \left( {\frac{e\phi }{{kT_{e} }}} \right) $$
(18)

Beside, in the limit α = 0, Tsallis pure density is recovered as

$$ N_{e} \left( \phi \right) = N_{e0} \left\{ {1 + \left( {q - 1} \right)\frac{e\phi }{{kT_{e} }}} \right\}^{{\frac{1}{q - 1} + \frac{1}{2}}} $$
(19)

it is useful to determine the integral \( \left\langle {v_{x}^{2} } \right\rangle = \int {v_{x}^{2} f_{e} \left( {v_{x} } \right){\text{d}}v_{x} } \) over all permitted velocity as follow

$$ \begin{aligned} v_{x}^{2} & = \left\{ {\begin{array}{*{20}l} {\int_{{ - v_{\hbox{max} } }}^{{v_{\hbox{max} } }} {v_{x}^{2} f_{e} \left( {v_{x} } \right){\text{d}}v_{x} } } \hfill & {q > 1} \hfill \\ {\int_{ - \infty }^{ + \infty } {v_{x}^{2} f_{e} \left( {v_{x} } \right){\text{d}}v_{x} } } \hfill & { - 1 < q < 1} \hfill \\ \end{array} } \right. \\ & = \frac{{2\left( {35q^{2} - 46q + 60\alpha + 15} \right)}}{{\left( {7q - 5} \right)\left[ {12\alpha + \left( {5q - 3} \right)\left( {3q - 1} \right)} \right]}}N_{0} v_{t}^{2} \\ \end{aligned} $$
(20)

it is noted that the kinetic energy should be positive. So, the acceptable range for q is narrowed to the area that mean value of square velocity to be positive. Moreover, it is well known that the Cairns distribution for α > 0.25 presents unstable behavior as it develops side wings, possibly leading to a kinetic instability. One would not expect stable nonlinear structures such as solitons to be supported by such a linearly unstable situation. That implies a need to introduce a cutoff in α governed by this consideration [33]. Indeed Williams et al. [3] demonstrated that the region for nonextensive parameter in the case −1 < q < 1, is restricted to 0.6 < q < 1.

Using of Eq. (20), the pressure term in Eq. (5) is determined as

$$ P_{e} = \frac{{m_{0} }}{3}\int {v^{2} f_{e} \left( v \right){\text{d}}v} = \frac{{2\left( {35q^{2} - 46q + 60\alpha + 15} \right)}}{{3\left( {7q - 5} \right)\left[ {12\alpha + \left( {5q - 3} \right)\left( {3q - 1} \right)} \right]}}N_{0} kT_{e} $$
(21)

By replacing Eqs. (10), (21) in the momentum equation, Eq. (5) is written in the following model

$$ n_{e} \frac{\partial }{\partial t}\left( {\gamma u_{e} } \right) = n_{e} \frac{\partial }{\partial x}\left( {\phi - \gamma } \right) - \frac{{c_{se}^{2} }}{{c^{2} }}\frac{{\partial n_{e} }}{\partial x} $$
(22)

Now we apply the multiple scales technique [34] to treat Eqs. (7)–(10) and (22). According to this method, the amplitude of all wave harmonics such as density, velocity, scalar and vector potential will be assumed to have an envelope with the slower space/time evolution which are distinguish from the fast carrier wave (phase) dynamics. Let S = (n, u, Φ, A) is given by

$$ S = S^{(0)} + \sum\limits_{n = - \infty }^{n} {\varepsilon^{n} S^{(n)} } $$
(23)

where S (0) = (1, 0, 0, 0) indicates the equilibrium state of the system and ε is a smallness parameter which provides evolution equations for different harmonic amplitude in successive orders ε n. We suppose S (n), the perturbed state, contains fast and slow part as

$$ S^{(n)} = \sum\limits_{l = - \infty }^{\infty } {S_{l}^{\left( n \right)} \left( {X_{m \ge 1} ,T_{m \ge 1} } \right)\exp \left( {il(kx - \omega t)} \right)} $$
(24)

The fast variables of state depend on the phase ψ = kx − ωt, which k and ω are the normalized wave number and frequency of the pulse by k pe  = ω pe /c and ω pe . The slow part, enter the argument of the l-th harmonic amplitude \( S_{l}^{(n)} \), depends on the stretched space and time slowly, which are considered as

$$ X_{m} = \varepsilon^{m} x,\quad T_{m} = \varepsilon^{m} t $$
(25)

It must be noted that m = 0 corresponds to the fast carrier space/time scale, while m ≥ 1 corresponds to the slower envelope scales. Assuming variable independence, time and space differentiation are obtained as follow

$$ \frac{\partial }{\partial t} = \frac{\partial }{{\partial t_{0} }} + \varepsilon \frac{\partial }{{\partial T_{1} }} + \varepsilon^{2} \frac{\partial }{{\partial T_{2} }} + \cdots $$
(26)
$$ \frac{\partial }{\partial x} = \frac{\partial }{{\partial x_{0} }} + \varepsilon \frac{\partial }{{\partial X_{1} }} + \varepsilon^{2} \frac{\partial }{{\partial X_{2} }} + \cdots $$
(27)

For obtaining the set of reduced equations, using Eqs. (23)–(24), all parameters are defined as

$$ S = S^{\left( 0 \right)} + \varepsilon S_{0}^{\left( 1 \right)} + \varepsilon S_{1}^{\left( 1 \right)} e^{i\psi } + \varepsilon^{2} S_{0}^{\left( 2 \right)} + \varepsilon^{2} S_{1}^{\left( 2 \right)} e^{i\psi } + \varepsilon^{2} S_{2}^{\left( 2 \right)} e^{2i\psi } + \varepsilon^{3} S_{0}^{\left( 3 \right)} + \varepsilon^{3} S_{1}^{\left( 3 \right)} e^{i\psi } + \varepsilon^{3} S_{2}^{\left( 3 \right)} e^{2i\psi } + \varepsilon^{3} S_{3}^{\left( 3 \right)} e^{3i\psi } + c.c $$
(28)

For all state variables, the reality condition as \( S_{ - l}^{\left( n \right)} = S_{l}^{\left( n \right)*} \) is true. By replacing Eqs. (26)–(28) into Eqs. (7)–(10) and (22) and collect the terms of the same order in ε for l-th harmonic amplitudes, \( S_{l}^{(n)} \), the set of reduced equations are obtained which must be solved separately.

In the first order (n = 1) and for zeroth harmonic (l = 0), equations convert to

$$ n_{0}^{(1)} = u_{0}^{(1)} = A_{0}^{(1)} = 0 $$
(29)

For the first harmonic of the first order (n = 1, l = 1) the following relations are get

$$ - \omega n_{1}^{(1)} + ku_{1}^{(1)} = 0 $$
(30)
$$ - k^{2} \phi_{1}^{(1)} = n_{1}^{(1)} $$
(31)
$$ \left( {\omega^{2} - k^{2} } \right)A_{1}^{(1)} = A_{1}^{(1)} $$
(32)
$$ \omega u_{1}^{(1)} + k\phi_{1}^{(1)} = 0 $$
(33)

from Eq. (32) linear dispersion relation for the propagation of electromagnetic wave into plasma is obtained as ω 2 − k 2 = 1, indeed from other equations, we have

$$ n_{1}^{(1)} = u_{1}^{(1)} = \phi_{1}^{(1)} = 0 $$
(34)

It is obvious, there are not any perturbation in electron density, parallel velocity, and scalar potential in the first order.

For the second order and the zeroth harmonic amplitude, it is obtained

$$ n_{0}^{(2)} = u_{0}^{(2)} = A_{0}^{(2)} = \frac{{\partial \phi_{0}^{(1)} }}{{\partial X_{1} }} = 0 $$
(35)

For the second order and first harmonics (n = 2, l = 1) equations convert to

$$ n_{1}^{(2)} = u_{1}^{(2)} = \phi_{1}^{(2)} = 0 $$
(36)
$$ \frac{{\partial A_{1}^{(1)} }}{{\partial T_{1} }} + v_{\text{g}} \frac{{\partial A_{1}^{(1)} }}{{\partial X_{1} }} = 0 $$
(37)

Here \( v_{\text{g}} = \frac{k}{\omega } \), is the group velocity and this relation indicates, up to second order of ε, wave packet moves with constant group velocity.

Proceeding in the perturbation analysis, for (n = 2, l = 2) we have

$$ u_{2}^{(2)} = \frac{\omega }{k}n_{2}^{(2)} $$
(38)
$$ - 4k^{2} \phi_{2}^{(2)} = n_{2}^{(2)} $$
(39)
$$ \omega u_{2}^{(2)} = \frac{k}{2}\left( {A_{1}^{(1)} } \right)^{2} - k\phi_{2}^{(2)} + k\frac{{c_{se}^{2} }}{{c^{2} }}n_{2}^{(2)} $$
(40)

Then we could derive second harmonics in the density perturbation as a result of nonlinear self-interaction of wave envelope as

$$ n_{2}^{(2)} = \frac{{2k^{2} }}{{\left( {4\omega^{2} - 1 - 4k^{2} \frac{{c_{se}^{2} }}{{c^{2} }}} \right)}}\left( {A_{1}^{(1)} } \right)^{2} $$
(41)

Finally, for the third order perturbation following relations are obtained.

In the zeroth harmonics (n = 3, l = 0)

$$ \phi_{0}^{(2)} = \frac{{\left| {A_{1}^{(1)} } \right|^{2} }}{2} $$
(42)

This relation indicates that zeroth scalar potential is generated by nonlinear self-interaction of envelope.

For the first harmonic (n = 3, l = 1)

$$ n_{1}^{(3)} = u_{1}^{(3)} = \phi_{1}^{(3)} = 0 $$
(43)

And wave equation converts to

$$ i\left( {\frac{{\partial A_{1}^{(1)} }}{{\partial T_{2} }} + v_{\text{g}} \frac{{\partial A_{1}^{(1)} }}{{\partial X_{2} }}} \right) + \frac{1}{2\omega }\left( {\frac{{\partial^{2} A_{1}^{(1)} }}{{\partial X_{1}^{2} }} - \frac{{\partial^{2} A_{1}^{(1)} }}{{\partial T_{1}^{2} }}} \right) + \frac{3}{4\omega }\left| {A_{1}^{(1)} } \right|^{2} A_{1}^{(1)} - \frac{1}{2\omega }n_{2}^{(2)} A_{1}^{(1)*} = 0 $$
(44)

Using by Eqs. (37) and (41) in Eq. (44), the following equation is obtained

$$ i\left( {\frac{{\partial A_{1}^{(1)} }}{{\partial T_{2} }} + v_{\text{g}} \frac{{\partial A_{1}^{(1)} }}{{\partial X_{2} }}} \right) + P\frac{{\partial^{2} A_{1}^{(1)} }}{{\partial X_{1}^{2} }} + Q\left| {A_{1}^{(1)} } \right|^{2} A_{1}^{(1)} = 0 $$
(45)

where

$$ P = \frac{1}{{2\omega^{3} }} $$
(46)

and

$$ Q = \frac{3}{4\omega } - \frac{{k^{2} }}{{\omega \left( {4\omega^{2} - 1 - 4k^{2} \frac{{c_{se}^{2} }}{{c^{2} }}} \right)}} $$
(47)

are the dispersion and nonlinear coefficients, respectively. By introducing the coordinate transformation ξ = x − v g t and τ = t, Eq. (45) converts to the nonlinear Schrödinger equation as

$$ i\frac{\partial a}{\partial \tau } + P\frac{{\partial^{2} a}}{{\partial \xi^{2} }} + Q\left| a \right|^{2} a = 0 $$
(48)

where a represents the slower component of the vector potential as

$$ A \cong A_{1}^{(1)} {\text{e}}^{i(kx - \omega t)} + c.c = a{\text{e}}^{i(kx - \omega t)} + c.c $$
(49)

Equation (48) indicates the wave envelope modulation with the effects of dispersion and nonlinearity terms. It could be predicted different types of envelop excitation in the propagation of laser in plasma. We consider the solution as follow for the nonlinear Schrödinger equation.

$$ a = R\,{ \exp }\left( {i\Theta } \right) $$
(50)

then Eq. (48) converts to KdV equation as

$$ \frac{{\partial^{2} R}}{{\partial \xi^{2} }} + \frac{Q}{P}R^{3} - \frac{E}{P}R = 0 $$
(51)

where E is the positive constant value, Θ indicates the phase correction, and \( \partial\Theta /\partial x = v\left( {x,t} \right) \) [35].

The first integral of Eq. (51) is

$$ \frac{1}{2}\left( {\frac{\partial R}{\partial \xi }} \right)^{2} + \frac{Q}{P}R^{4} - \frac{E}{P}R^{2} = {\text{constant}} $$
(52)

which can be assumed as energy equation for pseudo-particle. So, the Sagdeev potential is as follow

$$ V\left( R \right) = \frac{Q}{P}R^{4} - \frac{E}{P}R^{2} $$
(53)

In the present paper we assume v = v 0 as a constant.

If in the above equation, (Q/P) > 0 and (E/P) > 0, the Sagdeev potential has a minimum and bright soliton is formed [36].

In this case R is satisfied the following boundary conditions in the \( \xi \)-space

$$ \mathop {\lim }\limits_{\xi \to \pm \infty } R\left( \xi \right) = 0 $$
(54)

and Eq. (51) has the following bright soliton answer as

$$ R\left( \xi \right) = R_{0} {\text{sech}}\left( {\frac{{\xi - v_{0} \tau }}{L}} \right) $$
(55)

where \( R_{0} = \sqrt {2E /Q} ,\,L = \sqrt {P /E} \) is the amplitude and width of the pulse respectively. \( v_{0} \) represents the bright soliton envelope group velocity. The amplitude and width of soliton are independent of velocity and LR 0 = (2P/Q)1/2 = constant.

On the other side, if in Eq. (51) (Q/P) < 0 and (E/P) < 0, bright soliton will not be formed in the plasma medium. In this case, we consider R with the following boundary condition

$$ \mathop {\lim }\limits_{\xi \to \pm \infty } R\left( \xi \right) = \left| {R_{0} } \right| $$
(56)

in which

$$ R\left( \xi \right) \equiv R_{0} + R_{1} \left( \xi \right) $$
(57)

where \( \mathop {\lim }\limits_{\xi \to \pm \infty } R_{1} \left( \xi \right) = 0 \)

As a result, dark soliton will be formed which intensity of wave packet is zero at the center of pulse and reaches a nonzero value at the boundary. The dark soliton can be express as follow

$$ R\left( \xi \right) = \left| {R_{0} \tanh \left( {\frac{{\xi - v_{0} \tau }}{L}} \right)} \right| $$
(58)

where \( R_{0} = \sqrt {2E /Q} ,\;L = \sqrt {P /E} \) are the amplitude and width of the pulse respectively. The amplitude of the pulse does not depend on velocity of the pulse as was discussed in the case of bright type soliton.

Result and discussion

The coupling between the transverse electromagnetic wave and plasma wave could lead to form the EM soliton. In this paper distribution function of electron is assumed to be mixed. The influence of nonextensive and nonthermal parameters on the structure of bright and dark solitons are discussed.

Equation (51) looks like as energy equation of a pseudo-particle. First term is kinetic energy, while two other terms refer to potential energy or Sagdeev potential. For determining soliton solution, Sagdeev potential should have at least one maximum or one minimum. If (Q/P) > 0 and (E/P) > 0, Sagdeev potential has a minimum and the bright soliton would be arisen. While for (Q/P) < 0 and (E/P) < 0 Sagdeev potential has two symmetric maximum on the two sides of R = 0 [36]. The sort of soliton (bright or dark) depends on sign of Q and P, consequently. It is obvious, P is positive, and the magnitude of its decreases as frequency increase. The dispersion term, P, is independent of value of nonextensive and nonthermal parameters. While, sign and value of nonlinear term, Q, depends on the fast varying frequency, population of nonthermal electrons and nonextensive parameters.

In Figs. 1, 2 and 3, the variation of nonlinear term, Q in Eq. (47), is plotted versus ω for kT e  = 1 MeV and α = 0.2 for two different region of nonextensive parameter. As it is mentioned, there are two different regions for q. The nonextensive parameter can vary in 0.6 < q < 1 or q > 1. Since the kinetic energy must be positive value, it is necessary that the nonextensive parameter to be more than 0.8 for α = 0.2 [3]. In Fig. 1, q is 0.8, 0.9 and 1. In the limit q = 1, distribution function tends to the nonthermal distribution function. It is shown, there are singularity in the nonlinear terms for all value of nonextensive parameters. The nonlinear term, Q, contains two nonlinear terms. The first term, Q 1 = 3/4ω stands on the relativistic nonlinearity. On the other hand, \( Q_{2} = k^{2} /\omega \left( {4\omega^{2} - 1 - 4k^{2} \frac{{c_{se}^{2} }}{{c^{2} }}} \right) \) indicates the electron density perturbation due to ponderomotive force and pressure. The relativistic nonlinearity diminishes as frequency increases, and it is invariable for all magnitude of q and α. The value and signs of the second term, Q 2, depends tightly on frequency, nonextensive and nonthermal parameters of plasma. The second nonlinear term, Q 2 is positive and less than relativistic nonlinearity in ω < ω 1. While, it is positive and is more than relativistic nonlinearity term, in the range ω 1 < ω < ω 2, where \( \omega_{1} = \sqrt {(3\beta^{2} + 0.25) / (3\beta^{2} - 2)} \), \( \omega_{2} = 0.5\sqrt {(1 - 4\beta^{2} ) /(1 - \beta^{2} )} \) and

$$ \beta^{2} = \frac{1}{3}\frac{{kT_{e} }}{{m_{e} c^{2} }}\frac{{2\left( {35q^{2} - 46q + 60\alpha + 15} \right)}}{{\left( {7q - 5} \right)\left[ {12\alpha + \left( {5q - 3} \right)\left( {3q - 1} \right)} \right]}} $$
(59)
Fig. 1
figure 1

Variation of Q is plotted versus ω for kT e  = 1 MeV, α = 0.2 and q = 0.8, 0.9 and 1

Full size image
Fig. 2
figure 2

Variation of Q is plotted versus ω for kT e  = 1 MeV, α = 0.2 and q = 1.2, 1.3 and 1.4

Full size image
Fig. 3
figure 3

Variation of Q is plotted versus ω for kT e  = 1 MeV, α = 0.2 and q = 1.5, 2 and 5

Full size image

Therefore, the nonlinear term in ω 1 < ω < ω 2 is negative and the dark EM soliton could be developed. In the steady nonthermal parameter, by increasing q, its region be wider. It is noted, out of mentioned region, Q 2 is negative, so the nonlinear term is positive. As a result, the bright EM soliton could be performed for all value of nonextensive parameter.

By increasing of nonextensive parameter, more than 1, feature of mixed distribution function is substituted. In the region q > 1, raising of nonextensive parameter makes reducing of probability of high energy electron’s existence. In α = 0.2 and q = 1.1, there is singularity in the nonlinear term. Whereas, for q ≥ 1.2 in the same nonlinear parameter, Q declines as frequency increases. In Fig. 2, the variation of Q is shown versus ω for kT e  = 1 MeV, α = 0.2 and q = 1.2, 1.3 and 1.4. As it is shown, for q = 1.2, and ω approximately more than 2.2, the nonlinear term is negative. It indicates, the dark EM soliton is formed in plasma. But, for q = 1.3 and q = 1.4, the nonlinear term is positive for all frequency, so only bright EM soliton is performed. This figure, denotes, for α = 0.2, by increasing of the nonextensive parameter from 1.2 to 1.3, dark soliton converts to the bright soliton.

In Fig. 3, the variation of Q is plotted versus ω for kT e  = 1 MeV, α = 0.2 and q = 1.5, 2 and 5. The second nonlinear term, in the plasma with α = 0.2 and q ≥ 1.3 is positive and less than relativistic term, for all amount of frequency. So, the bright soliton is organized in this case. By increasing frequency, Q 2 increases in low frequency and then reduces in higher magnitude of frequency. Checking of the second nonlinearity term specifies that it decreases as nonextensive parameter raises. Therefore, as q increases, the influence of pressure term diminishes. a result, in the region q > 1.3, nonlinear term, Q, increases by enhancement of q for steady value of α.

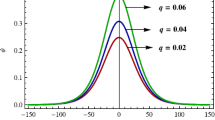
In this paper, the distribution function of electrons are assumed to obey Cairns–Tsallis model. In mixed model, there are two flexible parameters to vary, nonthermal and nonextensive. In Fig. 4, the variation of Q is shown versus ω for kT e  = 1 MeV for steady nonextensive parameter. The nonthermal parameter is 0, 0.1 and 0.2 for q = 0.9. In the mixed model, when nonthermal parameter tends to zero, the density of electrons convert to nonextensive distribution function. It indicates, for pure nonextensive distribution with q = 0.9, the nonlinear term decrease as frequency arises. The nonlinear term is positive, so bright soliton is formed. The positive nonlinearity requires the relativistic nonlinearity to be more than perturbation of density (Q 1 > Q 2). By increasing nonthermal parameter, population of high energy electrons grow. It represents, there are singularity for q = 0.9, α = 0.1 and α = 0.2. Therefore, accretion of the nonthermal parameter results to form the dark soliton in the limited region of frequency. By increasing of nonthermal parameter, the allowed region of frequency to perform of dark EM soliton improves and it is shifted to higher frequency.

Fig. 4
figure 4

Variation of Q is plotted versus ω for kT e  = 1 MeV, q = 0.9, α = 0, 0.1 and 0.2

Full size image

In Fig. 5, the variation of Q is plotted versus ω for kT e  = 1 MeV and state value of nonextensive parameter. The nonthermal parameter is 0, 0.1 and 0.2 for q = 1.2. It is shown, by increasing frequency, the nonlinear term falls. So, by increasing of nonthermal parameter, the nonlinear term reduces. For α = 0 and 0.1, the nonlinear term is positive for all value of frequency. Therefore, the effects of relativistic nonlinear term is more than perturbation density. As the nonthermal parameter and population of high energy particle enhance, the influence of density perturbation, Q 2, raises. It could be result that the influence of pressure decreases, while the nonlinear term increases. In q = 1.2 for α = 0 and 0.1, only bright soliton could be formed. By increasing nonthermal parameter the amplitude of the bright soliton amplifies. As the frequency increases, the nonlinear term becomes negative. So, the bright soliton converts to dark soliton in α = 0.2.

Fig. 5
figure 5

Variation of Q is plotted versus ω for kT e = 1 MeV, q = 1.2, α = 0, 0.1 and 0.2

Full size image

The contour of P/Q versus q and α is shown in Fig. 6 for ω = 1 and kT e  = 1 MeV. The coefficient of P/Q is positive except in the narrow region, between two lines. Then it is shown, for most of value of nonthermal and nonextensive parameters in the plasma with mixed distribution function, the bright soliton is formed. In Fig. 7 the variation of P/Q versus q and α is plotted for ω = 1 and kT e  = 1 MeV. In Fig. 7a, 0.8 < q < 1 and 0.1 < α < 0.2, while in Fig. 7b 1.3 < q < 1.5 and 0 < α < 0.2. As it is shown, in Fig. 6 for both of these regions the factor of P/Q is positive and the bright soliton is created in plasma. The amplitude and width of the bright soliton is independent of the velocity and LR 0 = (2P/Q)1/2 = constant [11]. As it is shown in Fig. 7, by increasing of the nonextensive parameter, P/Q decreases, so LR 0 reduces. While, growth of the nonthermal parameter has contrary effect on P/Q. In both regions of q, increasing of the nonthermal electrons lead to raise of P/Q and LR 0.

Fig. 6
figure 6

Variation of P/Q is plotted versus α and q for ω = 2

Full size image
Fig. 7
figure 7

Variation of P/Q is plotted versus α and q for ω = 2

Full size image

Conclusion

In the present paper, the role of mixed electron on properties of the relativistic electromagnetic soliton is investigated. Results show that two types of soliton, bright and dark, may be formed in the interaction of laser pulse and plasma, with mixed distribution of function. In the propagation of laser pulse into plasma, relativistic effect and perturbation of electron density modify the nonlinear term. If nonlinear term is positive, the bright soliton establishes, otherwise the dark soliton forms. Parameter of nonextensive and nonthermal of electrons and frequency of the pulse, adapt the sign and value of the nonlinear term. The nonextensive parameter is a real number, and it must be more than 0.6, while the nonthermal parameter varies in the range 0 till 0.25. It is shown by variation of nonextensive and nonthermal parameters, the sign and magnitude of the nonlinear term changes, so the properties of soliton vary. The effects of the nonthermal and nonextensive parameters are contradictory. Growing of the nonthermal electrons, increase P/Q, so the amplitude of soliton increases. While rising of the nonextensive electrons decrease P/Q, and the amplitude of soliton decreases.