Introduction

In the recent years, investigations on Schrödinger equation with position dependent mass, have been attached many attentions [1–3]. The local mass distributions is an ordinary feature in cosmology and in describing the large scale characteristics of the universe. The concept of local mass has important consequences in the scalar tensor theories of gravity. This concept has interesting features in the gravitational quantum field theories [4]. The local mass concept also has been proliferated in more applicable sciences such as the material science and condensed matter physics. The footprints of position dependent mass can be seen in the researches concerned to semiconductors [5–8], quantum wells and quantum dots [9–12], quantum liquids [13], and impurities in crystals [14].

Several methods have been applied to solve the Schrödinger equation, among which are the factorization scheme [15, 16], the path integral formulation [17], the supersymmetry approach [18], the algebraic way [19], the power series expansion [20, 21], the two-point quasi-rational approximation method [22], the shifted large-N procedure [23], the transfer matrix method [24, 25], the asymptotic iteration method [26–28], the Nikiforov-Uvarov approach [29–32], the approximation of perturbation [33] and the auxiliary field method [34].

One of the most effective methods for solving the Schrödinger equation with different sort of spherically symmetric potentials is the Laplace transformation method [35]. The advantage of this method is that a second order differential equation reduces to a first order differential equation. It was Schrödinger who used this technique for the first time in quantum physics to solve the radial eigenfunction of hydrogen atom [36]. The method has become commonly employed ever since to solve various kind of the spherically symmetric potentials [37–44].

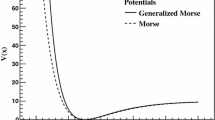
One of the significant potential for describing the vibrational and rotational movements of the diatomic molecules, is the Morse potential [45]. Solutions of the Schrödinger equation with position dependent mass for the Morse potential are investigated by applying different methods in [46–53].

A mass function has been investigated in [54] of the form \(m=m_0/(1-\delta e^{-\alpha (\frac{r-r_0}{r_0})})^2\) where \(\delta \) is a free parameter and \(0\le \delta <1\). They approximately find the solutions in the presence of the q-deformed Morse potential and by applying the Nikiforov- Uvarov method and by using the Ben Daniel and Duke Hamiltonian [55]. They discussed numerically the solutions in details. Here we consider, a similar mass function of the form \(m/m_0=a/(1+b e^{\alpha (\frac{r-r_0}{r_0})})^2\) where \(r_0\) is the equilibrium position of a typical diatomic molecule and \(\alpha \) characterizes the potential acting range. We have not apply any estimation except the Pekeris approximation. Also, We apply the point canonical transformation method [48, 56] to get ride of the first derivative of the wave function. In this way, we can suitably separate the terms contained the mass function from the terms of the field derivatives. Then, by applying some simple constraints, on the terms included the mass function, we construct the mass function in such a way that the corresponding equation can be solved via the Laplace transformation method of [40, 43].

The organization of this paper is as follows: In section two, we first introduce the initial form of the mass function with undetermined parameters. Then by considering the desired form of the Schrödinger equation which is most solvable with the Laplace transforms, we setup some constrains on our mass parameters to find the final form of the mass distribution. The parameters of the Morse potential become untouched. Then, in section three we solve the equation and introduce a possible bound state solution of the model. Finally, in the discussions and results section, the energy spectrums are presented and plotted.

A possible mass distribution

The most general form of Hamiltonian for the position dependent mass \(m=m(\mathbf r )\), is given by [5, 50]:

$$\begin{aligned} H=\frac{1}{4(a+1)}\left\{ {a\left[ \frac{1}{m}{} \mathbf P ^2+\mathbf P ^2\frac{1}{m}\right] }+ m^{\alpha } \mathbf P m^{\beta }{} \mathbf P m^{\gamma } + m^{\gamma } \mathbf P m^{\beta }{} \mathbf P m^{\alpha }\right\} +V(\mathbf r ), \end{aligned}$$
(1)

where \(\mathbf P \) denotes the momentum operator and V(r) is an arbitrary potential. Also \(\alpha \), \(\beta \), \(\gamma \) and a are the ambiguity parameters satisfying the constrain \(\alpha +\beta +\gamma =-1\). Let us consider a spherically symmetric mass function and potential function, respectively, \(m=m({\sf{r}})\) and \(V=V({\sf{r}})\) with \({\sf{r}}\) being the radial coordinate.

On account of the differentiating properties of the momentum operator \(\mathbf P \), one find the commutation relation:

$$\begin{aligned} {}[{\mathbf{P}} ,f({\textsf{r}})]={\mathbf{P}} f-f{\mathbf{P}} =-i{\hbar} \frac{{\rm d}f}{{\rm d}{{\textsf{r}}}}{\hat{{\textsf{r}}}}\, \end{aligned}$$
(2)

where f(r) is an arbitrary function of the radial coordinate r and \(\hat{r}\) is the radial unit vector. Using Eqs. (2), (1) turns into:

$$\begin{aligned} H=\frac{1}{2m}{} {\mathbf {P ^2}}+ \frac{i\hbar }{2}\frac{1}{m^2}\frac{{\rm d}m}{{\rm d}{\sf{r}}}{} {\mathbf {P}} _{\mathbf{r }}+U_{\alpha ,\beta ,\gamma ,a}({\sf{r}}) \end{aligned}$$
(3)

where

$$\begin{aligned} U_{\alpha ,\beta ,\gamma ,a}({\sf{r}})=-\frac{\hbar ^2}{4m^3(a+1)}\left[ (\alpha +\gamma -a)m\frac{{\rm d}^2 m}{{\rm d}{\sf{r}}^2}+2(a-\alpha -\gamma -\alpha \gamma )\left( \frac{{\rm d}m}{{\rm d}{\sf{r}}}\right) ^2\right] + V({\sf{r}}). \end{aligned}$$
(4)

In a special case, the effective potential \(U_{\alpha ,\beta ,\gamma ,a}({\sf{r}})\) can be reduced to \(U_{\alpha ,\beta ,\gamma ,a}({\sf{r}})=V({\sf{r}})\) by imposing some conventional constrain on the ambiguity parameters namely: \((\alpha +\gamma -a)=0\) and \((a-\alpha -\gamma -\alpha \gamma )=0\) which has two possible solutions (i) \(\alpha =0\) and \(a=\gamma \) or (ii) \(a=\alpha \) and \(\gamma =0\) [50]. Here, we are interested in this case where the Schrödinger equation yields:

$$-\frac{\hbar ^2}{2m}\left[ \nabla ^2-\frac{1}{m}\frac{{\rm d}m}{{\rm d}{\textsf{r}}}\nabla_{\sf{r}} \right] \varphi ({\mathbf {r}})=\left[ E-V({\textsf{r}}) \right]\varphi({\mathbf{r}}). $$
(5)

In the spherically symmetric case, which is considered here, the wave function can be separated to the following form:

$$\begin{aligned} \varphi (\mathbf r )=\frac{1}{\sf{r}}\psi _{\ell }({\sf{r}})\mathrm {Y}_{\ell m}(\theta ,\phi ). \end{aligned}$$
(6)

Inserting Eq. (6) into (5), the first term can be expressed as:

$$\begin{aligned} \nabla ^2 \varphi ({\mathbf {r}} )= \frac{\mathrm {Y}_{\ell m }(\theta ,\phi ) }{\sf{r} } \left[ \frac{d^2}{{\rm d}{\sf{r}}^2}-\frac{\ell (\ell +1)}{r^2} \right] \psi _{\ell }({\sf{r}} ) \end{aligned}$$
(7)

and the second term as

$$\begin{aligned} \frac{1}{m}\frac{{\rm d}m}{{\rm d}{\sf{r}}}\nabla _{\sf{r}} \varphi ({\mathbf {r}} )=-\frac{ \mathrm {Y}_{\ell m}(\theta ,\phi )}{{\sf{r}}~ m}\frac{{\rm d}m}{{\rm d}{\sf{r}}}\left( \frac{1}{{\sf{r}}}-\frac{d}{{\rm d}{\sf{r}}}\right) \psi _{\ell }({\sf{r}} ). \end{aligned}$$
(8)

Finally, inserting Eqs. (7) and (8), the radial wave equation turns into

$$\begin{aligned} \left[ \frac{d^2}{{\rm d}{\sf{r}}^2}-\frac{1}{m}\frac{{\rm d}m}{{\rm d}{\sf{r}}} \left( \frac{d}{{\rm d}{\sf{r}}}-\frac{1}{\sf{r}}\right) -\frac{\ell (\ell +1)}{{\sf{r}}^2}\right] \psi _{\ell }({\sf{r}})=-\frac{2m}{\hbar ^2}\left[ E -V({\sf{r}} )\right] \psi _{\ell }({\sf{r}} ). \end{aligned}$$
(9)

The first derivative can be eliminated from the right hand side of Eq. (9) by using the transformation:

$$\begin{aligned} \psi _{\ell }({\sf{r}})=\sqrt{m({\sf{r}})} \phi _{\ell }({\sf{r}}). \end{aligned}$$
(10)

This technique is based on the point canonical transformation method, [48, 56]. Substituting Eq. (10) in Eq. (9), one obtain

$$\begin{aligned} \frac{{\rm d}^2\phi _{\ell }}{ {\rm d}{\sf{r}}^2}+\left[ \frac{1}{2m}\frac{{\rm d}^2m}{{\rm d}{\sf{r}}^2}-\frac{3}{4} \left( \frac{1}{m}\frac{{\rm d}m}{{\rm d}{\sf{r}}}\right) ^2+\frac{1}{{\sf{r}}~m}\frac{{\rm d}m}{{\rm d}{\sf{r}}} -\frac{\ell (\ell +1)}{{\sf{r}}^2} \right] \phi _{\ell }=-\frac{2m}{\hbar ^2}\left[ E -V({\sf{r}})\right] \phi _{\ell }. \end{aligned}$$
(11)

The Morse potential [45], can be written as

$$\begin{aligned} V({\sf{r}})=V_1e^{-\alpha r}+V_2e^{-2\alpha r}, \end{aligned}$$
(12)

where

$$\begin{aligned} r=\frac{{\sf{r}}-{\sf{r}}_{0}}{{\sf{r}}_{0}}, \end{aligned}$$
(13)

and \({\sf{r}}_{0}\) is the equilibrium position of molecules and the dimensionless parameter \(\alpha \) characterizes the potential acting range. We suppose that \(V_1\) and \(V_2\) are two general potential parameters which in the traditional Morse potential are given by \(V_1=-2D\) and \(V_2=D\) with D describing the depth of the potential. In the Pekeris approximation it is convenient to expand the centrifugal potential barrier term of Eq. (11) as follows:

$$\begin{aligned} \frac{\ell (\ell +1)}{{\sf{r}}^2}=\frac{\ell (\ell +1)}{{\sf{r}}_{0}^2(1+r)^2}\cong \frac{\ell (\ell +1)}{{\sf{r}}_{0}^2}\left( C_{0}+C_{1}e^{-\alpha r}+C_{2}e^{-2\alpha r}\right) , \end{aligned}$$
(14)

where

$$\begin{aligned} C_{0}=1-\frac{3}{\alpha }+\frac{3}{\alpha ^2},\quad C_{1}=\frac{4}{\alpha }-\frac{6}{\alpha ^2},\quad C_{2}=-\frac{1}{\alpha }+\frac{3}{\alpha ^2}. \end{aligned}$$
(15)

In the same manner, we expand the term \(\frac{1}{{\sf{r}}~m}\frac{{\rm d}m}{{\rm d}{\sf{r}}}\) in Eq. (11) as follows:

$$\begin{aligned} \frac{1}{{\sf{r}}~m}\frac{{\rm d}m}{{\rm d}{\sf{r}}}=\frac{1}{{\sf{r}}_0~m}\frac{{\rm d}m}{{\rm d}{\sf{r}}}\frac{1}{(1+r)}\cong \frac{1}{{\sf{r}}_0~m}\frac{{\rm d}m}{{\rm d}{\sf{r}}}\left( B_{0}+B_{1}e^{-\alpha r}+B_{2}e^{-2\alpha r}\right) , \end{aligned}$$
(16)

where

$$\begin{aligned} B_{0}=1-\frac{3}{2\alpha }+\frac{1}{\alpha ^2},\quad B_{1}=\frac{2}{\alpha }-\frac{2}{\alpha ^2},\quad B_{2}=\frac{1}{\alpha ^2}-\frac{1}{2\alpha }. \end{aligned}$$
(17)

Substituting Eqs. (12–14) and (16) into (11), and applying

$$\begin{aligned} y=k e^{-\alpha r},\,\,\,\, \end{aligned}$$
(18)

where k is a constant parameter, yields:

$$\begin{aligned} \left( y^2 \frac{d^2}{{\rm d}y^2}+y\frac{d}{{\rm d}y}+ \Upsilon _m~\right) \phi _{\ell }= \frac{\ell (\ell +1)}{\alpha ^2}\left( C_{0}+\frac{C_{1}}{k}y+\frac{C_{2}}{k^2}y^2\right) \phi _{\ell }. \end{aligned}$$
(19)

Here all the mass dependent terms are placed into \(\Upsilon _m\) as:

$$\begin{aligned} \Upsilon _m=\frac{y^2}{2m} \frac{{\rm d}^2m}{{\rm d}y^2} -\frac{3y^2}{4m^2}\left( \frac{{\rm d}m}{{\rm d}y}\right) ^2+\frac{y}{m}\frac{{\rm d}m}{{\rm d}y}\left[ \frac{1}{2} -\frac{1}{\alpha }\left( B_0+\frac{B_1}{k} y+\frac{B_2}{k^2} y^2\right) \right] -\frac{m}{m_0}\left( \beta ^2+Gy+Fy^2\right) \end{aligned}$$
(20)

and

$$\begin{aligned} \beta ^2=-\frac{2 m_0{\sf{r}}_0^2E}{\alpha ^2\hbar ^2},\quad G=\frac{2m_0{\sf{r}}_0^2V_1}{k\alpha ^2\hbar ^2}, \quad F=\frac{2m_0{\sf{r}}_0^2V_2}{k^2\alpha ^2\hbar ^2}. \end{aligned}$$
(21)

where \(m_0\) is a mass dimensional parameter. Here, we use the following effective mass distribution:

$$\begin{aligned} \frac{m(y)}{m_0}=\frac{\tau }{(\gamma +\eta y)^2}, \end{aligned}$$
(22)

where \(\tau \), \(\gamma \) and \(\eta \) are constant parameters. In our procedure, we choose these parameters in such a way that \(\Upsilon _m\) in Eq. (20), which contains the mass function m, yields:

$$\begin{aligned} \Upsilon _m \equiv D_0+D_1y+D_2y^2 \end{aligned}$$
(23)

where \(D_0\), \(D_1\) and \(D_2\) are three parameters. Here we study the following two different sets of parameters which satisfies Eq. (23). The first set is characterized as:

$$\begin{aligned} \left\{ \begin{array}{lll} \eta =0, &{} \tau =\tau &{} \gamma =1\\ D_0=-\beta ^2~\tau , &{} D_1=-G\tau &{} D_2=-F\tau \end{array} \right. \end{aligned}$$
(24)

where G, F and \(\tau \) are free parameters. This case exactly corresponds to the constant mass case and for which we put \(G=-2kF\) and \(\tau =1\). This case has already been studied in [43], and we show that its solutions coincides with the results in the next section as well. The other possible set of the appropriate parameters have the following forms:

$$\begin{aligned} \left\{ \begin{array}{l} \eta = \frac{2B_2}{k(2B_1-\alpha k D_1)},\quad \tau =\tau ,\quad \gamma =1,\quad D_0=-\beta ^2~\tau ,\quad D_1=D_1\\ \\ G=\frac{-D_1^2\alpha ^2 k^2+ \left[ 2 k B_1 D_1+ \left( 4 D_0+2 \right) B_2 \right] \alpha -4 B_0 B_2}{\alpha k \left( D_1 \alpha k-2 B_1 \right) \tau },\quad D_2=\frac{2B_2}{\alpha k^2}\\ \\ F=\frac{2 B_2\left\{ D_1^{2}{\alpha }^{2}k^2+ \left[ \left( -2 D_0-2\right) B_2-2k B_1 D_1 \right) \alpha +4 B_0 B_2\right\} }{\alpha k^{2} \left( D_1\alpha k-2 B_1 \right) ^2\tau } \end{array} \right. \end{aligned}$$
(25)

where \(\tau \) and \(D_1\) are free parameters.

Substituting Eq. (23) in (19) yields:

$$\begin{aligned} y^2 \frac{{\rm d}^2\phi _{\ell }}{{\rm d}y^2}+y\frac{{\rm d}\phi _{\ell }}{{\rm d}y}-\left( \mu _{\ell }^2 - \chi _{\ell }^2~ y + \nu _{\ell }^2~ y^2\right) \phi _{\ell }=0, \end{aligned}$$
(26)

where:

$$\begin{aligned} \mu _{\ell }^2=-D_0+\frac{\ell (\ell +1)}{\alpha ^2}C_{0},\quad \chi _{\ell }^2=D_1-\frac{\ell (\ell +1)}{\alpha ^2}\frac{C_{1}}{k},\quad \nu _{\ell }^2=-D_2+\frac{\ell (\ell +1)}{\alpha ^2}\frac{C_{2}}{k^2}. \end{aligned}$$
(27)

Bound state solutions

In the presence of the mass function (22) our Schrödinger equation turns into Eq. (26). To have finite solutions at large values of y, we should apply the following ansatz

$$\begin{aligned} \phi _{\ell }=y^{-\mu _{\ell }} f_{\ell }(y). \end{aligned}$$
(28)

Eq. (26) becomes

$$\begin{aligned} \left[ y \frac{d^2}{{\rm d}y^2}- (2\mu _{\ell }-1)\frac{d}{{\rm d}y}+(\chi _{\ell }^2-\nu _{\ell }^2 y) \right] f_{\ell }(y)=0. \end{aligned}$$
(29)

Here we use the Laplace transformation method to solve Eq. (29), [40, 43]. By applying Laplace transform \(F(s)=\) \(\mathcal {L}\) \([f(y)]=\int _{0}^{\infty } e^{-sy}f(y){\rm d}y\), [35], the following equation can be obtained

$$\begin{aligned} \left( s^2-\nu _{\ell }^2\right) \frac{d}{ds}F_{\ell }(s)+\left[ (2\mu _{\ell }+1)s-\chi _{\ell }^2\right] F_{\ell }(s)=0, \end{aligned}$$
(30)

Eq. (30) is a first order differential equation and its solutions are in the form

$$\begin{aligned} F_{\ell }(s)=N^{''}\left( s +\nu _{\ell } \right) ^{-2 \mu _{\ell } -1}\left( 1-\frac{2\nu _{\ell }}{s+\nu _{\ell }}\right) ^{\left[ \frac{\chi _{\ell }^2}{\nu _{\ell }}-(2\mu _{\ell }+1)\right] \big /2}, \end{aligned}$$
(31)

where \(N^{''}\) is a constant. Here \(\left[ \frac{\chi _{\ell }^2}{\nu _{\ell }}-(2\mu _{\ell }+1)\right] \) is a multi-valued function. To have a single valued wave function we impose the condition

$$\begin{aligned} \frac{\chi _{\ell }^2}{\nu _{\ell }}-(2\mu _{\ell }+1)=2n,\,\,\,\,n=0,\pm 1,\pm 2,\pm 3, \ldots . \end{aligned}$$
(32)

Here, the positive or negative values of n depends on the magnitude of \(\frac{\chi _{\ell }^2}{\nu _{\ell }}\). In fact, according to Eq. (28), the parameter \(\mu _{\ell }\) needs to be positive to have finite wave function at large y. However, according to Eq. (32), for sufficiently large values of \(\frac{\chi _{\ell }^2}{\nu _{\ell }}\) and for positive and negative values of n, we can find positive values of \(\mu \). But for smaller values of \(\frac{\chi _{\ell }^2}{\nu _{\ell }}\) only for the minus sign of n we can obtain positive values of \(\mu \).

Let us separately consider each sign of n in Eq. (32). To apply the inverse Laplace transformation to Eq. (31), it needs to be expanded in power series which yields

$$\begin{aligned} F(s) = \sum _{j=0}^{\infty } \frac{(2\nu _{\ell })^j}{j!}\left\{ \begin{array}{ll} N^{''}_+\frac{(-1)^j n!}{(n-j)!} (s+\nu _{\ell })^{-(2\mu _{n\ell }^{+}+1+j)} , &{}\quad {n>0;} \\ \\ N^{''}_-\frac{(-1)^{2j}(n+j-1)!}{(n-1)!} (s+\nu _{\ell })^{-(2\mu _{n\ell }^{-}+1+j)} , &{}\quad {n<0.} \end{array} \right. \end{aligned}$$
(33)

where \(N^{''}_{\pm }\) are two integrating constants and \( \mu _{n\ell }^{\pm }\), in according to Eq. (32), corresponds to positive or negative values of n. Now, applying the inverse Laplace transforms to Eq. (33) yields:

$$\begin{aligned} F(s) = \sum _{j=0}^{\infty } \frac{(2\nu _{\ell })^j y^{j} e^{-\nu _{\ell }y}}{j!} \left\{ \begin{array}{ll} N^{''}_+\frac{(-1)^j n!}{(n-j)!\Gamma (2\mu _{n\ell }^{+}+1+j)} y^{2\mu _{n\ell }^{+}} , &{}\quad {n>0;} \\ N^{''}_-\frac{(n+j-1)!}{(n-1)!\Gamma (2\mu _{n\ell }^{-}+1+j)}y^{2\mu _{n\ell }^{-}} , &{}\quad {n<0.} \end{array} \right. \end{aligned}$$
(34)

The series expansion of the confluent hypergeometric functions is given by

$$\begin{aligned} F(a,b,z)=1+\frac{a}{b}z+\frac{a(a+1)}{b(b+1)}\frac{z^2}{2!}+ \cdots =\sum _{j=0}^{\infty } \frac{(a+j-1)!\Gamma (b)}{(a-1)!\Gamma (b+j)}\frac{z^j}{j!}. \end{aligned}$$
(35)

Comparing Eq. (34) with Eq. (35), both solutions yield

$$\begin{aligned} f_{\ell }(y)= N^{'} y^{2\mu _{n\ell }} e^{-\nu _{\ell } y} F(-n,2\mu _{n\ell }+1,2y\nu _{\ell }), \end{aligned}$$
(36)

where \(N^{'}\) is a constant and \(\mu _{n\ell }\) is given by Eq. (32). Inserting \(f_{\ell }(y)\) from Eq. (36) into (28) and then (10), leads to

$$\begin{aligned} \psi _{n\ell }(y)= N_{n\ell }\sqrt{m(y)}~y^{\mu _{n\ell }} e^{-\nu _{\ell } y}F(-n,2\mu _{n\ell }+1,2y\nu _{\ell }). \end{aligned}$$
(37)

Here \(N_{n\ell }\) is the normalization constant and m(y) is given by Eq. (22). The parameter \(\mu _{n\ell }\) from Eq. (32) is given as

$$\begin{aligned} \mu _{n\ell }=\frac{\chi _{\ell }^2}{2\nu _{\ell }}-n -\frac{1}{2}, \end{aligned}$$
(38)

where \(\nu _{\ell }\) and \(\chi _{\ell }\) are given by Eq. (27), while the parameters \(D_0\), \(D_1\) and \(D_2\) depending on the first set or the second set, are given, respectively, by Eqs. (24) and (25).

Discussions and results

This study has introduced a procedure to find the bound states of the Morse like potentials via the Laplace transformation method. Our main strategy is to find an appropriate mass function for which one could establish the condition Eq. (23). In this way, the parameters of the model should be chosen in such a way that the condition would be satisfied. Our result is applicable for any kind of the mass function for which one can set the condition Eq. (23). We have examined two different set of appropriate parameters. The first one corresponds to the constant mass case and the second one relates to a more general mass function namely, Eq. (22).

To find the energy eigenvalues, we substitute \(\mu _{n\ell }\) from Eq. (38) into (27) and find \(D_0\). Then, science from Eqs. (24) and (25) \(D_0=-\tau \beta ^2\), the energy spectrum can be found by inserting \(D_0\) into (21). In this way, the energy spectrum, yields:

$$\begin{aligned} E_{n\ell }= -\frac{\alpha ^2 \hbar ^2}{2m_0{\sf{r}}_0^2}\left\{ \frac{\ell (\ell +1)}{\alpha ^2}C_0- \left[ n+\frac{1}{2}-\frac{1}{2\nu _{\ell }}\left( \frac{\ell (\ell +1)}{\alpha ^2 k}C_1-D_1\right) \right] ^2\right\} . \end{aligned}$$
(39)

where

$$\begin{aligned} \nu _{\ell }=\left[ -D_2+\frac{\ell (\ell +1)}{\alpha ^2 k^2}C_2\right] ^{\frac{1}{2}}. \end{aligned}$$
(40)

For the first set specified with Eq. (24), we obtain:

$$\begin{aligned} \left\{ \begin{array}{l} D_1=k/2, \\ D_2=-1/4, \end{array} \right. \end{aligned}$$
(41)

For the second set with Eq. (25), we have:

$$\begin{aligned} \left\{ \begin{array}{l} D_1\,\, : \,\,\hbox {arbitrary;} \\ D_2=2B_2/(\alpha k^2), \end{array} \right. \end{aligned}$$
(42)

Figures 1 and 2 shows the energy spectrum of the first and second cases, respectively. In these diagrams, the required parameters are supposed as \(\alpha =1.440\), \(k=34.9\), and \(\hbar ^2/(2m_0{\sf{r}}_{0}^2)=60.83 \) cm −1 which are appropriate for the hydrogen atoms. Fig. 1a, exactly coincides with the diagram has already been obtained for the constant mass problem [43]. Fig. 1b demonstrates an example of the energy spectrum for the considered dependent mass profile. In this diagram, the free parameter \(D_1\) is considered as \(D_1=0.1~k/2 \) and the other parameters are the same as for Fig. 1a. According to Fig. 1b, the energy spectrum for the considered mass profile is not so sensitive to the quantum number n, science the diagrams for \(n=0\) and \(n=7\) are not so different and are very close together. Fig. 2 presents the considered mass profile which has a maximum value at \({\sf{r}}=0\).

Fig. 1
figure 1

The energy spectrum versus the quantum number \(\ell \) for the constant mas (a) and for the considered mass profile (b)

Full size image
Fig. 2
figure 2

The mass function versus the relative distance \({\sf{r}}/{\sf{r}}_0\)

Full size image