Introduction

The carrier-mediated ferromagnetism observed in dilute magnetic semiconductors (DMS) has gained interest over the past decade due to the possibility of controlling the ferromagnetism and their potential applications in spintronics which use both the charge and spin degrees of freedom for electronic applications [1]. DMS materials such as (Ga, Mn) As, (In, Mn) As, (Ga, Mn) N have combined the magnetic and semiconducting properties in a single material [2].

Even though the origin of ferromagnetism in diluted magnetic semiconductor is not fully understood and explained yet, there are different theoretical models proposed to explain the ferromagnetism in DMS materials. The magnetic interactions between magnetic moments in (III, Mn) V and (Mn, IV) DMS systems are hole mediated in which the substitutional Mn produces the holes and acts as acceptors [3].

Ge (Group IV)-based DMS system have attracted a great deal of attention due to its high hole mobility and compatibility with the present silicon technology [4–6]. Recently Mn-doped Ge DMS system showing magnetic ordering was successfully grown by molecular beam epitaxy (MBE) technique which are a good candidates of Ge-based DMSs [7, 8]. Recently Xiu et al. [9] successfully fabricated self-assembled \({\rm Mn}_{x}{\mathrm{Ge}}_{1-x}\) DMSQDs (with \(x=0.05\)) without metallic precipitates such as \({\mathrm{Mn}}_{5}{\mathrm{Ge}}_{3}\) and \({\mathrm{Mn}}_{11}{\mathrm{Ge}}_{5}\) which showed electric field-controlled ferromagnetism, \(T_{C}\) above 400 K. The presence of such metallic clusters strongly affect the magnetic properties of the Mn-Ge DMS system [5]. In addition to the MBE technique, Mn-Ge DMS systems were prepared by ion implantation techniques, which shows carrier-mediated ferromagnetism due to high hole concentration [10, 11].

Control of the magnetic phase in DMS is one of the most important processes for magnetic recording and information storage. The use of electric field-controlled magnetization reduces power consumption for storage devices [12, 13]. Electric field control of ferromagnetism was so far demonstrated in a field effect transistor (FET) structure which have been used for non-volatile spin logic devices via carrier-mediated effect [9, 14].

In this work, we propose the Kondo Lattice model (KLM) type Hamiltonian to explain the ferromagnetism of the DMS Mn-Ge system, and we theoretically study the influence of electric field on the magnetic properties of MnxGe1 – x DMS, using the double time Green functions formalism. Magnetization and the critical temperature are studied in relation to the EEF. The paper is organized as follows. In section II, we present the model Hamiltonian which describes the DMS charier–charier interaction, carrier–Mn interaction and the Mn–Mn interaction. In the next section, the numerical results of various physical quantities showing the effect of the electric field are discussed. Finally the conclusion and summary are presented in the last section.

Model Hamiltonian

Our system consists of an Mn-Ge DMS system containing Mn as acceptor impurity inside. The Hamiltonian of the system will have the form

$${H}={H}_{\mathrm{ee}}+{H}_{I}+{H}_{\mathrm{mag}}$$
(1)

We assume a parabolic energy band for the carriers and the second quantized electron Hamiltonian, \({H}_{\mathrm{ee}}\) is given by

$${H}_{\mathrm{ee}}=\sum _{k\sigma }\epsilon _{k\sigma }c^{\dag }_{k\sigma }c_{k\sigma },$$
(2)

where \(c^{\dag }_{k\sigma }(c_{k\sigma })\) are Fermionic creation (annihilation) operators for carriers in the DMS. \(\epsilon _{k\sigma }\) is the energy of carriers with momentum k, band \(\sigma\) (moments \(\uparrow\) or \(\downarrow\)).

\({H}_{I}\) is the interaction Hamiltonian between the carriers and the localized magnetic ions which is Kondo Lattice Model (KLM) type Hamiltonian with the interaction of electric field with carrier spin and localized spin included, and can be written as

$${H}_{I}=-2J_{\mathrm{sd}}\sum _{m}{\mathbf S} _{m}\cdot \sigma _{m} -\mu _{e}{\mathbf E} \sum _{m}{\mathbf S} _{m}^{z}\sigma _{m}^{z}$$
(3)

The first term in \({H}_{I}\) is due to the interaction of the band carriers (holes) and the localized spin \({\mathrm{Mn}}^{2+}\) ions, expressed as Heisenberg type Hamiltonian, where \(J_{\mathrm{sd}}\) is exchange coupling between the confined holes and the \({\mathrm{Mn}}^{2+}\) ions impurity spins \(S_{m}\). \(\sigma _{m}\) represents the spin of the confined holes, which can be written as \(\sigma _{\alpha }= \frac{1}{2}\sum _{\sigma \sigma '}c^{\dag }_{m\sigma }{\varvec {\tau }}_{\sigma \sigma '}c_{m\sigma '}\), (\(\alpha =x,y,z\)), where \({\varvec {\tau }}\) are the matrix elements of the Pauli spin matrices. The second term arises from interaction of the holes and the localized moments with the external electric field (EEF) \(\mathbf E\). It is Ising type Hamiltonian. The mean electric polarization is assumed to be proportional to the z-component of the carriers and the localized spins.

\(\mathbf H _\mathrm{mag}\) is given by

$${H}_\mathrm{mag}=-\frac{1}{2}\sum _\mathrm{mn}I_\mathrm{mn}\mathbf S _{m}\cdot \mathbf S _{n}-g\mu _{\beta }H\sum _{m}\mathbf S _{m}^{z},$$
(4)

The first term in \(\mathbf H _\mathrm{mag}\) is the Hamiltonian of the localized \(\mathrm{Mn}^{+2}\) spins, where \(I_\mathrm{mn}\) is the exchange coupling between the localized spins \(S_{m}(S_{n})\) at different sites. The second term gives the Zeemann energy when the external magnetic field H has been applied in the z-direction, where g is Landé g factor and \(\mu _{\beta }\) is the Bohr magneton.

The spin operators in Hamiltonian can be written using the Holstein–Primakoff (HP) transformation as

$$S_{m}^{-}=\left( \sqrt{2xS-a_{m}^{\dag }a_{m}}\right) a_{m}^{\dag }$$
(5)
$$S_{m}^{+}=\left( \sqrt{2xS-a_{m}^{\dag }a_{m}}\right) a_{m}$$
(6)
$$S_{m}^{z}=xS-a_{m}^{\dag }a_{m},$$
(7)

where \(a_{m}^{\dag }(a_{m})\) are bosonic creation (annihilation) operators, x is the mean number of magnetic ions in the DMS system.

It is reasonable to use the approximation \(\sqrt{2xS-a_{m}^{\dag }a_{m}}\approx \sqrt{2xS}\) in HP transformation at low temperature. Restricting the involved momentum in the first Brillouin zone and Fourier transforming the Fermionic and bosonic operators, the effective Hamiltonian can then be written in second quantized form as

$$\begin{aligned} {H}_{eff}&= \left( \frac{\mu _{e}\mathbf E }{2N}-\frac{J_\mathrm{sd}}{N}\right) \sum _{\sigma ,k,q,q'}\sigma a_{q}^{\dag }a_{q'}c_{k-q\sigma }^{\dag }c_{k-q\sigma } \nonumber \\&\quad - \frac{J_{{\text{ sd }}\sqrt{2xS}}}{\sqrt{N}}\sum _{kq}\bigg (a_{q}^{\dag }c_{k\uparrow }^{\dag } c_{k+q\downarrow }+ a_{q}c_{k+q\downarrow }^{\dag }c_{k\uparrow }\bigg ) \nonumber \\&\quad - g\mu _{\beta }H \sum _{q}a_{q}^{\dag }a_{q}+xS\sum _{q}(I_{0}-I_{q})a_{q}^{\dag }a_{q} \end{aligned}$$
(8)

For the quasiparticle spectrum of the system described by the Hamiltonian in Eq. (8), we consider the following Green function (GF).

$$G_{q}(t,t')=\langle \langle a_{q}(t);a^{\dag }_{q}(t')\rangle \rangle$$
(9)

To evaluate the GF we use the general equation of motion method [15].

$$\omega \langle \langle a_{q}(t);a^{\dag }_{q}(t')\rangle \rangle _{\omega }= \frac{1}{2\pi }\langle [a_{q},a_{q}^{\dag }]\rangle + \langle \langle [a_{q}(t),H] ; a_{q}^{\dag }(t') \rangle \rangle _{\omega }$$
(10)
$$\begin{aligned} [a_{q}(t),H]&= \left( \frac{\mu _{e}E}{2N}-\frac{J_{\text{ sd }}}{N}\right) \sum _{kq'\sigma }a_{q'}c_{k-q\sigma }^{\dag }c_{k-q'\sigma } \nonumber \\&\quad - \frac{J_{\text{ sd }}\sqrt{2xS}}{\sqrt{N}}\sum _{k}c_{k\uparrow }^{\dag }c_{k+q\downarrow } \nonumber \\&\quad + \left [xS\sum _{q}(I_{0}-I_{q})+g\mu _{\beta }H \right ]a_{q} \end{aligned}$$
(11)

Using Eq. (11) into Eq. (10), the GF becomes

$$\begin{aligned} \omega \langle \langle a_{q}(t);a^{\dag }_{q}(t')\rangle \rangle _{\omega }&= \frac{1}{2\pi }+ \Lambda _{q}\langle \langle a_{q}(t);a^{\dag }_{q}(t')\rangle \rangle _{\omega }\nonumber \\&\quad - \frac{J_{\text{ sd }}\sqrt{2xS}}{\sqrt{N}}\sum _{k}\langle \langle c_{k\uparrow }^{\dag }c_{k+q\downarrow } ; a_{q}^{\dag }(t') \rangle \rangle _{\omega } \nonumber \\&\quad +\left( \frac{\mu _{e}E}{2N}-\frac{J_{\text{ sd }}}{N}\right) \sum _{kq'\sigma } \langle \langle a_{q'}c_{k-q\sigma }^{\dag }c_{k-q'\sigma } ;a^{\dag }_{q}(t')\rangle \rangle _{\omega }, \end{aligned}$$
(12)

where \(\Lambda _{q}=xS\sum _{q}(I_{0}-I_{q})+g\mu _{\beta }H\).

Employing the following decoupling procedure on the higher order GFs [15],

$$\begin{aligned} \langle \langle c_{k\uparrow }^{\dag }c_{k+q\downarrow } ; a_{q}^{\dag }(t') \rangle \rangle _{\omega }&= \langle \langle [c_{k\uparrow }^{\dag }c_{k+q\downarrow },H] ; a_{q}^{\dag }(t') \rangle \rangle _{\omega }\nonumber \\ &= (\langle c_{k\uparrow }^{\dag }c_{k\uparrow }\rangle -\langle c_{k+q\downarrow }^{\dag }c_{k+q\downarrow }\rangle )\langle \langle a_{q};a_{q}^{\dag }(t') \rangle \rangle _{\omega } \end{aligned}$$
(13)
$$\begin{aligned} \langle \langle a_{q'}c_{k-q\sigma }^{\dag }c_{k-q'\sigma }; a_{q}^{\dag }(t') \rangle \rangle _{\omega }&= \delta _{qq'}\langle c_{k-q\sigma }^{\dag }c_{k- q'\sigma }\rangle \langle \langle a_{q'}; a_{q}^{\dag }(t') \rangle \rangle _{\omega } \nonumber \\&= \langle c_{k-q\sigma }^{\dag }c_{k-q\sigma }\rangle \langle \langle a_{q}; a_{q}^{\dag }(t') \rangle \rangle _{\omega } \end{aligned}$$
(14)

Plugging Eqs. (13) and (14) into Eq. (12) the GF at \(q\rightarrow 0\) can be written in the form

$$G_{q}(\omega )=\frac{1}{2\pi }\frac{1}{\omega -\Lambda _{q}+m(2xSJ_\mathrm{sd}^{2}-J_\mathrm{sd}-\frac{\mu _{e}E}{2})},$$
(15)

where

$$m=\frac{1}{N}\sum _{k}(c_{k\uparrow }^{\dag }c_{k\uparrow }-c_{k-q\downarrow }^{\dag }c_{k-q\downarrow })=\frac{1}{N}\sum _{k}(c_{k-q\uparrow }^{\dag }c_{k-q\uparrow }-c_{k-q\downarrow }^{\dag }c_{k-q\downarrow }),$$
(16)

is the carrier spin polarization at \(q\rightarrow 0\).

From the poles of the GF we can obtain the excitation spectrum of the magnon as

$$\omega _{q}=xS\sum _{q}(I_{0}-I_{q})+g\mu _{\beta }H-m \left (2xSJ_\mathrm{sd}^{2}+J_\mathrm{sd}-\frac{\mu _{e}E}{2} \right )$$
(17)

The exchange integral \(I_{q}\) is given by

$$I_{q}=\frac{1}{N}\sum _{mn}I_{mn}e^{i\mathbf q \cdot (\mathbf R _{m}-\mathbf R _{n})}$$
(18)

The dispersion of the localized spin subsystem includes the simplest spin wave result when expanding \(I_{q}\) in the limit \(q \rightarrow 0\) which leads to the dispersion law \(\omega _q=D q^{2}\), where D is spin wave stiffness and is given by \(D=xS\sum _{m}(\hat{\mathbf{q }}\mathbf R _{m})^{2}I(|{R_m}|))\) and \(\hat{q}=\mathbf q /|q|\) is the unit vector.

The dispersion of the localized spin subsystem can then be written as

$$\omega _{q}=Dq^{2}+g\mu _{\beta }H+m\alpha -m\gamma ,$$
(19)

where

$$\alpha =\frac{\mu _{e}E}{2}$$
(20)

is called the external electric field parameter (EEFP), and

$$\gamma =2xSJ_\mathrm{sd}^{2}+J_\mathrm{sd}$$
(21)

is a parameter associated with the coupling of carrier spin and the localized magnetic spin.

The number of magnon excited at temperature T, can be calculated using the correlation function,

$$\langle a_{q}^{\dag }(t')a_{q}(t)\rangle =\lim _{\epsilon \rightarrow 0} i\int ^{\infty }_{\infty }\frac{e^{-i\omega (t-t')}}{e^{\beta \omega }-1}(G_{q}(\omega +\epsilon )-G_{q}(\omega -\epsilon ))\mathrm{d}\omega$$
(22)

The equal time correlation gives the number of excited magnon and is obtained as

$$\tilde{n}_{q}=\frac{1}{e^{\beta \omega _{q}}-1}$$
(23)

At a temperature T, the magnetization per site is given by

$$M(T)-M(0)=-g\mu _{\beta }\sum _{q}\langle \tilde{n}_{q} \rangle ,$$
(24)

where \(M(0)=g\mu _{\beta }nS\) is the magnetization at absolute zero where all spins are parallel.

For small values of q, the sum in (24) can be replaced by an integral over the whole value of the q-space and can be written as

$$M(T)-M(0)=-g\mu _{\beta }\frac{V}{(2\pi )^{3}}\int _{-\infty }^{\infty }\frac{d^{3}q}{{\text{ exp }}[\beta ({Dq^{2}+g\mu _{\beta }H+m\alpha -m\gamma })]}$$
(25)
$$\frac{M(T)}{M(0)}=1-AT^{3/2}\mathrm{exp}[-\beta (g\mu _{\beta }H+m\alpha -m\gamma )],$$
(26)

where \(\frac{M(T)}{M(0)}\) is the reduced magnetization and A is a constant given by

$$A=\frac{1}{16\pi ^{2}N_{m}S}\bigg (\frac{k}{IxS}\bigg )^{3/2}.$$
(27)

Based on the above frame work, we can calculate the critical temperature, the spin wave dispersion and the susceptibility of the localized spin.

Numerical result and discussion

Fig. 1
figure 1

Reduced magnetization (M(T)/M(0)) as a function of temperature for different values of EEF parameter, \(\alpha\)

Full size image
Fig. 2
figure 2

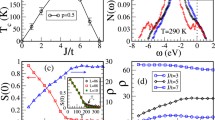
Electric field and temperature T dependence of \(R_\mathrm{Hall}\) proportional to the spontaneous magnetization taken from Ref. [16]

Full size image

Controlling the magnetization of magnetic devices using electric field will lead to new devices that will be energy efficient, fast and compact as compared to those devices tuned by electromagnets. The following material parameters are used for the analysis. \(J_\mathrm{sd}=2\;\mathrm{meV}, I=20\;\mathrm{meV}, a=5.77\;\)Å\(, m=0.9, S=5/2\).

In Fig. 1, we plot the reduced magnetization as a function of temperature in different values of the electric field parameters. The magnetization of the system tends to increase towards the temperature as the electric field parameter increases. The electric field increases the coupling between localized spin and the itinerant holes spins and produces spin-polarized carriers which in turn creates molecular field which is responsible to the higher magnetization of the Mn spins. The slow drop of the magnetization as compared to the Weiss mean field approximation is due to low temperature approximation and the ignorance of the strong spin fluctuation. This is in good agreement with experimental work of Ohno et al. [12] and Chiba et al. [16]. They reported that in the study of the anomalous Hall effect of the semiconductor field effect transistor (FET) structure, the hole-induced ferromagnetism can be turned on and off by EEF.

As seen from Fig. 2 the spontaneous magnetization is favored by negative electric field and the \(T_{C}\) will increase for higher magnitude of the (negative) electric field.

The other property that is affected by the application of EEF is spin wave dispersion gap. As can be seen from Fig. 3 the spin wave dispersion gap increases when the electric field parameters increases.

Fig. 3
figure 3

Spin wave dispersion as a function of wave vector, q

Full size image

The dependence of the reduced magnetization on the electric field is observed on Fig. 4. One can notice that the increase of magnetization of the system as electric field increases, which subsequently enhances the critical temperature, \(T_{C}\).

Fig. 4
figure 4

Reduced magnetization (M(T)/M(0)) as a function of EEF parameter, \(\alpha\)

Full size image
Fig. 5
figure 5

Critical temperature as a function of EEF parameter, \(\alpha\)

Full size image

Figure 5 is the plot of the variation of the critical temperature with the EEF. An increase in critical temperature is observed as the EEF increases. As can be seen from the curve, it is not a monotonic increase rather it is a parabolic increase, which shows there is a saturation for critical temperature at high values of the EEF, and this is also in agreement with [16] as shown in the inset of Fig. 2, which shows the variation of \(T_{C}\) with hole concentration p. (p is dependent on the electric field, i.e. the electric field increases the hole concentration).

Conclusions

We have shown that the magnetic properties of the DMS Mn-Ge system were greatly affected by the application of EEF. The magnetization shows an increase with increasing EEF. This confirms that the internal molecular field due to the carrier–Mn coupling leads to high curie temperature ferromagnetism. This could be explained by the fact that the EEF would accumulate large enough spin-polarized carriers which affect the orientation of the Mn ions and induce ferromagnetism. In addition, the critical temperature (\(T_{C}\)) and the spin wave dispersion gap increases with increasing EEF. These electric field-dependent magnetic properties will lead to the control of the magnetism by an electric field which is essential for the spintronics applications. In conclusion, we see that our system can be tuned by the external applied electric field.