Generalization of the analytical solution of neutron point kinetics equations with time-dependent external source

Abstract

Point reactor kinetics equations with one group of delayed neutrons in the presence of the time-dependent external neutron source are solved analytically during the start-up of a nuclear reactor. Our model incorporates the random nature of the source and linear reactivity variation. We establish a general relationship between the expectation values of source intensity and the expectation values of neutron density of the sub-critical reactor by ignoring the term of the second derivative for neutron density in neutron point kinetics equations. The results of the analytical solution are in good agreement with the results obtained with numerical solution.

Introduction

The neutron point kinetics (NPK) equations are a system of coupled nonlinear and stiff equations [1–3]. This system describes the nuclear parameters such as neutron density, reactivity and the precursor concentrations of delayed neutrons [4]. Calculations of these parameters are concerned with the reactor dynamics. The neutron density is one of the most important parameters in reactor dynamics [5–7]. According to the importance of neutron density in the cold start-up stage, the external neutron source makes a significant contribution to the reactor power [8]. In most reactors, the reactivity is introduced mainly by discontinuous transferring of control rods which is, in practice, a linear function. Applying too much reactivity will cause a high increase in reactor power and can result in an overpressure accident in the reactor core [9]. Therefore, one should carefully study the influence of external neutron source on the reactor power [10, 11]. So far, appropriate mathematical models have already been developed to study the sub-critical kinetics, such as including the constant external neutron source [6], approximation models [12–14] and prompt jump approximation (PJA) [9, 15, 16].

In this work we extend the analytical method to determine the effect of external source on the behavior of the neutron density during the start-up of a nuclear power reactor. The source of neutron is considered as a function of time.

This paper is organized as follows. In Sect. “Start-up process”, a brief description of the start-up process is presented. In Sect. “External neutron source contribution”, the mechanism of interaction between the control rod and external source is reviewed, and finally the authors discuss and interpret the results. The section is also followed by two appendices.

Start-up process

The start-up process of a reactor deals with the variation of reactivity in the system which occurs by raising the control rods in a discontinuous way [12]. So, the rule of neutron density variation is significant because it not only describes the relationship between lifting speed of the control rod, duration and speed of neutron density response, but also is helpful to the operator to control the reactor start-up from any accident [9, 17, 18]. The authors modified the analytical expressions for the calculation of neutron density from a set of physical and mathematical approximations [9, 12, 15]. Since the reactor is in sub-critical state in the cold start-up stage, the external neutron source cannot be ignored. Due to the low average temperature in the reactor core, here, the effect of temperature feedback can be ignored [9, 19]; consequently, the NPK equations with the external neutron source term for one group of delayed neutrons can be written as follows [8, 11, 12, 16]:

$$\begin{array}{cc}& \frac{\mathrm{d}n(t)}{\mathrm{d}t}=\frac{\mathit{\rho }(t)-\mathit{\beta }}{l}n(t)+\mathit{\lambda }c(t)+q(t)\hfill \\ \hfill & \frac{\mathrm{d}c(t)}{\mathrm{d}t}=\frac{\mathit{\beta }}{l}n(t)-\mathit{\lambda }c(t)\hfill \end{array}$$

(1)

where $n(\mathrm{neutron}{\mathrm{cm}}^{-3})$ is the neutron density, $c(\mathrm{neutron}{\mathrm{cm}}^{-3})$ is the precursor concentrations, $\mathit{\beta }$ is the total fraction of delayed neutrons, $\mathit{\lambda }({\mathrm{s}}^{-1})$ is the decay constant of delayed neutrons, $l(\mathrm{s})$ is the prompt neutron generation time, $\mathit{\rho }$ is the reactivity as a function of time, and $q(neutronc{m}^{-3}{s}^{-1})$ is the external neutron source.

To have a general solution, the variation of external neutron source with respect to time is considered. Let us first consider the external neutron source defined as the ratios of polynomials of degree $N$:

$$\begin{array}{c}\hfill q(t)=\sum _{n=0}^N{q}_n{t}^n\end{array}$$

We denote their reactivity by:

$$\begin{array}{c}\hfill \mathit{\rho }(t)=\left\{\begin{array}{cc}{\mathit{\rho }}_0+rt& 0\le t<t_0\\ {\mathit{\rho }}_0+r{t}_0& t\ge t_0\end{array}\right.\end{array}$$

(2)

where ${\mathit{\rho }}_0$ is the initial subcritical reactivity, $r({\mathrm{s}}^{-1})$ represents the ramp reactivity addition rates and $t_0(\mathrm{s})$ is the time for taking out the rods.

Eliminating the dependency of precursor concentration, the differential equation that governs the neutron density during the withdrawal of the control rods is given by [9, 12]:

$$\begin{array}{c}\hfill l\frac{{\mathrm{d}}^{2}n(t)}{\mathrm{d}{t}^2}=(\mathit{\rho }-\mathit{\beta }-\mathit{\lambda }l)\frac{\mathrm{d}n(t)}{\mathrm{d}t}+\left(\mathit{\lambda }\mathit{\rho }+\frac{\mathrm{d}\mathit{\rho }(t)}{\mathrm{d}t}\right)n(t)+l\left(\mathit{\lambda }q(t)+\frac{\mathrm{d}q(t)}{\mathrm{d}t}\right)\end{array}$$

(3)

Since $l\frac{{\mathrm{d}}^{2}n(t)}{\mathrm{d}{t}^2}$ is much smaller than the other terms in Eq. (3), we “Ignore the second term derivative” (ISD). So, the only approximation which we used in the calculations is ISD [9, 12]. According to the ISD, one can write:

$$\begin{array}{c}\hfill (\mathit{\rho }-\mathit{\beta }-\mathit{\lambda }l)\frac{\mathrm{d}n(t)}{\mathrm{d}t}+\left(\mathit{\lambda }\mathit{\rho }+\frac{\mathrm{d}\mathit{\rho }(t)}{\mathrm{d}t}\right)n(t)=-l\left(\mathit{\lambda }q(t)+\frac{\mathrm{d}q(t)}{\mathrm{d}t}\right).\end{array}$$

(4)

According to the data of some thermal reactors, i.e. $\mathit{\lambda }=0.001{\mathrm{s}}^{-1},\mathit{\beta }=0.0075,{\mathit{\rho }}_0=-0.006,l=0.0015\mathrm{s}$, the assumption of $\mathit{\beta }-\mathit{\rho }\gg \mathit{\lambda }l$ for very small ramp rate reactivities is valid [12]. To find the analytical solution, provided $n=n_1$, ${\mathit{\rho }}_1={\mathit{\rho }}_0+rt$, $k_1=\frac{\mathit{\lambda }{\mathit{\rho }}_0+r}{r}$ and $k_2=\frac{\mathit{\beta }-{\mathit{\rho }}_0}{r}$ , the equivalent form of Eq. (4) is rearranged as follows:

$$\begin{array}{c}\hfill \frac{\mathrm{d}{n}_1}{\mathrm{d}t}+\left(\frac{k_1+\mathit{\lambda }t}{t-k_2}\right)n_1=-\frac{l}{r(t-k_2)}\sum _{n=0}^N(\mathit{\lambda }{q}_n+(n+1)q_{n+1})t^n.\end{array}$$

(5)

Considering ($u=t-k_2$, $\mathit{\eta }=k_1+\mathit{\lambda }{k}_2-1$) [12], Eq. (5) reduces to:

$$\begin{array}{c}\hfill n_1(t)=\frac{e^{-\mathit{\lambda }u}}{u^{\mathit{\eta }+1}}\left(-\frac{l}{r}\int \mathrm{d}t{u}^{\mathit{\eta }}{e}^{\mathit{\lambda }u}\sum _{n=0}^N\sum _{m=0}^n\left(\begin{array}{c}n\\ m\end{array}\right)k_2^m(\mathit{\lambda }{q}_n+(n+1)q_{n+1})u^{n-m}+A\right).\end{array}$$

One can write (for more details see “Appendix A”):

$$\begin{array}{c}\hfill n_1(t)=\frac{e^{-\mathit{\lambda }u}}{u^{\mathit{\eta }+1}}\left(\sum _{n=0}^N\sum _{m=0}^n{a}_{nm}\mathit{\gamma }(\mathit{\eta }+n-m+1,-\mathit{\lambda }u)+A\right)\end{array}$$

(6)

$$\begin{array}{c}\hfill a_{nm}=\left(\left(-\frac{l}{r}\right){\left(-\frac{1}{\mathit{\lambda }}\right)}^{n+\mathit{\eta }-m+1}{k}_2^m(\mathit{\lambda }{q}_n+(n+1)q_{n+1})\right)\left(\begin{array}{c}n\\ m\end{array}\right).\end{array}$$

It is possible to determine the integration constant $(A)$ by using initial condition, $(n_1(0)=n_0)$, and so we have:

$$\begin{array}{c}\hfill A=\left(-\sum _{n=0}^N\sum _{m=0}^n{a}_{nm}\mathit{\gamma }(\mathit{\eta }+n-m+1,-\mathit{\lambda }u)+\frac{n_0{(-k_2)}^{\mathit{\eta }+1}}{e^{\mathit{\lambda }{k}_2}}\right).\end{array}$$

(7)

For $t=t_0$, the reactivity will reach a constant value $({\mathit{\rho }}_2={\mathit{\rho }}_0+r{t}_0)$. At this time, neutron density is equal to $n_2(t)=n_2$. Therefore, in this stage of introducing reactivity, the differential equation is given by:

$$\begin{array}{c}\hfill \frac{\mathrm{d}{n}_2}{\mathrm{d}t}+s{n}_2=\sum _{n=0}^N{b}_n{t}^n,\end{array}$$

(8)

where $s=\frac{\mathit{\lambda }({\mathit{\rho }}_0+r{t}_0)}{{\mathit{\rho }}_0+r{t}_0-\mathit{\beta }}$ and $b_n=-\frac{l(\mathit{\lambda }{q}_n+(n+1)q_{n+1})}{{\mathit{\rho }}_0+r{t}_0-\mathit{\beta }}$. Finally, the solution of Eq. (8) can be obtained from the integrating factor method (for more details see “Appendix B”):

$$\begin{array}{c}\hfill n_2(t)=\left(e^{-st}\left(\sum _{n=0}^N{b}_n{\left(-\frac{1}{s}\right)}^{n+1}\mathrm{\Gamma }(n+1,-st)+B\right)\right).\end{array}$$

(9)

The integral constant can be calculated by applying the continuity condition ($n_2(t_0)=n_1(t_0)$):

$$\begin{array}{cc}& B=\frac{e^{s{t}_0-\mathit{\lambda }(t_0-k_2)}}{{(t_0-k_2)}^{\mathit{\eta }+1}}\left(\sum _{n=0}^N\sum _{m=0}^n{a}_{nm}[\mathit{\gamma }(\mathit{\eta }+n-m+1,-\mathit{\lambda }(t_0-k_2))\right.\hfill \\ \hfill & \left.-\mathit{\gamma }(\mathit{\eta }+n-m+1,\mathit{\lambda }{k}_2)]-\sum _{n=0}^N{b}_n{\left(-\frac{1}{s}\right)}^{n+1}\mathrm{\Gamma }(n+1,-s{t}_0)+\frac{n_0{(-k_2)}^{\mathit{\eta }+1}}{e^{\mathit{\lambda }{k}_2}}\right).\hfill \end{array}$$

(10)

In summary, utilizing Eqs. (6) and (9), the neutron density was calculated when the core of the reactor was interpolated by an external source at the start-up stage. In the following, the neutron density was calculated for the case of a sinusoidal source, which is very close to a real system. In addition, the constant source was also considered to examine the validity of the obtained results.

External neutron source contribution

The analytical solution is calculated with two terms: one as a function of sinusoidal fluctuation in the external source, and the other as a function of constant source. Using the sinusoidal solution, the importance of the source term in the reactor kinetics analysis is better manifest.

Constant external neutron source

By calculating the neutron density for constant source, $(q=q_0)$, we have tried to show that the obtained result reduces to Palma et al.’s result [12]. From density equation definition of Eq. (6), we can write:

$$\begin{array}{c}\hfill n_1(t)=\left(\frac{e^{-\mathit{\lambda }u}}{u^{\mathit{\eta }+1}}(a_{00}\mathit{\gamma }(\mathit{\eta }+1,-\mathit{\lambda }u)+A)\right)\end{array}$$

(11)

where constants $a_{00}$ and $A$ are defined by:

$$\begin{array}{c}\hfill a_{00}=\frac{l{q}_0}{r{(-\mathit{\lambda })}^{\mathit{\eta }}},A=\left(\frac{-l{q}_0}{r{(-\mathit{\lambda })}^{\mathit{\eta }}}\mathit{\gamma }(\mathit{\eta }+1,\mathit{\lambda }{k}_2)+\frac{n_0{(-k_2)}^{\mathit{\eta }+1}}{e^{\mathit{\lambda }{k}_2}}\right).\end{array}$$

The complete solution of Eq. (8) with external constant source is given by:

$$\begin{array}{c}\hfill n_2(t)=\left(e^{-st}\left(\left(-\frac{b_0}{s}\right)\mathrm{\Gamma }(1,-st)+B\right)\right)\end{array}$$

(12)

In deriving $n_2(t)$, we used the continuity condition. In Eq. (12), $B$ is the integration constant given in terms of the incomplete gamma function as:

$$\begin{array}{c}\hfill B=\left(\frac{e^{s{t}_0-\mathit{\lambda }(t_0-k_2)}}{{(t_0-k_2)}^{\mathit{\eta }+1}}(a_{00}\mathit{\gamma }(\mathit{\eta }+1,\mathit{\lambda }(k_2-t_0))+A)+\left(\frac{b_0}{s}\right)\mathrm{\Gamma }(1,s{t}_0)\right).\end{array}$$

Therefore, Eqs. (11) and (12) are in agreement with previous results [Eqs. (16), (24) [12]]. These solutions are expressed in terms of incomplete gamma function and related to the probability integral of the chi-squared distribution, as discussed and tabulated by Abramowitz and Stegun [20].

Sinusoidal fluctuation

Due to fluctuation of neutron source around a constant value, the source is time dependent. Accounting for the sinusoidal external neutron source, $q(t)=q_0\sin \mathit{\omega }t$ ($\mathit{\omega }=\frac{2\mathit{\pi }}{T}$, where $\mathit{\omega }({\mathrm{s}}^{-1})$ and $T(\mathrm{s})$ are angular frequency and period of source, respectively) can be useful for indicating the environment effects in neutron density [16]. Let us recall Eq. (6) for neutron density coefficients:

$$\begin{array}{c}\hfill a_{nm}={\left(-\frac{1}{\mathit{\lambda }}\right)}^{\mathit{\eta }+2n-m+1}\left(\frac{l{q}_0}{r}\right){\left(\frac{{(-1)}^n{k}_2^m{\mathit{\omega }}^{2n+1}}{m!(2n-m+1)!}\right)}_{2n+1\ge m}\end{array}$$

(13)

$$\begin{array}{c}\hfill b_{nm}={\left(-\frac{1}{\mathit{\lambda }}\right)}^{\mathit{\eta }+2n-m+1}\left(-\frac{l{q}_0}{r}\right){\left(\frac{{(-1)}^n{k}_2^m{\mathit{\omega }}^{2n+1}}{m!(2n-m)!}\right)}_{2n\ge m}.\end{array}$$

(14)

Neutron density can be presented as:

$$\begin{array}{cc}& n_1(t)=\frac{e^{-\mathit{\lambda }u}}{u^{\mathit{\eta }+1}}\left(\sum _{n=0}^N\sum _{m=0}^{2n+1}{a}_{\mathrm{rm}\mathrm{nm}}\mathit{\gamma }(\mathit{\eta }+2n-m+2,-\mathit{\lambda }u)\right.\hfill \\ \hfill & \left.+\sum _{n=0}^N\sum _{m=0}^{2n}{b}_{\mathrm{nm}}\mathit{\gamma }(\mathit{\eta }+2n-m+1,-\mathit{\lambda }u)+A\right).\hfill \end{array}$$

(15)

After imposing the initial condition, $n_1(0)=n_0$, one can determine the constant $A$ from Eq. (15). So, we have:

$$\begin{array}{c}\hfill A=\frac{n_0{(-k_2)}^{\mathit{\eta }+1}}{e^{\mathit{\lambda }{k}_2}}-\left(\sum _{n=0}^N\sum _{m=0}^{2n+1}{a}_{\mathrm{nm}}\mathit{\gamma }(\mathit{\eta }+2n-m+2,\mathit{\lambda }{k}_2)\right.\\ \hfill \left.+\sum _{n=0}^N\sum _{m=0}^{2n}{b}_{\mathrm{nm}}\mathit{\gamma }(\mathit{\eta }+2n-m+1,\mathit{\lambda }{k}_2)\right).\end{array}$$

The solution of Eq. (8), in the second stage from insertion of reactivity, can be calculated from the integration factor method:

$$\begin{array}{c}\hfill n_2(t)=e^{-st}\left(\sum _{n=0}^N(c_n\mathrm{\Gamma }(2n+2,-st)+d_n\mathrm{\Gamma }(2n+1,-st))+B\right)\end{array}$$

(16)

where

$$\begin{array}{c}\hfill c_n=\left(-\frac{l{q}_0\mathit{\lambda }}{{\mathit{\rho }}_0+r{t}_0-\mathit{\beta }}\right)\left(\frac{{(-1)}^n{\mathit{\omega }}^{2n+1}}{(2n+1)!}\right){\left(\frac{1}{s}\right)}^{2n+2}\end{array}$$

$$\begin{array}{c}\hfill d_n=\left(\frac{l{q}_0\mathit{\lambda }}{{\mathit{\rho }}_0+r{t}_0-\mathit{\beta }}\right)\left(\frac{{(-1)}^n{\mathit{\omega }}^{2n+2}}{(2n)!}\right){\left(\frac{1}{s}\right)}^{2n+1}.\end{array}$$

In Eq. (16), $B$ is the integration constant given in terms of the incomplete gamma functions, which can be obtained from continuity condition $(n_1(t_0)=n_2(t_0))$:

$$\begin{array}{cc}& B=\frac{e^{s{t}_0-\mathit{\lambda }(t_0-k_2)}}{{(t_0-k_2)}^{\mathit{\eta }+1}}\left(\sum _{n=0}^N\sum _{m=0}^{2n+1}{a}_{\mathrm{nm}}\mathit{\gamma }(\mathit{\eta }+2n-m+2,\mathit{\lambda }(k_2-t_0))\right.\hfill \\ \hfill & \left.+\sum _{n=0}^N\sum _{m=0}^{2n}{b}_{\mathrm{nm}}\mathit{\gamma }(\mathit{\eta }+2n-m+1,\mathit{\lambda }(k_2-t_0))+A\right)-(c_n\mathrm{\Gamma }(2n+2,-s{t}_0)\hfill \\ \hfill & +d_n\mathrm{\Gamma }(2n+1,-s{t}_0)).\hfill \end{array}$$

Equations (15) and (16) represent the complete solutions of Eqs. (15) and (8) in the presence of the sinusoidal external neutron source.

Results and discussions

Neutron external source play an important role during the start-up of a nuclear reactor. Therefore, the analytical solutions of neutron point kinetics equations in the presence of an external source are important in predicting the variation of neutron population during the start-up of a nuclear reactor. Here, the analyses are presented for the thermal reactor with the following parameters [9, 12]: $\mathit{\lambda }=0.001{\mathrm{s}}^{-1}$, $l=0.0015s$, $\mathit{\beta }=0.0075$, $r=0.0001{\mathrm{s}}^{-1}$, ${\mathit{\rho }}_0=-0.006$, and $t_0=10s$. Equations (6) and (9) are the solutions of the neutron point kinetics equations with one-group delayed neutron during the start-up of the thermal reactor in a two-stage insertion of reactivity. They are valid for any function that can be expressed by a power series. Due to fluctuation of the neutron source around a mean value, the source is actually time dependent. The general solutions of NPK equations can well describe neutron density response to any external neutron source, both quantitatively and qualitatively. To verify the validity of the analytical solutions, the variation of neutron density with constant and sinusoidal external neutron source was calculated. Specially, for $n=0$ and $m=0,$ the neutron density was obtained in the presence of a constant source [see Eqs. (11), (12)]. This result is in line with Palma et al.’s work [12]. In this work, numerical calculations were carried out with generalized Runge–Kutta (GRK) method. The relative percentage errors (RPEs) of the neutron density using analytical and numerical solutions are defined as follows:

$$\begin{array}{c}\hfill {(RPEs)}_{12}=|\frac{n_1(t)-n_2(t)}{n_1(t)}|\times 100\end{array}$$

$$\begin{array}{c}\hfill {(RPEs)}_{13}=|\frac{n_1(t)-n_3(t)}{n_1(t)}|\times 100,\end{array}$$

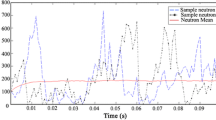
wherethe neutron densities of $n_1,n_2$ and $n_3$ are the solutions of numerical calculations without ISD, with ISD and analytical calculation with ISD, respectively. According to Table 1, the RPEs are smaller than 1 %, and the resultant RPEs are acceptable for engineering applications. So, the results of the analytical calculations are in a good agreement with the numerical results (see Fig. 1). Studying neutron density with conditions close to the critical state and small ramp rate reactivities $(r\ll 1)$ is important for reactor control and safety. Effective multiplication factor $(k_{\mathrm{eff}})$ values, close to the critical state is shown in Fig. 2. As an example, Fig. 3 shows the numerical and analytical solution results for $r={10}^{-5}{\mathrm{s}}^{-1},{\mathit{\rho }}_0=-0.003$ and $k_{\mathrm{eff}}=0.9965$, which are in good agreement with each other. Data in Table 2 show that the RPEs of the numerical and analytical solution are less than 0.5 % and also the RPEs decrease for $k_{\mathrm{eff}}⟶1$ and $r\ll 1$. So, the ISD approximation is valid for neutronic calculations very close to criticality and $r\ll 1$.

Table 1 The neutron densities and the relative errors for two-stage insertion of reactivity in the presence of a constant external neutron source

Table 2 The neutron densities and the relative errors for the insertion of ramp reactivity in the presence of a constant external neutron source very close to criticality

For $n=2k+1$ and $k=0,1,2,...$ the power series external source is:

$$\begin{array}{c}\hfill q(t)=\left(\sum _{n=0}^N{a}_n{t}^n\right)\equiv \left(\sum _{k=0}^N{a}_{2k+1}{t}^{2k+1}\right)=q_0\sin (\mathit{\omega }t).\end{array}$$

(17)

Such a phenomenon is also explained by Hetrick [16]. As a result, in the case of sinusoidal source with a small amplitude of oscillations, the constant source approximation is applicable at the start-up process [21, 22].

Fig. 1

Comparison of the analytical solution with the numerical solutions for $r=0.0001{\mathrm{s}}^{-1}$, ${\mathit{\rho }}_0=-0.006$, $q={10}^9\frac{\mathrm{neutron}}{{\mathrm{cm}}^3\mathrm{s}}$ and $t_0=10\mathrm{s}$ in the presence of a constant external neutron source

Fig. 2

Multiplication factor as a function of time and initial reactivity for very small ramp rate reactivity $(r=0.00001{\mathrm{s}}^{-1})$

Fig. 3

Multiplication factor as a function of time and initial reactivity for very small ramp rate reactivity $(r=0.00001{\mathrm{s}}^{-1})$

As an example, the neutron density using analytical solution for $n=20$, $m=0,..9$, $T=50\mathrm{s}$ and $q_0={10}^8$ (blue dashed-dotted line) was compared with numerical results, with ISD and without ISD in Fig. 4. After raising the control rods and during sturt-up, $10\mathrm{s}\le t\le 200\mathrm{s}$, the neutron density increases with time, as shown in Fig. 5. Regarding Table 3, the RPEs do not reach 1 %. Therefore, the results of numerical and analytical methods are the same.

Table 3 The neutron densities and the relative errors for two-stage insertion of reactivity in the presence of a sinusoidal external neutron source

Fig. 4

Comparison of the analytical solution with the numerical solutions for $r=0.0001{\mathrm{s}}^{-1}$, ${\mathit{\rho }}_0=-0.006$, $q_0={10}^8\frac{\mathrm{neutron}}{{\mathrm{cm}}^3\mathrm{s}}$, $T=50\mathrm{s}$ and $t_0=10\mathrm{s}$ in the presence of a sinusoidal external neutron source

Fig. 5

The variation of neutron density during start-up for $r=0.0001{\mathrm{s}}^{-1}$, ${\mathit{\rho }}_0=-0.006$, $q_0={10}^8\frac{\mathrm{neutron}}{{\mathrm{cm}}^3\mathrm{s}}$, $T=50\mathrm{s}$ and $0\le t\le 200\mathrm{s}$ in the presence of a sinusoidal external neutron source, which shows an increase in the neutron density with time, as expected

Conclusion

Since the external neutron source term is very important at the start-up stage, it cannot be ignored. Due to the random nature of the external neutron source, we can take a time-dependent source. Therefore, in this work, an analytical solution is presented for any neutron external source that can be found in terms of a power series. Analytical solutions in a general form are as in Eqs. (6) and (9). In particular, analytical solutions are obtained for the constant [12] and sinusoidal sources [16]. Numerical and analytical results in both cases are in a good agreement with each other.

Appendices

Appendix A

Using transformation of variable $u=t-k_2$ and replacing in Eq. (5), we have:

$$\begin{array}{c}\hfill \frac{\mathrm{d}{n}_1}{\mathrm{d}t}+\left(\frac{\mathit{\eta }+1}{u}+\mathit{\lambda }\right)n_1=-\frac{l}{ru}\sum _{n=0}^N(\mathit{\lambda }{q}_n+(n+1)q_{n+1}){(u+k_2)}^n,\end{array}$$

(18)

where $\mathit{\eta }=k_1+\mathit{\lambda }{k}_2-1$. Also using binomial expansion as follows:

$$\begin{array}{c}\hfill {(u+k_2)}^n=\left(\sum _{m=0}^n\left(\begin{array}{c}n\\ m\end{array}\right)k_2^m{u}^{n-m}\right),\end{array}$$

one can write:

$$\begin{array}{c}\hfill \frac{\mathrm{d}{n}_1(t)}{\mathrm{d}t}+\left(\frac{\mathit{\eta }+1}{u}+\mathit{\lambda }\right)n_1=\left(-\frac{l}{r}\sum _{n=0}^N\sum _{m=0}^n\left(\begin{array}{c}n\\ m\end{array}\right)k_2^m(\mathit{\lambda }{q}_n+(n+1)q_{n+1})u^{n-m-1}\right),\end{array}$$

where constant $d_{\mathrm{nm}}$ are defined as follows:

$$\begin{array}{c}\hfill d_{\mathrm{nm}}=\left(-\frac{l}{r}\left(\begin{array}{c}n\\ m\end{array}\right)k_2^m(\mathit{\lambda }{q}_n+(n+1)q_{n+1})\right)\end{array}$$

$$\begin{array}{c}\hfill \frac{\mathrm{d}{n}_1(t)}{\mathrm{d}t}+\left(\frac{\mathit{\eta }+1}{u}+\mathit{\lambda }\right)n_1=\sum _{n=0}^N\sum _{m=0}^n{d}_{\mathrm{nm}}{u}^{n-m-1}.\end{array}$$

(19)

Equation (19) can be solved through the use of the integrating factor method. Therefore, we get:

$$\begin{array}{c}\hfill n_1(t)=\frac{e^{-\mathit{\lambda }u}}{u^{\mathit{\eta }+1}}\left(\sum _{n=0}^N\sum _{m=0}^n{d}_{\mathrm{nm}}\int du{e}^{\mathit{\lambda }u}{u}^{\mathit{\eta }+n-m}+A\right).\end{array}$$

(20)

Using the transformation of variable $y=-\mathit{\lambda }u$ and $\mathit{\alpha }=\mathit{\eta }+n-m+1$, we have:

$$\begin{array}{c}\hfill n_1(t)=\frac{e^{-\mathit{\lambda }u}}{u^{\mathit{\eta }+1}}\left(\sum _{n=0}^N\sum _{m=0}^n{d}_{nm}{\left(-\frac{1}{\mathit{\lambda }}\right)}^{\mathit{\eta }+n-m+1}{\int }_0^{t}dy{e}^{-y}{y}^{\mathit{\alpha }-1}+A\right)\end{array}$$

(21)

$$\begin{array}{c}\hfill a_{\mathrm{nm}}=d_{\mathrm{nm}}{\left(-\frac{1}{\mathit{\lambda }}\right)}^{\mathit{\eta }+n-m+1},\end{array}$$

where

$$\begin{array}{c}\hfill \mathit{\gamma }(\mathit{\alpha },t)={\int }_0^t\mathrm{d}y{e}^{-y}{y}^{\mathit{\alpha }-1}.\end{array}$$

(22)

The solution of Eq. (21) can be written as:

$$\begin{array}{c}\hfill n_1(t)=\frac{e^{-\mathit{\lambda }u}}{u^{\mathit{\eta }+1}}\left(\sum _{n=0}^N\sum _{m=0}^n{a}_{nm}\mathit{\gamma }(\mathit{\eta }+n-m+1,-\mathit{\lambda }u)+A\right).\end{array}$$

(23)

Appendix B

Incomplete gamma function is defined as:

$$\begin{array}{c}\hfill \mathrm{\Gamma }(\mathit{\alpha },t)={\int }_t^{\infty }\mathrm{d}y{e}^{-y}{y}^{\mathit{\alpha }-1}.\end{array}$$

(24)

Equation (9) can be solved through the use of the integrating factor method. Therefore we get:

$$\begin{array}{c}\hfill n_2(t)=e^{-st}\left(\sum _{n=0}^N{b}_n\int \mathrm{d}t{e}^{st}{t}^n+B\right).\end{array}$$

(25)

Using $y=-st$, one can write:

$$\begin{array}{c}\hfill n_2(t)=e^{-st}\left(\sum _{n=0}^N{b}_n{\left(-\frac{1}{s}\right)}^{n+1}\int \mathrm{d}y{e}^{-y}{y}^n+B\right)\end{array}$$

(26)

, so we have:

$$\begin{array}{c}\hfill n_2(t)=e^{-st}\left(\sum _{n=0}^N{b}_n{\left(-\frac{1}{s}\right)}^{n+1}\mathrm{\Gamma }(n+1,-st)+B\right).\end{array}$$

(27)