The static properties and form factors of the deuteron using the different forms of the Wood–Saxon potential

Abstract

The basic properties and form factors of the deuteron system are investigated for the different forms of the Wood–Saxon potential. We have used the Nikiforov-Uvarov (NU) method for analytical solution of the radial Schrodinger equation. A comparison of the calculated values with experimental results are given. It is shown that the obtained results for the modified form of the Wood–Saxon potential are very close to the experimental results in comparison with other forms of the potential.

Introduction

The internal structure of the nucleon has been the subject of intensive experimental and theoretical studies for several decads. The internal structure is conveniently described in terms of electromagnetic form factors (FFs). The form factors are a measurable and physical manifestation of the nature of the nucleons’ constituents and the dynamics that binds them together. The elastic electron–deuteron scattering is one of the processes that probe mentioned structure. The deuteron electromagnetic form factors allow us to describe interaction between the deuteron and electromagnetic field [1]. Different aspects of the underlying nuclear structure of the deuteron can be obtained through analysis of scattering of various probes at different energy scales. As a relevant example, consider elastic electron–deuteron scattering. The form factor describes the structure and spatial extension of a nucleus, because in real life nuclei are not point like. The deuteron form factor $F_{\mathrm{D}}\left(q^2\right)$ provides an ideal illustration of the continuality between nuclear and particle physics at the microscopic level. At low momentum transfer, where the nucleons can be treated as point-like objects and are the essential degrees of freedom, the usual effective potential Schrodinger theory is appropriate, and meson exchange effects provide the framework for the nuclear interaction. The deuteron electromagnetic form factors allow us to describe quantifiable an interaction between the deuteron and electromagnetic field. Form factors can be calculated in terms of information about electron elastic scattering by deuteron [2, 3]. Our goal in this project is to study the properties and form factors of deuteron system. So, this paper is organized as follows: “Deuteron form factors” introduces deuteron form factors. In “NU (Nikiforov-Uvarov) method”, the theoretical framework of the NU method is briefly discussed. The solution of the Schrodinger equation for Standard, Generalized, and modified Wood–Saxon potentials via mentioned method are presented in “Calculations”. In “Numerical results and applications”, we will apply our results to calculate the statics properties and form factors of deuteron, and finally we summarize the paper and discuss future perspectives of the study in “Conclusion”.

Deuteron form factors

The elastic electron-deuteron cross-section in the one-photon exchange approximation is given by [4–6]

$$\begin{array}{c}\hfill \frac{\mathrm{d}\mathit{\sigma }}{\mathrm{d}\mathrm{\Omega }}={\mathit{\sigma }}_{\mathrm{M}}\left[A(Q^2)+B(Q^2){tan}^2\frac{\mathit{\theta }}{2}\right]\end{array}$$

(1)

with

$$\begin{array}{c}\hfill A(Q^2)=G_{\mathrm{c}}^2(Q^2)+\frac{8}{9}{\mathit{\eta }}^2{G}_{\mathrm{Q}}^2(Q^2)+\frac{2}{3}\mathit{\eta }{G}_{\mathrm{M}}^2(Q^2)\end{array}$$

(2)

$$\begin{array}{c}\hfill B(Q^2)=\frac{4}{3}\mathit{\eta }(1+\mathit{\eta })G_{\mathrm{M}}^2(Q^2)\end{array}$$

(3)

$$\begin{array}{c}\hfill \mathit{\eta }=\frac{Q^2}{4M_{\mathrm{d}}^2},\end{array}$$

(4)

where $Q^2=4E{E}^{\prime }{sin}^2\frac{\mathit{\theta }}{2}$ is the four-momentum transfer squared, $E$ is the incoming electron energy, $\mathit{\theta }$ is the electron scattering angle, $E^{\prime }$ is the scattered electron energy in the lab rest frame, $\mathit{\eta }=\frac{Q^2}{4M_{\mathrm{d}}^2}$ , and $M_{\mathrm{d}}$ is the deuteron mass.

The expression ${\mathit{\sigma }}_{\mathrm{M}}={(\frac{\mathrm{d}\mathit{\sigma }}{\mathrm{d}\mathrm{\Omega }})}_{\mathrm{Mott}}$ is a scattering cross-section by non-structure spin-free particle derived by Mott. Three terms $(G_{\mathrm{c}},G_{\mathrm{Q}},G_{\mathrm{M}})$ are the form factors making contribution to the full cross-section. They are due to charge, quadrupole moment, and magnetic moment of the deuteron.

Calculation of deuteron form factors and static properties require a deuteron wave function [7, 8]. The best non-relativistic wave function are calculated from Schrodinger equation. An analytical solution of radial Schrodinger equation is of high importance in non-relativistic quantum mechanics, because the wave function contains all necessary information for full description of a quantum system. There are only few potentials for which the radial Schrodinger equation can be solved explicitly for $n$ and $l$. So far, many methods were developed, such as supersymmetry (SUSY) [9, 10], Nikiforov-Uvarov (NU) method [11] the Pekeris approximation [12].

NU (Nikiforov-Uvarov) method

The NU method provides an exact solution of the non-relativistic Schrodinger equation for certain kinds of potentials [13, 14]. This method is based on the solution of generalized second-order differential linear equation with special orthogonal functions and for any given real or complex potential, the one-dimensional Schrodinger equation is reduced to a generalized equation of the hypergeometric with an appropriate $S=S(r)$ coordinate transformation. Thus it can be written in the following form [11]:

$$\begin{array}{c}\hfill F^{\prime \prime }(s)+\frac{\mathit{\tau }(s)}{\mathit{\sigma }(s)}{F}^{\prime }(s)+\frac{\tilde{\mathit{\sigma }}(s)}{{\mathit{\sigma }}^2(s)}F(s)=0,\end{array}$$

(5)

where $\mathit{\sigma }(s)$ and $\tilde{\mathit{\sigma }}(s)$ are polynomials at most second degree, and $\tilde{\mathit{\tau }}(s)$ is a first degree polynomials. We use the following transformation:

$$\begin{array}{c}\hfill F(s)=\mathit{\varphi }(s)y(s)\end{array}$$

(6)

This selection reduces the Schrodinger equation (5), to an equation of the hypergeometric type:

$$\begin{array}{c}\hfill \mathit{\sigma }(s)y^{″}(s)+\mathit{\tau }(s)y^{\prime }(s)+\mathit{\lambda }y(s)=0\end{array}$$

(7)

$\mathit{\varphi }(s)$ satisfies $\frac{{\mathit{\varphi }}^{\prime }(s)}{\mathit{\varphi }(s)}=\frac{\mathit{\pi }(s)}{\mathit{\sigma }(s)}$ and $y(s)$ is the hypergeometric type function whose polynomial solutions are given by Rodrigues relation:

$$\begin{array}{c}\hfill y_n(s)=\frac{B_{\mathrm{n}}}{\mathit{\rho }(s)}\frac{{\mathrm{d}}^n}{\mathrm{d}{\mathit{s}}^n}[{\mathit{\sigma }}^n(s)\mathit{\rho }(s)]\end{array}$$

(8)

$B_{\mathrm{n}}$ is the normalization constant and the weight function $\mathit{\rho }(s)$ must satisfy the condition:

$$\begin{array}{c}\hfill \frac{\mathrm{d}}{\mathrm{d}\mathit{s}}(\mathit{\sigma }\left(s\right)\mathit{\rho }(s))=\mathit{\tau }(s)\mathit{\rho }(s)\end{array}$$

(9)

The function $\mathit{\pi }(s)$ and the parameter $\mathit{\lambda }$ are defined as

$$\begin{array}{c}\hfill \mathit{\pi }(s)=\frac{\acute{\mathit{\sigma }}(s)-\tilde{\mathit{\tau }}(s)}{2}\pm \sqrt{{\left(\frac{\acute{\mathit{\sigma }}(s)-\tilde{\mathit{\tau }}(s)}{2}\right)}^2-\tilde{\mathit{\sigma }}(s)+k\mathit{\sigma }(s)}\end{array}$$

(10)

and

$$\begin{array}{c}\hfill \mathit{\lambda }=k+{\mathit{\pi }}^{\prime }(s)\end{array}$$

(11)

Here, $\mathit{\pi }(s)$ obviously is a polynomial depended on the transformation function $s\left(r\right).$ On the other hand, to find the value of k, the expression under the square root must be square of a polynomial. This is possible only if its discriminant is zero. Hence, a new eigenvalue equation for the Schrodinger equation becomes

$$\begin{array}{c}\hfill {\mathit{\lambda }}_n+n{\mathit{\tau }}^{\prime }\left(s\right)+\frac{n\left(n+1\right)}{2}{\mathit{\sigma }}^{″}\left(s\right)=0\left(n=0,1,2,...\right),\end{array}$$

(12)

where

$$\begin{array}{c}\hfill \mathit{\tau }\left(s\right)=\tilde{\mathit{\tau }}\left(s\right)+2\mathit{\pi }\left(s\right)\end{array}.$$

(13)

Calculations

Standard Wood–Saxon potential

Woods and Saxon [15] introduced a potential to study elastic scattering of 20 MeV protons by medium and heavy nuclei. The Wood–Saxon potential is a reasonable potential for nuclear shell model and hence attracts lots of attention in nuclear physics. The spherical Wood–Saxon potential that was used as a major part of nuclear shell model, has received a lot of attention in nuclear mean field model, and plays an essential role in microscopic physics [16]. The standard Wood–Saxon potential is given by [17]:

$$\begin{array}{c}\hfill V(r)=\frac{V_0}{1+exp\left(\frac{r-R}{a}\right)},\end{array}$$

(14)

where $R,V_0$ and $a$ are mean radius, wall depth potential, and skin thickness, respectively.

Let us consider the radial part of Schrodinger equation with mentioned potential:

$$\begin{array}{c}\hfill \frac{{\mathrm{d}}^2\mathrm{R}}{\mathrm{d}{\mathit{r}}^2}+\frac{2\mathit{\mu }}{{ħ}^2}[E+V_{\mathrm{total}}(r)]R(r)=0\end{array}$$

(15)

$$\begin{array}{c}\hfill V_{\mathrm{total}}\left(r\right)=\frac{V_0}{1+exp\left(\frac{r-R}{a}\right)}-\frac{{ħ}^{2}l(l+1)}{2\mathit{\mu }{r}^2},\end{array}$$

(16)

where $l$ is the angular momentum number, $\mathit{\mu }$ is the reduced mass, $E_{n,l}$ is the appropriate energy eigenvalue, and $\frac{1}{r^2}$ is the centrifugal term.

Now, we want to solve the Eq. (15) for the $l\ne 0$ cases using NU method and Pekeris approximation to the centrifugal for $l$ states [15–18]. The approximation is based on the expansion of the centrifugal barrier in the series of exponentials depending on the internuclear distance, keeping terms up to second order. We now replace the centrifugal term according to the Pekeris approximation with expression:

$$\begin{array}{c}\hfill {\tilde{V}}_l(x)=\mathit{\gamma }\left(D_0+D_1{(1+exp\left(\mathit{\alpha }x\right))}^{-1}+D_2{(1+exp\left(\mathit{\alpha }x\right))}^{-2}\right),\end{array}$$

(17)

where $x=\frac{\left(r-R\right)}{R}$, $\mathit{\alpha }=\frac{R}{a}$, and $D_i$ is the coefficients $\left(i=0,1,2\right)$. In the $x=0$, the expression of (16) can be expanded up to the terms $x^3$,

where

$$\begin{array}{cc}\hfill {\tilde{V}}_l(x)& =\mathit{\gamma }\left(D_0+\frac{D_1}{2}+\frac{D_2}{4}-x\left(\frac{D_1\mathit{\alpha }}{4}+\frac{D_2\mathit{\alpha }}{4}\right)\right)\hfill \\ \hfill & +\mathit{\gamma }\left(x^2\left(\frac{D_2{\mathit{\alpha }}^2}{16}\right)+x^3\left(\frac{D_1{\mathit{\alpha }}^3}{48}+\frac{D_2{\mathit{\alpha }}^3}{48}\right)+...\right)\hfill \end{array}$$

(18)

$$\begin{array}{c}\hfill D_0=1-\frac{4}{\mathit{\alpha }}+\frac{12}{{\mathit{\alpha }}^2},D_1=\frac{8}{\mathit{\alpha }}-\frac{48}{{\mathit{\alpha }}^2},D_2=\frac{48}{{\mathit{\alpha }}^2}\end{array}$$

(19)

We now can take the potential ${\tilde{V}}_l$ instead of the centrifugal term in the $V_{\mathrm{total}}$ and solve the Schrodinger equation. We substitute (17) into (15) and using a new variable of the form

$$\begin{array}{c}\hfill S\left(r\right)=exp\left(\frac{r-R}{a}\right)\end{array}$$

(20)

we obtain the following:

$$\begin{array}{cc}& \frac{{\mathrm{d}}^2\mathrm{R}\left(\mathrm{s}\right)}{\mathrm{d}{\mathit{s}}^2}+\frac{\left(s+1\right)}{s\left(s+1\right)}\frac{\mathrm{d}\mathit{R}\left(\mathrm{s}\right)}{\mathrm{d}\mathit{s}}+\frac{1}{s^2{\left(s+1\right)}^2}\hfill \\ \hfill & +\left[-{\mathit{\epsilon }}^2{s}^2\left({\mathit{\beta }}^2-2{\mathit{\epsilon }}^2\right)s+\left({\mathit{\beta }}^2-{\mathit{\chi }}^2-{\mathit{\epsilon }}^2\right)\right]R\left(s\right)=0,\hfill \end{array}$$

(21)

where

$$\begin{array}{cc}\hfill {\mathit{\epsilon }}^2& =\frac{-2\mathit{\mu }{a}^2\left(E-\mathit{\gamma }{D}_0\right)}{{ħ}^2},{\mathit{\beta }}^2=\frac{2\mathit{\mu }{a}^2\left(V_0-\mathit{\gamma }{D}_1\right)}{{ħ}^2}\hfill \\ \hfill {\mathit{\chi }}^2& =\frac{2\mathit{\mu }{a}^2\mathit{\gamma }{D}_2}{{ħ}^2},\mathit{\gamma }=\frac{{ħ}^{2}l\left(l+1\right)}{2\mathit{\mu }{R}^2}\hfill \end{array}$$

(22)

are dimensionless parameters.

According to the NU method, we can obtain $\mathit{\pi }\left(s\right)$ , $\mathit{\lambda }$ and ${\mathit{\lambda }}_n$:

$$\begin{array}{cc}\hfill \mathit{\pi }(s)& =\pm \left\{\frac{s}{2}\pm \frac{1}{2}\left[\sqrt{\mathit{\alpha }}+\left(\sqrt{1+4{\mathit{\chi }}^2}+2\sqrt{\mathit{\alpha }}\right)s\right]\right\}\hfill \\ \hfill k_{+}& =2{\mathit{\chi }}^2-{\mathit{\beta }}^2+\sqrt{\mathit{\alpha }\left(1+4{\mathit{\chi }}^2\right)}\hfill \\ \hfill \mathit{\pi }(s)& =\pm \left\{\frac{s}{2}\pm \frac{1}{2}\left[\sqrt{\mathit{\alpha }}-\left(\sqrt{1+4{\mathit{\chi }}^2}-2\sqrt{\mathit{\alpha }}\right)s\right]\right\}\hfill \\ \hfill k_{-}& =2{\mathit{\chi }}^2-{\mathit{\beta }}^2-\sqrt{\mathit{\alpha }\left(1+4{\mathit{\chi }}^2\right)},\hfill \end{array}$$

(23)

where $\mathit{\alpha }=\left({\mathit{\epsilon }}^2+{\mathit{\chi }}^2-{\mathit{\beta }}^2\right)$.

$$\begin{array}{c}\hfill \mathit{\lambda }=2{\mathit{\chi }}^2-{\mathit{\beta }}^2+\left(1+\sqrt{1+4{\mathit{\chi }}^2}\right)\left(\frac{1}{2}+\sqrt{{\mathit{\chi }}^2+{\mathit{\epsilon }}^2-{\mathit{\beta }}^2}\right)\end{array}$$

(24)

$$\begin{array}{c}\hfill {\mathit{\lambda }}_n=-n\left(1+n+2\sqrt{{\mathit{\chi }}^2+{\mathit{\epsilon }}^2-{\mathit{\beta }}^2}+\sqrt{1+4{\mathit{\chi }}^2}\right)\end{array}$$

(25)

Comparing (24) and (25), the exact energy eigenvalues of the radial Schrodinger equation with WS potential are obtained as follows:

$$\begin{array}{cc}\hfill E_{n,l}& =\mathit{\gamma }{D}_0+{\mathit{\beta }}^2-{\mathit{\chi }}^2\hfill \\ \hfill & -\frac{{ħ}^2}{2\mathit{\mu }{a}^2}{\left[\frac{{\mathit{\beta }}^2-2{\mathit{\chi }}^2+n\left(n+1\right)}{\left(1+2n+\sqrt{1+4{\mathit{\chi }}^2}\right)}-\frac{\left(2n+1\right)}{2}\right]}^2,\hfill \end{array}$$

(26)

where substitute the values of $\mathit{\gamma }$, $D_0$, $D_1$, $D_2$, ${\mathit{\beta }}^2$ and ${\mathit{\chi }}^2$ from (19) and (22). The corresponding eigenfunction as follows:

$$\begin{array}{cc}\hfill R_{n,l}\left(s\right)& =C_n\frac{{\left(1+s\right)}^{\frac{1}{2}\left(1+\sqrt{1+4{\mathit{\chi }}^2}\right)}{s}^{\sqrt{{\mathit{\chi }}^2-{\mathit{\beta }}^2+{\mathit{\epsilon }}^2}}}{n!{\left(1+s\right)}^{\sqrt{1+4{\mathit{\chi }}^2}}{s}^{2\sqrt{{\mathit{\chi }}^2-{\mathit{\beta }}^2+{\mathit{\epsilon }}^2}}}\hfill \\ \hfill & \times \frac{{\mathrm{d}}^{\mathit{n}}}{\mathrm{d}{\mathit{s}}^{\mathit{n}}}\left[{\left(1+s\right)}^{n+\sqrt{1+4{\mathit{\chi }}^2}}{s}^{n+2\sqrt{{\mathit{\chi }}^2+{\mathit{\epsilon }}^2-{\mathit{\beta }}^2}}\right],\hfill \end{array}$$

(27)

where $C_n$ is the new normalization constant and it is determined by the condition ${\int }_0^{\infty }{R}_n\left(s\right)ds=1$.

Generalized Wood–Saxon potential

We consider the following potential which is a generalization of the Wood–Saxon potential and it is given by [19]:

$$\begin{array}{c}\hfill V\left(r\right)=-V_1\frac{exp\left(-\left(\frac{r-R}{a}\right)\right)}{1+exp\left(-\left(\frac{r-R}{a}\right)\right)}+V_2\frac{exp\left(-2\left(\frac{r-R}{a}\right)\right)}{1+exp\left(-2\left(\frac{r-R}{a}\right)\right)},\end{array}$$

(28)

where $r$ stands for the center-of-mass distance between the projectile nucleus and the target nucleus. The other parameters in the potential $R=r_0{A}^{\frac{1}{3}}$ are the radius of the corresponding spherical nucleus or the width of the potential, A is the target mass number, $r_0$ is the radius parameter, $V_1$ is the potential depth of the Coulombic part [i.e., the first term on the right-hand side of (28)], $a$ is the diffuseness of the nuclear surface, and finally $V_2$ is an introduced parameter for the second part of (28) (transforms like potential barrier).

Now, rewriting (15) by employing the convenient transformation

$$\begin{array}{c}\hfill S\left(r\right)=\frac{1}{1+e^{-\left(\frac{r-R}{a}\right)}}\end{array}$$

(29)

The radial Schrodinger equation for the generalized Wood–Saxon potential is as follows:

$$\begin{array}{cc}& \frac{{\mathrm{d}}^2\mathrm{R}\left(\mathrm{s}\right)}{\mathrm{d}{\mathit{s}}^2}+\frac{\left(1-2s\right)}{s\left(1-s\right)}\frac{\mathrm{d}\mathit{R}\left(\mathrm{s}\right)}{\mathrm{d}\mathit{s}}+\frac{1}{s^2{\left(1-s\right)}^2}\hfill \\ \hfill & \left[-{\mathit{\chi }}^2{s}^2+\left(2{\mathit{\chi }}^2-{\mathit{\beta }}^2\right)s+\left({\mathit{\beta }}^2-{\mathit{\chi }}^2-{\mathit{\epsilon }}^2\right)\right]=0,\hfill \end{array}$$

(30)

where ${\mathit{\chi }}^2$, ${\mathit{\beta }}^2$, ${\mathit{\epsilon }}^2$ and $\mathit{\gamma }$ are dimensionless parameters. According to the previous section, we calculate the $\mathit{\pi }\left(s\right)$, $E_{n,l}$, $R_{n,l}$ and write briefly

$$\begin{array}{cc}\hfill \mathit{\pi }\left(s\right)& =\pm \left[\sqrt{{\mathit{\epsilon }}^2+{\mathit{\chi }}^2-{\mathit{\beta }}^2}+\left(\mathit{\epsilon }-\sqrt{{\mathit{\epsilon }}^2+{\mathit{\chi }}^2-{\mathit{\beta }}^2}\right)s\right]\hfill \\ \hfill k_{+}& ={\mathit{\beta }}^2-2{\mathit{\epsilon }}^2+2\mathit{\epsilon }\sqrt{{\mathit{\epsilon }}^2+{\mathit{\chi }}^2-{\mathit{\beta }}^2}\hfill \\ \hfill \mathit{\pi }\left(s\right)& =\pm \left[\sqrt{{\mathit{\epsilon }}^2+{\mathit{\chi }}^2-{\mathit{\beta }}^2}+\left(\mathit{\epsilon }-\sqrt{{\mathit{\epsilon }}^2+{\mathit{\chi }}^2-{\mathit{\beta }}^2}\right)s\right]\hfill \\ \hfill k_{-}& ={\mathit{\beta }}^2-2{\mathit{\epsilon }}^2-2\mathit{\epsilon }\sqrt{{\mathit{\epsilon }}^2+{\mathit{\chi }}^2-{\mathit{\beta }}^2}\hfill \end{array}$$

(31)

$$\begin{array}{cc}\hfill E_{n,l}& =\mathit{\gamma }{D}_0-\left(\frac{V_2-\mathit{\gamma }{D}_2}{(n^2+{\mathit{\chi }}^2+(n+\frac{1}{2})(1\pm \sqrt{1+4{\mathit{\chi }}^2}))}\right)\hfill \\ \hfill & \times {\left(\frac{(n^2+{\mathit{\chi }}^2+(n+\frac{1}{2})(1\pm \sqrt{1+4{\mathit{\chi }}^2}))+{\mathit{\beta }}^2-{\mathit{\chi }}^2}{2\mathit{\chi }}\right)}^2\hfill \end{array}$$

(32)

$$\begin{array}{cc}\hfill R_{n,l}\left(s\right)& =C_n\frac{{\left(1-s\right)}^{\mathit{\epsilon }}{s}^{\sqrt{{\mathit{\chi }}^2-{\mathit{\beta }}^2+{\mathit{\epsilon }}^2}}}{n!{\left(1-s\right)}^{2\mathit{\epsilon }}{s}^{2\sqrt{{\mathit{\chi }}^2-{\mathit{\beta }}^2+{\mathit{\epsilon }}^2}}}\hfill \\ \hfill & \times \frac{{\mathrm{d}}^{\mathit{n}}}{\mathrm{d}{\mathit{s}}^{\mathrm{n}}}\left[s^{n+2\sqrt{{\mathit{\epsilon }}^2+{\mathit{\chi }}^2-{\mathit{\beta }}^2}}{\left(1-s\right)}^{n+2\mathit{\epsilon }}\right]\hfill \end{array}$$

(33)

Modified form of Wood–Saxon potential

In order to modify this potential for $l\ne 0$, it is necessary to add two terms to generalized potential, so we have a modified potential as follows [20]:

$$\begin{array}{cc}\hfill V_{\mathrm{mod}}\left(r\right)& =\frac{-V_1}{1+exp\left(\frac{r-R}{a}\right)}+\frac{V_2}{{\left(1+exp\left(\frac{r-R}{a}\right)\right)}^2}\hfill \\ \hfill & +\mathit{\xi }coth\left(\frac{r-R}{a}\right)+\mathit{\eta }{coth}^2\left(\frac{r-R}{a}\right)\hfill \end{array}$$

(34)

the parameters $V_1$, $V_2$, $\mathit{\xi }$ and $\mathit{\eta }$ are real constant values. It is required to remind the third and fourth terms in Eq. (34), in limit $r-R\ll a$ reformed as $\frac{1}{r}$ and $\frac{1}{r^2}$, respectively. These forms are corresponding to the coulombian repulsive potential and its square. In this section, using the NU method, we solve analytically the radial part of time-independent Schrodinger equation with angular momentum $l\ne 0$, for this modified shape of generalized Wood–Saxon potential.

By considering a new transformation as

$$\begin{array}{c}\hfill S\left(r\right)=\frac{1}{1+e^{\left(\frac{r-R}{a}\right)}}\end{array}$$

(35)

and according to the previous section the $E_{n,l}$, $R_{n,l}$ are calculated and write briefly:

$$\begin{array}{cc}\hfill E_{n,l}& =\mathit{\gamma }{D}_0-\left(\frac{V_1-\mathit{\gamma }{D}_1}{{\mathit{\beta }}^2}\right)\hfill \\ \hfill & \left({\left(\frac{{\mathit{\alpha }}^2+{\mathit{\beta }}^2-{\mathit{\chi }}^2}{\sqrt{1+4{\mathit{\lambda }}^2+4{\mathit{\chi }}^2}+2n-1}\right)}^2-\left({\mathit{\alpha }}^2+{\mathit{\lambda }}^2-{\mathit{\beta }}^2\right)\right)\hfill \\ \hfill \end{array}$$

(36)

where

$$\begin{array}{cc}\hfill {\mathit{\epsilon }}^2& =\frac{-2\mathit{\mu }{a}^2\left(E-\mathit{\gamma }{D}_0\right)}{{ħ}^2},{\mathit{\beta }}^2=\frac{2\mathit{\mu }{a}^2\left(V_1-\mathit{\gamma }{D}_1\right)}{{ħ}^2}\hfill \\ \hfill {\mathit{\chi }}^2& =\frac{2\mathit{\mu }{a}^2\left(V_2+\mathit{\gamma }{D}_2\right)}{{ħ}^2},\mathit{\gamma }=\frac{{ħ}^{2}l\left(l+1\right)}{2\mathit{\mu }{R}^2}\hfill \\ \hfill {\mathit{\alpha }}^2& =\frac{2\mathit{\mu }{a}^2\mathit{\xi }}{{ħ}^2},{\mathit{\lambda }}^2=\frac{2\mathit{\mu }{a}^2\mathit{\eta }}{{ħ}^2}\hfill \end{array}$$

(37)

$$\begin{array}{cc}\hfill R_{n,l}(s)& =\hfill \\ \hfill & C_n\frac{{(s(1-s))}^{\sqrt{{\mathit{\alpha }}^2+{\mathit{\epsilon }}^2+{\mathit{\lambda }}^2-{\mathit{\beta }}^2}}{(1-2s)}^{\frac{1}{2}(1+\sqrt{1+4{\mathit{\chi }}^2+4{\mathit{\lambda }}^2})}}{n!{(s(1-s))}^{2\sqrt{{\mathit{\alpha }}^2+{\mathit{\epsilon }}^2+{\mathit{\lambda }}^2-{\mathit{\beta }}^2}}{(1-2s)}^{\sqrt{1+4{\mathit{\chi }}^2+4{\mathit{\lambda }}^2}}}\hfill \\ \hfill & \times \frac{{\mathrm{d}}^{\mathit{n}}}{\mathrm{d}{\mathit{s}}^{\mathit{n}}}\left[{(s(1-s))}^{n+2\sqrt{{\mathit{\alpha }}^2+{\mathit{\epsilon }}^2+{\mathit{\lambda }}^2-{\mathit{\beta }}^2}}{(1-2s)}^{n+\sqrt{1+4{\mathit{\chi }}^2+4{\mathit{\lambda }}^2}}\right]\hfill \\ \hfill \end{array}$$

(38)

The S and D state wave functions determined from these of three potentials are shown in Figs. 1, 2 and 3, standard,generalized, and modified forms of the potential, respectively. Also S and D states of the deuteron for the wave function obtained from experimental data are shown in Fig. 4. In the next section, we will apply these results to calculate the statis properties and form factors of deuteron.

Numerical results and applications

In the non-relativistic impulse approximation, the charge monopole, $G_{\mathrm{C}}(q)$, charge quadrupole, $G_{\mathrm{Q}}(q)$, and magnetic dipole, $G_{\mathrm{M}}(q)$, form factors of the deuteron that may be expressed in terms of the deuteron wave function and nucleon isoscalar form factor as follows [21, 26, 27]:

$$\begin{array}{c}\hfill G_{\mathrm{C}}\left(q\right)=2G_{\mathrm{E}}\int \left[u^2(r)+w^2(r)\right]j_0\left(\frac{qr}{2}\right)\mathrm{d}\mathit{r}\end{array}$$

(39)

$$\begin{array}{c}\hfill G_{\mathrm{Q}}\left(q\right)=4G_{\mathrm{E}}\int \left[u(r)w(r)-\frac{w^2(r)}{\sqrt{8}}\right]j_2\left(\frac{qr}{2}\right)\mathrm{d}\mathit{r}\end{array}$$

(40)

$$\begin{array}{c}\hfill G_{\mathrm{M}}\left(q\right)=\frac{M_{\mathrm{d}}}{M_{\mathrm{p}}}\left(2G_{{\mathrm{M}}_0}{C}_{\mathrm{S}}+G_{\mathrm{E}}{C}_{\mathrm{L}}\right)\end{array}$$

(41)

where

$$\begin{array}{c}\hfill C_{\mathrm{L}}=\frac{3}{2}\int w^2(r)\left[j_0\left(\frac{qr}{2}\right)+j_2\left(\frac{qr}{2}\right)\right]\mathrm{d}\mathit{r}\end{array}$$

(42)

$$\begin{array}{cc}\hfill C_{\mathrm{S}}& =\int \left[u^2(r)-\frac{w^2(r)}{2}\right]j_0\left(\frac{qr}{2}\right)\mathrm{d}\mathit{r}\hfill \\ \hfill & +\frac{1}{\sqrt{2}}\int w(r)\left[u(r)+\frac{w(r)}{\sqrt{2}}\right]j_2\left(\frac{qr}{2}\right)\mathrm{d}\mathit{r}\hfill \end{array}$$

(43)

$$\begin{array}{c}\hfill 2G_{{\mathrm{M}}_0}=G_{{\mathrm{M}}_{\mathrm{p}}}+G_{{\mathrm{M}}_{\mathrm{n}}},2G_{\mathrm{E}}=G_{{\mathrm{E}}_{\mathrm{p}}}+G_{{\mathrm{E}}_{\mathrm{n}}},\end{array}$$

(44)

where $u(r)$ and $w(r)$ are the radial wave functions of the bound state, while $j_0,j_2$ are spherical Bessel functions.

The charge form factor for the neutron was assumed to be zero, while the charge form factor for the proton was parameterized as

$$\begin{array}{c}\hfill G_{{\mathrm{E}}_{\mathrm{p}}}=\frac{1}{{\left(1+0.054844q^2\right)}^2},\end{array}$$

(45)

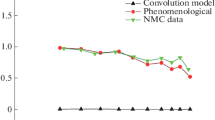
where $q$ is the momentum transfer in ${\mathrm{fm}}^{-1}$ units and the magnetic form factors for the nucleon were determined on the basic of the scaling law, $G_{{\mathrm{M}}_{\mathrm{p}}}={\mathit{\mu }}_{\mathrm{p}}{G}_{{\mathrm{E}}_{\mathrm{p}}}$ and $G_{{\mathrm{M}}_{\mathrm{n}}}={\mathit{\mu }}_{\mathrm{n}}{G}_{{\mathrm{E}}_{\mathrm{p}}}$. Now, substituting the obtained wave functions (Eqs. 27, 33, and 38) into Eqs. (39), (40), and (41) leads to the form factors of the deuteron. The mentioned form factors of the deuteron as a function of $q$ for various of the Wood–Saxon potential are calculated and the obtained results are shown in Figs. 5, 6 and 7.

One can evaluate the electric quadropole moment using the obtained wave functions which is expressed as

$$\begin{array}{c}\hfill Q_{\mathrm{d}}=\frac{1}{\sqrt{50}}\int \left(u(r)w(r)-\frac{w^2(r)}{\sqrt{8}}\right)r^2\mathrm{d}\mathit{r}\end{array}$$

(46)

The obtained results are given in Table 1.

The deuteron magnetic moment can be expressed in terms of the nucleon moments and the $\mathrm{D}$-state probability $P_{\mathrm{D}}$ [22], as follows:

$$\begin{array}{cc}& {\mathit{\mu }}_{\mathrm{d}}={\mathit{\mu }}_{\mathrm{n}}+{\mathit{\mu }}_{\mathrm{p}}-\frac{3}{2}\left({\mathit{\mu }}_{\mathrm{n}}+{\mathit{\mu }}_{\mathrm{p}}-\frac{1}{2}\right)P_{\mathrm{D}}\hfill \\ \hfill & P_{\mathrm{D}}=\int w^2(r)\mathrm{d}\mathit{r}\hfill \end{array}$$

(47)

With use of the obtained wave functions, the deuteron magnetic moment is determined (see Table 1).

Finally, in the non-relativistic form the deuteron size maybe characterized by a charge reduced $r_{\mathrm{ch}}$ and by a matter radius $r_{\mathrm{m}}$. The $\mathrm{rms}$ charge radius $r_{\mathrm{ch}}$ is related to the matter $\mathrm{rms}$-radius $r_{\mathrm{m}}$ by [22]

$$\begin{array}{c}\hfill r_{\mathrm{ch}}^2=r_m^2+\mathrm{\Delta }{r}_{\mathrm{m}}^2+r_{\mathrm{p}}^2+r_{\mathrm{n}}^2+\frac{3}{4}{\left(\frac{ħ}{m_{\mathrm{p}}}\right)}^2\end{array}$$

(48)

$$\begin{array}{c}\hfill r_{\mathrm{m}}^2=\frac{1}{4}\int \left[u^2(r)+w^2(r)\right]r^2\mathrm{d}\mathit{r},\end{array}$$

(49)

where $u(r)$ and $w(r)$ are the $\mathrm{S}$ and $\mathrm{D}$ components of the NR deuteron wavefunction, respectively. $r_{\mathrm{m}}$ is the matter radius, $\mathrm{\Delta }{r}_{\mathrm{m}}^2$ is the effect of the meson exchange current plus other non-classical effects, and $r_{\mathrm{p}}$ and $r_{\mathrm{n}}$ are the root-mean-square radii of the proton and neutron, respectively. The obtained results are shown in Table 1.

Conclusion

We have used the Nikiforov-Uvarov (NU) method for analytical solution of the radial Schrodinger equation. The NU method provides an exact solution of the non-relativistic Schrodinger equation for certain kinds of potentials. With the use of the mentioned method, the wave function are obtained for Standard, Generalized, and modified Wood–Saxon potentials. A comparison of the calculated values with experimental values is given. Then we applied our results to calculate the static properties and form factors of deuteron system. It is shown that the obtained results for modified form of the Wood–Saxon potential are very close to the experimental results with other forms of the potential. Our estimations indicate that the obtained wave function for modified potential provides relatively accurate values for form factors and static properties of deuteron system, emphasizing on the importance of the wave function and the nucleon-nucleon interaction model.

Fig. 1

S and D states of the deuteron wave function for the standard Wood–Saxon potential

Fig. 2

S and D states of the deuteron wave function for the generalized Wood–Saxon potential

Fig. 3

S and D states of the deuteron wave function for the modified Wood–Saxon potential

Fig. 4

S and D states of the deuteron wave function from experimental data [23]

Fig. 5

Charge monopole form factor of the deuteron, $G_{\mathrm{C}}$, as a function of $q$ for the various versions of the WS potential

Fig. 6

Charge quadrupole form factor of the deuteron, $G_{\mathrm{Q}}$, as a function of $q$ for the various versions of the WS potential

Fig. 7

Magnetic dipole form factor of the deuteron, $G_{\mathrm{M}}$, as a function of $q$ for the various versions of the WS potential

Table 1 The calculated values of electric quadrupole moment, magnetic dipole moment, $\mathrm{D}$ state percentage, matter and charge radius for deuteron system comparison with experimental values