Abstract
ZnO nanoparticles were synthesized from chitosan and zinc chloride by a precipitation method. The synthesized ZnO nanoparticles were characterized by Fourier transform infrared spectroscopy, X-ray diffraction peak profile analysis, Scanning electron microscopy, Transmission electron microscopy and Photoluminescence. The X-ray diffraction results revealed that the sample was crystalline with a hexagonal wurtzite phase. We have investigated the crystallite development in ZnO nanoparticles by X-ray peak profile analysis. The Williamson–Hall analysis and size–strain plot were used to study the individual contributions of crystallite sizes and lattice strain ϵ on the peak broadening of ZnO nanoparticles. The parameters including strain, stress and energy density value were calculated for all the reflection peaks of X-ray diffraction corresponding to wurtzite hexagonal phase of ZnO lying in the range 20°–80° using the modified form of Williamson–Hall plots and size–strain plot. The results showed that the crystallite size estimated from Scherrer’s formula, Williamson–Hall plots and size–strain plot, and the particle size estimated from Transmission electron microscopy analysis are very much inter-correlated. Both methods, the X-ray diffraction and Transmission electron microscopy, provide less deviation between crystallite size and particle size in the present case.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
The wide band gap semiconductors, viz. GaN, ZnO, InN, AlN, have gained more attention among semiconductor materials, because of their potential application in optoelectronic devices in both the visible and UV regions, such as light emitting diodes (LEDs) and laser diodes. Zinc oxide (ZnO) is a wide band gap semiconductor, which has been studied extensively due to its fundamental and technological importance. It has wide band gap energy (3.37 eV), large exciton binding energy and excellent chemical stability; all these properties suggest a great possible practical applications viz. in gas sensors, ceramics, field-emission devices and luminescent materials [1–3]. The large exciton binding energy of ZnO allows an intense near-band-edge excitonic emission at room temperature and higher temperatures [4]. Recently, ZnO has gained interest for spintronic applications due to its ferromagnetic behavior at room temperature when doped with transition metals [5]. Recent reports from our lab [6, 7] revealed that ZnO nanoparticles can be used as reinforcing agent in polymers, activator and accelerator instead of micro ZnO in the vulcanization of rubber materials, for producing highly stable and improved properties of the final products. Moreover, the ZnO content in vulcanized rubber can be reduced to 10 times if nanosized ZnO is used instead of the conventional micro ZnO [8], and this approach helps to reduce the release of toxic zinc metal into the environment [6].
Particle size and crystal morphology play important roles in these applications, which have driven the attention of researchers on the synthesis of nanocrystalline ZnO. Many methods were reported [9] such as sol–gel, solo-chemical processes, precipitation, combustion synthesis, DC thermal plasma synthesis, spray pyrolysis, pyrolysis, and hydrothermal synthesis to prepare ZnO nanopowders. The particle size and morphology of ZnO nanoparticles will vary with the synthetic route adopted for the synthesis.
It was understood that a perfect crystal would extend in all directions to infinity; however, no crystals are perfect due to their finite size. This deviation from perfect crystallinity is the reason for broadening of the diffraction peaks of materials. There are two main properties extracted from peak width analysis viz. crystallite size and lattice strain. Crystallite size is a measure of the size of a coherently diffracting domain, and the crystallite size of the particles is not generally the same as the particle size due to the presence of polycrystalline aggregates. The various techniques used for the measurement of particle size rather than the crystallite size are direct light scattering (DLS), scanning electron microscopy (SEM), and transmission electron microscopy (TEM) analysis. Lattice strain is a measure of the distribution of lattice constants arising from crystal imperfections, such as lattice dislocation. There are other sources of strain, which are the grain boundary triple junction, coherency stresses, contact or sinter stresses, stacking faults, etc. [10]. The X-ray line broadening is used for the investigation of dislocation distribution.
X-ray peak profile analysis (XPPA) was used to estimate the micro-structural quantities and correlate them to the observed material properties. Although XPPA is an averaging method, it still holds a dominant position in crystallite size determination. XPPA is a simple and powerful tool to estimate the crystallite size and lattice strain [11]. The crystallite size and lattice strain affect the Bragg peak in different ways and both these effects increase the peak width, peak intensity and shift the 2θ peak position accordingly. There are other methods reported in the literature to estimate the crystallite size and lattice strain, which are the pseudo-Voigt function, Rietveld refinement, and Warren-Averbach analysis [12–14]. However, the Williamson–Hall (W–H) analysis is a simplified integral breadth method employed for estimating crystallite size and lattice strain, considering the peak width as a function of 2θ [15]. The size–strain parameters can be also obtained by considering an average ‘size–strain plot’ (SSP) method. The XPPA is an average method and is important for the determination of crystallite size apart from TEM analysis.
The present work describes a facile route for the synthesis of ZnO nanoparticles from chitosan and ZnCl2 by a precipitation method. We have found that this is a cost-effective and new method for the synthesis of ZnO nanoparticles. The structure and morphology of ZnO nanoparticles were investigated by FTIR, XRD, SEM, TEM and Photoluminescence (PL). The XPPA was carried out for estimating the crystallite size, lattice strain, lattice stress and lattice strain energy density of ZnO nanoparticles based on modified W–H plots using uniform deformation model (UDM), uniform stress deformation model (USDM), uniform deformation energy density model (UDEDM) and another method viz. size–strain plot (SSP) and thereby correlating them to the presently observed physicochemical properties of nanocrystalline ZnO. Literature reports revealed that a detailed study using these models on the synthesized ZnO nanoparticles annealed at 550 °C is not yet reported. This study reveals the importance of SSP and W–H models in the determination of crystallite size of ZnO nanomaterials.
Experimental details
Materials
Chitosan was provided by M/s. India Sea Foods, Cochin, Kerala, India. Zinc chloride and sodium hydroxide were supplied by M/s. S. D. Fine Chem. Ltd. Mumbai, India. ZnO nanoparticles were synthesized from chitosan, zinc chloride and sodium hydroxide.
Synthesis of ZnO nanoparticles
ZnO nanoparticles were synthesized from zinc chloride and chitosan [16]. This is a new synthetic approach and in the present synthetic procedure, we have optimized the reaction conditions to facilitate the formation of Zn–chitosan complex and also to increase the yield of the ZnO nanoparticles. We have optimized the concentrations of ZnCl2, chitosan and NaOH, pH of the reaction medium, reaction temperature and stirring time for complexation of Zn–chitosan complex and precipitation of Zn(OH)2 out of the complex. About 5 g of ZnCl2 was dissolved in 100 ml 1 % acetic acid to form 5 % solution, and another 1 % solution of chitosan was prepared in 1 % acetic acid. Both the solutions were mixed and stirred for 21 h. After this, stoichiometric amount of NaOH (5 %) was added drop wise to the above reaction mixture with constant stirring. The whole mixture was then allowed to digest for 24 h at room temperature. During this time, OH− and Cl− ions were diffused through the medium and white gel-like precipitate of Zn(OH)2 was formed. This was filtered and washed thoroughly with distilled water to remove unreacted chitosan and other by-product like NaCl. This was then dried at 100 °C and annealed at 550 °C for 4 h in a muffle furnace to get ZnO nanocrystals. The yield of ZnO nanocrystals obtained by this method is about 90 %. The new synthetic route has the following advantages: the reaction can be carried out under moderate conditions, yield of the product is very good and particles of nanometer size can be attained, which make this method promising for large-scale production.
Chitosan is a linear polymine having reactive amino groups and hydroxyl groups and hence can easily form chelates with transition metal ions. In the present reaction, chitosan acts as a chelating agent for Zn2+ ions to form Zn–chitosan complex.
Characterization methods
FTIR (Schimadzu IR-470 IR spectrophotometer) spectrum of the ZnO nanoparticles was recorded in the range 4000–400 cm−1 using KBr pellet. XRD was recorded with the help of Bruker D-8 Advance (λ = 1.54060 Angstrom, Cu-Kά) machine, using pure Al2O3 as reference. SEM images were recorded using FE-SEM SUPRA-25 ZEISS analyser. HRTEM was taken with JEOL-JEM 3010 instrument; the ZnO nanoparticles were dispersed in acetone by ultrasonic bath and a drop of it was deposited on carbon-coated copper grid and was analyzed under an accelerating voltage of 200 kV. Photoluminescence (PL) spectrum of ZnO nanoparticles was recorded at room temperature using RF-5301 PC-Spectroflurophotometer-P/N 206.81601 consisting of Xenon arc lamp as the excitation source at excitation wavelength (λex = 355 nm). The luminescence is dispersed with a monochromator and recorded using a CCD detector.
Results and discussion
The synthesized ZnO nanoparticles were characterized as follows.
Structural studies
The IR spectrum of ZnO nanoparticles (Fig. 1a) was recorded using KBr pellet. The bands correspond to ν (Zn–O) appeared at 1,018 and 488 cm−1.
The XRD pattern of prepared ZnO nanoparticles was taken. All the XRD peaks were indexed by hexagonal wurtzite phase of ZnO (JCPDS Card No. 01-089-0510) as shown in Fig. 1b. XRD pattern indicates the formation of hexagonal wurtzite phase of ZnO which is in agreement with the electron diffraction results. The peak broadening in the XRD pattern clearly indicates that small nanocrystals are present in the samples. There is no evidence of bulk remnant materials and impurity. Nine peaks appear at different 2θ values as shown in the Fig. 1b. The sharp diffraction peaks indicate the good crystallinity of the prepared particles.
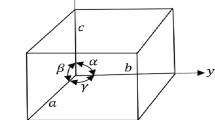
As ZnO crystallizes in the wurtzite structure in which the oxygen atoms are arranged in a hexagonal close packed type with zinc atoms occupying half the tetrahedral sites. Zn and O atoms are tetrahedrally coordinated to each other and have, therefore, an equivalent position. The zinc structure is open with all the octahedral and half the tetrahedral sites empty. According to Bragg’s law [11],
where n is the order of diffraction (usually n = 1), λ is the X-ray wavelength and d is the spacing between planes of given Miller indices h, k and l. In the ZnO hexagonal structure, the plane spacing d is related to the lattice constants a, c and the Miller indices by the following relation [11],
With the first-order approximation, n = 1;
The lattice constant a for 〈100〉 plane is calculated by [11],
For the 〈002〉 plane, the lattice constant c is calculated by [11],
The lattice constants (a = b = 3.2299 Angstrom and c = 5.1755 Angstrom, c/a = 1.6024) and diffraction peaks corresponding to the planes 〈100〉, 〈002〉, 〈101〉, 〈102〉, 〈110〉, 〈103〉 obtained from X-ray diffraction data are consistent with the JCPDS data of ZnO. The interplanar spacing (dhk l) calculated from XRD is compared with JCPDS data card and corresponding 〈h k l〉 planes, percentage of variation of d and full width at half-maximum (FWHM) values for some major XRD peaks are summarized in Table 1.
Crystallite size and strain
Scherrer method
XRD peak profile analysis is a simple and powerful method to evaluate the peak broadening with crystallite size and lattice strain due to dislocation. The breadth of the Bragg peak is a combination of both instrument and sample-dependent effects. For an accurate analysis for size and strain effects, the instrumental broadening must be accounted. The diffraction pattern from the line broadening of a standard material such as alumina (Al2O3) was collected to decouple the above-mentioned contributions and to determine the instrumental broadening. The instrumental corrected broadening [17] βhkl corresponding to each diffraction peak of ZnO was calculated using the relation,
In particular, the ZnO 〈101〉 diffraction peak is much stronger than the ZnO 〈002〉 peak. This indicates that the formed ZnO nanocrystals have a preferential crystallographic 〈101〉 orientation. The average crystallite size was calculated from XRD peak width of 〈101〉 based on the Debye–Scherrer equation [18],
where β hkl is the integral half width, K is a constant equal to 0.90, λ is the wave length of the incident X-ray (λ = 0.1540 nm), D is the crystallite size, and θ is the Bragg angle. The average crystallite size calculated for synthesized ZnO nanoparticles was 27.49 nm. The crystallite size is assumed to be the size of a coherently diffracting domain and it is not necessarily the same as particle size.
The dislocation density (δ), which represents the amount of defects in the sample is defined as the length of dislocation lines per unit volume of the crystal and is calculated using the Eq. [18],
where D is the crystallite size. The dislocation density (δ) is 14.76 × 10−4 (nm)−2.
The Zn–O bond length L is given by [19],
where u is the positional parameter in the wurtzite structure and is a measure of the amount by which each atom is displaced with respect to the next along the ‘c’ axis. ‘u’ is given by
The correlation between the c/a ratio and u is that when the c/a ratio decreases, the u increases in such a way that those four tetrahedral distances remain nearly constant through a distortion of tetrahedral angles. The Zn–O bond length calculated is 1.9654 Å; whereas the reported Zn–O bond length in the unit cell of ZnO and neighboring atoms is 1.9767 Å [20]. The calculated bond length agrees with the Zn–O bond length in the unit cell.
Estimation of microstrain (ε)
Williamson–Hall (W–H) methods
Uniform deformation model (UDM)
In Williamson–Hall approach, the line broadening due to finite size of coherent scattering region and the internal stress in the prepared film is also considered. According to Williamson and Hall, the diffraction line broadening is due to crystallite size and strain contribution. However, the XPPA by W–H methods is a simplified method which clearly differentiates between size-induced and strain-induced peak broadening by considering the peak width as a function of 2θ [15]. The strain-induced broadening in powders due to crystal imperfection and distortion was calculated using the formula,
From Eqs. (7) and (11), it was confirmed that the peak width from crystallite size varies as and strain varies as tan θ. Now, the total peak broadening is represented by the sum of the contributions of crystallite size and strain present in the material and can be written as [21],
where is due to the contribution of crystallite size, is due to strain-induced broadening and is the width of the half-maximum intensity of instrumental corrected broadening. The instrumental corrected broadening of each diffraction peak is calculated using Eq. (6) as given above. If we assume that the particle size and strain contributions to line broadening are independent to each other and both have a Cauchy-like profile, the observed line breadth is the sum of Eqs. (7) and (11) and given as [22],
By rearranging Eq. (13), we get
The Eq. (14) is Williamson–Hall equation, which represents the uniform deformation model (UDM). Equation (14) assumes that the strain is uniform in all crystallographic directions and known as uniform deformation model (UDM). In this model the crystal is considered as isotropic in nature and it is assumed that the properties of material are independent of the direction along which it is measured. The values of β hkl cosθ hkl on y-axis were plotted as a function of 4sinθ hkl on x-axis, and from the linear fit of the data, the crystalline size D was estimated from the y-intercept, and the microstrain ε, from the slope of the linear fit (Fig. 2). The UDM for ZnO nanoparticles is shown in Fig. 2. This strain may be due to the lattice shrinkage that was observed in the calculation of lattice parameters.
Uniform stress deformation model (USDM)
In many cases, the assumption of homogeneity and isotropy is not fulfilled. To incorporate more realistic situation, an anisotropic approach is adopted. Therefore, Williamson–Hall equation is modified by an anisotropic strain ε. In uniform stress deformation model (USDM), the lattice deformation stress is assumed to be uniform in all crystallographic directions, and assuming a small microstrain to be present in the particles. In USDM, the Hooke’s law refers to the strain and there is a linear proportionality between the stress and strain as given by σ = εY hkl or ε = σ/Y hkl , where σ is the stress of the crystal, ε is anisotropic microstrain, this will depend on the crystallographic directions and Y hkl is the modulus of elasticity or Young’s modulus. This equation is just an approximation and is valid for a significantly small strain; when strain is increased, the particles deviate from this linear proportionality. In this approach, the Williamson–Hall equation is modified [22] by substituting the value of ε in Eq. (14), we get
For a hexagonal crystal, Young’s modulus is given by the following relation [13, 14],
where ‘a’ and ‘c’ are lattice parameters; s11, s13, s33 and s44 are the elastic compliances of ZnO with values 7.858 × 10−12, −2.206 × 10−12, 6.940 × 10−12 and 23.57 × 10−12 m2 N−1, respectively [23]. Young’s modulus, Y hkl , for hexagonal ZnO nanoparticles was calculated as ~127 GPa. Plotting β hkl cosθ hkl as a function of 4sinθ/Y hkl (Fig. 3), the uniform deformation stress σ can be estimated from the slope of the linear fit and y-intercept gives the crystallite size. The strain ε can be calculated if Young’s modulus, Y hkl , of hexagonal ZnO nanoparticles is known.
Uniform deformation energy density model (UDEDM)
There is another model called the uniform deformation energy density model (UDEDM) that can be used to determine the energy density of a crystal. In Eq. (14), the crystals are assumed to have a homogeneous, isotropic nature; however, in many cases, the assumption of homogeneity and isotropy is not justified. Moreover, the constants of proportionality associated with the stress–strain relation are no longer independent when the strain energy density ued is considered. For an elastic system that follows Hooke’s law, the energy density ued (energy per unit volume) as a function of strain is ued = (ε2Y hkl )/2. Then, Eq. (15) can be rewritten according to the energy and strain relation as [22],
Plot of β hkl cosθ hkl versus 4sinθ hkl (2/Y hk )1/2 was done (Fig. 4) and the anisotropic energy density ued was estimated from the slope of the linear fit and the crystallite size D from the y-intercept. Previously, we knew that σ = εY hkl and ued = (ε2Y hkl )/2, where the stress σ was calculated as ued = (σ2/2Y hkl ). The lattice strain can be calculated by knowing the Y hkl value.
Size–strain plot (SSP)
The W–H plots described that the line broadening was basically isotropic. This emphasizes that the diffracting domains were isotropic due to the contribution of microstrain. In the cases of isotropic line broadening, a better evaluation of the size–strain parameters can be obtained by considering an average ‘size–strain plot’ (SSP) [24]. This method has a benefit that less importance is given to data from reflections at high angles where the precision is usually lower. In this method, it is assumed that the ‘strain profile’ is explained by a Gaussian function and the ‘crystallite size’ profile by a Lorentzian function [25] and is given by,
where d hkl is the lattice distance between the 〈h k l〉 planes, Vs is the apparent volume weighted average size and ϵa is a measure of the apparent strain which is related to the root-mean-square (RMS) strain ϵRMS,
For spherical crystallites the volume average true size is given by Dv = Vs 4/3.
The corresponding SSP for ZnO nanoparticles was obtained by plotting (d hkl β hkl cosθ hkl )2 on y-axis with respect to (d 2 hkl β hkl cosθ hkl ) on the x-axis (Fig. 5) for all peaks of ZnO nanoparticles with the wurtzite hexagonal phase from 2θ = 20º–80º. In this method, the volume-averaged true crystallite size Dv was estimated from the slope of the linear fit, and the RMS strain estimated from the intercept was negligible (Table 2).
According to the literature report [26], the Williamson–Hall plot showed that, the line broadening was essentially isotropic and that the least-squares line through the points had a positive slope and a non-zero intercept. This indicates that diffracting domains are isotropic and there is also a microstrain contribution. For a better evaluation of the size–strain parameters, an average ‘size–strain plot’ (SSP) method was considered as explained above. Comparing W–H and SSP methods in the present case, the lattice strain ϵ calculated from the W–H and SSP methods was found to be comparable and in agreement with each other (Table 2). Moreover, the crystallite size D obtained from the SSP method is in good agreement with the values obtained from W–H models and TEM (Table 2). However, the SSP method is the most suitable one compared to W–H methods, because less importance is given to data from reflections at high angles and the data points lay very close to the linear fit.
Comparing the 3 W–H models, UDM considers the homogeneous isotropic nature of the crystal, whereas USDM and UDEDM models consider the anisotropic nature of the crystallites. In USDM and UDEDM, it may be noted that though both Eqs. (15) and (17) are taken into account in the anisotropic nature of the elastic constant, they are essentially different. According to Eq. (15), it is assumed that the deformation stress has the same value in all crystallographic directions allowing ued to be anisotropic, while in Eq. (17), it is assumed that the deformation energy to be uniform in all crystallographic directions treating the deformation stress σ to be anisotropic. However, it was understood from the plots (Figs. 3, 4) using Eqs. (15) and (17) that, a given sample may result in different values for lattice strain and crystallite size. Thus, for a given sample, W–H plots can be plotted using Eqs. (6, 7, 11–17). Furthermore, the average crystallite sizes estimated from the y-intercept of the graphs for the UDM, USDM, UDEDM models were found to be 35.35, 36.28 and 36.09 nm, respectively. The average values of crystallite size obtained from UDM, UDSM, and UDEDM are almost similar, which indicate that the inclusion of strain in various forms of W–H methods has a very small effect on the average crystallite size of ZnO nanoparticles. However, the average crystallite size obtained from Scherrer’s formula and W–H analysis shows a small variation because of the difference in averaging the particle size distribution. It can be noted that the values of the average crystallite size obtained from the above three methods are in good agreement with the results of the TEM analysis (Table 2). Our results are more appropriate than the reported literature [27]. We suggest that these three methods are also suitable models for the evaluation of the crystallite size of ZnO nanoparticles. Rosenberg et al. [28] observed that for metallic samples with cubic structures, the uniform deformation energy model is suitable. We have made a comparison of the estimated microstrain ε values of ZnO nanoparticles annealed at 450 °C reported by Dole et al. [29] by W–H models, with that of our present values. The higher values of estimated microstrain ε in our case indicate polycrystalline nature of the films. The polycrystalline films will show a larger value of ε indicating more strain on the lattice. As the annealing temperature of ZnO nanocrystal is at 550 °C, the microstrain ε is high and the films are more polycrystalline in nature. This study reveals the importance of models in the determination of particle size of ZnO nanoparticles. The average crystallite size and the strain values obtained from UDM, UDSM, UDEDM and SSP methods were found to be accurate and comparable, as the entire high-intensity points lay close to the linear fit.
Estimation of RMS strain
The Wilson method [30] was employed to compute the maximum or upper-limit ε hkl , and root-mean-square (RMS) microstrains εRMS along the 〈h k l〉 crystallographic directions using the following relations:
The upper-limit microstrain was derived from the Bragg’s law by Wilson [30, 31] and the root-mean-square microstrain was derived from the upper-limit microstrain with the assumption of a Gaussian microstrain distribution. By substituting the value of ε hkl in Eq. (21), the root-mean-square (RMS) lattice strain is given by the equation:
Here, d and d 0 represent the observed and ideal interplanar spacing values, respectively. Figure 6 shows the plot of RMS strain against variation in the interplanar spacing for the uniform deformation energy density model. Theoretically, if the strain values agree, all the points should lie on a straight line with an angle of 45° to the x-axis. The RMS strain linearly varies with the strain calculated from the interplanar spacing, which indicates that there is no discrepancy on the 〈h k l〉 planes in the nanocrystalline nature [21]. The lattice strain in the nanocrystalline ZnO nanoparticles may arise from the excess volume of grain boundaries due to dislocations. The X-ray diffraction line broadening arises from dislocations and plastic deformation. The non-uniform strains are pictured as a distribution of d-spacings and lead to XRD peak broadening. It was already mentioned that the XRD peak broadening is mainly due to microstrains, small grain sizes (<100 nm), stacking faults and machine limitation. The XRD peak broadening was considered to be only a function of crystallite size, microstrains and instrumental broadening. The development of lattice strain is caused by varying displacement of the atoms with respect to their reference-lattice positions. In other words, the origin of microstarin is related to lattice ‘misfit’. The diffraction peak shape is related to crystallite size and the crystallite size is related to root-mean-square (RMS) strain. The higher the RMS strain, the smaller is the crystallite size, and the RMS strain is a measure of the lattice distortion.
Texture coefficient
The quantitative information concerning the preferential crystal orientation can be obtained from the texture coefficient, TC, which can be defined as [32],
where TC(hkl) is the texture coefficient, I(hkl) is the intensity of the XRD of the sample and n is the number of diffraction peaks considered. I0(hkl) is the intensity of the XRD reference of the randomly oriented grains. If TC(hkl) ≈ 1 for all the 〈hkl〉 planes are considered, then the nanoparticles are with a randomly oriented crystallite similar to the JCPDS reference, while values higher than 1 indicate the abundance of grains in a given 〈hkl〉 direction. Values 0 < TC(hkl) < 1 indicate the lack of grains oriented in that direction. As TC(hkl) increases, the preferential growth of the crystallites in the direction perpendicular to the 〈hkl〉 plane is greater.
Morphological studies
The SEM image of ZnO nanoparticles is shown in Fig. 7. The individual ZnO nanoparticles have the length about 90–185 nm range and the diameter 20–90 nm range.
The bright field TEM images of ZnO nanoparticles are shown in Fig. 8. The size parameters from TEM images indicate that the morphology of ZnO nanoparticles is identical to that observed in SEM image. The HRTEM images of ZnO nanoparticles and the corresponding selected area electron diffraction (SAED) were shown in Figs. 8a, b, respectively. The SAED ring pattern indicates that the phase of ZnO nanoparticles was polycrystalline in structure, and the distance between crystalline planes was consistent with the standard pattern for a wurtzite ZnO crystal structure. However, HRTEM lattice image (Fig. 8c) showed that each particle has a single crystalline structure. The particle size distribution of ZnO nanoparticles varies from 20 to 90 nm with an average particle size of 30 nm. Figure 8d represents particle size distribution based on TEM images. However, the diffraction lines clearly indicate the nanoscale crystallinity of the ZnO particles with randomly oriented polycrystalline. Compared to bulk ZnO crystal, the ZnO nanoparticles have large fraction of atoms occupying the surface sites and the presence of imperfect lattice.
Photoluminescence (PL)
PL is the emission of light as a result of excitation by a light source. The sample absorbs photon from a monochromatic source such as a laser or Xe lamp, which results in electron excitation from the valence band to the conduction band. Excited electrons may lose their energy by a non-radiative recombination and radiative recombination process. In photoluminescence, the radiative recombination of free carriers will result.
The PL study at room temperature provides information of different energy states available between valence and conduction bands responsible for irradiative recombination. Figure 9 shows the PL emission (λex = 355 nm) from our synthesized ZnO nanoparticles. Two emission bands are clearly shown in Fig. 9. One is a relatively narrow and weak UV emission band, which is observed about 390 nm. The other one is a stronger and broader visible emission band about 470 nm.
The UV emission is originated from excitonic recombination corresponding to the near band gap emission of ZnO. The intensity of UV emission was negligible in this experiment. The short life time of free exciton arises from the high oscillator strength of the transition and the fast non-radiative trapping of excited charge carriers. This fact suggests that the exciton emission is greatly affected by the trapping of charge carries at the surface sites. Thus, the weak UV emission in this experiment resulted from the higher trapping rate of charge carriers at the surface sites relative to the fast radiative recombination rate.
The visible emissions of ZnO nanoparticles were originated from the intrinsic defects such as oxygen vacancy, oxygen interstitial, zinc vacancy, zinc interstitial and antisite oxygen in ZnO crystal. The blue band at 470 nm may appear due to lattice defects related to oxygen and zinc vacancies or interstitials [33]. The stronger the intensity of the blue luminescence, the more the intrinsic defects (oxygen and zinc vacancies or interstitials). The intensity of the visible emission is mainly depend on the surface states. Shalish et al. [34] have reported that below a certain size the luminescence properties are entirely dominated by properties of the surface. The intense visible peak at room temperature photoluminescence spectrum indicates that the large surface area of ZnO was exposed to air and that a large amount of surface states related to oxygen vacancies. The room temperature photoluminescence spectroscopy indicates that large amount of surface states related to oxygen vacancies are present in the sample.
Conclusions
ZnO nanoparticles with hexagonal wurtzite structure were synthesized from ZnCl2 and chitosan by a precipitation method and characterized by FTIR, powder XRD, SEM, TEM and PL. The X-ray peak broadening of ZnO nanoparticles annealed at 550 °C was due to the small crystallite size and lattice strain. The peak broadening was analyzed by the Scherrer’s equation, SSP and modified forms of W–H models viz. UDM, UDSM, and UDEDM. The lattice strain ϵ calculated from the W–H and SSP methods was found to be comparable and in agreement with each other, and the crystallite size D obtained from the SSP method is in good agreement with the values obtained from W–H methods and TEM. The SSP method is found to be the most suitable one for the estimation of lattice strain ϵ and crystallite size D compared with W–H methods. Among W–H methods, UDM considers the homogeneous isotropic nature of the crystal where as USDM and UDEDM models consider the anisotropic nature of the crystallites. The average values of crystallite size obtained from UDM, UDSM, and UDEDM are almost similar, which indicate the inclusion of strain in various forms of W–H analysis has a very small effect on the average crystallite size of ZnO nanoparticles. It was also observed that, a small variation in the average crystallite size obtained from Scherrer’s formula and W–H analysis was due to the difference in averaging the particle size distribution. The above-explained methods were helpful in determining the crystallite size, strain, stress, and energy density value, and among them SSP method is highly preferable to define the crystal perfection.
The SEM and TEM images showed identical morphology of ZnO nanoparticles and the particle size distribution of ZnO nanoparticles varies from 20 to 90 nm with an average particle size of 30 nm. The crystallite size estimated from Scherrer’s formula, W–H and SSP methods was in good agreement with that of the average particle size estimated from TEM analysis. Both the methods, XRD and TEM, provide less deviation between crystallite size and particle size in the present case. The PL spectrum exhibited a relatively narrow and weak UV emission band at 390 nm and a stronger and broader visible emission band at 470 nm. The PL spectroscopy indicated that a large amount of surface states related to oxygen vacancies are present. Since ZnO has wide range of applications in various fields, this new method with high purity and excellent yield will find importance in the industrial level.
References
Hingorani, S., Pillai, V., Kumar, P., Muntai, M.S., Shah, D.O.: Microemulsion mediated synthesis of Zinc Oxide nanoparticles for varistor studies. Mater. Res. Bull. 28, 1303–1310 (1993)
Sakohara, S., Ishida, M., Anderson, M.A.: Visible luminescence and surface properties of nanosized ZnO colloids prepared by hydrolyzing zinc acetate. J. Phys. Chem. B 102, 10169–10175 (1998)
Zhao, X., Zhang, S.C., Li, C., Zheng, B., Gu, H.: Application of zinc oxide nanopowder for two-dimensional micro-gas sensor array. J. Mater. Synth. Process. 5, 227 (1997)
Madelung, O., Schulz, M., Weiss, H.: Landolt-Börnstein New Series. Springer, Berlin (1982)
Pearton, S.J., Heo, W.H., Ivill, M., Norton, D.P., Steiner, T.: Dilute magnetic semiconducting oxides. Semicond. Sci. Technol. 19, R59–R74 (2004)
Bindu, P., Biji, NM., Sabu, Thomas,: Natural rubber nanocomposites: Role of nano ZnO in natural rubber in 2nd International Symposium on Advanced Materials and Polymers for Aerospace and Defense Applications SAMPADA, Pune, India (2008)
Bindu, P, Joseph, R, Sabu, Thomas: Natural Rubber Nanocomposites: Influence of Nano ZnO in the Cure Characteristics and Rubber-Filler Interactions, International Conference on Latest in Polymers-LAP, J. J, Murphy Research Centre, Rubber Park, Kochi, India (2010)
Heideman, G., Datta, R.N., Noordermeer, J.W.M., van Baarle, B.: Influence of Zinc Oxide during different stages of sulfur vulcanization: Elucidated by model compound studies. J. Appl. Polym. Sci. 95, 1388–1404 (2005)
Niasari, M.S., Davar, F., Mazaheri, M.: Preparation of ZnO nanoparticles from [bis (acetylacetonato) zinc (II)]–oleylamine complex by thermal decomposition. Maters. Lett. 62, 1890–1892 (2008)
Ungar, T.: Characterization of nanocrystalline materials by x-ray line profile analysis. J. Mater. Sci. 42, 1584–1593 (2007)
Cullity, B.D., Stock, S.R.: Elements of X-ray diffraction, 3rd edn. Prentice Hall, New Jersey (2001)
Rietveld, H.M.: Line profiles of neutron powder diffraction peaks for structure refinement. Acta. Crystallogr. 22, 151–152 (1967)
Balzar, D., Ledbetter, H.J.: Voigt function modeling in Fourier analysis of size and strain broadened X-ray diffraction peaks. Appl. Crystallogr. 26, 97–103 (1993)
Warren, B.E., Averbach, B.L.: The effect of cold-work distorsion on X- ray pattems. J. Appl. Phys. 21, 595 (1950)
Suryanarayana, C., Norton, M.G.: X-ray diffraction: a practical approach. Plenum Press Publishing, New York (1998)
Aswathy, KV.: Nano ZnO: A Novel Modifier for Thermoplastics Ph.D. Thesis, Cochin University of Science & Technology, Kochi-22, Kerala, India (2008)
Rogers, K.D., Daniels, P.: An X-ray diffraction study of the effects of heat treatment on bone mineral microstructure. Biomaterials 23, 2577–2585 (2002)
Saleem, M., Fang, L., Ruan, H.B., Wu, F., Huang, Q.L., Xu, C.L., Kong, C.Y.: Effect of zinc acetate concentration on the structural and optical properties of ZnO thin films deposited by sol-gel method. Intl. J. Phy. Sci. 7(23), 2971–2979 (2012)
Barret, C.S., Massalski, T.B.: Structure of Metals. Pergamon Press, Oxford (1980)
Seetawan, U., Jugsujinda, S., Seetawan, T., Ratchasin, A., Euvananont, C., Junin, C., Thanachayanont, C., Chainaronk, P.: Effect of calcinations temperature on crystallography and nanoparticles in ZnO disk. Maters. Sci. Appls. 2, 1302–1306 (2011)
Biju, V., Sugathan, N., Vrinda, V., Salini, S.L.: Estimation of nano crystalline silver from X-ray diffraction line broadening. J. Mater. Sci. 43, 1175–1179 (2008)
Pandiyarajan, T., Karthikeyan, B.: Cr doping induced structural, phonon and excitonic properties of ZnO nanoparticles. J. Nanopart. Res. 14, 647 (2012)
Nye, JF.: Physical properties of Crystals: their representation by tensors and matrices. Oxford, New York (1985)
Prince, E., Stalick, J.K.: Accuracy in powder diffraction II. NIST Spec. Publ. 597, 567 (1992)
Tagliente, M.A., Massaro, M.: Strain-driven (002) preferred orientation of ZnO nanoparticles in ion-implanted silica. Nucl. Instrum. Methods Phys. Res. B 266, 1055–1061 (2008)
Williamson, G.K., Hall, W.H.: X-ray line broadening from filed aluminium and wolfram. Acta Metall 1, 22–31 (1953)
Yogamalar, R., Srinivasan, R., Vinu, A., Ariga, K., Bose, A.C.: X-ray peak broadening analysis in ZnO nanoparticles. Sol. State. Commun. 149, 1919–1923 (2009)
Rosenberg, Yu.: Machavariant, VSh, Voronel, A, Garber, S, Rubshtein, A, Frenkel, AI, Stern, EA: strain energy density in the X-ray powder diffraction from mixed crystals and alloys. J. Phys. Cond. Mater. 12, 8081–8088 (2000)
Mote, V.D., Purushotham, Y., Dole, B.N.: Williamson-Hall analysis in estimation of lattice strain in nanometer-sized ZnO particles. J. Theoret. Appl. Phys. 6, 6 (2012)
Wilson, A.C.J.: X-ray Optics. UK, London (1949)
Ortiz, A.L., Shaw, L.: X-ray diffraction analysis of a severely plastically deformed aluminum alloy. Acta Mater. 52, 2185–2197 (2004)
Ilican, S., Caglar, Y., Caglar, M.: Preparation and characterization of ZnO thin films deposited by sol-gel spin coating method. J. Optoelectro. Adv. Mater. 10, 2578–2583 (2008)
Hu, J.Q., Ma, X.L., Xie, Z.Y., Wong, N.B., Lee, C.S., Lee, S.T.: Characterization of Zinc Oxide crystal whiskers grown by thermal evaporation. Chem. Phys. Lett. 344, 97–100 (2001)
Shalish, I., Temkin, H., Narayanamurti, V.: Size-dependent surface luminescence in ZnO nanowires. Phys. Rev. 69, 1–4 (2004)
Acknowledgments
One of the authors, Dr. Bindu P thanks the Department of Science and Technology (DST), New Delhi, India, for the award of Young Scientist Fellowship and financial assistance for carrying out the research project. Authors are thankful to Prof. Subhadra Patanair, Former Head, Department of Mathematics, S. N. M. College Maliankara, Ernakulam, India and Prof. (Dr.) Chacko Jacob, Materials Science Centre, Indian Institute of Technology (IIT), Kharagpur, India for valuable suggestions and help.
Conflict of interest
Both the authors declare that they have no competing interests.
Authors’ contributions
BP carried out all the experiments, characterizations, data analysis, calculations and conceptualized the research. ST provided facilities for carrying out the research. Both authors read and approved the final manuscript.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
About this article
Cite this article
Bindu, P., Thomas, S. Estimation of lattice strain in ZnO nanoparticles: X-ray peak profile analysis. J Theor Appl Phys 8, 123–134 (2014). https://doi.org/10.1007/s40094-014-0141-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40094-014-0141-9