Introduction

Over the past decade, the number of natural disasters, such as tornados, floods, forest fires, and extreme cold, has increased and affected millions of people’s lives and cities, leaving a lot of their assets and resources damaged. Due to the growth of the population and the development of the cities, the number of people who are at risk has increased in recent years (Bozorgi-Amiri et al. 2013). According to Baskaya et al. (2017), 106,654 people died and more than 216 million have been affected by natural disasters from 2003 to 2012. In addition, it is estimated that the financial damage during these years has been around $157 billion.

Here, it is revealed that how humanitarian relief supply chain in disaster management is important to control the flow of resources to provide the affected people with relief. Determining the appropriate location for storing the relief items before a disaster and planning the distribution of pre-positioned relief items in post-disaster are two challenging issues. Besides, considering cost, time, and quality as essential criteria increases the complexity and importance of managing disaster in the point of operation management (Bozorgi-amiri et al. 2013). Demands for relief items, such as water, food, and blanket, normally increase after a disaster strikes. Providing these relief items in sufficient quantity and at the right time is vital to save human lives. Preparedness planning includes purchasing items and pre-positioning them. The response planning includes delivering supplies to the demand points and purchasing extra supplies (Pradhananga et al. 2016).

Disaster management usually consists of four parts: mitigation, preparedness, relief, and recovery. Mitigation is the effort taken to save the human life including understanding the consequences of risks and organization of resources. Preparedness is the set of operations performed to get prepared before a disaster, and consequently the risks reduce. Preparedness efforts include the improvement in response operation, by training people, and preparedness planning. Disaster management often encounters conflicting objectives such as maximizing the efficiency of emergency aids and minimizing the costs of logistic activities. Thus, the problem is much complicated with respect to the existence of high degrees of uncertainty.

Distributing relief items to the affected areas is one of the most important steps in humanitarian operations, which can be disrupted because of total/partial damage to warehouses’ capacity, distribution centres, suppliers, and infrastructures. This could result in unmet relief item demands and finally death in the affected areas (Çelik 2016). Thus, it is vital to consider the humanitarian logistic network vulnerability to diminish the risk of disruption when a disaster strikes. In this paper, we have formulated a multi-objective two-stage stochastic programming in order to design a humanitarian relief supply chain including relief suppliers, central warehouses (CWs), local distribution centres (LDCs), and affected areas. CWs and LDCs should be established and located in pre-disaster. Generally, LDCs can be considered reliable and unreliable. A disaster might affect unreliable LDCs, and they might lose some portions of their capacity (Ransikarbum and Mason 2016). On the contrary, reliable LDCs are safe in disasters, but their establishment cost is much higher than unreliable ones. The proposed model selected the location of CWs and reliable and unreliable LDCs among the candidate locations. Moreover, it determined the quantity of relief items pre-positioned in them by suppliers in pre-disaster. Also, the proposed model, in post-disaster, determines the quantity of relief items purchased from the suppliers and relief items sent from reliable LDCs to unreliable LDCs. Another feature of this model is considering the following factors: appropriate multi-period planning for the distribution of relief items in the response phase of the relief chain, uncertainties about the demands in the affected areas (Tabrizi and Razmi 2013), cost parameters, and transportation time. The costs in this study include the fixed cost of establishing local and central distribution warehouses, the cost of transporting relief items between the local and central distribution warehouses, the cost of transporting relief items from local or central distribution warehouses to the demand points, penalty costs for the unmet demands in the affected areas, and the cost of transporting relief items between local distribution centres (lateral transhipment). To cope with the imprecise parameters in the present model, we applied a method that was proposed by Jiménez et al. (2007). The remainder of this paper is presented as follows. The literature review is presented in “Literature review” section. “Problem description” section addresses the problem description and the model development. The solution procedures including multi-objective programming (MOP) and the possibilistic programming method are discussed in “Possibilistic programming” section. Numerical examples are presented in “Multi-objective programming” section. Computational results and sensitivity analyses are presented in “Numerical experiments” section. Managerial insights are developed in “Case study” section. Finally, the conclusion and further research are presented in “Managerial insights” section.

Literature review

The most relevant literature corresponding to the current work is reviewed in this section with focusing on humanitarian relief chain (HRC) published work.

Mete and Zabinsky (2010) proposed a two-stage stochastic programme which accounts for determining storage locations of medical supplies and their required inventory levels in the first stage (i.e., pre-disaster) and distributing pre-positioned medical supplies to the affected areas in the second stage (i.e., post-disaster). Rawls and Turnquist (2010) proposed a two-stage stochastic mixed-integer model in order to pre-position relief items in pre-disaster. They examined a real-world case study for the hurricane threat located at Gulf Coast area of the USA and developed an L-shaped method to solve some big problems. Rawls and Turnquist (2011) developed their previous model (Rawls and Turnquist 2010) by considering the service quality constraints to ensure that the unmet demands would be at their minimum level. Bozorgi-Amiri et al. (2013) proposed a multi-objective robust stochastic programming in order to optimize humanitarian relief operations in both the preparedness (e.g., pre-positioning) and response phases simultaneously (and distribution). Tirado et al. (2014) proposed the lexicographical dynamic flow model to solve the problem of relief item distribution in a humanitarian logistic supply chain. They tried to involve the criteria that were related to cost, time, and equity to obtain a better response in disasters. Barzinpour and Esmaeili (2014) proposed a multi-objective two-echelon HRC for the preparedness phase of HRC. They proposed some objectives for maximizing the covered demand and minimizing the total facility location costs and minimizing storing, transportation, and shortage costs. Azad et al. (2014) designed a robust reliable HRC network considering random disruptions for distribution centres and transportation modes. They assumed that a disruption might partially disrupt the capacity of supply facilities. Thus, they divided the distribution centres into reliable and unreliable facilities whose capacity might be affected by the disruption. Camacho-Vallejo et al. (2015) proposed a bi-level mathematical programming for distributing international aid in post-disaster and minimizing the shipping costs of the relief items that are received by foreign countries and non-profit international organizations. Tofighi et al. (2016) presented a two-stage stochastic model for pre-positioning the relief items in pre-disaster and distributing them in post-disaster considering the fuzziness and randomness nature of the disaster. Ahmadi et al. (2015) proposed a two-stage stochastic mixed-integer linear model to determine the location of distribution centres in the first stage and the location of local distribution centres and the vehicle routing strategy in the second stage, considering possible scenarios of road destruction.

To investigate the benefits of transhipment opportunities into HRC, Baskaya et al. (2017) developed three mathematical models: direct shipment model, lateral transhipment model, and maritime lateral transhipment model. They concluded that considering lateral transhipment could significantly increase the efficiency of the HRC. To address uncertainties in some important parameters, such as demand, supply, and all the cost parameters, Zokaee et al. (2016) presented a robust three-echelon relief chain model consisting of suppliers, distribution centres, and demand points. The proposed model selects the appropriate locations for locating relief centres and determines optimal distribution flows of the relief items. Their presented objective functions set to minimize operating costs and maximizing equity among demand points. He and Zhuang (2016) proposed a robust model for balancing pre- and post-disaster operations to improve the cost efficiency while enhancing fairness among beneficiaries. Cavdur et al. (2016) developed a two-stage stochastic programming for the facility location in the response phase which minimizes the total travelled distance, unmet demands, and the total number of facilities. Rezaei-Malek et al. (2016a, b) presented a multi-objective mixed-integer programming to determine the right decisions for selecting the location of warehouses, distributing commodities to the affected people, ordering policies for renewing the perishable stocks, and pre-positioning the quantity of medical commodities. Alem et al. (2016) proposed a two-stage stochastic network flow model to minimize the total cost of pre-positioning stocks and minimizing the unmet demands. Decisions such as pre-positioning relief items and fleet sizing are made in the first stage. Accordingly, budget allocations to provide the required relief items are addressed in the second stage. Bozorgi-Amiri and Khorsi (2016) proposed a scenario-based two-stage multi-objective multi-period model in order to integrate pre- and post-disaster emergency operations. Determining the facility location and pre-positioning the relief items are modelled through the first stage. In addition, vehicle routing for distributing pre-positioned relief items is considered in the second stage. The developed model consists of three objectives: minimizing the shortages, transportation time, and all the operation costs. Rodríguez-Espíndola et al. (2017) utilized geographical information systems (GISs) to develop a multi-objective optimization model. They aimed to determine the optimal location of emergency relief facilities and the quantity of relief items, which need to be pre-positioned. In addition, they considered the relief item distribution problem in their model with the aim of minimizing all the operation costs. Haghi et al. (2017) proposed a robust multi-objective programming model for pre- and post-disaster. In relief item distribution centres and health centres, the quantity of goods should be calculated in pre-disaster. In addition, planning for the distribution of relief items and casualty transfer to the medical centres are the other aspects of their work. Manopiniwes and Irohara (2017) developed a multi-objective stochastic linear mixed-integer model in order to integrate the emergency operations in both pre- and post-disaster phases. Facility location and pre-positioning relief items in pre-disaster and distributing stocks, vehicle routing, and evacuation planning are all noticed in post-disaster decisions. Mohammadi and Yaghobi (2017) proposed a bi-objective stochastic model to design an emergency medical service logistic network with the aim of minimizing the total transportation time by considering route’s disruptions and transportation costs. The proposed mathematical model tries to determine the appropriate locations for transfer points, medical supplies, distribution centres and to make decisions related to the allocation strategy between facilities and the flow of medical supplies. Fereiduni and Shahanaghi (2017) proposed a two-stage multi-period robust model to design a HRC. The first stage decisions include selecting proper suppliers for supplying relief items and determining the location of central and local warehouse and pre-positioning levels. Also, the second-stage decisions consist of determining the relief item flows among central and local warehouses, determining relief item flows from local warehouse to demand points, and quantity of relief items which are sent from suppliers to demand points. Condexia et al. (2017) developed a two-stage stochastic model considering managing risk in humanitarian operations. The first stage of the proposed model determines the location of distribution centres and pre-positioning levels, and the second stage associates with distributing relief items to demand points. Also, Elci and Noyan (2018) developed a chance-constrained two-stage stochastic programming model with considering risk management in order to design a HRC. The proposed model determines capacity and location of supply facilities and finds pre-positioning levels by incorporating risk measures. Yahyaei and Bozorgi-Amiri (2018) proposed a mixed-integer linear model to design a reliable HRC. Remarkably, they divided the supply facilities into reliable and unreliable warehouses. The facility location and distribution planning is formulated through a robust programming. Rezaei-Malek et al. (2016a, b) developed a HRC network design associated with the facility location, pre-positioning, and distributing relief items in the preparedness and response phases. They utilized a two-stage stochastic programming to model the inherited uncertainty existing in some input parameters.

In this paper, we propose a two-stage stochastic programming for integrating relief pre-positioning and distribution planning, considering the lateral transhipment and disruption in supply facilities. Hereby, humanitarian organizations can mitigate the impact of relief items scarcity. Another significant point of this work is designing the post-disaster operations in multi-periods and in a dynamic way by which humanitarian organizations can find an optimal distribution plan in the first 72 h after a disaster strikes.

In brief, the main contributions of this paper are as follows:

  • Involving disruptions while designing the HRC;

  • Enhancing the responsiveness of HRC, considering lateral transhipment;

  • Designing the dynamic (i.e., multi-period) post-disaster operations;

  • Dealing with possibilistic and stochastic uncertainties;

  • Implementing the proposed model for a case study.

Problem description

In the aftermath of a disaster and in the early stages (i.e., the first 72 h), pre-positioned relief items should be distributed to the affected areas in order to save lives and mitigate the negative impacts of the disaster. On the other hand, lack of resources such as pre-positioned relief items might cause some difficulties. Therefore, it is essential to plan an efficient and effective emergency response considering the distribution of relief items in multi-periods, because the new information can be used for future periods once it is known. This viewpoint can help humanitarian organizations to increase the relief chain responsiveness and deal with the uncertainties properly in post-disaster.

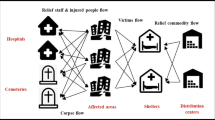
A typical relief supply chain includes relief suppliers, central warehouses (CWs), and local distribution centres (LDCs). Suppliers’ capacity is limited, and they can provide humanitarian organizations with relief items in short lead-time in pre- and post-disaster. CW and LDCs’ locations should be chosen, among candidate locations, in pre-disaster. To account supply disruptions, LDCs can be divided into reliable and unreliable facilities. A disaster might affect unreliable LDCs and damage some portions of their capacity (Ransikarbum and Mason 2016). On the other hand, reliable LDCs are safe in disasters, but their establishment costs are higher than unreliable ones. In pre-disaster, humanitarian organizations pre-position the required relief items in CWs and LDCs using suppliers. After a disaster, pre-positioned relief items are sent from CWs to LDCs and from LDCs to the demand points (i.e., the affected areas). CWs must be opened with large storage capacities, and they play a strategic role in the relief supply chain. Hence, they must be safe. In addition, LDCs should be located close to the potential demand points because their responsibility is sending the relief items to the demand points.

As the scarcity of relief items might result in death and increase the number of injured people, it is vital to estimate the proper inventory level of CWs and LDCs for pre-positioning relief items. On the other hand, since the severity of future disasters is not predictable, two-stage stochastic programming can be utilized to solve such problems (Tofighi et al. 2016). Notably, unmet demands might exist in post-disaster due to the lack of relief items (Bozorgi-amiri et al. 2013). For overcoming this difficulty, humanitarian organizations can exploit the lateral transhipment among LDCs. Thus, an LDC can provide more relief items from other LDCs and in this way reduce the unmet demands remarkably. Therefore, using lateral transhipment can enhance the responsiveness of a relief supply chain and reduce the overall unsatisfied relief demands. Figure 1 shows the proposed HRC.

Fig. 1
figure 1

General schema of the considered HRC

Full size image

Coping with uncertainties is another important part while configuring relief supply chains. As input parameters might be imprecise due to the unavailability of historical data, possibilistic programming is a proper method to deal with fuzzy parameters. Also, some parameters may have a stochastic nature which might have been inherited from the randomness of events. The historical data are sufficiently available for such parameters. In this paper, to deal with the fuzzy parameters, such as the cost of establishing warehouses, transportation costs between CWs and LDCs, etc., possibilistic approaches are used. Also, to estimate possible future scenarios in post-disaster a two-stage stochastic approach is used.

Related assumptions considered in this paper are provided in “Assumptions” section.

Assumptions

  • The costs related to the relief item shortages have been considered in post-disaster.

  • Transportation costs are relief item-dependent and scenario-dependent.

  • Transhipments among LDCs are permitted. Relief items can be sent from reliable LDCs to unreliable ones in the case of a shortage (lateral transhipments.)

  • Distribution of relief items in the response phase has been assumed multi-period.

  • Suppliers can supply relief items in the post-disaster and distribute them to the LDCs.

  • Lateral transhipments between LDCs and the procurement of relief items from suppliers are not allowed in the first period of response phase.

Indices

I

The index of a supplier

J

The index of a candidate location for CWs

K

The index of a candidate location for the reliable LDCs

L

The index of a candidate location for the unreliable LDCs

M

The index of LDCs

D

The index of demand points

C

The index of relief items

S

The index of disaster scenarios

T

The index of time periods

Parameters

\(\widetilde{g}_{j}\)

The fixed cost of establishing a CW in the location j

\(\widetilde{fr}_{k}\)

The fixed cost of establishing a reliable LDC in the location k

\(\widetilde{fu}_{l}\)

The fixed cost of establishing an unreliable LDC in the location l

\(\widetilde{aq}_{c}\)

The unit inventory holding cost of the relief item c

\(\widetilde{pc}_{ic}\)

The supplying cost of the relief item c from the supplier i in pre-disaster

\(\widetilde{pc}_{cit}^{s}\)

The supplying cost of the relief item c from the supplier i under the scenario s

\(\widetilde{tc}_{ij}^{s}\)

The unit transportation cost from the supplier i to the CW j under the scenario s

\(\widetilde{tc}_{im}^{s}\)

The unit transportation cost from the supplier i to the LDC m under the scenario s

\(\widetilde{tc}_{jm}^{s}\)

The unit transportation cost from the CW j to the LDC m under the scenario s

\(\widetilde{tc}_{md}^{s}\)

The unit transportation cost from the LDC m to the demand point d under the scenario s

\(\widetilde{tc}_{kl}^{s}\)

The unit transportation cost from the LDC k to the LDC l under the scenario s

\(\widetilde{\varPi }_{cdt}^{s}\)

The unit penalty cost for the shortage of the relief item c in the period t under the scenario s

\(cap_{ic}\)

The capacity of the supplier i to supply the relief item c

\(w_{cm}\)

The capacity of the LDC m (m3) for the storage of the relief item c

\(V_{cj}\)

The capacity of the CW j (m3) for the storage of the relief item c

\(v_{c}\)

The volume of the relief item c (m3)

\(\phi_{ms}\)

The percentage of the storage capacity of the LDC m which might be disrupted under the scenario s. LDCs in a reliable location are not affected by a disaster, then: \(\phi_{ks} = 0\quad \forall k\)

\(\widetilde{D}_{cdt}^{s}\)

The demand of the relief item c in the demand point d in the period t under the scenario s

\(p_{s}\)

The probability of the scenario s

M

A big number

Decision variables

First-stage variables:

\(qc_{cij}\)

The quantity of the relief item c supplied from the supplier i and pre-positioned in the CW j in pre-disaster

\(ql_{cim}\)

The quantity of the relief item c procured from the supplier i in pre-disaster and pre-positioned in the LDC m

\(zr_{k}\)

1 if an LDC is located in a reliable location k; otherwise 0

\(zu_{l}\)

1 if an LDC is located in an unreliable location l; otherwise 0

\(\delta_{j}\)

1 if a CW is located in the location j; otherwise 0

Second-stage variables:

\(Q_{cimt}^{s}\)

The quantity of the relief item c sent from the supplier i to the LDC m in the period t under the scenario s

\(y_{cjmt}^{s}\)

The quantity of the relief item c sent from the CW j to the LDC m in the period t under the scenario s

\(x_{cmdt}^{s}\)

The quantity of the relief item c sent from the LDC m to the demand point d in the period t under the scenario s

\(u_{cklt}^{s}\)

The quantity of the relief item c sent from the reliable LDC k to the unreliable LDC l in the period t under the scenario s

\(il_{cmt}^{s}\)

The inventory level of the relief item c available in the LDC m at the time period t under the scenario s

\(b_{cdt}^{s}\)

The shortage of the relief item c in the demand point d in the period t under the scenario s

Model formulation

$$\begin{aligned} & \hbox{min} z = \sum\limits_{j}^{{}} {\widetilde{g}_{j} } \delta_{j} + \sum\limits_{l}^{{}} {\widetilde{fu}_{l} zu_{l} } + \sum\limits_{k}^{{}} {\widetilde{fr}_{k} zr_{k} } + \sum\limits_{i}^{{}} {\sum\limits_{j}^{{}} {\sum\limits_{c}^{{}} {\widetilde{pc}_{ic} qc_{cij} } } } + \sum\limits_{i}^{{}} {\sum\limits_{m}^{{}} {\sum\limits_{c}^{{}} {\widetilde{pc}_{ic} ql_{cim} } } } \\ & + \sum\limits_{i}^{{}} {\sum\limits_{j}^{{}} {\sum\limits_{c}^{{}} {\widetilde{aq}_{c} qc_{cij} } } } + \sum\limits_{i}^{{}} {\sum\limits_{m}^{{}} {\sum\limits_{c}^{{}} {\widetilde{aq}_{c} ql_{cim} + } } } \\ & \sum\limits_{s}^{{}} {p_{s} } \left( \begin{aligned} \sum\limits_{i}^{{}} {\sum\limits_{m}^{{}} {\sum\limits_{t}^{{}} {(\widetilde{pc}_{cit}^{s} + \widetilde{tc}_{im}^{s} )Q_{cimt}^{s} } } } \hfill \\ \sum\limits_{j}^{{}} {\sum\limits_{m}^{{}} {\sum\limits_{c}^{{}} {\sum\limits_{t}^{{}} {\widetilde{tc}_{jm}^{s} y_{cjmt}^{s} + \sum\limits_{m}^{{}} {\sum\limits_{d}^{{}} {\sum\limits_{c}^{{}} {\sum\limits_{t}^{{}} {\widetilde{tc}_{md}^{s} x_{cmdt}^{s} + \sum\limits_{k}^{{}} {\sum\limits_{l}^{{}} {\sum\limits_{c}^{{}} {\sum\limits_{t}^{{}} {\widetilde{tc}_{kl}^{s} u_{cklt}^{s} + } } } } } } } } } } } } \hfill \\ \sum\limits_{d}^{{}} {\sum\limits_{c}^{{}} {\sum\limits_{t}^{{}} {\widetilde{\varPi }_{cdt}^{s} b_{cdt}^{s} } } } \hfill \\ \end{aligned} \right). \\ \end{aligned}$$
(1)

Objective function (1) aims to minimize the total cost of opening LDCs and CWs, the purchasing cost of relief items and storing them in the pre-disaster phase, and also the purchasing and the transportation cost of relief items from a supplier to the LDCs, the transhipment cost of relief items from the CWs to the LDCs, and from the LDCs to the demand points in post-disaster. Besides, the cost of lateral transhipments among LDCs and the relief item shortage costs are considered in the formulation:

$$\hbox{max} z_{2} = \min_{d,c,s} \left( {\sum\limits_{m}^{{}} {\sum\limits_{t}^{{}} {P_{S} \frac{{x_{cmdts} }}{{\widetilde{D}_{cdt}^{s} }}} } } \right).$$
(2)

Equation (2) aims to maximize fairness among demand points. Notably, it maximizes the minimum rate of satisfied demands by distributing relief items to demand points during periods:

$$\sum\limits_{i}^{{}} {v_{c} qc_{cij} \le V_{cj} \delta_{j} } \quad \forall j,c$$
(3)
$$\sum\limits_{i}^{{}} {v_{c} ql_{cim} \le w_{cm} zr_{k} } \quad \forall k,m = k,c$$
(4)
$$\sum\limits_{i}^{{}} {v_{c} ql_{cim} \le w_{cm} zu_{l} } \quad \forall l,m = l,c.$$
(5)

Constraints (3), (4), and (5) represent the amount of relief items purchased from the suppliers for each LDC and CW in pre-disaster, and it should not exceed the capacity of CWs and LDCs, respectively.

$$\sum\limits_{m}^{{}} {ql_{cim} + \sum\limits_{j}^{{}} {qc_{cij} } \le cap_{ci} } \quad \forall i,c.$$
(6)

Constraint (6) limits the total relief items sent from a supplier in the pre-disaster phase.

$$\sum\limits_{i}^{{}} {ql_{cim} } + \sum\limits_{j}^{{}} {y_{cjmt}^{s} } = \sum\limits_{d}^{{}} {x_{cmdt}^{s} } + il_{cmt}^{s} \quad \forall m,c,s,t = 1$$
(7)
$$\sum\limits_{i}^{{}} {Q_{cimt}^{s} } + \sum\limits_{j}^{{}} {y_{cjmt}^{s} } + il_{cm(t - 1)}^{s} = \sum\limits_{d}^{{}} {x_{cmdt}^{s} } + il_{cmt}^{s} + \sum\limits_{l}^{{}} {u_{cklt}^{s} } \quad \forall k,m = k,c,t,s$$
(8)
$$\sum\limits_{i}^{{}} {Q_{cimt}^{s} } + \sum\limits_{j}^{{}} {y_{cjmt}^{s} } + il_{cm(t - 1)}^{s} + \sum\limits_{k}^{{}} {u_{cklt}^{s} = } \sum\limits_{d}^{{}} {x_{cmdt}^{s} } + il_{cmt}^{s} \quad \forall l,m = l,c,t,s.$$
(9)

Constraints (7), (8), and (9) ensured the inventory balance limitation in reliable and unreliable LDCs. The quantity of relief items sent from suppliers to an LDC in the period t, and relief items remaining from the previous period and also the relief items sent through the lateral transhipment to the LDC should be equal to the relief items sent from the LDC to the demand point, relief items remaining at the end of the period t, in addition to the relief items sent from one LDC to another one.

$$\sum\limits_{m}^{{}} {x_{cmdt}^{s} } + b_{cdt}^{s} = \widetilde{D}_{cdt}^{s} \quad \forall d,c,t,s.$$
(10)

Equation (10) is the demand constraint for relief items in the demand points in multi-periods.

$$\sum\limits_{m}^{{}} {\sum\limits_{t}^{{}} {Q_{cimt}^{s} } } \le cap_{ci} \quad \forall i,c,s.$$
(11)

Constraint (11) limits the total relief items sent from a supplier to LDCs in the response phase.

$$\sum\limits_{m}^{{}} {\sum\limits_{t}^{{}} {y_{cjmt}^{s} } } \le V_{cj} \delta_{j} \quad \forall j,c,s.$$
(12)

Constraint (12) shows the limitation for sending relief items from CWs and LDCs.

$$\sum\limits_{i}^{{}} {Q_{cimt}^{s} \le Mzr_{k} } \quad \forall k,m = k,c,t,s$$
(13)
$$\sum\limits_{i}^{{}} {Q_{cimt}^{s} \le Mzu_{l} } \quad \forall l,m = l,c,t,s.$$
(14)

Constraints (13) and (14) ensured that relief items could be sent to the reliable and unreliable LDCs from suppliers if the LDCs have been established.

$$\sum\limits_{d}^{{}} {x_{\text{cmdt}}^{s} } + \sum\limits_{l}^{{}} {u_{\text{cklt}}^{s} } \le il_{\text{cmt}}^{s} \quad \forall k,m = k,c,t,s$$
(15)
$$\sum\limits_{d}^{{}} {x_{cmdts} } \le il_{cmt}^{s} \quad \forall l,m = l,c,t,s.$$
(16)

Constraint (15) expresses the quantity of relief items sent from a reliable LDC to the demand point. Constraint (16) restricts the quantity of relief items sent from an unreliable LDC to the demand point, and it should be less than the quantity of relief items available in the unreliable LDC.

$$\sum\limits_{j}^{{}} {y_{cjmt}^{s} } + \sum\limits_{i}^{{}} {ql_{cim} } \le w_{cm} \phi_{ms} \quad \forall m,c,t = 1,s$$
(17)
$$\sum\limits_{j}^{{}} {y_{cjmt}^{s} } + \sum\limits_{i}^{{}} {q_{cimt}^{s} + } il_{cm(t - 1)}^{s} \le w_{cm} \quad \forall k,m = k,c,t,s$$
(18)
$$\sum\limits_{j}^{{}} {y_{cjmt}^{s} } + \sum\limits_{i}^{{}} {q_{cimt}^{s} } + \sum\limits_{k}^{{}} {u_{cklt}^{s} } + il_{cm(t - 1)}^{s} \le w_{cm} \phi_{ms} \quad \forall l,m = l,c,t,s.$$
(19)

Constraints (17), (18), and (19) ensured the fact that the quantity of the relief items sent from suppliers and CWs to the LDCs should be less than the capacity of the reliable and unreliable LDCs.

$$\sum\limits_{d}^{{}} {x_{cmdt}^{s} } \le Mzr_{k} \quad \forall k,m = k,c,t,s$$
(20)
$$\sum\limits_{d}^{{}} {x_{cmdt}^{s} } \le Mzu_{l} \quad \forall l,m = l,c,t,s.$$
(21)

Constraints (20) and (21) ensured that the relief items could be sent to the demand point from reliable and unreliable LDCs if the LDCs have been opened.

$$u_{cklt}^{s} \le Mzr_{k} \begin{array}{*{20}c} {} & {\forall k,m = k,} \\ \end{array} c,t,s$$
(22)
$$u_{cklt}^{s} \le Mzu_{l} \begin{array}{*{20}c} {} & {\forall l,m = l,c,t,s} \\ \end{array} .$$
(23)

Constraints (22) and (23) express that relief items can be transported from a reliable LDC k to an unreliable one l if the LDC k and l have been opened.

$$qc_{cij} ,ql_{cim} ,Q_{cimt}^{s} ,y_{cjmt}^{s} ,x_{cmdt}^{s} ,u_{cklt}^{s} ,il_{cmts}^{s} ,b_{cdt}^{s} \ge 0$$
(24)
$$zr_{k} ,zu_{l} ,\delta_{j} \in \left\{ {0,1} \right\}.$$
(25)

Constraints (24) and (25) define the eligible domain of decision variables.

The above-proposed model is nonlinear by the max–min form of the second objective function. This objective function can be linearized using a new positive variable λ and a new constraint. Then, the second objective function can be rewritten as:

$$\begin{aligned} & \hbox{max} \lambda \\ & \lambda \le \sum\limits_{m}^{{}} {\sum\limits_{t}^{{}} {P_{S} \frac{{x_{cmdts} }}{{\widetilde{D}_{cdt}^{s} }}} \quad \forall d,c,s} \\ & \lambda \ge 0. \\ \end{aligned}$$
(26)

Solution methodologies

As the proposed two-stage stochastic programming model in the previous section is MOP and contains imprecise input parameters, first it must be converted to a single-objective programming (SOP). Afterwards, we can obtain its equivalent crisp model (ECM) through an efficient possibilistic programming. The utilized possibilistic programming approaches and multi-objective are both described in this section.

Possibilistic programming

As mentioned before, there is not enough historical data about some input parameters and we encounter some imprecise parameters. To cope with these imprecise parameters, such as the demand of relief items, cost parameters, and transportation times, in optimization models, it is necessary to adopt an efficient method to obtain the ECM of the proposed model. Torabi et al. (2018) state that possibilistic approaches are among the most applicable methods to tackle such uncertainties in relief chains and also, we used two-stage stochastic approach to develop the model because of the nature of disaster including pre- and post-disaster phases. Thus, our model benefits from stochastic optimization. On the other hand, it is possible that decision makers encounter imprecise input parameters (scenario-dependents or scenario-independents) because of unavailability of historical data (Sherafati and Bashiri 2016; Khalaj et al. 2013; Mehrbod and Miao 2015). Therefore, we encounter epistemic uncertainty and a useful approach is necessary to encounter imprecise parameters. For two reasons, possibilistic programming approach is used to deal with such uncertainty:

  • The possibilistic programming approach deals with epistemic uncertainty in input parameters. This approach is proper when there is a lack of knowledge about the exact values of parameters even if we approximate the values of uncertain parameters by historical data but due to the dynamic nature of the relief chain problems, they do not necessarily behave according to the historical data (Mousazadeh et al. 2018).

  • A large number of published works find possibilistic programming useful while designing HRCs to deal with such uncertainty (Tofighi et al. 2016; Torabi et al. 2018).

Thus, in this paper a method proposed by Jiménez et al. (2007) is used because Jimenez approach provides decision makers with flexible intervals while adjusting possibilistic parameters. Thus, they can obtain numerous and reliable solutions. Secondly, this method prevents model from increasing complexity, because neither new variables nor new constraints will be added to the model in comparison with other approaches such as robust programming (Jiménez et al. 2007).

According to Jiménez et al. (2007), proper fuzzy distribution for possibilistic parameters should be determined. For this purpose, assume \(\zeta\) is a triangular fuzzy parameter that can be represented as \(\zeta = (\zeta^{p} ,\zeta^{m} ,\zeta^{o} )\). Notably, \(\zeta^{m}\) is the most likely value, \(\zeta^{o}\) is the optimistic value, and \(\zeta^{p}\) is the pessimistic value of the fuzzy parameter \(\zeta\). Accordingly, such a definition of a fuzzy number is utilized to reformulate the presented model based on Jiménez et al. (2007) method to obtain the auxiliary crisp model. One of the advantages of this method is that it provides the decision maker with a satisfaction degree of possibilistic constraints. Let us assume that \(\alpha\) denotes the satisfaction degree for such constraints. Additionally, this method has two basic principles: I: the expected value and II: the expected interval. To clarify these principles, consider the following membership function of the fuzzy number \(\tilde{\zeta }\) as Eq. (27):

$$(x) = \left\{ {\begin{array}{*{20}l} {f_{\zeta } (x) = \frac{{x - \zeta^{p} }}{{\zeta^{m} - \zeta^{p} }}} \hfill & {{\text{if}}\;\;\zeta^{p} \le x \le \zeta^{m} } \hfill \\ 1 \hfill & {{\text{if}}\;\;x = \zeta^{m} } \hfill \\ {g_{\zeta } (x) = \frac{{\zeta^{o} - x}}{{\zeta^{o} - \zeta^{m} }}} \hfill & {{\text{if}}\;\;\zeta^{m} \le x \le \zeta^{0} } \hfill \\ 0 \hfill & {{\text{if}}\;\;x \le \zeta^{p} \;{\text{or}}\;x \ge \zeta^{0} } \hfill \\ \end{array} } \right..$$
(27)

The expected interval (EI) and the expected value (EV), according to Jiménez et al. (2007), can be calculated by Eqs. (28) and (29):

$${\text{EI}}(\tilde{\zeta }) = \left[ {E_{1}^{\zeta } } \right.\,\,\left. {E_{2}^{\zeta } } \right] = \left[ {\int_{0}^{1} {f_{\zeta }^{ - 1} (x){\text{d}}x\,\,\,\,\left. {\int_{o}^{1} {g_{\zeta }^{ - 1} (x){\text{d}}x} } \right]} } \right. = \left[ {\frac{1}{2}} \right.(\zeta^{p} + \zeta^{m} )\,\,\,\,\,\left. {\frac{1}{2}(\zeta^{o} + \zeta^{m} )} \right]$$
(28)
$${\text{EV}}(\tilde{\zeta }) = \frac{{E_{1}^{\zeta } + E_{1}^{\zeta } }}{2} = \frac{{\zeta^{p} + 2\zeta^{m} + \zeta^{o} }}{4}.$$
(29)

Now, assume that \(\tilde{a}\) and \(\tilde{b}\) are a pair of fuzzy numbers; then, the satisfaction degree can be defined as Eq. (30):

$$\mu_{M} (x) = (\tilde{a},\tilde{b}) = \left\{ {\begin{array}{*{20}l} 1 \hfill & {{\text{if}}\;\;E_{1}^{a} > E_{2}^{b} } \hfill \\ {\frac{{E_{2}^{a} - E_{1}^{b} }}{{E_{2}^{a} - E_{1}^{b} - (E_{1}^{a} - E_{1}^{a} )}}} \hfill & {{\text{if}}\;\;0 \in \left[ {E_{1}^{a} - E_{2}^{b} \left. {E_{2}^{a} - E_{1}^{b} } \right]} \right.} \hfill \\ 0 \hfill & {{\text{if}}\;\;E_{2}^{a} < E_{1}^{b} } \hfill \\ \end{array} } \right.$$
(30)

If \(\mu_{M} \left( {\tilde{a},\left. {\tilde{b}} \right)} \right. \ge \alpha\), then we could claim that \(\tilde{a}\) is equal to, or bigger than \(\tilde{b}\), at least with the degree of \(\alpha\) by which we could show \(\tilde{a} \ge_{\alpha } \tilde{b}\). Again, given \(\tilde{a}\) and \(\tilde{b}\) as a couple of fuzzy numbers, we can say that \(\tilde{a}\) is equal to \(\tilde{b}\) if \(\tilde{a} \le_{{\frac{\alpha }{2}}} \tilde{b}\) and \(\tilde{a} \ge_{{\frac{\alpha }{2}}} \tilde{b}\). Now, assume that model (31) is a representative of a possibilistic mathematical model:

$$\begin{aligned} & \hbox{min} z = \tilde{c}^{t} x \\ & \tilde{a}_{i} x \ge \tilde{b}_{i} x\;\;i = 1, \ldots ,l \\ & \tilde{a}_{i} x = \tilde{b}_{i} x\;\;i = l + 1, \ldots ,m \\ & x \ge o. \\ \end{aligned}$$
(31)

According to Jiménez et al. (2007), the above inequality possibilistic constraints can be converted to Eqs. (32–34):

$$[(1 - \alpha )E_{2}^{{a_{i} }} + \alpha E_{1}^{{a_{i} }} ]x \ge (1 - \alpha )E_{1}^{{b_{i} }} + \alpha E_{2}^{{b_{i} }} \quad i = 1, \ldots ,l$$
(32)
$$\left[ {\left( {1 - \frac{\alpha }{2}} \right)E_{1}^{{a_{i} }} + \frac{\alpha }{2}E_{2}^{{a_{i} }} } \right]x \le (1 - \frac{\alpha }{2})E_{2}^{{b_{i} }} + \frac{\alpha }{2}E_{1}^{{b_{i} }} \quad i = 1 + l, \ldots ,m$$
(33)
$$[(1 - \frac{\alpha }{2})E_{2}^{{a_{i} }} + \frac{\alpha }{2}E_{1}^{{a_{i} }} ]x \ge (1 - \frac{\alpha }{2})E_{1}^{{b_{i} }} + \frac{\alpha }{2}E_{2}^{{b_{i} }} \quad i = l + 1, \ldots ,m.$$
(34)

Thus, according to the above reformulations and the expected value of a triangular fuzzy number, which is presented by Eq. (29), the ECM model of (31) can be obtained as (35):

$$\begin{aligned} & {\hbox{min}} \,{\text{EV}}(\tilde{c})x \\ & [(1 - \alpha )E_{2}^{{a_{i} }} + \alpha E_{1}^{{a_{i} }} ]x \ge (1 - \alpha )E_{1}^{{b_{i} }} + \alpha E_{2}^{{b_{i} }} \quad i = 1, \ldots ,l \\ & [(1 - \frac{\alpha }{2})E_{1}^{{a_{i} }} + \frac{\alpha }{2}E_{2}^{{a_{i} }} ]x \le (1 - \frac{\alpha }{2})E_{2}^{{b_{i} }} + \frac{\alpha }{2}E_{1}^{{b_{i} }} \quad i = 1 + 1, \ldots ,m \\ & [(1 - \frac{\alpha }{2})E_{2}^{{a_{i} }} + \frac{\alpha }{2}E_{1}^{{a_{i} }} ]x \ge (1 - \frac{\alpha }{2})E_{1}^{{b_{i} }} + \frac{\alpha }{2}E_{2}^{{b_{i} }} \quad i = 1 + 1, \ldots ,m. \\ \end{aligned}$$
(35)

Based on the interpretations above, the final equivalent crisp model of our problem can be expressed as follows:

$$\begin{aligned} & \hbox{min} z = \sum\limits_{j}^{{}} {\left(\frac{{g_{j}^{o} + 2g_{j}^{p} + g_{j}^{m} }}{4}\right)\delta_{j} + \sum\limits_{k}^{{}} {\left(\frac{{fr_{k}^{o} + 2fr_{k}^{p} + fr_{k}^{m} }}{4}\right)zr_{k} + \sum\limits_{l}^{{}} {\left(\frac{{fu_{l}^{o} + 2fu_{l}^{p} + fu_{l}^{m} }}{4}\right)zu_{l} } } } \\ & + \sum\limits_{i}^{{}} {\sum\limits_{j}^{{}} {\sum\limits_{c}^{{}} {\left(\frac{{pc_{ic}^{o} + 2pc_{ic}^{p} + pc_{ic}^{m} }}{4}\right)qc_{cij} } } } + \sum\limits_{i}^{{}} {\sum\limits_{m}^{{}} {\sum\limits_{c}^{{}} {\left(\frac{{pc_{ic}^{o} + 2pc_{ic}^{p} + pc_{ic}^{m} }}{4}\right)ql_{cim} } } } \\ & + \sum\limits_{i}^{{}} {\sum\limits_{j}^{{}} {\sum\limits_{c}^{{}} {\left(\frac{{aq_{c}^{o} + 2aq_{c}^{p} + aq_{c}^{m} }}{4}\right)qc_{cij} } + \sum\limits_{i}^{{}} {\sum\limits_{m}^{{}} {\sum\limits_{c}^{{}} {\left(\frac{{aq_{c}^{o} + 2aq_{c}^{p} + aq_{c}^{m} }}{4}\right)ql_{cim} } } } } } \\ & \sum\limits_{s}^{{}} {p_{s} \left( \begin{aligned} \sum\limits_{i}^{{}} {\sum\limits_{m}^{{}} {\sum\limits_{c}^{{}} {\sum\limits_{t}^{{}} {\left(\frac{{pc_{cim}^{so} + 2pc_{cim}^{sp} + pc_{cim}^{sm} }}{4} + \frac{{tc_{im}^{so} + 2tc_{im}^{sp} + tc_{im}^{sm} }}{4}\right)Q_{cimt}^{s} } } } } \hfill \\ + \sum\limits_{j}^{{}} {\sum\limits_{m}^{{}} {\sum\limits_{c}^{{}} {\sum\limits_{t}^{{}} {\left(\frac{{tc_{jm}^{so} + 2tc_{jm}^{sp} + tc_{jm}^{sm} }}{4}\right)y_{cjmt}^{s} } } } } \hfill \\ \sum\limits_{m}^{{}} {\sum\limits_{d}^{{}} {\sum\limits_{c}^{{}} {\sum\limits_{t}^{{}} {\left(\frac{{tc_{md}^{so} + 2tc_{md}^{sp} + tc_{md}^{sm} }}{4}\right)x_{cmdt}^{s} } } } } \hfill \\ + \sum\limits_{k}^{{}} {\sum\limits_{l}^{{}} {\sum\limits_{c}^{{}} {\sum\limits_{t}^{{}} {\left(\frac{{tc_{kl}^{so} + 2tc_{kl}^{sp} + tc_{kl}^{sm} }}{4}\right)u_{cklt}^{s} } } } } \hfill \\ + \sum\limits_{d}^{{}} {\sum\limits_{c}^{{}} {\sum\limits_{t}^{{}} {\left(\frac{{\varPi_{cdt}^{so} + 2\varPi_{cdt}^{sp} + \varPi_{cdt}^{sm} }}{4}\right)b_{cdt}^{s} } } } \hfill \\ \end{aligned} \right)} \\ \end{aligned}$$
(36)
$$\sum\limits_{m}^{{}} {x_{cmdt}^{s} } + b_{cdt}^{s} \ge \left( {\frac{\alpha }{2}} \right)\left( {\frac{{D_{cdt}^{sm} + D_{cdt}^{so} }}{2}} \right) + \left( {1 - \frac{\alpha }{2}} \right)\left( {\frac{{D_{cdt}^{sp} + D_{cdt}^{sm} }}{2}} \right)$$
(37)
$$\sum\limits_{m}^{{}} {x_{cmdt}^{s} } + b_{cdt}^{s} \le \left( {1 - \frac{\alpha }{2}} \right)\left( {\frac{{D_{cdt}^{sm} + D_{cdt}^{so} }}{2}} \right) + \left( {\frac{\alpha }{2}} \right)\left( {\frac{{D_{cdt}^{sp} + D_{cdt}^{sm} }}{2}} \right).$$
(38)

The crisp form of Eq. (26) is represented below:

$$\lambda \le \sum\limits_{m}^{{}} {\sum\limits_{t}^{{}} {P_{S} \frac{{x_{cmdts} }}{{(1 - \alpha )\left( {\frac{{D_{cdt}^{sm} + D_{cdt}^{so} }}{2}} \right) + (\alpha )\left( {\frac{{D_{cdt}^{sp} + D_{cdt}^{sm} }}{2}} \right)}}} \forall d,c,s} .$$
(39)

Multi-objective programming

As the proposed model is an MOP, it is essential to adopt an efficient method in order to convert the MOP to SOP. In this paper, TH method proposed by Torabi and Hassini (2008) is applied which is developed based on the interactive fuzzy possibilistic programming. TH method enables decision makers to obtain a set of optimal solutions and select the most appropriate one. To elaborate on the method, let us assume the general form of the following MOP model:

$$\begin{aligned} & \hbox{min} f(x) = [f_{1} (x),f_{2} (x), \ldots ,f_{m} (x)] \\ & {\text{st}}: \\ & x \in F(x), \\ \end{aligned}$$
(40)

where \(F(x)\) denotes the feasible solution. Torabi and Hassini (2008) proposed model (41) as the SOP of model (40):

$$\begin{aligned} & \hbox{max} \lambda (x) = \gamma \lambda_{0} + (1 - \gamma )\sum\limits_{i}^{{}} {w_{i} } \mu_{i} (x) \\ & {\text{st}}: \\ & \lambda_{0} \le \mu_{i} (x)\;\;\;\forall i = 1, \ldots ,m \\ & x \in F(x),\lambda_{0} ,\gamma \in [0,1]. \\ \end{aligned}$$
(41)

\(\mu_{i} (x)\) represents the satisfaction degree of the ith objective function which can be calculated using Eq. (42). \(w_{i}\) indicates the importance of ith objective function where \(\sum\nolimits_{i}^{{}} {w_{i} } = 1\) and \(\lambda_{0}\) expresses the minimum satisfaction degree of the objective functions. Moreover, \(\gamma\) shows the coefficient compensation. For more details about the parameters, see Torabi and Hassini (2008).

According to TH method, Fig. 2 indicates the fuzzy membership function for the objective functions in the form of minimization (Torabi and Hassini; 2008). Where \(Z_{i} (x)\) is the value of the objective function, \(Z_{i}^{pis}\) is the most possible of it and \(Z_{i}^{nis}\) is the worst value that can be obtained from the objective function:

$$\mu_{i} (x) = \left\{ {\begin{array}{*{20}l} 1 \hfill & {Z_{i} (x) \le Z_{i}^{pis} } \hfill \\ {\frac{{Z_{i}^{nis} - Z_{i} (x)}}{{Z_{i}^{nis} - Z_{i}^{pis} }}} \hfill & {Z_{i}^{pis} \le Z_{i} (x) \le Z_{i}^{nis} } \hfill \\ 0 \hfill & {Z_{i} (x) \ge Z_{i}^{nis} } \hfill \\ \end{array} } \right\}.$$
(42)
Fig. 2
figure 2

Membership function of a minimization-type objective function

Full size image

In addition, the fuzzy membership function for an objective function is presented in the form of maximization in Eq. (43):

$$\mu_{i} (x) = \left\{ {\begin{array}{*{20}l} 1 \hfill & {Z_{i} (x) \ge Z_{i}^{pis} } \hfill \\ {\frac{{Z_{i} (x) - Z_{i}^{nis} }}{{Z_{i}^{pis} - Z_{i}^{nis} }}} \hfill & {Z_{i}^{pis} \le Z_{i} (x) \le Z_{i}^{nis} } \hfill \\ 0 \hfill & {Z_{i} (x) \le Z_{i}^{nis} } \hfill \\ \end{array} } \right\}.$$
(43)

Numerical experiments

To validate the proposed model, a comprehensive numerical example is provided in this section. The proposed model is solved using CPLEX solver in GAMS 24.3, and then the results are reported. The details of the considered problem are summarized in Table 1. Three major relief items are water, food, and shelter.

Table 1 Details of the numerical example
Full size table

Table 2 represents the number of scenarios and the probability of occurrence for each one. The parameters of the numerical experiment, which are summarized in Tables 3 and 4, are generated randomly using uniform distribution.

Table 2 Possible scenarios
Full size table
Table 3 Demand of relief items and the capacity of suppliers
Full size table
Table 4 Parameters for an experimental design
Full size table

It is noteworthy to mention that the centre of the fuzzy parameters is generated randomly using the distribution mentioned in Tables 3 and 4. Moreover, the right and left spreads are considered as 10 per cent of the centres.

Results and sensitivity analyses

One of the most important parameters for evaluating the performance of the crisp counterpart model is α as the minimum acceptance satisfaction degree of the constraints which is known as the constraints’ confidence level. Table 5 shows the sensitivity analyses for α and denotes its effects on the objective functions. As can be seen from Table 5, when the minimum degree of the satisfaction level increases, the optimal value of the first objective function, which indicates the cost of the relief chain, increases and the optimal value of the second objective function, which represents the fairness, decreases. Therefore, it is better for decision makers to set a medium value for α which results in the average total cost of the relief chain and fairness.

Table 5 Results in sensitivity analyses on confidence level
Full size table

Table 6 represents the effectiveness of using transhipment strategies. Eliminating transhipment opportunity increases the number of located reliable LDCs and decreases the number of located unreliable LDCs. As can be concluded from Table 6, using transhipment decreases the total cost of the chain, because the unmet demands are minimized as much as possible in post-disaster. In other words, using transhipment might increase the cost of relief distributions, while it eliminates the unmet demands, saves more lives, and avoids penalty costs as much as possible. In the proposed model, the multiple sourcing policy is used for allocating demand points to LDCs to send relief items from LDCs to demand points. The distance between LDCs and demand points is incorporated in the transportation cost.

Table 6 Results of solving test problem
Full size table

To solve the multi-objective model, selecting the most suitable value for the parameters such as \(\gamma\) and \(w_{1}\) is vital since we want to make a trade-off between conflict objective functions while converting MOP to SOP. Here, there is a conflict between the total cost of the relief chain and fairness. Torabi and Hassini (2008) explained that considering the coefficient compensation parameter (\(\gamma\)) with the value more than 0.5 leads to an increase in the minimum satisfaction degree of the objective function (\(\lambda_{0}\)). As a result, more balanced compromised solutions are obtained, whereas selecting the value of \(\gamma\) less than 0.5 leads to the acquirement of the unbalanced compromised solutions, because TH tries to find solutions with a higher satisfaction degree of objective functions with a higher relative importance weight.

Table 7 shows the sensitivity analysis results associated with the coefficient parameters of TH method (\(\gamma\) and \(w_{i}\)). Generally speaking, increasing the value of \(\gamma\) leads to an increase in the satisfaction degree of the first objective function (the total cost of the relief chain) and a decrease in the satisfaction degree of the second objective function (fairness). Thus, selecting the lower value for the coefficient parameter, the first objective function, which calculates the total cost of the relief chain, increases and the second objective function, which is related to fairness, decreases. Also, selecting a higher value for \(\gamma\) causes a decrease in the total cost of the relief chain and an increase in fairness. According to the results, if a decision maker wishes to make a balanced trade-off between the objective functions (the cost of HRC and fairness) he/she should not select the medium value for \(\gamma\). Besides, as can be seen in Table 7, changing the value of the parameters \(\gamma\) and \(w_{1}\) can produce different balanced and unbalanced solutions based on which a decision maker can select the most suitable solutions for the problem. Figure 3 shows that increasing the value of relative importance of the first objective function, which indicates the cost of the relief chain, increases the satisfaction degree of SOP. It means that to obtain better solutions for SOP one can increase the relative importance of the first objective function. In addition, increasing the value of \(\gamma\) decreases the satisfaction degree of the SOP model.

Table 7 Sensitivity analyses on parameters of TH method
Full size table
Fig. 3
figure 3

Sensitivity analysis for compromising the parameter and relative importance of the total relief chain

Full size image

Figure 4 demonstrates the total quantity of transhipped relief items from the reliable LDCs to the unreliable ones in post-disaster during three periods in each scenario. The quantity of relief items that are transhipped in the second period is larger than that of others. Also, as can be concluded from Fig. 5, the total shortage of relief items in the affected areas in the third period is larger than that in the first and second periods in each scenario. Thus, it is important to increase the number of established warehouses in order to prevent the occurrence of shortages in the third scenario because of the high severity of the disaster. Notably, the humanitarian organizations can use the national and international aids to establish more warehouses. In order to decrease the total shortages and to gain better responses in post-disaster, the following suggestions are presented:

Fig. 4
figure 4

Total transhipments in post-disaster (m3)

Full size image
Fig. 5
figure 5

Total shortages in post-disaster (m3)

Full size image

  • As our numerical example shows, the number of established CWs and LDCs is not sufficient to pre-position the proper quantity of relief items, and the HO should increase the number of established warehouses. Notably, increasing the number of established warehouses increases the total cost of HRC. Thus, the HO should be provided with enough budget through some public monetary and governmental donations in pre-disaster.

  • When a disruption occurs, unreliable LDCs lose some portions of their supply capacities. Thus, increasing the fortification level of the unreliable LDCs can play an important role in post-disaster to meet the relief item demands.

Case study

In this section, in order to evaluate the performance of the proposed model, a case study of Iran is presented and solved. Due to the fact that Tehran is located surrounded by major faults, the design of a proper HRC is necessary to prevent from massive destructions. Several earthquakes have been occurred in Tehran, but due to the small size of the city and the low population in those years, the impact of those crises has not been very high. Experts predict that a high-magnitude earthquake might annihilate human lives and infrastructures massively. Tehran is surrounded by three major faults called Mosha, North of Tehran, and Rey, whose movement would result in a high-magnitude earthquake (Tofighi et al. 2016). Also, movement of two or more faults will results in an intense earthquake which is called floating model. The possibility of earthquake occurrence due to the movement of each of these faults on day and night is considered in different scenarios and is shown in Table 8. In this study, tents, water, and food are considered as relief items and cities like Golestan, Mazandaran, Isfahan, and Gilan are considered as locations that suppliers are located in. Tehran has 22 districts, and they have been considered as demand points. Tables 9 and 10 represent the volume of each unit of relief items occupied and the supply capacity for the supply relief items. Another data for the case study are borrowed from Tofighi et al. (2016) and Torabi et al. (2018).

Table 8 Probabilities of different earthquake scenarios
Full size table
Table 9 Volume occupied by relief items (103 units)
Full size table
Table 10 Capacity of suppliers for each commodity (103 units)
Full size table

The results of the case study

In this section, the results of the solved case study using the proposed model are presented in order to design a HRC for Tehran. Results represent that six candidate points are selected as central CWs in Qom, Qazvin, Semnan, Karaj, Arak, and Mazandaran and LDCs are selected in 1, 2, 5, 6, 8, 11, 16, 19, 21, 22 points which are shown in Fig. 6.

Fig. 6
figure 6

Selected locations for establishing CWs and LDCs

Full size image

The results of quantity of pre-positioned relief items are summarized in Tables 11 and 12 for CWs and LDCs prior to the occurrence of the disaster.

Table 11 Results of the storage amount of commodities in CWs (103 units)
Full size table
Table 12 Results of the storage amount of commodities in LDCs (103 units)
Full size table

Figure 7 shows the objective function changes (i.e., the HRC costs) versus variations in a unit of transportation costs between relief facilities. It is observed that increasing the total transportation costs between relief facilities results in increasing the HRC cost. Also, Fig. 8 shows the variation of the objective function versus the shortage cost of a deficiency unit. Accordingly, increasing shortage costs will increase the HRC costs. As expected, results are reasonable and represent that the model performance is logical.

Fig. 7
figure 7

Total cost versus changing the unit transportation cost

Full size image
Fig. 8
figure 8

Total cost versus changing the unit shortage cost

Full size image

Managerial insights

Based on the conducted sensitivity analyses, the following managerial insights are presented:

  1. 1.

    Incorporating multi-period planning can enhance the responsiveness of the relief chain in post-disaster because the new information gained can be used for future periods once it is known.

  2. 2.

    Considering lateral transhipment as a strategy among LDCs can decrease the total relief item shortages and enhance the responsiveness of the relief chain.

  3. 3.

    If a decision maker wishes to make a medium trade-off between the total cost of HRC and fairness, it would be a good idea to set a medium value for the confidence level of the constraints which results in obtaining medium values for the total cost of fairness.

  4. 4.

    If a decision maker selects a lower value for the coefficient compromise parameter, the satisfaction degree of SOP model will increase.

  5. 5.

    If a decision maker chooses a higher value for the relative importance of the first objective function (i.e., the total cost of HRC), the satisfaction degree of the SOP model will increase. As a result, choosing lower values for the compromise parameter and higher values for the relative importance of the first objective function can bring about better solutions for the SOP model.

Conclusion

Disasters have negative impacts on individuals and affect millions of people worldwide. Appropriate planning of humanitarian relief chains can reduce these negative impacts. In this paper, a bi-objective two-stage stochastic programming model was presented to design humanitarian relief chains, which brings about maximizing fairness and minimizing the total cost of HRC. The proposed model integrates pre-positioning relief items in pre-disaster and distributing relief items in post-disaster, considering lateral transhipment among LDCs in order to reduce the relief item shortages. We proposed to use reliable and unreliable LDCs while establishing warehouses in the cities.

As the proposed model is bi-objective, TH method was used to solve the model and to obtain its equivalent SOP model. In addition, an efficient possibilistic programming method was adopted to deal with the imprecise input parameters. Imprecise parameters might be scenario-dependent or independent. To show the effectiveness of the developed model, a numerical example and a case study are provided and solved. Numerical experiments showed how the total cost of chain could be reduced in pre- and post-disaster by using lateral transhipment. In addition, sensitivity analyses were conducted to show the effects of varying key parameters. Finally, useful managerial insights are presented based on the conducted sensitivity analyses. It is interesting to extend the proposed model to the perishable relief items. Also, involving disruption risks in roads and last mile distribution and vehicle routing problem can be studied in the future.