Abstract
Certain inventory items are living organisms, for example livestock, and are therefore capable of growing during the replenishment cycle. These items often serve as various saleable food items downstream in supply chains. The purpose of this paper is to develop a lot sizing model for growing items if the supplier of the items offers incremental quantity discounts. A mathematical model is derived to determine the optimal inventory policy which minimises the total inventory cost in both the owned and rented facilities. A solution procedure for solving the model is developed and illustrated through a numerical example. Sensitivity analysis is performed to demonstrate the response of the order quantity and total costs to some key input parameters. Incremental quantity discounts result in reduced purchasing costs; however, ordering very large quantities has downsides as well. The biggest downsides include the increased holding costs, the risks of running out of storage capacity and item deterioration since the cycle time increases if larger quantities are purchased. Owing to the importance of growing items in the food supply chains, the model presented in this article can be used by procurement and inventory mangers when making purchasing decisions.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Background
Inventory management is concerned with ensuring that the right quantity of goods is available at the right time (i.e. when customers demand the goods). The two major decisions in inventory management are the quantity and timing of the orders. These decisions were first addressed by Harris (1913). Harris proposed the model popularly referred to as the economic order quantity (EOQ) which seeks to balance the fixed cost of ordering items against the variable cost of keeping stock, thereby determining the best quantity to order per procurement cycle.
While the basic EOQ model has found some practical applications, it makes a number of assumptions which do not reflect most real-life inventory systems. In order to model more realistic systems, various researchers have revised the classic EOQ model by relaxing the model assumptions in some ways (Holmbom and Segerstedt 2014). In an attempt to create a new variant of the EOQ model, this paper proposes an inventory system where the items being ordered grow during the course of the inventory replenishment cycle, and the vendor offers incremental quantity discount.
Literature review
Growing items
Rezaei (2014) was the first researcher known to have incorporated item growth into inventory theory by developing an EOQ model for growing items. Rezaei (2014)’s proposed inventory system had two distinct periods, namely growth and consumption periods. During the growth period, the ordered live items are fed and raised until they reach an acceptable weight for sale. The items are then slaughtered and put on sale during the consumption period. The increase in weight experienced by growing items during the growth period is what differentiates them from conventional items, whose weights do not change if they are not consumed or more items are added to the system. In the context of this study, growth is quantified only through an increase in weight.
Zhang et al. (2016) formulated an inventory model for growing items in a carbon-constrained environment. Their model used the same basic assumptions, including the growth and feeding functions, as Rezaei (2014)’s model, and they extended that model by assuming that the company under study operates in a country where carbon taxes are legislated. The carbon tax is based on the amount of emissions released into the atmosphere as a result of the company's inventory holding, ordering and transportation activities.
Building on Rezaei (2014)’s work, Nobil et al. (2018) studied an inventory system for growing items where shortages are allowed and fully backordered. The model presented by Nobil et al. (2018) differed from Rezaei (2014)’s model in two ways. Firstly, in the former, shortages are allowed and fully backordered, and secondly, the growth function of the items was approximated by a linear function in former model as opposed to using Richards (1959)’s growth curve as was the case in the latter.
Sebatjane and Adetunji (2018) extended Rezaei (2014)’s model by incorporating item quality. Their model was formulated under the assumption that a certain proportion of the ordered growing items is of inferior quality. In addition, this model investigated three different growth functions, namely logistic, linear and split linear.
Incremental quantity discounts
EOQ models with quantity discounts were first proposed by Hadley and Whitin (1963). Quantity discounts are usually offered by suppliers as a means of encouraging buyers to purchase larger volumes. In inventory theory, suppliers usually offer one of two types of quantity discounts. These are all-units quantity discounts, which result in reduced purchasing cost for the entire order if the quantity ordered is above a particular quantity called the break point; and incremental quantity discounts where the reduced purchasing cost only applies to items bought above the break point.
Lal and Staelin (1984) studied an integrated vendor–buyer inventory system taking into account incremental quantity discounts and pricing policies. The aim of their model was to determine the buyer’s order quantity and the optimal price the vendor should charge in order to minimise total system costs.
Most inventory models which consider incremental quantity discounts assume that demand is deterministic. This is seldom true in most real-life inventory systems. This prompted Abad (1988) to develop inventory models with incremental quantity discounts under two non-constant demand patterns, namely constant-price elasticity and linear demand functions.
Guder et al. (1994) relaxed two assumptions in the basic EOQ model with incremental quantity discounts to create a new model. As opposed to the basic model which considers only one type of item, their model considered multiple items. Secondly, they assumed that there is a capacity limit on the number of items that can be ordered.
When discounts are taken into account during the modelling of inventory systems, they are considered to be offered only on the basis of purchasing quantity discounts. This changed when Tersine et al. (1995) developed an inventory model which considered both quantity and freight volume discounts. They studied an inventory system which considers a company which is offered incremental and all-units discounts based on the quantity of stock ordered. Furthermore, the company’s logistics provider offers freight discounts based on the amount of stock transported from the supplier to the company.
Rubin and Benton (2003) studied an integrated vendor–buyer inventory system with multiple items, incremental quantity discounts and full backordering of shortages. In addition, constraints on the available storage space and budget were also taken into account.
Haksever and Moussourakis (2008) formulated a multi-item inventory model with incremental quantity discounts taking into account a number of constraints, including maximum purchasing cost of each item, maximum number of items of each type that can be ordered and maximum number of items that can be purchased in each price break. The model also investigated whether a common cycle time for all the different types of items could reduce the total costs.
Hosseini et al. (2013) presented a joint pricing and ordering inventory model under stochastic lead times. The authors used genetic algorithm to determine the optimal order quantity and pricing. An extension of this model which considered arbitrage and marketing plans was solved by Ghasemy-Yaghin et al. (2015) using credibility-based fuzzy optimisation.
Lee et al. (2013) studied an integrated vendor–buyer inventory system considering both all-units and incremental quantity discounts. This model was different from vendor–buyer inventory model with quantity discounts because it also took into account supplier selection. The model was aimed at evaluating a number of suppliers who offer different quantity discounts to the buyer, and the EOQ is based on the supplier who offers the best deal (i.e. results in the lowest total system costs).
Zhang et al. (2014) incorporated advance payments to the literature. They formulated an EOQ model under the assumption that the buyer pays for the stock before it is delivered. This situation might occur in cases where the supplier is powerful. In addition to modelling the case of full advance payment, the authors also investigated partial advanced payment (i.e. a portion of the payment can be paid at a later date).
Taleizadeh et al. (2015) developed an inventory model with incremental quantity discounts under two different shortage conditions. In the first case, shortages are considered to be fully backordered (i.e. all the customers are willing to wait for the backordered stock to arrive), and in the second case (partial backordering), it was assumed that some of the customer are not willing to wait for the backordered stock and in this case a lost sales cost is taken into account.
Tamjidzad and Mirohammadi (2015) incorporated stochastic demand and budget constraints to the basic inventory model with incremental quantity discounts. It was assumed that the demand rate follows a Poisson distribution and that the budget allocated to the purchasing stock is limited.
Bohner and Minner (2017) formulated a vendor–buyer inventory model with supplier selection. It was assumed that the buyer has a number of potential supplier offering various types of discounts, including all-units and incremental, for purchasing larger volumes of stock with different purchasing cost structures. Furthermore, all the suppliers had an associated failure risk (i.e. likelihood of not delivering order as promised) and multiple inventory items were considered.
Mohammadivojdan and Geunes (2018) studied the newsvendor problem (i.e. single period inventory model) with multiple vendors and various types of discounts. The model assumed that the vendors offered incremental and all-units discounts for purchasing the items and carload discounts for transporting the items to the buyer. In addition, the capacity of each of the suppliers was assumed to be limited.
A review of literature on inventory management for growing items suggests that incremental quantity discounts have not been incorporated into the EOQ model for growing items. This paper aims to address this gap in the literature by developing an EOQ model for growing items with incremental quantity discounts. A comparison of the proposed inventory system and related published works in the literature is provided in Table 1, which also shows the contributions of this paper to inventory management research for growing items.
Study relevance
Price discount models are important in the food chain. This is because a number of food items like livestock and fish products are greatly influenced by time. It may be necessary to consume the food items within a limited time period (usually the shelf life). This is motivated by the inherent nature of most food items. In addition, most food items are functional products, and for such product categories, profit is usually driven by sales volume rather than margins. This usually means most food items are, therefore, produced in volumes in order to take advantage of economy of scale to drive down the unit cost as a result of the fairly large overhead costs.
This is enough motivation for vendors within this chain to provide quantity discounts in many instances so that the food items are moved away from them to the next level of the supply chain as quickly as possible in order to avoid loses due to spoilage and deterioration.
It has, however, been observed that there seems to have been no study that has considered the implication of marginal discount on the lot sizing policy of growing items. This is probably because growing items models in inventory management is a relatively young area and researchers are just beginning to study it. Also, it is important to focus on incremental discount because all quantity discount is more straightforward with standard algorithm, and hence, more commonly studied than the marginal discount pricing models.
This study seeks to fill this gap as such lot sizing model may be important for the procurement manager in charge of decisions in the supply chain of fresh food items especially because quantity discount is not uncommon in this area.
Organisation
The rest of this paper is organised as follows. Section 2 provides a brief description of the proposed inventory system as well as the notations and assumptions used when formulating the mathematical model. The mathematical formulation of the problem is given in Sect. 3. A numerical example is presented in Sect. 4 to illustrate the proposed solution procedure and to provide managerial insights through a sensitivity analysis. The paper is then concluded in Sect. 5.
Problem definition, assumptions and notations
Problem definition
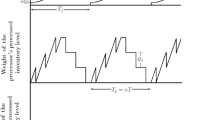
The proposed inventory system considers a situation where a company orders a certain number of items which are capable of growing during the course of the inventory planning cycle, for example livestock. The supplier of the newborn items offers the purchasing company incremental quantity discounts over fixed price breaks. Under the incremental quantity discounts pricing structure, the discounted purchasing costs only apply to the incremental quantity. Figure 1 represents the typical behaviour of an inventory system for growing items. In order for growth to occur, the company needs to feed the items. Every replenishment cycle can be divided into two periods, namely the growth and the consumption periods. During the growth period (shown as period t in Fig. 1), ordered newborn items are fed and raised until they grow to a certain target weight. Once the weight of items reaches the target weight, the growth period ends and the items are slaughtered. During the consumption period (shown as period T in Fig. 1), the slaughtered items are kept in stock and sold to market. The company incurs feeding cost during the growth period, and it incurs holding costs for keeping the slaughtered items in stock. All the inventoried items are consumed within the cycle time, T, at which point the items in the next inventory cycle would have completed their growth phase (i.e. the items in the next cycle will have grown to the target weight and are ready for sale). The company wants to determine the optimal number of newborn items to order at the beginning of the growth cycle in order to minimise total inventory costs (i.e. the sum of the purchasing, setup, feeding and holding costs).
The company needs to determine the optimal number of live newborn items to order at the beginning of a growing cycle and the frequency of placing orders which minimises the total cost (i.e. the sum of the setup, purchasing, feeding and holding costs). The proposed inventory system is studied as a cost minimisation problem, with the total cost being the objective function, and the cycle time (and the order quantity) as the decision variable(s)—since both are jointly determined.
Assumptions
The following assumptions are made when formulating the mathematical model:
-
The ordered items are capable of growing prior to being slaughtered.
-
A single type of item is considered.
-
Feeding costs are incurred for feeding and growing the items during the growth period. These costs are proportional to the weight gained by the items.
-
Holding costs are incurred for the duration of the consumption period.
-
The supplier of the live newborn items offers incremental quantity discounts.
-
Demand is a deterministic constant.
Notations
The notations employed in the formulation of the mathematical model are given in Table 2.
Model formulation
Mathematical model
When a new growing cycle begins, a company purchases Y newborn items, each weighing \(w_0\), which are capable of growing during the replenishment cycle. The total weight of the inventory at this point, \(Q_0\), is determined by multiplying the weight of each of the items by the number of items ordered (i.e. \(Q_0=Yw_0\)). The company feeds the items and they grow to a target weight of \(w_1\). This marks the end of the growth period, and at this point the items are slaughtered. The total weight of the inventory at the time of slaughter is \(Q_1=Yw_1\). The behaviour of the inventory system over time is depicted in Fig. 1. As a way of encouraging larger order sizes, the company’s supplier offers incremental quantity discounts. The discount cost structure is
where Y represents the number of newborn items purchased and \(y_1\), \(y_2\),...,\(y_m\) represent the order quantities at which the unit purchasing cost changes (i.e. the price breaks).
Growth and consumption occur over the periods t and T, respectively, and hence, the company incurs feeding and holding over those respective time periods. The demand rate, D, and the weight of the inventory level at the beginning of the consumption period, \(Q_1=Yw_1\), are used to determine the cycle time as
Item growth follows a pattern which can be represented by four stages. In the first stage, which occurs when a new growth cycle begins, the items experience slower growth. The second stage is characterised by faster growth, while in the third stage, growth is slower as the items approach maturity. In the final stage, the items are fully matured and they have reached peak weight and they do not experience considerable weight gains. This pattern of growth, common in most growing items and depicted by Fig. 1, can be represented by the logistic function (Hossein-Zadeh and Golshani 2016). The logistic growth function relates the weight of items with time. It has three parameters, denoted by \(\alpha\), \(\beta\) and \(\lambda\), which represent the asymptotic weight of the items, the integration constant and the exponential growth rate, respectively. The weight of the items as a function of time is given by
The items are slaughtered when their weight reaches the target weight (i.e. \(w_1\)) following the conclusion of the growth period t. From Eq. (2), the duration of the growth period (i.e. the slaughter age) is determined as
Purchasing cost per unit time
Define \(y_1=0,y_2,\ldots ,y_j,y_{j+1},\ldots ,y_m\) as the order quantities at which the purchase cost per weight unit changes and there are m such changes, called price breaks. When a supplier offers incremental quantity discounts, the purchasing cost per weight unit, \(p_j\), is the same for all Y values in \([y_j,y_{j+1})\). The purchasing cost per weight unit decreases from one price break to the next (i.e. \(p_1>p_2>\cdots>p_j>p_{j+1}>\cdots >p_m\)).
Let Y be in the jth price break (i.e. \(y_j\le Y<y_{j+1}\)). The purchasing cost per cycle for Y items, each weighing \(w_0\), in this price break is given by
Define \(R_j\) as the sum of the terms in Eq. (4) which are independent of Y, and thus
Equation (4) can be rewritten as
Dividing Eq. (6) by the cycle time, as given in Eq. (1), yields an expression for the average unit purchasing cost per unit time, denoted by PCU, as
Food procurement cost per unit time
The feeding cost per cycle is computed as the product of the number of items to be fed, the feeding cost per weight unit and the area under the growth/feeding period as given in Fig. 1. Thus,
Substituting Eq. (2) into Eq. (8) yields
Dividing Eq. (9) by the cycle time, as given in Eq. (1), yields an expression for the feeding cost per unit time, FCU, given by
Setup cost per unit time
Every time the company places an order for live newborn items, it incurs a cost of K for setting up the growth and feeding facilities. The setup cost per cycle is thus
The setup cost per unit time, SCU, is determined by dividing the setup cost by the cycle time as
Holding cost per unit time
The holding cost per cycle, HC, is computed from Fig. 1 using the area under the consumption period (since the holding cost is incurred for the slaughtered inventory) and thus
The holding cost per unit time, HCU, is computed by dividing Eq. (13) by Eq. (1), hence
Total cost per unit time
The total cost per unit time, TCU, is computed by summing Eqs. (7), (10), (12) and (14) and therefore
Through rearranging the terms, Eq. (15) becomes
Model constraints
Two constraints ensure the feasibility of the proposed inventory system. The first constraint ensures that the items are ready for consumption at the required time. The second constraint ensures the feasibility of the optimal order quantity, meaning that the optimal quantity \(Y_j\) is acceptable for each price break region and must fall between the price breaks \(y_j\) and \(y_{j+1}\).
Constraint 1 In order to ensure that the slaughtered items are ready for sale during the consumption phase, the duration of the growth phase should be less than or equal to the duration of the consumption phase. This results in a constraint (on the duration of the consumption phase) being formulated as
Through substituting t from Eq. (3), Eq. (17) becomes
Constraint 2 In order to ensure that the order quantity determined falls within the range of the given price break, a constraint on the order quantity is formulated as
Solution
Determination of the decision variables
The optimal order quantity for the proposed inventory system is determined by setting the first derivative of the objective function to zero. Thus,
The optimal cycle time is computed by substituting Eq. (20) into Eq. (1), and the result is
Proof of convexity of the objective function
The second derivative of the objective function, as given in Eq. (16), yields
To prove that Eq. (22) is positive definite, it suffices to show that \(R_j-p_jw_0y_j\) cannot be negative. This would be done using the principle of mathematical induction.
From Eq. (6), total purchasing cost for any range \(y_{j-1}\le Y \le y_j\) is governed by
where also \(R_j\) is defined in Eq. (5). \(R_j\) can be rewritten as
Hence, the total purchasing cost, PC, can also be rewritten as
Equation (24) can be rewritten to look like Eq. (22) as
Equation (25) is the general form of the purchasing cost function for \(j\ge 2\).
Base case is \(j=2\).
By definition, \(R_1=0\) and \(y_1=0\), hence
Observe also that \(p_1>p_2\), since by definition \(p_{j-1}>p_j \forall j\). Hence, all terms are zero or positive. Therefore, the nonnegativity holds for the base case.
Let us assume that the case holds for any j, then we show that it holds for any \(j+1\) for which \(y_j\le Y \le y_{j+1}\) is true, then
Equation (27) can be rewritten for the range \(j+1\) as
which is the desired form. So, the function also holds and this proves the nonnegativity of Eq. (22) which is the Hessian function of the total cost function.
Computational algorithm
The solution to the EOQ model for growing items with incremental quantity discounts is determined using the following algorithm:
-
Step 1 Compute Y for each j using Eq. (20). Denote this as \(Y_j\).
-
Step 2 Check each \(Y_j\)’s feasibility. They are feasible if \(y_j\le Y < y_{j+1}\). Infeasible \(Y_j\)’s are disregarded and only the feasible ones proceed to Step 3.
-
Step 3 For each feasible Y, compute the corresponding T using Eq. (21).
-
Step 4 Check the feasibility of each computed \(Y_j\) with regard to the cycle time. Each \(Y_j\) is feasible if \(T\ge t\). Infeasible \(Y_j\)’s are disregarded and only the feasible ones proceed to Step 5.
-
Step 5 Compute TCU using Eq. (16) for all the feasible \(Y_j\)’s. The \(Y_j\) value which results in the lowest TCU is the EOQ.
-
Step 6 End.
Numerical results
Numerical example
The proposed inventory system is applied to a numerical example which considers a company which purchases newborn day-old (i.e. newborn) lambs, feeds/grows them until they reach a targeted weight and then puts them on sale. The following parameters are utilised to analyse the proposed inventory system:
-
Demand rate, D = 100,000 kg/year
-
Setup cost, K = 75,000 ZAR/cycle
-
Holding cost, h = 10 ZAR/kg/year
-
Feeding cost, c = 2.5 ZAR/kg/year
-
Approximated weight of newborn lamb, \(w_0\) = 6.8 kg/sheep
-
Approximated weight of sheep at the time of slaughtering, \(w_1\) = 35 kg/sheep
-
Asymptotic weight, \(\alpha\) = 41 kg
-
Integration constant, \(\beta\) = 5
-
Exponential growth rate, \(\lambda\) = 7.3 /year
The purchasing cost structure is given in Table 3.
The proposed solution algorithm is illustrated by applying it to the numerical example. The procedure is outlined as follows:
-
Step 1 Compute Y for each j using Eq. (20).
$$\begin{aligned} R_1= & {} 0\\ R_2= & {} 25(1001-0)6.8=170170\\ R_3= & {} 34 170+20(1501-1001)6.8=238170\\ R_4= & {} 47 770+0.021(2001-1501)6.8=289170\\ Y_1= & {} \sqrt{\frac{2\left( 0-25\times 6.8\times 0+75 000\right) 100000}{10\times {35}^2}}=1106.6\\ Y_2= & {} \sqrt{\frac{2\left( 170170-20\times 6.8\times 201+75 000\right) 100000}{10\times {35}^2}}=1334.2\\ Y_3= & {} \sqrt{\frac{2\left( 238170-15\times 6.8\times 301+75 000\right) 100000}{10\times {35}^2}}=1616.6\\ Y_4= & {} \sqrt{\frac{2\left( 289170-10\times 6.8\times 401+75 000\right) 100000}{10\times {35}^2}}=1929.8\\ \end{aligned}$$ -
Step 2 Check each \(Y_j\)’s feasibility. They are feasible if \(y_j\le Y < y_{j+1}\). Infeasible \(Y_j\)’s are disregarded and only the feasible ones proceed to Step 3.
$$\begin{aligned}&0\le Y_1=1106.6 \not< 1001\\&1001\le Y_2=1334.2< 1501\\&1501\le Y_3=1616.6 < 2001\\&2001\not \le Y_4=1929.8 \end{aligned}$$Thus \(Y_2\) and \(Y_3\) are feasible.
-
Step 3 For each feasible Y, compute the corresponding T using Eq. (21).
$$\begin{aligned} T_2= & {} \sqrt{\frac{2\left( 170170-20\times 6.8\times 201+75 000\right) 100000}{10\times {100000}^2}}=0.4670\\ T_3= & {} \sqrt{\frac{2\left( 238170-15\times 6.8\times 301+75 000\right) 100000}{10\times {100000}^2}}=0.5658 \end{aligned}$$ -
Step 4 Check the feasibility of each computed \(Y_j\) with regard to the cycle time. Each \(Y_j\) is feasible if \(T\ge t\). Infeasible \(Y_j\)’s are disregarded and only the feasible ones proceed to Step 5.
$$t=-\frac{\ln \left[ \frac{1}{5}\left( \frac{41}{35}-1\right) \right] }{7.3}=0.4621$$Thus \(Y_2\) and \(Y_3\) are feasible since \(T_2\ge t\) and \(T_3\ge t\).
-
Step 5 Compute TCU using Eq. (16) for all the feasible \(Y_j\)’s. The \(Y_j\) value which results in the lowest TCU is the EOQ.
$$\begin{aligned} {\mathrm{TCU}}_2= & {} \,\frac{1001\times 6.8\times 100000}{35} +\frac{100000}{1334.2\times 35}\\&\times \left[ 170170-1001\times 6.8\times 1001+75000\right] \\&+\,10\left[ \frac{1334.2\times 35}{2}\right] +\frac{2.5\times 100000\times 41}{35}\left\{ 0.4621\right. \\&\left. +\,\frac{1}{7.3}\left[ \ln {\left( 1+5 {\mathrm{e}}^{-7.3 \times 0.4621}\right) }-\ln {(1+5)}\right] \right\} \\= & {}\, 925332.82\\ {\mathrm{TCU}}_3= & {} \,\frac{1501\times 6.8\times 100000}{35} +\frac{100000}{1616.6\times 35}\\&\times \left[ 238170-1501\times 6.8\times 1501+75000\right] \\&+\,10\left[ \frac{1616.6\times 35}{2}\right] +\frac{2.5\times 100000\times 41}{35}\left\{ 0.4621\right. \\&\left. +\,\frac{1}{7.3}\left[ \ln {\left( 1+5 {\mathrm{e}}^{-7.3 \times 0.4621}\right) }-\ln {(1+5)}\right] \right\} \\= & {} \,927018.08 \end{aligned}$$\(Y^*=Y_2\) since \({\mathrm{TCU}}_2<{\mathrm{TCU}}_3\).
-
Step 6 End.
Based on the results of the numerical example, some of which are summarised in Table 4, the company should place an order for 1335-day-old lambs at the beginning of each cycle. This order quantity lies in the 1501–2001 price break, and therefore, the company will pay 25, 20 and 15 ZAR per kg for the first 1000, the next 500 and the remaining 117, respectively. Based on the targeted slaughter weight, the items should be grown for 0.4621 years (169 days). Orders should be replenished every 0.4670 years (171 days). Following this optimal inventory policy, the company will incur a total cost of 925,332.83 ZAR per year.
Figure 2 shows the response of the total cost function to different order quantities. There are four curves corresponding to the four price breaks. Each curve is valid for a given order quantity interval. The valid interval for each curve is represented by a solid line.
Comparison with the basic EOQ for growing items (i.e. without incremental quantity discounts)
In order to investigate the cost savings, if any, resulting from a supplier offering incremental quantity discounts, the proposed model is compared with the basic EOQ model for growing items as proposed by Rezaei (2014). Since Rezaei (2014) used a different growth function than the one used in this paper, the feeding costs between the two models will be different. To counter this, Rezaei (2014)’s model is restated using the same growth function as used in this paper. The total cost per unit time in the base model (i.e. without incremental quantity discounts) equals
and the EOQ is given by
The parameters used for the numerical example are applied to the base model in order to achieve a fair comparison, and the results are presented in Table 5.
Although the quantity of newborn items ordered at the beginning of a cycle increased by \(2.1\%\) as a result of incremental quantity discounts, the total cost decreased by \(1.9\%\). The effect of incremental discounts on the holding cost costs was negative (i.e. they increased), and it was positive on both the setup and the purchasing costs. Overall, having a supplier who offers incremental quantity discounts reduced the total costs of managing inventory, and therefore, quantity discounts are a viable alternative for reducing procurement costs.
Sensitivity analysis
Sensitivity analyses are performed on the major input parameters in order to investigate their impacts on the decision variables and to provide managerial insights for improving inventory management.
Increasing the setup cost increases both the EOQ and the total costs, as shown in Table 6. The EOQ shifted into different price breaks as a result of the changes to the setup costs. Managers can offset the increase in the total cost by purchasing larger quantities (i.e. placing orders less frequently). However, this should be done in moderation because if too much stock is ordered the holding cost will increase and this will lead to an increase in total costs.
Increasing the holding cost increases the total cost and reduces the EOQ, as shown in Table 7. The effect of decreasing the holding cost on the EOQ is substantial because the EOQ shifts into different price breaks. As a result of the shift in price breaks, the total costs decrease because of the lower purchasing cost per unit weight in the new price break. This shift into a lower price breaks offsets the increased holding costs (due to the increase in the EOQ as a result of ordering larger quantities).
Table 8 shows that the total costs increase with the increase in feeding costs, whereas the EOQ is not affected by changes in the feeding cost. The feeding is essentially the cost of procuring feedstock for the items, and it is very difficult for managers to reduce this cost since it is set by the feedstock suppliers. Nonetheless, managers can reduce this cost through procuring larger volumes (of the items’ feedstock) which normally have discounted pricing.
Increasing the lower bound for the order quantity in each price break increases both the EOQ and the total costs, as shown in Table 9. The changes to the total costs are minimal most likely because the EOQ remains in the same price break. Managers do not have much control over the discount quantity structure as it is determined by the supplier, but if it happens that the suppliers reduce the lower bounds on the order quantities in each price break it is beneficial for managers to order less items.
Table 10 shows that increasing the purchasing cost decreases the EOQ and increases the total costs. In fact, the EOQ shifts into different price breaks, and consequently, the effect on the average cost is significant as well. By reducing purchasing costs, managers can save significantly on their average total costs by ordering larger quantities. While this will result in an increase in the holding cost, the savings which result from lower purchasing cost more outweigh the impact of the increased holding cost.
Conclusion
This paper combined the concepts behind the basic EOQ model for growing items and the EOQ model for conventional items under incremental quantity discounts in an attempt to formulate a new EOQ model. The biggest contribution made by this paper to the literature on inventory modelling for growing items is the incorporation of incremental quantity discounts. This addition to literature is important because suppliers often offer discounts for purchasing larger volumes of stock. The cost structure, in terms of both the purchasing cost in each price break and the lower bounds for the order quantities in each price break, was shown to have a significant impact on the order quantity and the average total cost of managing inventory. This indicates that incremental quantity discounts have considerable impact on inventory management and this presents operations managers with opportunities to reduce costs through better procurement practices. However, certain factors need to be considered when purchasing larger volumes, namely the available storage space, deterioration and the available procurement budget.
The proposed inventory system did not take into account issues like deterioration, growing and storage facility capacity and budget constraints. These factors are important when purchasing larger quantities because in certain instances, management might be forced to lease extra capacity if they purchased more items than can be grown and stored in their owned facilities. This will certainly increase costs and negate the benefit of purchasing larger quantities. The model presented in this paper can be extended to include capacity limits, budget limits, among other popular EOQ extensions. Deterioration becomes increasingly important if larger quantities are purchased, extensions which account for deterioration during the consumption period are another possible area for future research as they represent more realistic inventory systems.
References
Abad P (1988) Joint price and lot size determination when supplier offers incremental quantity discounts. J Oper Res Soc 39:603–607
Bohner C, Minner S (2017) Supplier selection under failure risk, quantity and business volume discounts. Comput Ind Eng 104:145–155
Ghasemy-Yaghin R, Ghomi Fatemi S, Torabi S (2015) A hybrid credibility-based fuzzy multiple objective optimisation to differential pricing and inventory policies with arbitrage consideration. Int J Syst Sci 46:2628–2639
Guder F, Zydiak J, Chaudhry S (1994) Capacitated multiple item ordering with incremental quantity discounts. J Oper Res Soc 45:1197–1205
Hadley G, Whitin T (1963) Analysis of inventory systems. Prentice-Hall, Upper Saddle River
Haksever C, Moussourakis J (2008) Joint price and lot size determination when supplier offers incremental quantity discounts. Eur J Oper Res 184:930–945
Harris F (1913) How many parts to make at once. Fact Mag Manag 10:135–136
Holmbom M, Segerstedt A (2014) Economic order quantities in production: from Harris to economic lot scheduling problems. Int J Prod Econ 155:82–90
Hossein-Zadeh N, Golshani M (2016) Comparison of non-linear models to describe growth of Iranian Guilan sheep. Revista Colombiana de Ciencias Pecuarias 29:199–209
Hosseini Z, Ghasemy-Yaghin R, Esmaeli M (2013) A multiple objective approach for joint ordering and price planning problem with stochastic lead times. J Ind Eng Int 9:1–14
Lal R, Staelin R (1984) An approach for developing an optimal discount pricing policy. Manag Sci 30:1524–1529
Lee A, Kang H, Hong W (2013) An integrated model for lot sizing with supplier selection and quantity discounts. Appl Math Model 37:4733–4746
Mohammadivojdan R, Geunes J (2018) The newsvendor problem with capacitated suppliers and quantity discounts. Eur J Oper Res 271:109–119
Nobil A, Sedigh A, Cardenas-Barron L (2018) A generalized economic order quantity inventory model with shortage: case study of a poultry farmer. Arab J Sci Eng. https://doi.org/10.1007/s13369-018-3322-z
Rezaei J (2014) Economic order quantity for growing items. Int J Prod Econ 155:109–113
Richards F (1959) A flexible growth function for empirical use. J Exp Bot 10:290–301
Rubin P, Benton W (2003) A generalized framework for quantity discount pricing schedules. Decis Sci 34:173–188
Sebatjane M, Adetunji O (2018) Economic order quantity model for growing items with imperfect quality. Oper Res Perspect. https://doi.org/10.1016/j.orp.2018.11.004
Taleizadeh A, Stojkovska I, Pentico D (2015) An economic order quantity model with partial backordering and incremental discount. Comput Ind Eng 82:21–32
Tamjidzad S, Mirohammadi S (2015) Optimal (\(r, q\)) policy in a stochastic inventory system with limited resource under incremental quantity discount. Comput Ind Eng 103:59–69
Tersine R, Barman S, Toelle R (1995) Composite lot sizing with quantity and freight discounts. Comput Ind Eng 28:107–122
Zhang Q, Tsao Y, Chen T (2014) Economic order quantity under advance payment. Appl Math Model 38:5910–5921
Zhang Y, Li L, Tian X, Feng C (2016) Inventory management research for growing items with carbon-constrained. In: Chinese control conference, pp 9588–9593
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Sebatjane, M., Adetunji, O. Economic order quantity model for growing items with incremental quantity discounts. J Ind Eng Int 15, 545–556 (2019). https://doi.org/10.1007/s40092-019-0311-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40092-019-0311-0