Cooperative aggregate production planning: a game theory approach

Abstract

Production costs in general, and workforce and inventory costs in particular, constitute a large fraction of the operating costs of many manufacturing plants. We introduce cooperative aggregate production planning as a way to decrease these costs. That is, when production planning of two or more facilities (plants) is integrated, they can interchange workforce and products inventory; thus, their product demands can be satisfied at lower cost. This paper quantifies the cost saving and synergy of different coalitions of production plants by a new linear model for cooperative aggregate planning problem. The developed approach is explicated with a numerical example in which inventory and workforce levels of different coalitions of facilities are evaluated. Afterward, a key question would be how the cost saving of a coalition should be divided among members. We tackle the problem using different methods of cooperative game theory. These methods are implemented in the numerical example to gain an insight into properties of the corresponding game results.

Introduction

In the real world, production plants (manufacturing facilities) often should take decisions regarding levels of inventory capacity, employment, and production levels, before demand is known. Aggregate production planning (APP) addresses the question, “How should a company best use the equipment and facilities that it currently has?” (Chopra and Meindl 2007). Accurate demand forecast and supply constraints are two key important inputs of APP. The goal of APP indeed is satisfying demands over a planning horizon with the minimum cost. APP, however, is an extra-firm operational problem rather than intra-firm one. Thus, modern production plans are viewed as a set of collaborative agreements between manufacturers’ network (Argoneto et al. 2008).

Aggregating production plan (APP) considers minimizing costs, levels of inventory, alteration of human resource level, wage of additional work for production, changes in production rate, number of machine start-up, idle time of plant and work force and maximizing revenue and costumer services in high priority (Baykasoglu 2001).

Traditionally, much of APP is concentrated on a single company and may not always be focused on the cooperation among a set of production plants. Currently, many types of products are manufactured by cooperation of several producers. This means that most of plants use the various site production facilities in order to make economic competitive advantages. It is possible that particular segment of a family product is produced in different sites. The events like defection of device, the absence of operator, lack of expert work force can be of the reasons of allocation to different sites or plants. For example, agricultural production cooperatives, also called farmers co-ops, are activities in which a group of farmers that pool resources to improve their productivity and responsiveness to market demands (Cobia 1989). Several successful benchmarks of agricultural production cooperatives exist around the world such as Longo Mai cooperatives, Kibbutzim and Nicaraguan production cooperatives (Ruben and Lerman 2005).

Numerous reasons exist that lead production plants to work together such as different operational conventions, globalization of markets are geographically dispersed and locally specific constraints (like capacity), prevention from wasting of investment (inventory, production, maintenance and work force), legislation constraints (worker), access to experienced labor force (regarding high-tech products), instant and economical communications, competition pressures of other producers and risk reduction (Kogan and Tapiero 2007). Cooperation among plants enables them to coordinate their production and maximize their profits (Barron 2013). This study attempts to address the following research questions:

• How can cooperative aggregate production planning (Co-APP) be formulated?

• How should benefits of cooperation of Co-APP be fairly distributed?

Cooperative game theory (CGT) primarily deals with coalition of players that coordinate their activities to enjoy the synergy of cooperation (Barron 2013; Branzei et al. 2008). CGT establishes a mathematical framework for fair and reasonable allocations of the cooperation benefits to each member of a coalition. By considering the production plants as a set of players, we first quantify the synergy of the Co-APP; then, we use CGT methods to assign the cooperation benefits to the companies. The difference of cooperation in this study with multi-site studies is in terms of superadditivity feature (Asgharpour 2014) which is defined when two production plants make a cooperative coalition. In such relationship, for each members of coalition it is feasible to earn minimum effectiveness that each plant gained before arranging the coalition. However, in most of the time, the earned benefits after cooperation are more than the benefit of cooperation in multi-model. Indeed in multi-site model, the features of each site optimize independently. However, cooperation of the sites causes the total revenue that is greater than or equal to independent revenue. In conventional approach of optimization, the problem will be optimized by different methods. In case of multiple problems, each of them has identical optimum solution. However in game theory’s problem, for each player there is a distinct optimization problem which is solved concurrently. The strategy of each player will affect both the other players’ problem and the final optimum solution simultaneously.

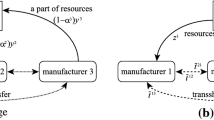
This study is a specific model of multi-site APP. The most important distinctions of the multi-site structure (a) with CO_APP (b) in Fig. 1 are as follows:

• The inventory on each site in the multi-site belongs to the same site, but in cooperation there is a possibility of replacement of inventory between them.

• The workforces in each site in the multi-site belong to the same site, but in cooperation there is the possibility of replacing the workers between them.

Fig. 1

The distinct framework of the multi-site APP and CO-APP

Therefore, these differences, while reducing costs, increase job security and workers’ skills and allow factories to use higher-tech equipment. The plants are moving with the maximum use of multi-skill workforce and minimizing inventory for lean production.

The reminder of the paper is organized as follows. “Literature review” section reviews the related literature. “Prerequisites and assumptions” section describes the prerequisites and assumptions. “Mathematical programming approaches” section presents the formulations of basic APP and Co-APP. Cost-saving opportunities of Co-APP are also examined using an illustrative example. “Collaborative frameworks for Co-APP” section discusses the methods of CGT for allocating the cost savings to production plants. “Conclusion and further research” section provides the conclusions and several directions for future research.

Literature review

Survey of aggregate production planning and its modeling approaches

Holt et al. (1955) introduced the concept of APP. From the mid-1950s, a number of researchers have studied APP, its modeling techniques and the related applications. Nam and Logendran (1992) presented a detailed survey about APP models and methodologies.

Some researchers focused on application of APP in multi-site environments. In the category of multi-site APP models, various solution approaches exist to tackle the real-world industrial planning problems including robust optimization (Mirzapour Al-E-Hashem et al. 2011), simple linear programming (Kanyalkar and Adil 2005; Proto and de Mesquita 2006; Wu and Williams 2003), stochastic programming (Leung et al. 2003b, 2006) and goal programming (Kanyalkar and Adil 2007; Leung et al. 2003a; Torabi and Hassini 2009). Kanyalkar and Adil (2005) generated a linear programming model for a multi-plant aggregate production and dynamic distribution problem. Proto and de Mesquita (2006) developed a mixed-integer linear programming model to deal with an aggregate production and distribution planning problem considering multiple production and distribution sites for application in cement industry. Utilizing time-staged linear programming technique, Wu and Williams (2003) analyzed multi-site APP problem. Leung et al. (2006) suggested a stochastic programming approach to consider multi-site APP under an uncertain environment. Leung et al. (2003b) addressed a multi-site APP problem employing a stochastic model under uncertain environment for application in a multinational lingerie company. Kanyalkar and Adil (2007) recommended a mixed-integer linear goal programming model to solve an aggregate multi-item, multi-plant procurement, production and distribution problem. Leung et al. (2003a) developed a goal programming approach to handle the problem of APP for a multinational lingerie company with multiple manufacturing factories.

Several groups of researchers have considered supply chain-oriented APP problems. Several solution techniques have been utilized by the researchers to manage practical APP problems in a supply chain network like robust optimization (Kanyalkar and Adil 2010; Mirzapour Al-E-Hashem et al. 2011; Niknamfar et al. 2014), simple linear programming (Mirzapour Al-e-hashem et al. 2012), stochastic programming (Mirzapour Al-e-hashem et al. 2013), fuzzy programming (Aliev et al. 2007; Paksoy et al. 2010; Pathak and Sarkar 2012; Torabi and Hassini 2009; Yaghin et al. 2012), bi-level programming, system dynamics approach (Mendoza et al. 2014) and heuristic algorithm (Pal et al. 2011). Kanyalkar and Adil (2010) presented a robust optimization methodology for aggregate planning of a multi-site procurement–production–distribution system. Mirzapour Al-E-Hashem et al. (2011) considered a robust multi-objective mixed-integer nonlinear programming model to tackle a APP problem in a supply chain under uncertainty. Niknamfar et al. (2014) developed a robust optimization method for an aggregate production–distribution planning in a three-level supply chain. Mirzapour Al-e-hashem et al. (2012) suggested a mixed-integer linear programming model to solve an aggregate production–distribution planning problem in a green supply chain. Mirzapour Al-e-hashem et al. (2013) proposed a stochastic programming approach to solve a multi-period multi-product multi-site APP problem in a green supply chain for a medium-term planning horizon under the assumption of demand uncertainty. Aliev et al. (2007) provided a genetic algorithm solution based on fuzzy programming for aggregate production–distribution planning in a supply chain. Paksoy et al. (2010) modeled a supply chain network design problem with fuzzy demand and capacities in production environment using the concept of aggregate production–distribution planning. Employing a fuzzy mixed-integer programming model, Pathak and Sarkar (2012) dealt with a supply chain network design problem in the field of aggregate production–distribution planning. Considering an interactive fuzzy goal programming approach, Torabi and Hassini (2009) tackled a multi-objective, multi-site production planning problem by integrating procurement and distribution plans in a multi-echelon supply chain network. Yaghin et al. (2012) utilized a hybrid fuzzy multiple objective technique to consolidate markdown pricing planning and APP in a two echelon supply chain. Mendoza et al. (2014) recommended a novel method to evaluate different APP strategies in a manpower-intensive supply chain considering system dynamics approach. Applying swarm-based heuristics, Pal et al. (2011) modeled a problem of aggregate purchasing, manufacturing and shipment planning for a supply chain extending over three echelons. Gholamian et al (2015) use the mixed-integer linear programming/fuzzy optimization for solution fuzzy-mathematical model to incorporate four objectives. Making trade-off between production costs and green principles seen in research Entezaminia et al. (2016), Jing et al. (2016) use the GA for solution multi-site problem.

In review papers on subject of aggregated production planning, the whole aspects are categorized (Cheraghalikhania et al (2018)). In Table 1, we present the summary of multiple APP researches. Also, we provide another summary about objective function in Table 2.

Table 1 Summary of conducted research on subject of multiple APP

Table 2 APP models classification based on the type of data and the number of objective functions

Survey of cooperative game-theoretic models

The methods of CGT can be used for assigning the cost saving to cooperating companies. Charles and Hansen (2008) proposed a theoretic cost-saving framework based on CGT for global cost minimization and cost assignment in an enterprise network. They proved that under classical concave cost functions for all participants, the cost allocation computed by the activity-based costing method is rational and stable. Frisk et al. (2010) evaluated cost-saving opportunity of cooperation among several forest companies in Sweden. They used the methods of CGT to fairly distribute total cost saving among participants. Lozano et al. (2013) adopted CGT to recognize the cost-saving opportunities of different logistic companies that may be achieved when they merge their transportation requirements. They suggested a linear transportation problem to quantify the cost savings of the possible coalitions. Hennet and Mahjoub (2010) provided convincing interpretations of fair sharing of profit in a supply network formation. Hafezalkotob and Makui (2015) studied cooperation benefits of owners of logistic network under capacity uncertainty. They showed that the flow of logistic network becomes more reliable when the owners make coalitions. They also presented a number of CGT methods to allocate benefits of cooperation to the owners. Similarly, Naseri and Hafezalkotob (2016) evaluated cooperative network flow problem with pricing decisions. They investigated shapely value, τ-value, core center and minmax core methods to allocate the extra benefits of cooperation and compared the results. By considering total supply chain inventory costs, Mohammaditabar et al. (2016) used CGT to evaluate decentralized supplier selection problem between a buyer and a set of supplier. They found that a stable solution for the cooperative model exists that yields total supply chain cost as the centralized model. Zibaei et al. (2016) proposed a mathematical model for a vehicle routing problem that was managed by multi-owners. The cost savings obtained from cooperation among owners were computed, and cooperative game theory methods were presented for allocating the cost savings to the cooperating owners. Fardi et al. (2019) developed a mixed-integer programming (MIP) formulation for a cooperative inventory routing problem (Co-IRP) considering uncertainty, and the methods of CGT can be used for assigning the cost saving to cooperating companies. Baogui and Minghe (2017) developed a differential oligopoly game, and the impact of oligopoly which product prices are sticky and water right trading occurs is used to study. Cellini and Lambertini (2007) investigate a dynamic oligopoly game where goods are differentiated and prices are sticky, while profits are increasing in a larger level of production and the speed of price adjustment. Heidari Gharehbolagh et al. (2017) investigate the model of maximum flow problem in the presence of many unreliable sources with the objective of participating in the game.

In Table 3, we present the summary of the research done with the game method that is ready.

Table 3 The review table of the game theory in research dimensions

Research gap

Reference to conducted literature review, there is lack of study based on aggregate product planning among manufacturing plants and the studies mostly focused on APP in a plant or multi-site that aim to reduce the production cost in terms of labor cost, contractual cost, etc., satisfying the demands (public demands is dividable along sites) or can be executed by upgrading the logistic services such as transportation. Therefor this study tries to reduce the production cost using cooperation and coordination among multi-plants regarding sharing of inventories and workforce to increase the satisfaction of demands (the demands of each plant are independent of the other plants) that eventually would be beneficial for whole plants and facilities, and various costs of production will contribute through them.

The continuous and unnecessary changes of workforce (hiring/firing) applied to previous models, cause some limitations and prohibitions by the governing rules of labor union and increase the cost at the national level (the rules for paying unemployment benefits; more info: Jimeno et al. 2018). In this model, Co-APP with possibility of workforce substitution among plants has advantages like preventing the multitude of recruitment and layoff, enhancement of the job security and reducing the hiring cost and firing’s penalties. On the other hand, training of expert workforce is a time- and cost-consuming task. The substitution of work force in addition to reducing the cost in terms of mentioned items will increase the production efficiency. The substitution of products among the plants in seasonal and emotional demands needs to be answered during the application period, or in cases where production facilities are not capable of producing high capacity due to lack of storage space, increased satisfaction of demand estimation and reduced accumulation capital and production costs and ultimately high profits (win-win games). Prior to commencement of the game, the plant by investigation about benefits of cooperation has the right to choose whether they want to cooperate or not. In multi-site model regarding the cost of implementation such as the overhead cost of establishment, the declining of cooperation was impossible.

The cost saving of Co-APP is quantified by a new mathematical programming model for coalitions of production plants, which indicates the result of cooperation synergy. We propose several methods of CGT to calculate the positive results of saving.

Prerequisites and assumptions

Multi-plants produce substitutable products and satisfy the market demand. The objective function of each production plants is to minimize the total cost incurred while meeting demand during the planning horizon. The cost incurred includes cost of hiring and layoff, cost of regular and overtime labor, and cost of inventory. When the production plants form a coalition, they can cooperatively plan their inventories and workforce. Figure 2 illustrates the Co-APP structure of four plants during the planning horizon.

Fig. 2

The framework of the Co-APP for four plants in the planning horizon

The Co-APP is formulated based on the following assumptions:

Assumption 1

The horizon of production planning is finite and can be characterized by multiple periods of time. The time frameworks of production planning procedure are similar for the production plants.

Assumption 2

Parameters of production planning procedure of all plants are deterministic. Moreover, the forecasts of demands and parameters relating to employment, overtime and inventory levels about all companies are known in advance.

Assumption 3

Mathematical programming models for traditional and Co-APP are formulated based on the linear relationship in input data. We also assume that the plants desire very high level of customer service; thus, all demands of customers should be met. Consequently, revenues obtained over the planning horizon are fixed, and minimizing cost over the planning horizon in the objective function is equivalent to maximizing profit.

Assumption 4

The products of different firms (plants) are fully substitutable. That is, when several production plants form a coalition, the product demand from the coalition can be fulfilled by inventory of each member. Thus, the inventory of the members of a coalition can be managed in a centralized manner.

Assumption 5

We consider cooperation among homogeneous manufacturers. It means that the production process and technologies of plants are similar such that an employee of one plant can work in other plants. This assumption can be especially acceptable in low-tech industries such as brick production, canned fish production. When the production plants join the coalition, they may exchange their workforce to improve their production planning efficiency.

Assumption 6

According to the main assumption of CGT, the utility obtained from Co-APP model is considered as transferable. The simplifying assumption is frequently made in the CGT (Myerson 1991); thus, these games are also called transferable utility games (TUGs).

Mathematical programming approaches

Basic aggregate production planning problem

The APP problem typically determines when to hire and fire, how much inventory to hold, when to use overtime and undertime, and so on such that the cost of the plan becomes minimum. Let us first review the basic linear programming (LP) model of the APP problem. Many LP formulations have been proposed for the APP problem, and we concentrate on a basic formulation. A set of symbols and notations used in the APP formulation are discussed as follows (Jacobs et al. 2011):

t:

the index of time period,

$C_{\text{H}}$:

the cost of hiring a worker,

$C_{\text{F}}$:

the cost of firing a worker,

$C_{\text{W}}$:

the wage cost of a worker in a period,

$C_{\text{R}}$:

the unit production cost per period on regular time,

$C_{\text{O}}$:

the unit production cost per period on overtime,

$C_{\text{I}}$:

the cost per period of carrying one unit of inventory,

H_t:

the number of workers hired in period t,

F_t:

the number of workers fired in period t,

P_t:

the number of units produced on regular time in period t,

O_t:

the number of units produced on overtime in period t,

W_t:

the number of workers employed in period t,

I_t:

the number of units stored in inventory (on-hand inventory) at the end of period t,

D_t:

the number of units of demand in period t,

A₁:

the number of units that one worker can produce in a period on regular time,

A₂:

the maximum number of units that one worker can produce in a period on overtime,

A₃:

the initial workforce level,

A₄:

the initial inventory level,

A₅:

the desired workforce level at the end of the planning horizon,

A₆:

the desired inventory level at the end of each period,

T:

the number of time periods over the planning horizon

Basically, APP integrates the production planning, the workforce planning and the inventories planning as follows (Jacobs et al. 2011):

$$\text{TC} = \hbox{min} \,\,\sum\limits_{t \in T} {\left( {C_{\text{H}} H_{t} + C_{\text{W}} W_{t} + C_{\text{F}} F_{t} + C_{\text{R}} P_{t} + C_{\text{O}} O_{t} + C_{\text{I}} I_{t} } \right)} ,$$

(1)

$${\text{s}} . {\text{t}} .\quad I_{t - 1} + P_{t} + O_{t} - D_{t} = I_{t} ,\quad \forall \,t \in T,$$

(2)

$$P_{t} \le A_{1} \,W_{t} ,\quad \forall \,t \in T,$$

(3)

$$O_{t} \le A_{2} \,W_{t} ,\quad \forall \, \,t \in T,$$

(4)

$$W_{t - 1} + H_{t} - F_{t} = W_{t} ,\quad \forall \,t \in T,$$

(5)

$$H_{t} ,F_{t} ,W_{t} ,O_{t} ,I_{t} \ge 0,\quad \forall \,t \in T,$$

(6)

$$W_{0} = A_{3} ,\quad I_{0} = A_{4} ,\quad W_{T} = A_{5} ,\quad I_{T} = A_{6} .$$

(7)

Objective function (1) minimizes the total costs of hiring, firing, wages, overtime and relative inventory for T periods. Constraint (2) denotes the inventory balance relationship in each period. Constraint (3) ensures that production in regular time does not exceed the maximum allowed production quantity of regular time. Similarly, Constraint (4) limits the overtime production quantity. Constraint (5) represents the workforce balance relationship in each period. Constraint set (7) is initializing conditions.

Cooperative aggregate production planning problem

We now develop a Co-APP problem for a coalition of production plants. Let set K = {1, 2, …, k, …, n} represents the set of plants. The production plants (manufacturing facilities) are also called players, and these terms may be used interchangeably throughout the paper. A coalition of plants can cooperatively manage production capacity, employment levels and inventory investment through the planning horizon. A set of S_m ⊆ K represents a coalition of plants that plan to cooperate. The basic APP model can be developed for coalition S_m of players. We first define the following notations:

t:

the index of time period,

k:

the index of production plants (i.e., players),

$C_{{{\text{H}},k}}$:

the cost of hiring a worker by plant k,

$C_{{\text{F},k}}$:

the cost of firing a worker by plant k,

$C_{{{\text{W}},t}}$:

the wage cost of a worker in a period by plant k,

$C_{{\text{R},k}}$:

the production cost per period on regular time of plant k,

$C_{{\text{O},k}}$:

the production cost per period on overtime of plant k,

$C_{{{\text{I}},k}}$:

the cost per period of carrying one unit of inventory by plant k,

H_k,t:

the number of workers hired in period t by plant k,

F_k,t:

the number of workers fired in period t by plant k,

P_k,t:

the number of units produced by plant k on regular time in period t,

O_k,t:

the number of units produced by plant k on overtime in period t,

W_k,t:

the number of workers employed by plant k in period t,

I_k,t:

the number of units stored in inventory (on-hand inventory) by plant k at the end of period t,

D_k,t:

the number of units of demand for products of plant k in period t,

A₁:

the number of units that one worker can produce in a period on regular time,

A₂:

the maximum number of units that one worker can produce in a period on overtime,

A_k,3:

the initial workforce level of plant k,

A_k,4:

the initial inventory level of plant k,

A_k,5:

the desired workforce level for plant k at the end of the planning horizon,

A_k,6:

the desired inventory level for plant k at the end of each period,

T:

the number of time periods over the planning horizon

The formulation of Co-APP for coalition S_m is presented as follows:

$$\text{TC}(S_{m} ) = \hbox{min} \,\,\sum\limits_{{k \in S_{m} }} {\sum\limits_{t \in T} {\left( {C_{{\text{H},k}} H_{k,t} + C_{{\text{W},t}} \,W_{k,t} + C_{{\text{F},k}} F_{k,t} + C_{{\text{R},k}} P_{k,t} + C_{{\text{O},k}} O_{k,t} + C_{{\text{I},k}} I_{k,t} } \right)} } ,$$

(8)

$${\text{s}} . {\text{t}} .\quad \sum\limits_{{k \in S_{m} }} {\left( {I_{k,t - 1} + P_{k,t} + O_{k,t} - D_{k,t} } \right)} = \sum\limits_{{k \in S_{m} }} {I_{k,t} } ,\quad \forall \,t \in T,$$

(9)

$$P_{k,t} \le A_{1} \,W_{k,t} ,\quad \forall \,k \in S_{m} ,\quad t \in T,$$

(10)

$$O_{k,t} \le A_{2} \,W_{k,t} ,\quad \forall \,k \in S_{m} ,\quad t \in T,$$

(11)

$$\sum\limits_{{k \in S_{m} }} {\left( {W_{k,t - 1} + H_{k,t} - F_{k,t} } \right)} = \sum\limits_{{k \in S_{m} }} {W_{k,t} } ,\quad \forall \,\,t \in T,$$

(12)

$$H_{k,t} ,F_{k,t} ,\,W_{k,t} ,O_{k,t} ,I_{k,t} \ge 0,\quad \forall \, k \in S_{m} ,\quad t \in T,$$

(13)

$$W_{k,0} = A_{k,3} ,\quad I_{k,0} = A_{k,4} ,\quad W_{k,T} = A_{k,5} ,\quad I_{k,T} = A_{k,6} .$$

(14)

Objective function (8) minimizes the total costs of hiring, firing, wages, overtime and relative inventory of the coalition for T periods. Constraint (9) is the inventory balance relationship for the coalition in each period, which implies that the participant plants cooperatively manage their inventories. Constraints (10) and (11) limit regular time and overtime production quantity of each participant plant to the maximum thresholds. Constraint (12) denotes the workforce balance relationship of the coalition in each period that means that the participant plants cooperatively manage workforce levels. Constraint set (7) is initializing conditions. Constraints (9) and (12) guarantee that the plants of a coalition can internally exchange their inventory and labor to level their production and inventory plans. This cooperation can reduce the cost of hiring, firing, wages, overtime and relative inventory of a coalition with respect to noncooperative situations (i.e., the model of “Basic aggregate production planning problem” section). The cooperative aggregate production problem (Co-APP) (8)–(14) is a simple and straightforward problem regarding two following aspects.

We note that APP (1)–(7) is a simple mathematical programming problem. Indeed, Co-APP (8)–(14) is a development of APP for multiple companies. Therefore, only one dimension (for companies as players) is added to the traditional APP model. Objective function (8) computes the sum of production costs for all cooperating companies, and constraints (9)–(14) are actually developed forms of (2)–(7) for the cooperating companies.

We note that traditional APP (1)–(7) is a linear programming (LP) problem with real decision variables. Thus, the problem can be effectively and quickly solved by solver package such as Lingo (or GAMS). Co-APP (8)–(14) also adds a dimension to the traditional APP; therefore, it is simple LP, as well. Because Co-APP is LP with real variables, it is not a complex problem (neither NP-hard nor NP-complete) and can be solved in a polynomial time with linear programming solver package. Therefore, Co-APP with high number of companies can be effectively solved.

The novelty of this study is, first, to solve Co-APP problem (8)–(14) for each production plant independently (i.e., noncooperation situations), Second is to solve the model of all coalitions of two plants. Afterward, we solve the model of all coalitions of three plants, and so on, until reaching the grand coalition. The optimal cost for any coalition of plants should be lower than the sum of the individual minimum production planning costs of the participants of the coalition, i.e.,

$$\text{TC}(S_{m} ) \le \sum\limits_{{k \in S_{m} }} {\text{TC}\left( {\left\{ k \right\}} \right)} .$$

(15)

The optimal total cost of APP for production plant k, i.e., TC({k}), is obtained from solving problem (8)–(14) for that plant. The cost saving CS(S_m) of coalition S_m is the difference between coalitional minimum cost and the sum of the separate minimum costs, that is

$$\text{CS}(S_{m} ) = \sum\limits_{{k \in S_{m} }} {\text{TC}\left( {\left\{ k \right\}} \right)} - \text{TC}(S_{m} ).$$

(16)

The synergy of Co-APP reduces the total cost. The cost saving should be evaluated with respect to the total cost of the collaborating plants. Therefore, the following criterion is a more reliable measure for the synergy of a coalition:

$${\text{Synergy}}\;(S_{m} ) = \frac{{\text{CS}(S_{m} )}}{{\text{TC}(S_{m} )}} = \frac{{\sum\nolimits_{{k \in S_{m} }} {\text{TC}\left( {\left\{ k \right\}} \right)} }}{{\text{TC}(S_{m} )}} - 1.$$

(17)

The larger the cost saving CS(S_m), the higher the synergy of plants will be. Equation (17) can be adopted to evaluate and quantify the synergy of Co-APP of each coalition of plants. Thus, it can be utilized as an argument to motivate this type of cooperation.

We present a real numerical example to evaluate and quantify the synergy among production plants. We study a canned fish-producing company in the southern coast of Iran. This company has established three production plants that process the fresh tuna fishes. The company sells the products of the plants with three different brand names; however, these products are substitutable in the market. Because the production processes and products of the plants are almost similar, the plants can interchange inventories and workers to reduce the production costs.

According to Table 4, the plants deal with high seasonal demands. We assume that these plants decide to use aggregate planning to overcome the obstacle of seasonal demand and minimize costs. The options of plants for handling the seasonality are adding workers during the peak months and building up inventory during the slow months. The details about the parameters utilized in the numerical example are presented in Table 5. One worker can produce 10 or 8 units of product in one period on regular time or overtime, respectively.

Table 4 The demand forecast (unit) of three plants in the numerical example

Table 5 The parameters of three plants in the numerical example

The senior managers of these production plants aim to coordinate their aggregate production plans to reduce their costs. In this example we study how coordination between APP of the plants of the company may yield extra profit for them. In this regard, we solve Co-APP problem (8)–(14) for possible coalitions of three plants. The detailed results of the models are listed in Table 6. Figure 3 presents a comparison between workforce levels in the extreme cases of no cooperation and full cooperation (grand coalition). Figure 4 illustrates inventory levels in these two extreme cases. The total costs TC(S_m) and corresponding cost saving (16) and synergy (17) are shown in Table 7.

Table 6 Optimal results of Co-APP for each of the possible coalitions

Fig. 3

Workforce levels of plants in noncooperative situation and grand coalition

Fig. 4

Inventory levels of plants in noncooperative situation and grand coalition

Table 7 Optimal cost of Co-APP and synergy for each of the possible coalitions

The following observations and managerial insights are derived from the numerical example:

• (i) In all periods of planning horizon, the plants’ workforce level of basic APP is higher than workforce level of Co-APP problem. Furthermore, the inventory of production plants reduces when the plants cooperate. Therefore, the exchanges of inventory and workforce decrease the total cost of Co-APP.

• (ii) In the grand coalition, the fluctuation in workforce levels is lower than noncooperative situation. In particular, the number of dismissals reduces because of Co-APP (i.e., instead of dismissal, the workers can be exchanged among the cooperating plants). Therefore, the job security and satisfaction of workers can be dramatically increased because of plants’ cooperation.

• (iii) Coalition among plants may result in a significant cost saving (i.e., 25%) which is a convincing argument to motivate cooperation.

• (iv) Table 4 demonstrates that the collaborative effects of coalitions are not equal for their plants. For instance, considering the viewpoint of plant 1, joining to plant 2 generates lower synergy (11%) as compared to plant 3 (26%). These differences depend on the pattern of demands and cost parameters of the plants.

Collaborative frameworks for Co-APP

Once the total cost, cost saving and synergy are computed for all coalitions of the production plants, the problem is addressing this question “how to distribute the cost saving of the cooperation among different plants?” This is not a simple problem because it is not clear how much the contribution of each plant to the cost saving of a coalition is. Thus, we require a theoretically grounded approach and the one most appropriate and well-known would be CGT (Reinhardt and Dada 2005; Bartholdi and Kemahlıoglu-Ziya 2005; Lozano et al. 2013; Asgari et al. 2013; Frisk et al. 2010; Hafezalkotob and Makui 2015; Mohammaditabar et al. 2016). For this purpose, some basic definitions and concepts related to CGT are briefly reviewed first; then, we will use these solution concepts in Co-APP. Even though several CGT solution concepts exist, we will focus here only on some of them including the Shapley value, the equal cost saving method (ECSM), the minmax core and the τ-value.

Given the grand coalition, K, CS(K) represents the possible cost saving when all production plants cooperate. Now, let x_k be cost saving allocated to plant k ∊ K such that $\sum\nolimits_{k\in K} x_{k}\leq CS(K)$. A vector $\overrightarrow {x} = (x_{1} ,x_{2} , \ldots ,x_{n} )$ is an imputation for cost-saving assignment if it meets the individual rationality condition x_k ≥ CS({k}) for all k ∊ K and efficiency condition$\sum\nolimits_{k\in K} x_{k}\leq CS(K)$, respectively (Barron 2013). An imputation shows how CS(K) should be split among the plants (i.e., players) such that no one will reject the allocated assignment. The set of all imputations for the cooperative game is defined as

$$X = \left\{ {\overrightarrow {x} = (x_{1} ,x_{2} , \ldots ,x_{n} )\left| {x_{k} \ge v(\left\{ k \right\}),\sum\limits_{k \in K} {x_{k} } } \right. = \text{CS}(K)} \right\}.$$

(18)

The main challenge of CGT is to assign payoff CS(K) among the players in a fair manner. Based on different interpretations of fairness, earlier researchers have proposed different solution concepts. We adopted some of them for the cost-saving allocation problem of Co-APP, but the interested readers may refer to Barron (2013), Branzei et al. (2008), Gilles (2010) and Lozano et al. (2013) for more information.

For imputation $\overrightarrow {x} \in X$, the satisfaction of coalition S_m ⊆ K is equal to

$$F_{S} (S_{m} ,\overrightarrow {x} ) = \sum\limits_{{k \in S_{m} }} {x_{i} } - \text{CS}(S_{m} ).$$

(19)

The satisfaction of coalition S_m represents the extra shares of allocated cost savings that members of the coalition can obtain compared to the cost saving of the coalition. Relative satisfaction of a coalition is computed as ${{F_{S} (S_{m} ,\overrightarrow {x} )} \mathord{\left/ {\vphantom {{F_{S} (S_{m} ,\overrightarrow {x} )} {\text{TC}(S_{m} )}}} \right. \kern-0pt} {\text{TC}(S_{m} )}}$. The core of the game is a set of imputations such that all coalitions are satisfied from assigned cost saving, i.e.,

$${\text{core}}(0) = \left\{ {\overrightarrow {x} \in X\left| {F_{S} (S_{m} ,\overrightarrow {x} ) \ge 0,\,\forall S_{m} \subseteq K} \right.} \right\} = \left\{ {\overrightarrow {x} \in X\left| {\,\sum\limits_{{k \in S_{m} }} {x_{i} } \ge \text{CS}(S_{m} ),\,\forall S_{m} \subseteq K} \right.} \right\}.$$

(20)

The core represents the set of feasible imputations that each coalition obtains at the least cost saving associated with that coalition. The game is called stable if the core is nonempty. Besides, for a given real number ɛ, $\varepsilon$-core is defined as:

$${\text{core}}(\varepsilon ) = \left\{ {\overrightarrow {x} \in X\left| {F_{S} (S_{m} ,\overrightarrow {x} ) \ge \varepsilon ,\,\forall S_{m} \subset K,\,S_{m} \ne K,S_{m} \ne \varnothing } \right.} \right\}.$$

(21)

Core method may not provide a single point for assignment of the cost saving to the plants. The least core method shrinks the core space at the same rate from each side of boundary until a single point (imputation) is obtained. The least core is achieved by solving the following LP problem:

$${\text{Maximize}}\,\,{\text{z}}$$

(22)

subject to:

$$\begin{aligned} & F_{{s_{m} }} (\text{CS},\overrightarrow {x} ) = \sum\limits_{{k \in S_{m} }} {x_{i} } - \text{CS}(S_{m} ) \ge z,\quad {\text{for}}\;{\text{all}}\,S_{m} \subset K,\quad S_{m} \ne K, \\ & \overrightarrow {x} \in X. \\ \end{aligned}$$

(23)

Interpretation of fairness in $\varepsilon {\text{ - core}}$ method is maximizing the minimum satisfaction of players in all coalitions. Shapley (1950) formulated another fair assignment method based on the value that each member adds to coalition. An imputation $\overrightarrow {x} = (x_{1} ,x_{2} , \ldots ,x_{n} )$ represents Shapley value if:

$$\,x_{i} = \sum\limits_{\begin{subarray}{l} S_{m} \subseteq \,K \\ i \subseteq \,S_{m} \end{subarray} } {\left[ {{\text{CS}}(S_{m} ) - {\text{CS}}(S_{m} - \left\{ i \right\})} \right]} \frac{{(\left| {S_{m} } \right| - 1)!(n - \left| {S_{m} } \right|)!}}{n!},\quad i = 1,2, \ldots ,n,$$

(24)

in which |S_m| represents the number of members in coalition S_m.

We also suggest a novel allocation method that provides similar relative cost saving to production plants. This method is based on the equal profit method introduced by Frisk et al. (2010). We call the method equal cost saving method (ECSM) that minimizes the maximum difference in pairwise cost saving of the plants. The ECSM is formulated as follows:

$${\text{Minimize}}\,\,{\text{z}}$$

(25)

subject to:

$$z \ge \left| {x_{i} - x_{j} } \right|,\quad \forall (i,j) \in K,$$

(26)

$$\sum\limits_{{i \in S_{m} }} {x_{i} } \ge {\text{CS}}(S_{m} ),\quad {\text{for}}\,{\text{all}}\,S_{m} \subset K,\quad S_{m} \ne K,$$

(27)

$$\sum\limits_{i \in K} {x_{i} } = {\text{CS}}(K).$$

(28)

The z variable measures the largest difference between cost-saving assignments (see constraint (26)) that should be minimized in objective function (25). Constraints (27)–(28) ensure the stability of the assignment because it should belong to core space.

Another solution approach for the cooperative games is upper vector M(K, CS) and lower vector m(K, CS). For each Player k ∊ K, the k-th coordinate M(K, CS), i.e., M_k, is the maximum value of payoff also called utopia payoff. M_k represents the marginal contribution of player k in the grand coalition, i.e., $M_{k} = {\text{CS}}(K) - {\text{CS}}(K\backslash \left\{ k \right\})$. For each player k ∊ K, the k-th coordinate m(K, CS), i.e., m_k, represents the minimum value for the player’s payoff defined by $m_{k} = \max_{{S_{m} :k^{{\prime }} \in S_{m} }} \left\{ {{\text{CS}}\left( {S_{m} } \right) - \sum\nolimits_{{k^{{\prime }} \in S_{m} \backslash \left\{ k \right\}}} {M_{{k^{{\prime }} }} } } \right\}$. We refer (M_k, m_k) as the maximum and minimum rights for cost-saving allocation for the plant k. Moreover, τ-value method defines imputation $\overrightarrow {\tau } = (\tau_{1} ,\tau_{2} , \ldots ,\tau_{n} )$ such that:

$$\tau_{k} = m_{k} + \alpha (M_{k} - m_{k} ),$$

(29)

in which α ∊ [0, 1] is uniquely determined by $\sum\nolimits_{k\in K} \tau_{k}= CS(K)$.

Now, we utilize the methods of CGT for assignment of cost saving in the numerical example. Table 8 illustrates the cost-saving assignment (imputations) achieved by various CGT methods including the Shapley value, the upper and lower vectors, the τ-value, the least core and ECSM. These results are obtained based on characteristics function (CSs) of Table 7. Except the last two methods, all of these numerical results have been computed using TUGlab platform (Mirás Calvo and Sánchez Rodríguez 2006). The results of the last two columns are obtained by solving least core problem (22)–(23) and ECSM problem (25)–(28) by Lingo 11 package.

Table 8 Assignment of the coalition cost saving according to methods of CGT

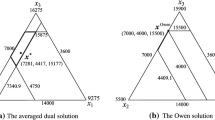
According to cost savings in Table 7, imputation set (18) and core set (20) for the numerical example are expressed as follows:

$$\begin{aligned} &X = \left\{ {\overrightarrow {x} = (x_{1} ,x_{2} ,x_{3} )\left| {x_{1} ,x_{2} ,x_{3} \ge 0,\,\,x_{1} + x_{2} + x_{3} = 1382933.33} \right.} \right\}, \\ &{\text{core}}(0) = \left\{ {\overrightarrow {x} \in X\left| {\,x_{1} + x_{2} \ge 431500,\,\,x_{1} + x_{3} \ge 542944.44,\,\,x_{2} + x_{3} \ge 1021333.33} \right.} \right\}. \\ \end{aligned}$$

From x₃ = 1,382,933.33 − x₁ − x₂, we know that the imputation and core sets can be rewritten as follows:

$$\begin{aligned} &X = \left\{ {\overrightarrow {x} = (x_{1} ,x_{2} ,1382933.33 - x_{1} - x_{2} )\left| {x_{1} ,x_{2} \ge 0,\,\,x_{1} + x_{2} \le 1382933.33} \right.} \right\}, \\ &{\text{core}}(0) = \left\{ {\overrightarrow {x} \in X\left| {x_{1} + x_{2} \ge 431500,\,\,x_{2} \le 839988.89,\,\,x_{1} \le 361600.03} \right.} \right\}. \\ \end{aligned}$$

The cost-saving allocations X (feasible imputations) can be illustrated in a triangle, as plotted in Fig. 5. The shaded area represents core(0) (the stable imputations). The points in the figure show the solutions of Shapley value, τ-value, ECSM and the least core methods. Although all solutions are stable, the various methods come up with rather different cost-saving allocations.

Fig. 5

Illustration of the solutions through different methods

For the imputations presented in Table 8, Table 9 lists the corresponding satisfaction values for each coalition, i.e., $F_{{s_{m} }} ({\text{CS}},\overrightarrow {x} )$, and the relative values, i.e., ${{F_{{s_{m} }} ({\text{CS}},\overrightarrow {x} )} \mathord{\left/ {\vphantom {{F_{{s_{m} }} ({\text{CS}},\overrightarrow {x} )} {{\text{TS}}(S_{m} )}}} \right. \kern-0pt} {{\text{TS}}(S_{m} )}}$. We know from Table 9 that the absolute and relative satisfactions of the coalitions reduce as the coalitions grow. That is, when the size of a coalition increases, the benefits to be gained from adding new members decline. In the real cases, the cost savings of Co-APP for a large number of plants may not outweigh the complexity involved in the cooperation of the multiple plants.

Table 9 Coalition satisfactions for different methods of CGT

The least core method intends to maximize the minimum satisfaction of the coalitions. Table 9 also demonstrates the minimum satisfaction among the coalition for each method. Because of the definition of the least core, this method provides the largest minimum satisfaction (i.e., 180,799.96 (4%)). Therefore, the least core technique imposes fairness via the maximization of the minimum satisfaction of all coalitions of plants.

From the results of the numerical example, we know that CGT approach presents useful tools to assign extra benefits of cooperation of plants. The methods of CGT help to choose the best allocation system to maximize the plants’ satisfaction. The fair allocation of the extra benefits encourages the production plants to continue their participation.

We compute mean absolute deviation (MAD) between the cost-saving allocations to evaluate the dissimilarity between the four CGT methods. MAD measure for two imputations $\overrightarrow {x} = (x_{1} ,x_{2} , \ldots ,x_{n} )$ and $\overrightarrow {{x^{{\prime }} }} = \left( {x_{1}^{{\prime }} ,x_{2}^{{\prime }} , \ldots ,x_{n}^{{\prime }} } \right)$ is computed by

$${\text{MAD}}(\overrightarrow {x} ,\overrightarrow {{x^{{\prime }} }} ) = \frac{n}{{{\text{CS}}(K)}}\sum\limits_{k} {\left| {x_{k} - x_{k}^{{\prime }} } \right|} .$$

(30)

Table 10 demonstrates the MAD measures for each pair of the CGT methods. The table indicates that the solutions of CGT methods are not generally close. From the table, we know that solutions of Shapley value, τ-value and ESCM are rather close; however, the least core gives a different solution. This conclusion is drawn from Fig. 5, as well.

Table 10 Similarity between solutions of CGT methods, measured by MAD

Conclusion and further research

The traditional APP models have often been studied for analyzing the production planning of one production plant. This paper presented a new mathematical programming model for APP problems of multiple cooperating plants. We quantified the cost-saving opportunity of the cooperation of plants caused by decreases in inventory and workforce levels. It was found that the job security and satisfaction of workers can be dramatically raised because of plants’ cooperation. Several methods of CGT including Shapley value, τ-value, the least core and equal cost saving methods were utilized for assignment of cost saving to cooperating plants. We found that fair allocation of cooperation cost saving can ensure the production plants satisfaction.

Various directions and suggestions exist for future research in the field. First of all, this study considers that inventories and workforce are fully interchangeable among cooperating production plants. However, in some real situations, products and workforce may be partially substitutable; thus, considering this assumption can be a fascinating extension of the study. Secondly, generalizing the proposed model to take account of uncertainty over cost and/or demand parameters is also an interesting extension. Finally, this study assumes that the cost parameters of the plants are common knowledge; however, it is unlikely that the plants would be privy to the real cost parameters. This situation would lead to a collaborative game model under asymmetric information that is interesting but challenging.