Modeling and solving multi-skilled resource-constrained project scheduling problem with calendars in fuzzy condition

Abstract

In this study, we aim to present a new model for the resource-constrained project scheduling problem (RCPSP) considering a working calendar for project members and determined the skill factor of any member using the efficiency concept. For this purpose, the recyclable resources are staff resources where any person with multiple skills can meet the required skills of activities in a given time. Then, considering uncertainty condition for parameters, it provided a fuzzy scheduling model and validated models by solving different examples. The proposed mathematical programming model optimizes the allocation of limited resources to project activities for scheduling purposes in an essential activity in the real condition of scheduling problems. Moreover, the proposed model can decrease the risk of deviation from scheduling by allocating members with higher skill factors to critical activities. Then, considering uncertainty condition for parameters, it provided a fuzzy scheduling model and validated models by solving different examples. Considering fuzzy conditions for the calendar of the project and multi-skill operators are firstly considered in this paper. Also, the recyclable resources are staff resources which are being considered for the model concurrently in response to the risks of availability to resources and delay in completing the project under uncertainty. The results derived from the model solved by CPLEX indicated a decreased need for employment and shortened project completion duration. Assuming the uncertainty of available resource capacity at any time, the results obtained from the fuzzy model for the value of objective function were evaluated under the influence of the resource calendar and showed the benefits. Effect of the multi-skill members with calendar constraints on the model is tested, and the advantages are determined.

Introduction and literature review

According to experience, resources are the main factor in any project. In the event of the limited capacity of resources, scheduling problem converts to the resource-constrained project scheduling problem (RCPSP). Although RCPSP is a powerful model, it cannot cover all cases and conditions of real situations. Therefore, many researchers have developed more generalized scheduling problems, most of which use RCPSP as the start point (Yaghoubi et al. 2013). During recent years, a new version of RCPSP has been introduced to the literature, which includes the simultaneous solving of two scheduling and human resource allocation problems. This problem is sometimes called the multi-skilled project scheduling problem (MSPSP). In its standard state, this is the problem of defining practicable scheduling for activities considering precedence relations which are only the multi-skilled human resource type.

Almeida et al. (2019) compared several integer and mixed integer linear programming formulations for the multi-skill resource-constrained project scheduling problem. Maghsoudlou et al. (2017) investigated a version of the multi-skilled resource-constrained project scheduling problem by a bi-objective optimization model to minimize total costs of processing and minimize reworking risks of activities. Arashpour et al. (2018) analyzed the cost-effectiveness of deploying multi-skilled resources with the aim of improving production flexibility. Pinha and Ahluwalia (2019) considered constraint resource for multi-skilled resources and proposed a heuristic framework. In a research by Tao and Dong (2018), an AND–OR network is used to propose a multi-mode multi-skilled resource-constrained project scheduling as a bi-objective linear integer program which minimized the makespan and the total cost. Studies and researches on RCPSP have been conducted with different purposes. Kassandra and Suhartono (2018) discussed in RCPSP with a fuzzy trapezoidal number expressing the optimistic and pessimistic view of activity duration. Wang et al. (2017) assumed that the activity duration is a stochastic variable, and proposed two new robustness measures to analyze the performance of priority rules under a stochastic environment. Chakrabortty et al. (2016) proposed a reactive rescheduling procedure without having any disruption information in advance. Namazian and Yakhchali (2016) investigated a project portfolio selection problem based on the schedule of the project in the uncertain nature of durations of the activities. Mehmanchi and Shadrokh (2013) with considering the effect of learning and forgetting on the human skills developed an exponential learning function by assuming the efficiency of employees performing. Shahnazari-Shahrezaei et al. (2013) presented a multi-objective manpower scheduling model regarding the lack of clarity on the target values of employers’ objectives and employees’ preferences. Calendar-based project scheduling activity is called calendarization.

In a research by Kreter et al. (2016), resources were extended by the concept of break calendars in order to incorporate the possible absence of renewable resources and can be regarded as a modern study on RCPSP where the problem was modeled only by binary variables and was solved by meta-heuristic algorithms. Allahverdi (2016) studied on no-wait process, and Cheng et al. (2015) considered multi-mode resource-constrained project scheduling problem that only allowed non-preemptive activity splitting. Tavana et al. (2014) proposed a new multi-objective multi-mode model for solving discrete time–cost-equality trade-off problems with preemption and generalized precedence relations. Gomes et al. (2014) addressed the RCPSP with the precedence relations and aimed to minimize two criteria: the makespan and the total weighted start time of the activities. Wang et al. (2014) introduced a multi-objective optimization model for multi-project scheduling on critical chains such as overall duration financing costs and robustness. Artigues et al. (2013) presented MILP formulation for RCPSPs based on the concept of the event, Start/End formulation and the On/Off formulation, and Hartmann and Briskorn (2010) presented an overview of primitive RCPSPs. Different methods and approaches were used for solving the mentioned problems simultaneously or separately. Each of the methods has disadvantages and advantages. The exact methods have the ability to obtain and guarantee optimal result. In these methods, all solving problem spaces are searched to find the optimal answer from solution space. In addition, for overcoming the computational problems of the methods, approximate methods are proposed. In these methods, instead of the whole space of problem solving, a part of it is searched so they do not guarantee the optimal results and try to achieve a good approximate answer, but they are quick methods and at the right time they achieve a good answer for large problems. Kazemipoor et al. (2013) proposed an efficient scatter search and Tabu search algorithms for multi-mode multi-skilled resource-constrained scheduling problem. In Ciro et al. (2015), a fuzzy ant colony optimization method was proposed due to the difficulty to fix the different parameters of a MILP model. Cheng et al. (2014) integrated the fuzzy C-means clustering technique and the chaotic technique into the differential evolution (DE) algorithm to develop the fuzzy clustering chaotic-based differential evolution (FCDE) algorithm. Shahriari (2016) presented the existing meta-heuristic solution procedures to solve the multi-mode resource-constrained project scheduling problem. Messelis and De Causmaecker (2014) investigated the construction of an automatic algorithm selection tool for the MMRCPSP. Kaiafa and Chassiakos (2015) employed a genetic algorithm for the optimization goals by minimizing the total cost. Luna et al. (2014) analyzed the scalability of eight multi-objective algorithms when they are applied to the mentioned problem using instances of increasing size. Jia and Seo (2013a) proposed two alternative approaches, applying the facility layout problem (FLP) concept and integrating the permutation-based artificial bee colony algorithm to effectively tackle the RCPSP. Jia and Seo (2013b) proposed an improved particle swarm optimization (PSO) algorithm for the RCPSP. Ranjbar et al. (2013) designed a set of priority rules and applied branch and band algorithm. Zamani (2013) proposed a genetic algorithm for solving the RCPSP. Sanaei et al. (2013) introduced the firefly algorithm for RCPSP. Bas and Kahraman (2009) studied the fuzzification of Weingartner’s pure capital rationing model and its analysis.

Although activity preemption is not allowed in the basic MSPSP, meaning that activities are not allowed to be interrupted once they are started until accomplishment, some researchers allowed activities to be preempted at discrete milestones in the project horizon (Azimi and Azouji 2017). Franck et al. (2001) introduced the concept of calendars in MMRCPSP and considered a binary parameter which determines whether activities can be executed in a specific time period or not. They also suggested using a minimum time of execution for activities before preemption. Schwindt and Trautmann (2000) allowed activity preemption, yet only due to calendar breaks and also suggested a similar approach which allows activities to be interrupted due to varying resource capacities (i.e., resource vacations). Cheng et al. (2015) emphasized on the varying capacity of renewable resources by introduction non-preemptive activity splitting.

The basic MSPSP assumes that the demand for renewable resources and resource capacities is constant during activity execution. However, in a more practical case, resource requests may change along with activities progress (Drexl and Gruenewald 1993).

In this regard, standard MSPSP assumes that the resource supply remains constant over the time. This assumption may be too far from practical situations, where resource capacities might change in response to changing the availability of labors due to vacations or varying availability of equipment due to maintenance (Buddhakulsomsiri and Kim 2007). The basic MSPSP assumes that resource capacities remain constant throughout the project lifecycle; however, in some cases, resource capacities may change over the time due to working hours and maintenance policies. Khalilzadeh et al. (2012) considered the renewable resources to be rented. Each renewable resource is available in predetermined sequential time periods and is not available out of those periods.

Fuzzy techniques are used when problem parameters/variables are not only imprecise but also vague. When problem parameters are not known and historical data are not sufficient to extract distribution functions, fuzzy methods can be used. In this regard, Zhang and Xing (2010) and Baradaran et al. (2012) applied fuzzy variables in order to estimate activity durations and cost. Sajadi et al. (2017) and Xu et al. (2012) considered the environmental impacts of large construction projects by means of fuzzy linguistic variables. Zheng et al. (2013) also utilized fuzzy linguistic variables in order to prioritize activities with uncertain durations.

The search is mainly performed in light of the following notions: project scheduling, resource constraint, multi-skilled and scarce resources, efficiency, fuzzy planning. A comparative of recent researches are given in Table 1.

Table 1 Summary of the literature review

This problem has attracted the attention of many scholars and triggered the development of accurate and innovative scheduling techniques. The project scheduling problem is a set of activities where the problem is scheduled by meeting precedence and resource limitations and optimizing the considered objective function. Despite remarkable advances in recent years, different areas of this problem suffer shortages. In the past researches, basically, one or two assumptions were considered as a start point of MSPSP problem. But we need to develop a model that takes more assumptions to get closer to real-world issues. So the aim of this paper is to present a scheduling model with the aim of minimizing the completion duration of a resource-constrained project considering a multi-skilled human resource approach. Project is scheduled by defining working calendars for the available time of human resource and by prioritizing the allocation of human resources to activities, considering the definitions of efficiency and skill factor of human resources. Finally, considering the uncertain and fuzzy calendar for resources as well as considering available resources at any time, the model gets closer to the real condition in order to obtain an optimal solution.

In order to investigate on those assumptions, which have gained very little attention, a preliminary search is indicated for the purpose of simultaneously implementing these innovations in a single model:

• (1) defining working calendars

• (2) prioritizing the allocation of human resources for critical activities

• (3) defining efficiency and skill factor of human resources

• (4) considering fuzzy calendar for resources.

Problem description

This paper evaluates a problem considering staff resources (human resource). Human resources are allocated to activities in a manner that at any time, each resource is working only on one activity. Human resources are capable of performing multiple skills. If the skills can be simultaneously performed on only one activity, the need for human resource for that activity will be less. Moreover, the working calendar is defined for human resources where they are not available in some days or work on another project. A project can be defined as a set of n activities that require time and recyclable resources for execution. This project includes n + 1 activities named from 0 to n. The dummy activity of 0 shows the project start time, and the dummy activity of n denotes project finish time. Activity i is determined by the processing time d_i, where d_i∈N. In all dummy activities, such as activities i and 0, d_i = 0

S_i∈N and C_i denote the start and finish time of each activity, respectively. We assume that the project initiates just at time zero (s₀ = 0). Project duration is shown by S_n. A vector starting from the start time (S = S_i) and i = 0, 1, …, i where S_i ≥ 0 and S₀ = 0 is called a schedule. In a project network G (N, A), set N indicates the set of activities, and set A indicates precedence relations between activities. In this study, the precedence relations are of finish-to-start type with time lags = 0. M_t is the set of available recyclable resources at any time, independent from their skill factor ($\beta_{m}^{k}$). $R_{i,k}$ indicates the amount of resource k required for executing activity i, which is used during “operation phase.” Operation phase consists of all times in which worker m is engaged in activity i. For the dummy activity $R_{i,k}$ = 0 and for all members m∈M, the resource calendar is as follows:

Definition 1

A calendar for $m \in M$ is a stepped function $\left[ {0,\left. \tau \right)} \right. \to \left\{ {0,1} \right\}$, cal_m(t)$\left[ {0,\left. \tau \right)} \right. \to \left\{ {0,1} \right\}$which is continuous from the right in jump points and is defined as follows:

$${\text{Cal}}_{m} \left( t \right) = \left\{ {\begin{array}{*{20}l} 1 \hfill & {{\text{If}}\,{\text{time}}\,t\,{\text{is}}\,{\text{a}}\,{\text{workday}}\,{\text{for}}\,{\text{resource}}\,m} \hfill \\ 0 \hfill & {{\text{If}}\,{\text{time}}\,t\,{\text{is}}\,{\text{an}}\,{\text{un}}\,{\text{workday}}\,{\text{for}}\,{\text{resource}}\,m} \hfill \\ \end{array} } \right..$$

Activities’ calendar can be determined based on resources calendar so that each activity i follows the relevant calendar and determines the completion duration of activity i as follows:

$$C_{i} = S_{i} + d_{i} = S_{i} + \sum\limits_{{t = S_{i} }}^{{S_{i} + d_{i} - 1}} {C_{i} \left( t \right)}$$

(1)

In this study, project resources are multi-skilled resources with different skill factors in each skill. In the evaluation of multi-skilled human resource, we face three problems:

• The total number of members allocated to the project activities at any time should not exceed the capacity of available human resource

• By determining resources allocated to activities, decreased resource allocation is expectable

• Project activity scheduling is optimized by the resource-constrained project scheduling problem

In this problem, the skill factor of each parameter is calculated considering their efficiency.

Definition 2

Efficiency indicates the extent to which a project is benefited from its resources compared to the best possible performance in a section of time. Efficiency is calculated by the following ratio considering the expected output:

$${\text{Efficiency}} = \frac{{{\text{Actual}}\,{\text{output}}}}{{{\text{Expected}}\,{\text{output}}}} = {\text{Output/input}}$$

(2)

Efficiency is defined as a measure ranging from 0 to 1 and is shown as percent (0% to 100%). As a general measure, it should be obtained by a combination of inputs and outputs. The skill factor of each parameter can be <1, = 1 and > 1. By calculating efficiency, the skill factor of members is calculated using the following relation:

$$\beta_{m}^{k} = \frac{{{\text{Efficiency}}\,{\text{of}}\,{\text{member }}\,m\,{\text{in}}\,{\text{performing}}\,{\text{skill}}\,k}}{{{\text{Mean}}\,{\text{expected}}\,{\text{efficiency}}\,{\text{for}}\,{\text{performing}}\,{\text{skill}}\,k}}$$

(3)

In practice, members can perform several skills. The simultaneous performance of multiple skills for an activity is rational and members can realize expectations. For example, a member cannot engage in both administrative and technical departments at the same time. This means that members can perform skills of the same category. We define parameter G_i as the category of similar skills of each activity and introduce it to the model. According to the previous results, being multi-skilled promotes productivity, quality and continuity and gives more flexibility to managers in the job allocation process. Moreover, members cannot engage in two activities at the same time, and if they are allocated to one skill, they will be completely engaged in that until its completion.

Model formulation

The mathematical model of mixed integer planning for MSPSP is formulated as follows:

Table 2 defines symbols, and Table 3 defines parameters.

Table 2 Symbols

Table 3 Parameters

Scalars:

BN = Very big number

Variables:

$x_{i,m}^{t}$ = if member m is engaged in activity i at time t, $x_{i,m}^{t}$ = 1; otherwise $x_{i,m}^{t}$ = 0

$y_{i,m}^{k}$ = if member m is allocated to activity i in order to perform skill k,$y_{i,m}^{k}$ = 1; otherwise $y_{i,m}^{k}$ = 0

$Q_{i}$ = if activity i is a critical activity, $Q_{i}$ = 1; otherwise $Q_{i}$ = 0

S_i and $C_{i}$ denote the start and end of activity i, respectively. The start of the dummy activity $\left( {S_{n + 1} } \right)$n + 1 shows project completion duration.

$$z = \hbox{min} s_{n}$$

(4)

Subject to

$$s_{i} \le x_{i,m}^{t} \times t$$

(5)

$$\sum\limits_{i = 1}^{n} {x_{i,m}^{t} \le 1} \quad \forall \,m \in M,\forall t \in T$$

(6)

$$\sum\limits_{i = 1}^{n} {x_{i,m}^{t} \le z_{m}^{t} } \quad \forall \,m \in M,\forall \,t \in T$$

(7)

$$\sum\limits_{i = 1}^{n} {\sum\limits_{m = 1}^{M} {x_{i,m}^{t} \le M_{t} } } \quad \forall \,t \in T$$

(8)

$$\sum\limits_{t = o}^{T} {x_{i,m}^{t} } \times G_{i} = y_{i,m}^{k} \times d_{i} \quad \forall \,i \in I,\;\forall m \in M,\;\forall k \in K$$

(9)

$$\sum\limits_{k = 1}^{K} {\sum\limits_{m = 1}^{M} {y_{i,m}^{k} \times v_{k}^{m} } } = \sum\limits_{k = 1}^{K} {U_{i,k} \times R_{i,k} } \quad \forall \,i \in I$$

(10)

$$s_{i} + d_{i} \le s_{{i^{\prime}}} + {\text{BN}}\left( {1 - {\text{predii}}^{{\prime }} } \right)\quad \forall i,i^{\prime} \in N$$

(11)

$${\text{LS}}_{i} - {\text{ES}}_{i} \ge 1 - Q_{i} \quad \forall i \in I$$

(12)

$$\varphi_{m}^{k} \times Q_{i} \le \beta_{m}^{k} + \left( {1 - y_{i,m}^{k} } \right){\text{BN}}\quad \forall i \in I,\forall m \in M,\forall k \in K$$

(13)

$$c_{i} - s_{i} = d_{i} \quad \forall i \in I$$

(14)

$${\text{ES}}_{i} \le S_{i} \le {\text{LS}}_{i} \quad \forall i \in I$$

(15)

$${\text{EF}}_{i} \le C_{i} \le {\text{LF}}\quad \forall i \in I$$

(16)

$$\left( {x_{i,m}^{t} } \right),\left( {y_{i,m}^{k} } \right),Q_{i} \in \left\{ {0,1} \right\}$$

(17)

$$\left( {S_{i} } \right),\left( {C_{i} } \right) \ge 0$$

Constraint (4) is defined to assure that in the objective function, execution scheduling is minimized. Constraint (5) is defined to determine start time of each activity. If person m, at time t is engaged in activity i, then variable $x_{i,m}^{t}$ will take 1. The multiplication on this variable with t indicates the time of work on activity i. So the least of these times is the start time of activity. Constraint (6) is defined to assure that every member can engage only in a single activity at any time in order to avoid activity interference. Constraint (7) is defined to assure that the constraints of the defined calendar are observed because separate calendars are defined for resources. Constraint (8) assures that the capacity of the available human resource does not exceed. Constraint (9) is defined to assure that if a member is allocated to activity i in order to perform skill k, he/she will be engaged in that activity until the completion of that activity. Constraint (10) is defined to assure that all required resources of an activity are supplied. Constraint (11) is defined to assure that the defined precedence relations are observed. Constraint (12) is defined as critical activities. Constraint (13) is defined to assure that only members whose skill factor is equal to, or larger than, the mean skill factor, are allocated to critical activities. Constraint (14) is defined as non-preemptive activities. Constraints (15) and (16) indicate the earliest and latest time for the start and end of activities. Relation (17) determines variables type.

Fuzzy modeling approach

Manpower scheduling is a complicated problem to solve that strives to satisfy employers’ objectives and employees’ preferences as much as possible by generating fairly desirable schedules. But sometimes, objectives and preferences may not be determined precisely. This point makes the manpower for scheduling activities to be a fuzzy number.

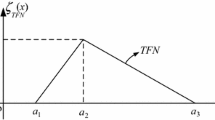
Data can change in the real world. Furthermore, the smallest change to input data can change optimization to a large extent. This uncertainty of scheduling can impose additional costs and stop the supply of schedule requirements. A fuzzy model is used when some elements of a problem are uncertain and ambiguous. Considering the real-world uncertainty, if the uncertainties can be considered in the model, optimal results will be obtained in real condition. To conduct this procedure, parameter M_t that is the number of available human resources, nonnegative real numbers and the most important parameter in the model is defined as a fuzzy number with the following fuzzy membership function as shown in Fig. 1.

Fig. 1

Triangular membership function

In this way, the objective function and relation (8) are converted to the following fuzzy forms:

$$\hbox{min} \widetilde{{S_{n + 1} }}$$

(18)

$$\sum\limits_{i = 1}^{n} {\sum\limits_{m = 1}^{M} {x_{i,m}^{t} } } \le \widetilde{{M_{t} }}\quad \forall t \in T$$

(19)

Considering $\widetilde{{Z_{0} }} = \left( {z_{0} - z^{\prime}_{o} ,z_{o} ,z_{0} + z^{\prime}_{o} } \right)$ as the ideal level of fuzzy objective function, relation (18) is replaced by the following relations:

$$s_{n + 1} \widetilde{ \ge }\widetilde{{z_{0} }}$$

(20)

In the following, we state a relation derived from Proposition 1 and is used to solve the adopted model:

$$\alpha \le \mu \left( {\sum\limits_{i = 1}^{n} {\sum\limits_{m = 1}^{M} {X_{i,m}^{t} ,\widetilde{{z_{0} }}} } } \right)\quad {\text{if}}\,{\text{and}}\,{\text{only}}\,{\text{if}}\quad z_{0}^{ - L} \left( \alpha \right) \le S_{n + 1}$$

(21)

Proposition 1

Assume that$\widetilde{A}$and$\widetilde{B}$are two normal and compressed fuzzy sets and$\alpha \in \left( {0,1} \right),T\left( {x,y} \right) = \hbox{min} \left\{ {x,y} \right\}$. Then,$\mu \left( {\widetilde{A,}} \right.\left. {\widetilde{B}} \right) \ge \alpha$if and only if$\sup \left[ {\widetilde{B}} \right] \ge \inf \left[ {\widetilde{A}} \right]$.

Assuming the above proposition, we define the following two relations:

$$A^{ - L} \left( \alpha \right) = {\text{Inf}}\left\{ {a \in R\left| {a \in \left[ {\widetilde{A}} \right]} \right.} \right\}$$

(22)

$$A^{ - R} \left( \alpha \right) = {\text{Sup}}\left\{ {a \in R\left| {a \in \left[ {\widetilde{A}} \right]} \right.} \right\}$$

(23)

Relation (21) simply shows that the aforementioned fuzzy relations are the equivalents of the following relations:

$$- s_{n + 1} \ge z_{0}^{ - L}$$

(24)

Subject to

$$\sum\limits_{i = 1}^{n} {\sum\limits_{m = 1}^{M} {x_{i,m}^{t} } } \le M_{t}^{ - R} \left( \alpha \right)\quad \forall t \in T$$

(25)

In this way, the objective function can be considered as a non-fuzzy constraint. By introducing the objective function, the following model is derived.

$$\hbox{max} - S_{n + 1}$$

(26)

Subject to

$$\sum\limits_{i = 1}^{n} {\sum\limits_{m = 1}^{M} {x_{i,m}^{t} } } \le M_{t}^{ - R} \left( \alpha \right)\quad \forall t \in T$$

(27)

By replacing $M_{t}^{ - R} \left( \alpha \right) = M_{t} + \left( {1 - \alpha } \right)M^{\prime}_{t}$ in the above model, the fuzzy scheduling problem is finally converted to the following certain scheduling problem:

$$\hbox{max} - S_{n}$$

(28)

Subject to

Constraints (5)–(7)

$$\sum\limits_{i = 1}^{n} {\sum\limits_{m = 1}^{M} {x_{i,m}^{t} } } \le M_{t} + \left( {1 - \alpha } \right)M^{\prime}_{t} \quad \forall t \in T$$

(29)

Constraints (9)–(17)

Computational experiments

This section first calculates members’ skill factor and efficiency by an example. Then, it defines working calendar for resources and performs necessary numerical calculation for categorizing similar activates and the number of available members at any time. Then, the model is solved in GAMS Win32 (24.1.2) using Cplex12 solver.

Numerical example 1

A project with 20 activities is defined to establish customer information system of company alpha. The duration of activities is known, and precedence relations are shown in Fig. 2 as finish-to-start relations.

Fig. 2

AON network

Figure 3 shows a part of the problem data. This figure shows precedence relations, activities transposition and required human resource for activities.

Fig. 3

Gantt chart—example 1

Each activity demands different skills. Table 4 shows the number of skill resources required for performing activities including:

Table 4 Number of resource for skill k in activity i − R_ik

• (1) network specialist

• (2) administrative specialist

• (3) informatics manager

• (4) administrative manager

• (5) installations technician.

The total number of human resources was considered to be 8. Resource calendar is defined as follows and members should be allocated to activities using this calendar. The completion duration of activities is determined under the influence of the required resource. Considering Definition 1 of Sect. 2, resource calendar is sketched as follows.

$${\text{Cal}}_{1} \left( t \right) = {\text{Cal}}_{2} \left( t \right) = {\text{Cal}}_{4} \left( t \right)$$

In Fig. 4, Y-axis indicates human resources which are in the same group in terms of availability, and X-axis shows the time horizon of the project. According to the figure, network specialist, administrative specialist and administrative manager are available from the first day to the 16th day. Following two non-working days and four working days, they are not available for 3 days and again are available from the 26th day to the 31st day of the project. Therefore, they should be allocated to activities in a manner that the completion duration of the activity for human resource is one working day. A similar working calendar is defined for other human resources.

Fig. 4

Resource calendars

Given available human resource in each day, scheduling should be practiced in a manner that the number of members allocated to activities in each day does not exceed the capacity of available resources. In Fig. 5, Y-axis indicates total available resources in each day and X-axis shows project time. Therefore, the number of members allocated to activities in each day should not exceed total available resources on that day.

Fig. 5

Resource profile

According to previous section explanations, Table 5, G_i categorizes similar required skills of activities. This categorization is practiced in terms of the possibility of doing skills at the same time. For example, although member 1 is able to serve as a network specialist and informatics manager at the same time, it is impossible to him to do both jobs because network specialist should work in administration department, while informatics manager should work in informatics department. As another example, activity 3 demands a network specialist and an installations technician. If a member is able to perform both skills at the same time, it will be possible to perform this activity only with one member, instead of two members, because the simultaneous performance of the activities does not conflict with the problem assumptions.

Table 5 Similar required skills of activities G_i

Each member has a specific skill factor in performing skill k of activity i. Since time is the most important factor of scheduling problems, members’ efficiency is calculated considering the time required by members to perform a skill.

$${\text{Efficiency}}\;{\text{of}}\;{\text{member}}\;m = \frac{{{\text{Duration}}\,{\text{required}}\,{\text{for}}\,{\text{the}}\,{\text{completion}}\,{\text{of}}\,{\text{skill}}\,k\,{\text{by}}\,{\text{member}}\,m}}{{{\text{Expected}}\,{\text{duration}}\,{\text{for}}\,{\text{the}}\,{\text{completion}}\,{\text{of}}\,{\text{skill}}\,k}}$$

(30)

Considering mean efficiency of skills required for project activities, i.e., the ratio of member m efficiency in skill k to mean expected efficiency of scheduling specialist and experts, a skill factor is defined for each member using relation (30). The risk of deviation from the schedule may be decreased by allocating members with higher skill factors to critical activities.

Each activity demands a certain level of skill. This means that if member m is allocated to activity i, he/she shall possess the minimum skill level required for performing that activity. This is due to the fact that some activities lie inside the critical path of a project, and they should be performed accurately, correctly and timely. Therefore, members who can perform them with the minimum possible deviation risk should be allocated to such activities. Table 6 defines a mean skill level required for each activity. In addition, a skill factor is derived for each member considering the concept of efficiency. For example, the efficiency of member M1 is calculated using relation (30), and the obtained value is 0.55. The project executor defines a mean efficiency for performing each skill. For example, the mean skill of an administrative specialist is K1 = 0.5. According to this definition, each member has a specific skill factor for performing each skill. $\beta_{1}^{1}$ = 1.1 is defined for activities that are inside the critical path of the project. Therefore, members who are allocated to such activities should possess the skill factor of $\beta_{m}^{k}$ = 1.1 or above. In this way, deviation risk may decrease.

Table 6 Skill Factor $\beta_{m}^{k}$

This problem was solved in GAMSWin32 (24.1.2) using Cplex12 solver. It can provide accurate solutions within acceptable times for small- and medium-scale problems. However, large-scale problems or problems with more than 100 activities demand longer times. Therefore, heuristic and meta-heuristic algorithms are recommended to execute them.

Analysis of the resource required on RCPSP and MSPSP (1)

By solving the above problem in GAMS, required resources at different times are derived. This clearly shows the effect of multi-skill members on the reduction in required resources at different times.

In Fig. 6, Y-axis shows the number of human resources required for the project and X-axis shows time. The number of human resources required for MSPSP shows a significant decrease compared to that of RCPSP. This can result in the optimized execution of the project due to:

Fig. 6

Comparison resources on RCPSP and MSPSP

• decreased employment cost

• decreased training costs

• decreased amount of salary and wage.

$U_{i,k}$ stands for skills that are required by each activity. $\beta_{m}^{k}$ stands for the skill factor of members in performing each activity. Given $U_{i,k}$ and $\beta_{m}^{k}$, the value of $y_{i,m}^{k}$ is determined for each member, each activity and each skill.

According to the outputs of the model variables, member m is allocated to activity i in order to perform some skills. In addition to the need for the activity for that skill, the allocated member is able to perform the skill. For example, in Table 8, we have Y_4,4,1 = 1. This means that member 4 is allocated to activity i = 4 in order to perform skill k = 1. This satisfies both availability and the ability to perform skill constraints. In contrast, in the case of Y_4,6,1 = 0, although member m = 6 is available at that time and can perform the skill, he/she is not allocated to the activity because activity i = 4 is a critical activity and the constraint of β = 1.1 should be met for this activity. In other words, members with higher skill factors for performing required skills of the critical path are allocated to critical activities. Table 7 shows critical activities, and Table 8 shows $y_{i,m}^{k}$ variables.

Table 7 Critical activities

Table 8 Outputs of variable $y_{i,m}^{k}$

Table 8 presents the list of allocation of resources to the activities in which the variables get the value 1 show the assignment of the required resource to the activity. Comparison of the value of the $y_{i,m}^{k}$ with the $U_{i,k}$, $\beta_{m}^{k}$ and $Q_{i}$ confirm the logical results of the model. This table also indicates the reduction in the required human resources. Resources 5 and 6 have not been assigned to any activity and are unnecessary resources which can be discounted from hiring.

Analysis calendar effect on project duration

Considering model output and $x_{i,m}^{t}$ values, the model accuracy can be assessed by observing calendar constraints. In addition, given activities start and end times and the required duration for the completion of activities and the duration of project completion are determined.

According to the values in Table 9, non-preemptive activities assumption is satisfied. For example, in Table 9, we have $x_{9,2}^{10}$ = 1 and $\beta_{m}^{k}$ = 1. This means that member 2 is allocated to activity i = 9 from the 10th day to the 11th day. Further definition of calendars has been prevented of stopping activities; therefore, the duration of the project has been reduced. For example, in activity 14, member 2 would not replace with member 4, leading to delay in both this activity and start time of the successor activities. Also for activity 18, member 7 has been replaced instead member 1. Accordingly, the time to do activities 14 and 18 creates 5 days lag in completing the project. Table 10 indicates that if the calendar is not defined, completion time of the project will be postponed.

Table 9 Outputs of variable $x_{i,m}^{t}$

Table 10 Stop results

The results of the uncertain number of available resources in each day can be evaluated using fuzzy scheduling model outputs. In the fuzzy state, the number of available human resource changes for different α values. This, in turn, changes the allocation of members to activities. Consequently, scheduling changes and the project completion duration may experience a delay. In better words, if member m has no choice to leave the project, or he/she is absent from time to time for unexpected and unpredicted reasons, it will be possible to update scheduling and use the uncertainty of available members in order to replace members in a manner that the project is completed with the minimum possible delay.

According to fuzzy model outputs, Table 11, any change to the number of available members in each day changes project scheduling. The overall time lag is originated from generated time lags between activities due to the necessity of supplying required human resource for that activity and the start of that activity.

Table 11 Fuzzy model outputs

However, according to the problem assumptions, members who are available until the completion time of the activities are allocated to the activities.

In certain cases, where the number of available human resource is given, the model solves the problem considering the minimum required members. In fuzzy case, however, if the number of the available human resource decreases, the model will solve the problem in a manner that in addition to satisfying problem assumptions, project completion delay is minimized.

Numerical example 2

In order to better investigate results and findings, a medium-scaled project is studied. This project has 60 activities with given completion duration, precedence relations and time lags, which are of finish-to-start type. Figure 7 illustrates a schematic view of the Gant Chart of this project in order to better understand precedence relations.

Fig. 7

Gantt chart—example 2

Each activity demands different skills. Table 12 shows the number of required resources of each skill for performing activities including:

Table 12 Number of resources for skill k in activity i − R_ik

• (1) network specialist

• (2) administrative specialist

• (3) informatics manager

• (4) administrative manager

• (5) installation technician.

The total number of human resources was considered to be 15. By defining the resource calendar in the following form, members should be allocated to activities in accordance with the calendar, and the complete duration of activities should be determined under the influence of required resources. Given available human resource in each day, project scheduling should be practiced in a manner that the number of members allocated to activities in each day does not exceed the capacity of available resources. Considering problem assumptions, members who are able to perform the required skills of activities are allocated to the activities. Table 13, G_i, categorizes similar required skills of activities. This categorization is practiced in terms of the possibility of doing skills at the same time.

Table 13 Similar required skills of activities G_i

Each member has a certain skill factor for performing skill k of activity i. Considering the concept of efficiency, Table 14, skill factors are defined for human resources proportional to the completion duration of each skill by each member.

Table 14 Skill factor

$${\text{Efficiency}}\,{\text{of}}\,{\text{member}}\,m = \frac{{{\text{Time}}\,{\text{of}}\,{\text{the}}\,{\text{completion}}\,{\text{of}}\,{\text{skill}}\,k\,{\text{by}}\,{\text{member}}\,m}}{{{\text{Expected }}\,{\text{completion}}\,{\text{time }}\,{\text{of}}\,{\text{skill}}\,k}}$$

A skill factor is defined for each member considering mean efficiency required for performing the skills of project activities as well as considering the ratio member m efficiency in skill k to mean efficiency expected by scheduling experts and specialists. By allocating members with higher skill factors to critical activities using relation (13), deviation risk may decrease.

Analysis of the resource required on RCPSP and MSPSP (2)

Solving the above problem in GAMS determines resources required at different times. This clearly shows the effect of multi-skill members on the reduction in resources required at different times.

In Fig. 8, Y-axis shows the number of human resources required for the project and X-axis shows time. The number of human resources required for MSPSP shows a significant decrease compared to that of RCPSP. This can result in the optimized execution of the project due to:

Fig. 8

Comparison required resources on RCPSP and MSPSP

• decreased employment cost

• decreased training costs

• decreased amount of salary and wage.

According to Table 15, the outputs of the model variables, member m is allocated to activity i in order to perform some skills where in addition to the need of the activity to that skill, the allocated member is able to perform the skill. Moreover, members with higher skill factors in performing skills required for critical path activities are allocated to critical activities. For example $y_{6,3}^{1}$, member 3 is allocated to activity 6 for skill 1 because it fulfills expected limits. Including having the skill and considering activity 6 as a critical activity, it has minimum required factor skill for this activity (1.1). As another example $y_{5,8}^{1}$, although activity 5 needs to skill 1, member 8 is not allocated to this activity because it does not the required skill.

Table 15 Some $y_{i,m}^{k}$ variables

Analysis calendar effect on project duration

Considering model output and $x_{i,m}^{t}$ values, the model accuracy can be assessed by observing calendar constraints. In addition, given activities start and end times and the duration required for the completion of activities, Table 16, the completion duration of project is determined.

Table 16 Some outputs of $x_{i,m}^{t}$ variables

In the following, $x_{i,m}^{t}$ results are analyzed in order evaluate that whether other assumptions of model are satisfied, and model targets are achieved.

According to the values in Table 16, non-preemptive activities assumption is satisfied. For instance $x_{3,1}^{1}$, duration of activity 3 is considered 3 so, as shown it is in processing in times 1, 2, 3 and for all the time after completing this process, the value is zero. For another example $x_{30,5}^{35}$, duration of activity 30 is considered 4 so for all the times before t = 35 and after t = 38, the variable will be zero.

Also definition of calendars has been prevented of stopping activities; therefore, the duration of the project has been reduced like the previous example. All outputs have been avoided mention for the reason that the scale of the problem is great.

The results of the uncertain number of available resources in each day can be evaluated using fuzzy scheduling model outputs.

According to Table 17, the fuzzy model outputs, any change to the number of available members in each day changes project scheduling. The overall time lag is originated from time lags between activities due to the necessity of supplying required human resource for that activity and the start of that activity. However, according to the problem assumptions, members who are available until the completion of the activities are allocated to the activities.

Table 17 Fuzzy model outputs

Conclusion and suggestions

In this research, we proposed a new mathematical model for the resource-constrained project scheduling problem in which the resources were not available in all times. For this purpose, a working calendar for the project workers was considered in which each person had multiple skills. Also, by assuming such parameter as a fuzzy one, we provided a fuzzy scheduling for the proposed model. The final goal was to assign limited resources to the activities in order to optimize scheduling purposes. In this paper, it was better to work with free resources that had enough skills to complete activities without any stop. This was very important issue for non-preemptive activities. In this way, considering the calendar for each person individually could be useful for planning both free and inaccessible resources. Considering the fuzzy conditions for the number of available resources in each time, enabled decision maker to anticipate some resources that were not available at sometimes and he would have timely decisions for the optimal use of resources. Indeed, the concept of efficiency and the skill factor were defined. Allocation of resources with higher skill factor to the critical activities ensured that the replacement strategy for resources could not reduce the quality of the project. The proposed model was tested in several examples with different size and acceptable results which were derived using CPLEX solver.

Considering our investigations, MSPSP can further be investigated in the following areas:

• Considering preemption conditions for activities.

• The addition of resource consumption cost in normal and overtime cases.

• Developing a multi-objective model considering new objectives such as cost cut.

• Allocating multi-skilled members for scheduling project portfolio.

• Providing approaches to resource leveling in the above model.

• Considering other parameters as uncertain parameters, including completion duration of activities.