Optimal overhaul–replacement policy for a multi-degraded repairable system sold with warranty

Abstract

In this research, we study an optimal overhaul–replacement policy of a multi-degraded repairable system sold with a free replacement warranty. In the proposed replacement policy, a maintenance action and failure are dependent on a system degradation level and the system age, and hence the replacement model will provide more effective maintenance decisions. Failure of the system is modeled using a rate of occurrence of failure for the system, which is as a function of a degradation level of the system and its age. We develop the optimal replacement policy for a multi-degraded repairable system from the buyer’s point of view, who plans to use the system for a horizon planning T. The buyer conducts a periodic evaluation and selects an appropriate maintenance option based on the revealed system condition together with the system operational age. At each evaluation point, three alternative decisions are available, i.e., keep running the system, overhaul, or replace it with a new one. We formulate the sequential decision (keep, overhaul, or replace) problem as a dynamic programming model and obtain an optimal policy that minimizes total cost over T. Numerical examples are presented using several hypothetical data sets to illustrate the structure of optimal solution and its sensitivity against the change in parameter values. The main contribution of the paper is to offer a decision tool that will help in deciding the overhaul–replacement action based on the degradation level and the operational age of the system.

Introduction

Maintenance is an activity to keep or to recover the performance of a system to a functioning state to accomplish its intended function. For a system with an increasing rate of failure and a high failure cost (which is very much greater than a preventive maintenance cost), it is more efficient to do a preventive maintenance before failure occurs. The effective preventive maintenance (pm) for a production system will decrease the number of failures, and hence it minimizes the total maintenance cost and provides economic benefits. Many maintenance optimization models which consider the cost–benefit trade-off have been studied, and some of them have been widely applied in practice (see Pierskalla and Voelker 1976; Valdez-Flores and Feldman 1989; Wang 2002; Chouhan et al. 2013 to name a few). The stages involved to study the preventive maintenance policies are generally (1) pm policy formulation, (2) failure and cost modeling, (3) model formulation, and (4) analysis to find an optimal solution with an objective function being the maximization of reliability/availability or cost minimization.

A warranty is a contractual agreement between a manufacturer and a buyer to set up liability in case of a premature failure of an item or inability to perform its intended function. One type of warranty that is usually offered for repairable products is the free replacement warranty (FRW) (Blischke and Murthy 1994). Many products are sold with warranty in which the manufacturers agree to give free maintenance services or compensation to the buyer when the product fails during the warranty period (Shafiee and Chukova 2013). It followed that most research on warranty and maintenance optimization studied is done from the manufacturer’s point of view (Jack and Dagpunar 1994; Jack et al. 2009; Wang et al. 2015), and some works consider the interests of the manufacturer and the buyer (Wang et al. 2017; Iskandar et al. 2016). From the buyer’s point of view, especially those who buy assets and use them to support their businesses, after-sale services (such as warranty, spare parts availability, and repair and maintenance) are important factors to attain their business performances. Among these, the warranty has been considered as an important means to influence the buyer’s decision at the time of purchase—more attractive warranty term will give more influence to purchase the product. However, the study of a replacement (or maintenance policy) policy with warranty consideration from the buyer’s point of view is still relatively limited. Sahin and Polatoglu (1996) and Jung and Park (2003) propose maintenance strategy post-warranty period; Pascual and Ortega (2006) consider optimal replacement and overhauls decision with imperfect maintenance; and (Soemadi et al. 2014) consider sequential do-nothing, overhaul, and replacement decision for a repairable system. To our knowledge, warranty studies on the maintenance of multi-degraded systems from the buyer’s point of view have not been considered in previous works.

In many maintenance policies studied, it is considered that a system has one of two conditions, i.e., operating or fail state, while in a multi-degraded system, the system may in one of many different intermediate operating states between working perfectly gradually deteriorate until eventually breakdown states. Gradual system degradation over time can be caused by wear, fatigue, and corrosion (Zhang et al. 2016), different operating environment (Sidibe et al. 2017), or internal and external shock (Yang et al. 2017). Furthermore, system failure can be classified based on its severity, for example critical failure and degraded failure. A critical state means loss of a major function, and a degraded state means that some degradation has started, but the overall system is still capable of performing its function. If a system has a degraded failure, it often follows that a critical failure is more likely to occur. The existence of any dependence on the occurrence of degraded and critical failures that affect the estimates of the system ROCOF (rate occurrence of failure) has been considered by Hokstad and Frovig (1996). Maintenance can be classified according to the degree to which the operating conditions of an item are restored by, i.e., perfect maintenance, minimal repair, and imperfect maintenance (Pham and Wang 1996). An overhaul represents an imperfect maintenance action. The system failure rate after overhaul is improved but not to as good as new condition (Pascual and Ortega 2006). Doyen and Gaudoin (2004) propose a reduction in system failure intensity and virtual system age reduction. Amari et al. (2006) and Moustafa et al. (2004) have considered imperfect maintenance for a multi-degraded system (written as minor maintenance or minimal maintenance) which improves the system degradation one level better.

The study of maintenance for multi-degraded systems has often been raised in the condition-based maintenance (CBM) strategy literature where most of the models developed seek the optimal solution minimizing the total cost. Moustafa (2002) considers a multistate semi-Markovian deteriorating system under continuous inspection with no random failure. Amari et al. (2006) use semi-Markov decision process formulation to provide an optimal cost-effective maintenance policy that must be taken for each status encountered, as well as the next optimal inspection schedule. Kurt and Kharoufeh (2010) study a system that deteriorates according to a discrete-time Markov process with a limit on the number of repairs that can be performed before replacement since each repair makes the system more susceptible to future deterioration. Caballé et al. (2015) propose a strategy for a system subject to degradation and sudden shocks, with a certain degradation threshold, assuming the dependence on the competing causes of failure. Zhang et al. (2016) consider inspection-based PM policy of a system with non-stationary degradation feature and the state detection delay. Sidibe et al. (2017) consider second-hand systems with an uncertainty of their age and degradation levels and being operated in a secondary environment that is more severe than operating conditions of their first lifetimes. Yang et al. (2017) propose optimal preventive replacement interval, inspection interval, and number of inspections for a system with internal deterioration and sudden shocks. Some model has been developed to maximize the system performance. Soro et al. (2010) determine the inspection periodicity to maximize the overall production rate of the system. Khatab et al. (2012) propose imperfect maintenance strategy for a continuously monitored degrading system to maximize the average system availability. Soro et al. (2012) develop a model for evaluating the availability, the production rate, and the reliability function of systems subjected to minimal repairs and imperfect preventive maintenance. Kumar et al. (2018) propose semi-Markov process modeling on steady-state availability analysis for a given maintenance strategy. Works in multi-degraded system consider that degradation can be represented by some conditions and can be identified by continuous monitoring (Moustafa 2002), or by inspection. Some works assumed that inspection can reveal the system condition perfectly (Amari et al. 2006; Yang et al. 2017), only partially (Huynh et al. 2011; Moghaddass and Zuo 2014), or delayed (Zhang et al. 2016). Transition rate between two degradation states can be considered as constant (Amari et al. 2006), or otherwise expressed as time increases and modeled as nonhomogeneous Poisson process (Moghaddass and Zuo 2014; Kumar et al. 2018). In addition to degradation failures, the system can also fail randomly due to Poisson failure (Zhang et al. 2016; Kumar et al. 2018), shock failure (Yang et al. 2017; Huynh et al. 2011; Caballé et al. 2015), or catastrophic failure (Moghaddass and Zuo 2014). These failures make the system stop working and can be considered as critical failures. The critical failure of any stage also has been modeled to have an exponential distribution that depends on the system degradation level (Zhang et al. 2016; Yang et al. 2017; Kumar et al. 2018).

To our knowledge, all replacement models discussed previously do not consider a system degradation level in selecting a maintenance action required and modeling failures. In general, a maintenance action (degree of maintenance needed to restore (or to maintain)) and a system failure are dependent not only on the degradation level experienced by the system (e.g., wear or corrosion level) but also on the age of the system. As a result, in this paper, we propose a new replacement model in which a maintenance action and failure are influenced by a system degradation level and the system age. This model can be viewed as the extension of the replacement model developed by Soemadi et al. (2014)—to the case of a multi-degraded system. Our contribution to previous work in replacement policy multi-degradation system modeling is to integrate the observed degradation level of the system and the system age to provide more representative maintenance decisions (i.e., the maintenance action chosen is not only based on the level of system degradation but also based on the age of the equipment). In addition, in terms of warranty study, the paper will provide the optimal maintenance and replacement policy for a multi-degraded warranted product from the buyer’s point of view. As a result, the main contribution of the paper is to provide a decision tool that will help the owner of the equipment (or machine) in deciding the optimal replacement policy based on the degradation level and the operational age of the system. We use a dynamic programming model that has been applied by Hartman and Rogers (2006), Nodem et al. (2011), Cheng et al. (2013) and Okamura et al. (2014) to formulate the decision problem, and obtain an optimal sequential decision. The outline of the paper is organized as follows. The first section describes the background of the research and indicates the research gap. In the second section, we present the characterization of the system, and model formulation and model analysis show the existence of the optimal solution in the third section. In the fourth section, we provide numerical examples illustrating the optimal solution and discuss the results. Finally, in the fifth section we give conclusions and provide extensions for further research.

System description

The following notations will be used to formulate the proposed model.

c₁:

Minimal repair cost charged per system failure during the warranty

c₂:

Minimal repair cost charged per system failure after the warranty expires

c₃:

Overhaul cost

c₄:

Replacement cost

$e_{i} \left( t \right)$:

Salvage (or trade-in) value of system at degradation levels i and age t

$h_{i} \left( t \right)$:

Expected number of failures during s for a system with operating age t and degradation level i

i:

Degradation level at j

$i^{{\prime }}$:

Degradation level at j + 1

j:

Evaluation point at the beginning of any operation interval, j = 0, 1, …N

K:

Keep operated until next evaluation point

k:

Minimum level of degradation for replacement decision

N:

Number of system evaluations during the respective planning period (N integer)

O:

Overhaul

R:

Replace

$S_{j}$:

System state at j, $S_{j} = \left( {i,t} \right)$, $i = 0,1, \ldots m,$ and $t = 0,s, \ldots js$

$S_{{jx_{j} }}$:

New system state at j, after decision x_j is chosen

s:

Operation interval between two evaluation points (s = T/N)

T:

Planning horizon

t:

System operational age at an evaluation point j, $t = 0,s, \ldots js$

p(i,i’):

Transition probability from i to $i^{{\prime }}$

w:

Warranty period, $w = n \cdot s$ (n = 1, 2, …)

x_j:

Decision alternatives at j, x_j = {K, O, R}

$\gamma (t)$:

Minimal repair cost charged per system failure at age t

$\rho_{i} (\tau )$:

System ROCOF at degradation level i.

System degradation and system failures

We consider a repairable revenue generating system, e.g., production machine that is planned to operate for finite horizon planning $T$ and evaluated periodically. During T, there are N evaluation points between operating intervals s as shown in Fig. 1. Accordingly, $s = T/N$ (N takes integer values) and j (j = 1,2, …, N) are the evaluation points. At the beginning of the planning horizon, a new system begins to run and at j = N the system operation is stopped.

Fig. 1

Planning horizon, operation intervals, and evaluation points

We assume that the system is subjected to degradation i {i = 0,1,2, …m}, where i = 0 is the best condition as that of a new system and i = m is at the worst level. An example of a system being considered is a heavy equipment or truck used in mining or plantation fields that is planned to be operated during certain planning horizon and periodically evaluated to maintain its performance. The equipment is used to serve a very large operating area, with variations either in workload, field location, driver’s skills, or in the condition of road and weather. These operating environments simultaneously trigger the degradation of the system and can be revealed at evaluation points. The equipment may not always be operated on the same site. Consequently, these variations in operating environments may result in the change in equipment degradation. At the same time, due to usage and aging, various system components experience wear and tear that may lead to failure during system operation. In this paper, the change in degradation level is modeled by the difference in the system ROCOF. We define a system degradation level at j, given by its ROCOF $\rho_{i} \left( \tau \right)$, and the corresponding age at j and expected number of failures are shown in Fig. 2. We assume that the levels of degradation are finite and the transition probabilities of the various levels are known, and the system can still be operated at any levels of degradation. In other words, a production equipment with the highest level of degradation can still be used technically, but the probability to fail while it is in operation will be very high. In some cases, the equipment is forced to run in order to achieve a delivery date, even if it is under the highest degradation condition. The degradation level of the system i is revealed only at the point of evaluation j; therefore, we assume that the occurrence of a system transition is viewed as a discrete random event. Throughout the operating period s, the system experiences failures that can be minimally repaired so that the system is restored immediately after the failure. The time required to conduct minimal repair is assumed negligible; then, the occurrence of failures during any operation interval s follows a nonhomogeneous Poisson process (Nakagawa 2005). If the system age is t and its degradation level is i, then the expected number of failures during (j, j + 1) is given by (1):

Fig. 2

Illustration of ROCOF, operational age, evaluation point, and corresponding system failures

$$ \begin{aligned} & h_{i} \left( t \right) = \int_{t}^{t + s} {\rho_{i} (\tau ){\text{d}}\tau } \\ & t \le \tau \le t + s,\;{\text{for}}\;t = s,2s, \ldots js. \\ \end{aligned} $$

(1)

System state and state transition

We define $S_{j}$ as system states at j that represented by the system degradation level $i$ and the system age $t$. Thus, $S_{j} = \left( {i,t} \right),i = 0,1, \ldots m,$ and $t = 0,s, \ldots js$. We model the rate of occurrences of failure at (j, j + 1) represented by a point process with a ROCOF $\rho_{i} \left( \tau \right)$, an increasing function of $\tau$ (Hokstad and Frovig 1996). The higher the system degradation level means the more possibility of failure to occur, so $\rho_{i + 1} (\tau ) > \rho_{i} (\tau )$. The probability of transit from i to $i^{\prime}$ is denoted by transition probability $p\left( {i,i^{\prime}} \right)$. During any operation interval (j, j + 1), the degradation level i may stay to the same level or move to the worse one $i^{\prime}$. Then, $p\left( {i,i^{\prime}} \right) > 0, \forall i^{\prime} \ge i$ and $\sum\nolimits_{{i^{{\prime }} = i}}^{m} p \left( {i,i^{{\prime }} } \right) = 1$.

Decision alternatives

Based on the degradation level revealed at an inspection point, one of the following maintenance actions is taken, i.e., (1) do nothing and keep the system running until next inspection point; (2) an overhaul is performed which incurred some cost but improve the system degradation to one level better (Moustafa et al. 2004); (3) replacement is performed which requires a notable cost but significantly reduces minimal repair costs during the warranty period. At each point of evaluation j, a decision $x_{j}$ can be chosen based on system state $S_{j}$. It is assumed that overhaul and replacement decisions are meant only for a relatively worse degradation level ($i > k$) and after the system warranty expired $t > w$ so $x_{j}$ can be written as (3):

$$ x_{j} = \left\{ {\begin{array}{*{20}l} {K:{\text{keep}}\;{\text{operating}}\;{\text{the}}\;{\text{system}}} \hfill & {\forall \left( {i,t} \right)} \hfill \\ {O:{\text{overhaul}}\;{\text{the}}\;{\text{system}}} \hfill & {i \ge k,\quad t \ge w} \hfill \\ {R:{\text{replace}}\;{\text{the}}\;{\text{system}}} \hfill & {i \ge k,\quad t \ge w} \hfill \\ \end{array} } \right. $$

(2)

Let $S_{j}$ be the system state at any stage j. We assume that once a decision at j is chosen the time needed to execute $x_{j}$ is very small (and hence it is ignored). By this assumption, the benefit of decision chosen at j is at once obtained as well in the operation period (j, j + 1). The reveal system state at evaluation point j is $S_{j}$, and after $x_{j}$ is chosen the new system state is written as $S_{{j, x_{j} }}$. At the next evaluation point j + 1, $S_{{j, x_{j} }}$ may shift to $S_{j + 1}$ as shown in Fig. 3.

Fig. 3

Illustration of system state at the beginning of j, new state at j due to $\varvec{x}_{\varvec{j}}$, and possible state at j + 1

Considering the limitation of x_j in relation to system states as given in (2), the relationship between $S_{j}$, decision $x_{j}$ and post-decision state $S_{{j, x_{j} }}$ is shown in Table 1.

Table 1 Relationship of $S_{j}$, possible x_j, new state $S_{{j, x_{j} }}$, and $S_{j + 1}$

Benefit of warranty

There are several costs of interest to buyers over the lifetime of revenue generating system, i.e., purchase, maintenance, and repair costs, following the expiration of the warranty period, operating costs, and disposal costs (Blischke and Murthy 1994). The important role of the warranty is to protect buyers from purchasing defective products. Warranty policies offered by the manufacturer can be grouped into two types—i.e., one- and two-dimensional warranty policies. In one-dimensional policy, the warranty is characterized by time interval named the warranty period, and the two-dimensional policy is characterized by a region in the two-dimensional plane where one axis stands for age and the other for usage. The warranty benefits to the buyer are protective, since within the warranty period if the product fails the manufacturer agrees to repair or replace the failed product at no cost, such that the buyer only suffers the cost due to system interference caused by repair activity. Once this period expires, the buyer will be charged for spare parts, maintenance, and other services to keep the system’s availability (Wang et al. 2017). The system considered is sold under a one-dimension free replacement warranty with period w. For simplification, w is an integer multiplication of s (w = n·s). Any failure that occurs during w will be repaired with no charges, but in such situation, there is still acquired some cost to buyer, c₁ due to disturbances in the system operation, e.g., disruptions of the system activity, change in planned production schedule, less desirable system performance after reparation which might affect availability and product quality. Although the seller still bears the cost of repairs during the warranty period, these various losses incurred by system failure are suffered by the buyer. After the warranty expired $(t > w)$ in case of system failure, total minimal repair cost and another cost due to disturbances in the system operation c₂ should be paid by the owner, where c₁ < c₂. Let γ denote the minimal repair cost per failure incurred, then depending on the warranty status of the system the value of γ is written as follows:

$$ \gamma = \left\{ {\begin{array}{*{20}l} {c_{1} ,} \hfill & {t < w} \hfill \\ {c_{2} ,} \hfill & {t \ge w.} \hfill \\ \end{array} } \right. $$

(3)

Dynamic programming formulation and analysis

Evaluation points j (j = 1, …N) are decision points. At the last evaluation point, the system operation is ended, and then the number of decision period in our model is N − 1. Evaluation and decisions are made throughout planning horizon T. At any j, the system state is evaluated, and based on the revealed state a decision $x_{j}$ is selected that may change the system state at once. While it is being run, the system state transition is occurred corresponding to a certain probability. The combinations of system states and alternative decisions produce many possible policies. Using dynamic programming, the problem can be solved efficiently. The objective of the model is to minimize the total expected costs over T.

Using dynamic programming terminologies, stages in this problem refer to evaluation points j, j = 1,2…N − 1, that have some possible states $S_{j} = \left( {i,t} \right)$ and $x_{j}$ denote the decision chosen at the jth stage. We define minimal repair cost during warranty as $c_{1}$, and after the warranty expired as $c_{2}$. Decision cost depends on $x_{j}$, i.e., no cost for do-nothing, $c_{3}$ for overhaul, and $c_{4}$ for replacement, and we assumed that $c_{1} < c_{2} < c_{3} < c_{4}$. At j = 0, a new system starts to run, and then $S_{0} = \left( {0,0} \right)$. Let $F_{j} \left( {i,t} \right)$ be the expected total cost from j to N. It follows that $F_{j} \left( {i,t} \right)$ is the summation of decision costs at j, the associated minimal repair cost during $\left( {j,j + 1} \right)$, and the best expected total costs for the remaining stages (stage j + 1 onwards). Let $F_{j}^{*} \left( {i,t} \right)$ be the best value of $F_{j} \left( {i,t} \right)$ given by optimal decision $x_{j}^{*}$, and let any system at state $\left( {i,t} \right)$ can be sold for $e_{i} \left( t \right)$; it follows that the associated costs at j for each $x_{j}$ can be obtained as given in Table 2.

Table 2 Costs at j and the remaining stages due to decision $x_{j}^{{}}$

We assumed that degradation levels i can be observed at any j. Keeping the system to operate until the next evaluation point will not change the degradation level as well as the system age and give rise to the number of failures during (j, j + 1). Conducting overhaul will create a cost of c₂ and reduces system degradation one level better, so the expected number of failures in the next interval operation is relatively decreasing. Conducting replacement requires a cost of c₃ which is higher than the overhaul cost, but it gives significant benefits both from decrease in system failures and from reduction in minimal repair costs due to warranty services. The model is developed to find the best sequential decision $\varvec{x}_{\varvec{j}}^{\varvec{*}}$ (j = 1, …N − 1) that minimizes the total expected cost over T. We seek the optimal sequential decisions (keep, overhaul, or replace) that minimize $F_{0}^{*} \left( {0,0} \right)$. From Table 1, we develop $F_{j}^{*} \left( {i,t} \right)$ costs equation at stage j for any state $\left( {i,t} \right)$ that minimizes the total ownership costs at stage j and onward by choosing x_j. The recursive equations of dynamic programming formulation for j = 0, …, N − 1 are then given by:

$$ F_{j}^{*} \left( {i,t} \right) = \hbox{min} \left\{ {\begin{array}{*{20}l} {x_{j} = K} \hfill & {\gamma h_{i} \left( t \right) + \mathop \sum \limits_{{i^{\prime} = i}}^{m} p\left( {i,i^{\prime}} \right)F_{j + 1}^{*} \left( {i^{\prime},t + s} \right),\forall \left( {i,t} \right)} \hfill \\ {x_{j} = O} \hfill & {c_{3} + \gamma h_{i - 1} \left( t \right) + \mathop \sum \limits_{{i^{\prime} = i - 1}}^{m} p\left( {i - 1,i^{\prime}} \right)F_{j + 1}^{*} \left( {i^{\prime},t + s} \right),i \ge 2,t \ge w} \hfill \\ {x_{j} = R} \hfill & {c_{4} - e_{i} \left( t \right) + \gamma h_{0} \left( 0 \right) + \mathop \sum \limits_{{i^{\prime} = 0}}^{m} p\left( {0,i^{\prime}} \right)F_{j + 1}^{*} \left( {i^{\prime},s} \right),i \ge 2,t \ge w} \hfill \\ \end{array} } \right. $$

(4)

At the end of the planning period (j = N), $F_{N}^{*} \left( t \right)$, the system operation is ended and the buyer gets the salvage value that is given by:

$$ F_{N}^{*} \left( {i,t} \right) = - e_{i} \left( t \right) $$

(5)

Using backward approach, we obtain the optimal total costs at j and its optimal decision $x_{j}^{*}$ from j = N − 1, j = N − 2, up to j = 1. Possible combinations of degradation level and system age of our proposed model result in a quite a lot of possible states in each stage. By using backward induction, the problem is solved efficiently without tracking every possible policy. The more the level of system degradations, and the longer the planning horizon period results in the larger dimension of the problem to solve. In such situations, we need to develop solution method that is supported by a computer program. For a small dimension problem, we can solve the model by using Microsoft Excel. In the following section, we carry out model analysis to prove the existence of an optimal solution and some required condition for a replacement decision.

Existence of optimal solution

For $F_{j}^{*} \left( {i,t} \right)$, given by (4), there exists an optimal solution that minimizes $F_{0}^{*} \left( {0,0} \right)$, given by the decision policy $\pi^{*} = \left\{ {x_{0}^{*} , x_{1}^{*} , \ldots , x_{N - 1}^{*} } \right\}$. We use an induction proof to show the existence of an optimal solution for our model. First, we denote at any stage j the space states $S_{j}$, i.e., the system’s degradation level and system’s age as $S_{j} = \left( {i_{j} ,t_{j} } \right)$, $i_{j} \in I. I = \left\{ {1,2, \ldots m} \right\}$, $t_{j} \in T_{j}$. $T_{j} = \left\{ {s, 2s, \ldots js} \right\}$. Let $G_{{j,x_{j} }} \left( {i_{j} ,t_{j} } \right)$ is the current stage’s costs, i.e., cost due to decision $x_{j}$ and the expected minimal repair cost of $\left( {j, j + 1} \right)$.

$$ G_{{j,x_{j} }} \left( {i_{j} ,t_{j} } \right) = \left\{ {\begin{array}{*{20}l} {\gamma h_{i} \left( {t_{j} } \right),} \hfill & {x_{j} = K} \hfill \\ {c_{3} + \gamma h_{i - 1} \left( {t_{j} } \right),} \hfill & {x_{j} = O} \hfill \\ {c_{4} + \gamma h_{0} \left( 0 \right),} \hfill & {x_{j} = R} \hfill \\ \end{array} } \right. $$

(6)

At any operation interval $\left( {j,j + 1} \right)$, the degradation levels $i$ only can change into the same or the worse level $i^{\prime}$ with probability $p_{{ii^{\prime}}}$. Depending on the decision taken at the current stage $x_{j}$, all possible states at stage $(j + 1)$ are $(S_{j + 1} )$:

$$ \left( {S_{j + 1} } \right) = \left\{ {\begin{array}{*{20}l} {\left( {i^{\prime},t_{j} + s} \right),} \hfill & {i^{\prime} = \left\{ {i_{j} , i_{j} + 1, \ldots m} \right\},\quad {\text{for}}\;x_{j} = K} \hfill \\ {\left( {i^{\prime},t_{j} + s} \right),} \hfill & {i^{\prime} = \left\{ {i_{j} - 1, \ldots m} \right\},\quad {\text{for}}\;x_{j} = O} \hfill \\ {\left( {i^{\prime},s} \right),} \hfill & {i^{\prime} = \left\{ {0, 1, \ldots m} \right\},\quad {\text{for}}\;x_{j} = R} \hfill \\ \end{array} } \right. $$

(7)

Using (6) and (7), we can rewrite (4), the best total costs at a particular stage j onward, as:

$$ F_{j}^{*} \left( {S_{j} } \right) = F_{{jx_{j}^{*} }} \left( {S_{j} } \right) = \mathop {\hbox{min} }\limits_{{x_{j} \in \left\{ {K,O,R} \right\}}} \left( {G_{{j,x_{j} }} \left( {S_{j} } \right) + \mathop \sum \limits_{{i_{j + 1} }}^{m} p_{{i_{j} i_{j + 1} }} F_{j + 1}^{*} \left( {S_{j + 1} } \right)} \right) $$

(8)

Using the principle of optimality, we can show that for any j (j = 0,1, 2, …N − 1) if there exists a decision $x_{j}$ for a certain $S_{j}$ that satisfies (8), then we can find $x_{j - 1}^{*}$.

For j = N;

At the last stage, the system is sold. The possible states at N, i.e.,$\left( {S_{N} } \right) = \left( {i_{N} ,t_{N} } \right)$, are finite, $i_{N} = \left\{ {1,2, \ldots m} \right\}$ and $t_{N} = \left\{ {s,2s, \ldots Ns} \right\}$. The salvage value of the system depends on its state $\left( {S_{N} } \right)$, and we can rewrite (5) as:

$$ F_{N}^{*} \left( {i_{j} ,t_{j} } \right) = F_{N} \left( {i_{N} ,t_{N} } \right) = - e_{{i_{N} }} \left( {t_{N} } \right) $$

(9)

Using $F_{N}^{*} \left( {i_{N} ,t_{N} } \right)$, we proceed to show the existence of an optimal solution at j = N − 1.

For j = N − 1;

At j = N − 1, the finite states space is $\left( {S_{N - 1} } \right) = \left( {i_{N - 1} ,t_{N - 1} } \right)$, $i_{N - 1} = \left\{ {1,2, \ldots m} \right\}$ and $t_{N - 1} = \left\{ {s,2s, \ldots \left( {N - 1} \right)s} \right\}$. Using (8), the optimal expected cost of stage N − 1 can be expressed as:

$$ F_{{N - 1x_{N - 1}^{*} }} \left( {S_{N - 1} } \right) = \mathop {\hbox{min} }\limits_{{x_{j} \in \left\{ {K,O,R} \right\}}} \left( {G_{{N - 1,x_{N - 1} }} \left( {S_{N - 1} } \right) + \mathop \sum \limits_{{i_{N} }}^{m} p_{{i_{N - 1} i_{N} }} F_{N}^{*} \left( {S_{N} } \right)} \right) $$

(10)

From any state $\left( {S_{N - 1} } \right)$, there exists at least one feasible $x_{N - 1} \in \left\{ {K,O,R} \right\}$ that facilitates movement to one $S_{N}$ in the subsequent stage. Hence, it follows that from all feasible solutions $x_{N - 1}$ there is at least one $x_{N - 1}^{*}$ that gives the minimum total costs for the last period to go. As a result, at j = N − 1 the optimal solution $x_{N - 1}^{*}$ can be obtained for all $\left( {i_{N - 1} ,t_{N - 1} } \right) \in S_{N - 1}$ which represent all possible states in stage N − 1. Continuing the backward process until stage 0, we will certainly obtain $F_{{0x_{0}^{*} }} \left( {S_{0} } \right)$ and optimal decision sequences for the remaining stages, i.e., $\pi^{*} = \{ x_{0}^{*} ,x_{1}^{*} , \ldots ,x_{N - 1}^{*} \}$ that minimizes $F_{0}^{*} \left( {0,0} \right)$.

Necessary condition for replacement decision

For any j and t (t ≥ w), we can perform replacement with cost c₄, which reduces the system degradation level from i to 0. We assumed that replacement is only conducted after the warranty expired and the system salvage value is zero. The necessary condition at j where replacement is better than do-nothing can be obtained using Eq. (4) as follows:

$$ c_{2} (h_{i} (t) - h_{0} (t)) + \left[ {\mathop \sum \limits_{{i^{\prime} = i}}^{m} p\left( {i,i^{\prime}} \right) \times F_{j + 1}^{*} \left( {i^{\prime},t + s} \right) - \mathop \sum \limits_{{i^{\prime} = 0}}^{m} p\left( {0,i^{\prime}} \right) \times F_{j + 1}^{*} \left( {i^{\prime},t + s} \right)} \right] > c_{4} $$

(11)

We analyze conditions required to satisfy (11). Since h_i(t) and F_j(i,t) are increasing functions in i and t, both LHS terms of (11) are also increasing in i and t. The first term shows minimal repair cost reduction in j due to replacement, and the second term stands for the additional benefit of the remaining stages. The first term becomes large if failure rate gaps between system levels are significant. The second term will increase if there is a great system tendency to move to the worse level. Thus, to accomplish (11), both gaps between (λ_i − λ_i−1) and $\left( {p\left( {i,i^{\prime}} \right) - p\left( {i - 1,i^{\prime}} \right)} \right)$ must be sufficiently large to yield cost reduction either at j or at the remaining stages. From (4), we also obtain that the necessary condition for replacement is better than overhaul at j as follows:

$$ (c_{3} ) + \left( {c_{2} h_{i - 1} (t) - c_{1} h_{0} (0)} \right) + \left( {\mathop \sum \limits_{{i^{\prime} = i - 1}}^{m} p\left( {i - 1,i^{\prime}} \right)F_{j + 1}^{*} \left( {i^{\prime},t + s} \right) + \mathop \sum \limits_{{i^{\prime} = 0}}^{m} p\left( {0,i^{\prime}} \right)F_{j + 1}^{*} \left( {i^{\prime},s} \right)} \right) > c_{4} $$

(12)

The first term of the LHS of (12) is overhaul cost. The second term stands for the disparity of minimal repair cost at j between overhaul and replacement decisions. This term always has a positive value since $h_{i - 1} \left( t \right)$ never approaches $h_{0} \left( 0 \right)$, i.e., the performance of the post-overhaul system cannot be as good as the new system. The third term stands for cost disparities in the remaining stages between overhaul and replacement decisions. This value will increase as the probability of transition to the worse degradation level is increased. Then, there are two conditions needed for the decision to replace. First, physical requirements, i.e., degradation level of the system, are more likely to get worse, and failure rate gaps between the degradation levels are significant. Secondly, economic requirements, i.e., replacement cost, are not extremely high compared to overhaul cost.

Warranty effect to replacement decision

Considering zero system salvages value and w = 1, we develop that the necessary condition at j for replacement is better than overhaul using (4) and (2) as follows:

$$ \left( {c_{2} h_{i - 1} \left( t \right) - c_{1} h_{0} \left( 0 \right)} \right) + \left( {\mathop \sum \limits_{{i^{\prime} = i - 1}}^{m} p\left( {i - 1,i^{\prime}} \right)F_{j + 1}^{*} \left( {i^{\prime},t + s} \right) - \mathop \sum \limits_{{i^{\prime} = 0}}^{m} p\left( {0,i^{\prime}} \right)F_{j + 1}^{*} \left( {i^{\prime},s} \right)} \right) > c_{4} - c_{3} $$

(13)

Both LHS terms of (13) are nonnegative, since h(t) and F_j(t) are increasing functions in t, and c₂ > c₁. The first term of LHS is the current stage benefit, and the second term is the remaining stage benefits. The necessary condition to choose the replacement at j can be satisfied with the accomplishment of (13) by either or both terms. We examine effects of overhaul and warranty benefits to obtain buyer’s sequential overhaul–replacement decisions. Corresponding to replacement decision, there is a saving, $\left( {c_{2} - c_{1} } \right)$ for any failure during warranty period. The first term value will increase as the difference between $c_{2}$ and $c_{1}$ increases which represents the greater warranty benefits the buyer receives in the warranty period. For w = 1, this saving is obtained simply in the current stage. Then, to analyze the buyer’s underlying decision to replace by j we only consider accomplishment of (13) by the current benefits shown in Eq. (14).

$$ \left( {c_{2} h_{i - 1} \left( t \right) - c_{1} h_{0} \left( 0 \right) > (c_{4} - c_{3} } \right) $$

(14)

Satisfaction of (14) depends on the gap between c₂ and c₁ that is associated with how significant is the repair cost reduction during the warranty period, and differences between $h_{i - 1} \left( t \right)$ and $h_{0} \left( 0 \right)$ that show the disparities of expected number of failures between the overhaul decision and the replacement decision. The decline gives in the RHS of (14) similar contribution. This situation shows necessary conditions to choose replacement, i.e., a significant repair cost reduction during warranty period, and a moderate price of a new system. This situation shows necessary conditions to choose replacement, i.e., a significant repair cost reduction during warranty period, and a moderate price of a new system. In addition to the more general situation where w > 1, we can see also that the second term value of (13) also increases for a longer warranty period. Thus, it is seen that the benefits obtained by the buyer affect the choice of a decision to make a replacement.

Numerical examples

To obtain the optimal solution, we need data including technical characteristics of system degradation, i.e., its possible levels m, the transition probability P, and system failure intensity at any level of degradation $\rho_{i} \left( \tau \right)$. Economic data include the cost of system minimal repair, both within the warranty period and after the warranty expired, system overhaul costs, and system replacement costs. We also need data given by the seller/manufacturer, i.e., the price of the new system, the length of the warranty period, and the various repair costs that will be borne by him in the warranty period.

In the following numerical examples, we consider a system which will be used for the next 15 years and evaluated each year. With the system aging, the deterioration gets worse. Based on the available data over the system life, there are three degradation levels. Overhaul decision will reduce system degradation one level better. Hence, we have T = 15, N = 15, s = 1, m = 2. We assumed that each deterioration level is represented by an increasing intensity function $\rho_{i} \left( \tau \right) = \alpha \beta_{i} \cdot \tau^{\beta i - 1}$, where $\alpha = 2$, and $\beta_{i} = \left( {1.25,1.5,1.75} \right)$, i = 0,1,2, where i = 0 is the best state. During warranty period, part of minimal repair cost is borne by the seller, so we model warranty parameters by its length w and percentage of minimal repair cost $r = c_{1} /c_{2}$.

We consider combination aspects of our model, i.e., system degradation, warranty, and also the model analysis in the previous section, and developed some data set as follows. First, to analyze behavior of optimal solutions to different failure parameters we ignore the warranty (w = 0 and r = 1) and create set data 1 with three scenarios of probability transition matrix $(P,P^{\prime}, \;{\text{and}}\;P^{{\prime \prime }} )$, and set 2 with another scenarios value of intensity functions parameter, $(\beta^{{\prime }} \;{\text{and}}\;\beta^{{\prime \prime }} )$. To test solution behavior toward different replacement cost $(c4^{'} \;{\text{and}}\;c4^{''} )$, set data 3 is developed. Lastly, to present the influence of system warranty on the model solution we create set data 4 with $r = 50\%$ for two scenarios warranty length $(w^{\prime},w^{\prime\prime})$. Table 3 presents all the scenarios.

Table 3 Set data for numerical examples

The optimal solution obtained is sequential decisions that give minimum expected total cost over T. The jth decision depends on the revealed state at the jth evaluation point. Possible states that may occur at any stages depend on selected decisions on earlier stages and their transition probabilities. Actually, it is possible to present the whole optimal decisions’ structure directly from the solution of dynamic programming, but in order to ease the discussion, we choose to do the following two things. First, instead of showing up all sequential decisions along T, we represent them in terms of the age of the system at j + 1 due to decision choose at j. Keep decision can be detected from constantly increasing of system age in the next stage, while replacement decision on j − 1 will change the system age to one year in the next stage at j. Next, to ease discussion of decision behavior we limit to the relation of the system age and the decision choose at j for each level of system degradation. The solution obtained for each data set is presented in Figs. 4, 5, 6, and 7. Overhaul decision that changes the system degradation one level better at j and does not affect the system age is marked with a circle. Figure 4a shows that when the system is not degraded (the system remains in its best condition) the decisions are do-nothing until the last evaluation point. Once the system age reaches 2 years (or 4 years) and detected to shift to the worst state (or the medium state) replacement should be conducted. Next, for the system remains at a medium level of degradation the optimal policies are to do system replacement three times along T, i.e., when the system age reaches 4 years, so we can see that in j = 5, 9, and 13 the system age is 1 year.

Fig. 4

System age at stage j under best decision at j − 1 for set data 1

Fig. 5

System age at stage j under best decision at j − 1 for set data 2

Fig. 6

System age at stage j under best decision at j − 1 for set data 3

Fig. 7

System age at stage j under best decision at j − 1 for set data 4

In the worst situation, system replacement should be done every two years and overhaul conducted just once at 13th stages. From Fig. 4a–c, we observe that as the system is more likely to degrade, overhaul decision is suggested to be more often. Using this figure as a reference, we can do the same simple logical approach to choose the subsequent best decisions for any state revealed on the next inspection points.

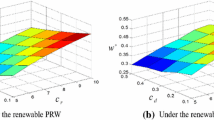
Figure 5 shows the effect of increasing failure rate to the model solution, meaning that the model responds to a higher system failure rate by doing sequential overhaul–replacement decisions more often. Figure 6 shows the sensitivity of the model solution toward the change of replacement cost. It can be seen that a higher replacement cost will decrease the frequency of replacement and is compensated by an increasing frequency of overhaul. In Fig. 7, we see that the decision to replace is sensitive to the warranty benefit. The longer the warranty period, the more the replacement conducted at the end of the warranty period as shown in the medium and the high level of system degradation case.

We summarized the optimal solution of all scenarios in Table 4.

Table 4 Summary of the optimal solution at the best and the worst situations

Conclusion

In this article, we propose the optimal replacement policy for a warranted repairable system in which both the maintenance action and the rate of system failure are affected by the level of degradation and its operational age. The dynamic programming formulation allows us to represent the system state as a combination of all possible degradation levels and its operational age throughout the evaluation points. In the same time, the model also can accommodate the different ROCOF for each system degradation level. The discussion has shown that there is a logical relationship between the system degradation level and its operational life to the optimal maintenance decision. From the sensitivity analysis, the results show that an older system with a low degradation tends to be kept with an overhaul, while a relatively new system with a severe degradation level tends to be replaced. The structure of the optimal solution provides a dynamic maintenance schedule based on the state of the system which can be used to support maintenance decision-making practice. To use the model, one need data of system degradation levels and the system ROCOF, system degradation transition probability, as well as various cost parameters. Also, one needs a sound method for modeling system degradation levels and their effects to the system ROCOF. This study can be extended in the following ways by considering two-dimensional warranty policy, the limitation of overhaul frequencies (Kurt and Kharoufeh 2010), overhaul alternatives with respect to system degradation and system age (Pascual and Ortega 2006), etc. Maintenance policy optimization that takes into account the buyer’s benefit of warranty is an interesting topic to be researched. This indicates that further study in this area is still open for more development.