Abstract
A debutanizer column is an integral part of any petroleum refinery. Online composition monitoring of debutanizer column outlet streams is highly desirable in order to maximize the production of liquefied petroleum gas. In this article, data-driven models for debutanizer column are developed for real-time composition monitoring. The dataset used has seven process variables as inputs and the output is the butane concentration in the debutanizer column bottom product. The input–output dataset is divided equally into a training (calibration) set and a validation (testing) set. The training set data were used to develop fuzzy inference, adaptive neuro fuzzy (ANFIS) and regression tree models for the debutanizer column. The accuracy of the developed models were evaluated by simulation of the models with the validation dataset. It is observed that the ANFIS model has better estimation accuracy than other models developed in this work and many data-driven models proposed so far in the literature for the debutanizer column.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Today, in a wide array of processes, it is difficult to achieve continuous online monitoring. The prime reason is the low reliability or unavailability of hardware sensors. This results in huge revenue loss to the industry due to low-quality products which could have been otherwise prevented in presence of continuous monitoring. In order to counter this problem, various industries are now incorporating soft sensor models to achieve quality monitoring. There is increasing use of soft sensors in process industries such as petroleum refinery (Wang et al. 2013; Shokri et al. 2015), cement (Pani and Mohanta 2014, 2016), polymer (Shi and Liu 2006; Ahmed et al. 2009; Chen et al. 2013; Sharma et al. 2017), metallurgy (Gui et al. 2005; Zhang et al. 2013; Markopoulos et al. 2016), bioprocesses (Steinwandter et al. 2016) and plasma etching process (Zakour and Taleb 2017).
A debutanizer column is used to remove the lighter fractions from gases, which are the overhead distillate coming from the distillation unit. The debutanizer column lacks real-time monitoring system for the butane (C4) composition. Adding to the nonlinearity of the process, the control of product quality tends to become a tricky issue in the refinery. For the prediction of the bottom product composition of the debutanizer column, various models have been reported in the past. Significant among them are backpropagation neural network (Fortuna et al. 2005; Pani et al. 2016), partial least square (PLS; Ge and Song 2010; Zheng et al. 2016), support vector regression (SVR; Ge and Song 2010), principal component regression (PCR; Ge et al. 2014), supervised latent factor analysis (Ge 2016; Yao and Ge 2017), probabilistic regression (Yuan et al. 2015) and state-dependent ARX (Bidar et al. 2017) techniques for modeling of debutanizer column.
Literature survey on modeling of debutanizer column reveals that various types of PCR, PLS, probabilistic regression, ARX and backpropagation neural network models are reported. However, so far, the techniques of fuzzy inference modeling and regression tree-based modeling techniques have not been investigated for the debutanizer column. Therefore, in this work, the performances of fuzzy inference, adaptive neuro fuzzy (ANFIS) and regression tree models are reported for the debutanizer column. The required input output data are obtained from the World Wide Web shared by Fortuna et al. (2007). The data were statistically divided into a training set and a validation set using Kennard–Stone algorithm (Kennard and Stone 1969). The training set was used to develop Mamdani and Sugeno-type fuzzy inference model, adaptive neuro fuzzy inference model and regression tree models. All developed models are examined with unknown data (validation set data) to assess the estimation accuracy of the models. The performances of the developed models were analyzed and compared by computing various statistical model evaluation parameters such as mean absolute error (MAE), root-mean-squared error (RMSE) and correlation coefficient (R). It was found that the adaptive neuro fuzzy model is able to estimate the butane content in the bottom stream of the debutanizer column with good accuracy. The accuracy of the ANFIS model reported here is even better than many other data-driven models proposed so far in the literature.
The main contribution of this research is proposing a model (with good accuracy of prediction) for the LPG recovery unit of refinery. The use of the model will help to overcome the problem of time delay arising due to the hardware sensor. This will result in improved process efficiency with maximization of LPG production. The rest of the article is organized as follows. Process description section contains the process description for the debutanizer column and the scope of inferential model application in the process. Details of the modeling techniques applied in this research are presented in Methodology section followed by results and discussion in Results and discussion section. Finally, concluding remarks are presented in Conclusion section.
Process description
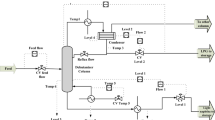
A debutanizer column is present in various processing units of a refinery. The column is used to remove the lighter fractions from gasoline in the production of LPG and gasoline. For instance, it is a part of the atmospheric and vacuum crude distillation unit, cracking and coking units. Unstabilized naphtha is fed to the debutanizer column. The products coming out from the column are LPG as the top product and gasoline/stabilized naphtha as the bottom product. A simplified schematic flowsheet of the debutanization process is shown in Fig. 1. The detailed process flowsheet can be referred to in Fortuna et al. (2005).
Scope of the present research work
The butane (C4) content in the bottom product needs to be minimized for better performance of the process (maximizing LPG in the top product). This requires continuous monitoring of C4 content in the bottom product. A gas chromatograph is used in the process to achieve this. But this hardware sensor is located in the overhead of the deisopentanizer column rather than being in the bottom flow line coming from the debutanizer column. This results in a time delay of 30–75 min in the composition measurement (Fortuna et al. 2005). Therefore, to overcome this problem of time delay, an inferential process model can be incorporated in the bottom flow of debutanizer column to achieve real-time monitoring of C4 content from the knowledge of other process inputs. The various process inputs influencing the C4 content in the bottom stream are listed in Table 1. The output to be predicted by the soft sensor model is the C4 content present in the debutanizer column bottom product.
Methodology
The required process input–output data were obtained from the internet resource mentioned in (Fortuna et al. 2007). This has a total of 2394 observations (samples). This dataset was split equally into a training set consisting of 1197 samples and a validation set of the same dimension. The training set was used for model development, and the validation set was meant for subsequent model performance assessment. The splitting was done so as to ensure that the training set becomes a proper representative of the entire set. The widely used distance-based statistical technique, the Kennard–Stone algorithm (Kennard and Stone 1969), was used for data division. The following modeling techniques were followed in this research for modeling of the debutanizer column.
Classification and regression tree (CART) model development
CART method involves the progressive binary splits of various estimations of classification variable to generate a decision tree. Every estimation of every indicator variable is taken into account as a potential split and the ideal split is chosen in view of impurity criterion. A set of explanatory variables or predictors are used to study the variation of the new data. Recursive binary splits are made on the data creating mutually exclusive subgroups containing objects with similar properties. An extremely intriguing preferred standpoint of CART is the likelihood to manage vast quantities of both categorical and numerical factors. Another favorable position is that no assumption about the hidden circulation of the predictor factors is required (even categorical variables can be utilized). Eventually, CART gives a graphical representation, which makes the understanding of the outcomes simple. Five elements are necessary to develop a classification tree (Breiman et al. 1984): (1) a set of binary questions, (2) a measure to optimize the split, (3) a stop-splitting rule, (4) a rule for assigning termination code classification and (5) a method to prune the tree back. The structure of a typical CART model is shown in Fig. 2 (Breiman et al. 1984).
The tree growing procedure in CART is roughly analogous to a stepwise linear regression procedure which consists of the following steps: (1) defining an initial set of variables, (2) choosing the fitting method of least squares, (3) defining the threshold P values for new variables to be entered or removed from the equation, (4) backward elimination of variables and selection of the best multi-variable model based on the adjusted R2 values.
The designed training set was used to build up the CART model for the debutanizer model. The resulting model is shown in Fig. 3.
However, because of the large dimension data set (1197 objects), the initial CART model is highly complex with a very high number of nodes. This model produces very accurate prediction for the training data but largely fails to predict accurately when supplied with unknown data (the objects of validation set). This is the well-known overfitting problem. The determination of a smaller tree, got from the maximal one, is therefore essential for successful modeling. The choice of the ideal tree is accomplished by a tree pruning methodology. Many techniques were used to generate the optimal model like examination of resubstitution error, cross-validation, control depth, evaluating root-mean-squared error (RMSE), correlation coefficient (R) and mean absolute error (MAE).
Resubstitution error is difference between the predictions of the model and that of the response training data. High resubstitution error signifies lower accuracy in predictions. However, great predictions for new data aren’t assured by having low resubstitution error.
Tree was cross-validated to see how accurate it could predict for the new data; training data were split into 10 parts at random. On 9 parents of the data, 10 new trees were trained. Predictive accuracy for each newly developed tree was examined on the data which was not there in the training. The technique gives a decent gauge on how accurate is developed model.
A leafy tree with depth (many nodes) is generally very precise on the training data. However, the model is not ensured to demonstrate a tantamount exactness on a test set. A deep tree’s test accuracy is frequently far not as much as its training (resubstitution) accuracy as it tends to overtrain (or overfit). Conversely, a shallow tree does not achieve high training precision.
The regression tree model after improvement is presented in Fig. 4.
Mamdani and Sugeno fuzzy inference model development
The entire activity of fuzzy inference model designing is a sequence of five steps: fuzzification of the input (predictor) process variables, application of the appropriate AND or OR operator in the antecedent, implication from the antecedent to the consequent by application of the fuzzy if then rule, aggregation of the consequents across the rules to get the output (response) process variable in fuzzified form and finally defuzzification of the fuzzified output (Jang et al. 1997; Pani and Mohanta 2014).
In the fuzzification step, membership functions were decided to create valid fuzzy sets to accommodate all inputs. The membership functions can take many forms such as trapezoidal, triangular, Gaussian bell shape, etc. (Jang et al. 1997). In this work, triangular membership functions were used for both the inputs and output. Training data used for the model were normalized so that all input and output data points lie in the broad range of 0–1. Every crisp variable was then classified into 5 fuzzy variables namely VS (Very Small), S (Small), M (Medium), L (Large) and VL (Very Large) depending upon its value.
Table 2 summarizes the membership functions and the range of values for classifying under a particular linguistic variable for all seven inputs and the output.
After fuzzification of the inputs (and outputs for Mamdani-type fuzzy model) as mentioned in Table 2, OR type fuzzy operator is applied to get a single number that represents the result of the antecedent for a rule which has multiple parts in its antecedent. The input to the fuzzy OR operator is two or more membership values from fuzzified input variables and the output is a single crisp value (the maximum of all inputs).
After the FIS was designed as per the requirements of our process, the next step was to add rules to it based on the training set. The conventional means to do that would require feeding the fuzzy logic toolbox with the linguistic variable for each data point based on its value individually.
In our case, we had 7 input variables and 1 output variable for a total of 1197 rows. So for adding rules, we needed 8 × 1197 = 9567 data points, classify them to linguistic variables based on their values and then finally add them row by row individually to the GUI provided by the fuzzy logic toolbox of MATLAB. It was really a cumbersome task to add rules in this manner. Moreover, this was not a one-time task! If we needed to change the training set at any point of our research, we would have to do the entire task again. The task was hence a time taking one. To eliminate the manual addition of rules, a function was written to make the process of rule building easy and replicable for any training set. It was called the RuleMatrix method. The function takes a training set as parameter and returns a rule matrix for that training set. A rule matrix is nothing but a set of rules defined for a particular training set in the form of a matrix. For a system with m number of inputs and n number of outputs, there are exactly m + n + 2 columns in the rule list.
The first m columns are for the inputs of the system. The next n columns are for the outputs of the system. Each column contains a number that refers to the index of the membership function for that variable. The m + n + 1 column contains the weight applied to each rule. As specified earlier, it is 1 for each rule in our case. The m + n + 2 column contains a 1 if the fuzzy operator for the rule’s antecedent is AND. It contains a 2 if the fuzzy operator is OR. AND was used as the fuzzy operator in our case for the rules.
The rule matrix was then added to the FIS through a single line of code. This has made the entire process easy, reproducible and adaptable for different training sets by just changing one line in the entire code.
For development of Sugeno-type fuzzy model, the prime difference is in the definition of membership values for output variable which was defined to constant values in the range 0–1 (zero-order Sugeno fuzzy model). The mam2sug MATLAB function method takes a Mamdani-type FIS as parameter and returns a corresponding zero-order Sugeno-type FIS for the process. The resulting Sugeno-type FIS has output membership functions with values corresponding to the centroids of that in Mamdani-type FIS passed as parameter. It uses weighted-average defuzzification method and the product implication method. All the other properties like the input membership functions and the rule definitions of the resulting FIS are identical to the Mamdani-type FIS passed to it.
Adaptive neuro fuzzy inference (ANFIS) model development
This technique was first proposed by Jang (1993) and has subsequently become one of the most popular hybrid modeling techniques combining neural network and fuzzy inference concepts. ANFIS takes a Sugeno-type FIS as input and then trains its membership function parameters. The initial fuzzy model is required to determine the number of inputs, linguistic variable and the number of rules in the tuned final model. The FIS must have the following properties for the ANFIS to support it:-
-
1.
Only zeroth- and first-order Sugeno-type FIS.
-
2.
Output membership functions uniformly of the same type, i.e., linear or constant. The FIS must have a single output.
-
3.
Number of output membership function must be equal to the number of rules, i.e., no two rules can share the same output membership function.
-
4.
Have the same weight for each rule, i.e., 1.
The Sugeno-type FIS designed earlier will not be supported by the ANFIS. It is because the FIS had 350 rules while the number of output membership functions was 5. This clearly hints at rule sharing which is not supported by the ANFIS.
Hence a new FIS had to be designed such that it complies with all the requirements for it to be supported by the ANFIS. The number of rules can be reduced and fine-tuned by using various clustering methods on the training data.
Clustering methods analyze the intrinsic grouping in a dataset. The two most widely used methods are grid partitioning and subtractive clustering.
In grid partitioning technique, the antecedents of the fuzzy rules are formed by partitioning the input space into numerous fuzzy regions. It is a rather subjective approach because the user has to initially specify the number of clusters in which the variables will be partitioned into. The product of number of clusters for each input variables then gives the total number of rules.
The grid partitioning method leads to a problem when the number of inputs is large. The method requires enumerating all possible combinations of input membership functions to generate rules, and hence, the number of rules blows up in the case of more inputs. In our case of 7 inputs, each with say 5 membership functions, this method will lead to 78,125(= 55) rules. Hence, the number of rules grows exponentially with the increase in number of inputs. Such systems then are infeasible for any training. This exponential blowing up of number of rules with the increase in number of inputs is often referred to as the ‘curse of dimensionality.’
So keeping in mind the above constraint, the number of membership function for the 7 inputs of the debutanizer column was kept as low as 2. That led to 128 (= 27) rules and could be further trained using ANFIS. The membership functions were marked S and L denoting ‘small’ and ‘large,’ respectively. The model was chosen to be a zeroth-order Sugeno model. The membership functions were chosen to be of the triangular type.
The above fuzzy model obtained by grid partitioning was trained by updating the consequent parameters of the rules by least square estimation algorithm and the premise parameters by the backpropagation gradient descent algorithm. This is also known as the hybrid learning algorithm.
The curse of dimensionality renders the grid partitioning method impractical for large number of inputs. For instance, if the above fuzzy model was attempted with 3 membership functions for each input, the number of rules would have exceeded 2000. Therefore, the number of membership functions was restricted in the case of grid partitioning algorithm.
A much more intuitive technique is the subtractive clustering algorithm. Subtractive clustering is a one pass algorithm that estimates the number of clusters and the cluster centers for the input–output pair in the data set. It works by determining regions of high densities in the data space. A point is chosen to be the cluster center if it has maximum no. of neighbors. User specifies a fuzzy radius till which the points are left out, and the algorithm tries to find the next cluster center in the remaining points. In this manner, all the data points are examined.
This algorithm does not lead to the dimensionality issue. Number of rules and antecedent membership functions are first determined by the rule extraction method. Linear least squares estimation is then used to determine the consequent of each rule.
This algorithm requires the user to specify the radius of influence of the cluster centers for each input. This values lies between 0 and 1 considering the entire data set as a unit hypercube. Also the accept ratio and the reject ratios needs to be specified which instructs the algorithm to accept the data points as cluster centers if their density potential lies above the accept ratio and reject them if the potential lies below the reject ratios.
For the final model generated using subtractive clustering, the radii of influence were set to 0.22 for all inputs. The accept ratio was set to be 0.6, and the reject ratio was set to 0.1. This generates a Sugeno FIS with 54 membership functions and 54 rules.
Results and discussion
The initial regression tree model was developed with the leaf size of 1. Though it has good accuracy, the model is extremely complex. As the leaf size was increased error also increased, i.e., model became less accurate. For the given data when Min leaf size vs cross-validated error graph was generated, it was found out that the cross-validated error was least for the 77.5 min leaf size. The best leaf size is 77.5 or 78. Therefore, leaf size of 78 was decided to be somewhat optimum at which the model is relatively much simpler and at the same time does not have very high error value.
The resubstitution loss is the MSE (mean squared error) of prediction. This was computed to be 0529.
The cross-validated loss was computed to be 0.0177, which signifies a common predictive error of model to be 0.133. This signifies that simple resubstitution loss is typically lower than cross-validated loss.
The optimal regression tree generated gives very high resubstitution error and is much smaller. Yet, it gives comparable precision. Even though cross-validation error was low for the generated model other errors [root-mean-squared error (RMSE), correlation coefficient (R), mean absolute error (MAE)] were really high as compared to the original model.
The performances of the Mamdani and Sugeno-type fuzzy models are not satisfactory when developed from such a huge data set of 1197 samples. However, an increase in the number of rules (which will also add to added complexity and computational effort) may result in a better model.
Both grid partitioning and subtractive clustering techniques were applied for ANFIS modeling. Both kinds of ANFIS models were trained for 30 epochs. The value of error drops with each training epoch. The models trained using the training set were validated by the test set. The value of error goes down for the test set too with the number of training epoch till it finally converges to a constant value. The RMSE values converged at 0.109 and 0.105 for training set and the test set, respectively, for the grid partition-based ANFIS model. For the subtractive clustering based model, the RMSE values converged at 0.0539 and 0.0672 for training set and the test set, respectively.
The predicted values were compared with the actual values in the data, and the values of MAE, RMSE and R were computed for different models. The formulas used for computation of various statistical parameters are mentioned below:
Mean absolute error is a quantity used to evaluate how close the predictions are to the output. It is given by: \({\text{MAE}} = \frac{{\mathop \sum \nolimits_{i = 1}^{N} \left| {y_{i} - \widehat{y}_{i} } \right|}}{N}\).
Root-mean-squared error gives an index to analyze the precision with which the model predicts the output. It is given by: \({\text{RMSE}} = \sqrt { \frac{{\mathop \sum \nolimits_{i = 1}^{N} \left( {y_{i} - \widehat{y}_{i} } \right)^{2} }}{N}}\) where yi and \(\widehat{y}_{i}\) are actual and predicted values, respectively, N is the no. of rows.
Correlation coefficient provides an index to measure the linear dependence between two vectors X and Y. It gives a value ranging from − 1 to +1. The value 1 signifies total positive linear correlation, 0 no linear correlation, whereas − 1 signifies total negative linear correlation. For a sample, the correlation coefficient is given by: \(R = \left( {\frac{{\sum \left( {y - \overline{y} } \right)\left( {\widehat{y} - \overline{{\widehat{y}}} } \right)}}{{\sqrt {\sum \left( {y - \overline{y} } \right)^{2} \sum \left( {\widehat{y} - \overline{{\widehat{y}}} } \right)^{2} } }}} \right)\)yi \(\widehat{y}_{i}\) are actual and predicted values, respectively, N is the no. of rows.
The prediction performances of all models for the validation data are presented in Table 3.
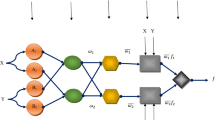
From Table 3, it is quite clear that the proposed adaptive neuro fuzzy inference model designed using subtractive clustering algorithm regression tree model, Mamdani and Sugeno fuzzy inference models and a few other models (neural network, just in time and principal component regression) reported in the literature for the same process and using the same benchmark dataset. The structure of the proposed ANFIS model is shown in Fig. 5. The model has 7 inputs, 1 output and a total of 54 rules.
Error analysis of the proposed ANFIS model
The accuracy of the designed ANFIS model is further tested by conducting rigorous error analysis between the actual and model-predicted output values (i.e., butane content in the debutanizer column bottom product stream). It may be noted that all the error analysis is done by simulation of the model to unknown inputs (validation data). The actual values and the predicted values by the ANFIS model are shown in Fig. 6.
Table 3 and Fig. 6 indicate that the predicted output of the ANFIS model is quite close to the actual output values. However, the accuracy of the model is further tested by conducting error analysis of model residuals. Two kinds of error analysis are reported in this work which are presented in Figs. 7 and 8.
In simulation of the model with the validation set input data, Fig. 7 presents the plot of model residuals (i.e., difference between actual output and model-predicted output). It is clear that the residuals are perfectly random in nature without any particular trend w.r.t the sample number (or time instances). Figure 8 shows the normal probability plot of the prediction errors which indicates that most of the errors’ probability values match satisfactorily with the analytic line. Randomness and normal distribution of the prediction errors are important requirements of a good model (Ljung 1998). Table 3 and Figs. 6 to 8 indicate that the ANFIS model simulation with unknown inputs results in outputs whose error values are less, randomly distributed and come from a normal distribution.
Conclusion
Data-driven models were developed in the present work for real-time monitoring of butane (C4) content in the bottom stream of debutanizer column. Mamdani and Sugeno-type fuzzy inference models, regression tree-based model and adaptive neuro fuzzy model were developed. All models were analyzed by assessing their prediction performances with unknown data. It was found that the neuro fuzzy model reported in this work results in better performance than other models developed in this work and developed in earlier works reported in literature. The good performance of the neuro fuzzy model makes it a suitable option for being used for real-time monitoring in petroleum refineries.
References
Ahmed F, Nazir S, Yeo YK (2009) A recursive PLS-based soft sensor for prediction of the melt index during grade change operations in HDPE plant. Korean J Chem Eng 26(1):14–20
Aimin M, Peng L, Lingjian Y (2015) Neighborhood preserving regression embedding based data regression and its applications on soft sensor modeling. Chemometr Intell Lab Syst 147:86–94
Bidar B, Sadeghi J, Shahraki F, Khalilipour MM (2017) Data-driven soft sensor approach for online quality prediction using state dependent parameter models. Chemometr Intell Lab Syst 162:130–141
Breiman L, Friedman J, Stone CJ, Olshen RA (1984) Classification and regression trees. CRC Press, Hoboken
Chen WL, Huang CY, Huang CY (2013) Finding efficient frontier of process parameters for plastic injection molding. J Ind Eng Int 9(1):25
Fan M, Ge Z, Song Z (2014) Adaptive Gaussian mixture model-based relevant sample selection for JITL soft sensor development. Ind Eng Chem Res 53(51):19979–19986
Fortuna L, Graziani S, Xibilia MG (2005) Soft sensors for product quality monitoring in debutanizer distillation columns. Control Eng Pract 13(4):499–508
Fortuna L, Graziani S, Rizzo A, Xibilia MG (2007) Soft sensors for monitoring and control of industrial processes. Springer, Berlin
Ge Z (2014) Active learning strategy for smart soft sensor development under a small number of labeled data samples. J Process Control 24(9):1454–1461
Ge Z (2016) Supervised latent factor analysis for process data regression modeling and soft sensor application. IEEE Trans Control Syst Technol 24(3):1004–1011
Ge Z, Song Z (2010) A comparative study of just-in-time-learning based methods for online soft sensor modeling. Chemometr Intell Lab Syst 104(2):306–317
Ge Z, Huang B, Song Z (2014) Nonlinear semisupervised principal component regression for soft sensor modeling and its mixture form. J Chemom 28(11):793–804
Gui WH, Li YG, Wang YL (2005) Soft sensor for ratio of soda to aluminate based on PCA-RBF multiple network. J Cent South Univ Technol 12(1):88–92
Jang JS (1993) ANFIS: adaptive-network-based fuzzy inference system. IEEE Trans Syst Man Cybern 23(3):665–685
Jang JSR, Sun CT, Mizutani E (1997) Neuro-fuzzy and soft computing: a computational approach to learning and machine intelligence. Prentice Hall, India
Kennard RW, Stone LA (1969) Computer aided design of experiments. Technometrics 11(1):137–148
Ljung L (1999) System Identification: theory for the User, 2nd edn. Englewood Cliffs, NJ, Prentice-Hall, USA
Markopoulos AP, Georgiopoulos S, Manolakos DE (2016) On the use of back propagation and radial basis function neural networks in surface roughness prediction. J Ind Eng Int 12(3):389–400
Pani AK, Mohanta HK (2014) Soft sensing of particle size in a grinding process: application of support vector regression, fuzzy inference and adaptive neuro fuzzy inference techniques for online monitoring of cement fineness. Powder Technol 264:484–497
Pani AK, Mohanta HK (2016) Online monitoring of cement clinker quality using multivariate statistics and Takagi–Sugeno fuzzy-inference technique. Control Eng Pract 57:1–17
Pani AK, Amin KG, Mohanta HK (2016) Soft sensing of product quality in the debutanizer column with principal component analysis and feed-forward artificial neural network. Alex Eng J 55(2):1667–1674
Sharma GVSS, Rao RU, Rao PS (2017) A Taguchi approach on optimal process control parameters for HDPE pipe extrusion process. J Ind Eng Int 13(2):215–228
Shi J, Liu XG (2006) Product quality prediction by a neural soft-sensor based on MSA and PCA. Int J Autom Comput 3(1):17–22
Shokri S, Sadeghi MT, Marvast MA, Narasimhan S (2015) Improvement of the prediction performance of a soft sensor model based on support vector regression for production of ultra-low sulfur diesel. Pet Sci 12(1):177–188
Steinwandter V, Zahel T, Sagmeister P, Herwig C (2017) Propagation of measurement accuracy to biomass soft-sensor estimation and control quality. Anal bioanal chem 409:693–706
Wang Y, Chen C, Yan X (2013) Structure and weight optimization of neural network based on CPA-MLR and its application in naphtha dry point soft sensor. Neural Comput Appl 22(1):75–82
Yao L, Ge Z (2017) Locally weighted prediction methods for latent factor analysis with supervised and semisupervised process data. IEEE Trans Autom Sci Eng 14(1):126–138
Yuan X, Ye L, Bao L, Ge Z, Song Z (2015) Nonlinear feature extraction for soft sensor modeling based on weighted probabilistic PCA. Chemometr Intell Lab Syst 147:167–175
Zakour SB, Taleb H (2017) Endpoint in plasma etch process using new modified w-multivariate charts and windowed regression. J Ind Eng Int 13(3):307–322
Zhang Shuning, Wang Fuli, He Dakuo, Chu Fei (2013) Soft sensor for cobalt oxalate synthesis process in cobalt hydrometallurgy based on hybrid model. Neural Comput Appl 23(5):1465–1472
Zheng J, Song Z, Ge Z (2016) Probabilistic learning of partial least squares regression model: theory and industrial applications. Chemometr Intell Lab Syst 158:80–90
Zhu J, Ge Z, Song Z (2015) Robust supervised probabilistic principal component analysis model for soft sensing of key process variables. Chem Eng Sci 122:573–584
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Siddharth, K., Pathak, A. & Pani, A.K. Real-time quality monitoring in debutanizer column with regression tree and ANFIS. J Ind Eng Int 15, 41–51 (2019). https://doi.org/10.1007/s40092-018-0276-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40092-018-0276-4