Abstract
In this paper, a bi-level game-theoretic model is proposed to investigate the effects of governmental financial intervention on green supply chain. This problem is formulated as a bi-level program for a green supply chain that produces various products with different environmental pollution levels. The problem is also regard uncertainties in market demand and sale price of raw materials and products. The model is further transformed into a single-level nonlinear programming problem by replacing the lower-level optimization problem with its Karush–Kuhn–Tucker optimality conditions. Genetic algorithm is applied as a solution methodology to solve nonlinear programming model. Finally, to investigate the validity of the proposed method, the computational results obtained through genetic algorithm are compared with global optimal solution attained by enumerative method. Analytical results indicate that the proposed GA offers better solutions in large size problems. Also, we conclude that financial intervention by government consists of green taxation and subsidization is an effective method to stabilize green supply chain members’ performance.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Environmental pollution, especially air pollution, is one of the obvious environmental health threats in different countries, contributing to a number of illnesses, such as asthma, and in some cases leading to premature death (Ilyas et al. 2010). Also, many of these environmental impacts have been studied by researchers (Sokolova and Caballero 2012, 2009). Concerns about the impact of environmental pollution on health and the economy have resulted in measures to mitigate emissions of the most harmful pollutants, such as particle pollution (acids, organic chemicals, metals, and soil or dust particles) and ozone (O3), which affects the respiratory system. Despite national and international interventions and reductions in major pollutant emissions, the health impacts of environmental pollution are not likely to decrease in the years ahead, unless proper and drastic action is taken.
However, governments have various policy options for the aim of recovering environmental condition (water, soil, and especially air quality), such as imposing strict standards on air pollutant emissions or managing and supervising fuel quality. Many of these policy options have been studied and analyzed to see whether they are effective in decreasing environmental pollution (Tolga Kaya and Kahraman 2011; Roberts 2013; Chen et al. 2013). It is obvious that in the years to come, the prices of health care from environmental pollution will become considerable without adequate efforts. Hence, proper and opportune environmental policies should be performed in order to manage and control the environmental issues that cause harmful effects on human health.
With due attention to the evident facts regarding the green supply chain (GSC) and green supply chain management (GSCM) concepts, and its many elements, there have been various definitions over the years. We will use the term GSCM in this paper and can define it as a series of regulations and interventions in the supply chain achieved by attempting to minimize the environmental impact from the suppliers to the end users (Basu and Wright 2008). It is also stated as a win–win strategy, through which economic benefits can be increased by reducing environmental impact (Zhu and Cote 2004; Zhu et al. 2008).
In recent years, the field of GSCM has been growing with an interest from both academia and industry, and therefore, the literature on this field in various applications is very diverse. An important point of view in GSCM is that it is not just about being environment-friendly. It is also about good business sense and increasing profits. In other words, the green point of view can serve as a powerful cost reduction tool by eliminating waste. For instance, in transportation, decreasing vehicle fuel consumption cuts emissions and saves on fuel costs. Managers of supply chain (SC) can improve the performance of SC’s processes while minimizing adverse environmental effects when they collaborate with environmental managers to improve these processes. Combining the views of environmental and SC managers is a natural fit. Indeed, a number of organizations have been doing it for some time (Wilkerson 2005).
GSCM has an important role in improving global environments and industrial ecology, but despite this significant role, integration of chain member operations stays challenging and a great part of this problem is a result of economic motivation deficiency. Though, without government supervision and legislation-based enforcement, SC members, such as manufacturers and suppliers, may only attempt to reach their business intentions to satisfying end-customer demands. To these manufacturers and suppliers, increasing benefits obtained from supplying and producing green products are negligible.
Accordingly, this work investigates how GSC members such as manufacturer and supplier act under governmental intervention with tariff legislation consisting of taxes and subsidies for both raw materials and final products. In our model, with the assumption of government financial supervision to reduce environmental pollution, the supplier provides raw materials and sales it to the manufacturer, who produces various products with different levels of environmental pollution and then sales products to the market. The market demand for products is assumed to be uncertain, while the price of raw material and product is uncertain, too.
The remainder of this paper is organized as follows. The “Literature review” section briefly expresses the related literature. The “Mathematical formulation” section presents the proposed problem scope, assumptions, and bi-level game-based GSCM model. The “Solution methodology” section describes steps of genetic algorithm (GA) as a proposed solution methodology used in this study to solve the problem. The “Results and discussion” section deals with the solving procedure of the proposed model and derives equilibrium solutions to characterize chain member actions under government financial intervention. Finally, the “Conclusions and further study” section gives conclusions and suggestions for the future research.
Literature review
In this section, we will introduce the literature review of concepts in this paper, including GSC and GSCM, game theory and its application to GSC, uncertainties in demand and price, BLP, and also GA which will be expressed subsequently.
GSCM has been introduced when issues of improving long-term economic profits and global environmental performance have been discussed among researchers in this field (Sheu et al. 2005). GSCM can be defined as a combination of environmental and supply chain management (SCM) activities, including product design, material selection, manufacturing processes, final product delivery, and end-of-life product management (Srivastava 2007).
GSC literatures have expressed this fact that GSCM concentrate on all of SC participants involves from suppliers to manufacturers, customers, and reverse logistics throughout the so-called closed-loop SC. So, more green operations, materials, or products might be attained (Bowen et al. 2001; Zhu and Sarkis 2004; Kumar et al. 2013). The main goal of GSCM is to reduce and hopefully minimize the global environmental impacts of SC processes generated by the whole SC participants from the suppliers to the end users. It is an effective strategy in which through decreasing environmental impacts, economic benefits can be increased (Zhu and Cote 2004; Zhu et al. 2008).
Adequate literature exists about a variety of aspects of GSCM (Carter and Ellram 1998; Srivastava 2007; Seuring and Müller 2008; Hafezalkotob 2015, 2017). The early literature focuses on the necessity, exigency, and importance of GSCM. GSCM began with an emphasis on some aspects of SCM that were more managerial instead of technological and not useful, such as logistics (Murphy et al. 1994; Szymankiewicz 1993), purchasing (Drumwright 1994), and reverse logistics (Barnes 1982; Pohlen and Farris 1992). Also, different kinds of methods and techniques have been used for problem formulation in this field, such as linear programming (Fleischmann 2001; Hu et al. 2002) that is one of the most common methods used for problem formulation, nonlinear programming (NLP) (Richter and Dobos 1999; Sarkis and Cordeiro 2001), and also dynamic programming (Klausner and Hendrickson 2000; Inderfurth et al. 2001; Richter and Weber 2001; Kiesmuller and Scherer 2003).
In addition, there has been a variety of studies that investigate game theory application to GSC. Modern game theory was introduced by Von Neumann and Morgenstern (1944) when they published “The Theory of Games and Economic Behavior.” After that, game theory has been stated as a mathematical and logical methodology to use in varying research fields, such as SCM, GSCM, economics and business, marketing, political science, and psychology, as well as logic and biology. This theory was developed extensively in the 1950s by many scholars.
Most of the researches on decision-making procedures of GSC are mainly based on the framework of game theory (Barari et al. 2012; Katsaliaki et al. 2014). Game theory has been used in SC problems; in particular, coordination, economic stability, and the SC efficiency have been discussed by different authors. In comparison with SC, game theory applications to GSCM are still under development.
Savaskan et al. (2004) investigated the game process of three models that characterize three used product collection procedures to investigate potential channel decisions and profits that have been obtained by channel members under product remanufacturing circumstances. Also, Savaskan and Van Wassenhove (2006) extended their model for a relatively more comprehensive closed-loop SC framework that has one manufacturer and two competing retailers. Rezaee et al. (2017) presented a model using multi-objective programming based on the integrated simultaneous data envelopment analysis–Nash bargaining game. Moreover, Esmaeilzadeh and Taleizadeh (2016) studied the optimal pricing decisions in a two-echelon supply chain under two scenarios. Then, the relationships between the manufacturers and the retailer were modeled by the MS-Stackelberg and MS-Bertrand game-theoretic approach. Various researchers have investigated the effects of government intervention on green supply chain. According to Zhu and Dou (2007), the game model of their study proposes that it would be better for government to increase the environmental regulations to make organizations and firms to implement environmental management. Also, Sheu (2011) investigated the problem of negotiations between producers and reverse logistics (RL) suppliers for cooperative agreements under government intervention. The author has concluded that over-intervention by a government may result in adverse effects on chain members’ profits and social welfare. The other researches in this subject can also be stated (Chen and Sheu 2009; Fenglan 2010; Liu et al. 2008; Yali 2010; Gong et al. 2007; Mitra and Webster 2008; Zhu and Dou 2007; Xiao-xi and Wei-qing 2012; Mahmoudi et al. 2014; Ghaffari et al. 2016; Hafezalkotob and Mahmoudi 2017).
According to assumptions about uncertain price and demand in this study, we introduce some of related studies subsequently. Uncertainty is expressed as a known and unknown confidence range of the imperfect information available at the present state. A large number of literatures exist about a variety of fields about uncertainties and among all; demand and price uncertainties are the main types of uncertainties that affect the operations of the SC. Some of these studies are declared subsequently.
Li et al. (2009) considered a supply contracting problem in which the buyer firm faces non-stationary stochastic price and demand. This study indicated that the selection of suppliers is particularly affected by price uncertainty. Moreover, Awudu and Zhang (2013) proposed a stochastic production planning model for a biofuel SC under demand and price uncertainties. Demands of end products are uncertain with known probability distributions, and the prices of end products follow geometric Brownian motion (GBM). Benders decomposition (BD) method with Monte Carlo simulation technique is applied to solve the proposed stochastic production planning model. In addition, Paul et al. (2014) developed an EOQ model for a coordinated two-level SC under energy (gasoline) price uncertainty and defective items in transshipment. The authors show that as the gasoline price uncertainty increases, both the total cost and shipment size increase. So, this indicates that the gasoline price influences the SC coordination.
To solve problems dealing with uncertainties, researchers have suggested a number of methods, including scenario programming (Wullink et al. 2004; Chang et al. 2007), robust optimization (Bertsimas and Thiele 2006; Leung et al. 2007; Mulvey et al. 1999), stochastic programming (Popescu 2007; Santoso et al. 2005), fuzzy approach (Petrovic et al. 1999; Schultmann et al. 2006; Liang 2008), and computer simulation and intelligent algorithms (Kalyanmoy 2001; Coello 2005). No individual algorithm dominates others, and different strategies are suitable for different situations. In this study, we utilized stochastic programming to deal with uncertainties in market demand, raw material price, and product price.
Another related field utilized in this study is bi-level programming problem (BLPP) that includes two players at different levels that consist of the leader and the follower. We can regard BLPP as a static version of the noncooperative, two-player game called Stackelberg problem introduced by Stackelberg (1952). BLP was introduced in mathematical programming field by Bracken and Mcgill (1973) in the 1970s and since then various studies have been done to review the subject (Colson et al. 2007; Vicente and Calamai 2004). Also, there are several methods to solve BLPPs that have been used by researchers such as branch-and-bound method (Bard and Falk 1982), penalty functions method (Aiyoshi and Shimizu 1981), and Karush–Kuhn–Tucker (KKT) conditions (Herskovits et al. 2000; Bianco et al. 2009; Li and Wang 2011). In addition, there have been some evolutionary algorithm studies in this field (Wang et al. 2005; Li and Wang 2007; Koh 2007; Wang et al. 2008). In this study, we have transformed the BLP model into a single-level NLP problem by replacing the lower-level optimization problem with its KKT conditions.
Also, a lot of numerical algorithms have been developed by a number of authors to solve multi-level programming. So, considering the NP-hardness of BLPP (Hansen et al. 1992), several authors proposed various algorithms to solve it (Colson et al. 2005; Bard and Moore 1990; Maiti and Roy 2016).
Candler and Townsley (1982) presented an implicit enumeration scheme to solve the problem. Bard (1983) offered a grid search algorithm which exhibits the desirable property of monotonicity. The proposed algorithm is based on two sets of necessary conditions developed and combined to provide an operational check for stationarity and local optimality.
Bard and Moore (1990) presented a branch-and-bound algorithm based on Kuhn–Tucker conditions to solve the problem. Gendreau et al. (1996) proposed an adaptive search method related to the Tabu search meta-heuristic to solve the linear BLPP. Esogbue (1999) proposed a GA for a special nonlinear BLP. And Savard and Gauvin (1994) gave the steepest descent direction for quadratic nonlinear BLPPs. Several researches used meta-heuristics for BLPP, such as Li et al. (2005) which developed a new algorithm based on particle swarm optimization (PSO) to solve BLPP, which combines two variants of PSO to solve the upper-level and lower-level programming problems interactively and cooperatively.
The effects of governmental financial intervention on the cooperation green supply chain are rarely investigated by pioneering researchers in GSCM and related areas. This paper presents a multi-product multi-level game-theoretic green supply chain model with uncertainties in market demand, material, and product sale price formulated in a BLPP. This paper considers a single decision variable named tariff which takes the positive and negative values to determine tax and subsides, respectively. Since it is not possible to solve a multi-level model in mathematical terms because of its NP-hardness, we propose an efficient meta-heuristic algorithm to solve this problem.
Mathematical formulation
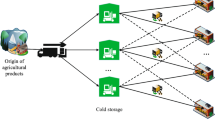
In the process of solving the problem, we regard a decentralized noncooperative decision system in which one leader (government) and two followers with equal position (supplier and manufacturer) are involved. We assume that the government and followers may have their own decision variables and objective functions. Therefore, the followers could control how to optimize their objective functions and the government can only control the reactions of followers through its own decision variables. The structure of GSC in this paper is shown in Fig. 1.
Definition of sets and notations
In this GSC, material supplier provides I types of raw materials. Manufacturer can purchase I types of material from supplier to produce J types of products to satisfy market demand. Under stochastic raw material sale price, product sale price, and stochastic market demand with limited production, our goal is to determine the supply and production quantity of the entire GSC so as to maximize the profit of the entire GSC, while maximizing the government’s income, and manage the environmental pollution cost.
Sets and indices
- I :
-
The set of raw materials (i = 1, …, n);
- J :
-
The set of products (j = 1, …, m);
Decision variables
- t i :
-
The tariff of raw material i (government’s decision variable), − ∞< ti<+ ∞;
- T j :
-
The tariff of product j (government’s decision variable), − ∞< Tj<+ ∞;
- q i :
-
The supply of raw material i (supplier’s decision variable), qi≥ 0;
- Q j :
-
The production of product j (manufacturer’s decision variable), Qj≥ 0;
Notations
- GNI:
-
The government net income;
- MPCi:
-
The environmental pollution cost of raw material i;
- PPCj:
-
The environmental pollution cost of product j;
- UB:
-
The upper bound of environmental pollution cost;
- Π S :
-
The supplier’s objective function;
- \( \tilde{w}_{i} \) :
-
The stochastic sale price of raw material i;
- c i :
-
The total supply expenses per unit for raw material i;
- γ :
-
The constant risk aversion coefficient of supplier;
- capsi:
-
The supply capacity for raw material i;
- Π M :
-
The manufacturer’s objective function;
- \( \tilde{P}_{j} \) :
-
The stochastic sale price of product j;
- e j :
-
The total production expenses per unit for product j;
- λ :
-
The constant risk aversion coefficient of manufacturer;
- capmj:
-
The production capacity for product j;
- α ij :
-
The consumption coefficient of raw material i in product j;
- \( \tilde{D}_{j} \) :
-
The stochastic market demand of product j;
- R S :
-
The minimum acceptable profit of supplier;
- R M :
-
The minimum acceptable profit of manufacturer;
- M :
-
A very large positive constant;
Assumptions
The goal of this work is to analyze the impact of governmental intervention via green legislation and financial instrument to persuade GSC members for green product production. To achieve this goal, several assumptions involved in this paper are described below.
-
Market demand, raw material sale price, and product sale price are uncertain.
-
GSC produces various products with different pollution levels.
-
Model formulation is based on Stackelberg, monopoly and vertical integration.
ti and Tj as tariff decision variables of government are considered free decision variables for both raw materials and final products, respectively. Therefore, we assume that positive values of ti and Tj represent taxes for raw materials and final products; similarly, the negative values of ti and Tj denote subsidies for raw materials and final products, respectively. Consequently, if the value of tariff is positive, it works as a profit element for government and a cost element for GSC members; on the other hand, if the value of tariff is negative, it would be a cost element for government and a profit element for GSC members.
The MPCi and PPCj represent environmental pollution cost of raw materials’ procurement and final products’ production, respectively. For generalization purpose of the model, we do not restrict the environmental pollution cost of raw materials and final products to specific elements. They may be all kinds of pollution costs caused by industrial activities like economic and medical expenses.
BLP formulation
A bi-level game-based model is constructed in this section to formulate the problem of interaction between government and SC. The optimization process consists of two levels: (1) an upper-level optimization of the government income and (2) a lower-level optimization of supplier and manufacturer profit. First level maximizes the government’s objective function to derive the solutions for ti and Tj.
Second level maximizes the supplier’s profit under uncertain raw material sale price and also maximizes the manufacturer’s profit under uncertain product sale price and market demand. Supplier decides about the amount of raw material procurement (qi), and similarly, manufacturer decides about the amount of final product production (Qj).
Now, let us consider government problem first. The upper-level model is used to optimize the government’s problem that is formulated as follows:
The government’s objective function is given as Eq. (1). As described in assumptions, ti and Tj are free decision variables for the government. Thus, if government assigns taxes to raw materials and final products, it acts like a profit element; and if government assigns subsidies to raw materials and final products, it acts like a cost element. Further, there are some constraints for the government. Constraint (2) sets the limitation on environmental pollution cost. It shows that the environmental cost caused by raw material procurement and final product manufacturing cannot exceed a specified upper bound. This upper bound may change depending on various legislations in different countries considering their environmental and economic conditions. Constraints (3) and (4) are individual rationality constraint (IR) under which supplier and manufacturer would like to supply raw materials and manufacture final products, respectively; otherwise, they reject it and withdraw from the market. These inequalities point out the GSC members’ interest to have long-term relationships with government. They express that a minimum profit should be considered for supplier and manufacturer in any situation.
The lower-level optimization model of supplier can be formulated as follows:
The supplier provide qi (i =1, 2, …, I) units of the ith raw material at the cost of ci (i =1, 2, …, I), respectively. The supplier’s decision variables are raw material procurement qi, and his profit function is given by Eq. (5). Furthermore, there are some constraints for the supplier, which includes constraint (6) that indicates procurement capacity, and constraint (7) that shows raw material production’s value is a nonnegative number.
Now let us describe the lower-level optimization model of manufacturer that can be formulated as follows:
The manufacturer purchases qi (i =1, 2, …, I) units of the ith raw material at the price of wi (i =1, 2, …, I), respectively, and she manufactures Qj (j =1, 2, …, J) units of the jth material at the cost and price of ej and pj (j =1, 2, …, J), respectively. Therefore, the manufacturer decides about production unit Qj to maximize his profit which is given by Eq. (8). Moreover, manufacturer encounters with some constraints in production procedures. Constraint (9) indicates this fact that raw material’s consumption in the process of manufacturing final products cannot be more than the available raw material provided by the supplier. Constraint (10) states that the amount of final product’s production must be more than the uncertain market demand. Constraints (11) and (12) assure that production quantities are feasible for the manufacturer.
Product sale price, material sale price, and market demand uncertainties
Demand and price uncertainties are the main types of uncertainties that affect the operations of the SC. Hence, it is assumed that the market demand, product price, and raw material price are uncertain parameters. Raw material price uncertainty defines the probability that price of a material might change during the planning horizon. We assume that sale price of raw material i is represented by a normal distribution considering mean (\( \bar{w}_{i} \)), and variance (σ 2 i ) as follows:
Thus, considering the supplier’s risk sensitivity, we assume that the supplier estimates her utility via the mean–variance value function of her random profit as follows (Tsay 2002; Gan et al. 2005; Lee and Schwarz 2007; Xiao and Yang 2008):
Equation (14) expresses that the supplier will make a trade-off between the mean and the variance of her random profit. The part γVar(ΠS) is the risk cost of supplier and γ denotes the attitude of supplier toward uncertainty. The increscent of γ results in an increase in conservativeness in supplier’s actions. Therefore, we can rewrite Eq. (5) as follows:
In a similar manner, we assume that sale price of product j is represented by a normal distribution considering mean (\( \bar{P}_{j} \)) and variance (σ 2 j ) as follows:
Thus, Eq. (8) can be rewritten as follows:
The third uncertain parameter in this paper is market demand of final products j. Market demand \( \tilde{D}_{j} \) for product j is normally distributed with known means and variances, \( \mu_{{D_{j} }} \) and \( \sigma_{{D_{j} }}^{2} \) where
Thus, constraint (10) is reformulated as follows:
where αj is the confidence level. That is, if αj = 0.05, then the manufacturer seeks to satisfy market demand at least 95% of the time and F−1(αj) is the cumulative distribution function (cdf) of the standard normal distribution.
Reformulation the whole problem as a single-level NLP
As described before, the whole problem is a BLPP that the government in upper level considered to be the leader. Also, the supplier and manufacturer in second level regarded as followers. To solve the bi-level programming problem, a single-level NLP is obtained by replacing the lower-level problem by its KKT optimality conditions and further linearizing the complementary terms. It can be shown that ΠS and ΠM are concave functions (refer to the “Appendix”). Such reformulations using KKT optimality conditions have been well studied for solving the problems, and after deriving KKT conditions for the above problem we achieve a single-level nonlinear problem. The reformulated optimization model is shown as follows:
As the lower-level optimization problem given by (5)–(11) is concave and continuous, we can replace it with its KKT conditions and rewrite the proposed bi-level problem as an NLP given in (20)–(35), where (20)–(23) are the part corresponding to the former upper level, (24)–(25) are the derivatives of the Lagrangian of the lower level, (26)–(29) are the complementarity conditions, and (30)–(35) are the constraints of the lower level. To simplify the mathematical model, we linearize Eqs. (26)–(29) by replacing each one with two linear constraints as follows:
Solution methodology
Traditional and classical techniques of optimization for an NLP are not efficient when the practical search space is too large, and there are too many decision variables. Hence, we chose a meta-heuristic method (GA) to solve the problem. GA is a population-based search method that moves from one set of points called population to another set of points in a single iteration with probable improvement by using set of control operators. GA is viewed as function optimizer, though problem ranges to which GA is applied are quite extensive features (Haupt and Haupt 2004). GA simulates natural selection, using imitative processes of the nature such as crossover, mutation, or selection. The GA begins with generating a random population of solutions to research the problem’s solution space. This method produces sequential populations of alternative solutions, until a solution is found with satisfactory results.
Each GA employs some basic components to solve a given problem such as chromosome representation, initial population production, fitness function, genetic operators, selection strategy, and parameters values. These ingredients are described in the following sections. In this study, all of the parameters are adjusted based on experimental data. The procedure followed for the GA is explained as follows:
Chromosome representation In the GA, each individual solution is shown by a chromosome consists of genes. Each chromosome is called a solution for the optimization problem, and in this research, each chromosome consists of I raw material tariff, J product tariff, I raw material procurement, J product production, and four KKT variables, respectively, as an array with the size of (4I + 4J) summarized as follows:

Initialization Initialization is an essential step for any evolutionary algorithm. In this research, first we define the parameters for the GA, including the population size and the maximum number of iterations. Afterwards, we generate an initial random population of chromosomes.
Fitness function Fitness function is a function that assigns a fitness value to the individual chromosome. It quantifies the optimality of a chromosome so that a particular solution or chromosome can be ranked against all other solutions. In this research, this function is same as the objective function of government, i.e., Eq. (20). As a result, first we evaluate the fitness value of each chromosome in the population and, then, order the fitness values from the largest to the least.
Selection strategy The plan for selecting chromosomes to create the next generation is described by selection strategy. Generally, the beginning operator that applied on population is selection strategy. There are different selection strategies that basically perform a same thing. They choose some chromosomes from current population using different mechanisms to be the parents of the new generation. These mechanisms include roulette wheel selection, tournament selection, rank selection, and some others. In this research, rank selection is employed. Therefore, we first rank the population according to their fitness value and afterwards the specific number of best answers will be selected for a new generation.
Heuristic operator A proposed heuristic function is used as an operator before crossover and mutation operators to produce new offspring. In this operator for each column of solution matrix (i.e., for each decision variable), we replace each gene of the column with mean value of the genes in the higher chromosomes.
Crossover One of the most important mechanisms of GA is crossover. New offspring is produced by joining genes of selected parents. If the new offspring gets the best features from each parent, it may be better than the parents. In this study, the crossover operates as follows: firstly, a point (r) is randomly selected for each column of solution matrix (i.e., for each decision variable); secondly, the genes are written in reverse from the point (r + 1) to the last element in that column. The reason we choose and change genes from one column is because we should compare genes (decision variables) with similar ones due to the different intervals for each decision variable. Afterward, we check the feasibility of the new offspring; if the new solution was feasible, we consider it as a part of new generation.
Mutation Mutation operator makes a new mutated chromosome by making a random modification. Mutation operator is used from one generation of population to the next, to avoid getting trapped in local optimum. In this study, the mutation operates as follows: first, for each column of solution matrix (i.e., for each decision variable), two points (r1, r2) are randomly selected, and then, each point is replaced by the other one. Subsequently, the feasibility of the new offspring is checked; if the new solution was feasible, we regard it as a part of new generation.
Termination criterion Termination is the criterion by which the GA decides to continue searching or stop it. In this paper, after a fixed number of iterations of the algorithm, it will stop searching and the best produced solution that has been recorded in the algorithm is reported as the best solution to NLP by the proposed GA. The pseudocode for the GA method is represented in Fig. 2.
In this algorithm, G(t) represents a population of chromosomes in t-th generation, G′(t) displays the population of chromosomes after implementing heuristic operator and so on. Also, Z represents a set of chromosomes in the current generation which is selected by the algorithm.
Results and discussion
In this section, some test problems with different sizes are solved to show the application of the model as well as efficiency of its solution algorithm. The sizes of the test problems are presented in Table 1. The test problems are solved with different GA parameters including Popsize and iteration to test the quality of the solutions obtained through the proposed GA. Moreover, to investigate the validity and feasibility of the proposed method, small-sized problems are solved by enumerative method. In this technique, given that all the decision variables are considered to be discrete, the whole solution space has been searched to find the optimal solution for the problem. For small size problems, the enumerative method provides better results but with worst computational time. Some larger-size problems which cannot be solved by enumerative method are only solved by the proposed GA. The computational results acquired from the proposed GA with different Popsize and iteration is displayed in Table 2. Additionally, results obtained from enumerative method have been compared with the average of solution values in each type of problem in Table 3. The authors could not attain results of enumerative method in problem type III, due to the length of time. With the propose of summarizing the paper, the data set used for the test problems in Tables 2 and 3 has not been presented. But it is available with the authors if needed. In addition, MATLAB 7.12 is used to implement the proposed GA and also enumerative method. MATLAB is a functional software and has been used in different kinds of fields (Valipour 2014, 2016a, b; Valipour et al. 2013a, b, 2017).
The accuracy of the GA solutions is expressed by the value of the error percentage in the last column of Table 3 This error percentage is calculated by the following equation:
Table 3 clearly indicates that the proposed GA offers better solutions in large size problems according to computational time. According to the results shown in Table 3, solutions obtained from the proposed GA and enumerative method in smaller sizes (2.2) are approximately equal (~ %1.2 error). However, by increasing the size of the problem (3.3), difference between the solution values in two different methods is increased at a low rate (~ 1.7%). Based on the solutions presented in Table 3, the proposed GA can be effectively employed for the large size problems. As shown in the last column of Table 3, the error percentage in size 2.2 and 3.3 is under 2%. Also, Fig. 3 compares the best solutions obtained by the proposed GA and enumerative method in different sizes.
Numerical example
In this section, we solve a numerical example in the field of gasoline production. In this example, a GSC is taken into account, including a supplier and a manufacturer. The supplier procures two raw materials for gasoline production consisting of benzene and aromatics.
With the global phase out of leaded gasoline, different additives have replaced the lead compounds. In order to sustain octane levels in producing gasoline, oil companies replaced lead with something almost as bad: aromatic hydrocarbons, or simply aromatics, mainly comprised of benzene, toluene, and xylene. However, concern over its negative health effects have led to stringent regulation of all gasoline’s aromatic compounds. In this study, we consider benzene and aromatics in general, as two individual gasoline’s raw materials.
Also, the manufacturer produces gasoline with Euro 2 and Euro 4 standards. European emission regulations for light-duty and heavy-duty vehicles are commonly referred to as Euro 2… Euro 6. The Euro standards require vehicle producers to reduce the exiting polluting emission levels in a more effective manner by making certain technical changes in their vehicles. As gasoline quality was required alongside Euro stages, government should make an attempt to persuade SC’s members to raise the quality of their products in order to meet air quality requirements. The goal is to make GSC members achieve better emission standards and improve public health. Consequently, in this study gasoline with Euro 4 standard is considered to be a green product. Default parameters for government, supplier, and manufacturer as well as GA are listed below:
-
UB = 54,000
-
\( \gamma \) = 0.1
-
\( \lambda \) = 0.5
-
\( R_{\text{S}} \) = 12,000
-
\( R_{\text{M}} \) = 15,000
-
Iteration= 60
-
Popsize= 25
Furthermore, other data used for numerical example are shown in Tables 4, 5, 6 and 7 as follows:
Numerical analysis
We have implemented the proposed GA to solve the NLP in the platform of MATLAB 7.12 using information in Tables 4, 5, 6 and 7 which contain sample data. The best solution obtained by proposed GA is shown in Table 8 and its variable values in Table 9.
As expressed before, negative values of ti and Tj state that government (leader) assigns subsidies to raw materials procurement and final products production, respectively. On the other hand, positive values of ti and Tj declare that government levies green taxes on GSC members. As shown in the highlighted cells in Table 9, raw material tariff (t) values and the first product tariff (T) value are positive and the second product tariff (T) value is negative. Thus, in this example government should levy green taxes on both raw materials (benzene and aromatics) and one of the final products (i.e., gasoline with Euro 2 standard) and, on the other hand, assigns subsidies to the other final product (i.e., gasoline with Euro 4 standard).
From the obtained results, we conclude that the objective value (GNI) is dependent on the maximum permitted value of environmental pollution cost (UB); therefore, it is meaningful to examine the sensitivity of approximate objective value with respect to UB. We choose five values of UB for a same problem, that is, UB1= 54,000, UB2= 50,000, UB3= 46,000, UB4= 42,000, and UB5= 38,000, and calculate the approximate objective values as shown in Fig. 4. It indicates that the objective value will decrease with the reduction in the value of UB.
Also, the sensitivity of raw materials and products tariff values has been examined with respect to UB. It implies that when UB is decreased, the amount of taxes (i.e., positive values of tariff) assigned to regular raw materials and final products is increased and also the amount of subsides (i.e., negative values of tariff) assigned to green ones is intensified by the government to persuade GSC members to raise the quality of their products. These results are displayed in Figs. 5 and 6. From the obtained results, we conclude that the proposed GA offers better solutions in large size problems according to computational time. Also, the error percentage in all sizes is under 2%. Therefore, the results obtained from the proposed method are completely accurate.
Conclusions and further study
The modeling in this study focused on Stackelberg game between the government as a leader and the GSC members (supplier and manufacturer) as followers. To solve the bi-level game-theoretic model, a GA was designed to resolve the single-level model obtained from KKT conditions for the lower level. Feasibility and validity of the proposed method were evaluated by solving several test problems using enumerative method and comparing them with results of the proposed GA. In addition, the results indicated that the computational time in the proposed GA is considerably lesser than that in enumerative method. The proposed method for bi-level GSC has attained its objectives including the maximization of government net income considering the environmental pollution cost, as well as the maximization of supplier and manufacturer income in the second level of the bi-level plan. Implementing the proposed GA approach for bi-level Stackelberg game-based GSC model, we determined the values of green taxes and subsides (using tariff decision variable) by which government financial and environmental intervention could be planned and also GSC members could decide about procurement and production values for green and non-green products.
There are many other aspects, which should be explored in the future studies. For example, more than two members can be considered for GSC such as retailer and distributer. Also, we can utilize a multi-objective model with considering government net income and environmental pollution cost as objectives and then solve the model by the use of multi-objective GA or other suitable methods. Another future study could be developing the model by considering more than one GSC.
References
Aiyoshi E, Shimizu K (1981) Hierarchical decentralized systems and its new solution by a barrier method. IEEE Tran Syst Man Cybern 11:444–449
Awudu I, Zhang J (2013) Stochastic production planning for a biofuel supply chain under demand and price uncertainties. Appl Energy 103:189–196
Barari S, Agarwal G, Zhang WJ, Mahanty B, Tiwari MK (2012) A decision framework for the analysis of green supply chain contracts: an evolutionary game approach. Expert Syst Appl 39(3):2965–2976
Bard JF (1983) An algorithm for solving the general bilevel programming problem. Math Oper Res 8:260–272
Bard J, Falk J (1982) An explicit solution to the multi-level programming problem. Comput Oper Res 9:77–100
Bard JT, Moore JT (1990) The mixed integer linear bilevel programming problem. Oper Res 38:911–921
Barnes JH (1982) Recycling: a problem in reverse logistics. J Macromark 2(2):31–37
Basu R, Wright JN (2008) Total supply chain management. Butterworth-Heinemann, London
Bazaraa MS, Sherali HD, Shetty CM (2006) Nonlinear programming: theory and algorithms, 3rd edn. Wiley, Hoboken, pp 113–114
Bertsimas D, Thiele A (2006) A robust optimization approach to inventory theory. Oper Res 54(1):150–168
Bianco L, Caramia M, Giordani S (2009) A bilevel flow model for hazmat transportation network design. Transp Res C Emerg 17(2):175–196
Bowen FE, Cousin PD, Lamming RC, Faruk AC (2001) The role of supply management capabilities in green supply. Prod Oper Manag 10(2):174–189
Bracken J, McGill J (1973) Mathematical programs with optimization problems in the constraints. Oper Res 21:37–44
Candler W, Townsley R (1982) A linear two-level programming problem. Comput Oper Res 9:59–76
Carter CR, Ellram LM (1998) Reverse logistics—a review of the literature and framework for future investigation. Bus Logist 19(1):85–102
Chang MS, Tseng YL, Chen JW (2007) A scenario planning approach for the flood emergency logistics preparation problem under uncertainty. Transp Res E Logist 43(6):737–754
Chen YJ, Sheu JB (2009) Environmental-regulation pricing strategies for green supply chain management. Transp Res E Logist 45(5):667–677
Chen Y, Jin GZ, Kumar N, Shi G (2013) The promise of Beijing: evaluating the impact of the 2008 Olympic Games on air quality. J Environ Econ Manag 66(3):424–443
Coello CAC (2005) An introduction to evolutionary algorithms and their applications. Advanced distributed systems. Springer, Berlin
Colson B, Marcotte P, Savard G (2005) Bilevel programming: a survey. 4OR-Q J Oper Res 3:87–107
Colson B, Marcotte P, Savard G (2007) An overview of bilevel optimization. Ann Oper Res 153:235–256
Drumwright M (1994) Socially responsible organisational buying: environmental concern as a noneconomic buying criterion. J Market 58(8):1–19
Esmaeilzadeh A, Taleizadeh AA (2016) Pricing in a two-echelon supply chain with different market powers: game theory approaches. J Ind Eng Int 12:119
Esogbue AO (1999) Cluster validity for fuzzy criterion clustering. Comput Math Appl 37(11–12):95–100
Fenglan L (2010) An analysis of the dynamic game model between government and enterprises of green supply chain. In: International conference on management and service science (MASS), pp 1–4
Fleischmann M (2001) Quantitative models for reverse logistics. Springer, Berlin
Gan XH, Sethi SP, Yan HM (2005) Channel coordination with a risk-neutral supplier and a downside-risk-averse retailer. Prod Oper Manag 14(1):80–89
Gendreau M, Marcotte P, Savard G (1996) A hybrid Tabu_Ascent algorithm for the linear bilevel programming problem. J Global Optim 9:1–14
Ghaffari M, Hafezalkotob A, Makui A (2016) Analysis of implementation of Tradable Green Certificates system in a competitive electricity market: a game theory approach. J Ind Eng Int 12(2):185–197
Gong Y, Tang J, Chen J (2007) A dynamic game analysis on the incomplete information in enterprises’ reverse logistics. In: International conference on transportation engineering, pp 533–538
Hafezalkotob A (2015) Competition of two green and regular supply chains under environmental protection and revenue seeking policies of government. Comput Ind Eng 82:103–114
Hafezalkotob A (2017) Competition, cooperation, and coopetition of green supply chains under regulations on energy saving levels. Transp Res Part E 97:228–250
Hafezalkotob A, Mahmoudi R (2017) Selection of energy source and evolutionary stable strategies for power plants under financial intervention of government. J Ind Eng Int 13(3):357–367
Hansen B, Jaumard B, Savard G (1992) New branch and bound rules for linear bilevel programming. SIAM J Sci Stat Comput 13:1194–1217
Haupt RL, Haupt SE (2004) Practical GAs, 2nd edn. Wiley, New Jersey
Herskovits J, Leontiev A, Dias G, Santos G (2000) Contact shape optimization: a bilevel programming approach. Struct Multidiscip Optim 20:214–221
Hu L, Cao Y, Cheng C, Shao H (2002) Sampled-data control for time-delay systems. J Franklin Inst 339:231–238
Ilyas SZ, Khattak AI, Nasir SM, Qurashi T, Durrani R (2010) Air pollution assessment in urban areas and its impact on human health in the city of Quetta, Pakistan. Clean Technol Environ Policy 12:291–299
Inderfurth K, de Kok AG, Flapper SDP (2001) Product recovery in stochastic remanufacturing system with multiple reuse options. Eur J Oper Res 133:130–152
Kalyanmoy D (2001) Multi-objective optimization using evolutionary algorithms. Wiley, New York
Katsaliaki K, Mustafee N, Kumar S (2014) A game-based approach towards facilitating decision making for perishable products: an example of blood supply chain. Expert Syst Appl 41(9):4043–4059
Kiesmuller GP, Scherer CW (2003) Computational issues in a stochastic nite horizon one product recovery inventory model. Eur J Oper Res 146(3):553–579
Klausner M, Hendrickson CT (2000) Reverse logistics strategy for product take-back. Interfaces 30:156–165
Koh A (2007) Solving transportation bi-level programs with differential evolution. In: 2007 IEEE congress on evolutionary computation (CEC-2007), pp 2243–2250
Kumar S, Luthra S, Haleem A (2013) Customer involvement in greening the supply chain: an interpretive structural modeling methodology. J Ind Eng Int 9:6
Lee JY, Schwarz LB (2007) Leadtime reduction in a (Q, r) inventory system: an agency perspective. Int J Prod Econ 105:204–212
Leung SCH, Tsang SOS, Ng WL, Wu Y (2007) A robust optimization model for multi-site production planning problem in an uncertain environment. Eur J Oper Res 181(1):224–238
Li H, Wang Y (2007) A GA for solving a special class of nonlinear bilevel programming problems. In: Shi Y, Albada G, Dongarra J, Sloot P (eds) Computational science AI ICCS 2007, Lecture notes in computer science, vol 4490, pp 1159–1162
Li H, Wang Y (2011) An evolutionary algorithm with local search for convex quadratic bilevel programming problems. Appl Math Inf Sci 5(2):139–146
Li H, Zhang A, Zhao M, Xu Q (2005) Particle swarm optimization algorithm for FIR digital filters design. Acta Electron Sin 33(7):1338–1341
Li S, Murat A, Huang W (2009) Selection of contract suppliers under price and demand uncertainty in a dynamic market. Eur J Oper Res 198(3):830–884
Liang TF (2008) Integrating production-transportation planning decision with fuzzy multiple goals in supply chains. Int J Prod Res 46(6):1477–1494
Liu, M., Ye, H., Qi, X., Shui, W. (2008). Analysis on trilateral game of green supply chain. In: Logistics: the emerging frontiers of transportation and development in China, pp 575–581
Mahmoudi R, Hafezalkotob A, Makui A (2014) Source selection problem of competitive power plants under government intervention: a game theory approach. J Ind Eng Int 10:59
Maiti SK, Roy SK (2016) Multi-choice stochastic bi-level programming problem in cooperative nature via fuzzy programming approach. J Ind Eng Int 12:287
Mitra S, Webster S (2008) Competition in remanufacturing and the effects of government subsidies. Int J Prod Econ 111(2):287–298
Mulvey JM, Vanderbei RJ, Zenios SA (1999) Robust optimization of large-scale systems. Oper Res 43(2):264–281
Murphy PR, Poist RF, Braunschweig CD (1994) Management of environmental issues in logistics: current status and future potential. Transp J 34(1):48–56
Paul S, Wahab MIM, Cao XF (2014) Supply chain coordination with energy price uncertainty, carbon emission cost, and product return. Int Ser Oper Res Manag Sci 197:179–199
Petrovic D, Roy R, Petrovic R (1999) Supply chain modeling using fuzzy sets. Int J Prod Econ 59(1–3):443–453
Pohlen TL, Farris MT (1992) Reverse logistics in plastics recycling. Int J Phys Distrib Logist Manag 22(7):35–47
Popescu I (2007) Robust mean–covariance solutions for stochastic optimization. Oper Res 55(1):98–112
Rezaee MJ, Yousefi S, Hayati J (2017) A multi-objective model for closed-loop supply chain optimization and efficient supplier selection in a competitive environment considering quantity discount policy. J Ind Eng Int 13:199
Richter K, Dobos I (1999) Analysis of EOQ repair and waste disposal problem with integer setup. Int J Prod Econ 59:463–467
Richter K, Weber J (2001) The reverse Wagner/Whitin model with variable manufacturing and remanufacturing cost. Int J Prod Econ 71:447–456
Roberts S (2013) Have the short-term mortality effects of particulate matter air pollution changed in Australia over the period 1993–2007? Environ Pollut 182:9–14
Santoso T, Ahmed S, Goetschalckx M, Shapiro A (2005) A stochastic programming approach for supply chain network design under uncertainty. Eur J Oper Res 167(1):96–115
Sarkis J, Cordeiro J (2001) An empirical evaluation of environmental efficiencies and firm performance: pollution prevention versus end-of pipe practice. Eur J Oper Res 135:102–113
Savard G, Gauvin J (1994) The steepest descent direction for nonlinear bilevel programming problem. Oper Res Lett 15:265–270
Savaskan RC, Van Wassenhove LN (2006) Reverse channel design: the case of competing retailers. Manage Sci 52(1):1–14
Savaskan RC, Bhattacharya A, Van Wassenhove LN (2004) Closed-loop supply chain models with product remanufacturing. Manage Sci 50(2):239–252
Schultmann F, Frohling M, Rentz O (2006) Fuzzy approach for production planning and detailed scheduling in paints manufacturing. Int J Prod Res 44(8):1589–1612
Seuring S, Müller M (2008) From a literature review to a conceptual framework for sustainable supply chain management. J Clean Prod 16(15):1699–1710
Sheu JB (2011) Bargaining framework for competitive green supply chains under governmental financial intervention. Transp Res E Logist 47:573–592
Sheu JB, Chou YH, Hu CC (2005) An integrated logistics operational model for green-supply chain management. Transp Res E Logist 41(4):287–313
Sokolova MV, Caballero AF (2009) Modeling and implementing an agent-based environmental health impact decision support system. Expert Syst Appl Part 2 36(2):2603–2614
Sokolova MV, Caballero AF (2012) Evaluation of environmental impact upon human health with DeciMaS framework. Expert Syst Appl 39(3):3469–3483
Srivastava SK (2007) Green supply-chain management: a state-of-the-art literature review. Int J Manag Rev 9(1):53–80
Stackelberg HV (1952) The theory of the market economy. Oxford University Press, Oxford
Szymankiewicz J (1993) Going green: the logistics Dilemma. Logist Inf Manag 6(3):36–43
Tolga Kaya T, Kahraman C (2011) An integrated fuzzy AHP-ELECTRE methodology for environmental impact assessment. Expert Syst Appl 38(7):8553–8562
Tsay AA (2002) Risk sensitivity in distribution channel partnerships: implications for manufacturer return policies. J Retail 78:147–160
Valipour M (2014) Application of new mass transfer formulae for computation of evapotranspiration. J Appl Water Eng Res 2(1):33–46
Valipour M (2016a) How much meteorological information is necessary to achieve reliable accuracy for rainfall estimations? Agriculture 6(4):53
Valipour M (2016b) Variations of land use and irrigation for next decades under different scenarios. Irriga Braz J Irrig Drain 1(1):262–288
Valipour M, Banihabib ME, Behbahani MR (2013a) Comparison of the ARMA, ARIMA, and the autoregressive artificial neural network models in forecasting the monthly inflow of Dez dam reservoir. J Hydrol 476:433–441
Valipour M, Mousavi M, Valipour R, Rezaei E (2013b) A new approach for environmental crises and its solutions by computer modeling. In: The 1st international conference on environmental crises and its solutions, at Kish Island, Iran
Valipour M, Gholami Sefidkouhi MA, Raeini-Sarjaz M (2017) Selecting the best model to estimate potential evapotranspiration with respect to climate change and magnitudes of extreme events. Agric Water Manag 180(A):50–60
Vicente LN, Calamai PH (2004) Bilevel and multilevel programming: a bibliography review. J Global Optim 5(3):291–306
Von Neumann J, Morgenstern O (1944) Theory of games and economic behavior. Princeton University Press, Princeton
Wang Y, Jiao YC, Li H (2005) An evolutionary algorithm for solving nonlinear bilevel programming based on a new constraint-handling scheme. IEEE Tran Syst Man Cybern C 35(2):221–232
Wang G, Wan Z, Wang X, Lv Y (2008) GA based on simplex method for solving linear-quadratic bilevel programming problem. Comput Math Appl 56(10):2550–2555
Wilkerson T (2005) Can one green deliver another? Harvard Business School Publishing Corporation. http://www.supplychainstrategy.org/. Accessed 15 Jan 2018
Wullink G, Gademann AJRM, Hans EW, Van Harten A (2004) Scenario-based approach for flexible resource loading under uncertainty. Int J Prod Res 42(24):5079–5098
Xiao T, Yang D (2008) Price and service competition of supply chains with risk-averse retailers under demand uncertainty. Int J Prod Econ 114:187–200
Xiao-xi W, Wei-qing X (2012) Evolutionary game analysis of the reverse supply chain based on the government subsidy mechanism. In: Second international conference on business computing and global informatization (BCGIN), pp 99–102
Yali LU (2010) Research on evolutionary mechanisms of green supply chain constraints by macro-environment. In: ICLEM, pp 1009–1016
Zhu QH, Cote RP (2004) Integrating green supply chain management into an embryonic eco industrial development: a case study of the Guitang Group. J Clean Prod 12:1025–1035
Zhu Q, Sarkis J (2004) Relationships between operational practices and performance among early adopters of green supply chain management practices in Chinese manufacturing enterprises. J Oper Manag 22(3):265–289
Zhu QH, Dou YJ (2007) Evolutionary game model between governments and core enterprises in greening supply chains. Syst Eng Theory Pract 27(12):85–89
Zhu QH, Sarkis J, Lai KH (2008) Confirmation of a measurement model for green supply chain management practices implementation. Int J Prod Econ 111:261–273
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
This appendix contains the proof of the concavity of \( \varPi_{\text{S}} \) and \( \varPi_{\text{M}} \). According to (Bazaraa et al. 2006), \( \varPi_{\text{S}} \) and \( \varPi_{\text{M}} \) are concave if and only if their Hessian matrix is negative semidefinite (NSD), that is, we have \( d^{t} H_{{\varPi_{\text{S}} }} d \le 0 \) and \( d^{t} H_{{\varPi_{\text{M}} }} d \le 0 \) for all \( d \in {\mathbb{R}}^{n} ,\;d \ne 0 \). Thus, we prove their concavity as follows.
For supplier objective function we have:
It is obvious that \( d^{t} H_{{\varPi_{\text{S}} }} d \le 0 \). So, supplier’s Hessian matrix (\( H_{{\varPi_{\text{S}} }} \)) is negative semidefinite. Therefore, \( \varPi_{\text{S}} \) is concave. Similarly, for manufacturer objective function we have:
It is obvious that \( d^{t} H_{{\varPi_{\text{M}} }} d \le 0 \). So, manufacturer’s Hessian matrix (\( H_{{\varPi_{\text{M}} }} \)) is negative semidefinite. Therefore, \( \varPi_{\text{M}} \) is concave.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Hafezalkotob, A., Zamani, S. A multi-product green supply chain under government supervision with price and demand uncertainty. J Ind Eng Int 15, 193–206 (2019). https://doi.org/10.1007/s40092-018-0271-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40092-018-0271-9