Download PDF

Retrieval–travel-time model for free-fall-flow-rack automated storage and retrieval system

Open Access
Technical Article
First Online:
Received:
Accepted:
  • 213 Downloads

Abstract

Automated storage and retrieval systems (AS/RSs) are material handling systems that are frequently used in manufacturing and distribution centers. The modelling of the retrieval–travel time of an AS/RS (expected product delivery time) is practically important, because it allows us to evaluate and improve the system throughput. The free-fall-flow-rack AS/RS has emerged as a new technology for drug distribution. This system is a new variation of flow-rack AS/RS that uses an operator or a single machine for storage operations, and uses a combination between the free-fall movement and a transport conveyor for retrieval operations. The main contribution of this paper is to develop an analytical model of the expected retrieval–travel time for the free-fall flow-rack under a dedicated storage assignment policy. The proposed model, which is based on a continuous approach, is compared for accuracy, via simulation, with discrete model. The obtained results show that the maximum deviation between the continuous model and the simulation is less than 5%, which shows the accuracy of our model to estimate the retrieval time. The analytical model is useful to optimise the dimensions of the rack, assess the system throughput, and evaluate different storage policies.

Keywords

Automated storage/retrieval systems (AS/RS) Free-fall-flow-rack AS/RS (FF-flow-rack AS/RS) Travel time Throughput Drug distribution Modelling 
Download article PDF

Introduction

Over the last years, automated storage/retrieval systems (AS/RSs) have become the focus of many companies and distribution centers, through the major advantages, they offer such as reducing delivery time, savings in labour costs and floor space, faster and more reliable operation of the warehouse, the decrease of handling errors, and improved throughput level. AS/RS are mainly introduced to eliminate walking that accounted for 70% of manual retrieval time (Lee 1997). AS/RS are widely used in a variety of industries, as an essential component in a flexible manufacturing system (FMS) (Van Den Berg et al. 2000). Moreover, AS/RS can be classified as mechatronic systems (Sharma and Sharma 2015).

According to the Material Handling Institute of America, an automated storage and retrieval system (AS/RS) consists of a variety of material and control systems that handle store and retrieve loads with precision, accuracy, and great speed (Material Handling Institute 1977). In general, an AS/RS includes the following main components: storage racks, aisles, storage and retrieval (S/R) machines, pick-up/drop-off (P/D) stations, and the control system. Racks are composed of bins that can store loads. Aisles are the spaces between the racks. Storage and retrieval machines are fully automated cranes that can pick-up and drop-off loads. Pick-up/drop-off (P/D) stations are used for incoming and outgoing loads. The control system is the responsible for managing storage and retrieval operations.

AS/RS structures are designed according to their different size, weight, and volume of loads to be handled, and characterized of the warehouse. These different structures include unit-load AS/RS, mini-load AS/RS, man-on-board AS/RS, carousel AS/RS, deep-lane AS/RS, multi-aisle AS/RS, mobile-rack AS/RS, and flow-rack AS/RS.

To reduce the installation cost and to increase the performances of the AS/RSs, a new variant of flow-rack AS/RS has been developed, which consists of a free-fall-flow-rack AS/RS (FF-flow-rack AS/RS). This new kind of AS/RS was introduced by Mekapharm (Mekapharm 2016). It can operate without any storage/retrieval machines, which are replaced by the combination of two movements: vertical movement performed by the free fall of items and horizontal movement achieved by a conveyor. As opposed to the traditional flow-rack AS/RS, the system used (S/R) machines that travel simultaneously horizontally and vertically.

The main objective of this paper is to develop an analytical expression of expected retrieval–travel time. This research will be useful for the decision-maker to optimise the rack dimensions, evaluate the system throughput, and compare different storage policies. To evaluate the developed expression (based on a continuous approach) for its accuracy, we compare the results obtained from the expression with those obtained from the computer simulations (based on a discrete model).

The expected travel time of S/R machine is considered as the most important factor when evaluating the performance of an AS/R system. Since 1976, research on the modelling of travel time has been widely investigated. For this reason, several researchers have produced many articles in this area. Sarker and Babu (1995) and Roodbergen and Vis (2009) had presented a survey of AS/RS.

The literature on the modelling of the travel time for a unit-load AS/RS shows a variety of approaches. Hausman et al. (1976) were the first who have proposed the travel-time model of the single-command cycle. The authors assumed a square-in-time continuous rack. They were considered random, full turnover, and class-based storage assignment policies. This study was extended by Graves et al. (1977) by modelling the travel time model of dual-command cycle for the same assumptions. The most interesting approach to this issue has been proposed by Bozer and White (1984). They developed the expected single and dual travel time models of rectangular rack under a random storage and for different positions input/output point. In addition, various dwell-point strategies for the storage/retrieval machine were examined.

These researchers do not take into account all operational characteristics of an AS/RS such as acceleration and deceleration of the S/R machine and the rack configuration. Therefore, Hwang and Lee (1990) presented travel-time models that integrated the operating characteristics of the S/R machine, including constant acceleration and deceleration rate, and the maximum-velocity restriction. Chang et al. (1995) continued Bozer and White (1984) study by including acceleration and deceleration instead of assuming constant speed. This work was extended by Wen et al. (2001); they have considered class-based and full-turnover-based storage assignment policies. In the paper of Chang and Wen (1997), the authors studied the impact of the rack configuration on the expected travel time. Recently, Bortolini et al. (2015) extended the analytical models that are already proposed by the literature to compute the expected travel time of (AS/RS) in three-class-based storage. The authors determined the analytical closed form of the mean travel time for both the single-command (SC) and the dual-command (DC) cycles varying the warehouse shape factor and the ABC turnover curve.

For the flow-rack AS/RS, much research has been done. By the inspiration of Bozer and White (1984) previous work, Sari et al. (2005) presented mathematical models for the expected travel time for a flow-rack AS/RS, which used two (S/R) machines. The first model is developed using a continuous approach and compared with a discrete model for accuracy via simulation. The authors conclude that the expressions based on the continuous approach are extremely practical due to the difference in computation time. After that, Sari (2010) performed a comparative study between unit-load AS/RS and flow-rack AS/RS. The author considered two comparison parameters: space‘s use and travel time. Xu et al. (2015) developed the dual cycle and quadruple cycle travel time models for the traditional single-deep single-AS/RS and double-deep dual-shuttle AS/RS. Through a comparison between the two systems, the authors find that the efficiency of the system has a significant improvement using dual-shuttle S/R machine. In a recent paper, Hachemi and Besombes (2013) extended the problem of retrieval sequencing for flow-rack AS/RS by integrating the product expiry date. They introduced an optimisation method as decision process, which performs a real-time optimisation into two phases and formulated as an integer program.

To decrease the travel time for the flow-rack AS/RS, many researchers have proposed various methods. Sari et al. (2007) studied the impact of P/D stations and restoring conveyor locations on expected retrieval-time and classified their optimal positions. Meghelli-Gaouar and Sari (2010) used a two class-based storage policy for the flow-rack AS/RS, where each item is assigned to the same bin as closely as possible to the P/D point. This work was extended by Bessenouci et al. (2012) by developing two metaheuristic algorithms (tabu search and simulated annealing) applied to the control of the S/R machine. Hachemi and Alla (2008) presented an optimisation method of retrieval sequencing where the AS/RS was depicted by a coloured Petri net model. By considering dual cycle coupled with lower mid-point S/R crane dwell-point policy, Xu et al. (2017) has developed a continuous travel-time model for DC in 3D compact storage system; then, he has used the analytical models to optimise system dimensions.

Recently, Sari and Bessnouci (2012) proposed a new kind of flow-rack AS/RS: using a single machine for storage and retrieval operations instead of two machines. They developed analytical-travel-time models of the storage and retrieval machine under randomized storage assignment. Two dwell-point positions were considered. Otherwise, De Koster et al. (2008) used a lifting mechanism on the opposite face of the S/R machine for a flow-rack AS/RS. They presented a closed-form expression of expected retrieval–travel time for single-command cycles and derived an approximate travel-time expression for dual-command cycles of the system. In addition, Chen et al. (2015) designed a bi-directional-flow-rack (BFR) in which bins in adjacent columns slope to opposite directions. They have developed a travel-time model for BFR systems. An extension of Sari and Bessnouci (2012)work was proposed by Hamzaoui and Sari (2015), which determined optimal dimensions of the same AS/RS design minimizing expected travel times of the S/R machine using an enumeration technique.

Other studies have been undertaken to present travel time for many AS/RS types, such as the autonomous vehicle S/R system (AVS/RS), multi-aisle AS/RS, split-platform AS/RS (SP-AS/RS), and the multiple in-the-aisle pick positions (MIAPP-AS/RS).

The first study on the performances of an AVS/RS was proposed by Malmborg (2002), who modelled the travel time of an AVS/RS according to the number of aisles, tiers, vehicles, and lifts, by considering a random storage policy, and a tier-to-tier configuration. Marchet et al. (2012) criticized the previously mentioned work for the fact that they did not take into account the transaction cycle time and waiting times in the calculation of analytical model, which have been integrated to the model proposed by Marchet et al. (2012). Manzini et al. (2016) present analytic models for expected cycle time of a deep-lane unit-load AVS/RS that performing single- and dual-command cycles.

Ghomri et al. (2009) proposed an analytical expression for the average time of a single cycle of a multi-aisle AS/RS, while Lerher et al. (2010) presented analytical-travel-time models of multi-aisle AS/RS for the computation of travel time for both the single-command (SC) and the dual-command (DC) cycles (these models consider the operating characteristics of the storage and retrieval machine such as acceleration and deceleration and the maximum velocity. Ouhoud et al. (2016) developed travel-time models for single-cycle displacements of S/R machine in multi-aisle AS/RS by taking into account class-based storage policy. Guezzen et al. (2013) presented two analytical models to estimate travel time for mobile-rack AS/RS; these models are validated for accuracy by simulation.

Hu et al. (2005) have presented a new kind of S/R mechanism (SP-AS/RS) that enables AS/RS to efficiently handle very heavy loads. They have presented a continuous travel-time model for the new AS/RS under the stay dwell-point policy. While Liu et al. (2016) presented a continuous travel time model for the dual-command cycle of the same system under various input and output (I/O) dwell-point policy. Ramtin and Pazour (2015) developed expected travel time models for MIAPP-AS/RS, with different operating policies and different physical configurations. Dukic et al. (2015) presented the throughput model for dual-tray Vertical Lift Module (VLM) AS/RS. Accuracy of the model was tested using comparison with results obtained by simulation models. Khojasteh and Son (2016) addressed an order picking problem in a multi-aisle unit-load AS/RS served by a single S/R machine, the authors formulated the problem as a nonlinear programming model and developed a heuristic called the STD heuristic to find the optimal solution.

Summarizing, in the literature, several travel-time models have been developed and various types of AS/RS have been presented. To our knowledge, no study deals with the modelling of the retrieval time of the FF-flow-rack AS/RS due to its recent large-scale introduction in the drugs distribution in pharmacies. Therefore, an assessment of its performance is necessary, and for this system, it offers advantages in terms of economy (does not need an S/R machine) and the possibility of simultaneous retrieval of multiple products. For this purpose, this paper develops an analytical retrieval–travel-time model for this type of AS/RS, to evaluate the system performances.

The rest of this paper is structured as follows. In the next section, we will describe the structure and operations of the FF-flow-rack AS/RS. The retrieval–travel-time models for the FF-flow-rack AS/RS are presented in Sect. 3. In Sect. 4, a validation study of the continuous model by computer simulations is offered. Our conclusions are proposed in the final section (Sect. 5).

System structure and configuration

A new kind of flow-rack AS/RS was introduced by Mekapharm company® (Mekapharm 2016). It is mainly used for the automation of the drug distribution in pharmacies and in all the areas of handlings products that support the free-fall movement. We shall refer to the new type of AS/RS, the free-fall-flow-rack AS/RS, or FF-flow-rack AS/RS.

In the flow-rack AS/RS proposed by Sari et al. (2005), the authors used a two S/R machines. While De Koster et al. (2008) used a lifting mechanism on the opposite face of the S/R machine, Sari and Bessnouci (2012) used a single S/R machine for handling loads. In this section, we present a new type of flow-rack AS/RS, which consists of FF-flow-rack AS/RS. The main difference between the FF-flow-rack AS/RS and the other types of flow-rack AS/RS is that the FF-flow-rack AS/RS is used, for the product transport, a combination between the free-fall movement and a transport conveyor, while the other systems use S/R machine that moves according to a Tchebychev travel.

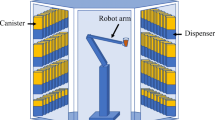
As illustrated in Fig. 1, the FF-flow-rack AS/RS include the following components: a deep rack, which is composed of multitude sloping bins, that uses a gravitational conveyor equipped with rolling wheels to allow the sliding of products by gravity from the storage to the picking side of the system. Each bin is composed of a plurality of segments (locations) that contains several identical products (the same SKU: Stock Keeping Unit) placed one after the other. A pick-up station is located on the storage face, and a drop-off station is located on the retrieval face. A transport conveyor used to connect the rack to the drop-off station. An operator or a storage machine allows the storage of items.
Fig. 1

Typical configuration of FF-flow-rack AS/RS

The work method (storage and retrieval operation) of the FF-flow-rack AS/RS is as follows: The storage operation which is performed by a storage machine or an operator, where the products are handled from the pick-up station to store it in the adequate bin. The retrieval operation consists of two phases: The first one is the ejection of the product, where it is achieved by the excitement of the electromagnet of the bin containing the desired product. This will cause the free fall of the product on the transport conveyor. The second phase is the transport of this product by the conveyor until reaching the drop-off station (See Fig. 3).

The ejection of a product leads to the progressive sliding by the gravity of all other products in the bin, as shown in Fig. 2, that illustrates the layout of products inside the bin. As it was mentioned in the retrieval operation, the retrieval–travel time of an FF-flow-rack AS/RS includes two steps: the time required for the free fall of the desired product and time to transport it.
Fig. 2

Product disposition inside a storage bin

As detailed in Fig. 1, the dimensions of the rack are: length \((L),\) height \((H),\) and depth \((D).\) The rack has \((N_{\text{L}} )\) bins in each tier and \((N_{\text{c}} )\) bins in each column. Each bin has \((M)\) storage segments. Since the use of a person for the storage operation, the maximum height of the rack should be less than 3 m, for practical and ergonomic reasons.

The dedicated storage assignment policy is used, where each bin is dedicated to a particular product because of the storage policy constraint required in pharmacies and distribution centers.

FF-flow-rack AS/RS advantages

Compared with the classic flow-rack AS/RS presented by Sari et al. (2005), the free-fall flow-rack AS/RS offers many advantages. The differences between them are summarized in Table 1 and further explanations are in the following statements:
Table 1

Differences between the free-fall flow-rack AS/RS and the classic flow-rack AS/RS

 

Free-fall flow-rack AS/RS

Flow-rack AS/RS

Throughput

High

Low

Average retrieval–travel time

Low

High

Delivery capacity

High

Low

Fault tolerance

Low

High

Initial investment

Low

High

Rapidity

High

Low

  • According to a comparative study carried out recently by Metahri and Hachemi (2017) between the FF-flow-rack and the classic one, improved throughput, which can be up to 90%.

  • The reduction of average retrieval–travel time can reach 38%, when using the FF-flow-rack (Metahri and Hachemi 2017).

  • With the FF-flow-rack, each bin is independent from the others; therefore, many items can be retrieved at the same time.

  • In the classic flow-rack, all bins are inaccessible once the S/R machine is failed. However, in the FF-flow-rack, if the electromagnet of a bin is out of service, only that bin is affected.

  • FF-slow rack offers a 40% reduction of the initial investment due to the replacement of the S/R machine by the combination between the free-fall movement and the transport conveyor (according to Rosenblatt et al. 1993; it represents approximately 40% or more than according to the system’s cost).

  • With the classic flow-rack, the S/R machine travels back and forth to retrieve an item. While, with the FF-flow-rack, the destocking of a product is made by the combination between the free-fall movement and the conveyor, which are too fast. Therefore, the new FF-flow-rack offers better rapidity of delivery.

Especially, in the pharmaceutical distribution, this system offers a high speed in the preparation and delivery of customer orders (reducing preparation time). In addition, this system presents the advantage to give to the pharmacists more time to advise their customers for the taking of the prescribed drug (Mekapharm 2016).

In the following section, we will present the retrieval–travel-time models of this system.

Retrieval–travel-time models

This part presents the original contribution of this study. It consists of the modelling of the expected retrieval-time of the FF-flow-rack AS/RS. For this, we start by giving some assumptions and notations that are needed in our approach, and then, we present the retrieval–travel-time models (continuous model and discrete model).

This paper is based on the following assumptions, which respect the real nature of the system:
  1. (1)

    The rack is considered to be a continuous rectangular pick face where drop-off station is located at the lower left-hand corner.

     
  2. (2)

    The rack length, height, and depth are known.

     
  3. (3)

    Constant velocity is assumed for the transport conveyor.

     
  4. (4)

    We consider only the retrieval operations, since the response-time constraints are stronger on the retrieval operations than those on the storage operations, which are usually not time-critical (Roodbergen and Vis 2009).

     
  5. (5)

    According to pharmacy practice, a dedicated storage policy is used, which means that each product type is assigned to a fixed bin. However, we assumed a random retrieval policy, which means that any product within the pick face has the same probability to be retrieved. Thus, the storage and retrieval are independent operations.

     
  6. (6)

    The time of the translation by the gravity of load inside a bin is usually deterministic. Thus, the sliding time can be added after the calculation of the expected retrieval time.

     
  7. (7)
    We assume uniform demands distributions; that is, all the products have the same picking frequency. We consider the uniform demands distribution for these reasons:
    1. -

      To study and explore the system behaviour in a general manner.

       
    2. -

      The lack of prior information of the customer’s requests.

       
    3. -

      It is typically used in the literature by several authors (Bozer and White 1984; Sari et al. 2005; Liu et al. 2016).

       
     
The following notations are introduced:
\(L,H,D\)

The length, height, and depth of the rack

\(l,h,d\)

The length, height, and depth of a storage segment

\(N_{\text{L}}\)

The number of bins per line

\(N_{c}\)

The number of bins per column

\(N_{\text{PF}}\)

The total number of bins in pick face

\(M\)

The number of segments in each bin

\(N\)

The total number of bins

\((i,j)\)

The bin coordinates

\(V_{\text{c}}\)

The speed of the transport conveyor

\(g\)

The acceleration due to gravity

\(t_{\text{v}}^{'}\)

The vertical travel time from a bin to the impact point on the transport conveyor

\(t_{\text{h}}^{'}\)

The horizontal travel time from the impact point to the drop-off station

\(t_{g}^{'}\)

The total travel time from a bin to the drop-off station

\(t_{\text{v}}\)

The vertical travel time from the farthest line to the impact point

\(t_{\text{h}}\)

The horizontal travel time from the farthest impact point to the drop-off station

\(E(T_{v}^{'} )\)

The mean of the vertical travel time

\(E(T_{h}^{'} )\)

The mean of the horizontal travel time

\(E(T_{g}^{'} )\)

The expected retrieval–travel time

\(A \left( {t_{g}^{'} } \right)\)

The average retrieval–travel time

It should be mentioned that the retrieval–travel time of all items: \(N\) stored in the rack become the retrieval–travel time of items \(N_{\text{PF}}\) stored only in the pick face, since we have assumed that a dedicated storage policy was used, and the items were automatically moved from the storage to the picking side of the rack by gravity.

Continuous model

Our idea consists in dividing the retrieval–travel time of a location \((i,j)\) in a two-travel time (vertical and horizontal) where the locations \((i,j)\) are uniformly distributed. Therefore, the expected retrieval time is the sum of the mean values of each travel time. As stated in the assumption part, the pick face is supposed as a continuous rectangle. In this case, the discrete coordinates \((i,j)\) become continuous coordinates noted \((i,j).\)

As illustrated in Fig. 3, the displacement of an item in the FF-flow-rack AS/RS is different from the displacement of the S/R machine in the traditional flow-rack AS/RS. Thus, the total travel time \(t_{\text{g}}^{'}\) of an item from the storage bin to the drop-off station is the sum of two travels.
Fig. 3

Depiction of the product movements in the retrieval face (continuous face)

To calculate the expected retrieval–travel time, let \((t_{\text{h}}^{'} ,t_{\text{v}}^{'} )\) denote the temporal coordinate of the retrieval point \((x,y),\) where \(\left( x \right)\) and \((y)\) are independently generated and uniformly distributed. The total travel time \(t_{\text{g}}^{'}\) from this point \((x,y)\) to the drop-off station is: \(t_{\text{g}}^{'} = t_{\text{v}}^{'} + t_{\text{h}}^{'} .\) By assuming that: \(T_{\text{v}}^{'}\) presents the continuous random variable associated with the vertical travel time \(t_{v}^{'}\) and \(T_{\text{h}}^{'}\) presents the continuous random variable associated with the horizontal travel time \(t_{\text{h}}^{'} .\) Now, let \(g (t) = g(T_{\text{v}}^{'} = t)\) and \(G(t) = P\left( {T_{\text{v}}^{'} \le t} \right)\) denote the probability density function and cumulative distribution function of the random variable \(T_{\text{v}}^{'} ,\) respectively. In addition, let \(w\left( t \right) = w\left( {T_{\text{h}}^{'} = t} \right)\) and \(W (t) = P (T_{\text{h}}^{'} \le t)\) denote the probability density function and cumulative distribution function of the random variable \(T_{\text{h}}^{'} ,\) respectively.

The calculation of \(E(T_{v}^{'} )\)

The vertical movement is due to the free fall of the desired product, and thus, it is not a uniform movement but a uniformly accelerated movement. The formula of the free fall is as follows:
$$y = \frac{1}{2}g( t_{v}^{\prime } )^{2} ,$$
(1)
where \(y\) represents the vertical distance between the retrieval point and the conveyor.
We have assumed that
$$C = \sqrt {\frac{2}{g}} .$$
(2)
Therefore
$$t_{v}^{\prime } = C \sqrt y .$$
(3)

Suppose that Y presents the continuous random variable associated with vertical distance \(y,\) and let \(f (y) = f(Y = y)\) and \(F\left( y \right) = P(Y \le y)\) denote the probability density function and cumulative distribution function of the random variable \(Y,\) respectively. Recognizing that \(Y\) is uniformly distributed between \(0\) and \(H,\) while \(T_{v}^{'}\) follows a probability law that can be determined as follow:

Determination of the cumulative distribution function \(G\;(t)\)

We have \(G\left( t \right) = P\left( {T_{v}^{'} \le t} \right)\) and \(T_{v}^{'} = C \sqrt Y .\)

Therefore,
$$G\left( t \right) = P (T_{v}^{'} \le t) = P\left( C \sqrt Y \le t \right).$$
(4)
So,
$$G\left( t \right) = P(T_{v}^{'} \le t) = P\left( {Y \le \frac{t^{2}}{{C^{2} }}} \right).$$

Recall that, \(F\left( y \right) = P\left( {Y \le y} \right);\) and from Eq. (3): \(y = \frac{1}{{C^{2} }}t^{2} .\)

Therefore,
$$G\left( t \right) = P(T_{v}^{'} \le t) = F\left( {Y \le \frac{1}{{C^{2} }}t^{2} } \right).$$
(5)

Determination of the probability density function \(g (t)\)

As we assume that \(T_{\text{v}}^{'}\) is a continuous random variable, we have: \(g\left( t \right) = \frac{{{\text{d}}G(t)}}{{{\text{d}}t}} = G'(t).\)

Hence
$$g\left( t \right) = G^{ '} \left( t \right) = F '\left( {Y \le \frac{1}{{C^{2} }}t^{2} } \right).$$
(6)
Then
$$g\left( t \right) = \frac{2 t}{{C^{2} }} F'\left( {Y \le \frac{{t^{2} }}{{C^{2} }}} \right)\,{\text{where}}:f\left( y \right) = \frac{{{\text{d}}F(y)}}{{{\text{d}}t}} = F'(y).$$
(7)
Thus
$$g\left( t \right) = \frac{2t}{{C^{2} }}f\left( {Y = \frac{{t^{2} }}{{C^{2} }}} \right).$$
(8)
For randomized retrieval policy, the vertical coordinate locations are assumed to be uniformly distributed. Thus, the probability density \(f\left( y \right)\) of the continuous random variable \(Y\) can be represented as a usual uniform law between 0 and H, as follows:
$$f\left( y \right) = P\left( {Y = ~y} \right) = \left\{ {\begin{array}{ll} {\frac{1}{H}} & {{\text{if}}\;~0 \le y \le H} \\ 0 & {{\text{else}}} \\ \end{array} } \right.$$
(9)
Hence
$$f\left( {Y = \frac{{t^{2} }}{{C^{2} }}} \right) = P\left( {Y = \frac{{t^{2} }}{{C^{2} }}} \right) = \left\{ {\begin{array}{*{20}c} {\frac{1}{H}} & {{\text{if}}\;~0 \le \frac{{t^{2} }}{{C^{2} }} \le H} \\ 0 & {{\text{else}}} \\ \end{array} } \right.$$
Thus,
$$f\left( {Y = \frac{{t^{2} }}{{C^{2} }}} \right) = P\left( {Y = \frac{{t^{2} }}{{C^{2} }}} \right) = \left\{ {\begin{array}{*{20}c} {\frac{1}{H}} & {{\text{if}}\;0 \le t \le C\sqrt H } \\ 0 & {{\text{else}}} \\ \end{array} } \right.$$
(10)
Substituting Eq. (10) into Eq. (8) yields:
$$g\left( t \right) = P\left( {T_{{\text{v}}}^{'} = t} \right) = \left\{ {\begin{array}{*{20}c} {\frac{{2~}}{{H~C^{2} }}t} & {{\text{if}}\;0 \le t \le C\sqrt H } \\ 0 & {{\text{else}}} \\ \end{array} } \right.$$
(11)
Consequently
$$G\left( t \right) = P\left( {T_{{\text{v}}}^{'} \le t} \right) = \left\{ {\begin{array}{*{20}l} 0 \hfill & {{\text{if}}\;t \le 0} \hfill \\ {\frac{{2~}}{{H~C^{2} }}t} \hfill & {{\text{if}}\;0 \le t \le C\sqrt H } \hfill \\ 1 \hfill & {{\text{if}}\;t \ge C\sqrt H } \hfill \\ \end{array} } \right.$$
(12)
The mean \(E(T_{v}^{'} )\) of the continuous random variable \(T_{v}^{'}\) is obtained as follows,
$$E(T_{v}^{'} ) =\int \limits_{ - \infty }^{ + \infty } t g\left( t \right) {\text{d}}t.$$
(13)
Thus
$$E(T_{v}^{'} ) = \mathop \int \limits_{ - \infty }^{0} tg\left( t \right){\text{d}}t + \mathop \int \limits_{0}^{C\sqrt H } tg\left( t \right){\text{d}}t + \mathop \int \limits_{C\sqrt H }^{ + \infty } tg\left( t \right){\text{d}}t.$$
As
$$\mathop \int \limits_{ - \infty }^{0} t g\left( t \right) {\text{d}}t + \mathop \int \limits_{C\sqrt H }^{ + \infty } t g\left( t \right) {\text{d}}t = 0.$$

Therefore, Eq. (13) can be reduced to the following equation as follows:

$$E(T_{\text{v}}^{'} ) = \mathop \int \limits_{0}^{C\sqrt H } tg\left( t \right){\text{d}}t .$$
Therefore,
$$E(T_{v}^{'} ) = \frac{2}{3}C\sqrt H .$$
(14)

The calculation of \(E(T_{\text{h}}^{'} )\)

The horizontal movement is due to the translation of the desired product from the impact point to the drop-off station by the transport conveyor; thus, it is a uniform movement. The horizontal travel time \(t_{h}^{'}\) can be calculated as follows.
$$t_{\text{h}}^{ ' } = \frac{x}{{V_{\text{c}} }},$$
(15)
where \(x\) represents the horizontal distance between the impact point and the drop-off station.

We recognize that the random variable \(T_{h}^{'}\) is uniformly distributed between 0 and \(t_{\text{h}} ,\) where: \(t_{\text{h}} = \frac{L}{{V_{\text{c}} }}.\)

For randomized retrieval policy, the horizontal coordinate locations are assumed to be uniformly distributed. Thus, the probability density function \(w\left( t \right)\) of this horizontal displacement follows a usual uniform law between 0 and \(t_{\text{h}} ,\) where:
$$w\left( t \right) = P(T_{\text{h}}^{'} = t) = \left\{ {\begin{array}{*{20}c} {\frac{1}{{t_{\text{h}} }} } & {{\text{if}}\,0 \le t \le t_{h} } \\ 0 & {\text{else}} \\ \end{array} } \right..$$
(16)
Consequently
$$W\left( t \right) = P(T_{\text{h}}^{'} \le t) = \left\{ {\begin{array}{*{20}c} 0 & {\text{if}} & {t \le 0} \\ {\frac{1}{{t_{\text{h}} }} } & {\text{if}} & {0 \le t \le t_{h} } \\ 1 & {\text{if}} & {t \ge t_{h} } \\ \end{array} } \right..$$
(17)
The mean \(E\left( {T_{\text{h}}^{'} } \right)\) of the continuous random variable \(T_{\text{h}}^{'}\) is obtained as follows:
$$E(T_{h}^{'} ) = \mathop \int \limits_{ - \infty }^{ + \infty } t w\left( t \right) {\text{d}}t.$$
(18)
Hence
$$E(T_{h}^{'} ) = \mathop \int \limits_{ - \infty }^{0} t w\left( t \right){\text{d}}t + \mathop \int \limits_{0}^{{t_{h} }} t w\left( t \right) {\text{d}}t + \mathop \int \limits_{{t_{h} }}^{ + \infty } t w\left( t \right) {\text{d}}t.$$
As,
$$\mathop \int \limits_{ - \infty }^{0} t w(t){\text{d}}t + \mathop \int \limits_{{t_{h} }}^{ + \infty } t w(t){\text{d}}t = 0.$$
Therefore, Eq. (18) can be reduced to the following equation:
$$E(T_{\text{h}}^{ '} ) = \mathop \int \limits_{0}^{{t_{h} }} \frac{t}{{t_{h} }}{\text{d}}t.$$
Therefore
$$E (T_{\text{h}}^{'} ) = \frac{1}{2}t_{\text{h}} .$$
(19)
Recall that, \(t_{\text{h}} = \frac{L}{{V_{\text{c}} }}.\) Therefore,
$$E (T_{\text{h}}^{'} ) = \frac{L}{{2 V_{\text{c}} }}.$$
(20)

The expected retrieval–travel time \(E(T_{\text{g}}^{'} )\) is obtained as follows.

Knowing that: \(T_{\text{g}}^{'}\) is the random continuous variable associated with \(t_{\text{g}}^{'} .\)
$$E(T_{\text{g}}^{'} ) = E(T_{\text{v}}^{'} + T_{\text{h}}^{'} ) = E(T_{\text{v}}^{'} ) + E(T_{\text{h}}^{'} ).$$
(21)
Substituting Eq. (14) and Eq. (20) into Eq. (21) yields:
$$E(T_{\text{g}}^{ '} ) { = }\frac{2}{3}C\sqrt H + \frac{1}{{2 V_{\text{c}} }}L.$$
(22)

Discrete model

We use the discrete rack face approach (the coordinates of the locations are integers in this case) to evaluate the expected retrieval–travel time of the FF-flow-rack AS/RS, which presents an exact model that will be used in a computer simulation to validate the continuous model. For this, we calculate the sum of the retrieval time of each bin, then dividing this sum by the total number of segments.

The vertical travel time (\(t'_{v}\)) of a particular item stored in position \((i,j)\) to reach the impact point can be calculated as follows.

From Eq. (1), we obtain:
$$t_{\text{v}}^{\prime } = {\text{C}}\sqrt {j.h} ,$$
(23)
where \((j.h)\) represents the vertical distance between the retrieval bin and the impact point on the conveyor.
The horizontal travel time \((t_{\text{h}}^{\prime } )\) needed to transport the same item to the drop-off station is as follows:
$$t_{\text{h}}^{\prime } = \frac{i.l}{\text{Vc}},$$
(24)
where \((i.l)\) represents the horizontal distance between the impact point and the drop-off station.
As illustrated in Fig. 4, the total travel time \(t_{\text{g}}^{\prime }\) that item needed to reach the drop-off station is the sum of the vertical travel time (\(t_{v}^{\prime }\)) and the horizontal travel time (\(t'_{h}\)):
Fig. 4

Depiction of the product movements in the retrieval face (discrete face)

$$t_{\text{g}}^{\prime } = \left( {\frac{i.l}{\text{Vc}}} \right) + {\text{C}}\sqrt {j.h} .$$
(25)
Thus, the average retrieval–travel time \(A \left( {t_{\text{g}}^{'} } \right)\) for all locations is as follows:
$$A ( t_{\text{g}}^{\prime } ) = \frac{1}{{N_{\text{L}} N_{\text{c}} }}\mathop \sum \limits_{i = 1}^{{N_{L} }} \mathop \sum \limits_{j = 1}^{{N_{c} }} \left[ {\left( {\frac{i.l}{Vc}} \right) + C\sqrt {j.h} } \right].$$
(26)

Simulation and validation results

The expected retrieval–travel time model presented in Sect. 4.1 provides approximate values, since it was based on a continuous approximation of the probability laws modelling the displacement of a product. To validate the accuracy of this model, we carried out a comparison between the results obtained from the continuous model with those obtained from a computer simulation that based on the discrete model presented in Sect. 4.2.

Simulation is typically used in the literature to validate the accuracy of approximate AS/RS models (Bozer and White 1984; Sari et al. 2005; Hu et al. 2005; Manzini et al. 2016), and supply chain models (Chiadamrong and Piyathanavong 2017). According to Rao and Naikan (2014), the computer simulation is used to represent the dynamic behavior of systems in the most realistic sense. In our case, the advantage of the computer simulation is to emulate the random behaviour of the retrieval operations in the FF-flow-rack AS/RS. The discrete model is used to calculate the retrieval–travel time of each retrieval operation. The computer simulation that developed using (MATLAB R2010a) software is shown in Fig. 5.
Fig. 5

Diagram of the computer simulation

In the computer simulation, a sequence of 1 million retrieval operations has been performed \((r = 10^{6} ),\) to calculate the average retrieval time. Twenty different configurations of the FF-flow-rack AS/RS have been simulated. For each configuration, it is assumed that the width \((l)\) and the height \((h)\) of each storage segment are 20 cm and 10 cm, respectively. Moreover, we will vary the speed velocity of the transport conveyor \((V_{\text{c}} ).\)

The results of the comparison between the simulation and the continuous model are summarized in Tables 2, 3, and 4. Column 2, 3, and 4 of these tables represent, respectively, the number of bins per line \((N_{\text{L}} )\) and per column \((N_{\text{c}} ),\)) and total number of bins in the pick face \((N_{\text{PF}} )\). While Column 5, 6, and 7 represent, respectively, the retrieval–travel time calculated by simulation and by continuous model \(E(T_{\text{g}}^{'} )\) and deviation between them.
Table 2

Comparison between continuous model and simulation results with Vc = 1 m/s

Configurations

\(N_{\text{L}}\)

\(N_{\text{C}}\)

\(N_{\text{PF}}\)

Simulation

\(E(T_{\text{g}}^{'} )\)

Deviation (%)

1

20

24

480

2.5768

2.4663

4.2855

2

52

27

1404

5.8061

5.6946

1.9208

3

54

27

1458

6.0073

5.8946

1.8757

4

32

25

800

3.7886

3.6759

2.9723

5

36

26

936

4.1968

4.0854

2.6559

6

50

25

1250

5.5895

5.4759

2.0322

7

26

24

624

3.1793

3.0663

3.5518

8

48

24

1152

5.3812

5.2663

2.1348

9

28

25

700

3.3888

3.2759

3.3288

10

44

25

1100

4.9892

4.8759

2.2695

11

42

26

1092

4.7965

4.6854

2.3174

12

40

27

1080

4.6044

4.4946

2.3842

13

38

26

988

4.3990

4.2854

2.5822

14

56

27

1512

6.2059

6.0946

1.7929

15

34

24

816

3.9769

3.8663

2.7799

16

30

26

780

3.5993

3.4854

3.1651

17

22

24

528

2.7792

2.6663

4.0614

18

24

26

624

2.9993

2.8854

3.7986

19

46

25

1150

5.1934

5.0759

2.2620

20

58

27

1566

6.4117

6.2946

1.8268

Table 3

Comparison between continuous model and simulation results with Vc = 2 m/s

Configurations

\(N_{\text{L}}\)

\(N_{\text{C}}\)

\(N_{\text{PF}}\)

Simulation

\(E(T_{\text{g}}^{'} )\)

Deviation (%)

1

20

24

480

1.5289

1.4663

4.0931

2

52

27

1404

3.1555

3.0946

1.9284

3

54

27

1458

3.2563

3.1946

1.8954

4

32

25

800

2.1394

2.0759

2.9664

5

36

26

936

2.3473

2.2854

2.6390

6

50

25

1250

3.0404

2.9759

2.1205

7

26

24

624

1.8302

1.7663

3.4911

8

48

24

1152

2.9283

2.8663

2.1176

9

28

25

700

1.9393

1.8759

3.2691

10

44

25

1100

2.7406

2.6759

2.3573

11

42

26

1092

2.6508

2.5854

2.4672

12

40

27

1080

2.5567

2.4946

2.4276

13

38

26

988

2.4476

2.3854

2.5410

14

56

27

1512

3.3578

3.2946

1.8820

15

34

24

816

2.2290

2.1663

2.8103

16

30

26

780

2.0479

1.9854

3.0547

17

22

24

528

1.6301

1.5663

3.9115

18

24

26

624

1.7475

1.6854

3.5577

19

46

25

1150

2.8388

2.7759

2.2147

20

58

27

1566

3.4550

3.3946

1.7462

Table 4

Comparison between continuous model and simulation results with Vc = 3 m/s

Configurations

\(N_{L}\)

\(N_{\text{C}}\)

\(N_{PF}\)

Simulation

\(E(T_{g}^{'} )\)

Deviation (%)

1

20

24

480

1.1791

1.1330

3.9115

2

52

27

1404

2.2752

2.2280

2.0782

3

54

27

1458

2.3405

2.2946

1.9615

4

32

25

800

1.5895

1.5426

2.9478

5

36

26

936

1.7318

1.6854

2.6831

6

50

25

1250

2.1882

2.1426

2.0824

7

26

24

624

1.3803

1.3330

3.4235

8

48

24

1152

2.1135

2.0663

2.2333

9

28

25

700

1.4558

1.4093

3.1937

10

44

25

1100

1.9886

1.9426

2.3135

11

42

26

1092

1.9312

1.8854

2.3732

12

40

27

1080

1.8755

1.8280

2.5329

13

38

26

988

1.7997

1.7520

2.6499

14

56

27

1512

2.4068

2.3613

1.8915

15

34

24

816

1.6456

1.5997

2.7939

16

30

26

780

1.5303

1.4854

2.9336

17

22

24

528

1.2453

1.1997

3.6683

18

24

26

624

1.3319

1.2854

3.4901

19

46

25

1150

2.0556

2.0093

2.2524

20

58

27

1566

2.4722

2.4280

1.7904

These results are also schematized in Figs. 6 and 7, where Fig. 6 represents a comparison between the results (expected retrieval–travel time) given by the continuous model with those given by the simulation, for multiple configuration and three speeds of the transport conveyor. Whereas, Fig. 7 shows the deviation (%) between the results of simulation and the continuous model of each configuration, with the three values of the transport conveyor speed.
Fig. 6

Comparison between results given by the continuous model and simulation for the three values of Vc

Fig. 7

Deviation between results given by the continuous model and simulation for the three values of Vc

The equation that describes the deviation is as follows:
$${\text{Deviation}}\;\left( \% \right) = \frac{{({\text{Simulation}}\_{\text{results}}) - ({\text{Continuous}}\_{\text{model}}\_{\text{results}})}}{{({\text{Simulation}}\_{\text{results}})}} \times 100\% .$$
(27)

We observe from Fig. 6 that the obtained results of both continuous model and simulation are near to each other, which prove that our analytical expression captures the real behaviour of the retrieval–travel time for the FF-flow-rack AS/RS.

Moreover, as it is illustrated in Fig. 7, it can be seen that the maximum deviation is less than 5%, showing that the continuous model gives a very good approximation to simulation results, which are more close to the real-rack nature. Because of lack of space, only the simulation results of 20 system configurations have been presented. However, the proposed model (continuous model) can estimate the retrieval time of a large range of system configurations with a very good accuracy.

We notice that the developed analytical expression allows a fast evaluation of the expected retrieval time, also the developed model can be really used to guide the decision-making process about design and control of the FF-flow-rack AS/RS.

In addition, the developed expression (Eq. 22) offers several applications in managing AS/RS. For example, it can be used to:

  • evaluate the throughput of the FF-flow-rack AS/RS for various configurations;

  • optimise the dimensions of the rack, where the developed expression represents the objective function to be minimized;

  • compare different storage assignment policies;

  • conduct a performance comparison between the FF-flow-rack and other types of AS/RS.

Conclusion

This paper has presented a new kind of flow-rack AS/RS, which is called free-fall-flow-rack AS/RS (FF-flow-rack AS/RS), which presents a novel material handling technology that can be used in several applications, from the distribution centers to the manufacturing industry.

The advantages of this FF-flow-rack AS/RS include high throughput, flexible configuration and a considerable reduction of the initial investment due to the replacement of the S/R machine by the combination between the free-fall movement and the transport conveyor for the retrieval of items. This system can be used in the case of items with low size and weight, such as the pharmaceutical products, food, textile, and electronic components. However, it is not recommended to use this kind of AS/RS in the case of voluminous and\or fragile products, because the free-fall of products can damage them.

In this study, we focused on evaluating the performance of the FF-flow-rack AS/RS by developing a continuous retrieval–travel-time model. This model has been compared for accuracy with a computer simulation based on a discrete model. It can be concluded that the developed model gives very satisfactory results, since the maximum deviation is less than 5%.

To our knowledge, this is the first study to deal with evaluating FF-flow-rack performance. Likewise, we hope that this research will be usefully employed in the future studies in this area.

Finally, in our future research, we will investigate the developed model, under different demand distributions to study the impact of the turnover rate of items on the retrieval time, which allows establishing new control techniques. In addition, we suggest optimising the dimensions of the FF-flow-rack AS/RS to minimize the expected retrieval–travel time.

Notes

Compliance with ethical standards

Conflict of interest

No potential conflict of interest was reported by the authors.

References

  1. Bessenouci HN, Sari Z, Ghomri L (2012) Metaheuristic based control of a flow rack automated storage retrieval system. J Intell Manuf 23(4):1157–1166CrossRefGoogle Scholar
  2. Bortolini M, Accorsi R, Gamberi M, Manzini R, Regattieri A (2015) Optimal design of AS/RS storage systems with three-class-based assignment strategy under single and dual command operations. Int J Adv Manuf Technol 79(9–12):1747–1759CrossRefGoogle Scholar
  3. Bozer YA, White JA (1984) Travel-time models for automated storage/retrieval systems. IIE Trans 16(4):329–338CrossRefGoogle Scholar
  4. Chang DT, Wen UP (1997) The impact on rack configuration on the speed profile of the storage and retrieval machine. IIE Trans 29(7):525–531Google Scholar
  5. Chang DT, Wen UP, Lin JT (1995) The impact of acceleration/deceleration on travel-time models for automated storage/retrieval systems. IIE Trans 27(1):108–111CrossRefGoogle Scholar
  6. Chen Z, Li X, Gupta JN (2015) A bi-directional flow-rack automated storage and retrieval system for unit-load warehouses. Int J Prod Res 53(14):4176–4188CrossRefGoogle Scholar
  7. Chiadamrong N, Piyathanavong V (2017) Optimal design of supply chain network under uncertainty environment using hybrid analytical and simulation modeling approach. J Ind Eng Int 13(4):465–478CrossRefGoogle Scholar
  8. De Koster RMB, Le-Duc T, Yugang Y (2008) Optimal storage rack design for a 3-dimensional compact AS/RS. Int J Prod Res 46(6):1495–1514CrossRefMATHGoogle Scholar
  9. Dukic G, Opetuk T, Lerher T (2015) A throughput model for a dual-tray Vertical Lift Module with a human order-picker. Int J Prod Econ 170:874–881CrossRefGoogle Scholar
  10. Ghomri L, Sari Zaki, Guezzen A, Tewfik SARI (2009) Continuous models for single and dual cycle times of a multi aisle automated storage and retrieval system. IFAC Proc 42(4):1061–1066CrossRefGoogle Scholar
  11. Graves SC, Hausman WH, Schwarz LB (1977) Storage-retrieval interleaving in automatic warehousing systems. Manage Sci 23(9):935–945CrossRefMATHGoogle Scholar
  12. Guezzen AH, Sari Z, Castagna P, Cardin O (2013) Travel time modeling and simulation of a mobile racks automated storage/retrieval system. Int J Eng Technol 5(3):420CrossRefGoogle Scholar
  13. Hachemi K, Alla H (2008) Pilotage dynamique d’un système automatisé de stockage/déstockage à convoyeur gravitationnel. J Eur Syst Autom (JESA) 42(5/2008):487–508Google Scholar
  14. Hachemi K, Besombes B (2013) Integration of products expiry dates in optimal scheduling of storage/retrieval operations for a flow-rack AS/RS. Int J Ind Syst Eng 15(2):216–233Google Scholar
  15. Hamzaoui MA, Sari Z (2015) Optimal dimensions minimizing expected travel time of a single machine flow rack AS/RS. Mechatronics 31:158–168CrossRefGoogle Scholar
  16. Hausman WH, Schwarz LB, Graves SC (1976) Optimal storage assignment in automatic warehousing systems. Manage Sci 22(6):629–638CrossRefMATHGoogle Scholar
  17. Hu YH, Huang SY, Chen C, Hsu WJ, Toh AC, Loh CK, Song T (2005) Travel time analysis of a new automated storage and retrieval system. Comput Oper Res 32(6):1515–1544CrossRefMATHGoogle Scholar
  18. Hwang H, Lee SB (1990) Travel-time models considering the operating characteristics of the storage and retrieval machine. Int J Prod Res 28(10):1779–1789CrossRefGoogle Scholar
  19. Khojasteh Y, Son JD (2016) A travel time model for order picking systems in automated warehouses. Int J Adv Manuf Technol 86(5–8):2219–2229CrossRefGoogle Scholar
  20. Lee HF (1997) Performance analysis for automated storage and retrieval systems. IIE Trans 29(1):15–28CrossRefGoogle Scholar
  21. Lerher T, Potrč I, Šraml M, Tollazzi T (2010) Travel time models for automated warehouses with aisle transferring storage and retrieval machine. Eur J Oper Res 205(3):571–583CrossRefMATHGoogle Scholar
  22. Liu T, Xu X, Qin H, Lim A (2016) Travel time analysis of the dual command cycle in the split-platform AS/RS with I/O dwell point policy. Flex Serv Manuf J 28(3):442–460CrossRefGoogle Scholar
  23. Malmborg CJ (2002) Conceptualizing tools for autonomous vehicle storage and retrieval systems. Int J Prod Res 40(8):1807–1822CrossRefMATHGoogle Scholar
  24. Manzini R, Accorsi R, Baruffaldi G, Cennerazzo T, Gamberi M (2016) Travel time models for deep-lane unit-load autonomous vehicle storage and retrieval system (AVS/RS). Int J Prod Res 54(14):4286–4304CrossRefGoogle Scholar
  25. Marchet G, Melacini M, Perotti S, Tappia E (2012) Analytical model to estimate performances of autonomous vehicle storage and retrieval systems for product totes. Int J Prod Res 50(24):7134–7148CrossRefGoogle Scholar
  26. Material Handling Institute. (1977). Consideration for planning and installing an automated storage/retrieval systems, Inc AS/RS document: 100 7MGoogle Scholar
  27. Meghelli-Gaouar N, Sari Z (2010) Assessment of performance of a class-based storage in a flow-rack AS/RS. J Stud Manuf 1(2–3):100–107Google Scholar
  28. Mekapharm (2016) http://mekapharm.com/apoteka/. Accessed 22 Oct 2016
  29. Metahri D, Hachemi K (2017) Automated storage and retrieval systems: A performances comparison between Free-fall-flow-rack and classic flow-rack. In: Systems and control (ICSC), 2017 6th international conference on IEEE, pp 589–594Google Scholar
  30. Ouhoud A, Guezzen A, Sari Z (2016) Experimental validation of travel time models for multi aisle automated storage and retrieval system in class-based storage. Electr Electr Autom 64(1):150–157Google Scholar
  31. Ramtin F, Pazour JA (2015) Product allocation problem for an AS/RS with multiple in-the-aisle pick positions. IIE Trans 47(12):1379–1396CrossRefGoogle Scholar
  32. Rao MS, Naikan VNA (2014) Reliability analysis of repairable systems using system dynamics modeling and simulation. J Ind Eng Int 10(3):69CrossRefGoogle Scholar
  33. Roodbergen KJ, Vis IF (2009) A survey of literature on automated storage and retrieval systems. Eur J Oper Res 194(2):343–362CrossRefMATHGoogle Scholar
  34. Rosenblatt MJ, Roll Y, Vered Zyser D (1993) A combined optimization and simulation approach for designing automated storage/retrieval systems. IIE Trans 25(1):40–50CrossRefGoogle Scholar
  35. Sari Z (2010) Performance evaluation of flow-rack and unit load automated storage & retrieval systems. Proc ISTEC 2010:605–615Google Scholar
  36. Sari Z, Bessnouci NH (2012) Design & modeling of a single machine flow rack AS. RS. In: Proceeding of IMHRC2012, Gardanne, FranceGoogle Scholar
  37. Sari Z, Saygin C, Ghouali N (2005) Travel-time models for flow-rack automated storage and retrieval systems. Int J Adv Manuf Technol 25(9–10):979–987CrossRefGoogle Scholar
  38. Sari Z, Grasman SE, Ghouali N (2007) Impact of pickup/delivery stations and restoring conveyor locations on retrieval time models of flow-rack automated storage and retrieval systems. Prod Plan Control 18(2):105–116CrossRefGoogle Scholar
  39. Sarker BR, Babu PS (1995) Travel time models in automated storage/retrieval systems: a critical review. Int J Prod Econ 40(2–3):173–184CrossRefGoogle Scholar
  40. Sharma RK, Sharma P (2015) Qualitative and quantitative approaches to analyse reliability of a mechatronic system: a case. J Ind Eng Int 11(2):253–268CrossRefGoogle Scholar
  41. Van Den Berg JP, Gademann AJRM (2000) Simulation study of an automated storage/retrieval system. Int J Prod Res 38(6):1339–1356CrossRefMATHGoogle Scholar
  42. Wen UP, Chang DT, Chen SP (2001) The impact of acceleration/deceleration on travel-time models in class-based automated S/R systems. IIE Trans 33(7):599–608Google Scholar
  43. Xu X, Shen G, Yu Y, Huang W (2015) Travel time analysis for the double-deep dual-shuttle AS/RS. Int J Prod Res 53(3):757–773CrossRefGoogle Scholar
  44. Xu X, Gong Y, Fan X, Shen G, Zou B (2017) Travel-time model of dual-command cycles in a 3D compact AS/RS with lower mid-point I/O dwell point policy. Int J Prod Res 11:1–22Google Scholar

Copyright information

© The Author(s) 2018

Open AccessThis article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.

Authors and Affiliations

  1. 1.Institute of Maintenance and Industrial SafetyUniversity of Oran 2 Mohamed Ben AhmedOranAlgeria

Personalised recommendations