Decentralized supply chain network design: monopoly, duopoly and oligopoly competitions under uncertainty

Abstract

This paper presents the competitive supply chain network design problem in which $n$ decentralized supply chains simultaneously enter the market with no existing rival chain, shape their networks and set wholesale and retail prices in competitive mode. The customer demand is elastic and price dependent, customer utility function is based on the Hoteling model and the chains produce identical or highly substitutable products. We construct a solution algorithm based on bi-level programming and possibility theory. In the proposed bi-level model, the inner part sets the prices based on simultaneous extra- and Stackleberg intra- chains competitions, and the outer part shapes the networks in cooperative competitions. Finally, we use a real-word study to discuss the effect of the different structures of the competitors on the equilibrium solution. Moreover, sensitivity analyses are conducted and managerial insights are offered.

Introduction

These days, competition is promoted from firms against firms to supply chains versus supply chains; globalization is a common phenomenon, markets become saturated, obstacles enter new markets, become lower and developing countries are trying to omit monopoly to enrol in the World Trade Organization (WTO) and countries are ratifying different foreign investment strategies and policies to attract international investors to their virgin markets and also a lot of entrepreneurs invite new products and consequently new markets. In these circumstances, investors are encountered with the opportunity of a lot of virgin markets that they can enter the market and design their chain in competitive modes. On the other hand, designing a supply chain in a centralized way needs a huge amounts of money and they may be interested in designing their chains in decentralized way to reduce their costs. So they are faced with the questions like the following: how can they design their supply chains in decentralized mode? How can they set the prices? How can they set the location of facilities? What is the effect of the leadership of the chains on the pricing and location decisions? What is the effect of competition intensity and promotions on their prices, market shares and profits? The aim of this paper is to answer the abovementioned questions.

According to Deloitte Consulting (1999), “no longer will companies compete against other companies but total supply chains will be against other supply chains”. A supply chain (SC) is a network of suppliers, manufacturers, warehouses and retailers organized to produce and distribute merchandise at the right quantities, to the right locations and at the right time in order to minimize total costs while satisfying service level requirements Simchi-Levi et al. (2003). Tayler (2003) mentioned that “the traditional company VS company competition is replaced by SC VS SC model and success now is based on assembling a team of competitors that can rise above the win/loss negotiations of conventional business relationship and work together to deliver the best product at the best price”. Above definitions reveal that there are different players in a network and each independent entity tries to maximize its own objective functions. In supply chain network design (SCND) physical structure of a network is shaped and has a great impact on SC’s overall performance, Simchi-Levi et al. (2003) consider SCND as the primary and most important step for decreasing (increasing) the whole cost (profit) of chains. According to SCND literature (e.g., Shen 2007; Meixell and Gargeya 2005; Beamon 1998), great deal of work has been done on monopoly assumption (Altiparmak et al. 2006; Torabi and Hassini 2008; Pishvaee and Rabbani 2011; Babazadeh et al. 2012; Rao et al. 2013; Tavakkoli-Moghaddam et al. 2013; Shankar et al. 2013; Badri et al. 2013; Özceylan et al. 2014; Vahdani and Mohamadi 2015; Yang et al. 2015; Sherafati and Bashiri 2016; Ardalan et al. 2016; Keyvanshokooh et al. 2016; Özceylan et al. 2016; Alizadeh Afrouzy et al. 2017; Chiadamrong and Piyathanavong 2017; Jeihoonian et al. 2017, Varsei and Polyakovskiy 2017). Although there are many examples of SC competition in real world including maritime shipping, automotive industry, online bookstores, pharmaceutical SC and retail industry Farahani et al. (2014), it is highly ignored in the literature. Competitive SCND (CSCND) is considering the impact of competitive markets in designing the network structure of a chain to improve its future competitiveness; Farahani et al. (2014) have done a review on CSCND.

To accompany with the needs of practical world and fill this important gap of the literature, this paper considers SCND under different types of competitions by the possibility of existing different number of rivals, different levels of competitions, cooperation between the chains and investigating the effects of them on SCND. The rest of this paper is structured as follows: “Literature review” presents literature review and our contributions, “Problem definition” describes our problem, “Solution approach” presents our solution approach, “Numerical example and discussion” gives the numerical results and discussion, and “Conclusion” presents the conclusion.

Literature review

Players and customers are the most important factors in CSCND. If no rival exists, the newcomer encounters a monopolistic market; if one rival exists, then duopolistic competition will occur and in case of more than one, existing rival oligopolistic competition will take place. According to the reactions of the rivals three main types of competitions exist in the literature:

• (1) Static competition: in this competition new entrant makes decisions and his decision variables regard the fact that no rival will show any reaction to his entry (Berman and Krass 1998; Aboolian et al. 2007a, b; Revelle et al. 2007). Plastria (2001) has done a review of this kind of competition.

• (2) Dynamic competition: if the rivals show reactions simultaneously, this type of competition occurs. Also this is usually related to operational characteristics and leads to Nash game; most of the dynamic games in SC literature are unconstrained models that solved by differential systems (Xiao and Yang 2008; Zhang 2006; Godinho and Dias 2010, 2013; Sinha and Sarmah 2010; Friesz et al. 2011, Jain et al. 2014; Chen et al. 2015; Nagurney et al. 2015; Mousavi et al. 2016; Santibanez-Gonzalez and Diabat 2016; Hjaila et al. 2016a; Jahangoshai Rezaee et al. 2017; Lipan et al. 2017).

• (3) Competition with foresight: in this competition, the rivals show reactions to the entry of new comer in sequential manner and usually this is related to strategic characteristics; this competition leads to bi-level or multi-level models and stackelberg games (Drezner and Drezner 1998; Plastria and Vanhaverbeke 2008; Kucukaydın et al. 2011, 2012, Zhang and Liu 2013; Yue and You 2014; Zhu 2015; Drezner et al. 2015; Taleizadeh and Charmchi 2015; Yang et al. 2015, Esmaeilzadeh and Taleizadeh 2016; Hjaila et al. 2016b; Aydin et al. 2016; Ezimadu and Nwozo 2017; Genc and Giovanni 2017. Eiselt and Laporte 1997; Krass and Pesch 2012 have done a review of this kind of competition.

Customer demand and customer utility function are another important elements that should be considered in CSCND. According to the literature customer demand can be inelastic or elastic, and elastic demand can depend on price, service, price and service, or price and distance (Farahani et al. 2014). On the other hand, deterministic utility function (introduced by Hotelling 1929) and random utility function (introduced by Huff 1964, 1966) are the most common functions in the CSCND, SC competition and competitive location literature. In deterministic utility model, the customers visit the facility with the highest utility, whereas in random utility they visit each facility by a certain probability that is directly related to the attractiveness level of the facility and inversely related to the attractiveness level of all the existing facilities.

Also in SC competition literature, there are three kinds of competitions: horizontal competition: competition between firms of one tier of a SC (Nagurney et al. 2002; Dong et al. 2004; Cruz 2008; Zhang and Zhou 2012; Qiang et al. 2013; Huseh 2015; Qiang 2015; Li and Nagurney 2016, Nagurney et al. 2016); vertical competition: competition between the firms of different tiers of a SC (Bernstein and Federgruen 2005; Anderson and Bao 2000; Chen et al. 2013, Wu 2013; Zhao and Wang 2015; Zhang et al. 2015; Bai et al. 2016; Bo and Li 2016; Esmaeilzadeh and Taleizadeh 2016; Li et al. 2016; Huang et al. 2016; Wang et al. 2017; Genc and Giovanni 2017; Chaeb and Rasti-Barzoki 2016); and SC versus SC: competition between SCs (Boyaci and Gallego 2004; Xiao and Yang 2008; Zhang 2006; Li et al. 2013; Chung and Kwon 2016).

Ezimadu and Nwozo (2017) used Sethi model to models the dynamic effect of the manufacturer and retailer’s advertising efforts on sale and by the help of control technique and stochastic differential game theory the players’ advertising strategies and the long-run value of the awareness share are obtained. Esmaeilzadeh and Taleizadeh (2016) proposed the optimal pricing decisions for two complementary products in a two-echelon supply chain composed of one retailer and two manufacturers under two scenarios. The relationships between the manufacturers and the retailer are modeled by the MS-Stackelberg and MS-Bertrand game-theoretic approach where the manufacturers are leaders and the retailers are followers. Ghaffari et al. (2016) used game theory to investigate three models to implement tradable green certificates system and formulated the competition between thermal and renewable power plants by cooperative, Nash and Stackelberg game models. Heydari and Norouzinasab (2015) proposed a discount model to coordinate pricing and ordering decisions in a two-echelon supply chain under stochastic price sensitive demand.

There are a little work on CSCND literature, Rezapour and Farahani (2010) developed a centralized SCND in the market underprice—dependent demand where a rival exists, derived equilibrium conditions and established finite dimensional variable inequality formulation. Rezapour et al. (2011) developed a model for duopolistic CSCND with sequential acting and variable delivered price under deterministic price dependent demand with rival chain presents. Rezapour et al. (2014) presented a bi-level model for CSCND with anticipating price and service level competition with the presence of existing rival. Rezapour and Farahani (2014) presented a bi-level model for CSCND in the presence of an existing rival where demand is elastic with respect to price and distance. Rezapour et al. (2015) presented a bi-level model for closed-loop SCND in price-dependent market demand with an existing SC, which only has a forward direction, but the new chain is a closed-loop SC. Fallah et al. (2015) presented a competitive closed-loop SCND problem in a price-dependent market under uncertainty and investigate the impact of simultaneous and Stackelberg competition between the chains. Fahimi et al. (2017a) presented a simultaneous competitive supply chain network design problem by attractiveness variables of the DCs and proposed an algorithm based on the Lemke and Howson algorithm and variational inequality formulation with the help of bi-level programming, the modified projection method and the possibility theory. Fahimi et al. (2017b) presented simultaneous decentralized competitive supply chain network design problem in virgin market and proposed a three-step algorithm based on variational inequality to solve the problem.

Contribution of this paper

This paper considers monopolistic, duopolistic and oligopolistic competitions and develops models and a solution approach for CSCND in the markets by the price-dependent demand and deterministic customer utility function. The contributions of this paper on SCND literature are as follows:

• 1. Instead of monopoly markets assumption which is highly used in the literature, we define three different market competitions: monopolistic, duopolistic or oligopolistic competitions and consider the effects on SCND.

• 2. We consider the chains enter the market simultaneously and make strategic decisions cooperatively and pricing decisions competitively which is rare in the literature.

• 3. Each SC can enter the markets and specify its market prices and structure in decentralized supply chain based on plants or DCs.

• 4. We introduce a bi-level model that the inner part is related to pricing decisions and outer part is related to location decisions.

• 5. The SCs do not have enough information about the market as they are newcomers so they have encountered with imprecise information and should cope with this uncertainty. So we use probabilistic chance constraint programming to handle this situation.

Problem definition

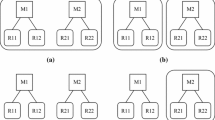
This paper describes a situation in which two independent investors want to enter virgin and price-dependent market by creating a two-tier SC including plants and distribution centers (DCs); in addition it may be the case that two or four more investors are planning to enter the market at the same time and produce either identical or highly substitutable products. These circumstances result in monopoly (in the case of two investors), duopoly (for four different investors) or oligopoly competitions (for six and more independent investors) (Fig. 1). As they are all newcomers into the virgin market, it is rational to consider that they do not have enough information about the parameters and are encountered with lack of knowledge and ill-known parameters; Liu and Iwamura (1998) mention that two types of uncertainty are available: if the distribution functions is found by experiments then probability theory and stochastic programming are used to cope with uncertainty, but if there is not enough information to obtain the distribution functions then possibility theory and fuzzy mathematical programming are used to model the situations. As in our problem the investors are encountered with high degree of uncertainty, we empowered our model by possibility theory and modeled the problem by fuzzy multi-level mixed integer linear programming. The chains should decide on two intrinsically different and important decisions as pricing (operational) and location (strategic one); therefore, three different games extra- and intra- of the chains can be defined; as each chain specifies a leader (it can be its plant or DC) to set the prices in simultaneous game between the chains and Stackelberg game intra the chains also for location decision, they will make their networks cooperatively with respect to obtained prices. This procedure will be done by converting the multi-level model of the problem into an integrated bi-level one. The following assumptions, indexes, parameters and variables are used to model the introduced problem:

Fig. 1

competition modes

Assumptions

• The candidate locations of plants are known in advance.

• The candidate locations of the DCs are known in advance.

• There are no common potential locations between the chains.

• The demand of each customer market is concentered at discrete point.

• Demand is elastic and price dependent.

• Customer utility function is based on price.

• The products are either identical or highly substitutable.

Parameters

$\widetilde{f\varUpsilon }_{i}^{{}}$ :

Fixed cost of opening a plant on location $i$ for SC1.

$\widetilde{{g\varPsi_{j} }}$ :

Fixed cost of opening a DC on location $j$ for SC1.

$\widetilde{f\chi }_{{i^{\prime}}}^{{}}$ :

Fixed cost of opening a plant on location $i^{\prime}$ for SC2.

$\widetilde{{g{\rm E}_{{j^{\prime}}} }}$ :

Fixed cost of opening a DC on location $j^{\prime}$ for SC2.

$\widetilde{{f{\rm H}}}_{{i^{\prime\prime}}}^{{}}$ :

Fixed cost of opening a plant on location $i^{\prime}$ for SC3.

$\widetilde{{g\varGamma_{{j^{\prime\prime}}} }}$ :

Fixed cost of opening a DC on location $j^{\prime}$ for SC3.

$\widetilde{{s\varUpsilon_{i} }}$ :

Unit production cost at plant $i$ for SC1.

$\widetilde{{s\chi_{{i^{\prime}}} }}$ :

Unit production cost at plant $i^{\prime}$ for SC2.

$\widetilde{{s{\rm H}_{{i^{\prime\prime}}} }}$ :

Unit production cost at plant $i^{\prime}$ for SC3.

$\widetilde{c\varUpsilon }_{ij}$ :

Unit transportation cost between plant $i$ and DC $j$ for SC1.

$\widetilde{c\varPsi }_{jk}$ :

Unit transportation cost between DC j and customer k for SC1.

$\widetilde{c\chi }_{{i^{\prime}j^{\prime}}}$ :

Unit transportation cost between plant $i^{\prime}$ and DC $j^{\prime}$ for SC2.

$\widetilde{{c{\rm E}}}_{{j^{\prime}k}}$ :

Unit transportation cost between DC $j^{\prime}$ and customer k for SC2.

$\widetilde{{c{\rm H}}}_{{i^{\prime\prime}j^{\prime\prime}}}$ :

Unit transportation cost between plant $i^{\prime}$ and DC $j^{\prime}$ for SC3.

$\widetilde{c\varGamma }_{{j^{\prime\prime}k}}$ :

Unit transportation cost between DC $j^{\prime}$ and customer k for SC3.

$\tilde{d}_{k}$ :

Demand of customer k.

$\widetilde{Cp\varUpsilon }_{i}$ :

Capacity of plant ${\text{i}}$.

$\widetilde{Cp\varPsi }_{j}$ :

Capacity of DC $j$.

$\widetilde{Cp\chi }_{{i^{\prime}}}$ :

Capacity of plant $i^{\prime}$.

$\widetilde{{Cp{\rm E}}}_{{j^{\prime}}}$ :

Capacity of plant $j^{\prime}$.

$\widetilde{{Cp{\rm H}}}_{{i^{\prime\prime}}}$ :

Capacity of plant $i^{\prime\prime}$.

$\widetilde{Cp\varGamma }_{{j^{\prime\prime}}}$ :

Capacity of plant $j^{\prime\prime}$.

$\widetilde{h\varPsi }_{j}$ :

Unit holding cost at DC $j$ in SC1.

$\widetilde{{h{\rm E}}}_{{j^{\prime}}}$ :

Unit holding cost at DC $j^{\prime}$ in SC2.

$\widetilde{h\varGamma }_{{j^{\prime\prime}}}$ :

Unit holding cost at DC $j^{\prime\prime}$ in SC3.

$P\varUpsilon$ :

Number of opened plants in SC1.

$P\chi$ :

Number of opened plants in SC2.

$P{\rm H}$ :

Number of opened plants in SC3.

$P\varPsi$ :

Number of opened DCs in SC1.

$P{\rm E}$ :

Number of opened DCs in SC2.

$P\varGamma$ :

Number of opened DCs in SC3.

$n$ :

Maximum number of plants in SC1.

$m$ :

Maximum number of DCs in SC1.

$n^{\prime}$ :

Maximum number of plants in SC2.

$m^{\prime}$ :

Maximum number of DCs in SC2.

$n^{\prime\prime}$ :

Maximum number of plants in SC3.

$m^{\prime\prime}$ :

Maximum number of DCs in SC3.

$l$ :

Number of available customers.

Decision variables

$\varUpsilon_{i}$ :

$\left\{ \begin{aligned} &1\quad {\text{ if SC1 opens a plant in location i}} \hfill \\ &0 \quad {\text{ else}} \hfill \\ \end{aligned} \right.$

$\varPsi_{j}$ :

$\left\{ \begin{aligned} &1 \quad {\text{ if SC1 opens a DC in location j}} \hfill \\ &0 \quad {\text{ else}} \hfill \\ \end{aligned} \right.$

$\chi_{{i^{\prime}}}$ :

$\left\{ \begin{aligned} &1 \quad {\text{ if SC2 opens a plant in location }}i^{\prime} \hfill \\ &0\quad {\text{ else}} \hfill \\ \end{aligned} \right.$

${\rm E}_{{j^{\prime}}}$ :

$\left\{ \begin{aligned} &1\quad {\text{ if SC2 opens a DC in location }}j^{\prime} \hfill \\ &0\quad {\text{ else}} \hfill \\ \end{aligned} \right.$

${\rm H}_{{i^{\prime\prime}}}$ :

$\left\{ \begin{aligned} &1\quad {\text{ if SC3 opens a plant in location }}i^{\prime\prime} \hfill \\ &0\quad {\text{ else}} \hfill \\ \end{aligned} \right.$

$\varGamma_{j''}$ :

$\left\{ \begin{aligned} &1\quad {\text{ if SC3 opens a DC in location }}j^{\prime\prime} \hfill \\ &0\quad {\text{ else}} \hfill \\ \end{aligned} \right.$

$y_{{ijki^{\prime}j^{\prime}}}$ :

$\left\{ \begin{aligned} &1\quad {\text{ if path }}ij \, i{\text{s opened to serve market }}k{\text{ in monopoly}} \hfill \\ &0\quad {\text{ otherwise}} \hfill \\ \end{aligned} \right.$

$y_{{ijki^{\prime}j^{\prime}}}$ :

$\left\{ \begin{aligned} &1\quad {\text{ if path }}iji^{\prime}j^{\prime} \, is{\text{ opened to serve market }}k{\text{ in doupoly}} \hfill \\ &0\quad {\text{ otherwise}} \hfill \\ \end{aligned} \right.$

$y_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}}$ :

$\left\{ \begin{aligned} &1 \quad i{\text{f path }}iji^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}{\text{ is opened to serve market }}k{\text{ in oligpoly}} \hfill \\ &0\quad {\text{ otherwise}} \hfill \\ \end{aligned} \right.$

$x\varUpsilon_{ij}$ :

Quantity of product shipped from plant i to DC j for SC1.

$x\varPsi_{jk}$ :

Quantity of product shipped from DC j to customer k for SC1.

$x\chi_{{i^{\prime}j^{\prime}}}$ :

Quantity of product shipped from plant $i^{\prime}$ to DC $j^{\prime}$ for SC2.

$x{\rm E}_{{j^{\prime}k}}$ :

Quantity of product shipped from DC $j^{\prime}$ to customer k for SC2.

$x{\rm H}_{{i^{\prime\prime}j^{\prime\prime}}}$ :

Quantity of product shipped from plant $i^{\prime\prime}$ to DC $j^{\prime\prime}$ for SC3.

$x\varGamma_{{j^{\prime\prime}k}}$ :

Quantity of product shipped from DC $j^{\prime\prime}$ to customer k for SC3.

$W\varUpsilon_{ij}^{{}}$ :

wholesale price of plant $i$ to DC $j$ in SC1.

$P\varPsi_{jk}^{{}}$ :

Retail price of DC $j$ to customer $k$ in SC1.

$W\chi_{{i^{\prime}j^{\prime}}}^{{}}$ :

Wholesale price of plant $i^{\prime}$ to DC $j^{\prime}$ in SC2.

$P{\rm E}_{{j^{\prime}k}}^{{}}$ :

Retail price of DC $j^{\prime}$ to customer $k$ in SC2.

$W{\rm H}_{{i^{\prime\prime}j^{\prime\prime}}}^{{}}$ :

Wholesale price of plant $i^{\prime\prime}$ to DC $j^{\prime\prime}$ in SC3.

$P\varGamma_{{j^{\prime\prime}k}}^{{}}$ :

Retail price of DC $j^{\prime\prime}$ to customer $k$ in SC3.

$W\varUpsilon_{ijk}^{{}}$ :

Wholesale price of SC1 by path $ijk$ in monopoly competition.

$P\varPsi_{ijk}^{{}}$ :

Retail price of SC1 by path $ijk$ in monopoly competition.

$W\varUpsilon_{{ijki^{\prime}j^{\prime}}}^{{}}$ :

Wholesale price of SC1 by path $ijki^{\prime}j^{\prime}$ in duopoly competition.

$P\varPsi_{{ijki^{\prime}j^{\prime}}}^{{}}$ :

Retail price of SC1 by path $ijki^{\prime}j^{\prime}$ in duopoly competition.

$W\chi_{{ijki^{\prime}j^{\prime}}}^{{}}$ :

Wholesale price of SC2 by path $ijki^{\prime}j^{\prime}$ in duopoly competition.

$P{\rm E}_{{ijki^{\prime}j^{\prime}}}^{{}}$ :

Retail price of SC2 by path $ijki^{\prime}j^{\prime}$ in duopoly competition.

$W\varUpsilon_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}}^{{}}$ :

Wholesale price of SC1 by path $ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}$ in oligopoly competition.

$P\varPsi_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}}^{{}}$ :

Retail price of SC1 by path $ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}$ in oligopoly competition.

$W\chi_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}}^{{}}$ :

Wholesale price of SC2 by path $ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}$ in oligopoly competition.

$P{\rm E}_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}}^{{}}$ :

Retail price of SC2 by path $ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}$ in oligopoly competition.

$W{\rm H}_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}}^{{}}$ :

Wholesale price of SC3 by path $ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}$ in oligopoly competition.

$P\varGamma_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}}^{{}}$ :

Retail price of SC3 by path $ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}$ in oligopoly competition.

$x\varUpsilon_{ijk}^{{}}$ :

Quantity of product shipped by path $ijk$ in monopoly competition for SC1.

$x\varUpsilon_{{ijki^{\prime}j^{\prime}}}^{{}}$ :

Quantity of product shipped by path $ijki^{\prime}j^{\prime}$ in duopoly competition for SC1.

$x\chi_{{ijki^{\prime}j^{\prime}}}^{{}}$ :

Quantity of product shipped by path $ijki^{\prime}j^{\prime}$ in duopoly competition for SC2.

$x\varUpsilon_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}}^{{}}$ :

Quantity of product shipped by path $ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}$ in oligopoly competition for SC1.

$x\chi_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}}^{{}}$ :

Quantity of product shipped by path $ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}$ in oligopoly competition for SC2.

$x{\rm H}_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}}^{{}}$ :

Quantity of product shipped by path $ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}$ in oligopoly competition for SC3.

Demand functions of DC $j,j^{\prime},j^{\prime\prime}$ for SC1, SC2 and SC3 in market $k$ in each competition mode are defined as follows:

Monopoly demand

$$\widetilde{D\varUpsilon }_{jk}^{{}} = \tilde{\alpha }_{SC1} \tilde{d}_{k} - \tilde{\delta }P\varUpsilon_{jk}^{{}} .$$

(1)

Duopoly demand

$$\widetilde{D\varUpsilon }_{jk}^{{}} = \tilde{\alpha }_{SC1} \tilde{d}_{k} - \tilde{\delta }P\varUpsilon_{jk}^{{}} + \tilde{\beta }(P\chi_{{j^{\prime}k}}^{{}} - P\varUpsilon_{jk}^{{}} )$$

(2)

$$\widetilde{D\chi }_{{j^{\prime}k}}^{{}} = \tilde{\alpha }_{SC2} \tilde{d}_{k} - \tilde{\delta }P\chi_{{j^{\prime}k}}^{{}} + \tilde{\beta }(P\varUpsilon_{jk}^{{}} - P\chi_{{j^{\prime}k}}^{{}} )$$

(3)

Oligopoly demand

$$\widetilde{D\varUpsilon }_{jk}^{{}} = \tilde{\alpha }_{SC1} \tilde{d}_{k} - \tilde{\delta }P\varUpsilon_{jk}^{{}} + \tilde{\beta }(P\chi_{{j^{\prime}k}}^{{}} + P\varGamma_{{j^{\prime\prime}k}} - P\varUpsilon_{jk}^{{}} )$$

(4)

$$\widetilde{D\chi }_{{j^{\prime}k}}^{{}} = \tilde{\alpha }_{SC2} \tilde{d}_{k} - \tilde{\delta }P\chi_{{j^{\prime}k}}^{{}} + \tilde{\beta }(P\varUpsilon_{jk}^{{}} + P\varGamma_{{j^{\prime\prime}k}}^{{}} - P\chi_{{j^{\prime}k}}^{{}} )$$

(5)

$$\widetilde{{D{\rm H}}}_{{j^{\prime\prime}k}}^{{}} = \tilde{\alpha }_{SC3} \tilde{d}_{k} - \tilde{\delta }P\varGamma_{{j^{\prime\prime}k}}^{{}} + \tilde{\beta }(P\varUpsilon_{jk}^{{}} + P\chi_{{j^{\prime}k}}^{{}} - P\varGamma_{{j^{\prime\prime}k}}^{{}} ).$$

(6)

$\tilde{d}_{k}$ is the potential market size (if prices were all zero),$\tilde{\alpha }_{{{\text{SC}}1}} ,\tilde{\alpha }_{{{\text{SC}}2}} ,\tilde{\alpha }_{{{\text{SC}}3}}$ are related to SC1, SC2 and SC3 brand reputations, $\tilde{\alpha }_{{{\text{SC}}1}} \tilde{d}_{k} ,\tilde{\alpha }_{{{\text{SC}}2}} \tilde{d}_{k} ,\tilde{\alpha }_{{{\text{SC}}3}} \tilde{d}_{k}$ are related to based demand for SC1, SC2 and SC3 if all prices were set to zero. If a SC reduces its price in market k the related demand will be increased; also there are two types of customers who can be gained, switching and marginal customers. Switching customers are those who will definitely buy the products by finding the one with the lowest price, but marginal customers will buy the product only if the price is below a certain level. $\tilde{\delta }$ is related to the switching customers and $\tilde{\beta }$ is related to marginal customers, also a unit reduction of price increases the demand function by $(\tilde{\delta } + \tilde{\beta })$.

Now we can formulate our presented problem as follows:

Plant’s model of SC1

$$P_{{_{\text{SC1}} }}^{\text{Plant}} : \, \hbox{max} \, Z_{1} = \sum\limits_{i} {\sum\limits_{j} {x\varUpsilon_{ij} W\varUpsilon_{ij}^{{}} } } \, - \left(\sum\limits_{i}^{{}} {\widetilde{f\varUpsilon }_{i}^{{}} \varUpsilon_{i} + } \sum\limits_{i}^{{}} {\sum\limits_{j}^{{}} {\widetilde{{s\varUpsilon_{i} }}x\varUpsilon_{ij} + \sum\limits_{i}^{{}} {\sum\limits_{j}^{{}} {\widetilde{c\varUpsilon }_{ij} x\varUpsilon_{ij} } \, } } } \right) s.t$$

(7)

$$\sum\limits_{i} {x\varUpsilon_{ij} } = \sum\limits_{k} {x\varPsi_{jk} } \quad \forall i$$

(8)

$$\begin{aligned} \sum\limits_{j}^{{}} x\varUpsilon_{ij} \le \widetilde{Cp\varUpsilon }_{i} \varUpsilon_{i} \qquad \forall i \hfill \\ \end{aligned}$$

(9)

$$\sum\limits_{i}^{{}} {\varUpsilon_{i} } = P\varUpsilon$$

(10)

$$x\varUpsilon_{ij} ,W\varUpsilon_{ij}^{{}} \ge 0,\varUpsilon_{i} = \left\{ {0,1} \right\}.$$

(11)

Term 7 represents the objective function of the plant of SC1 which includes profits captured by selling the product to the DCs minus the fixed cost of opening plants, the production cost of plants, the transportation cost between plants and DCs. Constraint 8 is related to flow balance; constraint 9 ensures that only opened plants can satisfy their related demands up to their capacity; constraint 10 ensures that only $P\varUpsilon$ plants are opened and constraint 11 is related to binary and non-negativity restrictions on the corresponding decision variables.DC’s model of SC

$$P_{\text{DC}}^{{{\text{SC}}1}} :{ \hbox{max} }Z_{2} = \sum\limits_{j} {\sum\limits_{k} {x\varPsi_{jk} P\varPsi_{jk} } } - \left( {\sum\limits_{{}} {\widetilde{{g\varPsi_{j} }}\varPsi_{j} } + \sum\limits_{j} {\sum\limits_{k} {\left( {\frac{{\widetilde{h\varPsi }_{j} }}{2}} \right)x\varPsi_{jk} } } + \sum\limits_{j} {\sum\limits_{k} {\widetilde{c\varPsi }_{jk} x\varPsi_{jk} } } } \right)\quad s.t$$

(12)

$$x\varPsi_{jk} = \widetilde{D\varUpsilon }_{jk} \quad {\forall }k$$

(13)

$$\sum\limits_{k}^{{}} {x\varPsi_{jk} } \le \widetilde{Cp\varPsi }_{j} \varPsi_{j} \quad {\forall }{\text{j}}$$

(14)

$$\sum\limits_{j}^{{}} {\varPsi_{j} = q} \varPsi$$

(15)

$$x\varPsi_{jk} ,P\varPsi_{jk}^{{}} \ge 0,\varPsi_{j} = \left\{ {0,1} \right\}$$

(16)

Term 12 represents the objective function of the DC of the SC1 which includes profits captured by selling the product to the customers minus the fixed cost of opening DCs and the holding cost at DCs and the transportation cost between DCs and the customers. Constraint 13 ensures that all customer demand is satisfied; Constraints 14 ensures that only opened DCs can satisfy their related demands up to their capacity; Constraint 15 ensures that only $q\varUpsilon$ DCs are open; and Constraint 16 is related to binary and non-negativity restrictions on the corresponding decision variables. SC2 and SC3 mostly have the same model presented in “Appendix 1, 2, 3 and 4”.

Solution approach

This section presents the solution approach to tackle the presented fuzzy multi-level mixed integer linear programming problem: most of multi-level and bi-level models in the literature are converted into a single-level problem usually by KKT conditions then will be solved by different methods, but this procedure is very hard, time-consuming and needs lots of computation calculations even for small scaled problem because the one-level problem is nonlinear and non-convex and resulted from KKT conditions and Lagrangian terms, but our approach is very easy to use and efficient for any problem size and there is no need to convert the model into a single one. We convert the problem into an integrated bi-level model (our formulation of the bi-level model is like Rezapour and Farahani (2014)) in which the inner part sets the equilibrium prices in simultaneous extra-the chains and Stackelberg intra-the chains competitions and outer level shapes the networks of the chains cooperatively. Also in each step we introduced the equivalent crisp one of the fuzzy models according to “Appendix 13”.

Modeling framework

Two parts of bi-level model are formulated for this problem, the inner part is a Nash equilibrium model determining the equilibrium prices (DCs and plants prices) by maximizing SCs profit in monopoly, duopoly and oligopoly competitions by considering the fact that each SC can be decentralized based on plant or DC mode.

There are firm interactions between the two parts of the model:

• Profit of the SCs is computed by the equilibrium prices in the inner model.

• Network structures of the SCs, that are specified in the outer model, determine the productions and distributions costs which affect the prices equilibrium in the inner part.

Pricing decision

This step deals with the inner part of the bi-level model which determines the equilibrium prices for the SCs; in fact according to each possible path (combination of one plant and one DC of the chains) the prices are calculated and according to the computed prices the best structure of each chain in the next step will be selected by the outer part of the model.

Two common strategies can occur as follows.

Decentralized pricing strategy based on plants

In this mode a Stackelberg game happens in the pricing strategy in which plants are the leader of the game; they decide the wholesale prices that maximize their profit given responses of the DCs and the DCs acting as followers and choose DC prices to maximize their profit, given the wholesale and market price the players will decide to open the paths with the highest profit and shape their network structure.

Monopoly competition

The plant and DC profit functions in market k are as follows:

Leader:

$$\begin{aligned} \pi_{\text{Plant}}^{\text{SC1}} & = \left( {W\varUpsilon_{ijk}^{{}} - EV(C\varUpsilon_{ij}^{SC1} ))(EV(\tilde{\alpha }\tilde{d}_{k} ) - EV(\tilde{\delta })P\varPsi_{ijk}^{{}} } \right), \\ & \hbox{max} \left\{ {\pi_{\text{Plant}}^{\text{SC1}} } \right\} \\ \end{aligned}$$

(17)

Follower:

$$\begin{aligned} \pi_{\text{DC}}^{{{\text{SC}}1}} & = (P\varPsi_{ijk}^{{}} - EV(\widetilde{C\varPsi }_{jk}^{{}} ) - W\varUpsilon_{ijk}^{{}} )(EV(\tilde{\alpha }\tilde{d}_{k} ) - EV(\tilde{\delta })P\varPsi_{ijk}^{{}} ), \\ & \hbox{max} \left\{ {\pi_{\text{DC}}^{{{\text{SC}}1}} } \right\} \\ \end{aligned}$$

(18)

where $EV(C\varUpsilon_{ij}^{SC1} ) = EV(\widetilde{{s\varUpsilon_{i} }}) + EV(\widetilde{c\varUpsilon }_{ij} )$ and $EV(\widetilde{C\varPsi }_{jk}^{{}} ) = EV(\frac{{\widetilde{h\varPsi }_{j} }}{2}) + EV(\widetilde{c\varPsi }_{jk} )$

Duopoly competition

In this competition mode the following models should be maximized sequentially in order to achieve the equilibrium prices:

Leaders:

$$\begin{aligned} \pi_{\text{Plant}}^{{{\text{SC}}1}} & = \left( {W\varUpsilon_{{jki^{\prime}j^{\prime}}} - EV(C\varUpsilon_{ij}^{{}} )} \right)\left( {EV(\tilde{\alpha }\tilde{d}_{k} ) - EV(\tilde{\delta })P\varPsi_{{ijki^{\prime}j^{\prime}}}^{{}} + EV(\tilde{\beta })(P{\rm E}_{{ijki^{\prime}j^{\prime}}}^{{}} - P\varPsi_{{ijki^{\prime}j^{\prime}}}^{{}} )} \right) \\ & \hbox{max} \left\{ {\pi_{\text{Plant}}^{{{\text{SC}}1}} } \right\}, \\ \end{aligned}$$

(19)

$$\begin{aligned} \pi_{\text{Plant}}^{{{\text{SC}}2}} & = (W\chi_{{ijki^{\prime}j^{\prime}}} - EV(\widetilde{C\chi }_{{i^{\prime}j^{\prime}}}^{{}} ))(EV((1 - \tilde{\alpha })\tilde{d}_{k} ) - EV(\tilde{\delta })P{\rm E}_{{ijki^{\prime}j^{\prime}}}^{{}} + EV(\tilde{\beta })(P\varPsi_{{ijki^{\prime}j^{\prime}}}^{{}} - P{\rm E}_{{ijki^{\prime}j^{\prime}}}^{{}} )) \\ & \hbox{max} \left\{ {\pi_{\text{Plant}}^{{{\text{SC}}2}} } \right\} \\ \end{aligned}$$

(20)

Followers:

$$\begin{aligned} \pi_{\text{DC}}^{{{\text{SC}}1}} & = \left( {P\varPsi_{{ijki^{\prime}j^{\prime}}}^{{}} - EV(\widetilde{C\varPsi }_{jk}^{{}} ) - W\varUpsilon_{{ijki^{\prime}j^{\prime}}}^{{}} )(EV(\tilde{\alpha }\tilde{d}_{k} ) - EV(\tilde{\delta })P\varPsi_{{ijki^{\prime}j^{\prime}}}^{{}} + EV(\tilde{\beta })(P{\rm E}_{{ijki^{\prime}j^{\prime}}}^{{}} - P\varPsi_{{ijki^{\prime}j^{\prime}}}^{{}} )} \right) \\ & \hbox{max} \left\{ {\left( {\pi_{\text{DC}}^{{{\text{SC}}1}} } \right)} \right\} \\ \end{aligned}$$

(21)

$$\begin{aligned} \pi_{\text{DC}}^{{{\text{SC}}2}} & = \left( {P{\rm E}_{{ijki^{\prime}j^{\prime}}}^{{}} - EV(\widetilde{{C{\rm E}}}_{{j^{\prime}k}}^{{}} ) - W\chi_{{ijki^{\prime}j^{\prime}}} )(EV((1 - \tilde{\alpha })\tilde{d}_{k} ) - EV(\tilde{\delta })P{\rm E}_{{ijki^{\prime}j^{\prime}}}^{{}} + EV(\tilde{\beta })(P\varPsi_{{ijki^{\prime}j^{\prime}}}^{{}} - P{\rm E}_{{ijki^{\prime}j^{\prime}}}^{{}} )} \right). \\ & \hbox{max} \left\{ {\pi_{\text{DC}}^{{{\text{SC}}2}} } \right\} \\ \end{aligned}$$

(22)

That $EV(\widetilde{C\chi }_{{i^{\prime}j^{\prime}}}^{{}} ) = EV(\widetilde{s\chi }_{{i^{\prime}}} ) + EV(\widetilde{c\chi }_{{i^{\prime}j^{\prime}}} ),EV(\widetilde{{C{\rm E}}}_{{j^{\prime}k}}^{{}} ) = \frac{{EV(\widetilde{{h{\rm E}}}_{{j^{\prime}}} )}}{2} + EV(\widetilde{{c{\rm E}}}_{{j^{\prime}k}} )$

Oligopoly competition

This competition mode is shown for three players. It can be clearly extended to more players. Similarly, the following models should be maximized sequentially in order to achieve the wholesale and market equilibrium prices:

Leaders:

$$\begin{aligned} \pi_{{{\text{Plant}} }}^{{{\text{SC}}1}} & = \left( {W\varUpsilon_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}} - EV(\widetilde{C\varUpsilon }_{ij} ))(EV(\tilde{\alpha }_{SC1} \tilde{d}_{k} ) - EV(\tilde{\delta })P\varPsi_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}} + EV(\tilde{\beta })(P{\rm E}_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}} + P\varGamma_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}} - P\varPsi_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}} )} \right), \\ & \hbox{max} \left\{ {\pi_{\text{Plant}}^{{{\text{SC}}1}} } \right\} \\ \end{aligned}$$

(23)

$$\begin{aligned} \pi_{\text{Plant}}^{{{\text{SC}}2}} & = \left( {W\chi_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}} - EV(\widetilde{C\chi }_{{i^{\prime}j^{\prime}}}^{{}} ))(EV(\tilde{\alpha }_{SC2} \tilde{d}_{k} ) - EV(\tilde{\delta })P{\rm E}_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}}^{{}} + EV(\tilde{\beta })(P\varPsi_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}} + P\varGamma_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}}^{{}} - P{\rm E}_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}}^{{}} )} \right) \\ & \hbox{max} \left\{ {\pi_{\text{Plant}}^{{{\text{SC}}2}} } \right\} \\ \end{aligned}$$

(24)

$$\begin{aligned} \pi_{\text{Plant}}^{{{\text{SC}}3}} & = \left( {W{\rm H}_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}}^{{}} - EV(\widetilde{{C{\rm H}}}_{{i^{\prime\prime}j^{\prime\prime}}}^{{}} ))(EV(\tilde{\alpha }_{SC3} \tilde{d}_{k} ) - EV(\tilde{\delta })P\varGamma_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}}^{{}} + EV(\tilde{\beta })(P\varPsi_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}} + P{\rm E}_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}}^{{}} - P\varGamma_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}}^{{}} )} \right) \\ & \hbox{max} \left\{ {\pi_{\text{Plant}}^{{{\text{SC}}3}} } \right\} \\ \end{aligned}$$

(25)

Followers:

$$\begin{aligned} \pi_{\text{DC}}^{{{\text{SC}}1}} & = \left( {P\varPsi_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}} - EV(C\varPsi_{jk}^{{}} ) - W\varUpsilon_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}}^{{}} )(EV(\tilde{\alpha }_{SC1} \tilde{d}_{k} ) - EV(\tilde{\delta })P\varPsi_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}} + EV(\tilde{\beta })(P{\rm E}_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}}^{{}} + P\varGamma_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}}^{{}} - P\varPsi_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}} )} \right) \\ & \hbox{max} \left\{ {\pi_{\text{DC}}^{{{\text{SC}}1}} } \right\} \\ \end{aligned}$$

(26)

$$\begin{aligned} \pi_{DC}^{SC2} = (P{\rm E}_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}}^{{}} - EV(\widetilde{{C{\rm E}}}_{{j^{\prime}k}}^{{}} ) - W\chi_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}}^{{}} )(EV(\tilde{\alpha }_{SC2} \tilde{d}_{k} ) - EV(\tilde{\delta })P{\rm E}_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}}^{{}} + EV(\tilde{\beta })(P\varPsi_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}} + P\varGamma_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}}^{{}} - P{\rm E}_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}}^{{}} )) \hfill \\ \hbox{max} \left\{ {\pi_{DC}^{SC2} } \right\} \hfill \\ \end{aligned}$$

(27)

$$\begin{aligned} \pi_{\text{DC}}^{{{\text{SC}}3}} & = \left( {P\varGamma_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}} - EV(\widetilde{C\varGamma }_{{j^{\prime\prime}k}} ) - W{\rm H}_{{jki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}} )(EV(\tilde{\alpha }_{SC3} \tilde{d}_{k} ) - EV(\tilde{\delta })P\varGamma_{{jki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}} + EV(\tilde{\beta })(P\varPsi_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}} + P{\rm E}_{{jki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}} - P\varGamma_{{jki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}} )} \right) \\ & \hbox{max} \left\{ {\pi_{\text{DC}}^{{{\text{SC}}3}} } \right\}, \\ \end{aligned}$$

(28)

where $EV(\widetilde{CH}_{{i^{\prime\prime}j^{\prime\prime}}} ) = EV(s{\rm H}_{{i^{\prime\prime}}} ) + EV(c{\rm H}_{{i^{\prime\prime}j^{\prime\prime}}} ),EV(\widetilde{C\varGamma }_{{j^{\prime\prime}k}} ) = \frac{{EV(\widetilde{h\varGamma }_{{j^{\prime\prime}}} )}}{2} + EV(\widetilde{c\varGamma }_{{j^{\prime\prime}k}} )$

Decentralized pricing strategy based on DCS

In this pricing mode another Stackelberg game happens in which DCs are the leaders and make decisions first. If they choose the market price, the product demands are fixed and the plants set their price equal to DC price leaving no profit for the DCs (Edirisinghe et al. 2011); thus they choose their margins $M$ at the first stage where in monopoly

$$M_{ijk}^{{{\text{SC}}1}} = P\varPsi_{ijk}^{{}} - W\varUpsilon_{ijk}^{{}} .$$

(29)

in duopoly

$$M_{{ijki^{\prime}j^{\prime}}}^{{{\text{SC}}1}} = P\varPsi_{{ijki^{\prime}j^{\prime}}}^{{}} - W\varUpsilon_{{ijki^{\prime}j^{\prime}}}^{{}} ,M_{{ijki^{\prime}j^{\prime}}}^{{{\text{SC}}2}} = P{\rm E}_{{ijki^{\prime}j^{\prime}}}^{{}} - W\chi_{{ijki^{\prime}j^{\prime}}}^{{}} .$$

(30)

and in oligopoly

$$M_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}}^{{{\text{SC}}1}} = P\varPsi_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}}^{{}} - W\varUpsilon_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}}^{{}} ,M_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}}^{{{\text{SC}}2}} = P{\rm E}_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}}^{{}} - W\chi_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}}^{{}} ,M_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}}^{{{\text{SC}}3}} = P\varGamma_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}}^{{}} - W{\rm H}_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}}^{{}}$$

(31)

Then at the second stage, the wholesale prices are chosen, given the DCs margin, therefore, giving the wholesale and market prices the players will decide to open the paths with the highest profit and shape their network structure.

Differentiating the terms and solving sequentially will result in equilibrium prices for the SCs

Location decisions

This step deals with the outer part of the bi-level model addressing the network design for the chains to shape in cooperative games; mathematical model of this part is presented as follows, in which the prices are given by the inner part and the definition of variables and objective functions are based on the possible paths to serve the markets (for example $x\varUpsilon_{ijk}$ is replaced instead of $x\varUpsilon_{ij} ,x\varPsi_{jk}$ in monopoly competition, expected values of trapezoidal fuzzy numbers are used to convert the model into a crisp one as well).

Monopoly competition

This mode is the simplest one, based on the power of each entity and according to the leader and follower game, their model will be solved sequentially.

Plant as the leader

$$Z_{\text{Plant}} : { }\sum\limits_{i} {\sum\limits_{j} {\sum\limits_{k} {\left[ {(W\varUpsilon_{ijk}^{*} - EV(C\varUpsilon_{ij}^{{}} ))x\varUpsilon_{ijk} } \right]} } } - \left(\sum\limits_{i} {EV(\widetilde{f\varUpsilon }_{i}^{{}} )\varUpsilon_{i} } \right) \quad s.t$$

(32)

(10, 15)

$$Z_{\text{DC}} = \sum\limits_{i} {\sum\limits_{j} {\sum\limits_{k} {\left[ {(P\varPsi_{ijk}^{*} - EV(\widetilde{C\varPsi }_{jk}^{{}} ) - W\varUpsilon_{ijk}^{*} )x\varUpsilon_{ijk} } \right]} } } - \sum\limits_{j} {EV(\widetilde{{g\varPsi_{j} }})\varPsi_{j} }$$

(33)

$$x\varUpsilon_{ijk} = D\varUpsilon_{ijk}^{*} y_{ijk} \quad {\forall }i,j,k$$

(34)

$$\sum\limits_{i} {\sum\limits_{j} {\sum\limits_{k} {y_{ijk} = 1} } } \quad {\forall }k$$

(35)

$$y_{ijk} \le \varUpsilon_{i} \varPsi_{j} \quad {\forall }i,j,k$$

(36)

$$\sum\limits_{j}^{{}} {\sum\limits_{k} {x\varUpsilon_{ijk} } } \le \left( {\varphi Cp\varUpsilon_{(1i)} + (1 - \varphi )Cp\varUpsilon_{(2i)} } \right)\varUpsilon_{i} \quad \forall i$$

(37)

$$\sum\limits_{j}^{{}} {\sum\limits_{k} {x\varUpsilon_{ijk} } } \le (\varphi Cp\varPsi_{(1j)} + (1 - \varphi )Cap\varPsi_{(2j)} )\varPsi_{j} \quad {\forall }j$$

(38)

$$x\varUpsilon_{ijk} , \ge 0,y_{ijk} ,\varUpsilon_{i} ,\varPsi_{j} = \left\{ {0,1} \right\}.$$

(39)

Term 32 represents the objective function of plant. Constraint 33 is related to objective function of DC. Constraint 34 is related to demand satisfaction. Constraint 35 ensures that only one path should be assigned to each customer. Constraint 36 ensures that a path cannot be opened unless the related plants and DCs of the chain are open. Terms 37, 38 are related to the capacity constraints of the SC, which changed to the crisp mode according to Appendix 13. Term 39 is related to the binary and non-negativity restrictions on the corresponding decision variables.

If the DC is set as the leader and the plant set as the follower in location step in this competition, the following model will be the result:

$$Z_{\text{DC}} : { }\sum\limits_{i} {\sum\limits_{j} {\sum\limits_{k} {\left[ {(P\varPsi_{ijk}^{*} - EV(\widetilde{C\varPsi }_{jk}^{{}} ) - W\varUpsilon_{ijk}^{*} )x\varUpsilon_{ijk} } \right]} } } - \sum\limits_{j} {EV(\widetilde{{g\varPsi_{j} }})\varPsi_{j} } \quad s.t$$

(40)

(10, 15, 34–39)

$$Z_{\text{Plant}} = \sum\limits_{i} {\sum\limits_{j} {\sum\limits_{k} {\left[ {\left( {W\varUpsilon_{ijk}^{*} - EV(C\varUpsilon_{ij}^{{}} )} \right)x\varUpsilon_{ijk} } \right]} } } - \left( {\sum\limits_{i} {EV(\widetilde{f\varUpsilon }_{i}^{{}} )\varUpsilon_{i} } } \right)$$

(41)

Term 40 represents the objective function of DC. Constraint 41 is related to objective function of the plant.

Duopoly competition

In this mode, the cooperation will be shaped between the leaders of the chains based on their power and four different models are achieved as follows:

Plants are the leaders of both chains

$$\begin{aligned} P_{\text{cop}}^{P\& P} & : { }\sum\limits_{i} {\sum\limits_{j} {\sum\limits_{{i^{\prime}}} {\sum\limits_{{j^{\prime}}} {\sum\limits_{k} {\left[ {(W\varUpsilon_{{ijki^{\prime}j^{\prime}}}^{*} - EV(C\varUpsilon_{ij}^{{}} ))x\varUpsilon_{{ijki^{\prime}j^{\prime}}} + (W\chi_{{ijki^{\prime}j^{\prime}}}^{*} - EV(\widetilde{C\chi }_{{i^{\prime}j^{\prime}}}^{{}} ))x\chi_{{ijki^{\prime}j^{\prime}}} } \right]} } } } } \\ & - \left(\sum\limits_{i} {EV(\widetilde{f\varUpsilon }_{i}^{{}} )\varUpsilon_{i} } + \sum\limits_{{i^{\prime}}} {EV(\widetilde{f\chi }_{{i^{\prime}}}^{{}} )\chi_{{i^{\prime}}} } \right) \quad s.t. \\ \end{aligned}$$

(42)

(10, 15, 73, 78)

$$Z_{\text{DC}}^{{{\text{SC}}1}} = \sum\limits_{i} {\sum\limits_{j} {\sum\limits_{{i^{\prime}}} {\sum\limits_{{j^{\prime}}} {\sum\limits_{k} {\left[ {(P\varPsi_{{ijki^{\prime}j^{\prime}}}^{*} - EV(\widetilde{C\varPsi }_{jk}^{{}} ) - W\varUpsilon_{{ijki^{\prime}j^{\prime}}}^{*} )x\varUpsilon_{{ijki^{\prime}j^{\prime}}} } \right]} } } } } - \sum\limits_{j} {EV(\widetilde{{g\varPsi_{j} }})\varPsi_{j} }$$

(43)

$$Z_{\text{DC}}^{{{\text{SC}}2}} = \sum\limits_{i} {\sum\limits_{j} {\sum\limits_{{i^{\prime}}} {\sum\limits_{{j^{\prime}}} {\sum\limits_{k} {\left[ {(P{\rm E}_{{ijki^{\prime}j^{\prime}}}^{*} - EV(\widetilde{{C{\rm E}}}_{{j^{\prime}k}}^{{}} ) - W\chi_{{_{{ijki^{\prime}j^{\prime}}} }}^{*} )x\chi_{{ijki^{\prime}j^{\prime}}} } \right]} } } } } - \sum\limits_{{j^{\prime}}} {EV(\widetilde{{g{\rm E}_{{j^{\prime}}} }}){\rm E}_{{j^{\prime}}} }$$

(44)

$$x\varUpsilon_{{ijki^{\prime}j^{\prime}}} = D\varUpsilon_{{ijki^{\prime}j^{\prime}}}^{*} y_{{ijki^{\prime}j^{\prime}}} \quad {\forall }i,j,i^{\prime},j^{\prime},k$$

(45)

$$x\chi_{{ijki^{\prime}j^{\prime}}} = D\chi_{{ijki^{\prime}j^{\prime}}}^{*} y_{{ijki^{\prime}j^{\prime}}} \quad {\forall }i,j,i^{\prime},j^{\prime},k$$

(46)

$$\sum\limits_{i}^{{}} {\sum\limits_{j}^{{}} {\sum\limits_{{i^{\prime}}}^{{}} {\sum\limits_{{j^{\prime}}}^{{}} {y_{{ijki^{\prime}j^{\prime}}} = 1} } } } \quad {\forall }k$$

(47)

$$y_{{ijki^{\prime}j^{\prime}}} \le \varUpsilon_{i} \varPsi_{j} \chi_{{i^{\prime}}} {\rm E}_{{j^{\prime}}} \quad {\forall }i,j,i^{\prime},j^{\prime},k$$

(48)

$$\sum\limits_{j}^{{}} {\sum\limits_{{i^{\prime}}} {\sum\limits_{{j^{\prime}}} {x\varUpsilon_{{ijki^{\prime}j^{\prime}}} } } } \le (\varphi Cp\varUpsilon_{(1i)} + (1 - \varphi )Cp\varUpsilon_{(2i)} )\varUpsilon_{i} \quad \forall i$$

(49)

$$\sum\limits_{i}^{{}} {\sum\limits_{{i^{\prime}}} {\sum\limits_{{j^{\prime}}} {\sum\limits_{k} {x\varUpsilon_{{ijki^{\prime}j^{\prime}}} } } } } \le (\varphi Cp\varPsi_{(1j)} + (1 - \varphi )Cp\varPsi_{(2j)} )\varPsi_{j} \quad {\forall }j$$

(50)

$$\sum\limits_{i}^{{}} {\sum\limits_{j} {\sum\limits_{{j^{\prime}}} {\sum\limits_{k} {x\chi_{{ijki^{\prime}j^{\prime}}} } } } } \le (\varphi Cp\chi_{{(1i^{\prime})}} + (1 - \varphi )Cp\chi_{{(2i^{\prime})}} )\chi_{{i^{\prime}}} \quad {\forall }i^{\prime}$$

(51)

$$\sum\limits_{i}^{{}} {\sum\limits_{j} {\sum\limits_{{i^{\prime}}} {\sum\limits_{k} {x\chi_{{ijki^{\prime}j^{\prime}}} } } } } \le (\varphi Cp{\rm E}_{{(1j^{\prime})}} + (1 - \varphi )Cp{\rm E}_{{(2j^{\prime})}} ){\rm E}_{{j^{\prime}}} {\forall }j^{\prime}$$

(52)

$$x\varUpsilon_{{ijki^{\prime}j^{\prime}}} ,x\chi_{{ijki^{\prime}j^{\prime}}} \ge 0,y_{{ijki^{\prime}j^{\prime}}} ,\varUpsilon_{i} ,\varPsi_{j} ,\chi_{{i^{\prime}}} ,{\rm E}_{{j^{\prime}}} = \left\{ {0,1} \right\}.$$

(53)

Term 42 represents the objective function which includes the objective functions of SC1 and SC2 plants. Constraints 43 and 44 are calculating the objective function of the DCs in the chains. Constraints 45 and 46 are related to demand satisfaction. Constraint 47 ensures that only one path should be assigned to each customer. Constraint 48 ensures that a path cannot be opened unless the related plants and DCs of SC1 and SC2 are open. Terms 49–52 are related to the capacity constraints of the SCs which changed to the crisp mode according to Appendix 13. Term 53 is related to the binary and non-negativity restrictions on the corresponding decision variables.

If the leader of SC1 and SC2 is their related DC and plant then the following model is achieved:

$$\begin{aligned} P_{\text{cop}}^{{{\text{DC}}\& P}} & : { }\sum\limits_{i} {\sum\limits_{j} {\sum\limits_{{i^{\prime}}} {\sum\limits_{{j^{\prime}}} {\sum\limits_{k} {\left[ {(P\varPsi_{{ijki^{\prime}j^{\prime}}}^{*} - EV(\widetilde{C\varPsi }_{jk}^{{}} ) - W\varUpsilon_{{ijki^{\prime}j^{\prime}}}^{*} )x\varUpsilon_{{ijki^{\prime}j^{\prime}}} + (W\chi_{{ijki^{\prime}j^{\prime}}}^{*} - EV(\widetilde{C\chi }_{{i^{\prime}j^{\prime}}}^{{}} ))x\chi_{{eike^{\prime}i^{\prime}}} } \right]} } } } } \\ & - \left(\sum\limits_{j} {EV(\widetilde{{g\varPsi_{j} }})\varPsi_{j} } + \sum\limits_{{i^{\prime}}} {EV(\widetilde{f\chi }_{{i^{\prime}}}^{{}} )\chi_{{i^{\prime}}} } \right)\quad s.t. \\ \end{aligned}$$

(54)

(10, 15, 73, 78, 45–53)

$$Z_{\text{plant}}^{{{\text{SC}}1}} = \sum\limits_{i} {\sum\limits_{j} {\sum\limits_{{i^{\prime}}} {\sum\limits_{{j^{\prime}}} {\sum\limits_{k} {\left[ {(W\varUpsilon_{{ijki^{\prime}j^{\prime}}}^{*} - EV(C\varUpsilon_{ij}^{{}} ))x\varUpsilon_{{ijki^{\prime}j^{\prime}}} } \right]} } } } } - \sum\limits_{i} {EV(\widetilde{f\varUpsilon }_{i}^{{}} )\varUpsilon_{i} }$$

(55)

$$Z_{\text{DC}}^{{{\text{SC}}2}} = \sum\limits_{i} {\sum\limits_{j} {\sum\limits_{{i^{\prime}}} {\sum\limits_{{j^{\prime}}} {\sum\limits_{k} {\left[ {(P{\rm E}_{{ijki^{\prime}j^{\prime}}}^{*} - EV(\widetilde{{C{\rm E}}}_{{j^{\prime}k}}^{{}} ) - W\chi_{{_{{ijki^{\prime}j^{\prime}}} }}^{*} )x\chi_{{ijki^{\prime}j^{\prime}}} } \right]} } } } } - \sum\limits_{{j^{\prime}}} {EV(\widetilde{{g{\rm E}_{{j^{\prime}}} }}){\rm E}_{{j^{\prime}}} } .$$

(56)

Term 54 represents the objective function which includes the objective functions of DC of SC1 and plant of SC2. Constraints 55 and 56 are calculating the objective function of the plant of SC1 and DC of SC2 correspondingly.

Whenever the Plant of SC1 and DC of SC2 are set as the leaders of their chains to shape their network in cooperation mode, the following model is obtained:

$$\begin{aligned} P_{\text{cop}}^{{P\& {\text{DC}}}} & : { }\sum\limits_{i} {\sum\limits_{j} {\sum\limits_{{i^{\prime}}} {\sum\limits_{{j^{\prime}}} {\sum\limits_{k} {\left[ {(W\varUpsilon_{{ijki^{\prime}j^{\prime}}}^{*} - EV(C\varUpsilon_{ij}^{{}} ))x\varUpsilon_{{ijki^{\prime}j^{\prime}}} + (P{\rm E}_{{ijki^{\prime}j^{\prime}}}^{*} - EV(\widetilde{{C{\rm E}}}_{{j^{\prime}k}}^{{}} ) - W\chi_{{_{{ijki^{\prime}j^{\prime}}} }}^{*} )x\chi_{{ijki^{\prime}j^{\prime}}} } \right]} } } } } \quad s.t \\ & - \left(\sum\limits_{i} {EV(\widetilde{f\varUpsilon }_{i}^{{}} )\varUpsilon_{i} } + \sum\limits_{{j^{\prime}}} {EV(\widetilde{{g{\rm E}_{{j^{\prime}}} }}){\rm E}_{{j^{\prime}}} }\right ) \\ \end{aligned}$$

(57)

(10, 15, 73, 78, 45–53)

$$Z_{\text{DC}}^{{{\text{SC}}1}} = \sum\limits_{i} {\sum\limits_{j} {\sum\limits_{{i^{\prime}}} {\sum\limits_{{j^{\prime}}} {\sum\limits_{k} {\left[ {(P\varPsi_{{ijki^{\prime}j^{\prime}}}^{*} - EV(\widetilde{C\varPsi }_{jk}^{{}} ) - W\varUpsilon_{{ijki^{\prime}j^{\prime}}}^{*} )x\varUpsilon_{{ijki^{\prime}j^{\prime}}} } \right]} } } } } - \sum\limits_{j} {EV(\widetilde{{g\varPsi_{j} }})\varPsi_{j} }$$

(58)

$$Z_{\text{Plant}}^{{{\text{SC}}2}} = \sum\limits_{i} {\sum\limits_{j} {\sum\limits_{{i^{\prime}}} {\sum\limits_{{j^{\prime}}} {\sum\limits_{k} {\left[ {(W\chi_{{ijki^{\prime}j^{\prime}}}^{*} - EV(\widetilde{C\chi }_{{i^{\prime}j^{\prime}}}^{{}} ))x\chi_{{ijki^{\prime}j^{\prime}}} } \right]} } } } } - \sum\limits_{{i^{\prime}}} {EV(\widetilde{f\chi }_{{i^{\prime}}}^{{}} )\chi_{{i^{\prime}}} } .$$

(59)

Term 57 represents the objective function which includes the objective functions of plant of SC1 and DC of SC2. Constraints 58 and 59 are calculating the objective function of the DC of SC1 and plant of SC2 correspondingly.

In the case of DCs as the leaders of the chain, we have the following:

$$\begin{aligned} P_{\text{cop}}^{{{\text{DC}}\& {\text{DC}}}} & : { }\sum\limits_{i} {\sum\limits_{j} {\sum\limits_{{i^{\prime}}} {\sum\limits_{{j^{\prime}}} {\sum\limits_{k} {\left[ {(P\varPsi_{{ijki^{\prime}j^{\prime}}}^{*} - EV(\widetilde{C\varPsi }_{jk}^{{}} ) - W\varUpsilon_{{ijki^{\prime}j^{\prime}}}^{*} )x\varUpsilon_{{ijki^{\prime}j^{\prime}}} + (P{\rm E}_{{ijki^{\prime}j^{\prime}}}^{*} - EV(\widetilde{{C{\rm E}}}_{{j^{\prime}k}}^{{}} ) - W\chi_{{_{{ijki^{\prime}j^{\prime}}} }}^{*} )x\chi_{{ijki^{\prime}j^{\prime}}} } \right]} } } } } \\ & - \left(\sum\limits_{j} {EV(\widetilde{{g\varPsi_{j} }})\varPsi_{j} } + \sum\limits_{{j^{\prime}}} {EV(\widetilde{{g{\rm E}_{{j^{\prime}}} }}){\rm E}_{{j^{\prime}}} } \right)\quad \text{s.t.} \\ \end{aligned}$$

(60)

(10, 15, 73, 78, 45–53)

$$Z_{\text{Plant}}^{{{\text{SC}}1}} = \sum\limits_{i} {\sum\limits_{j} {\sum\limits_{{i^{\prime}}} {\sum\limits_{{j^{\prime}}} {\sum\limits_{k} {\left[ {(W\varUpsilon_{{ijki^{\prime}j^{\prime}}}^{*} - EV(C\varUpsilon_{ij}^{{}} ))x\varUpsilon_{{ijki^{\prime}j^{\prime}}} } \right]} } } } } - \sum\limits_{i} {EV(\widetilde{f\varUpsilon }_{i}^{{}} )\varUpsilon_{i} }$$

(61)

$$Z_{\text{Plant}}^{{{\text{SC}}2}} = \sum\limits_{i} {\sum\limits_{j} {\sum\limits_{{i^{\prime}}} {\sum\limits_{{j^{\prime}}} {\sum\limits_{k} {\left[ {(W\chi_{{ijki^{\prime}j^{\prime}}}^{*} - EV(\widetilde{C\chi }_{{i^{\prime}j^{\prime}}}^{{}} ))x\chi_{{ijki^{\prime}j^{\prime}}} } \right]} } } } } - \sum\limits_{{i^{\prime}}} {EV(\widetilde{f\chi }_{{i^{\prime}}}^{{}} )\chi_{{i^{\prime}}} }$$

(62)

Term 6 represents the objective function which includes the objective functions of DCs of the chains. Constraints 61 and 62 are calculating the objective function of the plants of the chains.

Oligopoly competition

The models in this mode are mostly like duopoly, but the number of models extended to eight different models is presented in the Appendix 5–12.

Numerical example and discussion

This section is divided into two parts, “Numerical example” introduces our example and provides the results of different possible scenarios while “Discussion” fully discusses the example and derives managerial insights.

Numerical example

In this part, we use a real-word problem from Iranian industry in which two independent investors are planning to design a decentralized SC to produce and distribute a kind of oil seal used in washing machine. This seal has been imported to the country, but is not produced in the country; with respect to the market research that has been done by the investors according to specifications of the oil seal that can be produced in Iran this class of the product is virgin so they want to know the possible income from entering to the market in decentralized way by different leadership in pricing and location step (plant or DC being the leader). Moreover, they consider situations in which two or four more investors may enter the market at the same time, so they may encounter with monopoly, duopoly and oligopoly competitions

Decentralized based on plants and DCs are two main strategies in both pricing and location strategies that should be considered. According to modeling framework the prices will specify at first then with respect to the achievable market share and cost of the paths and by the cooperation between the entities of the chains, location decision will be made and the network structure will be shaped. The following distributions are used to extract the required parameters. The parameters are assumed to be trapezoidal fuzzy numbers, and there are some confidential considerations relating to the required parameters. Also four prominent values of the trapezoidal numbers are generated by uniform distributions in reasonable ranges that are very close to the real value of the parameters in the aforementioned industry. All the monetary values are in the Iranian currency (Rials). The following distributions are used to extract the required parameters.

Example 1

Monopoly competition

In this example, only SC1 exists and wants to enter the markets, it has 2 potential locations for plants, 2 for the DCs, wants to open one plant and one DC to satisfy markets, the elements of demand functions are as the follows:

$$EV(d_{1} ) = 1 1 5 6 0 5 ;EV(d_{2} ) = 1 0 7 7 9 5 ;\;EV(\delta ) = 0.03EV(d_{k} );\alpha = 1$$

As there is just one SC exists, four following scenarios are possible to happen based on pricing and location strategies:

Pricing strategies:

• 1. Decentralized (Plant leader)

• 2. Decentralized (DC leader)

Location decisions

• 1. Decentralized (Plant leader)

• 2. Decentralized (DC leader)

$$S = \left\{ {s_{1} = \left\{ {1,1} \right\},s_{2} = \left\{ {1,2} \right\},s_{3} = \left\{ {2,1} \right\},s_{4} = \left\{ {2,2} \right\}} \right\}$$

According to Table 2, if DC sets the price, it results to $s_{3} ,s_{4}$ by the 560485.5 profits for DC, 354612.9 and 915098.4 as the plant and total SC profits respectively. On the other hand, wherever plant is the leader of the chain $s_{1} ,s_{2}$ will be happened by the 568339.7, 283173.3, 851513 as the plant, DC and SC total profits (Table 1 shows the results). By comparing the achieved results, it is clear that if plant sets the price, then its profits will increase by 37.60% but DC and SC profits will decrease by 97.93 and 7.47%, therefore; being DC as the leader is the best profitable scenarios, but there should be a mechanism to share the obtained revenue between the plant and DC in order to motivate the plant to accept those scenarios.

Table 1 First and second scenarios

Table 2 Third and fourth scenarios

Example 2

Duopoly competitionIn this competition, two SCs (4 investors) enter the market simultaneously, they have two potential locations for plants and two for DCs that want to open one plant and one DC to capture the demand of two markets by the following parameters

$$EV(d_{1} ) = 1 1 5 6 0 5 ;EV(d_{2} ) = 1 0 7 7 9 5 ;EV(\delta ) = 0.03EV(d_{k} );EV(\beta ) = 0.05EV(d_{k} );EV(\alpha_{1} ) = 0.55;EV(\alpha_{2} ) = 0.45$$

Also they want to set the prices and locations according to the following scenarios:

Pricing strategies:

• 1. Decentralized (Plant leader)

• 2. Decentralized (DC leader)

Location decisions

• 1. DC cooperative with DC

• 2. DC cooperative with plant

• 3. Plant cooperative with plant

• 4. Plant cooperative with DC

$$S = \left\{ {s_{1} = \left\{ {1,1} \right\},s_{2} = \left\{ {1,2} \right\},s_{3} = \left\{ {1,3} \right\},s_{4} = \left\{ {1,4} \right\},s_{5} = \left\{ {2,1} \right\},s_{6} = \left\{ {2,2} \right\},s_{7} = \left\{ {2,3} \right\},s_{8} = \left\{ {2,4} \right\}} \right\}.$$

According to Tables 3, 4, 5, being plant as the leader results in more profits for SC1 while for SC2 being DC as the leader results in more SC profits. The best scenarios for SC1 are $s_{1}\; \text{and}\; s_{4}$ while they are the worst scenarios for SC2, $s_{5} ,s_{6} ,s_{7}\; \text{and}\;s_{8}$ are the best for SC2 though.

Table 3 First and fourth scenarios

Table 4 Second and third scenarios

Table 5 Fifth, sixth, seventh and eighth scenarios

Example 3

Oligopoly competition

In this competition, three SCs are considered to enter to the market simultaneously. They have two potential locations for plants and two for DCs that want to open one plant and one DC to capture the demand of two markets by the following parameters:

$$EV(d_{1} ) = 1 1 5 6 0 5 ;EV(d_{2} ) = 1 0 7 7 9 5 ;EV(\delta ) = 0.03d_{k} ;EV(\beta ) = 0.05d_{k} ;EV(\alpha_{1} ) = 0.30;EV(\alpha_{2} ) = 0.37;EV(\alpha_{3} ) = 0.33$$

Also they have eight different strategies for location decisions and two different pricing strategies which lead to the following 16 different scenarios:

Pricing strategies:

• 1. Decentralized (Plant leader)

• 2. Decentralized (DC leader)

Location decisions

• 1. DC cooperative with DC cooperative with DC

• 2. DC cooperative with DC cooperative with plant

• 3. DC cooperative with plant cooperative with DC

• 4. plant cooperative with DC cooperative with DC

• 5. Plant cooperative with plant cooperative with DC

• 6. Plant cooperative with DC cooperative with plant

• 7. DC cooperative with Plant cooperative with plant

• 8. Plant cooperative with Plant cooperative with Plant

$$S = \left\{ \begin{aligned} s_{1} = \left\{ {1,1} \right\},s_{2} = \left\{ {1,2} \right\},s_{3} = \left\{ {1,3} \right\},s_{4} = \left\{ {1,4} \right\},s_{5} = \left\{ {1,5} \right\},s_{6} = \left\{ {1,6} \right\},s_{7} = \left\{ {1,7} \right\},s_{8} = \left\{ {1,8} \right\}, \hfill \\ s_{9} = \left\{ {2,1} \right\},s_{10} = \left\{ {2,2} \right\},s_{11} = \left\{ {2,3} \right\},s_{12} = \left\{ {2,4} \right\},s_{13} = \left\{ {2,5} \right\},s_{14} = \left\{ {2,6} \right\},s_{15} = \left\{ {2,7} \right\},s_{16} = \left\{ {2,8} \right\} \hfill \\ \end{aligned} \right\}$$

According to Tables 6, 7, 8, 9, 10, 11, 12, 13 and 14, in scenarios $s_{1} ,s_{2} ,s_{3} ,s_{7} ,s_{12}$ only SC2 that has the biggest $EV(\alpha )$, has the positive total SC income, SC3 has never reached positive total income, although $EV(\alpha )$ is bigger than SC2 but it has higher fixed and variables costs that lead to negative total income that imply it is not profitable for SC3 to enter the market by the current situations and it should find some ways to reduce its cost or increase its $EV(\alpha )$ to obtain more market share or finds another market. The best income for SC2 happens in $s_{3} ,s_{7}$ while the pricing strategy and location decision are based on plant for this chain. $s_{10}$ is the best scenario for SC1 while the pricing strategy and location decisions are based on DC. On the other hand, in all the scenarios (except $s_{10}$ for SC1 and $s_{10} ,s_{12} ,s_{14} ,s_{15}$ for SC2) DC’s profits are negative that can be interpreted as the high level of competition and leads to low DC price in order to achieve more market share but with respect to DC’s costs, no profit will be gained by the DCs so there should be a mechanism to share plant’s profit between DCs, nonetheless; no DCs will have intention to enter the market.

Table 6 First and second scenarios

Table 7 Third and seventh scenarios

Table 8 Fourth and sixth scenarios

Table 9 Fifth scenario

Table 10 Eighth, eleventh, thirteenth and sixteenth scenarios

Table 11 Ninth scenario

Table 12 Tenth scenario

Table 13 Twelfth scenario

Table 14 Fourteenth and fifteent scenarios

Discussion

The former study considers CSCND problem in monopolistic, duopolistic, oligopolistic markets and investigates the effects of leadership of plant and DC in pricing and location decisions. Another important thing that can happen in a real world is the influence of the chains on the number of parameters $\tilde{\delta },\tilde{\beta }$ in demand functions. So in this part we consider $s_{5} ,s_{6} ,s_{7} ,s_{8}$ and discuss the sensitivity analysis of equilibrium wholesale and retail prices, number of profits of the plants and DCs and market shares of SCs with respect to $\tilde{\delta },\tilde{\beta }$. It is worth noting that the rest of the scenarios have the same parameters so the results can be extended to them similarly.

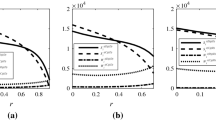
In this part, we study the behavior of the equilibrium wholesale and retail prices, number of profits of the plants and DCs and market shares of the chains with respect to competition intensity $\tilde{\beta }$ effect while the self-price parameter $\tilde{\delta }$ is set to $EV(\tilde{\delta }) = 0.03EV(\tilde{d}_{k} )$. Table 15 represents the change of the equilibrium wholesale and retail prices, number of profits of the plants and DCs and market shares of the chains with respect to the competition intensity effect.

Table 15 The change of the equilibrium wholesale and retail prices, amount of profits of the plants and DCs and market shares of SCs with respect to competition intensity effect

Figures 2, 3 and 4 show the sensitivity analysis of the optimal equilibrium wholesale and retail prices, number of profits of the plants and DCs and market shares of the chains with respect to competition intensity effect. According to these figures, by increasing the amount of the competition intensity parameter, the market shares of the chain will increase, but the prices and the total profits will decrease so the competition intensity parameter has a positive impact on market shares but negative impact on equilibrium prices and total profits.

Fig. 2

Amount of prices with respect to competition intensity effect

Fig. 3

Amount of market shares with respect to competition intensity effect

Fig. 4

Amount of profits with respect to competition intensity effect

Now we study the behavior of the equilibrium wholesale and retail prices, number of profits of the plants and DCs and market shares of the chains with respect to self-price effect while the competition intensity parameter is set to $EV(\beta ) = 0.05$.

Table 16 represents the change of the equilibrium wholesale and retail prices, number of profits of the plants and DCs and market shares of the chains with respect to the self-price effect.

Table 16 The change of the equilibrium wholesale and retail prices, amount of profits of the plants and DCs and market shares of SCs with respect to self-price effect

Figures 5, 6 and 7 show the sensitivity analysis of the equilibrium wholesale and retail prices, amount of profits of the plants and DCs and market shares of the chains with respect to the self-price effect. According to these figures, by increasing the amount of the self-price parameter, the market shares, the prices of the chain and total incomes will decrease; so the self-price parameter has a negative impact on equilibrium prices, total profits and market shares.

Fig. 5

Amount of prices with respect to self-price effect

Fig. 6

Amount of market shares with respect to self-price effect

Fig. 7

Amount of profits with respect to self-price effect

It is worth noting that in our case the change of self-price and competition intensity parameters have no effects on location decision variables, but changes in location decision variables by change in these parameters are possible, and in these circumstances the shape of the networks will change.

The following managerial insights can be derived from these sensitivity analyses:

• Reducing the self-price effect parameter will increase the market share of the chains; this can be achieved by increasing brand loyalty.

• Increasing the competition intensity effect parameter will decrease the marginal profits and consequently will decrease total profits of the chains.

• Increasing competition intensity effect parameters will increase the market share of the chains; this can be achieved by investigating marketing activities.

• To increase the demand and capture more market share, the chains should try to increase the competition intensity parameter and decrease the self-price parameter.

Conclusion

This paper considered a problem in which one, two or three SCs simultaneously are planning to enter the virgin and price dependent market in decentralized mode and set the prices simultaneously between the chains and Stackelberg intra-the chains competition and shape their networks in cooperative competitions. These conditions are modeled by fuzzy multi-level mixed integer linear programming then converted into an integrated bi-level model in which the inner part makes operational pricing decisions in sequential games and the outer part shapes the network of the chains cooperatively. These complicated situations are modeled in different scenarios. After that, we study a real-world problem, explore the scenarios and conduct sensitivity analyses to discuss the effect of competition intensity and self-price parameters on equilibrium wholesale and retail prices, number of profits of the plants, DCs, and market shares of the chains and the behavior of the equilibrium wholesale and retail prices, number of profits of the plants, DCs and market shares of the chains. We conclude that increasing brand loyalty by reducing self-price effect will increase the market shares of the chains and consequently result in more profits for the chains.

Closed-loop, sustainable, robust, green or stochastic decentralized CSCND problem or using fuzzy-hybrid system can be considered for future studies. Moreover, existence of a rival or another customer utility function like Huff gravity rule model can be good ideas for further research.

Appendices

Appendix 1

Plant’s model of SC2

$$P_{{{\text{SC}}2}}^{\text{Plant}} : \, \hbox{max} \, Z_{3} = \sum\limits_{{i^{\prime}}} {\sum\limits_{{j^{\prime}}} {x\chi_{{i^{\prime}j^{\prime}}} W\chi_{{i^{\prime}j^{\prime}}} } } \, - \left(\sum\limits_{{i^{\prime}}}^{{}} {\widetilde{f\chi }_{{i^{\prime}}}^{{}} \chi_{{i^{\prime}}} + } \sum\limits_{{i^{\prime}}}^{{}} {\sum\limits_{{j^{\prime}}}^{{}} {\widetilde{{s\chi_{{i^{\prime}}} }}x\chi_{{i^{\prime}j^{\prime}}} + \sum\limits_{{i^{\prime}}}^{{}} {\sum\limits_{{j^{\prime}}}^{{}} {\widetilde{c\chi }_{{i^{\prime}j^{\prime}}} x\chi_{{i^{\prime}j^{\prime}}} } \, } } } \right) \text{s.t.}$$

(65)

$$\sum\limits_{{i^{\prime}}} {x\chi_{{i^{\prime}j^{\prime}}} } = \sum\limits_{k} {x{\rm E}_{{j^{\prime}k}} } \quad {\forall }i^{\prime}$$

(66)

$$\sum\limits_{{j^{\prime}}}^{{}} {x\chi_{{i^{\prime}j^{\prime}}} } \le \widetilde{Cp\chi }_{{i^{\prime}}} \chi_{{i^{\prime}}} \quad {\forall }{\text{i}}$$

(67)

$$\sum\limits_{{i^{\prime}}}^{{}} {\chi_{{i^{\prime}}} } = P\chi$$

(68)

$$x\chi_{{i^{\prime}j^{\prime}}} ,W\chi_{{i^{\prime}j^{\prime}}}^{{}} \ge 0,\chi_{{i^{\prime}}} = \left\{ {0,1} \right\}.$$

(69)

Terms 51–61 are mostly like the terms 7–11

Appendix 2

Plant’s model of SC3

$$P_{SC3}^{Plant} : \, \hbox{max} \, Z_{3} = \sum\limits_{{i^{\prime\prime}}} {\sum\limits_{{j^{\prime\prime}}} {x{\rm H}_{{i^{\prime\prime}j^{\prime\prime}}} W{\rm H}_{{i^{\prime\prime}j^{\prime\prime}}} } } \, - \left( {\sum\limits_{{i^{\prime\prime}}} {\widetilde{{f{\rm H}}}_{{i^{\prime\prime}}} H_{{i^{\prime\prime}}} } + \sum\limits_{{i^{\prime\prime}}} {\sum\limits_{{j^{\prime\prime}}} {\widetilde{{s{\rm H}}}_{{i^{\prime\prime}}} x{\rm H}_{{i^{\prime\prime}j^{\prime\prime}}} + \sum\limits_{{i^{\prime\prime}}} {\sum\limits_{{j^{\prime\prime}}} {\widetilde{{c{\rm H}}}_{{i^{\prime\prime}j^{\prime\prime}}} x{\rm H}_{{i^{\prime\prime}j^{\prime\prime}}} } } } } } \right)\quad \text{s.t.}$$

(70)

$$\sum\limits_{{i^{\prime\prime}}} {x{\rm H}_{{i^{\prime\prime}j^{\prime\prime}}} } = \sum\limits_{k} {x\varGamma_{{j^{\prime\prime}k}} } \quad \forall i^{\prime\prime}$$

(71)

$$\sum\limits_{{j^{\prime\prime}}} {x{\rm H}_{{i^{\prime\prime}j^{\prime\prime}}} \le \widetilde{CpH}_{{i^{\prime\prime}}} {\rm H}_{{i^{\prime\prime}}} \quad \forall i}$$

(72)

$$\sum\limits_{{i^{\prime\prime}}} {{\rm H}_{{i^{\prime\prime}}} = P{\rm H}}$$

(73)

$$x{\rm H}_{{i^{\prime\prime}j^{\prime\prime}}} ,W{\rm H}_{{i^{\prime\prime}j^{\prime\prime}}} \ge 0,{\rm H}_{{i^{\prime\prime}}} = \left\{ {0,1} \right\}$$

(74)

Terms 62–66 are mostly like the terms 7–11

Appendix 3

DC’s model of SC2

$$P_{{{{\rm DC}}}}^{{{{\rm SC}}2}} :\,{{\rm max }}Z_{5} = \sum\limits_{{j^{\prime}}} {\sum\limits_{k} {x{\rm E}_{{j^{\prime}k}} P{\rm E}_{{j^{\prime}k}}^{{}} } } - \left( {\sum\limits_{{j^{\prime}}}^{{}} {\widetilde{{g{\rm E}_{{j^{\prime}}} }}{\rm E}_{{j^{\prime}}} {\text{ + }}\sum\limits_{{j^{\prime}}}^{{}} {\sum\limits_{k}^{{}} {\left( {\frac{{\widetilde{{h{\rm E}}}_{{j^{\prime}}} }}{2}} \right)x{\rm E}_{{j^{\prime}k}} } {\text{ }}} } + \sum\limits_{{j^{\prime}}}^{{}} {\sum\limits_{k}^{{}} {\widetilde{{c{\rm E}}}_{{j^{\prime}k}} x{\rm E}_{{j^{\prime}k}} } } } \right)\quad {{\rm s}}{\text{.t.}}$$

(75)

$$x{\rm E}_{{j^{\prime}k}} = \widetilde{D\chi }_{{j^{\prime}k}} \quad {\forall }k$$

(76)

$$\sum\limits_{k}^{{}} {x{\rm E}_{{j^{\prime}k}} } \le \widetilde{{Cp{\rm E}}}_{{j^{\prime}}} {\rm E}_{{j^{\prime}}} \quad {\forall }{\text{j}}$$

(77)

$$\sum\limits_{{j^{\prime}}}^{{}} {{\rm E}_{{j^{\prime}}} = q} {\rm E}$$

(78)

$$x{\rm E}_{{j^{\prime}k}} ,P{\rm E}_{{j^{\prime}k}}^{{}} \ge 0,{\rm E}_{{j^{\prime}}} = \left\{ {0,1} \right\}$$

(79)

Terms 67–71 are mostly like the terms 12–16

Appendix 4

DC’s model of SC3

$$P_{\text{DC}}^{{{\text{SC}}3}} : \, \hbox{max} \, Z_{6} = \sum\limits_{{j^{\prime\prime}}} {\sum\limits_{k} {x\varGamma_{{j^{\prime\prime}k}} P\varGamma_{{j^{\prime\prime}k}} } } - \left( {\sum\limits_{{j^{\prime\prime}}} {\widetilde{g\varGamma }_{{j^{\prime\prime}}} \varGamma_{{j^{\prime\prime}}} + \sum\limits_{{j^{\prime\prime}}} {\sum\limits_{k} {\left( {\frac{{\widetilde{h\varGamma }_{{j^{\prime\prime}}} }}{2}} \right)x\varGamma_{{j^{\prime\prime}k}} + \sum\limits_{{j^{\prime\prime}}} {\sum\limits_{k} {\widetilde{c\varGamma }_{{j^{\prime\prime}k}} x\varGamma_{{j^{\prime\prime}k}} } } } } } } \right)\quad \text{s.t.}$$

(80)

$$x{\rm H}_{{j^{\prime\prime}k}} = \widetilde{{D{\rm H}}}_{{j^{\prime\prime}k}} \quad {\forall }k$$

(81)

$$\sum\limits_{k} {x\varGamma_{{j^{\prime\prime}k}} } \le \widetilde{Cp\varGamma }_{{j^{\prime\prime}}} \varGamma_{{j^{\prime\prime}}} \quad \forall j$$

(82)

$$\sum\limits_{{j^{\prime\prime}}} {\varGamma_{{j^{\prime\prime}}} = q\varGamma }$$

(83)

$$x\varGamma_{{j^{\prime\prime}k}} ,P\varGamma_{{j^{\prime\prime}k}} \ge 0,\varGamma_{{j^{\prime\prime}}} = \left\{ {0,1} \right\}$$

(84)

Terms 72–76 are mostly like the terms 12–16

Appendix 5

The following model represents a situation in which the leaders of the chains are their related plants:

$$\begin{aligned} P_{\text{cop}}^{P\& P\& P} & : { }\sum\limits_{i} {\sum\limits_{j} {\sum\limits_{{i^{\prime}}} {\sum\limits_{{j^{\prime}}} {\sum\limits_{{i^{\prime\prime}}} {\sum\limits_{{j^{\prime\prime}}} {\sum\limits_{k} {\left[ {(W\varUpsilon_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}}^{*} - EV(C\varUpsilon_{ij}^{{}} ))x\varUpsilon_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}} + (W\chi_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}}^{*} - EV(\widetilde{C\chi }_{{i^{\prime}j^{\prime}}} ))x\chi_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}} + (W{\rm H}_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}}^{*} - EV(\widetilde{{C{\rm H}}}_{{i^{\prime\prime}j^{\prime\prime}}} ))x{\rm H}_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}} } \right]} } } } } } } \\ & -\left (\sum\limits_{i} {EV(\widetilde{f\varUpsilon }_{i} )\varUpsilon_{i} } + \sum\limits_{{i^{\prime}}} {EV(\widetilde{f\chi }_{{i^{\prime}}} )\chi_{{i^{\prime}}} } + \sum\limits_{{i^{\prime\prime}}} {EV(\widetilde{{f{\rm H}}}_{{i^{\prime\prime}}} ){\rm H}_{{i^{\prime\prime}}} } \right)\quad s.t \\ \end{aligned}$$

(85)

(10, 15, 33, 34, 45, 46, 60, 65, 70, 75)

$$Z_{\text{DC}}^{\text{SC1}} = \sum\limits_{i} {\sum\limits_{j} {\sum\limits_{{i^{\prime}}} {\sum\limits_{{j^{\prime}}} {\sum\limits_{{i^{\prime\prime}}} {\sum\limits_{{j^{\prime\prime}}} {\sum\limits_{k} {\left[ {(P\varPsi_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}}^{*} - EV(\widetilde{C\varPsi }_{jk}^{{}} ) - W\varUpsilon_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}}^{*} )x\varUpsilon_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}} } \right]} } } } } } } - \sum\limits_{j} {EV(\widetilde{{g\varPsi_{j} }})\varPsi_{j} }$$

(86)

$$Z_{\text{DC}}^{\text{SC2}} = \sum\limits_{i} {\sum\limits_{j} {\sum\limits_{{i^{\prime}}} {\sum\limits_{{j^{\prime}}} {\sum\limits_{{i^{\prime\prime}}} {\sum\limits_{{j^{\prime\prime}}} {\sum\limits_{k} {\left[ {(P{\rm E}_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}}^{*} - EV(\widetilde{{C{\rm E}}}_{{j^{\prime}k}}^{{}} ) - W\chi_{{_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}} }}^{*} )x\chi_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}} } \right]} } } } } } } - \sum\limits_{{j^{\prime}}} {EV(\widetilde{{g{\rm E}_{{j^{\prime}}} }}){\rm E}_{{j^{\prime}}} }$$

(87)

$$Z_{\text{DC}}^{{{\text{SC}}3}} = \sum\limits_{i} {\sum\limits_{j} {\sum\limits_{{i^{\prime}}} {\sum\limits_{{j^{\prime}}} {\sum\limits_{{i^{\prime\prime}}} {\sum\limits_{{j^{\prime\prime}}} {\sum\limits_{k} {\left[ {(P\varGamma_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}}^{*} - EV(\widetilde{C\varGamma }_{{j^{\prime\prime}k}} ) - W{\rm H}_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}}^{*} )x{\rm H}_{{eike^{\prime}i^{\prime}}} } \right]} } } } } } } - \sum\limits_{{j^{\prime\prime}}} {EV(\widetilde{g\varGamma }_{{j^{\prime\prime}}} )\varGamma_{{j^{\prime\prime}}} }$$

(88)

$$x\varUpsilon_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}} = D\varUpsilon_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}}^{*} y_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}} \quad {\forall }i,j,i^{\prime},j^{\prime},i^{\prime\prime},j^{\prime\prime},k$$

(89)

$$x\chi_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}} = D\chi_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}}^{*} y_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}} \quad {\forall }i,j,i^{\prime},j^{\prime},i^{\prime\prime},j^{\prime\prime},k$$

(90)

$$x{\rm H}_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}} = D{\rm H}_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}}^{*} y_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}} \quad {\forall }i,j,i^{\prime},j^{\prime},i^{\prime\prime},j^{\prime\prime},k$$

(91)

$$\sum\limits_{i} {\sum\limits_{j} {\sum\limits_{{i^{\prime}}} {\sum\limits_{{j^{\prime}}} {\sum\limits_{{i^{\prime\prime}}} {\sum\limits_{{j^{\prime\prime}}} {y_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}} = 1} } } } } } \quad {\forall }k$$

(92)

$$y_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}} \le \varUpsilon_{i} \varPsi_{j} \chi_{{i^{\prime}}} {\rm E}_{{j^{\prime}}} {\rm H}_{{i^{\prime\prime}}} \varGamma_{{j^{\prime\prime}}} \quad {\forall }i,j,i^{\prime},j^{\prime},i^{\prime\prime},j^{\prime\prime},k$$

(93)

$$\sum\limits_{j}^{{}} {\sum\limits_{{i^{\prime}}} {\sum\limits_{{j^{\prime}}} {\sum\limits_{{i^{\prime\prime}}} {\sum\limits_{{j^{\prime\prime}}} {\sum\limits_{k} {x\varUpsilon_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}} } } } } } } \le (\varphi Cp\varUpsilon_{(1i)} + (1 - \varphi )Cp\varUpsilon_{(2i)} )\varUpsilon_{i} \quad \forall i$$

(94)

$$\sum\limits_{i}^{{}} {\sum\limits_{{i^{\prime}}} {\sum\limits_{{j^{\prime}}} {\sum\limits_{{i^{\prime\prime}}} {\sum\limits_{{j^{\prime\prime}}} {\sum\limits_{k} {x\varUpsilon_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}} } } } } } } \le (\varphi Cp\varPsi_{(1j)} + (1 - \varphi )Cp\varPsi_{(2j)} )\varPsi_{j} \quad {\forall }j$$

(95)

$$\sum\limits_{i}^{{}} {\sum\limits_{j} {\sum\limits_{{j^{\prime}}} {\sum\limits_{{i^{\prime\prime}}} {\sum\limits_{{j^{\prime\prime}}} {\sum\limits_{k} {x\chi_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}} } } } } } } \le (\varphi Cp\chi_{{(1i^{\prime})}} + (1 - \varphi )Cp\chi_{{(2i^{\prime})}} )\chi_{{i^{\prime}}} \quad {\forall }i^{\prime}$$

(96)

$$\sum\limits_{i}^{{}} {\sum\limits_{j} {\sum\limits_{{i^{\prime}}} {\sum\limits_{{i^{\prime\prime}}} {\sum\limits_{{j^{\prime\prime}}} {\sum\limits_{k} {x\chi_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}} } } } } } } \le (\varphi Cp{\rm E}_{{(1j^{\prime})}} + (1 - \varphi )Cp{\rm E}_{{(2j^{\prime})}} ){\rm E}_{{j^{\prime}}} \quad {\forall }j^{\prime}$$

(97)

$$\sum\limits_{i}^{{}} {\sum\limits_{j} {\sum\limits_{{j^{\prime}}} {\sum\limits_{{i^{\prime}}} {\sum\limits_{{j^{\prime\prime}}} {\sum\limits_{k} {x{\rm H}_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}} } } } } } } \le (\varphi Cp{\rm H}_{{(1i^{\prime})}} + (1 - \varphi )Cp{\rm H}_{{(2i^{\prime})}} ){\rm H}_{{i^{\prime\prime}}} \quad {\forall }i^{\prime\prime}$$

(98)

$$\sum\limits_{i}^{{}} {\sum\limits_{j} {\sum\limits_{{j^{\prime}}} {\sum\limits_{{i^{\prime}}} {\sum\limits_{{i^{\prime}}} {\sum\limits_{k} {x{\rm H}_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}} } } } } } } \le (\varphi Cp\varGamma_{{(1j^{\prime\prime})}} + (1 - \varphi )Cp\varGamma_{{(2j^{\prime\prime})}} )\varGamma_{{j^{\prime\prime}}} \quad {\forall }j^{\prime\prime}$$

(99)

$$x\varUpsilon_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}} ,x\chi_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}} ,x{\rm H}_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}} \ge 0,y_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}} ,\varUpsilon_{i} ,\varPsi_{j} ,\chi_{{i^{\prime}}} ,{\rm E}_{{j^{\prime}}} ,{\rm H}_{{i^{\prime\prime}}} ,\varGamma_{{j^{\prime\prime}}} = \left\{ {0,1} \right\}.$$

(100)

Term 85 represents the objective function which includes the objective functions of plants of SC1, SC2 and SC3. Constraints 86–88 are calculating the objective function of the DCs in the chains. Constraints 89–91 are related to demand satisfaction. Constraint 92 ensures that only one path should be assigned to each customer. Constraint 93 ensures that a path could not be opened unless the related plants and DCs of the chains are open. Terms 94–99 are related to the capacity constraints of the SCs which changed to the crisp mode according to Appendix 13. Term 100 is related to the binary and non-negativity restrictions on the corresponding decision variables.

Appendix 6

The following model represents a situation in which the leaders of the chains are plant, plant and DC for SC1, SC2 and SC3 correspondingly:

$$\begin{aligned} P_{cop}^{P\& P\& DC} & : \, \sum\limits_{i} {\sum\limits_{j} {\sum\limits_{{i^{\prime}}} {\sum\limits_{{j^{\prime}}} {\sum\limits_{{i^{\prime\prime}}} {\sum\limits_{{j^{\prime\prime}}} {\sum\limits_{k} {\left[ {(W\varUpsilon_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}}^{*} - EV(C\varUpsilon_{ij} ))x\varUpsilon_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}} + (W\chi_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}}^{*} - EV(\widetilde{C\chi }_{{i^{\prime}j^{\prime}}} ))x\chi_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}} + (P\varGamma_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}}^{*} - EV(\widetilde{C\varGamma }_{{j^{\prime\prime}k}} ) - W{\rm H}_{{_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}} }}^{*} )x{\rm H}_{{eike^{\prime}i^{\prime}}} } \right]} } } } } } } \\ & - \left( {\sum\limits_{i} {EV(\widetilde{f\varUpsilon }_{i} )\varUpsilon_{i} } + \sum\limits_{{i^{\prime}}} {EV(\widetilde{f\chi }_{{i^{\prime}}} )\chi_{{i^{\prime}}} } + \sum\limits_{{j^{\prime\prime}}} {EV(\widetilde{g\varGamma }_{{j^{\prime\prime}}} )\varGamma_{{j^{\prime\prime}}} } } \right)\quad s.t \\ \end{aligned}$$

(101)

(10, 15, 33, 34, 45, 46, 60, 65, 70, 75, 81–88)

$$Z_{DC}^{SC1} = \sum\limits_{i} {\sum\limits_{j} {\sum\limits_{{i^{\prime}}} {\sum\limits_{{j^{\prime}}} {\sum\limits_{{i^{\prime\prime}}} {\sum\limits_{{j^{\prime\prime}}} {\sum\limits_{k} {\left[ {(P\varPsi_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}}^{*} - EV(\widetilde{C\varPsi }_{jk}^{{}} ) - W\varUpsilon_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}}^{*} )x\varUpsilon_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}} } \right]} } } } } } } - \sum\limits_{j} {EV(\widetilde{{g\varPsi_{j} }})\varPsi_{j} }$$

(102)

$$Z_{\text{DC}}^{{{\text{SC}}2}} = \sum\limits_{i} {\sum\limits_{j} {\sum\limits_{{i^{\prime}}} {\sum\limits_{{j^{\prime}}} {\sum\limits_{{i^{\prime\prime}}} {\sum\limits_{{j^{\prime\prime}}} {\sum\limits_{k} {\left[ {(P{\rm E}_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}}^{*} - EV(\widetilde{{C{\rm E}}}_{{j^{\prime}k}}^{{}} ) - W\chi_{{_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}} }}^{*} )x\chi_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}} } \right]} } } } } } } - \sum\limits_{{j^{\prime}}} {EV(\widetilde{{g{\rm E}_{{j^{\prime}}} }}){\rm E}_{{j^{\prime}}} }$$

(103)

$$Z_{\text{Plant}}^{{{\text{SC}}3}} = \sum\limits_{i} {\sum\limits_{j} {\sum\limits_{{i^{\prime}}} {\sum\limits_{{j^{\prime}}} {\sum\limits_{{i^{\prime\prime}}} {\sum\limits_{{j^{\prime\prime}}} {\sum\limits_{k} {\left[ {(W{\rm H}_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}}^{*} - EV(\widetilde{{C{\rm H}}}_{{i^{\prime\prime}j^{\prime\prime}}} ))x{\rm H}_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}} } \right]} } } } } } } - \sum\limits_{{i^{\prime\prime}}} {EV(\widetilde{{f{\rm H}}}_{{i^{\prime\prime}}} ){\rm H}_{{i^{\prime\prime}}} }$$

(104)

Term 101 represents the objective function which includes the objective functions of plant of SC1, plant of SC2 and DC of SC3. Constraints 102–104 are calculating the objective function of the DC of SC1, DC of SC2 and plant of SC3 correspondingly.

Appendix 7

The following model represents a situation in which the leaders of the chains are plant for SC1, DC, SC2 and plant for SC3 correspondingly:

$$\begin{aligned} P_{\text{cop}}^{P\& DC\& P} : { }\sum\limits_{i} {\sum\limits_{j} {\sum\limits_{{i^{\prime}}} {\sum\limits_{{j^{\prime}}} {\sum\limits_{{i^{\prime\prime}}} {\sum\limits_{{j^{\prime\prime}}} {\sum\limits_{k} {\left[ {(W\varUpsilon_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}}^{*} - EV(C\varUpsilon_{ij} ))x\varUpsilon_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}} + (P{\rm E}_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}}^{*} - EV(\widetilde{{C{\rm E}}}_{{j^{\prime}k}}^{{}} ) - W\chi_{{_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}} }}^{*} )x\chi_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}} + (W{\rm H}_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}}^{*} - EV(\widetilde{{C{\rm H}}}_{{i^{\prime\prime}j^{\prime\prime}}}^{{}} ))x{\rm H}_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}} } \right]} } } } } } } \hfill \\ - \left(\sum\limits_{i} {EV(\widetilde{f\varUpsilon }_{i}^{{}} )\varUpsilon_{i} } + \sum\limits_{{j^{\prime}}} {EV(\widetilde{{g{\rm E}_{{j^{\prime}}} }}){\rm E}_{{j^{\prime}}} } + \sum\limits_{{i^{\prime\prime}}} {EV(\widetilde{{f{\rm H}}}_{{i^{\prime\prime}}} ){\rm H}_{{i^{\prime\prime}}} } \right)\quad s.t \hfill \\ \end{aligned}$$

(105)

(10, 15, 33, 34, 45, 46, 60, 65, 70, 75, 81–88)

$$Z_{DC}^{SC1} = \sum\limits_{i} {\sum\limits_{j} {\sum\limits_{{i^{\prime}}} {\sum\limits_{{j^{\prime}}} {\sum\limits_{{i^{\prime\prime}}} {\sum\limits_{{j^{\prime\prime}}} {\sum\limits_{k} {\left[ {(P\varPsi_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}}^{*} - EV(\widetilde{C\varPsi }_{jk}^{{}} ) - W\varUpsilon_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}}^{*} )x\varUpsilon_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}} } \right]} } } } } } } - \sum\limits_{j} {EV(\widetilde{{g\varPsi_{j} }})\varPsi_{j} }$$

(106)

$$Z_{\text{Plant}}^{{{\text{SC}}2}} = \sum\limits_{i} {\sum\limits_{j} {\sum\limits_{{i^{\prime}}} {\sum\limits_{{j^{\prime}}} {\sum\limits_{{i^{\prime\prime}}} {\sum\limits_{{j^{\prime\prime}}} {\sum\limits_{k} {\left[ {(W\chi_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}}^{*} - EV(\widetilde{C\chi }_{{i^{\prime}j^{\prime}}}^{{}} ))x\chi_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}} } \right]} } } } } } } - \sum\limits_{{i^{\prime}}} {EV(\widetilde{f\chi }_{{i^{\prime}}}^{{}} )\chi_{{i^{\prime}}} }$$

(107)

$$Z_{\text{DC}}^{{{\text{SC}}3}} = \sum\limits_{i} {\sum\limits_{j} {\sum\limits_{{i^{\prime}}} {\sum\limits_{{j^{\prime}}} {\sum\limits_{{i^{\prime\prime}}} {\sum\limits_{{j^{\prime\prime}}} {\sum\limits_{k} {\left[ {(P\varGamma_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}}^{*} - EV(\widetilde{C\varGamma }_{{j^{\prime\prime}k}} ) - W{\rm H}_{{_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}} }}^{*} )x{\rm H}_{{eike^{\prime}i^{\prime}}} } \right]} } } } } } } - \sum\limits_{{j^{\prime\prime}}} {EV(\widetilde{{g\varGamma_{{j^{\prime\prime}}} }})\varGamma_{{j^{\prime\prime}}} }$$

(108)

Term 105 represents the objective function which includes the objective functions of the plant of SC1, DC of SC2 and plant of SC3. Constraints 102–104 are calculating the objective function of the DC of SC1, DC of SC2 and plant of SC3 correspondingly.

Appendix 8

The following model represents a situation in which the leaders of the chains are DC plant, plant for SC1, SC2 and SC3 correspondingly:

$$\begin{aligned} P_{\text{cop}}^{P\& P\& P} : { }\sum\limits_{i} {\sum\limits_{j} {\sum\limits_{{i^{\prime}}} {\sum\limits_{{j^{\prime}}} {\sum\limits_{{i^{\prime\prime}}} {\sum\limits_{{j^{\prime\prime}}} {\sum\limits_{k} {\left[ {(P\varPsi_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}}^{*} - EV(\widetilde{C\varPsi }_{jk} ) - W\varUpsilon_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}}^{*} )x\varUpsilon_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}} + (W\chi_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}}^{*} - EV(\widetilde{C\chi }_{{i^{\prime}j^{\prime}}} ))x\chi_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}} + (W{\rm H}_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}}^{*} - EV(\widetilde{{C{\rm H}}}_{{i^{\prime\prime}j^{\prime\prime}}} ))x{\rm H}_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}} } \right]} } } } } } } \hfill \\ - \left(\sum\limits_{j} {EV(\widetilde{{g\varPsi_{j} }})\varPsi_{j} } + \sum\limits_{{i^{\prime}}} {EV(\widetilde{f\chi }_{{i^{\prime}}}^{{}} )\chi_{{i^{\prime}}} } + \sum\limits_{{i^{\prime\prime}}} {EV(\widetilde{{f{\rm H}}}_{{i^{\prime\prime}}} ){\rm H}_{{i^{\prime\prime}}} } \right)\quad s.t \hfill \\ \end{aligned}$$

(109)

(10, 15, 33, 34, 45, 46, 60, 65, 70, 75, 81–88)

$$Z_{\text{Plant}}^{{{\text{SC}}1}} = \sum\limits_{i} {\sum\limits_{j} {\sum\limits_{{i^{\prime}}} {\sum\limits_{{j^{\prime}}} {\sum\limits_{{i^{\prime\prime}}} {\sum\limits_{{j^{\prime\prime}}} {\sum\limits_{k} {\left[ {(W\varUpsilon_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}}^{*} - EV(C\varUpsilon_{ij}^{{}} ))x\varUpsilon_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}} } \right]} } } } } } } - \sum\limits_{i} {EV(\widetilde{f\varUpsilon }_{i}^{{}} )\varUpsilon_{i} }$$

(110)

$$Z_{DC}^{SC2} = \sum\limits_{i} {\sum\limits_{j} {\sum\limits_{{i^{\prime}}} {\sum\limits_{{j^{\prime}}} {\sum\limits_{{i^{\prime\prime}}} {\sum\limits_{{j^{\prime\prime}}} {\sum\limits_{k} {\left[ {(P{\rm E}_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}}^{*} - EV(\widetilde{{C{\rm E}}}_{{j^{\prime}k}}^{{}} ) - W\chi_{{_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}} }}^{*} )x\chi_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}} } \right]} } } } } } } - \sum\limits_{{j^{\prime}}} {EV(\widetilde{{g{\rm E}_{{j^{\prime}}} }}){\rm E}_{{j^{\prime}}} }$$

(111)

$$Z_{\text{DC}}^{{{\text{SC}}3}} = \sum\limits_{i} {\sum\limits_{j} {\sum\limits_{{i^{\prime}}} {\sum\limits_{{j^{\prime}}} {\sum\limits_{{i^{\prime\prime}}} {\sum\limits_{{j^{\prime\prime}}} {\sum\limits_{k} {\left[ {(P\varGamma_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}}^{*} - EV(\widetilde{C\varGamma }_{{j^{\prime\prime}k}} ) - W{\rm H}_{{_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}} }}^{*} )x{\rm H}_{{eike^{\prime}i^{\prime}}} } \right]} } } } } } } - \sum\limits_{{j^{\prime\prime}}} {EV(\widetilde{{g\varGamma_{{j^{\prime\prime}}} }})\varGamma_{{j^{\prime\prime}}} }$$

(112)

Term 109 represents the objective function which includes the objective functions of the DC, DC plant for SC1, SC2 and SC3. Constraints 102–104 are calculating the objective function of the plant, DC and DC of SC1, SC2 and SC3 correspondingly.

Appendix 9

The following model represents a situation in which the leaders of the chains are DC, DC plant, DC for SC1, SC2 and SC3 correspondingly:

$$\begin{aligned} P_{\text{cop}}^{{{\text{DC}}\& {\text{DC}}\& {\text{DC}}}} : { }\sum\limits_{i} {\sum\limits_{j} {\sum\limits_{{i^{\prime}}} {\sum\limits_{{j^{\prime}}} {\sum\limits_{{i^{\prime\prime}}} {\sum\limits_{{j^{\prime\prime}}} {\sum\limits_{k} {\left[ {(P\varPsi_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}}^{*} - EV(\widetilde{C\varPsi }_{jk} ) - W\varUpsilon_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}}^{*} )x\varUpsilon_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}} + (P{\rm E}_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}}^{*} - EV(\widetilde{{C{\rm E}}}_{{j^{\prime}k}} ) - W\chi_{{_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}} }}^{*} )x\chi_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}} + (P\varGamma_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}}^{*} - EV(\widetilde{C\varGamma }_{{j^{\prime\prime}k}} ) - W{\rm H}_{{_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}} }}^{*} )x{\rm H}_{{eike^{\prime}i^{\prime}}} } \right]} } } } } } } \hfill \\ - \left(\sum\limits_{j} {EV(\widetilde{{g\varPsi_{j} }})\varPsi_{j} } + \sum\limits_{{j^{\prime}}} {EV(\widetilde{{g{\rm E}_{{j^{\prime}}} }}){\rm E}_{{j^{\prime}}} } + \sum\limits_{{j^{\prime\prime}}} {EV(\widetilde{{g\varGamma_{{j^{\prime\prime}}} }})\varGamma_{{j^{\prime\prime}}} }\right )\quad s.t \hfill \\ \end{aligned}$$

(113)

(10, 15, 33, 34, 45, 46, 60, 65, 70, 75, 81–88)

$$Z_{Plant}^{SC1} = \sum\limits_{i} {\sum\limits_{j} {\sum\limits_{{i^{\prime}}} {\sum\limits_{{j^{\prime}}} {\sum\limits_{{i^{\prime\prime}}} {\sum\limits_{{j^{\prime\prime}}} {\sum\limits_{k} {\left[ {(W\varUpsilon_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}}^{*} - EV(C\varUpsilon_{ij}^{{}} ))x\varUpsilon_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}} } \right]} } } } } } } - \sum\limits_{i} {EV(\widetilde{f\varUpsilon }_{i}^{{}} )\varUpsilon_{i} }$$

(114)

$$Z_{\text{plant}}^{{{\text{SC}}2}} = \sum\limits_{i} {\sum\limits_{j} {\sum\limits_{{i^{\prime}}} {\sum\limits_{{j^{\prime}}} {\sum\limits_{{i^{\prime\prime}}} {\sum\limits_{{j^{\prime\prime}}} {\sum\limits_{k} {\left[ {(W\chi_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}}^{*} - EV(\widetilde{C\chi }_{{i^{\prime}j^{\prime}}}^{{}} ))x\chi_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}} } \right]} } } } } } } - \sum\limits_{{i^{\prime}}} {EV(\widetilde{f\chi }_{{i^{\prime}}}^{{}} )\chi_{{i^{\prime}}} }$$

(115)

$$Z_{\text{plant}}^{\text{SC3}} = \sum\limits_{i} {\sum\limits_{j} {\sum\limits_{{i^{\prime}}} {\sum\limits_{{j^{\prime}}} {\sum\limits_{{i^{\prime\prime}}} {\sum\limits_{{j^{\prime\prime}}} {\sum\limits_{k} {\left[ {(W{\rm H}_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}}^{*} - EV(\widetilde{{C{\rm H}}}_{{i^{\prime\prime}j^{\prime\prime}}}^{{}} ))x{\rm H}_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}} } \right]} } } } } } } - \sum\limits_{{i^{\prime\prime}}} {EV(\widetilde{{f{\rm H}}}_{{i^{\prime\prime}}}^{{}} ){\rm H}_{{i^{\prime\prime}}} }$$

(116)

Term 113 represents the objective function which includes the objective functions of the DCs for SC1, SC2 and SC3. Constraints 114–115 are calculating the objective function of the plants for SC1, SC2 and SC3 correspondingly.

Appendix 10

The following model represents a situation in which the leaders of the chains are plant, DC, DC for SC1, SC2 and SC3 correspondingly:

$$\begin{aligned} P_{\text{cop}}^{{P\& {\text{DC}}\& P}} : { }\sum\limits_{i} {\sum\limits_{j} {\sum\limits_{{i^{\prime}}} {\sum\limits_{{j^{\prime}}} {\sum\limits_{{i^{\prime\prime}}} {\sum\limits_{{j^{\prime\prime}}} {\sum\limits_{k} {\left[ {(W\varUpsilon_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}}^{*} - EV(C\varUpsilon_{ij} ))x\varUpsilon_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}} + (P{\rm E}_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}}^{*} - EV(\widetilde{{C{\rm E}}}_{{j^{\prime}k}} ) - W\chi_{{_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}} }}^{*} )x\chi_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}} + (P\varGamma_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}}^{*} - EV(\widetilde{C\varGamma }_{{j^{\prime\prime}k}} ) - W{\rm H}_{{_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}} }}^{*} )x{\rm H}_{{eike^{\prime}i^{\prime}}} } \right]} } } } } } } \hfill \\ - (\sum\limits_{i} {EV(\widetilde{f\varUpsilon }_{i} )\varUpsilon_{i} } + \sum\limits_{{j^{\prime}}} {EV(\widetilde{{g{\text{E}}}}_{{j^{\prime}}} ){\rm E}_{{j^{\prime}}} } + \sum\limits_{{j^{\prime\prime}}} {EV(\widetilde{g\varGamma }_{{j^{\prime\prime}}} )\varGamma_{{j^{\prime\prime}}} } )\quad s.t \hfill \\ \end{aligned}$$

(117)

(10, 15, 33, 34, 45, 46, 60, 65, 70, 75, 81–88)

$$Z_{\text{DC}}^{{{\text{SC}}1}} = \sum\limits_{i} {\sum\limits_{j} {\sum\limits_{{i^{\prime}}} {\sum\limits_{{j^{\prime}}} {\sum\limits_{{i^{\prime\prime}}} {\sum\limits_{{j^{\prime\prime}}} {\sum\limits_{k} {\left[ {(P\varPsi_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}}^{*} - EV(\widetilde{C\varPsi }_{jk}^{{}} ) - W\varUpsilon_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}}^{*} )x\varUpsilon_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}} } \right]} } } } } } } - \sum\limits_{j} {EV(\widetilde{{g\varPsi_{j} }})\varPsi_{j} }$$

(118)

$$Z_{\text{plant}}^{{{\text{SC}}2}} = \sum\limits_{i} {\sum\limits_{j} {\sum\limits_{{i^{\prime}}} {\sum\limits_{{j^{\prime}}} {\sum\limits_{{i^{\prime\prime}}} {\sum\limits_{{j^{\prime\prime}}} {\sum\limits_{k} {\left[ {(W\chi_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}}^{*} - EV(\widetilde{C\chi }_{{i^{\prime}j^{\prime}}}^{{}} ))x\chi_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}} } \right]} } } } } } } - \sum\limits_{{i^{\prime}}} {EV(\widetilde{f\chi }_{{i^{\prime}}}^{{}} )\chi_{{i^{\prime}}} }$$

(119)

$$Z_{\text{Plant}}^{{{\text{SC}}3}} = \sum\limits_{i} {\sum\limits_{j} {\sum\limits_{{i^{\prime}}} {\sum\limits_{{j^{\prime}}} {\sum\limits_{{i^{\prime\prime}}} {\sum\limits_{{j^{\prime\prime}}} {\sum\limits_{k} {\left[ {(W{\rm H}_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}}^{*} - EV(\widetilde{{C{\rm H}}}_{{i^{\prime\prime}j^{\prime\prime}}} ))x{\rm H}_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}} } \right]} } } } } } } - \sum\limits_{{i^{\prime\prime}}} {EV(\widetilde{{f{\rm H}}}_{{i^{\prime\prime}}} ){\rm H}_{{i^{\prime\prime}}} }$$

(120)

Term 117 represents the objective function which includes the objective functions of the plant, DC and DC for SC1, SC2 and SC3. Constraints 118–120 are calculating the objective function of the DC, plant, plant of SC1, SC2 and SC3 correspondingly.

Appendix 11

The following model represents a situation in which the leaders of the chains are DC, plant, DC for SC1, SC2 and SC3 correspondingly:

$$\begin{aligned} P_{\text{cop}}^{{{\text{DC}}\& {\text{Plant}}\& {\text{DC}}}} :& \, \sum\limits_{i} {\sum\limits_{j} {\sum\limits_{{i^{\prime}}} {\sum\limits_{{j^{\prime}}} {\sum\limits_{{i^{\prime\prime}}} {\sum\limits_{{j^{\prime\prime}}} {\sum\limits_{k} {\left[ {(P\varPsi_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}}^{*} - EV(\widetilde{C\varPsi }_{jk} ) - W\varUpsilon_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}}^{*} )x\varUpsilon_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}} + (W\chi_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}}^{*} - EV(\widetilde{C\chi }_{{i^{\prime}j^{\prime}}} ))x\chi_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}} + (P\varGamma_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}}^{*} - EV(\widetilde{C\varGamma }_{{j^{\prime\prime}k}} ) - W{\rm H}_{{_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}} }}^{*} )x{\rm H}_{{eike^{\prime}i^{\prime}}} } \right]} } } } } } } \\ & - (\sum\limits_{j} {EV(\widetilde{{g\varPsi_{j} }})\varPsi_{j} } + \sum\limits_{{i^{\prime}}} {EV(\widetilde{f\chi }_{{i^{\prime}}}^{{}} )\chi_{{i^{\prime}}} } + \sum\limits_{{j^{\prime\prime}}} {EV(\widetilde{{g\varGamma_{{j^{\prime\prime}}} }})\varGamma_{{j^{\prime\prime}}} } )\quad s.t \\ \end{aligned}$$

(121)

(10, 15, 33, 34, 45, 46, 60, 65, 70, 75, 81–88)

$$Z_{\text{Plant}}^{{{\text{SC}}1}} = \sum\limits_{i} {\sum\limits_{j} {\sum\limits_{{i^{\prime}}} {\sum\limits_{{j^{\prime}}} {\sum\limits_{{i^{\prime\prime}}} {\sum\limits_{{j^{\prime\prime}}} {\sum\limits_{k} {\left[ {(W\varUpsilon_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}}^{*} - EV(C\varUpsilon_{ij}^{{}} ))x\varUpsilon_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}} } \right]} } } } } } } - \sum\limits_{i} {EV(\widetilde{f\varUpsilon }_{i}^{{}} )\varUpsilon_{i} }$$

(122)

$$Z_{\text{DC}}^{{{\text{SC}}2}} = \sum\limits_{i} {\sum\limits_{j} {\sum\limits_{{i^{\prime}}} {\sum\limits_{{j^{\prime}}} {\sum\limits_{{i^{\prime\prime}}} {\sum\limits_{{j^{\prime\prime}}} {\sum\limits_{k} {\left[ {(P{\rm E}_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}}^{*} - EV(\widetilde{{C{\rm E}}}_{{j^{\prime}k}}^{{}} ) - W\chi_{{_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}} }}^{*} )x\chi_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}} } \right]} } } } } } } - \sum\limits_{{j^{\prime}}} {EV(\widetilde{{g{\rm E}_{{j^{\prime}}} }}){\rm E}_{{j^{\prime}}} }$$

(123)

$$Z_{\text{Plant}}^{\text{SC3}} = \sum\limits_{i} {\sum\limits_{j} {\sum\limits_{{i^{\prime}}} {\sum\limits_{{j^{\prime}}} {\sum\limits_{{i^{\prime\prime}}} {\sum\limits_{{j^{\prime\prime}}} {\sum\limits_{k} {\left[ {(W{\rm H}_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}}^{*} - EV(\widetilde{{C{\rm H}}}_{{i^{\prime\prime}j^{\prime\prime}}}^{{}} ))x{\rm H}_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}} } \right]} } } } } } } - \sum\limits_{{i^{\prime\prime}}} {EV(\widetilde{{f{\rm H}}}_{{i^{\prime\prime}}}^{{}} ){\rm H}_{{i^{\prime\prime}}} }$$

(124)

Term 121 represents the objective function which includes the objective functions of the DC, plant DC for SC1, SC2 and SC3. Constraints 118–120 are calculating the objective function of the plant, DC plant of SC1, SC2 and SC3 correspondingly.

Appendix 12

The following model represents a situation in which the leaders of the chains are DC, DC plant for SC1, SC2 and SC3 correspondingly

$$\begin{aligned} P_{\text{cop}}^{{{\text{DC}}\& {\text{DC}}\& {\text{Plant}}}} & : \, \sum\limits_{i} {\sum\limits_{j} {\sum\limits_{{i^{\prime}}} {\sum\limits_{{j^{\prime}}} {\sum\limits_{{i^{\prime\prime}}} {\sum\limits_{{j^{\prime\prime}}} {\sum\limits_{k} {\left[ {\left( {P\varPsi_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}}^{*} - EV(\widetilde{C\varPsi }_{jk} ) - W\varUpsilon_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}}^{*} )x\varUpsilon_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}} + (P{\rm E}_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}}^{*} - EV(\widetilde{{C{\rm E}}}_{{j^{\prime}k}} ) - W\chi_{{_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}} }}^{*} } \right)x\chi_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}} + (W{\rm H}_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}}^{*} - EV(\widetilde{{C{\rm H}}}_{{i^{\prime\prime}j^{\prime\prime}}} ))x{\rm H}_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}} } \right]} } } } } } } \\ & - \left( {\sum\limits_{j} {EV(\widetilde{{g\varPsi_{j} }})\varPsi_{j} } + \sum\limits_{{j^{\prime}}} {EV(\widetilde{{g{\rm E}_{{j^{\prime}}} }}){\rm E}_{{j^{\prime}}} } + \sum\limits_{{i^{\prime\prime}}} {EV(\widetilde{{f{\rm H}}}{}_{{i^{\prime\prime}}}){\rm H}_{{i^{\prime\prime}}} } } \right)\quad s.t \\ \end{aligned}$$

(125)

(10, 15, 33, 34, 45, 46, 60, 65, 70, 75, 81–88)

$$Z_{\text{Plant}}^{{{\text{SC}}1}} = \sum\limits_{i} {\sum\limits_{j} {\sum\limits_{{i^{\prime}}} {\sum\limits_{{j^{\prime}}} {\sum\limits_{{i^{\prime\prime}}} {\sum\limits_{{j^{\prime\prime}}} {\sum\limits_{k} {\left[ {(W\varUpsilon_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}}^{*} - EV(C\varUpsilon_{ij}^{{}} ))x\varUpsilon_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}} } \right]} } } } } } } - \sum\limits_{i} {EV(\widetilde{f\varUpsilon }_{i}^{{}} )\varUpsilon_{i} }$$

(126)

$$Z_{\text{plant}}^{{{\text{SC}}2}} = \sum\limits_{i} {\sum\limits_{j} {\sum\limits_{{i^{\prime}}} {\sum\limits_{{j^{\prime}}} {\sum\limits_{{i^{\prime\prime}}} {\sum\limits_{{j^{\prime\prime}}} {\sum\limits_{k} {\left[ {(W\chi_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}}^{*} - EV(\widetilde{C\chi }_{{i^{\prime}j^{\prime}}}^{{}} ))x\chi_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}} } \right]} } } } } } } - \sum\limits_{{i^{\prime}}} {EV(\widetilde{f\chi }_{{i^{\prime}}}^{{}} )\chi_{{i^{\prime}}} }$$

(127)

$$Z_{DC}^{SC3} = \sum\limits_{i} {\sum\limits_{j} {\sum\limits_{{i^{\prime}}} {\sum\limits_{{j^{\prime}}} {\sum\limits_{{i^{\prime\prime}}} {\sum\limits_{{j^{\prime\prime}}} {\sum\limits_{k} {\left[ {(P\varGamma_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}}^{*} - EV(\widetilde{C\varGamma }_{{j^{\prime\prime}k}} ) - W{\rm H}_{{_{{ijki^{\prime}j^{\prime}i^{\prime\prime}j^{\prime\prime}}} }}^{*} )x{\rm H}_{{eike^{\prime}i^{\prime}}} } \right]} } } } } } } - \sum\limits_{{j^{\prime\prime}}} {EV(\widetilde{{g\varGamma_{{j^{\prime\prime}}} }})\varGamma_{{j^{\prime\prime}}} }$$

(128)

Term 125 represents the objective function which includes the objective functions of the DC, plant for SC1, SC2 and SC3. Constraints 126–128 are calculating the objective function of the plant, DC of SC1, SC2 and SC3 correspondingly.

Appendix 13

Assume there is a fuzzy number by the following membership function (Dubois and Prade 1987; Dubois 1987; Pishvaee et al. 2012):

$$\mu _{{\tilde{k}}} (x) = \left\{ \begin{gathered} l_{{\tilde{k}}} (x){\text{ }}if{\text{ }}k_{{(1)}} \le x \le k_{{(2)}} , \hfill \\ 1{\text{ }}if{\text{ }}k_{{(2)}} \le x \le k_{{(3)}} ,{\text{ }} \hfill \\ h_{{\tilde{k}}} (x){\text{ }}if{\text{ }}k_{{(3)}} \le x \le k_{{(4)}} , \hfill \\ 0{\text{ }}if{\text{ }}k_{{(4)}} \prec x{\text{ }}or{\text{ }}k \prec a_{{(1)}} \hfill \\ \end{gathered} \right.$$

(129)

Then the upper and lower expected value of $\left( {E_{{}}^{*} (\tilde{k}),E_{*}^{{}} (\tilde{k})} \right)$ by the means of Choquet integral are defined as follows:(Dubois and Prade 1987; Dubois 1987; Pishvaee et al. 2012):

$$E_{{}}^{*} (\tilde{k}) = k_{(3)} + \int_{{k_{(3)} }}^{{k_{(4)} }} {h_{{\tilde{k}}} (x)dx} ,$$

(130)

$$E_{{}}^{*} (\tilde{k}) = k_{(3)} + \int_{{k_{(3)} }}^{{k_{(4)} }} {h_{{\tilde{k}}} (x)dx} ,$$

(131)

Now the expected value [EV] and expected interval [EI] of $\tilde{k}$ can be defined as follows (Dubois and Prade 1987; Dubois 1987; Pishvaee et al. 2012):

$$EI = [k_{(2)} - \int_{{k_{(1)} }}^{{k_{(2)} }} {l_{{\tilde{k}}} (x)dx} ,k_{(3)} - \int_{{k_{(e)} }}^{{k_{(4)} }} {h_{{\tilde{k}}} (x)dx} ],$$

(132)

$$EV = \frac{1}{2}[k_{(2)} - \int_{{k_{(1)} }}^{{k_{(2)} }} {l_{{\tilde{k}}} (x)dx} + k_{(3)} - \int_{{k_{(e)} }}^{{k_{(4)} }} {h_{{\tilde{k}}} (x)dx} ]$$

(133)

If $\tilde{k}$ has the trapezoidal membership function then (Dubois and Prade 1987; Dubois 1987; Pishvaee et al. 2012)

$$EI(\tilde{k}) = \left[\frac{{k_{(1)} + k_{(2)} }}{2},\frac{{k_{(3)} + k_{(4)} }}{2}\right],$$

(134)

$$EV(\tilde{k}) = \left[\frac{{k_{(1)} + k_{(2)} + k_{(3)} + k_{(4)} }}{4}\right]$$

(135)

Now assume $w$ is a real number, the possibility (Pos) and necessity (Nec) of $\tilde{k} \le w$ can be defined as follows (Dubois and Prade 1987; Dubois 1987; Pishvaee et al. 2012):

$$Pos(\tilde{k} \le w) = \left\{ \begin{array}{ll} 1 &\quad if \, k_{(2)} \le w , { } \hfill \\ \frac{{w - k_{(1)} }}{{k_{(2)} - k_{(1)} }}&\quad if \, k_{(1)} \le w \le k_{(2)} , { } \hfill \\ 0 &\quad if \, k_{(1)} \ge w \, \hfill \\ \end{array} \right.$$

(136)

$$Nec(\tilde{k} \le w) = \left\{ \begin{array}{ll} 1 &\quad {\rm if} \, k_{(4)} \le w , { } \hfill \\ \frac{{w - k_{(3)} }}{{k_{(4)} - k_{(3)} }};&\quad {\rm if} \, k_{(3)} \le w \le k_{(4)} , { } \hfill \\ 0&\quad {\rm if} \, k_{(3)} \ge w \, \hfill \\ \end{array} \right.$$

(137)

It can be shown that for $\alpha \succ 0.5$, we have [Inuiguchi and Ramik (2000) and Pishvaee et al. (2012)]:

$$Pos(\tilde{k} \le w) \ge \alpha \Leftrightarrow w \ge (1 - \alpha )k_{(1)} + (\alpha )k_{(2)} ,$$

(138)

$$Nec(\tilde{k} \le w) \ge \alpha \Leftrightarrow w \ge (1 - \alpha )k_{(3)} + (\alpha )k_{(4)}$$

(139)

(126), (127) are directly applied to convert our fuzzy constraints into their equivalent crisp one. It is worth noting that necessity measure is more meaningful to satisfy the constraints. We applied this measure in the paper to cope with fuzzy constraints [Inuiguchi and Ramik (2000) and Pishvaee et al. (2012)].