Introduction

Currently, issues regarding pollution and environmental contamination are seriously considered in the supply chain systems. While developing countries have made significant attempts since the late 1970s to improve the air quality, air pollution still is increasing in many of those countries and the whole world in general. Air pollution needs immediate attention among all types of pollution. According to World Health Organization Report (2012), approximately 6% of total avoidable mortality around the world is due to intense air pollution. Global warming is also a consequence of increased emission of greenhouse gases which causes severe problems for people as well. Managing environmental impacts in supply chain results in financial development in macro economical system (Çiftçioglu and Almasifard 2015; Almasifard 2013), as well as organizational improvement. Hence, it is essential to consider large-scale technological practices and social, fiscal and political changes (Rezaei et al. 2015). Moreover, understanding the needs of sustainable and environmental-friendly supply chain network causes of more governmental pressure on manufacturers (Zavvar Sabegh et al. 2017; Gold et al. 2010).

Supply chain management refers to management and coordination of a complicated network of activities including providing final goods to the customers (Abbasi et al. 2016). Thus, effective supply chain management results in better customer satisfaction which is one of the main objectives of each industrial system (Khorasani 2014; Al-Tit 2015). Moreover, increasing variety among customers’ needs forces organizations to operate in an uncertain environment. Thus, they attempt to apply supply chain models which can control uncertain variables (Rao et al. 2013). For achieving an effective supply chain management some requirements should be met such as technology, agility of system, decision making ability, and inventory levels (Khorasani et al. 2015). Green supply chain management is also defined as green procurement, green manufacturing, green distribution channels and reverse logistics (Pishvaee and Razmi 2012).

The objective of green supply chain management is to eliminate or minimize waste (energy, hazardous greenhouse gas/chemical emissions, and solid waste). Under customer instructions agreed upon by the European Union and Japan, environmental problems have become a major concern of manufacturers. Green supply chain management helps organizations to develop strategies which lead to a higher level of profitability by reducing environmental risks and increasing environmental efficiency (Abbasi et al. 2016). Due to high contribution of steel industry to contamination of the environment, green supply chain implementation is particularly essential in this industry. Clemens (2001) declares that the steel industry is the biggest manufacturing source of environmental contamination in the US Therefore, application of green supply chain model results in lower contamination and costs related to environmental aspects of supply chain management. Moreover, a lack of implementation of green supply chain models in developing countries with large steel industry was studied by Zhu and Sarkis (2004) and Kumar and Shekhar (2015). Zhu and Sarkis (2004) revealed that just 4.8% of steel companies in China are applying green supply chain management. Kumar and Shekhar (2015) provided an assessment of the degree of implementation of green supply chain management in the state of Chhattisgarh steel manufacturers in India. According to their observation, a few steel manufacturers in that region applied green supply chain management. Providing a green supply chain model for steel industries in developing countries assists them to become more environmentally friendly and achieve a higher level of efficiency. Vahdani et al. (2012) provided an integrated facility location in closed-loop supply chain network for steel facilities using queuing theory and fuzzy multi-objective programming.

In case of uncertainties in the model, fuzzy multiple objectives can be applied in supply chain networks (Sherafati and Bashiri 2016; Rezaee et al. 2016). Specifically, Li et al. (2008) suggested a dual-objective mathematical programming approach (for maximizing profits and minimizing pollution) for supply chain. The objective of their model is optimization of distribution centers by considering the transportation cost and carbon pollutants caused by manufacturing and transportation. They also examined the effect of changes in crude oil prices on location decisions.

Neto et al. (2008) revealed a multi-objective programming model which simultaneously optimizes both goals (cost effectiveness and environmental effects) and establishes a trade-off between cost and environment. Environmental impacts (global warming, ecosystem toxicity, light-chemical oxidation, acidification and solid waste) are shown in the form of weighted values instead of absolute values to obtain optimal locations for facilities in the supply chain.

Ramudhin et al. (2009) revealed an extensive framework for eco-friendly supply chain systems. They suggested a mixed integer linear multi-objective programming model as a decision support tool for selection of suppliers and subcontractors, allocation of products to locations, utilization of capacity and configuration of transport as well as decisions to reduce carbon emissions in the supply chain.

Ioannis et al. (2012) examined the effect of green supply chain on network design and its cost. They developed strategic and tactical decisions to help managers evaluating the effect of environmental issues. In this case, they considered different types of vehicles. Consequently, they studied the decisions on the utilization of common vehicles and warehouses. Their model was implemented in a region of Eastern Europe. In most cases, the use of common warehouses and vehicles improved environmental and cost performance of companies. Pishvaee and Razmi (2012) developed a dual-objective model for green supply chain network with uncertainty condition. They used life cycle assessment (LCA)-based technique for a green design. Furthermore, a fuzzy method was presented to improve green supply chain network.

Boonsothonsatit et al. (2015) developed a decision support system based on multi-objective programming to design a green supply chain issue. They revealed a model with three objective functions in which fuzzy goal programming was applied. Coskun et al. (2016) used goal programming to design a green supply chain network. The authors classified customer behavior into three categories: green customers, incompatible customers, and red customers as well as environmental effects in the suggested model.

Talaei et al. (2016) developed an effective fuzzy programming model for a green supply chain network in the electronics industry. The authors suggested a dual-objective model and used ε-constraint approach to solve the model. Rezaee et al. (2017) developed a two-tiers stochastic programming model for green supply chain network. The authors considered demand and carbon price as random parameters in the introduced model.

Golpîra et al. (2017) developed a bi-level programming model for robust design of a green supply chain network. The authors considered risk parameters in the suggested model through conditional value at risk (CVaR) approach.

All the above mentioned studies are in the context of green supply chain systems. Nevertheless, none of them could insert uncertainty of parameters in their models as an important factor. Moreover, the importance of green supply chain design for many steel companies is neglected. Therefore, this study aimed to focus on design of a green supply chain network for steel manufacturing. This study develops a fuzzy dual-objective facility programming model of a green supply chain system. Facility programming is employed to model uncertainty of parameters in the network. In addition, the aggregation function (TH) is applied for solving two objective functions.

Problem statement and modeling

In this section, the main problem of the study is defined. Afterwards, the modeling methodology will be presented.

Many scholars endeavored to model the uncertainty in supply chains in recent times (e.g., Gupta and Maranas 2003; Santoso et al. 2005; Alonso-Ayuso et al. 2003; Kenne et al. 2012). However, Pishvaee and Razmi (2012) implied that only the classical facility location models are implemented in real-world cases. These classical models focused on minimization of establishment, operation, and transportation cost only. However, these models are not able to consider the availability of facilities due to uncertain parameters such as severe weather. On the other hand, steel manufacturing process is a significant source of toxic environmental persistent pollutants (Anderson and Fisher 2002). As mentioned above, a lack supply chain system design with consideration of environmental parameters was identified in the literature. Thus, this paper aims to develop a novel bi-objective model for deigning a green supply chain network within steel industry by considering different level of uncertainties. The novelty of this model is that it attempts to respond to the one of the research gaps in the field of supply chain management for steel industries, which is the minimization of environmental effects, by applying a unique hybrid solution for dual-objective optimization model, so that it can consider the uncertain parameters as well as the environmental effects on the steel manufacturing supply chain network.

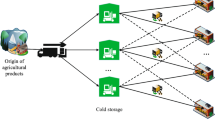
The problem considered in this study is a design of a single commodity supply chain network, including suppliers, production facilities and customers. This problem involves decisions related to supplier selection, production levels, allocation of customers to manufacturers, delivery rate from suppliers to manufacturers, and manufacturers to customers in a pull supply chain. The considered supply chain is related to steel industry which is perceived as a whole network. As the figure below shows, iron ore is transported from suppliers to manufacturers. Manufacturers transform the purchased iron ore to steel ingots and deliver them to the customers. Raw material is required in bulk; the iron ore from different mines should obtain the same certain fusion ratio as well. The studied steel supply chain network is shown in Fig. 1.

Fig. 1
figure 1

Three-level supply chain including supplier, manufacturer and customer

Full size image

Planning horizon is a single period. Customer demand is always uncertain. Customer demand can be determined in an interval. In this chain, customer demand, and the supplier, production, and casting capacities are considered as uncertain parameters of the chain. In order to guarantee a minimum rate of profitability of each manufacturer, a minimum acceptable ratio of production rate to production capacity (utilization factor) is considered for each of them. Although network configuration can be altered to operational planning live, planning horizon is limited to long-term and medium-term phase.

Assumptions of this problem are listed below:

  • The studied supply chain network is single commodity and single period;

  • Planning horizon is single period;

  • The supply chain network is a multilevel network including suppliers, manufacturing facilities and customers;

  • Customer service points are fixed and predetermined;

  • Supply chain parameters such as customer demand, production, transportation, and purchase costs as well as capacity of production facilities and suppliers are uncertain.

This problem tends to identify the number and optimal sites of manufacturing facilities and determine optimal value of product flow between them in order to minimize overall cost of the supply chain network and minimize environmental effects. The following symbols are used to develop the mathematical model (Table 1).

Table 1 The symbols of the mathematical model
Full size table

Based on the presented symbols, a mathematical model of the problem is suggested as follows.

Objective function 1

Minimizing total costs like fixed cost of establishment of production facilities and production costs, purchase of iron ore from mines and transportation of goods in the supply chain. The first term of the objective function (1) shows purchasing and delivery costs of iron ore from mines to production facilities. The second term of the objective function (1) shows delivery cost of goods from production facilities to customers and production cost of manufacturing facilities. The third term of the objective function (1) shows establishment cost of production facilities.

Objective function 2

Minimizing environmental effects of steel supply chain system. The first term of the objective function (2) shows total environmental effects of transportation of iron ore from suppliers to manufacturers. The second term of the objective function (2) shows total environmental effects of casting, production, and transportation of products from the manufacturers to the customers.

$${\text{Min}}\,Z_{1} = \sum\limits_{i} {(\tilde{P}_{i} + \tilde{C}_{ij}^{1} )X_{ij} + } \sum\limits_{j} {({\text{Cp}}\tilde{r}{\text{od}}_{j} + \tilde{C}_{jl}^{1} )Y_{jl} + } \sum\limits_{j} {\tilde{F}_{j} U_{j} }$$
(1)
$${\text{Min}}\,Z_{2} = \sum\limits_{i} {\sum\limits_{j} {{\text{ET}}_{ij}^{1} X_{ij} } + } \sum\limits_{j} {\sum\limits_{l} {({\text{EP}}_{i} + {\text{ET}}_{jl}^{2} )Y_{jl} } } ,$$
(2)
$$\begin{aligned} & {\text{s}} . {\text{t}} .\\ & \quad \quad \sum\limits_{j} {Y_{jl} } \ge \tilde{d}_{l} \quad \forall l, \\ \end{aligned}$$
(3)
$$\sum\limits_{j} {X_{ij} } \le c\tilde{p}r_{i} \quad \forall i$$
(4)
$$\sum\limits_{i} {\frac{{X_{ij} }}{{E_{i} }}}\,\ge \sum\limits_{l} {Y_{jl} } \quad \forall j,$$
(5)
$$\sum\limits_{l} {Y_{jl} } \le c\tilde{p}_{j} U_{j} \quad \forall j$$
(6)
$$U_{j} \, \in \{ 0,\,1\} ,\quad \forall j \in J,$$
(7)
$$X_{ij} ,Y_{jl} \ge 0,\quad \forall i \in I,\;\forall j \in J,\;\forall l \in L.$$
(8)

Constraint (3) ensures that each demand is met by manufacturers. Constraint (4) shows maximum capacity to supply iron ore by mines (suppliers). Constraint (5) ensures that fusion ratio of raw materials purchased by each manufacturer from iron ore mines matches the required ratio. Constraint (6) shows maximum production capacity of each production facility. Constraints (7) and (8) show binary decision variables and decision variables of product flow and the related constraints.

This section briefly explains fuzzy facility programming developed by Jimenez et al. (2007). Then, this approach is used to model cognitive uncertainties of parameters. To do this, let \(\tilde{c}\) be a triangular fuzzy number with the following membership function, where, \(c^{\text{p}}\), \(c^{\text{m}}\) and \(c^{\text{o}}\) are pessimistic, the most likely and the optimistic values, respectively (Özceylan and Paksoy 2014).

$$\mu_{{\tilde{c}}} (x) = \left\{ {\begin{array}{*{20}l} {f_{c} (x) = \hbox{max} \frac{{x - c^{\text{p}} }}{{c^{\text{m}} - c^{\text{p}} }}} \hfill & {{\text{if}}\;\;c^{\text{p}} \le x \le c^{\text{m}} } \hfill \\ 1 \hfill & {{\text{if}}\;\;x = c^{\text{m}} } \hfill \\ {g_{c} (x) = \hbox{max} \frac{{c^{\text{o}} - x}}{{c^{\text{o}} - c^{\text{m}} }}} \hfill & {{\text{if}}\;\;c^{\text{m}} \le x \le c^{\text{o}} } \hfill \\ 0 \hfill & {{\text{if}}\;\;x \le c^{\text{p}} \;{\text{or}}\;x \ge c^{\text{o}} } \hfill \\ \end{array} } \right..$$
(9)

This facility programming is developed based on concepts of the expected interval (EI) and the expected value (EV). These concepts can be achieved through the following equations:

$$\begin{aligned} {\text{EI}}(\tilde{c}) & = [E_{1}^{c} ,\,E_{2}^{c} ] = \left[ {\int\limits_{0}^{1} {f_{c}^{ - 1} (x){\text{d}}x,} \int\limits_{0}^{1} {g_{c}^{ - 1} (x){\text{d}}x,} } \right] = \left[ {\frac{{c^{\text{p}} + c^{\text{m}} }}{2},\frac{{c^{\text{m}} + c^{\text{o}} }}{2}} \right] \\ {\text{EV}}(\tilde{c}) & = \frac{{E_{1}^{c} + E_{2}^{c} }}{2} = \frac{{c^{\text{p}} + 2c^{\text{m}} + c^{\text{o}} }}{4}. \\ \end{aligned}$$
(10)

Now, consider the following fuzzy programming, where, all parameters are fuzzy triangular numbers.

$$\begin{aligned} {\text{Max}}\;z = \tilde{c}^{t} x \hfill \\ {\text{s}} . {\text{t}} .\hfill \\ \quad \tilde{a}_{i} x \ge \tilde{b}_{i} ,\quad i = 1,2, \ldots ,l \hfill \\ \quad \tilde{a}_{i} x = \tilde{b}_{i} ,\quad i = l + 1, \ldots ,m \hfill \\ \quad x \ge 0. \hfill \\ \end{aligned}$$
(11)

According to Jiménez (1996), certain α-parametric model using EI and EV definition is shown below:

$$\begin{aligned} & {\text{Min}}\;{\text{EV}}(\tilde{c})x \\ & [(1 - \alpha )E_{2}^{{a_{i} }} + \alpha E_{1}^{{a_{i} }} ]x \ge \alpha E_{2}^{{b_{i} }} + (1 - \alpha )E_{1}^{{b_{i} }} ,\quad i = 1, \ldots ,l \\ & \left[ {\left( {1 - \frac{\alpha }{2}} \right)E_{2}^{{a_{i} }} + \alpha E_{1}^{{a_{i} }} } \right]x \ge \frac{\alpha }{2}E_{2}^{{b_{i} }} + \left( {1 - \frac{\alpha }{2}} \right)E_{1}^{{b_{i} }} ,\quad i = l + 1, \ldots ,m \\ & \left[ {\frac{\alpha }{2}E_{2}^{{a_{i} }} + \left( {1 - \frac{\alpha }{2}} \right)E_{1}^{{a_{i} }} } \right]x \ge \left( {1 - \frac{\alpha }{2}} \right)E_{2}^{{b_{i} }} + \frac{\alpha }{2}E_{1}^{{b_{i} }} ,\quad i = l + 1, \ldots ,m \\ & x \ge 0. \\ \end{aligned}$$
(12)

Accordingly, dual-objective facility programming model suggested for green supply chain system presented as follows (Pishvaee and Razmi 2012):

$${\text{Min}}\,Z_{1} = \sum\limits_{i} {({\text{EV}}(\tilde{P}_{i} ) + {\text{EV}}(\tilde{C}_{ij}^{1} ))X_{ij} + } \,\sum\limits_{j} {({\text{EV}}({\text{Cp}}\tilde{r}{\text{od}}_{j} ) + {\text{EV}}(\tilde{C}_{jl}^{1} ))Y_{jl} + } \sum\limits_{j} {{\text{EV}}(\tilde{F}_{j} )U_{j} } ,$$
(13)
$${\text{Min}}\,Z_{2} = \sum\limits_{i} {\sum\limits_{j} {{\text{ET}}_{ij}^{1} X_{ij} } + } \sum\limits_{j} {\sum\limits_{l} {({\text{EP}}_{i} + {\text{ET}}_{jl}^{2} )Y_{jl} } } ,$$
(14)
$$\begin{aligned} & {\text{s}} . {\text{t}} .\\ & \quad \sum\limits_{j} {Y_{jl} } \ge \left[ {(1 - \alpha )E_{1} (\tilde{d}_{l} ) + \alpha E_{2} (\tilde{d}_{l} )} \right]\quad \forall l, \\ \end{aligned}$$
(15)
$$\sum\limits_{j} {X_{ij} } \le \left[ {\alpha E_{1} (c\tilde{p}r_{i} ) + (1 - \alpha )E_{2} (c\tilde{p}r_{i} )} \right]\quad \forall i,$$
(16)
$$\sum\limits_{i} {\frac{{X_{ij} }}{{E_{i} }}} \ge \sum\limits_{l} {Y_{jl} } \quad \forall j,$$
(17)
$$\sum\limits_{l} {Y_{jl} } \le \left[ {\alpha E_{1} (c\tilde{p}_{j} ) + (1 - \alpha )E_{2} (c\tilde{p}_{j} )} \right]U_{j} \quad \forall j,$$
(18)
$$U_{j} \in \{ 0,1\} ,\quad \forall j \in J,$$
(19)
$$X_{ij} ,Y_{jl} \ge 0,\quad \forall i \in I,\;\forall j \in J,\;\forall l \in L.$$
(20)

The proposed solution method

In literature, different methods have been used for solving multi-objective programming problems. Meanwhile, fuzzy approaches have been widely used. Min–max developed by Zimmermann (1978) is one of the first fuzzy approaches used for solving multi-objective optimization problems; however, this approach sometimes produces inefficient solutions (Lai and Hwang 1993). To solve this problem, Sakawa et al. (1987) developed a fuzzy interactive approach. In addition to this approach, Lai and Hwang (1993) suggested the augmented min–max approach. Torabi and Hassini (2008) also developed a one-step approach based on fuzzy concepts for solving linear multi-objective optimization problems; this is known as TH in the literature. These authors proved efficiency of their approach. In another study, Vahdani et al. (2012) developed a hybrid approach based on robust optimization and TH to solve multi-objective optimization problems where parameters are uncertain. The present study uses this hybrid approach to solve the considered dual-objective problem. This hybrid approach is implemented as follows:

  1. 1.

    All uncertain parameters and distribution functions related to each of them are identified.

  2. 2.

    The uncertain problem is developed; considering uncertain parameters, the suggested dual-objective facility programming model is written.

  3. 3.

    Positive ideal solution (PIS) and negative ideal solution (NIS) are determined for each objective function. To obtain PIS for each objective function, \(\left( {f_{1}^{\text{PIS}} ,x_{1}^{\text{PIS}} } \right)\) and \(\left( {f_{2}^{\text{PIS}} ,x_{2}^{\text{PIS}} } \right)\), the suggested facility programming model is solved for each objective function separately, and optimal values are determined; therefore, we have:

    $$\left. {\begin{array}{*{20}l} {f_{1}^{\text{PIS}} = \hbox{min} f_{1} } \hfill \\ {{\text{s}} . {\text{t}} .x \in X} \hfill \\ \end{array} } \right\} \Rightarrow (f_{1}^{\text{PIS}} ,x_{1}^{\text{PIS}} ),$$
    (21)
    $$\left. {\begin{array}{*{20}l} {f_{2}^{\text{PIS}} = \hbox{min} f_{2} } \hfill \\ {{\text{s}} . {\text{t}} .\;x \in X} \hfill \\ \end{array} } \right\} \Rightarrow \left( {f_{2}^{\text{PIS}} ,x_{2}^{\text{PIS}} } \right).$$
    (22)

Then, following equations are used to obtain NIS:

$$f_{1}^{\text{NIS}} = f_{1} (x_{2}^{\text{PIS}} ),$$
(23)
$$f_{2}^{\text{NIS}} = f_{2} (x_{1}^{\text{PIS}} ).$$
(24)
  1. 4.

    A linear membership function is obtained for each objective function based on following formula:

    $$\mu_{1} (x) = \left\{ {\begin{array}{*{20}l} 1 \hfill & {{\text{if}}\;\;f_{1} < f_{1}^{\text{PIS}} } \hfill \\ {\frac{{f_{1}^{\text{NIS}} - f_{1} }}{{f_{1}^{\text{NIS}} - f_{1}^{\text{PIS}} }}} \hfill & {{\text{if}}\;\;f_{1}^{\text{PIS}} \le f_{1} \le f_{1}^{\text{NIS}} } \hfill \\ 0 \hfill & {{\text{if}}\;\;f_{1} > f_{1}^{\text{NIS}} } \hfill \\ \end{array} } \right.,$$
    (25)
    $$\mu_{2} (x) = \left\{ {\begin{array}{*{20}l} 1 \hfill & {{\text{if}}\;\;f_{2} < f_{2}^{\text{PIS}} } \hfill \\ {\frac{{f_{2}^{\text{NIS}} - f_{2} }}{{f_{2}^{\text{NIS}} - f_{2}^{\text{PIS}} }}} \hfill & {{\text{if}}\;\;f_{2}^{\text{PIS}} \le f_{2} \le f_{2}^{\text{NIS}} } \hfill \\ 0 \hfill & {{\text{if}}\;\;f_{2} > f_{2}^{\text{NIS}} } \hfill \\ \end{array} .} \right.$$
    (26)

In fact, \(\mu_{h} (x)\), h = 1, 2, shows the degree to which hth objective function is met.

  1. 5.

    The suggested dual-objective facility programming model is converted to a single-objective mathematical programming model through aggregation function TH. Note that TH ensures that the solutions are efficient. TH can be obtained by the following formula:

    $$\begin{aligned} & {\text{Max}}\lambda (x) = \psi \lambda_{0} + (1 - \psi )\sum\limits_{h = 1}^{2} {\varphi_{h} \mu_{h} (x)} \\ & {\text{s}} . {\text{t}} .\\ & \quad \lambda_{0} \le \mu_{h} (x),\quad h = 1,2 \\ & \quad x \in F(x),\quad \lambda_{0} \;{\text{and}}\;\lambda \in [0,1] \\ \end{aligned}$$
    (27)

    where F(x) shows the eligible area related to constraints of the suggested dual-objective facility programming model. Moreover, \(\phi_{h}\) and ψ indicate importance of the hth objective function and coefficient of compensation, respectively. \(\mathop \sum \nolimits_{h = 1}^{2} \phi_{h} = 1, \quad \phi_{h} > 0\) is always true. In addition, the optimal value of the decision variable shows the lowest degree to which objective functions are met. TH aggregation function always attempts to compromise the value between the operator min and the operator sum based on ψ.

  2. 6.

    Values of uncertainty (ρ), coefficient of compensation (ψ) and relative importance of fuzzy objectives (\(\phi_{h}\)) are determined, and the single-objective model is solved. If solutions are acceptable for the decision-maker based on the values of these parameters, the algorithm will stop; otherwise, other solutions are searched by changing these parameters.

Implementation and evaluation

In this section, the validity of the presented green supply chain model as well as practicality of the proposed solution method is investigated via the data extraction from the considered case study. As noted earlier, the studied green supply chain has three different levels: suppliers, manufacturers and customers. There are nine suppliers in this chain including Chadormalu, Gol Gohar, Choghart, SAMARCO, KUDERMUKH, CARAJASE, CVRD, FERTECO and MBR. There are three manufacturers in this chain including Khuzestan Steel Company (KSC), Mobarake Steel Company (MSC) and Esfahan Steel Company (ESC). Moreover, there are ten customers in this chain including MSC, ESC, Kavian Steel, Iran National Steel Industrial Group, Arpco, Khuzestan Oxin Steel Co., Azarbayjan Steel Company, Khorasan Steel Complex Co., Amirkabir Khazar Steel Company, and Iran Alloy Steel. Each manufacturer requires an iron ore with certain fusion rate. In the chain, the first current commodity is iron ore, and the second is steel billet. Conversion ratio of each type of iron ore to the product depends on its fusion rate and it should be < 1.66. Here, this ratio is set at 1.66. The price per ton of iron ore is 130.28 $. The cost of transporting a ton of product per kilometer is 16. Transportation cost between two facilities is calculated by multiplying the cost of transporting one unit of product per distance (km) by the distance between the two facilities. Capacity of KSC, MSC and ESC is set at (540, 550, 560), (790, 800, 810) and (890, 900, 910) thousand tons, respectively. Purchase cost of one ton steel billet is (575.71, 578.57, 581.42), (578.57, 582.85, 587.14) and (581.71, 585.14, 588.57) US Dollar in KSC, MSC and ESC, respectively. Establishment cost of these production facilities is (156,857.1, 15,714.28, 157,428.57), (197,142.85, 20,000, 200,285.7) and (228,285.71, 228,571.42, 228,857.14) US Dollar, respectively.

Environmental effect of transporting one ton product per km is 173.3 and environmental effect of producing one kilo steel billet is set at 32.2 based on eco-indicator. Table 2 shows values of other parameters of the supply chain network.

Table 2 Values of parameters of steel supply chain network
Full size table

This study tends to develop and solve a model related to Iran steel supply chain, planning for manufacturer development, establishment of production facilities, and purchase rate of supplier in order to determine product flow between suppliers, manufacturers and customers. Tactical objectives of the problem are to determine delivery rate of any type of product from a node related to one level to the node related to the next level and to determine production levels.

To solve the suggested dual-objective facility programming problem by the hybrid solution in different α levels, it is required to obtain PIS and NIS for each objective function at any level of α. For this purpose, payoff tables and formula (21)–(24) are used (α = 0.10, 0.25, 0.5, 0.75,0.90, 1). Table 3 reports PIS and NIS for green supply chain network.

Table 3 PIS and NIS results for green supply chain network
Full size table

Then, membership function of each objective function is calculated in any level of α based on formulas (25) and (26). Final results can be calculated using aggregation function TH given in the Eq. (27). The table below shows the obtained results calculated using the software GAMS. This table shows optimal values of objective functions and membership degree of each objective function at different levels of α. To obtain the results presented in the table below,

$$\phi_{1} = \phi_{3} = \frac{1}{2}\;{\text{and}}\;\psi = 0. 5.$$

By comparing optimal values of objective functions (total costs and environmental effects of the network) at different levels of α, it can be concluded that the increase in α level increases total costs and environmental effects of supply chain network. This means that total costs and environmental effects increase when the model supports the network with higher further uncertainties. Table 4 shows the performance of the robust corresponding model to the absolute model.

Table 4 Performance of the robust corresponding model to the absolute model
Full size table

Figure 2 shows values of the first objective function, i.e., total costs of supply chain network at different levels of α.

Fig. 2
figure 2

Total cost of green supply chain network (first objective function) at different α levels

Full size image

Fig. 3 shows values of the second objective function, i.e., environmental effects of supply chain network at different levels of α.

Fig. 3
figure 3

Environmental effects of green supply chain network (second objective function) at different levels of α

Full size image

Conclusion

As mentioned earlier, moving toward a higher level of sustainability is a big concern not only for local small businesses, but also for multinational companies (Khorasani and Almasifard 2017). Different levels of sustainability in the supply chain system can influence the overall well-being of individuals and also change the environmental condition. Sustainability of a system is considered as a critical issue which cannot be reached only by considering environment and economic aspects of the whole process. For reaching a higher level of sustainability, social factors should be analyzed as well. Researchers endeavor to develop new green supply chain models for steel companies to turn them more environmental-friendly. Achieving this goal has positive influence on the social welfare of the whole economy. However, reaching this point is not feasible without new governmental policy and regulations. Demonstration of the importance of green supply chain network, which is leading to lower cost for the steel companies, also motivate managers and leadership of these industries to implement these new models.

This study endeavoured to present a development of a green supply chain network model under uncertainty of parameters such as customer demand as well as suppliers, production, and casting capacity. The novelty of presented model lies in two main aspects. First, presented model was dual-objective facility programming model which tended to minimize two objective functions, i.e., total cost of the supply chain and total environmental effects coincidently. Second, the facility programming was used to model uncertainty of parameters.

For finding an optimal solution for this model a TH aggregation function was applied to solve the problem and convert the two objective functions to one. The suggested dual-objective model was employed to model steel green supply chain. As the results show, the increase in α level increases values of two objective functions of total cost and total environmental effects; that is, the model provides further support against uncertainties.

We can argue that this developing discipline which is called supply chain management would in near future turn out to be a leading force in business success and flourish, so further research and investment in this specific field is essential. For future studies concentration on both dynamic and uncertainty of different parameters in the supply chain system is necessary. Additionally, simulation (for operation level) and optimization (for strategical level) tools should be used simultaneously. Consideration of distribution centers in the supply chain model can be perceived as another future direction of research which was out of scope of this study. It is necessary to remember that the value of creating a green supply chain is depending on the nature of the industry, so before any specific programming, studying the whole industry is an essential step.