Introduction

Redundancy is a well-known and widely used approach to enhancement of failure-sensitive systems which are subject to both dependent and independent failures. In most reliability analyses and mean time between failures (MTBF) evaluation models for redundant systems, components are considered independent of one another with respect to failure. This results in an incorrect and inaccurate evaluation of system features. Therefore, it is highly crucial to identify and consider dependent failures in the evaluation of reliability and MTBF of systems. Common cause failure (CCF) is one of the most important dependent failures in redundant systems, in which an intrinsic factor leads to the propagation of failure in all components, resulting in the simultaneous failure of components in the redundant system (Kančev and Čepin 2012). Failing to incorporate CCF into MTBF of redundant systems leads to irreversible damage. In March 22, 1975, negligence of CCF led to a fire that occurred in a nuclear power plant located in the state of Alabama, USA (Mortazavi et al. 2016). After this event, in order to prevent the recurrence of such incidents, extensive research was conducted on CCF, resulting in the development of various standards (Mosleh et al. 1988, 1998). As another example, one may refer to the failure of all four engines of the Boeing 747 in fight BA 009 on 24 June 1982 over the Indian Ocean (Tootell 1985). The engineers estimated the likelihood of all four engines failing during the same flight to be negligible; however, a CCF of volcano ash proved otherwise. Other catastrophic incidents resulted by ignoring the likelihood of dependent failures in redundant systems have been reported, e.g., the hydraulic pumps failure due to engine explosion in United Airlines DC-10 in July 1989 (Galison 2000).

Another variety of dependent failures in redundant systems is cascading failure (also known as load share); when a component in the redundant system fails, the intact components undergo greater load or the failure propagates through the system to other components; hence, their failure rates change. As an example, the costly collision of the space rocket Ariane 5 on 4 June 1996 was due to cascading failure (Gleick 1996). Ariane 5 and its precious cargo of four expensive satellites were destroyed due to an error in the rocket navigation computer that led to generation of a number which was too large for the system to calculate. This in turn resulted in handing over control to an identical redundant computer in which the same failure occurred. The out-of-control rocket changed direction to compensate for an estimated error and was finally destroyed in its own turbulence. The significance of the influence of cascading failures can be recognized through many examples of catastrophic incidents reportedly stem from this type of dependent failure, e.g., the explosion of Boeing 707, Pan Am flight 214, on 8 December 1963 and Boeing 747, TWA 800, on 17 July 1999 (Negroni 2013).

Considering the significant impact of dependent failures (CCF and cascading failure) on reliability of redundant systems, these types of failures substantially affect MTBF of such systems. Neglecting the role that these types of failures play may result in significantly misleading MTBF evaluation models which in turn lead to incorrect MTBF value. Therefore, this paper addresses these two important types of failures and incorporates those into a proposed model for MTBF evaluation of a 2-out-of-3 repairable redundant system.

The organization of the paper is as follows: In the next section, a review of the related literature is presented. In "Alpha factor model and capacity flow model" section, addresses the alpha factor model and capacity flow model. In "Formulating the model" section, the MTBF for 2-out-of-3 redundant repairable system is computed with CCF and cascading failure based on alpha factor model and capacity flow model and, also the developed MTBF function together with fuzzy parameter is discussed, and the NLP method is used to determine the membership function. In "Case study" section, in order to validate the proposed model, a case study on the redundant system of centrifugal pumps is presented. In "Comparison of results" section, the results of the developed model are compared with those of a model offered in previous studies and an analysis is carried out. Finally, "Discussion and conclusion" section, concludes the paper and presents some guidelines for future works.

Literature review

Studied extensively in recent years, the fuzzy theory is an efficient tool for considering uncertainty in reliability analyses (Purba et al. 2014; Sharma and Sharma 2015; Gupta et al. 2016; Kumar and Goel 2017). Due to uncertainty and imprecision, it is not easy to estimate dependent and independent failure rates. Therefore, different industries in the real world are interested in considering these rates as intervals (minimum failure rate and maximum failure rate) using the fuzzy theory and fuzzy numbers. Wu and Tsai (2000) developed weighted-based fuzzy clustering procedure to estimate time-to-failure distribution. The fuzzy reliability computation of single component is a fundamental problem. Jiang and Chen (2003) focused on the computation of the fuzzy reliability of a single component. The idea is that if the value of fuzzy reliability of a single component can be determined, it will be possible to compute the fuzzy reliability of the whole system by conventional methods. The general redundant system with the random fuzzy lifetime was considered by Zhao and Liu (2004). In their research, three system performances with random fuzzy lifetimes are studied. In addition, Liu et al. (2007) regarded component failure rate and lifetime as fuzzy variables and established mathematical models for non-repairable series and parallel systems. In another research by Liu et al. (2010), component lifetime and repair time were modeled by random fuzzy exponential distribution. In addition, system MTBF and mean time to repair (MTTR) were calculated. Liu et al. (2011) used bivariate exponential distribution, assuming that components have interdependent lifetimes.

To estimate lifetime and repair time, Liu et al. (2014) used random fuzzy exponential distribution and evaluated the availability of a redundant system with non-identical repairable components. González-González et al. (2016) used nonlinear regression to model a degradation process in order to predict mean time to failure (MTTF). To include uncertainty in the extrapolation process, they used trapezoidal fuzzy numbers to shape the time-to-failure estimation. Aghili and Hajian-Hoseinabadi (2017) introduced a flexible form of Markov process to evaluate the reliability of repairable systems. They then used fuzzy arithmetic calculations to incorporate uncertainty into their presented model. Some other studies focused on repairable systems with fuzzy repair rates. Chhoker and Nagar (2015) and Hu and Su (2016) developed frameworks for modeling, analyzing and predicting the reliability of redundant repairable systems with fuzzy parameters.

Redundant systems are in various types. Standby systems are one of the most widely used types of redundant systems, in which one or several components are put on standby mode. In case of failure of an operating component, the standby component replaces the failed component and prevents system breakdown. Ke et al. (2008) proposed a procedure to construct the MTTF membership function of a redundant repairable system with two primary components and one standby. They assumed component failures to be independent of one another. Lin et al. (2012) analyzed the reliability and MTBF of a redundant repairable system with one primary component, one standby component, and one unreliable service station. They assumed failure and repair rates to follow fuzzy exponential distributions. In the study by Huang et al. (2006), a parametric NLP approach is addressed to analyze the MTBF of a repairable system with switching failure and fuzzy parameters, assuming that components fail only due to their independent failure. Jahanbani Fard et al. (2017) applied the concepts of α-cuts and fuzzy algorithm to a repairable system with two primary units in parallel as one active and one standby redundancy with imperfect coverage. They proposed a method to construct membership functions for MTBF and availability using paired NLP models.

Lethal shocks cause redundant system components to fail simultaneously (simultaneous failure). In some studies, such shocks are known as common cause shock failure. Only few studies have investigated dependent failure with fuzzy parameters. Huang et al. (2008) addressed the fuzzy availability and fuzzy MTTF of a system with two components in series and parallel configurations. They categorized system failures into two groups of individual failures and common cause shock failures assuming failure rates to be fuzzy numbers with trapezoidal membership functions. Jain et al. (2012) investigated a repairable redundant system with imperfect coverage, common cause shock failure, reboots, and recovery, and determined the fuzzified reliability, availability, and MTTF. Jain (2016) studied a repairable redundant system with warm standby components and repair facility. He took into account the real system conditions including repair, repair delay, switching failure, and CCF. Taking these into consideration helped developing appropriate availability functions for the redundant system.

In most of the aforementioned researches, dependent failures are ignored. A few studies have merely hinted at a single kind of dependent variables (e.g., CCF or common cause shock failure). However, there are many redundant systems which are exposed to cascading failure as well as CCF. Dependent failures and reparability are among the features that should be taken into consideration in evaluation of MTBF of redundant systems in order to obtain realistic results. Hence, it is important to develop a method which incorporates these features into the MTBF function. Furthermore, it was demonstrated in this paper how dependent failures affect and reduce redundant system MTBF. If dependent failures are not incorporated into reliability analyses, reliability parameters are not correctly evaluated creating misleading results about the redundant systems. Some other studies have been silent regarding fuzzy failure rates, whereas engineers designing redundant systems would prefer the failure rates expressed as linguistic terms that can be effectively modeled as fuzzy numbers. Therefore, this research presents a method to evaluate the MTBF of a 2-out-of-3 redundant repairable system with independent failure, CCF, cascading failure, and fuzzy parameters.

Alpha factor model and capacity flow model

CCF, as a category of dependent failures, may significantly affect the reliability of redundant systems. The alpha-factor, originally developed by Mosleh et al. (1998), is a method for modeling CCF in k-out-of-n redundant systems. To clarify the formulations of the alpha-factor, capacity flow and the proposed models, Table 1 presents the notations used in the paper.

Table 1 Notations
Full size table

Figure 1 depicts the fault tree of a 2-out-of-3 redundant system with 3 identical components A, B and C that constitute a Common Cause Component Group (CCCG) which is a set of components subject to failures due to a common cause in addition to their independent failures. The minimal cut sets for the fault tree in Fig. 1 are:

Fig. 1
figure 1

The fault tree of 2-out-of-3 redundant system

Full size image
$$\{ A,B\} ,\{ A,C\} ,\{ B,C\} ,\{ A,B,C\}$$
(1)

Each component A, B and C is subject to CCF as well as independent failure. Figure 2 illustrates the fault tree for component A for which the minimal cut sets are as follows:

Fig. 2
figure 2

The fault tree of component A

Full size image
$$\{ A_{\text{I}} \} ,\{ C_{AB} \} ,\{ C_{AC} \} ,\{ C_{ABC} \}$$
(2)

Similarly, the minimal cut sets for components B and C are presented the following expressions, respectively.

$$\{ B_{\text{I}} \} ,\{ C_{AB} \} ,\{ C_{BC} \} ,\{ C_{ABC} \}$$
(3)
$$\{ C_{\text{I}} \} ,\{ C_{AC} \} ,\{ C_{BC} \} ,\{ C_{ABC} \}$$
(4)

In the above sets, A I, B I, and C I are the independent failures of components A, B, and C, respectively. Also, C AB , C AC , C BC , and C ABC are the failures of {A, B}, {A, C}, {B, C}, and {A, B, C} due to the common cause, respectively. Thus, the probability of failure in a 2-out-of-3 redundant system is

$$\begin{aligned} P(s) & = P(A_{\text{I}} )P(B_{\text{I}} ) + P(A_{\text{I}} )P(C_{\text{I}} ) + P(B_{\text{I}} )P(C_{\text{I}} ) \\ & \quad + P(C_{AB} ) + P(C_{AC} ) + P(C_{BC} ) + P(C_{ABC} ) \\ \end{aligned}$$
(5)

To simplify the above equation and without loss of generality and because the components are identical, it is assumed that

$$\begin{aligned} P(A_{\text{I}} ) & = P(B_{\text{I}} ) = P(C_{\text{I}} ) = Q_{1} \\ P(C_{AB} ) & = P(C_{AC} ) = P(C_{BC} ) = Q_{2} \\ P(C_{ABC} ) & = Q_{3} \\ \end{aligned}$$
(6)

Hence, the probability of failure of a 2-out-of-3 redundant system is

$$P(T) = 3(Q_{1} )^{2} + 3Q_{2} + Q_{3}$$
(7)

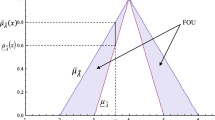
In alpha-factor model, two parameters Q T and α k are predefined. The former, \(Q_{\text{T}}\), is the total failure frequency of the system caused by independent failure and CCF and the latter, \(\alpha_{k}\), is a fraction of the total frequency of failure event including the failure of k components in the system. Kang et al. (2011), Zheng et al. (2013) and Hassija et al. (2014) have already proposed methods to estimate the value of α k . To estimate the parameter alpha (α), all of these methods require comprehensive data regarding independent failure and CCF. In most cases, however, α and Q T are not computed easily. There may be a lack of appropriate information regarding redundant system failure; therefore, Q 1, Q 2, and Q 3 cannot be computed accurately. Under such circumstances, these parameters are often expressed through linguistic terms. In other words, independent failure rate and CCF rate can be represented by triangular fuzzy numbers. Figure 3 illustrates the membership functions of fuzzy numbers considering independent failure rate, CCF rate, and repair rate as triangular fuzzy numbers.

Fig. 3
figure 3

The membership function for failure rates and repair rate

Full size image

A fuzzy membership function can be defined as a function presented by the following notation.

$$\mu_{{\tilde{A}}} :U \to [0,1]\quad u| \to \mu_{{\tilde{A}}} (u)$$
(8)

Let a, b and c be real numbers where a < b < c. The membership function of a triangular fuzzy number is presented by the following equation:

$$\mu_{{\tilde{A}}} = \left\{ \begin{aligned} \frac{x - a}{b - a}\quad a \le x \le b \hfill \\ 1\quad x = b \hfill \\ \frac{x - c}{b - c}\quad b \le x \le c \hfill \\ 0\quad {\text{others}} \hfill \\ \end{aligned} \right.$$
(9)

Another type of dependent failures is known as “cascading failure or load share”. When a component in a redundant system fails, the load on to the intact components increases which in turn changes the failure rate of the surviving components affecting the MTBF of the total system. The capacity flow model is proposed as an easy way for load share modeling (Yinghui and Jing 2008). It this model, a k-out-of-n system with n identical components is assumed. Load L is applied equally to all operation components. When all the components are in operation, the load on each component equals L/n. With the first component failure, load on operating components increases to L/(n − 1). The initial failure rate for all the components equals Q 1. Due to the increase in load following the failure of the first components, the failure rate of each intact components, x, equals Q * x , which is defined by

$$Q_{x}^{*} = \left( {\frac{n}{n - x}} \right)^{\gamma } .Q_{1} \quad x = 0,1, \ldots ,n - 1$$
(10)

In the above equation, x is the number of failed components in a redundant system and γ is the load factor. Load share exists in many redundant systems such as water pumps, electric generators, suspension bridge cables, and computer parts (e.g., CPUs, graphics cards, laptop RAMs).

Formulating the model

Assumptions

  • The system and the components have two states: they either work or fail.

  • Load share in centrifugal pumping 2-out-of-3 redundant system is detected by the use of technical measures.

  • Initially, all the system components operate (they are not failed).

  • After each repair, the system restarts and operates exactly the same as a newly installed and started system.

  • Component failure is repaired immediately after detection.

  • Failure rates and repair rate of the components are constant (component lifetime has exponential distribution).

  • Components are repaired individually (there is one repairman).

Using Markov chains, alpha-factor model and capacity flow model, a model can be developed to properly evaluate the MTBF of a 2-out-of-3 redundant repairable system. The main rule to evaluate MTBF is presented in the following equation. An MTBF evaluation requires system reliability as a function of time.

$${\text{MTBF}} = \int_{0}^{\infty } {R_{\text{T}} (t){\text{d}}t} + \int_{0}^{\infty } {t \times f(t){\text{d}}t}$$
(11)

Let P n (t) be the probability that n components fail at time t assuming n ∊ {0, 1, 2, 3} where t ≥ 0 and the process is a continuous-time homogeneous Markov chain in which the transition rates matrix is as follows.

$$W = \left[ {\begin{array}{*{20}c} { - (3Q_{1} + 3Q_{2} + Q_{3} )} & {3Q_{1} } & {3Q_{2} } & {Q_{3} } \\ \omega & { - (\omega + 2Q_{1}^{*} + 3Q_{2} + Q_{3} )} & {(2Q_{1}^{*} + 2Q_{2} )} & {(Q_{2} + Q_{3} )} \\ 0 & \omega & { - (\omega + Q_{2}^{*} + 2Q_{2} + Q_{3} )} & {(Q_{2}^{*} + 2Q_{2} + Q_{3} )} \\ 0 & 0 & \omega & { - \omega } \\ \end{array} } \right]$$
(12)

Considering the state transition matrix in Eq. (12), the Laplace transform techniques cannot be easily and effectively used to estimate the system reliability function. Therefore, a method is adopted to evaluate the MTBF of such systems (Wang et al. 2006; Sridharan 2006; Yen et al. 2013) and is formulated as:

$${\text{MTBF}} = E[T_{{P(0) \to P({\text{absorbing}})}} ] = P(0)( - W_{\text{absorbing}}^{ - 1} )\left[ {\begin{array}{*{20}c} 1 \\ 1 \\ \end{array} } \right]$$
(13)

In the above equation, the matrix, W t, which is the W transposed, is utilized for computing MTBF. Since the system is a 2-out-of-3, the rows and columns of matrix W t corresponding to the absorbing states, i.e., third and fourth column and the same rows, are removed and the new matrix is called W absorbing where

$$W_{\text{absorbing}} = \left[ {\begin{array}{*{20}c} { - (3Q_{1} + 3Q_{2} + Q_{3} )} & \omega \\ {3Q_{1} } & { - (\omega + 2Q_{1}^{*} + 3Q_{2} + Q_{3} } \\ \end{array} } \right]$$
(14)

The initial state vector is

$$P(0) = [P_{0} (0)P_{1} (0)] = [\begin{array}{*{20}c} 1 & 0 \\ \end{array} ]$$
(15)

Then, using Eq. (13) we have

$$\begin{aligned} {\text{MTBF}} & = f(Q_{1} ,Q_{2} ,Q_{3} ,\omega ) \\ & = \frac{{3Q_{1} }}{{9Q_{1} Q_{2} + 3Q_{1} Q_{3} + 6Q_{2} Q_{3} + 6Q_{1} Q_{1}^{*} + 6Q_{2} Q_{1}^{*} + 2Q_{3} Q_{1}^{*} + 3Q_{2} \omega + Q_{3} \omega + 9Q_{2}^{2} + Q_{3}^{2} }} \\ & \quad + \frac{{3Q_{2} + Q_{3} + 2Q_{1}^{*} + \omega }}{{3Q_{1} Q_{2} + 3Q_{1} Q_{3} + 6Q_{2} Q_{3} + 9Q_{1} Q_{1}^{*} + 6Q_{2} Q_{1}^{*} + 2Q_{3} Q_{1}^{*} + 3Q_{2} \omega + Q_{3} \omega + 9Q_{2}^{2} + Q_{3}^{2} }} \\ \end{aligned}$$
(16)

Since Q 1, Q 2, and Q 3 are triangular fuzzy numbers, the system MTBF equation is transformed to the following form:

$$\begin{aligned} {\text{M}}\tilde{T}{\text{BF}} & = f(\tilde{Q}_{1} ,\tilde{Q}_{2} ,\tilde{Q}_{3} ,\tilde{\omega }) \\ & = \frac{{3\tilde{Q}_{1} }}{{9\tilde{Q}_{1} \tilde{Q}_{2} + 3\tilde{Q}_{1} \tilde{Q}_{3} + 6\tilde{Q}_{2} \tilde{Q}_{3} + 6\tilde{Q}_{1} (1.5)^{\gamma } \tilde{Q}_{1} + 6\tilde{Q}_{2} (1.5)^{\gamma } \tilde{Q}_{1} + 2\tilde{Q}_{3} (1.5)^{\gamma } \tilde{Q}_{1} + 3\tilde{Q}_{2} \tilde{\omega } + \tilde{Q}_{3} \tilde{\omega } + 9\tilde{Q}_{2}^{2} + \tilde{Q}_{3}^{2} }} \\ & \quad + \frac{{3\tilde{Q}_{2} + \tilde{Q}_{3} + 2(1.5)^{\gamma } \tilde{Q}_{1} + \tilde{\omega }}}{{3\tilde{Q}_{1} \tilde{Q}_{2} + 3\tilde{Q}_{1} \tilde{Q}_{3} + 6\tilde{Q}_{2} \tilde{Q}_{3} + 9\tilde{Q}_{1} (1.5)^{\gamma } \tilde{Q}_{1} + 6\tilde{Q}_{2} (1.5)^{\gamma } \tilde{Q}_{1} + 2\tilde{Q}_{3} (1.5)^{\gamma } \tilde{Q}_{1} + 3\tilde{Q}_{2} \tilde{\omega } + \tilde{Q}_{3} \tilde{\omega } + 9\tilde{Q}_{2}^{2} + \tilde{Q}_{3}^{2} }} \\ \end{aligned}$$
(17)

By utilizing the above equation, MTBF can be expressed as a function based on fuzzy numbers. Therefore, according to Zadeh’s extension principle, the membership function for MTBF can be defined as follows:

$$\mu_{{f(\tilde{Q}_{1} ,\tilde{Q}_{2} ,\tilde{Q}_{3} ,\tilde{\omega })}} (z) = \sup \hbox{min} \left\{ {\mu_{{\tilde{Q}_{1} }} (Q_{1} ),\mu_{{\tilde{Q}_{2} }} (Q_{2} ),\mu_{{\tilde{Q}_{3} }} (Q_{3} ),\mu_{{\tilde{\omega }}} (\omega )|{\text{MTBF}} = f(Q_{1} ,Q_{2} ,Q_{3} ,\omega )} \right\}$$
(18)

Unfortunately, the membership function in the above equation cannot be presented in a usable form. In this paper, we adapted NLP modeling to deal with this problem. To apply this technique, according to the principle, the α-cuts as crisp intervals are utilized. These α-cuts can be written as follows:

$$\begin{aligned} \tilde{Q}_{1} (\alpha ) & = [X_{1\alpha }^{L} ,X_{1\alpha }^{U} ] = [\hbox{min} \{ Q_{1} |\mu_{{\tilde{Q}_{1} }} (Q_{1} ) \ge \alpha \} ,\hbox{max} \{ Q_{1} |\mu_{{\tilde{Q}_{1} }} (Q_{1} ) \ge \alpha \} ] \\ \tilde{Q}_{2} (\alpha ) & = [X_{2\alpha }^{L} ,X_{2\alpha }^{U} ] = [\hbox{min} \{ Q_{2} |\mu_{{\tilde{Q}_{2} }} (Q_{2} ) \ge \alpha \} ,\hbox{max} \{ Q_{2} |\mu_{{\tilde{Q}_{2} }} (Q_{2} ) \ge \alpha \} ] \\ \tilde{Q}_{3} (\alpha ) & = [X_{3\alpha }^{L} ,X_{3\alpha }^{U} ] = [\hbox{min} \{ Q_{3} |\mu_{{\tilde{Q}_{3} }} (Q_{3} ) \ge \alpha \} ,\hbox{max} \{ Q_{3} |\mu_{{\tilde{Q}_{3} }} (Q_{3} ) \ge \alpha \} ] \\ \tilde{\omega }(\alpha ) & = [X_{4\alpha }^{L} ,X_{4\alpha }^{U} ] = [{\text{m}}in\{ \omega |\mu_{{\tilde{\omega }}} (\omega ) \ge \alpha \} ,\hbox{max} \{ \omega |\mu_{{\tilde{\omega }}} (\omega ) \ge \alpha \} ] \\ \end{aligned}$$
(19)

To obtain the lower and upper bounds of the fuzzy numbers, NLP problems are constructed as follows:

$$\begin{aligned} {\text{M}}\tilde{T}{\text{BF}}_{\alpha }^{L} & = \hbox{min} f(Q_{1} ,Q_{2} ,Q_{3} ,\omega ) \\ & {\text{subject}}\;{\text{to}}\quad X_{1\alpha }^{L} \le Q_{1} \le X_{1\alpha }^{U} \\ X_{2\alpha }^{L} & \le Q_{2} \le X_{2\alpha }^{U} \\ X_{3\alpha }^{L} & \le Q_{3} \le X_{3\alpha }^{U} \\ X_{4\alpha }^{L} & \le \omega \le X_{4\alpha }^{U} \\ \end{aligned}$$
$$\begin{aligned} {\text{M}}\tilde{T}{\text{BF}}_{\alpha }^{U} & = \hbox{max} f(Q_{1} ,Q_{2} ,Q_{3} ,\omega ) \\ & {\text{subject}}\;{\text{to}}\quad X_{1\alpha }^{L} \le Q_{1} \le X_{1\alpha }^{U} \\ X_{2\alpha }^{L} & \le Q_{2} \le X_{2\alpha }^{U} \\ X_{3\alpha }^{L} & \le Q_{3} \le X_{3\alpha }^{U} \\ X_{4\alpha }^{L} & \le \omega \le X_{4\alpha }^{U} \\ \end{aligned}$$
(20)

By solving the above problems, given the α-cuts, the upper and lower boundaries for the MTBF membership function are determined for each α-cuts. Using the upper and lower boundaries for each α-cut, the membership function MTBF can be obtained. The highest membership function is one of the conventional methods used in most previous studies (Lee et al. 2001; Chen et al. 2013; D’Urso et al. 2017). In this paper, the highest membership value method is applied to defuzzify the fuzzy numbers through the following equation.

$$\mu_{{{\text{M}}\tilde{T}{\text{BF}}}} (z^{*} ) \ge \mu_{{{\text{M}}\tilde{T}{\text{BF}}}} (z)\quad \forall \quad z \in {\text{universe}}$$
(21)

Therefore, MTBF is determined by:

$${\text{MTBF}} = {\text{MTBF}}_{\alpha } \quad \alpha = 1$$
(22)

In addition, estimation of upper and lower boundaries of MTBF can provide useful insights for system designers and maintenance operators. The upper and lower bounds of MTBF are as follows:

$$\begin{aligned} {\text{MTBF}}_{{{\text{Upper}}\;{\text{boundary}}}} = {\text{MTBF}}_{\alpha }^{U} \quad \alpha = 0 \hfill \\ {\text{MTBF}}_{{{\text{Lower}}\;{\text{boundary}}}} = {\text{MTBF}}_{\alpha }^{L} \quad \alpha = 0 \hfill \\ \end{aligned}$$
(23)

Case study

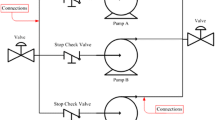
Centrifugal water pumps play an indispensable role in many industries, including nuclear industries (Kang et al. 2011), cooling towers (Alavi and Rahmati 2016), main water transfer routes (Mortazavi et al. 2016), etc. Centrifugal water pumps are utilized in the main water pipelines to compensate for water pressure drop. Failure of these pumps results in water outages/shortage in the water supply network which in turn may lead to significant losses. Specifically, drinking water outage has social, cultural, political and health consequences. Therefore, in recent years, the reliability of the water supply networks and equipment has been a point of attraction for both practitioners and researchers. In practice, it is common to use three pumps in parallel to prevent water outage in case of failure of a pump (Fig. 4). If two pumps out of the three pumps fail, there will be a water pressure drop or a water outage in the water supply network. In addition, because of the water pressure inside the pipes, the load is transferred to the intact pumps if one of the pumps fails (load share). The centrifugal water pumping is a redundant system that fails due to CCF as well as independent failure. CCCG in centrifugal pumping redundant system is presented in Fig. 5. One of the important features in the maintenance and inspection of systems is MTBF that presents an estimation of the time to failure of the system and provides the opportunity of starting the preventive maintenance. Furthermore, MTBF is tool in controlling the maintenance costs of the centrifugal water pumps.

Fig. 4
figure 4

The centrifugal pumping 2-out-of-3 redundant system

Full size image
Fig. 5
figure 5

CCCG for centrifugal pumping 2-out-of-3 redundant system

Full size image

Failure data regarding values of failure and repair rates are usually preferred to be expressed in linguistic terms which are easily and preferably expressed as triangular fuzzy numbers. Table 2 presents the failure and repair rates data of the centrifugal water pumping system and Fig. 6 presents the associated membership.

Table 2 Fuzzy failure and repair rates
Full size table
Fig. 6
figure 6

The membership function for failure rates and repair rate of centrifugal water pump system

Full size image

Figure 6 illustrates the membership function of failure rates and repair rate of centrifugal water pumps.

In this research, MATLAB® software is utilized to determine the α-cuts for independent failure rate, CCF rates, and repair rate. In the next step, fuzzy MTBF is calculated for the centrifugal pumping redundant system for 11 distinct values (See Table 3).

Table 3 MTBF values obtained by applying different α-cuts values
Full size table

It is concluded from Table 3 that for α = 1, the MTBF value of the centrifugal pumping redundant system is 41.99947 days. For possibility level α = 0, the MTBF range of the centrifugal redundant pumping system is approximately [MTBF L α=0  = 35.63052, MTBF U α=0  = 50.97627]. If Eq. (21) is used for defuzzification, MTBF equals 41.99947 days. All three values of MTBF L α=0 , \({\text{MTBF}}_{\alpha = 0}^{U}\), and MTBF α=1 can be beneficial for system designers and maintenance operators.

Comparison of results

As mentioned previously, neglecting dependent failures in MTBF evaluation of redundant systems leads to overrated results. Huang et al. (2008) posited that redundant systems fail due to independent failure and lethal shocks, each of which entails the failure of all redundant system components. In their studies, they only considered independent failure (Q 1) and common cause shock failure (Q 3). If MTBF for a 2-out-of-3 redundant system is evaluated following their approach, MTBF function is determined by the following equation.

$${\text{MTBF}} = \frac{{3Q_{1} }}{{6Q_{1}^{2} + 2Q_{1} Q_{3} + Q_{3} \omega }} + \frac{{2Q_{1} + \omega }}{{6Q_{1}^{2} + 2Q_{1} Q_{3} + Q_{3} \omega }}$$
(24)

Obviously, (Q 2) and (Q *1 ) rates are ignored in this function. In centrifugal water pumping systems, however, these two failure rates must be taken into consideration. In other words, it can be said that cascade failure and CCF both exist in these systems. If the redundant system consists of more than two components, in order to take CCF into consideration, models such as alpha-factor and MGL should be used (Beckman 1995).

In this research, failure rates and repair rate for the MTBF function are considered as triangular fuzzy numbers (Table 2); therefore, Eq. (24) is rewritten as Eq. (25). Using NLP, fuzzy MTBF values are computed for 11 distinct values. These values are presented in Table 4.

Table 4 MTBF values obtained by applying different α-cuts values ignoring Q *1 and Q 2
Full size table
$${\text{M}}{{\tilde{\rm T}}}{\text{BF}} = \frac{{3\tilde{Q}_{1} }}{{6\tilde{Q}_{1}^{2} + 2\tilde{Q}_{1} \tilde{Q}_{3} + \tilde{Q}_{3} \tilde{\omega }}} + \frac{{2\tilde{Q}_{1} + \tilde{\omega }}}{{6\tilde{Q}_{1}^{2} + 2\tilde{Q}_{1} \tilde{Q}_{3} + \tilde{Q}_{3} \tilde{\omega }}}$$
(25)

Figure 7 presents a column chart for lower and upper bounds as well as the center value for the fuzzy MTBF for both models. As illustrated, the lower bound of MTBF in the study by Huang et al. (2008) is higher than that of the model developed by the present study. This is because the former study only considered independent and common cause shock failures. A similar situation exists for upper bound of MTBF and center of MTBF values.

Fig. 7
figure 7

The comparison of MTBF for the two models

Full size image

Failure rate estimation is one of the most accurate (and most expensive) reliability analysis activities. An inaccurate estimation of failure rate leads to an inaccurate or incorrect evaluation of reliability, availability, MTTF, and MTBF of systems. In most cases, accelerated tests are utilized for accurate estimation of failure rates. It should be noted, however, that creating genuine conditions in these tests is considerably costly and sometimes not feasible. Therefore, it is more appropriate to consider failure rate values as intervals. Upper bound, lower bound, and central values for failure rates and repair rate can be expressed through triangular fuzzy numbers. As a result, MTTF and MTBF adopt upper bound, lower bound, and central values as well. More specifically, independent failure rate and dependent failure rates each can be expressed as triangular fuzzy numbers. The functioning condition of redundant systems causes them to undergo failure at different times. Therefore, it is possible to determine an interval for failure rate using previous failure data. In centrifugal water pumping redundant systems, fuzzy failure rates can also be collected by taking previous failure data into consideration. Repair rate can also be considered as triangular fuzzy numbers. In this case, the maintenance operator can determine an interval for the maintenance operation. Using the model presented in this paper, the MTBF of a redundant system with two types of dependent failures as well as fuzzy failure rates and fuzzy repair rate can be evaluated.

Discussion and conclusion

Most dependent failures reduce MTTF and MTBF in redundant systems. Therefore, the frequency of dependent failure events in redundant systems must be minimized and appropriate corrective actions must be taken. However, redundant systems undergo both independent failures and dependent failures. In this paper, using Markov chain and transposed matrix, the MTBF function for a 2-out-of-3 redundant system is developed by taking into consideration two types of dependent failures. First, the alpha-factor model and capacity flow model are briefly outlined. Since the failure rates are usually preferred to be expressed as linguistic terms, the failure and maintenance rates are expressed as triangular fuzzy numbers, and, the upper bound, lower bound, and central values for the fuzzy MTBF of a 2-out-of-3 redundant system are determined by applying Zadeh’s extension principle, concepts of α-cuts, and NLP. To validate the model, the results were compared with those obtained by the model developed by Huang et al. (2008). The comparison revealed that considering dependent failures in the MTBF function leads to the reduction of the MTBF of redundant systems. Obviously, by investigating and integrating dependent failures in MTBF evaluation models for redundant systems, more applicable and realistic MTBF models can be developed.

System failure in dynamic environment is another variety of dependent failures (XiaoFei and Min 2014). To evaluate the MTBF of redundant systems, it is assumed that the components operate in a static environment. Therefore, the models developed under such assumptions may not be appropriate for redundant systems operating in dynamic conditions. It is recommended that future studies develop a model to evaluate the MTBF of redundant system, incorporating CCF, cascade failure in dynamic environments. The dynamic model may also incorporate uncertainty of the real-world problems.