Introduction

As we know that at any retails or supermarket the occurrence of temporary stock-outs is a very common phenomenon in the categories of frequently purchased items and it is also very common to see at any retails or supermarket, customers who willing to purchase certain items will be willing to purchase the substitute items, if they faced the situation of the stock-outs. A survey report of Anupindi et al. (1998) also observed the same phenomenon, in which he found that 82–88% of buyer would be willing to buy the substitute items if the desired items are out of stock. The substitutable items in which sufficient deterioration can take place during the normal storage period of the units and consequently this loss must be taken into account when analyzing the inventory system of substitutable items, i.e. the effect of deterioration plays a vital role in the decision of ordering quantity of substitutable deteriorating items. When substitution will take place an additional cost is incurred, known as substitution cost. Such substitution costs may arise due to a variety of reasons: the cost of the reworking required on an item to make it substitutable for the other, loss of a customer’s goodwill due to substitution, etc. Deterioration of physical goods in stock is a very realistic feature and there is a big need to consider it in the inventory modelling of substitutable items. Tang and Yin (2007) categorizes the substitution as stock-out-based substitution, price-based substitution and assortment-based substitution. Recently, Kim and Bell (2011) categorizes the substitution as symmetrical substitution and asymmetrical substitution. As they define, the definition of these categories are: stock-out based substitution corresponds to a situation in which a customer may purchase another product as a substitute, when the preferred product is out of stock, price-based substitution corresponds to a situation in which a retailer uses different pricing to make certain products substitutable, assortment-based substitution occurs when products with similar attributes are substitutable while symmetrical substitution occurs when all of the unfulfilled demands of one items are completely fulfilled by the demands of the substitute items and asymmetrical substitution occur when partial fraction of unfulfilled demands are added to the demands of the substitutable item. Based on the categories defined as above, this paper lies in the category of asymmetrical stock-out-based substitution. In the recent years, little bit attention has been given in the research for the stock-out-based substitution within the EOQ setting under deterministic demand and to the best of our knowledge no one consider the concept of deterioration for the substitutable items with deterministic demand and joint replenishment. Recently, Salameh et al. (2014) developed the joint replenishment policy for substitution by considering the deterministic demand, closely related to this paper, but they have not considered the concept of deterioration which is more realistic to determine the accurate optimal ordering quantity in the current era of competitive business strategies. Large numbers of the literature are available in inventory modelling of substitutable and deteriorating item separately. Thus, in subsequent paragraph, first, we discuss about recent and previous advancement in the inventory modelling of deteriorating items then inventory modelling of substitutable items.

The journey of inventory modelling was started in second decade of nineteenth century when Harris (1915) developed the first inventory model and this model was generalized by Wilson (1934) by deriving the formula to obtain the economic order quantity (EOQ). The inventory of deteriorating items was first studied by Whitin (1957) in which he considered the fashion goods as deteriorating items. Further there are several researcher who gave different inventory model of deteriorating item under different realistic situations, the reader may refer the review paper on inventory of deteriorating items of Raafat (1991), Goyal and Giri (2003), Li et al. (2010) and Bakker et al. (2012) and Khanlarzade et al. (2014) for detailed review of the literature of inventory of deteriorating items. Recently, Taleizadeh (2014a, b) gave economic order quantity model for deteriorating and evaporating items with consecutive and advanced payment, respectively.

The first inventory model of substitutable item was studied by McGillivray and Silver (1978) by considering that all of the substitutable items have the same unit variable cost and shortage penalty. Parlar and Goyal (1984) developed the similar model for optimal ordering decisions for stochastic demands. Pasternack and Drezner (1991) numerically proved that if the products are not substitutable then the associated optimal order quantities can be larger or smaller. In this sequence, Drezner et al. (1995) developed an EOQ model with substitution for two substitutable products and compare the results with no substitution. Ernst and Kouvelis (1999) suggested an efficient numerical search algorithm for the optimal stocking levels for three partially substitutable products. Gurnani and Drezner (2000) extended the model of Drezner et al. (1995) for multiple products. Mishra and Raghunathan (2004) gave new explanation for why retailers might be interested in vendor-managed inventory and showed that vendor-managed inventory intensifies the competition between two manufacturers of competing brands. Under joint replenishment policy (JRP), Porras and Dekker (2008) provided a complete analysis and presented a new inventory model over JRP when a correction is made for the empty replenishment and Hong and Kim (2009) gave a genetic algorithm for JRP and devised an unbiased estimator to find out the exact cost. In continuation of this, Schulz and Telha (2011) theoretically showed that the JRP with constant demands may have no polynomial-time algorithm. Taleizadeh et al. (2015) gave Joint optimization of price, replenishment frequency, replenishment cycle and production rate in vendor-managed inventory system with deteriorating items. Recently, Krommyda et al. (2015), Salameh et al. (2014), Rasouli and NakhaiKamalabadi (2014), and Gerchack and Grosfeld (1999) developed inventory model for two substitutable item with deterministic demand, constant holding cost and fixed ordering cost but no one considered the effect of deterioration in inventory decision of substitutable items. Zhao et al. (2014) analyzed the pricing decision for two substitutable product with price-dependent probabilistic demand with fixed ordering cost and constant holding cost while Ye (2014), Huang and Ke (2014), Li et al. (2013), Li and You (2012), Hsieh (2011), and Xue and Song (2007) developed the inventory policy for multiple substitutable item with stochastic demand, fixed ordering cost and constant holding cost.

This paper makes the model of Krommyda et al. (2015), Salameh et al. (2014), and Rasouli and NakhaiKamalabadi (2014) more realistic and applicable by taking into account the effect of deterioration and cost of substitution on inventory of the substitutable items. Demand is considered as a constant function for both mutually substitutable items. If one of the items is out of stock then its demand will be fulfilled by the second item and if any demand is not met by substitutable item it will be completely lost. Both the products are order jointly and replenishment cycle is same for both the items.

The rest of the paper is organized as follows: In the next section, we describe the assumptions and notations used in the entire article, “Formulation and solution” Section gives the detail of mathematical formulation and solution procedure of the model, extensive numerical analysis and convexity shown graphically in “Numerical and sensitivity analysis” Section and article ends with summary and conclusions of the article.

Assumptions and notations

For the mathematical formulation of the inventory model, the following assumptions and notations are used.

Assumptions

  1. (a)

    The two items are ordered jointly in every ordering cycle.

  2. (b)

    The demand rates and deterioration rates are known and constant for both items.

  3. (c)

    The procurement lead time is zero and replenishment rates for both items are infinite.

  4. (d)

    When an item is completely depleted and it subsequently becomes out of stock and there is on-hand inventory of the second item available, then the second item while supplying its own demands substitutes the demands of the first item during stock-out period. This substitution need not be the full substitution. It can be limited to a fraction (known as the substitution rate) of the total demand of the first item during stock-out period. The remaining un-substituted demand of the first item is lost.

Notations

Notation is grouped into parameters of the model, intermediate variables, and derived functions.

Parameters

D 1, D 2

Demand rate of item 1 and item 2

θ

Deterioration rate

α 1, α 2

Substitution rate of item 1 by item 2

\(Q_{1}^{*} ,Q_{2}^{*}\)

Optimal ordering quantities of item 1 and item 2, respectively

A 1, A 2

Fixed ordering cost per order of item 1 and item 2

i

Rate of holding cost of item 1 and item 2

C 1, C 2

Item cost per unit of item 1 and item 2

C S12

Unit substitution cost for item 1 if substituted by item 2

C S21

Unit substitution cost for item 2 if substituted by item 1

π 1, π 2

Lost sale cost per unit of item 1 and item 2, respectively

Intermediate variables

p

Portion of time when substitution occur

z

Inventory level of item when other item is out of stock

t 1

Time when level of inventory of substituted item completely depleted

t 2

Time when level of inventory of substitute item completely depleted in case of no substitution

Derived functions

\(I_{1}^{1} (t)\)

Inventory level of item 1 when item 1 depletes before item 2 at time t, \(0 \le t \le t_{1}\)

\(I_{2}^{1} (t)\)

Inventory level of item 2 when item 1 depletes before item 2 at time t, \(0 \le t \le t_{1}\)

\(I_{3}^{1} (t)\)

Inventory level of item 2 when item 1 depletes before item 2 and substitution take place at time t, \(0 \le t \le t_{1} + p\)

\(I_{1}^{2} (t)\)

Inventory level of item 1 when item 2 depletes before item 1 at time t, \(0 \le t \le t_{2}\)

\(I_{2}^{2} (t)\)

Inventory level of item 2 when item 2 depletes before item 1at time t, \(0 \le t \le t_{2}\)

\(I_{3}^{2} (t)\)

Inventory level of item 1 when item 2 depletes before item 1 and substitution take place at time t, \(0 \le t \le t_{2} + p\)

TC11 (Q 1, Q 2)

Total cost with substitution in per ordering cycle of item 1

TC12 (Q 1, Q 2)

Total cost with substitution in per ordering cycle of item 2

TC (Q 1, Q 2)

Total cost with substitution in per ordering cycle of both item

TC1 (Q 1, Q 2)

Total cost per unit time with substitution in per ordering cycle of both item when item 1 deplete before item 2

TC2 (Q 1, Q 2)

Total cost per unit time with substitution in per ordering cycle of both item when item 1 deplete before item 2

TCWS (Q 1, Q 2)

Total cost per unit time without substitution

Formulation and solution

As stated before, we consider an inventory system for two mutually substitutable deteriorating items under the assumptions as mentioned in “Assumptions and notations” Section. At the beginning of the replenishment cycle, the retailer orders Q 1 and Q 2 units of item 1 and item 2, respectively, whose consumption rates are D 1 and D 2. The inventory level of both items gradually depletes due to deterioration and consumption rate. There are three possibilities cases,

Case 1

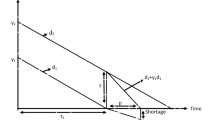
Item 1 depletes before item 2, i.e. if at time t 1 the inventory of item 1 is out of stock, as depicted in Fig. 1, then item 2 partially substitutes the item 1 with substitution rate α 1 and a portion of unmet demand for item 1 is assumed to be lost with the rate of (1 − α 1).

Fig. 1
figure 1

Graphical representation of first scenario of inventory model when t 1 < t 2

Full size image

Case 2

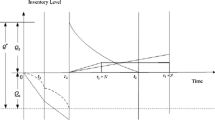
Item 2 depletes before item 1, i.e. if at time t 2 the inventory of item 2 is out of stock, as depicted in Fig. 2, then item 1 partially substitutes the item 2 with substitution rate α 2. A portion of unmet demand for item 2 is assumed to be lost with the rate of (1 − α 2).

Fig. 2
figure 2

Graphical representation of second scenario of inventory model when t 1 > t 2

Full size image

Case 3

The inventory level of both items becomes zero simultaneously and no substitution will take place, as depicted in Fig. 3.

Fig. 3
figure 3

Graphical representation of third scenario under joint replenishment

Full size image

Case 1 (Fig. 1 )

Item 1 is substituted by item 2 (t 1 < t 2).

As depicted in Fig. 1, the inventory level of both item is governed by the following differential equations

$$\begin{aligned} & \frac{{{\text{d}}I_{{_{1} }}^{1} \left( t \right)}}{{{\text{d}}t}} + \theta I_{{_{1} }}^{1} \left( t \right) = - D_{1} ;\quad 0 \le t \le t_{1} \\ & {\text{with}}\,{\text{boundary}}\,{\text{condition}}\,I_{1}^{1} (0) = Q_{1} \,{\text{and}}\,I_{1}^{1} (t) = 0. \\ \end{aligned}$$
(1)
$$\begin{aligned} & \frac{{{\text{d}}I_{{_{2} }}^{1} \left( t \right)}}{{{\text{d}}t}} + \theta I_{{_{2} }}^{1} \left( t \right) = - D_{2} ;\quad 0 \le t \le t_{1} \\ & {\text{with}}\,{\text{boundary}}\,{\text{condition}}\,I_{2}^{1} (0) = Q_{2} \,{\text{and}}\,I_{2}^{1} (t_{1} ) = I_{3}^{1} (t_{1} ). \\ \end{aligned}$$
(2)
$$\begin{aligned} & \frac{{{\text{d}}I_{{_{3} }}^{1} \left( t \right)}}{{{\text{d}}t}} + \theta I_{{_{3} }}^{1} \left( t \right) = - (D_{2} + \alpha_{1} D_{1} );\quad t_{1} \le t \le t_{1} + p \\ & {\text{with}}\,{\text{boundary}}\,{\text{condition}}\,I_{3}^{1} (t_{1} ) = I_{2}^{1} (t_{1} )\,{\text{and}}\,I_{3}^{1} (t_{1} + p) = 0. \\ \end{aligned}$$
(3)

The solutions of Eqs. (1)–(3) are

$$I_{{_{1} }}^{1} \left( t \right) = \frac{{D_{1} }}{\theta }\left( {{\text{e}}^{{\theta (t_{1} - t)}} - 1} \right);\quad 0 \le t \le t_{1}$$
(4)
$$I_{{_{2} }}^{1} \left( t \right) = \frac{{\left( {Q_{2} \theta + D_{2} } \right)}}{{\theta {\text{e}}^{\theta t} }} - \frac{{D_{2} }}{\theta };\quad 0 \le t \le t_{1}$$
(5)
$$I_{{_{3} }}^{1} \left( t \right) = \frac{{D_{2} + \alpha_{1} D_{1} }}{\theta }\left( {{\text{e}}^{{\theta (t_{1} + p - t)}} - 1} \right);\quad t_{1} \le t \le t_{1} + p$$
(6)

The cost components per cycle consist of (a) costs related to item 1 (b) costs related to item 2 (c) lost sale costs and (d) substitution costs.

  1. (a)

    The total cost associated with item 1 per ordering cycle consists of fixed ordering cost, purchase cost and holding cost, and can be expressed as

    $${\text{TC}}11(Q_{1} ,Q_{2} ) = \left( {A_{1} + C_{1} Q_{1} + \frac{{iC_{1} }}{{\theta^{2} }}\left( {\theta Q_{1} - D_{1} \ln \left( {\frac{{\theta Q_{1} + D_{1} }}{{D_{1} }}} \right)} \right)} \right).$$
    (7)
  2. (b)

    The total cost associated with item 2 per ordering cycle consists of fixed ordering cost, purchase cost and holding cost, and expressed as

    $${\text{TC}}12(Q_{1} ,Q_{2} ) = \left( {\begin{array}{*{20}l} {A_{2} + C_{2} Q_{2} + \frac{{iC_{2} }}{{\theta^{2} }}\left( {\theta Q_{2} - D_{2} \ln \left( {\frac{{\theta Q_{1} + D_{1} }}{{D_{1} }}} \right)} \right)} \hfill \\ { - \frac{{iC_{2} (D_{1} \alpha_{1} + D_{2} )}}{{\theta^{2} }}\ln \left( {\frac{{D_{1} (\alpha_{1} \theta Q_{1} + D_{1} \alpha_{1} + \theta Q_{2} + D_{2} )}}{{(D_{1} \alpha_{1} + D_{2} )(\theta Q_{1} + D_{1} )}}} \right)} \hfill \\ \end{array} } \right).$$
    (8)
  3. (c)

    The Lost sale cost is incurred due to demand for the item 1, which can be expressed as

    $${\text{Lost}}\,{\text{sale}}\,{\text{cost}} = \frac{{\pi_{1} D_{1} }}{\theta }\left( {(1 - \alpha_{1} )\ln \left( {\frac{{D_{1} (\alpha_{1} \theta Q_{1} + D_{1} \alpha_{1} + \theta Q_{2} + D_{2} )}}{{(D_{1} \alpha_{1} + D_{2} )(\theta Q_{1} + D_{1} )}}} \right)} \right).$$
    (9)
  4. (d)

    The substitution cost is incurred according to the number of units of item 1 substituted by item 2 at the rate of C S12 per unit substituted and can be expressed as

    $${\text{Substitution}}\,{\text{cost}} = \frac{{C_{S12} D_{1} \alpha_{1} }}{\theta }\left( {\ln \left( {\frac{{D_{1} (\alpha_{1} \theta Q_{1} + D_{1} \alpha_{1} + \theta Q_{2} + D_{2} )}}{{(D_{1} \alpha_{1} + D_{2} )(\theta Q_{1} + D_{1} )}}} \right)} \right).$$
    (10)

Thus, the total cost per ordering cycle TC (Q 1, Q 2), from Eqs. (7)–(10) is given as

$${\text{TC}}(Q_{1} ,Q_{2} ) = \left[ {\begin{array}{*{20}l} {A_{1} + A_{2} + C_{1} Q_{1} + C_{2} Q_{2} + \frac{{iC_{1} }}{{\theta^{2} }}\left( {\theta Q_{1} - D_{1} \ln \left( {\frac{{\theta Q_{1} + D_{1} }}{{D_{1} }}} \right)} \right)} \hfill \\ { + \frac{{iC_{2} }}{{\theta^{2} }}\left( {\theta Q_{2} - D_{2} \ln \left( {\frac{{\theta Q_{1} + D_{1} }}{{D_{1} }}} \right)} \right)} \hfill \\ { - \frac{{iC_{2} (D_{1} \alpha_{1} + D_{2} )}}{{\theta^{2} }}\ln \left( {\frac{{D_{1} (\alpha_{1} \theta Q_{1} + D_{1} \alpha_{1} + \theta Q_{2} + D_{2} )}}{{(D_{1} \alpha_{1} + D_{2} )(\theta Q_{1} + D_{1} )}}} \right)} \hfill \\ { + \frac{{\pi_{1} D_{1} }}{\theta }\left( {(1 - \alpha_{1} )\ln \left( {\frac{{D_{1} (\alpha_{1} \theta Q_{1} + D_{1} \alpha_{1} + \theta Q_{2} + D_{2} )}}{{(D_{1} \alpha_{1} + D_{2} )(\theta Q_{1} + D_{1} )}}} \right)} \right)} \hfill \\ { + \frac{{C_{S12} D_{1} \alpha_{1} }}{\theta }\left( {\ln \left( {\frac{{D_{1} (\alpha_{1} \theta Q_{1} + D_{1} \alpha_{1} + \theta Q_{2} + D_{2} )}}{{(D_{1} \alpha_{1} + D_{2} )(\theta Q_{1} + D_{1} )}}} \right)} \right)} \hfill \\ \end{array} } \right].$$
(11)

Finally, for case 1 (when t 1 < t 2), TC1 (Q 1, Q 2), the average total cost per unit time (say a year) is obtained by multiplying the total cost per ordering cycle by the average number of cycles per year \(\left( {{\theta \mathord{\left/ {\vphantom {\theta {\ln \left( {\frac{{\alpha_{1} \theta Q_{1} + D_{1} \alpha_{1} + \theta Q_{2} + D_{2} }}{{D_{1} \alpha_{1} + D_{2} }}} \right)}}} \right. \kern-0pt} {\ln \left( {\frac{{\alpha_{1} \theta Q_{1} + D_{1} \alpha_{1} + \theta Q_{2} + D_{2} }}{{D_{1} \alpha_{1} + D_{2} }}} \right)}}} \right)\) and is given as

$${\text{TC}}1(Q_{1} ,Q_{2} ) = \frac{\theta }{{\ln \left( {\frac{{\alpha_{1} \theta Q_{1} + D_{1} \alpha_{1} + \theta Q_{2} + D_{2} }}{{D_{1} \alpha_{1} + D_{2} }}} \right)}}\left( {\begin{array}{*{20}l} {A_{1} + A_{2} + C_{1} Q_{1} + C_{2} Q_{2} + \frac{{iC_{1} }}{{\theta^{2} }}\left( {\theta Q_{1} - D_{1} \ln \left( {\frac{{\theta Q_{1} + D_{1} }}{{D_{1} }}} \right)} \right)} \hfill \\ { + \frac{{iC_{2} }}{{\theta^{2} }}\left( {\theta Q_{2} - D_{2} \ln \left( {\frac{{\theta Q_{1} + D_{1} }}{{D_{1} }}} \right)} \right)} \hfill \\ { - \frac{{iC_{2} (D_{1} \alpha_{1} + D_{2} )}}{{\theta^{2} }}\ln \left( {\frac{{D_{1} (\alpha_{1} \theta Q_{1} + D_{1} \alpha_{1} + \theta Q_{2} + D_{2} )}}{{(D_{1} \alpha_{1} + D_{2} )(\theta Q_{1} + D_{1} )}}} \right)} \hfill \\ { + \frac{{\pi_{1} D_{1} }}{\theta }\left( {(1 - \alpha_{1} )\ln \left( {\frac{{D_{1} (\alpha_{1} \theta Q_{1} + D_{1} \alpha_{1} + \theta Q_{2} + D_{2} )}}{{(D_{1} \alpha_{1} + D_{2} )(\theta Q_{1} + D_{1} )}}} \right)} \right)} \hfill \\ { + \frac{{C_{S12} D_{1} \alpha_{1} }}{\theta }\left( {\ln \left( {\frac{{D_{1} (\alpha_{1} \theta Q_{1} + D_{1} \alpha_{1} + \theta Q_{2} + D_{2} )}}{{(D_{1} \alpha_{1} + D_{2} )(\theta Q_{1} + D_{1} )}}} \right)} \right)} \hfill \\ \end{array} } \right)$$
(12)

Case 2 (Fig. 2 )

Item 2 is substituted by item 1 (t 2 < t 1).

Following an approach analogous to case 1, for case 2 (when t 1 > t 2), TC2 (Q 1, Q 2), the average total cost per unit time (say a year) is

$${\text{TC}}2(Q_{1} ,Q_{2} ) = \frac{\theta }{{\ln \left( {\frac{{\alpha_{2} \theta Q_{2} + D_{2} \alpha_{2} + \theta Q_{1} + D_{1} }}{{D_{2} \alpha_{2} + D_{1} }}} \right)}}\left( {\begin{array}{*{20}l} {A_{1} + A_{2} + C_{1} Q_{1} + C_{2} Q_{2} + \frac{{iC_{2} }}{{\theta^{2} }}\left( {\theta Q_{2} - D_{2} \ln \left( {\frac{{\theta Q_{2} + D_{2} }}{{D_{2} }}} \right)} \right)} \hfill \\ { + \frac{{iC_{1} }}{{\theta^{2} }}\left( {\theta Q_{1} - D_{1} \ln \left( {\frac{{\theta Q_{2} + D_{2} }}{{D_{2} }}} \right)} \right)} \hfill \\ { - \frac{{iC_{1} (D_{2} \alpha_{2} + D_{1} )}}{{\theta^{2} }}\ln \left( {\frac{{D_{2} (\alpha_{2} \theta Q_{2} + D_{2} \alpha_{2} + \theta Q_{1} + D_{1} )}}{{(D_{2} \alpha_{2} + D_{1} )(\theta Q_{2} + D_{2} )}}} \right)} \hfill \\ { + \frac{{\pi_{2} D_{2} }}{\theta }\left( {(1 - \alpha_{2} )\ln \left( {\frac{{D_{2} (\alpha_{2} \theta Q_{2} + D_{2} \alpha_{2} + \theta Q_{1} + D_{1} )}}{{(D_{2} \alpha_{2} + D_{1} )(\theta Q_{2} + D_{2} )}}} \right)} \right)} \hfill \\ { + \frac{{C_{S21} D_{2} \alpha_{2} }}{\theta }\left( {\ln \left( {\frac{{D_{2} (\alpha_{2} \theta Q_{2} + D_{2} \alpha_{2} + \theta Q_{1} + D_{1} )}}{{(D_{2} \alpha_{2} + D_{1} )(\theta Q_{2} + D_{2} )}}} \right)} \right)} \hfill \\ \end{array} } \right)$$
(13)

Case 3 (Fig. 3 )

No Substitution.

Figure 3 illustrates the inventory levels for the case of no substitution. Under a joint replenishment policy, the inventories of both items deplete to zero simultaneously, i.e. Q 1/D 1 = Q 2/D 2. The average total cost per unit time for an inventory system without substitution under joint replenishment, TCWS (Q 1, Q 2), consists only of setup costs, purchase costs and holding costs and is given as

$${\text{TC}}_{\text{WS}} (Q_{1} ,Q_{2} ) = \frac{\theta }{{\ln \left( {\frac{{\theta Q_{1} + D_{1} }}{{D_{1} }}} \right)}}\left( {\begin{array}{*{20}l} {A_{1} + A_{2} + C_{1} Q_{1} + C_{2} Q_{2} + \frac{{iC_{1} }}{{\theta^{2} }}\left( {\theta Q_{1} - D_{1} \ln \left( {\frac{{\theta Q_{1} + D_{1} }}{{D_{1} }}} \right)} \right)} \hfill \\ { + \frac{{iC_{2} }}{{\theta^{2} }}\left( {\theta Q_{2} - D_{2} \ln \left( {\frac{{\theta Q_{1} + D_{1} }}{{D_{1} }}} \right)} \right)} \hfill \\ \end{array} } \right).$$
(14)

Solution procedure

To determine the optimal ordering quantities from total cost function. In the next section we will graphically show that the total cost function is a strictly convex function and using this property of total cost function, next we provide an algorithm to obtain the optimal ordering quantities.

Algorithm to obtain the optimal ordering quantities.

  • Step 1 Initialize all the parameters of the model.

  • Step 2 Solve the constraint optimization problem

    $$\begin{array}{*{20}c} {P_{1} :(Q_{1} ,Q_{2} )\,{\text{that}}\mathop {\hbox{min} }\limits_{{Q_{1} ,Q_{2} }} {\text{TC}}1(Q_{1} ,Q_{2} )\,{\text{subject}}\,{\text{to}}\,\frac{{Q_{1} }}{{D_{1} }} \le \frac{{Q_{2} }}{{D_{2} }}} \\ {\text{and}} \\ {P_{2} :(Q_{1} ,Q_{2} )\,{\text{that}}\mathop {\hbox{min} }\limits_{{Q_{1} ,Q_{2} }} {\text{TC}}2(Q_{1} ,Q_{2} )\,{\text{subject}}\,{\text{to}}\,\frac{{Q_{1} }}{{D_{1} }} \ge \frac{{Q_{2} }}{{D_{2} }}} \\ \end{array}$$

  • Step 3 Obtain the optimum solution by \((Q_{1}^{*} ,Q_{2}^{*} )\) = Min \((P_{1} ,P_{2} )\).

  • Step 4 Stop.

Numerical and sensitivity analysis

In this section, we provide a numerical example to illustrate the proposed model using Maple mathematical modelling package. In Numerical analysis, we use the parameter as defined in Table 1 unless otherwise mentioned.

Table 1 Initial parameters used for numerical analysis
Full size table

According the algorithm as defined above, we solve the constraint optimization problem as defined in step-2 by maple mathematical software. The outputs of step-2 are P 1: Q 1 = 116.08, Q 2 = 91.34, \({\text{TC}}1(Q_{1} ,Q_{2} )\) = 2000.79 and P2: Q 1 = 199.45, Q 2 = 19.34, \({\text{TC}}2(Q_{1} ,Q_{2} )\) = 2069.98. When comparing the total cost of both constraint optimization problems in step-3 of the algorithm then first optimization problems (P 1) lead to the optimal solution. Thus, the optimal ordering quantities in this case is \((Q_{1}^{*} ,Q_{2}^{*} )\) = (116.8, 91.34) and the optimal total cost is 2000.79. The optimal total cost of inventory model with no substitution under same assumptions using Eq. (14) with traditional calculus method the outputs are Q 1 = 178.70, Q 2 = 44.67, \({\text{TC}}2(Q_{1} ,Q_{2} )\) = 2096.98. Comparing the output (optimal total cost) of both inventory model then difference in optimal total cost and percentage improvement are 96.19 and 4.59, respectively.

To examine the nature of average total cost function, we plot the total cost function with varying order quantity of item 1 and item 2. The results are shown in Figs. 4, 5 and 6. As Figs. 4, 5 and 6 show that the average total cost function is strictly convex function. Thus, average total cost function (Eq. 12) always leads to the unique optimal solution.

Fig. 4
figure 4

Total cost (TC1) versus Q 1 at fixed Q 2

Full size image
Fig. 5
figure 5

Total cost (TC1) versus Q 2 at fixed Q 1

Full size image
Fig. 6
figure 6

Total cost (TC1) versus ordering quantity of item 1 and item 2

Full size image

Next, we carry out a sensitivity analysis of the optimal total cost and optimal ordering quantities according to given values of different parameter of the model. The percentage improvements in the optimal total cost according to the values of various parameters are also presented. The numerical results are given in Table 2.

Table 2 Sensitivity analysis optimal total cost and optimal ordering quantities
Full size table

Now, we investigate the decrease in total cost when substitution is possible and compared to the case without substitution with respect to various parameters of the system. The results are shown in Figs. 7, 8 and 9.

Fig. 7
figure 7

% improvement in TC over TCWS with ratios of item cost (C 1/C 2) and rate of holding Cost (i)

Full size image
Fig. 8
figure 8

% improvement in TC over TCWS with variation in shortage cost (π 1) and setup cost (A 1 = A 2)

Full size image
Fig. 9
figure 9

% improvement in TC over TCWS with cost of substitution (C S12) and substitution rate (α 1)

Full size image

While the extent and relative rate may vary, general nature of the percentage improvement in TC1 over TCWS follows the intuitive reasoning. The findings are presented in Table 3.

Table 3 Improvement in total optimal cost with substitution over total cost without substitution
Full size table

As we know that the main objective of an organization, dealing the inventory control, is to provide the right products to the right place, at the optimal price and time, and in the good quality with optimal quantity. With the help of this inventory model, which provides a detailed analysis of substitutable deteriorating items with numerical examples, manager can increase the firm’s capability and their performance to deal the inventory of their organizations.

Summary and conclusions

In this paper, we presented an inventory model for two substitutable deteriorating items under joint replenishment in each replenishment cycle. If at any moment of time, the inventory level of one item is out of stock then second item will partially substitute the first item and vice versa. A portion of unmet demand for both items is assumed to be lost and each substituted item incurs a cost of substitution. For the situation as mentioned above, we mathematically formulated an inventory model and developed a solution procedure to obtain the optimal ordering quantities.

The numerical analysis showed that as rate of holding cost, setup cost and deterioration rate increases, the percentage improvement in optimal total cost with substitution over without substitution also increases and if we increase the shortage cost or cost of substitution, the percentage improvement decreases in total optimal cost with substitution over without substitution while percentage improvement becomes constant when substitution rate of item 1 becomes equal or more from substitution rate of item 2.

In addition, as this paper only considered two deteriorated items, joint replenishment and same replenishment cycle, while future researches can focus on more than two items, different replenishment cycle for different items, multiple supplier and retailers, trade credit mechanism, supplier retailer cooperation, etc.