Introduction and literature review

Inventory models are really important to control demand and supply in many sectors such as business, industry, agriculture and trade. These models are very useful for the managers to minimize the total inventory cost, the response time to the requirements of their customers and maximize the sales. There are some particular situations that should be assumed to model the inventory system to determine demand and supply perfectly. One of these situations is that the customers are separated into two groups; the first one is the customers that do not change the vendor that they choose to fulfill their demand though they know that they should wait more than the regular time for their order. On the other hand the, second one is the customers that are not patient enough to wait to fulfill their demand; these customers prefer to receive their orders from the other vendors because they do not want to wait for the previous vendor or their demand is critical so their demand should be fulfilled soon. Because of the second group of customers a particular proportion of backordered items become lost sales so we have partial backordering instead of full backordering. Another assumption is a process of inspection because of the presence of some defective items in each order that a firm or enterprise receives. According to the inspection process that is provided in this paper we have three different situations regarding the number of defective items in the chosen sample that are explained in detail in the next section. In this section we provide a summary of the papers that are about the mentioned situations, partial backordering and inspection process. The basic inventory model was provided by Harris (1913). This model is called economic order quantity (EOQ) model that its aim is to minimize the total cost that includes holding cost and ordering cost. According to this model optimum order quantity is obtained according to the situation that the total cost is minimized. In this model it is assumed that all the items that are received as an order are perfect but we know in reality this situation is not possible, so in the next articles provided by other researcher presence of defective items in each order is considered. Salameh and Jaber (2000) are the first researchers that considered mentioned assumption and provided the inventory model according to it. They assumed that average percent (p) of all items that are in an order are defective. Also they assumed that the buyer inspects all the items to separate the defective items and the perfect items from each other; the buyer sells the defective items as a single batch at the end of the inspection time. After this article some researchers worked on the mentioned situation because of its simplicity and practical value, for instance, Goyal and Cárdenas-Barrón (2002) corrected the model provided by Salameh and Jaber (2000), Papachristos and Konstantaras (2006) extended mentioned model by considering shortage in the model and provided the new formulation for the inventory system, after them the model was revisited by Maddah and Jaber (2008); in addition to the mentioned works, there are many other articles that are provided by paying attention to the article that was provided by Salameh and Jaber (2000). Some researchers, for instance, Chang and Ho (2010), Eroglu and Ozdemir (2007), Hsu and Hsu (2013a, b), Rezaei (2005), Wee et al. (2007), considered shortage and backordered items in the model and extended the model according to these assumptions to make their model closer to the real world. In the original model (Salameh and Jaber 2000) it is assumed that the defective items are separated from the perfect items and sold with the lower price in comparison to the price for the perfect items in a different inventory condition, but there are some researchers such as Hayek and Salameh (2001), Konstantaras et al. (2007), Shekarian et al. (2014) that created another situation for defective items, they considered that the defective items are reworked and sold as perfect items with the same price as the perfect ones. Some researchers assumed that inspection is done for all items with constant rate and cost of inspection; however, some other researchers considered other possibilities, for example, Konstantaras et al. (2012), Wahab and Jaber (2010) worked on the learning impacts on inspection. Rezaei and Salimi (2012) provided an article and showed that in some particular situations it is better for the inventory system that supplier does the inspection and instead of it the buyer pays more price for the products. In reality, there are some errors that have occurred in the process of the inspection, some researchers such as Hsu and Hsu (2013a, b), Khan et al. (2011, 2014) considered this situation in their articles. Skouri et al. (2014) modeled the inventory system in the situations with full inspection, if there is no defective items in a received order it is acceptable but if there is even a defective item in a received order it is rejected and a new order will be received. Other situation that is not assumed in EOQ and EPQ model is that customers are differentiated in two groups, first group is the ones that their needs are not very important to be fulfilled. In this situation when the supplier does not provide these customers’ order by the lead time they could wait to receive their order. On the other hand, the second group of customers is not patient to receive their orders; or their needs are critical and it should be fulfilled by the lead time. This group of customers does not wait for the supplier to receive their order and choose another supplier. In this situation a fraction of backordered demand becomes lost items because of the second group of customers. Fabrycky and Banks (1967) provided the primary model associated to this assumption on the primary EOQ model. Montgomery et al. (1973) were the first researchers that developed the model for primary EOQ model with the situation that backordering is partial, also a solving approach is provided for this model. Mak (1987) provided a paper in which certain optimal policies for inventory system are provided while the quantity of backordered is not certain. There are some papers that their researchers considered that backordering proportion is based on the replenish time. For instance, Abad (1996, 2000, 2001, 2003, 2008) considered that in real world, more buyers wait to receive their order if the waiting time is short and provided five papers by considering this assumption. San Jose et al. (San José et al. 2007), Papachristos and Skouri (2000) provided their papers regarding partial backordering based on the replenish time. Besides some researchers provided their article according to the consideration that fraction of backlogging is based on the backlog size. For instance Padmanabhan and Vrat (1990, 1995), Ouyang et al. (2003), Chu and Chung (2004), Dye et al. (2006) assumed that the backordering probability has a negative relation with existed backlog size when a demand is received and provided their paper according to this assumption. Pentico and Drake (2009) provided an article that has a different approach for modeling the deterministic EOQ in the condition with partial backordered items which leads to the presence of some equations which are more like the ones associated with the primary EOQ model and its backordering development. Sarkar and Sarkar (2013) has provided a developed inventory model with partial backlogging, variation of deterioration time, also he considered demand as a dependent parameter on stock. Taleizadeh (2014) has improved an efficient order quantity model regarding evaporating item and its related payments and partial backordering. The articles that we mentioned in this section are summarized in Table 1. Also other related works published recently are by Dobson et al. (2017), Muriana (2016), Salehi et al. (2016), Taleizadeh et al. (2010a, b, c, 2011, 2012, Taleizadeh et al. 2013, Taleizadeh and Pentico 2013, Taleizadeh 2014b, Taleizadeh et al. 2015a, b, 2016). It should be noted that there are no articles that have considered both of the mentioned assumptions, partial backordering, presence of defective items and inspection. In reality, to access the precise process for inventory system and being successful, it is necessary to consider these assumptions because nowadays competition between the enterprises has been very intense and without such precise inventory model that includes many aspects of inventory system it is not possible for the companies to become successful. So in this paper to help the managers we provide the inventory model by considering the mentioned assumptions to make the model more similar to the real world and the answers that are obtained from the provided model are more reliable to cope with the fluctuations of the price, amount, etc.

Table 1 Summary of the inventory articles that are works on defective items and partial backordering
Full size table

Problem definition

There are some assumptions that should be considered to model the inventory system to access more efficient and usable results. One of these assumptions is inspection. There are some defective items in each order that a firm or enterprise receives, these items should be recognized and managers should choose the particular decision according to their inspection strategy. In this paper we consider an inspection approach that is explained in the following. In this approach we consider three levels for the number of defective items in each sample that is chose from each order randomly.

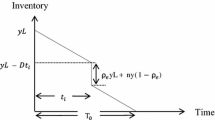
According to the number of defective items that are in an order we will decide what to do with the received order. According to the mentioned explanation we define three levels for the number of defective items in each sample, if this number is less than α 1 it is not necessary to inspect all the items, else if this number is between α 1 and α 2 all the items should be inspected and if this number is more than α 2 the order is rejected and another order without any defective items is received. We define these three levels because they can make the situation clearer for the managers. For example, the managers know if the number of defective items in a random sample chosen from each lot is lower than the particular number, it is beneficial that they ignore the inspection process and subsequently the inspection cost is eliminated. On the other hand, if the number of defective items in a sample would be between two particular numbers, it is beneficial that the inspection process is considered though it leads to inspection cost. Finally if the number of defective items in a sample becomes greater than the particular number, it is beneficial to return the lot to the supplier, because many defective items may exist in each lot (according to the chosen sample). Therefore, may affect their prestige if these lots are delivered to their customers. The rate of imperfect items in each order is p and regarding the number of defective items it has three levels, lower than p 1, between p 1 and p 2 and more than p 2. Another assumption is related to the customers. There are two types of customers. The first one is the customers that do not change the vendor that they have chosen before to fulfill their demand though they know that they should sometimes wait more than the regular time for their order. On the other hand, the second one is the customers that are not patient enough to wait to fulfill their demand; these customers prefer to receive their orders by the other vendors because they do not want to wait for the previous vendor or their demand is critical so their demand should be fulfilled soon. Because of the second ones a particular proportion of backordered items become lost sales so we have partial backordering instead of full backordering. We explain these assumptions in Fig. 1.

Fig. 1
figure 1

Process of the system

Full size image

In the following, we define notations that are used in the associated model.

Parameters:

D :

Demand in a year

\(c_{0}\) :

Ordering cost

\(c_{h}\) :

Holding cost per unit per year

\(c_{p}\) :

Unit purchasing cost

s :

Unit selling price

\(c_{b}\) :

The cost related to a unit of backordered items in a year

\(c_{g}\) :

Goodwill cost related to a unit of lost items

x :

Inspection rate during a unit of time

p :

Defective rate

d :

Cost of inspecting a unit per unit of time

θ :

Number of defective products in a sample of n items

n :

Size of the sample

r :

Cost for returning a defective item

R :

The cost that is paid because of the wrong rejection by the vendor

γ :

Fraction of backordered shortage

Independent decision variables

T :

Ordering cycle duration

φ :

The fraction of demand that is fulfilled from stock

Dependent decision variable

TP:

Total profit per cycle

ETP:

Expectation of total profit per cycle

E(.):

Mathematical expectation

f (p):

Function of probability density of defective rate

E[p]:

Expectation of defective rate

According to the mentioned explanations we have three situations regarding the number of defective items in each order. In the first situation, the number of defective items that are in the sample chosen from the lot is more than the upper line which is α 2, so the buyer rejects the lot and receives another order without any defective items. In this situation it is beneficial for the managers to return the lot to the supplier, because they conclude there are many defective items in each lot and it affects their prestige badly if these lots are delivered to their customer. In the second situation, the number of defective items is between α 1 and α 2 so the buyer inspects all the items because the mangers know that if the number of defective items in a sample becomes between two particular numbers it is beneficial that the inspection process is considered though it leads to inspection cost. The defective items are separated from the perfect items. Then perfect items are sold at the particular price within the cycle and the defective items are sold after the inspection time at the lower price than the perfect items. In the third situation the number of defective items that are in the sample is lower than the lower line, α 1, so the buyer does not intend to the inspection process and prefer to return the lot to the supplier. All the items are sold with the particular price that is determined for the perfect items. After selling the items customers can return the defective items and get the particular amount of money instead of it. Each of these situations has a particular probability that affects the formulation of the total revenue function. In the following, we explain these situations precisely.

The first situation: \(\theta > \alpha_{2}\)

The first case is the one that the number of imperfect products in a chosen sample is more than the upper limit that is α 2 and determined by the buyer and the supplier. In this situation all the items are rejected and new order is received that has not any imperfect items. The revenue of this case in a cycle is computed as following. \(sD\left[ {\varphi + \gamma (1 - \varphi )} \right]\): the amount of money that is received by selling products per unit of time, \(\frac{nd}{T}\): the cost of inspection of a sample per unit of time, \(\frac{{c_{0} }}{T}\): the ordering cost per unit of time, \(c_{p} D\left[ {\varphi + \gamma (1 - \varphi )} \right]\): cost of buying products per unit of time, \(\frac{{c_{h} DT\varphi^{2} }}{2}\): holding cost per unit of time, \(c_{g} D(1 - \gamma )(1 - \varphi )\): shortage cost that is related to lost sales per unit of time, \(\frac{{\gamma c_{b} DT(1 - \varphi )^{2} }}{2}\): shortage cost that is related to backorders per unit of time. Also there is a situation that buyers reject the lot wrongly, in other words the buyer rejects the lot while the number of defective items is less than α2, so the particular amount of money is considered for this situation that the buyer should pay to the supplier. The probability of this situation is computed as: \(\psi = pr(p \le p_{2} \left| {\theta \ge \alpha_{2} )} \right.\) and the penalty that the buyer should pay per cycle is computed as: \(\frac{\psi R}{T}\). So the total revenue per unit of time is obtained from the formulations above:

$$TP_{1} = sD\left[ {\varphi + \gamma (1 - \varphi )} \right] - \left[ {\frac{{c_{0} }}{T} + c_{p} D\left[ {\varphi + \gamma (1 - \varphi )} \right] + \frac{{c_{h} DT\varphi^{2} }}{2} + \frac{nd}{T} + c_{g} D(1 - \gamma )(1 - \varphi ) + \frac{{\gamma c_{b} DT(1 - \varphi )^{2} }}{2} + \frac{\psi R}{T}} \right]$$
(1)

The second situation: \(\alpha_{1} \le \theta \le \alpha_{2}\)

The second case is the one that the number of imperfect products in a chosen sample is between the lower limit and upper limit (\(\alpha_{1}\) and \(\alpha_{2}\)); in this situation all the items should be inspected to separate the defective items from the perfect items. Then he sells the perfect items with the particular price within the cycle and sells the defective items after the inspection time with the lower price than the perfect items. The revenue of this case is computed as the following. \(sD(1 - p)\left[ {\varphi + \gamma (1 - \varphi )} \right]\): the amount of money that is received per unit of time by selling the perfect units that are (1-p) percentage of all the units that are purchased, \(vpD\varphi\): the amount of money that is received per unit of time by selling the imperfect items that are p percentage of all the units that are purchased, \(\frac{{c_{0} }}{T}\): the ordering cost per unit of time, \(c_{p} D\left[ {\varphi + \gamma (1 - \varphi )} \right]\): cost of buying products per unit of time, \(dD\varphi\): cost of screening all units per unit of time(cost of inspection of the sample is computed in this part of total cost), \(\frac{{c_{h} D(1 - p)^{2} T\varphi^{2} }}{2}\): holding cost of the perfect units per unit of time, \(\frac{{c_{h} pD^{2} T\varphi^{2} }}{x}\): holding cost of the imperfect units in per unit of time, \(c_{g} D(1 - \gamma )(1 - \varphi )\): shortage cost that is related to lost sales per unit of time, \(\frac{{\gamma c_{b} DT(1 - \varphi )^{2} }}{2}\): shortage cost that is related to backorders per unit of time. So the total revenue per unit of time is obtained from the formulation below:

$$\begin{aligned} TP_{2} &= sD(1 - p)\left[ {\varphi + \gamma (1 - \varphi )} \right] + vpD\varphi \hfill \\ &\quad - \left[ {\frac{{c_{0} }}{T} + c_{p} D\left[ {\varphi + \gamma (1 - \varphi )} \right] + dD\varphi + \frac{{c_{h} D(1 - p)^{2} T\varphi^{2} }}{2} + \frac{{c_{h} pD^{2} T\varphi^{2} }}{x} + c_{g} D(1 - \gamma )(1 - \varphi ) + \frac{{\gamma c_{b} DT(1 - \varphi )^{2} }}{2}} \right] \hfill \\ \end{aligned}$$
(2)

The third situation: \(\theta \le \alpha_{1}\)

Finally, the third situation is the one that the number of imperfect products in a chosen sample is lower than the lower limit (\(\alpha_{1}\)) that is expected. In this situation none of the items is inspected and all the products are given to the customers as their orders with the price that is considered for the perfect products. Customers can receive the particular amount of money instead of the defective items that they return to the vendor. The revenue of this situation is computed as the following. \(sD\left[ {\varphi + \gamma (1 - \varphi )} \right]\): the amount of money that is received per unit of time by selling the perfect units that are (1 − p) percentage of all the units that are purchased, \(\frac{{c_{0} }}{T}\): the ordering cost per unit of time, \(c_{p} D\left[ {\varphi + \gamma (1 - \varphi )} \right]\): cost of buying products per unit of time, \(\frac{{c_{h} D(1 - p)^{2} T\varphi^{2} }}{2}\): holding cost of the perfect units per unit of time, \(\frac{nd}{T}\): the cost of inspection of a sample per unit per time, \(\frac{{c_{h} pD^{2} T\varphi^{2} }}{x}\): holding cost of the imperfect units per unit of time, \(c_{g} D(1 - \gamma )(1 - \varphi )\): shortage cost that is related to lost sales per unit of time, \(\frac{{\gamma c_{b} DT(1 - \varphi )^{2} }}{2}\): shortage cost that is related to backorders per unit of time, the total number of returned item is computed as (p + p 2 + p 3 + ···) and we know that \(\mathop {\lim }\limits_{m \to \infty } \left( {p + p^{2} + p^{3} + \cdots + p^{m} } \right) = \frac{p}{1 - p}\) so we have \(rD\varphi \frac{p}{1 - p}\) as a return cost of imperfect units per unit of time that the customers return them to a vendor. So the total revenue per unit of time is obtained from the formulation above:

$$\begin{aligned} TP_{3} &= sD(1 - p)\left[ {\varphi + \gamma (1 - \varphi )} \right] + vpD\varphi \hfill \\ & \quad - \left[ {\frac{{c_{0} }}{T} + c_{p} D\left[ {\varphi + \gamma (1 - \varphi )} \right] + \frac{nd}{T} + \frac{{c_{h} D(1 - p)^{2} T\varphi^{2} }}{2} + \frac{{c_{h} pD^{2} T\varphi^{2} }}{x} + rD\varphi \frac{p}{1 - p} + c_{g} D(1 - \gamma )(1 - \varphi ) + \frac{{\gamma c_{b} DT(1 - \varphi )^{2} }}{2}} \right] \hfill \\ \end{aligned}$$
(3)

In all these cases we consider two types of cost of shortage that has been explained before. In the following section, we provide the solution method according to the solution that has been provided by Pentico and Drake (2009).

Solution method

In this section we first derive the expected value of total profit for each case. The total profit function terms for the first case is the revenue received by selling products per unit of time, the cost of inspection of a sample per unit of time, the ordering cost per unit of time, cost of buying products per unit of time, holding cost per unit of time, lost sale and backorders costs per unit of time. For the second case these terms are the amount of money received per unit of time by selling the imperfect items that are p percentage of all units purchased, the ordering cost per unit of time, cost of buying products per unit of time, cost of screening all units per unit of time (cost of inspection of the sample is computed in this part of total cost), holding cost of the perfect units per unit of time, holding cost of the imperfect units per unit of time and backordered cost per unit of time. Finally, for the third case the related terms are the amount of money received per unit of time by selling the perfect units which are (1 − p) percentage of all purchased units, the ordering cost per unit of time, cost of buying products per unit of time, holding cost of the perfect units per unit of time, the cost of inspection of a sample per unit per time, holding cost of the imperfect units per unit of time, lost sales and backordered costs per unit of time. Moreover, each case is done with a certain probability computed according to the intervals related to the number of defective items in each sample and subsequently the numbers of defective items in each lot. So according to these probabilities and the related case for each one, the total profit per year that includes all three cases is obtained. Also we consider F and T as the decision variables. For the expectation of the first case we have:

$$ETP_{1} = sD\left[ {\varphi + \gamma (1 - \varphi )} \right]\, - \left[ {\frac{{c_{0} }}{T} + c_{p} D\left[ {\varphi + \gamma (1 - \varphi )} \right] + \frac{{c_{h} DT\varphi^{2} }}{2} + \frac{nd}{T} + c_{g} D(1 - \gamma )(1 - \varphi ) - \frac{{\gamma c_{b} DT(1 - \varphi )^{2} }}{2} - \frac{\psi R}{T}} \right]$$
(4)

For the second case we have:

$$\begin{aligned} ETP_{2} &= sD(E_{2} (1 - p))\left[ {\varphi + \gamma (1 - \varphi )} \right] + v(E_{2} (p))D\varphi \hfill \\ & \quad - \left[ {\frac{{c_{0} }}{T} + c_{p} D\left[ {\varphi + \gamma (1 - \varphi )} \right] + dD\varphi + \frac{{c_{h} D(E_{2} ((1 - p)^{2} ))T\varphi^{2} }}{2} + \frac{{c_{h} (E_{2} (p))D^{2} T\varphi^{2} }}{x} + c_{g} D(1 - \gamma )(1 - \varphi ) + \frac{{\gamma c_{b} DT(1 - \varphi )^{2} }}{2}} \right] \hfill \\ \end{aligned}$$
(5)

And finally for the third case we have:

$$\begin{aligned} ETP_{3} &= sD(E_{3} (1 - p))\left[ {\varphi + \gamma (1 - \varphi )} \right] + v(E_{3} (p))D\varphi \hfill \\ & \quad - \left[ {\frac{{c_{0} }}{T} + c_{p} D\left[ {\varphi + \gamma (1 - \varphi )} \right] + \frac{nd}{T} + \frac{{c_{h} D(E_{3} ((1 - p)^{2} ))T\varphi^{2} }}{2} + rD\varphi \left(E_{3} \left(\frac{p}{1 - p}\right)\right) + c_{g} D(1 - \gamma )(1 - \varphi ) + \frac{{\gamma c_{b} DT(1 - \varphi )^{2} }}{2}} \right] \hfill \\ \end{aligned}$$
(6)

To access a general optimum order quantity we combine three cases so the expected for p is calculated in three cases as below:

First case: \(\theta > \alpha_{2}\)

In this part we have formulated the expectation of the number of defective products in an order received by the vendor, while the number of defective items in the sample is more than \(\alpha_{2}\), \(\overline{E}_{1} (p)\) is computed as below:

$$\overline{E}_{1} (p) = \Pr (\theta \ge \alpha_{2} \cap p \le p_{1} )E_{{p \le p_{1} }} \left[ p \right] + \Pr (\theta \ge \alpha_{2} \cap p_{1} \le p \le p_{2} )E_{{p_{1} \le p \le p_{2} }} \left[ p \right] + \Pr (\theta \ge \alpha_{2} \cap p \ge p_{2} )E_{{p \ge p_{2} }} \left[ p \right]$$
(7)

Also in two next parts we have formulated this expectation for other situations mentioned before.

Second case: \(\alpha_{1} \le \theta \le \alpha_{2}\)

For the situation that the number of defective products in the sample is between \(\alpha_{1}\) and \(\alpha_{2}\) we will have:

$$\begin{aligned} \overline{E}_{2} (p) &= \Pr (\alpha_{1} \le \theta \le \alpha_{2} \cap p \le p_{1} )E_{{p \le p_{1} }} \left[ p \right] + \Pr (\alpha_{1} \le \theta \le \alpha_{2} \cap p \le p_{1} )E_{{p_{1} \le p \le p_{2} }} \left[ p \right] \hfill \\ & \quad + \Pr (\alpha_{1} \le \theta \le \alpha_{2} \cap p \le p_{1} )E_{{p \ge p_{2} }} \left[ p \right] \hfill \\ \end{aligned}$$
(8)

Third case: \(\theta \le \alpha_{1}\)

And if the number of defective products in the random sample is lower than \(\alpha_{1}\), we will have:

$$\overline{E}_{3} (p) = \Pr (\theta \le \alpha_{1} \cap p \le p_{1} )E_{p \le p1} \left[ p \right] + \Pr (\theta \le \alpha_{1} \cap p_{1} \le p \le p_{2} )E_{{p_{1} \le p \le p2}} \left[ p \right] + \Pr (\theta \le \alpha_{1} \cap p \ge p_{2} )E_{{p \ge p_{2} }} \left[ p \right]$$
(9)

And in this part we provide the total revenue as below:

$$\begin{aligned} {\text{ETP}} &= \Pr (\theta \ge \alpha_{2} )\left(\vphantom{\frac{1}{2}}sD\left[ {\varphi + \gamma (1 - \varphi )} \right] + \Pr (\alpha_{1} \le \theta \le \alpha_{2} )\left(\vphantom{\frac{1}{2}}sD(E_{2} (1 - p))\left[ {\varphi + \gamma (1 - \varphi )} \right] \right.\right.\hfill \\ & \quad + \Pr (\theta \le \alpha_{1} )\left(\vphantom{\frac{1}{2}}sD(E_{3} (1 - p))\left[ {\varphi + \gamma (1 - \varphi )} \right] + v(E_{3} (p))D\varphi + v(E_{2} (p))D\varphi \right.\hfill \\& \left. \quad - \left[ {\frac{{c_{0} }}{T} + c_{p} D\left[ {\varphi + \gamma (1 - \varphi )} \right] + \frac{{c_{h} DT\varphi^{2} }}{2} + \frac{nd}{T} + c_{g} D(1 - \gamma )(1 - \varphi ) + \frac{{\gamma c_{b} DT(1 - \varphi )^{2} }}{2} + \frac{\psi R}{T}} \right]\right) \hfill \\& \left.\quad - \,\left[ {\frac{{c_{0} }}{T} + c_{p} D\left[ {\varphi + \gamma (1 - \varphi )} \right] + dD\varphi + \frac{{c_{h} D(E_{2} ((1 - p)^{2} ))T\varphi^{2} }}{2} + \frac{{c_{h} (E_{2} (p))D^{2} T\varphi^{2} }}{x} + c_{g} D(1 - \gamma )(1 - \varphi ) + \frac{{\gamma c_{b} DT(1 - \varphi )^{2} }}{2}} \right]\right) \hfill \\& \left.\quad - \left[ {\frac{{c_{0} }}{T} + c_{p} D\left[ {\varphi + \gamma (1 - \varphi )} \right] + \frac{nd}{T} + \frac{{c_{h} D(E_{3} ((1 - p)^{2} ))T\varphi^{2} }}{2} + rD\varphi (E_{3} (\frac{p}{1 - p})) + c_{g} D(1 - \gamma )(1 - \varphi ) + \frac{{\gamma c_{b} DT(1 - \varphi )^{2} }}{2}} \right]\right) \hfill \\ \end{aligned}$$
(10)

ETP is a concave function (proof in “Appendix A”). To access optimum φ we set T as constant and we set \(\frac{{\partial {\text{ETP}}}}{\partial \varphi } = 0\) then we have:

$$\varphi^{*} (T) = \frac{{ - B_{1} - B_{2} (T)}}{{2A_{1} (T)}}$$
(11)

That \(B_{1}\), \(B_{2} (T)\) and \(A_{1} (T)\) are computed as below:

$$\begin{aligned} B_{1} &= \Pr (\theta \ge \alpha_{2} )(sD - sD\gamma - c_{p} D + c_{p} D\gamma + c_{g} D(1 - \gamma )) + \Pr (\alpha_{1} \le \theta \le \alpha_{2} )(sD(E_{2} (1 - p)) \hfill \\ & \quad - sD(E_{2} (1 - p))\beta + v(E_{2} (p))D - c_{p} D + c_{p} D\gamma - dD + c_{g} D(1 - \gamma )) \hfill \\ \end{aligned}$$
(12)

and

$$B_{2} (T) = - \Pr (\theta \ge \alpha_{2} )\gamma c_{b} DT - \Pr (\alpha_{1} \le \theta \le \alpha_{2} )\gamma c_{b} DT - \Pr (\theta \le \alpha_{1} )\gamma c_{b} DT$$
(13)

and

$$\begin{aligned} A_{1} (T) &= \Pr (\theta \ge \alpha_{2} )\left( - \frac{{c_{h} DT}}{2} - \frac{{\gamma c_{b} DT}}{2}\right) + (\Pr (\alpha_{1} \le \theta \le \alpha_{2} ) + \Pr (\theta \le \alpha_{1} ))\left( - \frac{{\gamma c_{b} DT}}{2}\right) \hfill \\ & \quad - \Pr (\alpha_{1} \le \theta \le \alpha_{2} )\frac{{c_{h} D(E_{2} ((1 - p)^{2} ))T}}{2} - \Pr (\theta \le \alpha_{1} )\frac{{c_{h} D(E_{3} ((1 - p)^{2} ))T}}{2} \hfill \\ \end{aligned}$$
(14)

Now we substitute φ in ETP to obtain the optimum T, so we have:

$${\text{ETP}} = A_{1} (T)(\varphi^{*} (T))^{2} + (B_{1} + B_{2} T)\varphi^{*} (T) + c(T)$$
(15)

That we computed \(c_{1}\), \(c_{2}\) and \(c_{3}\) as below:

$$c(T) = c_{1} + c_{2} T + c_{3} \frac{1}{T}$$
(16)

and

$$\begin{aligned} c_{1} = \Pr (\theta \ge \alpha_{2} )(sD\gamma - c_{p} D\beta - nd - c_{g} D(1 - \gamma ) - \psi R) + (\Pr (\alpha_{1} \le \theta \le \alpha_{2} ) + \Pr (\theta \le \alpha_{1} ))( - c_{p} D\gamma - c_{g} D(1 - \gamma )) \hfill \\ \,\,\,\,\,\,\,\,\, + \Pr (\alpha_{1} \le \theta \le \alpha_{2} )sD(E_{2} (1 - p))\gamma + \Pr (\theta \le \alpha_{1} )sD(E_{3} (1 - p))\gamma \hfill \\ \end{aligned}$$
(17)
$$c_{2} = - \frac{{\beta c_{b} D}}{2}(\Pr (\theta \ge \alpha_{2} ) + \Pr (\alpha_{1} \le \theta \le \alpha_{2} ) + \Pr (\theta \le \alpha_{1} ))$$
(18)
$$\begin{aligned} c_{3} = - (c_{0} + nd + \psi R)(pr(\theta \ge \alpha_{2} )) - c_{0} (pr(\alpha_{1} \le \theta \le \alpha_{2} )) - (c_{0} + nd)pr(\theta \le \alpha_{1} )) \hfill \\ \hfill \\ \end{aligned}$$
(19)

Now we obtain the optimum T by solving \(\frac{{\partial {\text{ETP}}}}{\partial T} = 0\), so we have:

$$T^{*} = \frac{{ - B_{1}^{2} + 4(\Pr (\theta \ge \alpha_{2} )( - \frac{{c_{h} D}}{2} - \frac{{\gamma c_{b} D}}{2}) + (\Pr (\alpha_{1} \le \theta \le \alpha_{2} ) + \Pr (\theta \le \alpha_{1} ))( - \frac{{\gamma c_{b} D}}{2}))c_{3} - \Pr (\alpha_{1} \le \theta \le \alpha_{2} )\frac{{c_{h} D(E_{2} ((1 - p)^{2} ))}}{2} - \Pr (\theta \le \alpha_{1} )\frac{{c_{h} D(E_{3} ((1 - p)^{2} ))}}{2}}}{{2(( - (\Pr (\theta \ge \alpha_{1} ) + \Pr (\alpha_{1} \le \theta \le \alpha_{2} ))\gamma c_{b} D - \Pr (\theta \le \alpha_{1} )\gamma c_{b} DT)^{2} - 8c_{2} (\Pr (\theta \ge \alpha_{2} )( - \frac{{c_{h} D}}{2} - \frac{{\gamma c_{b} D}}{2}) + \Pr (\theta \le \alpha_{1} ))( - \frac{{c_{h} D(E_{3} ((1 - p)^{2} ))}}{2} - \frac{{\gamma c_{b} D}}{2}))}}$$
(20)

In this section we have obtained the optimum quantity for the decision variables and total profit. In the following section we provide the numerical result.

Computational and practical results

We provide some numerical results according to the real case. This case is a dairy store that has partial backordering because of its impatient customers; also it absolutely has the defective items in each received order. The customers of this dairy store are separated into two groups: one group is the ones that their requirements are not critical, so when the vendor does not provide their order quantity in the right time they could wait to fulfill their order. On the other hand, there are some customers that are not patient to fulfill their orders, or their requirements are critical and they should be accessible at the right time. This group of customers does not wait for the vendor to fulfill their order and choose other vendor. In this situation a proportion of backordered demand that is associated with the second group of customers becomes lost sales, so shortage cost consists of two types of penalty. One of them is related to backordered demands and another one is related to lost sales. Also in each cycle the dairy store receives the lot that has the number of defective items so it is necessary for the vendor to consider the inspection process to recognize the defective items and choose a particular decision according to the certain strategy considered for the inspection process. So we use this real case to illustrate the given model and show how the sensitive parameters affect the total profit and decision variables. At first the buyer defines the particular number for n, \(\alpha_{1}\) and \(\alpha_{2}\). He considers n = 20, \(\alpha_{1}\) = 1 and \(\alpha_{2}\) = 4, also the buyer and the vendor should define the maximum limit that is considered as 0.15 in this paper and the buyer defines the minimum limit as 0.06. According to this information, we obtain \(E_{1} [p]\), \(E_{2} [p]\) and \(E_{3} [p]\). We have:

$$E\left[ p \right] = \frac{1}{b - a}\int_{a}^{b} {pdp} = \frac{{b^{2} - a^{2} }}{2(b - a)} = \frac{b + a}{2}$$
(21)
$$E\left[ {p^{2} } \right] = \frac{1}{b - a}\int_{a}^{b} {p^{2} dp} = \frac{{b^{3} - a^{3} }}{3(b - a)} = \frac{{a^{2} + b^{2} + ab}}{3}$$
(22)
$$E\left[ {\frac{p}{1 - p}} \right] = \frac{1}{ - a + b}\int_{a}^{b} {\frac{p}{1 - p}dp} = \frac{(\ln (1 - a) + a) - (\ln (1 - b) + b)}{ - a + b}$$
(23)
$$E\left[ {p \le 0.06} \right] = \frac{1}{0.06 - 0}\int_{0}^{0.06} {pdp} = \frac{{0.06^{2} - 0^{2} }}{2(0.06 - 0)} = \frac{0.06 + 0}{2} = 0.03$$
(24)
$$E\left[ {0.06 \le p \le 0.15} \right] = \frac{1}{0.15 - 0.06}\int_{0.06}^{0.15} {pdp} = \frac{{0.15^{2} - 0.06^{2} }}{2(0.15 - 0.06)} = \frac{0.15 + 0.06}{2} = 0.105$$
(25)
$$E\left[ {0.15 \le p \le 0.25} \right] = \frac{1}{0.25 - 0.15}\int_{0.15}^{0.25} {pdp} = \frac{{0.25^{2} - 0.15^{2} }}{2(0.25 - 0.15)} = \frac{0.25 + 0.15}{2} = 0.20$$
(26)

A sample of 20 products is chosen randomly and the probabilities of different situations according to the number of defective items in the chosen selection are obtained:

  1. a.

    If the number of defective products \(\theta\) is more or equal to \(\alpha_{2}\) = 4, the buyer rejects the order and receives another lot instead of it that it does not have any defective items.

  2. b.

    If the number of defective products \(\theta\) is equal to 2 or 3 all the items should be inspected.

  3. c.

    If the number of defective products \(\theta\) is lower or equal to \(\alpha_{1}\) = 1 no item is inspected.

The probability of being \(\theta\) defective items in a sample is calculated as follows:

$$f(\theta ;n,p) = \left( \begin{aligned} n \hfill \\ \theta \hfill \\ \end{aligned} \right)p^{\theta } (1 - p)^{n - \theta }$$
(27)

For instance we calculate the probability of the situation that \((\theta \le 1)\) and \(p = 0.01\):

$$F(1;20,0.010) = \Pr (\theta = 0) + \Pr (\theta = 0) = \left( \begin{aligned} 20 \hfill \\ 0 \hfill \\ \end{aligned} \right)0.010^{0} (1 - 0.010)^{20} + \left( \begin{aligned} 20 \hfill \\ 1 \hfill \\ \end{aligned} \right)0.010^{1} (1 - 0.010)^{19} = 0.983$$
(28)

We provide these probabilities in Fig. 2 for all situations.

Fig. 2
figure 2

The expectance of different number of defective products in a sample with 20 products

Full size image

According to Fig. 2, Table 2 is provided that considers all the situations; the probabilities of these different situations are provided in Table 2.

Table 2 The probability of different situation
Full size table

Now we compute \(E_{1} [p]\), \(E_{2} [p]\) and \(E_{3} [p]\) using Eqs. (7), (8), (9), (24), (25), (26) as follows:

$$E_{1} (p) = (0.004 \times 0.03) + (0.032 \times 0.105) + (0.963 \times 0.2) = 0.196$$
(29)
$$E_{2} (p) = (0.237 \times 0.03) + (0.460 \times 0.105) + (0.460 \times 0.2) = 0.117$$
(30)
$$E_{3} (p) = (0.796 \times 0.03) + (0.186 \times 0.105) + (0.018 \times 0.2) = 0.049$$
(31)

Now, we want to show how the different quantity of E(p) affects the total profit in Table 3, we set D = 50 units per year, v = 20$ per unit, x = 1 unite per minute, d = 0.5$ per unit, r = 15$ per unit, R = 70$, s = 50$ per unit, \(c_{p}\) = 25$ per unit, \(c_{b}\) = 1$ per unit, \(c_{g}\) = 2$ per unit, \(c_{o}\) = 10$ per order, \(\gamma\) = 0.4.

Table 3 Quantity of \(E_{3} [p]\), \(E_{2} [p]\), \(E_{3} [p]\) and E(p)
Full size table

As we see in Fig. 3 by increasing E(p) in the interval [0.01,0.03] the total profit increases, also by increasing E(p) in the interval [0.04, 0.11] the total profit increases too and finally in the last interval [0.12,0.20] the total profit decreases. But the total profit in the case that all the items are rejected is more than two other cases and the total profit in the case in which the lot is accepted and all the items are inspected is more than the total profit in the case in which the lot is accepted and no inspection happens. One of the sensitive parameters is \(\gamma\) and we analyze its effect on the duration of the cycle (T), the fraction of demand that is fulfilled from stock (φ) and the total profit (ETP). We set D = 50 units/year, v = 20 $ per unit, x = 1 unite per minute, d = 0.5$ per unit, r = 15$ per unit, R = 70$, s = 50$ per unit, \(c_{p}\) = 25$ per unit, \(c_{b}\) = 1$ per unit, \(c_{g}\) = 2$ per unit, \(c_{o}\) = 10$ per order, E(P) = 0.14.

Fig. 3
figure 3

Quantity of ETP versus different quantity of E(p)

Full size image

As we see in Table 6, ETP is below zero by quantity of \(\gamma\) that are more than 0.5, so we consider ETP as zero in these particular quantity of \(\gamma\). The changes of ETP according to the changes of \(\gamma\) are shown in Fig. 4.

Fig. 4
figure 4

ETP versus \(\gamma\)

Full size image

For the behavior of the decision variables we just consider \(\gamma\) as 0.1–0.5 because the quantity of ETP is more than zero. We provide the different quantity of T and φ in Tables 4 and 5, also the changes of them according to the changes of \(\gamma\) are shown in Figs. 5 and 6, respectively (Table 6).

Table 4 Quantity of \(T^{*}\) according to the different quantity of \(\gamma\)
Full size table
Table 5 Quantity of \(\varphi^{*}\) according to the different quantity of \(\gamma\)
Full size table
Fig. 5
figure 5

\(T^{*}\) versus \(\gamma\)

Full size image
Fig. 6
figure 6

\(\varphi^{*}\) versus \(\gamma\)

Full size image
Table 6 Quantity of ETP according to the different quantity of \(\gamma\)
Full size table

As we see in Figs. 4, 5 and 6, by increasing \(\gamma\) the optimum value of both decision variables φ and T, also expectation of total profit, ETP, decrease. Our purpose is to increase the expectation of the profit, so by considering the greater value for γ this purpose is accessible, though it should be noted that for this case these results are gained and absolutely for the other cases results could be changed. So according to considered cases, managers should set the sensitive parameters with the particular values to access the best results for their decision variables and expected value of the total profit. In this part, we provided some numerical results according to the data related to a diary store, analyze these results regarding the sensitive parameters to find out how this model can impact on the expectation of total profit and decision variables. It should be noted that we verify two conditions for the proof of the concavity of ETP (see “Appendix A”) to find out if it is concave or not according to the quantity of parameters, and it is found out that it is concave. Also this part is provided to find out how the provided model in this paper can improve the process. In reality, to access the precise process of inventory system and being successful among many companies, it is necessary to consider the assumptions that are provided in this paper to model the inventory system, partial backordering and particular process of inspection because of the defective items. Nowadays competition between the enterprises has been very intense and without such precise inventory model that includes many aspects of inventory system it is not possible to be successful. With the provided model in this paper we can make the customers more satisfied than before, also by considering the perfect strategy for inspection, managers can determine the decision variables perfectly. Additionally the cost of inventory system is determined more similar to the real world and the answers that are obtained from the provided model are more reliable to cope with the fluctuations of the price, amount, etc. Also responsiveness is an important factor that is considerable for the managers; with the provided model, this factor increases and absolutely customers are more satisfied. Additionally with this model managers can increase their system flexibility to respond to the changes and provide their certain services with the higher level, also demand and supply can be determined perfectly.

Conclusion

There are some assumptions that are really essential to be considered to model the inventory system. One assumption is that there are some defective items in each order that a firm or enterprise receives, these items should be recognized and managers decide what to do according to their inspection strategy. In this paper we consider an inspection approach that is explained in the following. In this approach we consider three levels of number of defective items in each sample that is chosen from each order randomly. According to the number of defective items that is in an order we decide what to do for with the order. According to the mentioned explanation we define three levels of defective items in each sample according to their numbers. If this number is less than α1 it is not necessary to inspect all the items, else if this number is between α1 and α2 all the items should be inspected and if this number is more than α2 the order is rejected and another order without any defective items is received. The rate of imperfect items in each order is p and regarding the number of defective items it has three levels, lower than p 1, between p 1 and p 2 and upper than p 2. Another assumption is related to the customers. There are two types of customers. The first one is the customers that do not change the vendor that they choose to fulfill their demand though they know that they should wait more than the regular time for their order. On the other hand the second one is the customers that do not be patient enough to wait to fulfill their demand; these customers prefer to receive their orders by the other vendors because they do not want to wait or their demand is critical so their demand should be fulfilled soon. Because of the second ones a particular proportion of backordered items become lost sales so we have partial backordering instead of full backordering. We have proposed the model by considering these assumptions and obtain the optimum quantity for the total profit and the decision variables. Next we have provided the numerical result to show how the sensitive parameter affects the total profit and decision variables, also how the different situations affect the total profit. This model is the first one that considers both partial backordering and the process of inspection simultaneously and is so helpful for the managers to cope with the fluctuations of the inventory system in the real world as we discussed in Sect. 5. All managers surely are interested to make the inventory system closer to the real world. There are some assumptions that make the model more complicated. For example, the demand rate and length of the cycle could be considered as stochastic variables, also the fraction of the backordered items could be provided by the particular distribution function to make the model more realistic. Although the selling price is considered as constant, it could be considered as a particular function of certain parameters.