Endpoint in plasma etch process using new modified w-multivariate charts and windowed regression

Abstract

Endpoint detection is very important undertaking on the side of getting a good understanding and figuring out if a plasma etching process is done in the right way, especially if the etched area is very small (0.1%). It truly is a crucial part of supplying repeatable effects in every single wafer. When the film being etched has been completely cleared, the endpoint is reached. To ensure the desired device performance on the produced integrated circuit, the high optical emission spectroscopy (OES) sensor is employed. The huge number of gathered wavelengths (profiles) is then analyzed and pre-processed using a new proposed simple algorithm named Spectra peak selection (SPS) to select the important wavelengths, then we employ wavelet analysis (WA) to enhance the performance of detection by suppressing noise and redundant information. The selected and treated OES wavelengths are then used in modified multivariate control charts (MEWMA and Hotelling) for three statistics (mean, SD and CV) and windowed polynomial regression for mean. The employ of three aforementioned statistics is motivated by controlling mean shift, variance shift and their ratio (CV) if both mean and SD are not stable. The control charts show their performance in detecting endpoint especially W-mean Hotelling chart and the worst result is given by CV statistic. As the best detection of endpoint is given by the W-Hotelling mean statistic, this statistic will be used to construct a windowed wavelet Hotelling polynomial regression. This latter can only identify the window containing endpoint phenomenon.

Introduction

The Plasma is partially ionized gas. Therefore, it contains electron energy which excites the atoms and molecules then de-energize in emitting photons. Under those circumstances, the plasma thus emits light. The etch process is employed in patterning of thin films to form significant features in chips such as gates and interconnect lines, and contact holes. With the industry moving toward greater circuit integration and multilevel metalization, the successful formation of these features with the necessity of achieving etch goals puts up Etch process as a critical challenge. Endpoint detection is employed to identify when the etched film has cleared the underlying film, at this moment, the process can be stopped, or modified to a more selective etch. The Optical spectra (profiles) will be monitored to detect the endpoint. As the traditional statistical process control (SPC) employs a single (or multiple) measurement(s) of a single unit to monitor any change in mean (or mean vector) or in variance (or covariance matrix), Monitoring profiles will gather a set of values over a range (sampling stage) having the shape of curve to detect the variation between successive curves. Monitoring profile is based on monitoring the prescribed functional relationship between a dependent (explicative) variable and one or more independent (explanatory) variables. In this paper, we have investigated and proposed several methods to enhance the endpoint detection especially when the open area to be etched is very small (0.1%) compared to the whole surface of wafer. In the first section, monitoring profile will be presented with previous works. The second section will be dedicated for the most used multivariate control charts (Hotelling and MEWMA charts). The third section exposes our proposed methodology, at the first time we start with the proposed algorithm named spectra peak selection (SPS) then we employ wavelet analysis to improve the quality of selected wavelengths (profiles) by de-correlating and suppressing noise from Optical spectra. We will use also three statistics (mean, standard deviation (SD) and coefficient of variation (CV)) to construct modified W-Hotelling and W-MEWA control charts using Chebyshevs inequality. Finally, we propose windowed wavelet polynomial regression based on the best statistic performance to be able to identify the convergence of endpoint event. Then results and discussion will be exposed and the final one presents the concluding remarks.

Monitoring profiles

Nowadays, monitoring process is simply to ensure about preserving the steadiness of the relationship between the main variable of interest (output) and one or more environmental variables or control variables (inputs) over the time, hence the application of classical SPC is not convenient. It should be noted that in some literature, the profile data are also referred as waveform signal, Jin and Shi (2001) and Zhou et al. (2006) or signature, Moroni and Pacella (2008). The mathematical expression of profile is given as follows:

$$\begin{aligned} Y_{i}=f(X_{i})+\varepsilon _{i}, \quad i=1, 2,\ldots ,n. \end{aligned}$$

(1)

where X represents one (or more) fixed independent variable(s), $\epsilon_i$ is random noise following independent and identically normal distribution with mean zero and common variance $\sigma ^2$, i the index the ith profile and f(.) is a linear or nonlinear function. In some cases, profile can be described effectively using linear regression model and in some others it would be suitable to use nonlinear regression model especially elastic and stretchable configuration of profiles.

Phase I and Phase II in monitoring profiles

To build statistical process control (SPC) chart, Woodall (2000) proposes two phases (the construction of Phase I is based on fixed historical profiles while the construction of Phase II is based on online data). A detailed distinction between tasks and aims of phase I and II are presented by Montgomery (2009), Kim et al. (2003), Zhu and Lin (2010), Zhang et al. (2013), Keramatpoura et al. (2014). Kang and Albin (2000) presented an efficient and extensive use of phase I and phase II. In phase I and after collecting waveform signals, one should study them to: first, understand the type of variation in a process over time to distinguish between the common variation within a profile and the variation between profiles. Second, evaluate the steady-state process by separating the in-control profiles from out-of-control profile (assignable causes) and remove samples associated with special causes; finally, to model the in-control (stable) process performance by estimating the steady profile (f(x0)) or/and unknown parameters of this model. In Phase II, the parameters of the constructed chart, are known (or estimated) from in-control process in Phase I, are used as the target profile. The main goal of this phase is to detect any change (shift) in the new process outcomes (profiles). The performance of a Phase II is given by the average run length (ARL). Remember that the run length is the number of samples taken before an out-of-control signal is given and the ARL represents the average number of time points needed for the procedure to signal a change in profiles. There are two Average run lengths (In and out). For in-control, ARL ($ARL_0$) is often controlled at a given level. If the out-of-control (OC) ARL ($ARL_1$) is shorter in detecting a specific profile change, the process will perform better. Huwang et al. (2015) exposed a new method for monitoring profiles if the response variable is both categorical and ordinal by exploring a proportional odds model and EWMA chart. Qi et al. (2016) proposed to monitor profiles using generalized linear models during Phase II in which the explanatory variables can be fixed design or random arbitrary design. They presented a new control chart based on the weighted likelihood ratio test.

Linear and nonlinear profiles

From the generated data, the endpoint is reached through the use of the signal trace (at the endpoint). The analysis of the OES measurements remains a challenge. This is due to the emitted light by the plasma containing rich emissions from many different species constructing the full spectral. To fill the void of controlling unique variable, the employ of monitoring profiles method is unavoidable. While, a specific reactant or product species is determined for a special process, the species concentration is tending to change over the time and more significantly at onset of the endpoint. Hence, the intensity of this OES wavelength light allied to this species is also presumed to vary at endpoint.

Linear profiles

Kang and Albin (2000) put forward two control charts for Phase II to monitor linear profiles. The first one, multivariate Hotelling $T^2$ control chart to identify the change in intercept or slope parameters; they had shown that the univariate EWMA chart for monitoring the residuals is more sensitive than their proposed chart. The second chart, based on the regression residuals using an EWMA chart combined with an R chart, named EWMA / R is employed to detect the possibility of extreme residuals shift undetected in any of the regression parameters (intercept, slope and error variance). The EWMA chart is put in use of controlling the average of the profile residuals, and the R chart identifies the largest and smallest residuals from each profile to detect any change in the noise behavior. Stover and Brill (1998) employed the Phase I Hotelling $T^2$ chart to detect change  based on vector containing the slope and the intercept specifications, in each profile. A next approach is made known by those authors combining the reduction dimension technique through the use of principal component analysis (PCA) to the coefficient vector, and the univariate SPC method only for the first retained component. The second technique was reviewed by Kim et al. (2003), who showed its failure to detect shift raised from other component except the first one. Kim et al. (2003) presented a Phase II method in monitoring the intercept, the slope, and the variance individually. Their main idea is to center the variable(s) (X or Y or both) to make least square estimators for intercept and slope independent of each other (remove the covariance between intercept and slope), and apply EWMA chart for each parameter noted $EWMA_3$ chart, subscript three refers to the three monitored parameters, the first two constructed based on the estimation of the least squares of the slope and the intercept, while the last one is based on the MSE of the residuals from each profile. They had proven, based on the simulation study, that the ARL of their chart performs better than the multivariate $T^2$ chart and the EWMA / R. Kang and Albin (2000) advised that their Phase II methods could be used in Phase I with estimated values of parameter substituted by the values of unknown parameters themselves. Mahmoud and Woodall (2004) presented and compared several control charts showing that the successive values of the Phase I $T^2$ statistic by Kang and Albin (2000) are dependent and they have proposed the use of a global F-statistic based on setting indicator variables in a multiple regression model to compare two or more regression lines. Another paper is presented by Mahmoud et al. (2007) in which they suggest a change-point method for monitoring linear profile data. Woodall et al. (2004) present an overview of monitoring profiles. Many models have also been used to represent profiles, such as simple linear regression (Aly et al. 2015; Noorossana et al. 2010; Zhang et al. 2009) and more complex model such as that presented by Abbas et al. (2016) exposed three newest univariate Bayesian EWMA control charts for the Y-intercepts, the slopes and the error variance during phase II using non-conjugate and conjugate priors. These control charts are used to monitor the Y-intercepts, the slope coefficients and increase in process standard deviations, respectively. They have found that the Bayesian control with conjugate prior charts gives a high performance in monitoring the Y-intercepts and slopes than the one with non-conjugate priors, while both priors perform almost equivalently in case of error variance.

Nonlinear profiles

Williams et al. 2003 studied Phase I on monitoring nonlinear profiles using nonlinear regression. They proposed using multivariate $T^2$ control charts to monitor all coefficients in the nonlinear model and compared several approaches in choosing the variance–covariance matrix. Williams et al. 2007 extended this methodology to nonlinear profiles with a non-immovable variance at set points to take apart a set of differences between variance of profiles. Shiau and Weng 2004 extended the linear profile to general forms of profiles using non-parametric regression. Hence, there is no assumption for the form of the profiles except the smoothness. They proposed an EWMA chart for detecting mean shifts, an R chart for variation changes, and an SD (standard deviation) chart for variation increases. Ding et al. 2006 indicated two main challenges in Phase I analysis of nonlinear profiles: (1) the high dimensionality of the data, and (2) how to separate in-control profiles from the out-of-control profiles. They proposed an independent component analysis (ICA) method for the dimension reduction and a change point-based method for the effective separation of in-control and out-of-control profiles. Shiau et al. 2009 propose for Phase I profile monitoring, using the usual Hotelling $T^2$ chart, a run of the mail accustomed to control chart designed for multivariate process data, by treating the principal component (PC) scores of a side-view obtained from PCA as the multivariate data. For Phase II process monitoring, they propose PC-score charts and a $T^2$ chart (different from the $T^2$ chart of Phase I). Some other non-wavelet papers are proposed to monitor nonlinear profiles, such as modified $T^2$ Hotelling chart based on spatial autoregressive regression models proposed by Colosimo et al. 2008; Williams et al. 2007 proposed spline-fitting to estimate profile. Qiu 2008 proposed a distribution-free technique to detect fluctuation in multivariate processes through the employ of a log-linear model to estimate the in-control distribution, and the use of a multivariate CUSUM chart to detect shifts. They proposed also in another paper Qiu et al. 2010 a non-parametric control chart when within profile is correlated to monitor profiles behavior. Some other authors proposed statistical methods based on the introduction of wavelet analysis, which will be presented shortly. The simple nonlinear regression is also studied by Chang and Yadama (2010), Paynabar et al. (2013).

Monitoring profile using wavelet transform

As mentioned previously, the application of wavelet method in detecting the change in functional data has been first used in the semiconductor production and in other industrial processes. Jin and Shi (1999) explored tonnage signals to identify shortcomings in a sheet-metal stamping process. Jin and Shi (2001) detected the variation between profiles and within profiles, by observing the change in the magnitudes of the coefficients of DWT’s profile. Lada et al. (2002) scrutinized quadruple mass spectrometry (QMS) samples of a expeditious thermal chemical vapor deposition (RTCVD) process to detect significant deviations from the nominal process. Ganesan et al. (2003) used acoustic emission signals to monitor de-lamination defect in nano-machining process. Jeong et al. (2006) expanded a wavelet-based statistical process control (SPC) procedure for dig-up out-of-control events that signal course of action abnormalities for monitoring complicated data. Chicken et al. (2009) used the change-point model based on wavelet analysis to monitor the change between the sequences of profiles. There is a good literature review of wavelet analysis in statistical process monitoring introduced by Ganesan et al. (2004).

Each collected profile is expressed as follows:

$$\begin{aligned} Y_{i}=f(x_{i})+\epsilon _{i} \end{aligned}$$

(2)

If this profile is conforming to the target profile (a steady-state process), it will be defined as:

$$\begin{aligned} Y_{i}=f_{0}(x_{i})+\epsilon _{i} \end{aligned}$$

(3)

where i index of the ith observation from n, the total number of observations; $f_{0}$ is the known standard signal, taken from in control process and established in Phase I; $\epsilon _{i}$ are independent and identically distributed normal (i.i.d.) random variables with mean zero and variance $\sigma ^{2}$.

To reduce the controlled coefficients with keeping the profile information, discrete wavelet analysis will be applied for each selected wavelength. Hence, the discrete wavelet transform (DWT) of y is given by:

$$\begin{aligned} d=Wy \end{aligned}$$

(4)

where $W=[h_{ij}]$ is the orthonormal wavelet transform matrix with dimension $n*n$ with element $h_{ij}$ representing the linear filter, for $i,j = 1, 2,\ldots ,n$. The matrix W is different according to the wavelet type, decomposition level and number of sample points n. The property of orthonormality of W allows us to get the original data Y from the inverse of DWT ($Y=W^{-1}d$) This obtained matrix $\mathbf d$ is composed by approximations ($\mathbf C _{L}$) and details ($\mathbf d _{L}$). Each wavelength is contaminated with noise ($\varvec{\epsilon }$) and expressed as follows:

$$\begin{aligned} \mathbf{d} =\theta_{0}+\eta \end{aligned}$$

(5)

where $\theta _{0}=Wf_{0}$ and $\eta = W\epsilon$ with $\eta \sim N_{n}(0, \sigma ^{2}I_{n})$ and $I_{n}$ is the identity matrix with dimension $n*n$, presented by Vidakovic (1999).

$$\begin{aligned} \mathbf{d}= & {} (\mathbf{c} _{L}, \mathbf{d} _{L},\mathbf{d} _{L+1},\ldots ,\mathbf{d} _{J} )^{T} \nonumber \\= & {} ((c_{L,0},\ldots ,c_{L,2^{L}-1})^{T}, (d_{L,0},\ldots ,d_{L,2^{L}-1})^{T},\ldots ,(d_{J,0},\ldots ,d_{J,2^{J}-1})^{T}) \end{aligned}$$

(6)

All these coefficients $(c_{L,0},\ldots ,d_{J,2^{J}-1})$ are wavelet coefficients at various scales. The most useful wavelets in discrete wavelet analysis are the Daubechies family. The orthonormal basis function for Haar wavelet Daubechies (first-order Daubechies wavelet transform) in $L^{2}(R)$ is as following:

$$\begin{aligned} \Psi (t)= & {} {\left\{ \begin{array}{ll} 1, &{} \quad 0\le t\le 0.5 \\ -1,&{} \quad 0.5\le t\le 1 \\ 0, &{} \quad \text {otherwise} \end{array}\right. } \end{aligned}$$

(7)

$$\begin{aligned} \Psi _{j,k} (t)= & {} {\left\{ \begin{array}{ll} 2^{\frac{-j}{2}}, &{} \quad 2^{j}k\le t\le 2^{j}(k+0.5) \\ -2^{\frac{-j}{2}}, &{} \quad 2^{j}(k+0.5)\le t\le 2^{j}(k+1) \\ 0, &{} \quad \text {otherwise} \end{array}\right. } \end{aligned}$$

(8)

The most useful wavelets in discrete wavelet analysis are the Daubechies family. It should be noticed that in semiconductor process especially Plasma etch process, wavelets are often employed as data pre-processing tool to de-correlate, de-noise, reduce the original data. A new paper combining wavelet and SPC to monitor process is presented by Cohen et al. (2015) in which they demonstrated that the Discrete Wavelet Transform (Haar wavelet) is equivalent to the X-bar-R chart and they have introduced a new control chart, named DeWave, to control the process variability.

The traditional multivariate control chart

One of most challenging tasks in semiconductor industry is to monitor several variables. The use of univariate method can offer the possibility to monitor unique variable. If the process is more sophisticated, one should control several key variables using multivariate control chart. In fact, it is impossible in practice to monitor SPC charts for every variable separately, and if one opts to construct many control charts for each variable to detect shifts in one of them, it will be a time consuming and will generate many false detection errors. The error type I for multivariate control chart can be expressed as follows:

$$\begin{aligned} \alpha _n=1-(1-\alpha )^n \end{aligned}$$

(9)

where $\alpha _n$ is the probability of type I error for n univariate charts, and $\alpha$ is the probability of type I error for each univariate chart computed from the control limits.

For the multivariate control chart, each run will be considered as a variable, two variables should be monitored and the last two other runs will be used as online data. In addition, it should be pointed out that to study the robustness of the result many variable arrangements are checked and the total run is 200.

Hotelling control chart

Introduction to $T^2$ chart

The Hotelling $T^2$ statistic is the multivariate extension of t values calculated for univariate data. The t value for an individual sample (x) is calculated as follows:

$$\begin{aligned} t=\frac{x-\bar{x}}{s} \end{aligned}$$

(10)

where t is the normalized range from specific sample (x) away from a given mean and given variance. The mean and the variance are usually unknown values and should be estimated based on some accumulated samples. If the sample size is very high, it goes to the characteristic z value. This latter is always computed from population distributions, and expressed as shown below:

$$\begin{aligned} z=\frac{x-\mu }{s} \end{aligned}$$

(11)

The t values follow t distribution while the z values are normally distributed. The t and z values are employed in the X-bar chart and it is an extension of the aforementioned chart. The name of multivariate X-bar chart is the Hotelling $T^2$ control chart. Hotelling $T^2$ statistic based on individual samples of x only is calculated as:

$$\begin{aligned} T_i^2=(x_{i.}-\bar{x_{i.}})^TS^{-1}(x_{i.}-\bar{x_{i.}}) \end{aligned}$$

(12)

where S is the sample covariance matrix. $T^2$ is the value for each unit time produced in the statistical range between point and the mean and this statistic $T^2$ is computed based on multivariate data set. The $T^2$ statistic is following an F distribution, so that the control limits for the $T^2$ control chart are:

$$\begin{aligned} \mathrm{UCL}= & {} \frac{(m-1)(m+1)}{m(m-n)}F_{(1-\alpha ,n,m-n)} \end{aligned}$$

(13)

$$\begin{aligned} \mathrm{LCL} = 0 \end{aligned}$$

(14)

where m is the number of samples in the ME interval from which the mean and covariance are calculated, the size of monitored variables is referred by n, and UCL and LCL are the upper and lower control limits, respectively. With large m, the control limits can be come closer to a Chi-squared distribution as:

$$\begin{aligned} \mathrm{UCL} = \chi _{\alpha ,n}^2 \end{aligned}$$

(15)

$$\begin{aligned} \mathrm{LCL} = 0 \end{aligned}$$

(16)

Practically, the $T^2$ control chart, under the normal condition, is able to identify the mean shift in an arbitrary direction away.

Application of Hotelling $T^2$ to detect endpoint in plasma etch process

As noted previously, the $T^2$ is the multivariate extension of the X-bar chart used to detect shifts from the target mean. For endpoint detection in Plasma etch process, the steady state of process is defined during the main etch and after the end initial transient interval. Then, the endpoint data (wavelength channels or time channels) are presented by the matrix X notation composed by four components: initial transient (IT), main etch (ME), endpoint (EP), and over etch (OE) and it is expressed as follows:

$$\begin{aligned} (\mathrm{Partitioning } \, \mathrm{ of } \, \mathrm{ Endpoint } \, \mathrm{ Data })\, X = \begin{bmatrix} X_{(\mathrm{IT})}\\ X_{(\mathrm{ME})}\\ X_{(\mathrm{EP})}\\ X_{(\mathrm{OE})} \end{bmatrix} \end{aligned}$$

(17)

where the columns of X represent the trace of a specific wavelength and the rows of X represent the time sample spectra. Then, the $T^2$ statistic is computed for each time sample point, i, using the following formula:

$$\begin{aligned} T_i^2= & {} (x_{i.}-\bar{x}_{i.})^T S^{-1}(x_{i.}-\bar{x}_{i.})\end{aligned}$$

(18)

$$\begin{aligned} S= & {} \frac{X^T_{(\mathrm{ME})}X_{(\mathrm{ME})}}{m-1} \end{aligned}$$

(19)

where S is the sample covariance matrix accounted from the main etch data only, and m is the number of samples in the main etch data. $T^2$ is equal to a scalar value for each time sample showing the distance away the main etch. Assuming the statistic $x_{i1},\ldots ,x_{ip}$ follows a multivariate normal distribution, the upper control limit (UCL) can be calculated from the F-statistic as:

$$\begin{aligned} \mathrm{UCL}=\frac{(m-1)(m+1)}{m(m-n)}F_{(1-\alpha ,m-n)} \end{aligned}$$

(20)

where n is the number of spectral channels. With a large number of spectra (n) gathered from the historical data, the F distribution will be tended by a Chi-squared distribution and expressed as below:

$$\begin{aligned} \mathrm{UCL}=\chi _{(\alpha , n)}^2 \end{aligned}$$

(21)

The multivariate exponentially weighted moving average (MEWMA) control chart

The extension of EWMA chart in several variables is called multivariate EWMA chart and noted MEWMA control chart, it was proposed by Lowry et al. (1992) and the EWMA vector $Z_i$ is defined as follows:

$$\begin{aligned} Z_i= r X_i + (1-r)Z_{i-1} \end{aligned}$$

(22)

where $X_i$; $i = 1,2\ldots ,n$ represents the ith observation on X, the r is the smoothing constant, $0 < r \le 1$ and $Z_0$ is the zero vector. The statistic $T_i$ of MEWMA control chart is given by:

$$\begin{aligned} T_{i}^2=Z_{i}^{'}\Sigma _{Z_i}^{-1}Z_{i} \end{aligned}$$

(23)

An out-of-control is detected on the ith sample if the plotted statistic $T_i$ exceeds the control limit L and the two main parameters of the MEWMA chart (L and r) are set to acquire a looked-for in-control $ARL_0$ value. The control limits are defined as follows:

T-squared control limit with known covariances:

$$\begin{aligned} \mathrm{UCL}=X^2_{\alpha ,p} \end{aligned}$$

(24)

T-squared control limit with covariances are estimated from k previous samples:

$$\begin{aligned} \mathrm{UCL}=\frac{P(k+1)(k-1)}{k(k-p)}F_{\alpha ,p,k-p} \end{aligned}$$

(25)

New proposed algorithm to select important spectra: spectra peak selection (SPS)

The sophisticated sensors and the development IC make the endpoint detection a hard task. As the optical emission spectroscopy (OES) is one of the ultimate known plasma etching sensors, it is unavoidable to use it. However, the OES data are typically high and rich with information, huge number of intensities for each run. To analyze and to understand them, the request to select important spectra is crucial and basic. As a result, selecting important OES data contributes to significant gains in terms of detecting endpoint. In this section, a new proposed algorithm, named Spectra Peak selection will be exposed; this algorithm is constructed to detect significant reactant or product species change and expressed as follows

For all runs Plasma etch step

For each wavelength

      For endpoint range.

        Determine peaks

       ENDFOR

     Determine the highest peak in absolute values.

   ENDFOR

  Rank peak in decreasing way.

  Selecting the first fifty important peaks.

ENDFOR

As a result, the application of this algorithm is done on wavelength channels (profiles). To illustrate for each run, the only first fifty wavelengths, and between 250, 999s and 252, 499 s, the fifty significant wavelengths for each variable will be used on constructing control chart. In Fig. 1, the full spectra are plotted to have an insight about the process. Figure 2 shows the extreme points (maximum in red and minimum in green) from 250.999 to 252.499 s (endpoint interval), in red color the points having highest peaks and in green color the lowest peak.

Fig. 1

Full spectra from the start of process to the end

Fig. 2

The intensities of wavelengths from $t=$250.999 to 252.499

Proposed W-Hotelling and W-MEWMA charts

The modified W-Hotelling

The statistic W-Hotelling is expressed as follows:

For wavelet-mean approximation:

$$\begin{aligned} T_i^2=(x_{i.}-\bar{x_{i.}})^T S^{-1}(x_{i.}-\bar{x_{i.}}) \end{aligned}$$

(26)

where $x_{i.}$ is the mean of notable wavelengths for each variable. The (.) in this study is two (2 variables), the constructed control chart are coming from two historical statistics. For each variable, i is index of observations, $\bar{x_{i.}}$ the mean of mean this statistic in main etch. $S^{-1}$ is the inverse matrix of covariance between two variables and it is square matrix with order two. The control limit noted CL is equal to the mean of the mean of notable wavelengths. This type of chart is employed to monitor the mean shift.

For wavelet-SD approximation:

$$\begin{aligned} T_i^2=(x_{i.}-\bar{x_{i.}})^T S^{-1}(x_{i.}-\bar{x_{i.}}) \end{aligned}$$

(27)

where $x_{i.}$ is the SD of notable wavelengths for each variable, two variables are studied. The i is index of observations for each variable, $\bar{x_{i.}}$ the mean of this statistic SD in main etch. $S^{-1}$ is the inverse matrix of covariance between two variables and it is square matrix with order two. The control limit noted CL is equal to the mean of SD of notable wavelengths. This type of chart is employed to monitor the variation in the variance shift.

For wavelet-CV approximation:

$$\begin{aligned} T_i^2=(x_{i.}-\bar{x_{i.}})^T S^{-1}(x_{i.}-\bar{x_{i.}}) \end{aligned}$$

(28)

where $x_{i.}$ the CV of notable wavelengths from each variable, two variables are studied. i is index of observations for each variable, $\bar{x_{i.}}$ the mean of this statistic CV in main etch. $S^{-1}$ is the inverse matrix of covariance between two variables and it is square matrix with order two. The control limit noted CL is equal to the mean of CV of notable wavelengths. This type of chart is employed to monitor the stable ratio ($SD/\mu$) if both $\mu$ and SD are not steady.

The modified W-MEWMA

The statistic W-MEWMA is expressed as follows:

For wavelet-mean approximation:

$$\begin{aligned} T_{i}^2=Z_{i}^{'}\Sigma _{Z_i}^{-1}Z_{i} \end{aligned}$$

(29)

where $Z_i$ is the statistic of EWMA chart expressed by:

$$\begin{aligned} Z_i= \lambda X_i + (1-\lambda )Z_{i-1} \end{aligned}$$

(30)

where smoothing parameter is noted by $\lambda$. For the first observation, $X_1$ is 0 (starting value) and $Z_0$ is mean of mean of $X_i$ in steady state (Main etch). The $x_{i.}$ is the mean of notable wavelengths from each variable. The control chart limits are constructed based on two variables. i is the number of observations in each variable, $\bar{x_{i.}}$ the mean of mean this statistic in main etch. $S^{-1}$ is the inverse matrix of covariance between two variables times ($\lambda /2-\lambda$) and it is square matrix with order two. The control limit noted CL is equal to the mean of the mean of notable wavelengths. This type of chart is employed to monitor the mean shift.

For wavelet-SD approximation:

$$\begin{aligned} T_{i}^2=Z_{i}^{'}\Sigma _{Z_i}^{-1}Z_{i} \end{aligned}$$

(31)

where $Z_i$ is the statistic of EWMA chart expressed by:

$$\begin{aligned} Z_i= \lambda X_i + (1-\lambda )Z_{i-1} \end{aligned}$$

(32)

where smoothing parameter is noted by $\lambda$. For the first observation, $X_1$ is 0 (starting value) and $Z_0$ is mean of SD of $X_i$ in steady state (Main etch). The $x_{i.}$ is the SD of notable wavelengths from each variable. The control chart limits are constructed based on two variables. i is the number of observations in each variable; $\bar{x_{i.}}$ the mean of SD this statistic in main etch. $S^{-1}$ is the inverse matrix of covariance between two variables times ($\lambda /2-\lambda$) and it is square matrix with order two. The control limit noted CL is equal to the mean of the SD of notable wavelengths. This type of chart is employed to monitor the variation in variance shift.

For wavelet-CV approximation:

$$\begin{aligned} T_{i}^2sub=Z_{i}^{'}\Sigma _{Z_i}^{-1}Z_{i} \end{aligned}$$

(33)

where $Z_i$ is the statistic of EWMA chart expressed by:

$$\begin{aligned} Z_i= \lambda X_i + (1-\lambda )Z_{i-1} \end{aligned}$$

(34)

where smoothing parameter is noted by $\lambda$. For the first observation, $X_1$ is 0 (starting value) and $Z_0$ is the mean of CV of $X_i$ in steady state (Main etch). The $x_{i.}$ is the CV of notable wavelengths from each variable. The control chart limits are constructed based on two variables: i is the number of observations in each variable, $\bar{x_{i.}}$ the mean of SD this statistic in main etch. $S^{-1}$ is the inverse matrix of covariance between two variable times ($\lambda /2-\lambda$) and it is square matrix with order two. The control limit noted CL is equal to the mean of the CV of notable wavelengths. This type of chart is employed to monitor the stable ratio ($SD/\mu$) if both $\mu$ and SD are not steady.

Construction chart procedure

The Daubechies family will be used since it has the easiest and advantageous properties. The Haar wavelet type is the most simplest and the oldest one, it is not the best wavelet in many monitoring industrial processes due to its property of discontinuity but it is ideal for step change detection.

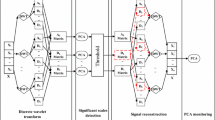
The different steps to construct control chart to monitor Profiles (Fig. 3)

Fig. 3

Monitoring endpoint using W-Hotelling and W-MEWMA

In phase I:

Step 1: Apply the proposed algorithm named Spectra Peak selection to select the significant reactant and product wavelengths, respectively.

Step 2: From the selected significant wavelengths, compute the control limit in Main etch interval.

In phase II: At this stage, it is an online-monitoring procedure

For etch run(s),

Step 1: Plot W-Hotelling (W-MEWMA) statistic in a chart.

Step 2: Detect endpoint when statistic crosses the control limit.

The control limit is given as follows:

$$\begin{aligned} \mathrm{UCL}=\mathrm{CL}+2*\mathrm{std(CL)} \end{aligned}$$

(35)

CL and std (CL) for Hotelling chart are mean and standard deviation of Hotelling statistic based on intervals ME. CL and std (CL) for MEWMA chart are mean and standard deviation of MEWMA statistic based on intervals ME.

It should be noted, for experts they have a previous knowledge about the representative wavelengths in plasma etch process. This work concentrated only on selected wavelengths could be able to detect the important wavelengths without specifying its associated gas. As a result, the main identified wavelengths (species) will be used in the future to be monitored on the same Plasma etch process operating in the same condition. The upper control limit is used as thresholded value by which if the process data cross this line in increasing or decreasing direction, then endpoint is detected. The following Fig. 3 presents the steps of constructing W-Hotelling and W-MEWMA.

Monitoring Hotelling regression

To detect the endpoint, the need to estimate a relation is felt. The profile will be studied according to two relations:

• 1. Polynomial order 2 (curve, $y = ax^2+b$).

• 2. Polynomial order 1 (linear regression $y = ax +b$).

where a and b refer to the slope and intercept, respectively. The independent variable is unit time, $i = 1,\ldots ,872$. The proposed dependent variable is W-mean-Hotelling statistic intensities. This choice is justified by first the power of Hotelling statistic to detect mean shift more than SD and CV shifts and second instead of monitoring each independently, the selection of the fifty important wavelengths to construct Hotelling will make the control of profile more easier and minimize the wrong individual variable detection. To estimate of each one of aforementioned relations, the decomposition level will not be associated with the optimal level. This is because the decomposed coefficient at optimal level could really damage the relation.

The proposed procedure is given below:

• 1. Compute W-mean Hotelling statistic for the historical data.

• 2. Keep only the W-mean Hotelling statistic values presenting steady state.

• 3. Estimate the target regression (profile) using in-control W-mean-Hotelling values.

• 4. Divide each online data onto window(s).

• 5. Estimate W-mean Hotelling relation for each window.

• 6. Identify the window to which the endpoint belongs.

It should be noted that the window size is equal to 100 intensities and it is the adequate size to estimate a reliable regression, based on Green (1991), Harris (1985) and Wilson Van Voorhis and Morgan (2007). The following Fig. 4 exposed the steps of constructing W-Hotelling profile for linear target profile.

Fig. 4

Monitoring endpoint using Linear W-Hotelling regression

Results and discussion

Results and discussion for W-Hotelling and W-MEWMA

To start for W-mean Hotelling and W-mean-MEMA the data process and control limits are constructed based on approximations. While for W-SD-Hotelling, W-SD-MEWMA, W-CV-Hotelling and W-CV-MEWMA charts, the monitored intensities and limits are computed based on details. The screen shot shows the first twenty six important wavelengths from one run after putting to use new proposed algorithm, with their peaks. Hotelling and MEWMA statistics for the selected wavelength will be calculated during the interval 50–872, at different levels of decomposition and with different wavelet types. The detection is reached when data cross the Upper control limit.

W-Hotelling Based on Figs. 5 and 6, the endpoint for W-mean Hotelling is detected on the right time; there is no time delay. The endpoint is reached when data cross thresholded W-mean-Hotelling value (UCL). There is no significant incidence on the result using db1 or db8. While, the levels of decomposition have an effect on the endpoint detection; only for the optimal level 6, EP is reached at the right moment.

Fig. 5

W-mean-Hotelling chart for db1 and 8, decomposed till level 3

Fig. 6

The W-mean-Hotelling control chart at the optimal level 6

Based on Figs. 7 and 8, W-CV-hotelling could not detect the EP at the right moment. While W-SD-Hotelling can detect the EP on the right time, there is no time delay.

Fig. 7

The W-CV Hotelling control chart

Fig. 8

The W-SD Hotelling control chart

W-MEWMA Based on Figs. 9, 10 and 11 there is no incidence if the level of decomposition or wavelet types are changed. It should be noted that for some control charts, the choice of other wavelet types could affect the detection of endpoint, especially, if the signal is nearest to the threshold and at the same time representing high fluctuations.

Fig. 9

The W-mean MEWMA control chart

Fig. 10

The W-CV MEWMA control chart

Fig. 11

The W-SD MEWMA control chart at two levels of decomposition and two wavelet types

As can be seen, W-CV-MEWMA is not steady and then it becomes steady, hence one could construct control limits from OE interval and then monitor the process which is moving from unstable to stable one. Figure 12 shows the Hotelling chart for level 3 and 6. Figure 13 presents Hotelling chart for W-mean using three different wavelet types of Daubechies family. Hence, there is no significant incidence on endpoint detection if different wavelet types (db1, db4, db8) are chosen. While, if there is an increase in the level of decomposition (from 1 to 8) till the optimal level, one moves from under-etched wafer to endpoint detection.

Fig. 12

The W-mean Hotelling for level 3 and 6

Fig. 13

The W-mean Hotelling for DB1, DB4, DB8

The W-Hotelling chart

For mean, there is no time delay.

For coefficient of variation, the endpoint is detected before the right moment.

For standard deviation, the endpoint is detectable on the right moment.

The W-MEWMA chart

For the mean and SD, the EP is detected on the right time.

For the CV, the EP is detected before the usual endpoint time.

Results and discussion based on monitoring wavelet windowed regression

Polynomial relation order 2

Figure 14 presents the estimated windowed profiles.

Fig. 14

Profile estimation function (f(x)) at level 3 and 6

Linear regression From in-control W-mean-Hotelling statistic, the target profile will be estimated. To estimate the aforementioned relation for the online data, the etch data will be divided in several windows, the size of each window is 100 points and the starting point is from the 40th point. The first fourty points refer to the initial transient state and then the main state process is attained which becomes approximately stable. Recall that the chosen size of windows or more precisely the sample size to estimate the relation is 100 based on A Rough Rule of Thumb for Determining Sample Sizes (Wilson Van Voorhis et al. 2007). From Fig. 15, the W-mean Hotelling profiles have the ability to detect the EP. The EP is detected in the first encountered profile corresponding to the profile change compared to the target mean.

Fig. 15

The estimated W-Hotelling linear function (f(x))

To point out, the W-mean-Hotelling regression is able to detect the endpoint. Both SD nd CV statistics are not able to detect EP if they are used as dependent variable. The size of window is 100 which is the most appropriate, if we increase or decrease it, the estimated regression will be erroneous and will conduct to false EPD. The starting point is from the 40th to preserve fixed window size till the end of process. This proposed method can only determine the window containing endpoint event. At the fifth window, the student statistic is significant referring to reliable statistic.

Conclusion

In this paper, we have tried to improve the endpoint detection in plasma etch process by employing in the first stage a new proposed algorithm named spectra peak section (SPS) and in the second stage we have combined wavelet analysis with modified multivariate charts (Hotelling and MEWMA). The results are investigated for 200 runs with different associations to ensure about the pertinence of the findings. Three statistics are investigated to detect the endpoint, mean, SD and CV. We have also investigated different wavelet types and for two different levels of decomposition. The findings for W-Hotelling chart, both w-mean Hotelling and w-SD Hotelling are able to detect the endpoint. For the coefficient of variation, when the limits are computed based on main etch, the right endpoint is undetectable but we can notice that this chart can be used as an indicator of the endpoint approaches or also the W-CV Hotelling could be constructed based on the over etch interval by which the endpoint is detected directly and easily if the process enters in a steady state. Moreover, only Hotelling for SD and CV are computed based on details coefficients because those coefficients are the most reliable and appropriate for monitoring variance. The same conclusion made by Hotelling is recorded for the MEWMA statistic. Then concerning the proposed estimated regression method, both estimated w-Hotelling regressions are able to identify the endpoint window only for the mean. The W-SD and W-CV Hotelling estimated regressions are not able to detect the change and hence to identify the non-target profile. In addition, to monitor the mean shift is beneficial to use directly the approximation coefficients while to monitor the SD and CV, it is appropriate to use detailed coefficients because the latter present high noise translated by high variance.