Introduction

Production based on the needs and customers’ satisfaction, as well as material and products flow cost control are considered the main goals of manufacturers in different industries. Moreover, for a constant presence in the current competitive markets, it is particularly important to develop the relationships between suppliers and big manufacturers, efficiency control, maximize the value of returned items, and guarantee their systematic disposal, as well as increase environmental and/or legal concerns. Due to the overall mentioned issues, the concept of reverse logistic and closed-loop supply chain (CLSC) is significantly important (Francas and Minner 2009). In fact, the reverse logistic in the CLSC involves the precise transport, on time, and accurate transition of customer’s usable and unusable products to the right unit through the supply chain. This type of supply chain requires an essential concern in environmental issues to enhance the performance of overall supply chain regarding consistency and business operational criteria (Das and Posinasetti 2015). During recent years, researchers have been interested in this process in CLSC optimization. For example, Lee et al. (2009) formulized a mathematical model for a general network of CLSC with a supplier defining optimal amount of process and disassembly centers. Shi et al. (2010) developed a mathematical model for optimizing regeneracy system profit by developing a solution approach based on Lagrangian and Gradient algorithm. Moreover, in another research, Shi et al. (2011) studied a CLSC network in which demand and returned items are uncertain. Roghanian and Pazhoheshfar (2014) suggested a potential model using integer linear programming for designing a multi-product reverse logistic network and estimating demand with the minimum cost in an uncertain environment applied by production and recycle centers. In another study, Kaya and Urek (2016) suggested a mixed integer nonlinear programming model along with innovative solutions for decision making in location, inventory control, and pricing problems in a CLSC. A review of studies on the subject reveals that most researchers were involved with formulization of CLSC networks using facility location while not many of them used supplier selection to configure an integrated CLSC. Accordingly, in their research, Amin and Zhang (2012) suggested a multi-objective integrated model for configuration and supplier selection in the CLSC. Afterwards, Ramezani et al. (2013) presented a stochastic multi-objective model for designing an onward three-level logistic network (including supplier, manufacturer, and distribution centers), as well as a bi-level reverse logistic network (including collector and disposal sites) considering profit optimization, quality level, and responding to customer. Bottani et al. (2015) examined a model with multi-objective optimization of CLSC asset management including a pallet supplier, manufacturer, and seven retails based on Economic Order Quantity (EOQ) policy. Zhang et al. (2015) proposed a dual channel closed-loop supply chain model that improves the sustainability of products. They also used a two-stage optimization technique and Nash bargaining game to evaluate the impact of retail services and the degree of customer loyalty to the retail channel on the pricing of players in the centralized and decentralized dual-channel supply chain.

In general, in a buyer–supplier system, inventory decision making is structured independently. Inventory control problems have been investigated in many studies (Taleizadeh et al. 2009, 2010a; Hsueh 2011). Suppliers sometimes offer special sale prices to decrease inventories of certain items (Kim and Hwang 1989; Taleizadeh et al. 2010b, 2012, 2013a; Duan et al. 2010). Therefore, the supplier sets its favorable policies based on the product’s output and demand while the buyer may set its favorable policies to calculate order from supplier. Besides, in a competitive environment, one policy for suppliers to hold shares in the market is offering customers some incentives like discounts (Dahel 2003; Kokangul and Susuz 2009; Taleizadeh et al. 2013b; Taleizadeh and Pentico 2014). Because a mass purchase buyer would like to buy a larger amount of products with a lower unit price. A supplier offering quantity discounts is a common strategy to entice the buyers to purchase more (Monahan 1984; Taleizadeh et al. 2015). The main assumption underlying this policy is that competition is dynamic and the existing competition features may change after a new competitor arrives. Kamali et al. (2011) developed a multi-objective mixed nonlinear integer programming model for the first time to coordinate the system of single buyer and multi-vendors’ multi-period with certain demand under all-unit quantity discount policy for vendors. In the study, they used quantity discount policy per every unit of products for vendors as an incentive factor against the buyer. Accordingly, Hammami et al. (2014) suggested a stochastic model for supplier selection aiming at optimization of multi-period system’s total cost with diverse buyers and quantity discount.

During last years, considering the increased necessity of availability assurance of an efficient and coordinated supply chain, supplier selection is as a basic component. Because, one of the most important relationships between the supply chain members is the coordination between the focal company and the suppliers (Yousefi et al. 2016). Studies on supplier selection are mostly focused on decision-making methods (Ho et al. 2010). In the CLSC, the relationship between manufacturer and supplier is set in a closed-loop while in reverse logistic, new parts are provided from external suppliers. The point is that, compared to open-loop supply chains (OLSC), criteria related to production performance and parts’ features should be more important in CLSCs and reverse logistics. Because not only parts and supplier criteria should be considered, but also process criteria such as process ability and flexibility are essential. Furthermore, criteria related to environment and environmental protection is among reverse logistic and CLSC goals (Amin and Zhang 2012). Therefore, a close attention should be paid to process elements in supplier selection process of reverse logistic.

Although many researches have been carried out on the supplier selection in the open-loop supply chain, supplier selection in a closed-loop supply chain is a new issue. Govindan et al. (2015) studied 33 articles on green supplier selection examining different criteria and methods up to 2011. In their perspective, popular approaches in green supplier selection include Analytic Hierarchy Process (AHP), Analytic Network Process (ANP), and Data Envelopment Analysis (DEA). Most of these methods have been offered for open-loop supply chain networks. Gradually, regarding the increased existing needs, researchers started either to make use of integrated methods or offer complicated mathematical models. For example, Kannan et al. (2013) used an integrated multi-criteria decision-making and multi-objective programming method for supplier selection and allocation in a certain green supply chain. On the other hand, due to the management focus on the efficiency and previous performance improvement in a competitive market, integrated approaches based on DEA are particularly important. To explain the competitive condition of market, an appropriate option is to use the game theory of cooperation, which has a considerable potential in management applications and supply chain performance improvement. Due to the ability of game theory to be integrated with most sciences, many studies have been executed in the field of designing and coordinating of supply chain’s different levels including effective designing and supply chain management (Talluri and Baker 2002), coordination of single-vendor multi-buyer supply chain (Chan and Kingsman 2007; Leng and Parlar 2010), and optimal supplier selection, pricing and inventory policy making in supply chain (Huang et al. 2012).

Therefore, from the previous studies, it can be concluded that for the first time, using multi-objective programming based on DEA–Nash bargaining game, the present study optimizes the CLSC with quantity discount policy and efficient supplier selection in a competitive environment. In fact, in this study, in addition to the maximization of profit, the concept of efficiency and competition, utilizing integrated DEA and Nash bargaining game approach has been added. In addition to synchronized evaluation and efficient supplier selection for different parts in a competitive environment, the proposed model makes decisions for set-up of refurbishing and disassembly sites. The general structure of the present study is as follows; the second section of the study is devoted to statement of the problem. The third section examines the proposed model. “Solution approach” prepares for an example to be tested in “Analysis of the results” in which computational results are presented and analyzed. Finally, in the last section, conclusion is presented along with suggestions for future more extended researches.

Statement of the problem

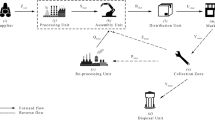
In this study, a CLSC network is studied that consist of disassembly and refurbishing sectors, as well as a sector for dispose of used products. Being under the control of manufacturer, this network’s production is in accordance with demand. After the product was used by the customer and some of them were returned, they are sent to the disassembly site. Afterwards, the returned products are separated into reusable and waste parts. The waste parts are sent to the disposal site while the reusable parts are sent to the refurbishing site to be remade and used as new parts in the inventory. It should be noted that disassembly, disposal and refurbishing sites have limited capacity. Meanwhile, according to demand and refurbished parts, the manufacturer attempts to purchase new parts from external suppliers. In the following, the operational flows between members in a CLSC network are shown in Fig. 1.

Fig. 1
figure 1

The operational flows between members in a CLSC network

Full size image

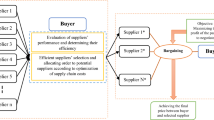
On the other hand, as expressed, one of the most essential relationships between members of the supply chain is coordinating manufacturer (buyer) and suppliers in the supply chain, including the CLSC. So, with coordination among the members can be achieved an efficient supply chain. In the meantime, selecting suppliers based on the perspective of the buyer and allocating orders to their suppliers are one of the main issues to optimize the supply chain in various aspects such as reducing costs in the various policies available on the market that each member considers it. The aim of this study is modeling selection of suppliers in the CLSC considering various dimensions of the real world and using mathematical methods. So in this study, in addition to the maximization of profit and minimization of defective and delivery delay rates (using multi-objective programing), the concept of efficiency and competition, utilizing integrated DEA and Nash bargaining game approach has been added. Also, in this study for consideration the available policies between members of the chain, it is assumed that external suppliers—to increase their sales—perform the quantity discount policy. Also, the buyer to produce final products, to increase customer satisfaction, consider a policy based on controlling the supplier evaluation criteria such as safety and green packaging in the form of efficiency. Likewise, the external suppliers try to achieve the minimum efficiency interested by buyers per each needed part due to the competitive environment. This competition so that suppliers competing with others to sell their parts and improve the supply parts criteria from the perspective of the buyer’s (green supply criteria) and on the other hand, buyer is trying to select a supplier that have necessary efficiency as green choice score and had a higher score in competition with others. Therefore, in this study in addition to purchase price, criteria such as efficiency (according to the CLSC criteria), defective, and delivery delay rates are of great importance in supplier selection and order allocation. Because, coordination and cooperation between the two resources of manufacturer namely refurbishing site and suppliers can affect the production rate and finally change the products cost. Moreover, lack of returned parts and new parts lead to an increase in the inventory maintenance costs. Therefore, another strategic decision is choosing the refurbishing site location. When there are several alternatives for parts refurbishing site, manufacturer prefers to select the one with the lowest cost. In the following, the proposed model based on the problem is presented so the results demonstrate selection of suppliers in the competitive environment, with selecting the refurbishing sites, and determine the number of products and parts in each sector of the CLSC network.

Proposed model

In this section, the CLSC is formulized using multi-objective programming model. The four-objective model is based on DEA–Nash bargaining game approach in which some efficient suppliers are selected within a competitive environment with considering quantity discount intervals, so that, the supply chain profit increases while delivery delay and defective rates decrease. Not only it can help to make decisions in supplier selection, as well as set-up of refurbishing and disassembly sites considering objectives such as profit optimization, but also it determines the number of products and parts in each network’s sector. In the following, assumptions, indexes, parameters, and the decision variables of the problem are presented in Table 1. Then, the problem is formulized as a mathematical four-objective model.

Table 1 Assumptions, indexes, parameters, and decision variables of the proposed model
Full size table

As mentioned above, the proposed model is a multi-objective programming model. The objective functions include total profit, defective rate, delivery delay rate, and efficiency in competitive environment that are investigated in the following.

Total profit

Objective function z 1 mentioned in Eq. (1) maximizes the total profit. The first section of this objective function indicates the profit resulted from product selling. The second section indicates the cost of buying parts from suppliers considering quantity policy. So that, when it falls into a discount interval, the proposed price is exerted to all purchase quantity. The third section indicates cost of disassembly taken place in disassembly site, and it consisted of disassembly cost of each unit multiply the number of parts to be disassembled. The cost of refurbishing and disposal sites is calculated in sections four and five. Furthermore, the sixth and seventh sections indicate the set-up cost of refurbishing and disassembly sites. It is to be noted that refurbishing sites are selected based on the maximum profit.

$${\text{Max}}\,z_{1} = \sum\limits_{j = 1}^{J} {P_{j} } (S_{j} - C_{j} ) - \sum\limits_{i = 1}^{I} {\sum\limits_{k = 1}^{K} {\sum\limits_{d = 1}^{{D_{ik} }} {r_{ikd} q_{ikd} } } } - \sum\limits_{i = 1}^{I} {f_{i} T_{i} } - \sum\limits_{i = 1}^{I} {\sum\limits_{l = 1}^{L} {O_{il} X_{il} } } - \sum\limits_{i = 1}^{I} {h_{i} } V_{i} - \sum\limits_{l - 1}^{I} {\sum\limits_{l = 1}^{L} {P_{il} y_{il} } } - \sum\limits_{j = 1}^{J} {d_{j} } y_{j}$$
(1)

Defective rate

Objective function z 2 mentioned in Eq. (2) minimizes the defective rate of parts bought from selected external suppliers. So that, as much as possible, suppliers with less defective rates are selected.

$${\text{Min}}\,z_{2} = \sum\limits_{i = 1}^{I} {\sum\limits_{k = 1}^{K} {S_{ik} q_{ik} } }$$
(2)

Delivery delay rate

Objective function z 3 mentioned in Eq. (3) minimizes the delivery delay rate of parts bought from selected external suppliers. So that, as much as possible, suppliers with less delivery delay rates are selected.

$${\text{Min}}\,z_{3} = \sum\limits_{i = 1}^{I} {\sum\limits_{k = 1}^{K} {H_{ik} q_{ik} } }$$
(3)

Efficiency in competitive environment

In today’s world, DEA is known as one of the most important methods for efficiency evaluation. In general, the efficiency is defined as the level and quality at which total interested goals are achieved (Färe et al. 1985). In 1957, Farrell (1957) suggested this method by measuring performance of one production unit. In his model, only one input and one output were considered. He failed to develop his model in multi-input/output conditions. Afterwards, other scientists like Lee et al. (2001) developed Farrell model proposing a new model that was able to measure efficiency considering multi-input/multi-output and was then named data envelopment analysis (DEA). This method in various fields such as energy systems (Rezaee et al. 2012a), manufacturing systems (Baghery et al. 2016; Rezaee et al. 2016a), banking systems (Shafiee et al. 2016) and healthcare systems (Rezaee et al. 2016b), have been used. In general, DEA popularity comes from its ability to examine complicated and often unclear relationships between several inputs and outputs. Principally, using mathematical models, efficiency of one unit is optimized over other units; that is, relative efficiency of each Decision Making Unit (DMU) is evaluated based on its inputs and outputs. However, it should be noted that the evaluated units should be quite equal, i.e., with quite similar inputs and outputs. In some cases, due to excess of decision-making units, too many linear programming models are required resulting in a time consuming solution process. In this regard, in their study of integrated locating-DEA models, Klimberg and Ratick (2008) proposed a model named Simultaneous Data Envelopment Analysis (SDEA) to remove the problem in 2008. Accordingly, in the present study, SDEA model is used to simultaneously calculate the efficiency of candidate suppliers.

On the other hand, this study made use of game theory to create a competitive environment between suppliers. This theory widely deals with multi-factor decision-making problems in the state of conflict and cooperation. Therefore, in this research, to demonstrate competitive state, Nash bargaining game is used which is known as a cooperative game. This game in various fields such as performance evaluation of health centers (Rezaee et al. 2012b), supplier evaluation (Wang and Li 2014), power plants evaluation (Rezaee 2015), network design (Avrachenkov et al. 2015), and comparison of operational and spatial efficiencies in urban transportation systems (Rezaee et al. 2016c), have been used. In Nash bargaining game, players (suppliers) try to find optimal solutions in a competition. In this regard, Nash (1950) suggested a bargaining solution known as Pareto optimization for bargaining game. Nash’s solution in a bargaining state is an agreement through which individuals’ utility multiplication is optimized. This model requires a feasible compact and convex set including some resultant vectors; so that, each individual result is larger than result obtained from single breakdown point. For traditional bargaining problem, Nash (1950) indicated that there is an exceptional solution called Nash solution that satisfies invariance quadruple conditions, Pareto optimization, independence of irrelevant alternative, and symmetry. This solution is attainable through solving the following optimization problem:

$$\mathop {\text{Max}}\limits_{{\mathop u\limits^{ \to } \in S,\mathop u\limits^{ \to } \ge \mathop b\limits^{ \to } }} = \prod\limits_{i = 1}^{I} {(u_{i} - b_{i} )}$$
(4)

The function mentioned in Eq. (4) leads to Nash solution when players’ utility u is attainable from the strategy set S. Also, the resulted utilities should be larger and/or equal to the minimum utility of players b. So in this section, aiming at efficiency optimization, supplier selection is examined using DEA model. This model aims to find states in which buyer who need different parts to produce their final product, seek efficient suppliers. In a competitive environment, it is assumed that the buyer defines a minimum efficiency level of supplier selection per each part. This issue creates a competitive environment for suppliers to build better parts according to buyer’s criteria. Combining SDEA with Nash bargaining game, and considering the minimum required efficiency per each part (E i ), we have the following objective function for supplier selection in a competitive environment:

$${\text{Max}}\,Z_{4} = \sum\limits_{i = 1}^{I} {\prod\limits_{k = 1}^{K} {\left( {(1 - e_{ik} ) - E_{i} } \right)} }$$
(5)

The above mentioned function seeks more efficient supplier selection for each part creating competition between suppliers. Constraints for this objective function, as well as for other objective functions are stated in the following.

$$q_{ik} = \sum\limits_{d = 1}^{{D_{ik} }} {q_{ikd} } \quad \forall i,k$$
(6)
$$q_{ikd} \le u^{\prime}_{ikd} y_{ikd} \quad \forall i,k,d$$
(7)
$$q_{ikd} \ge u_{ik,d - 1} y_{ikd} \quad \forall i,k,d$$
(8)
$$\sum\limits_{d = 1}^{{D_{ik} }} {y_{ikd} } \le 1\quad \forall i,k$$
(9)
$$\sum\limits_{d = 1}^{{D_{ik} }} {y_{ikd} } = y_{ik} \quad \forall i,k$$
(10)
$$\sum\limits_{j = 1}^{J} {q_{ij} } P_{j} = \sum\limits_{l = 1}^{L} {X_{il} } + \sum\limits_{k = 1}^{K} {q_{ik} } \quad \forall i$$
(11)
$$\sum\limits_{i = 1}^{I} {\sum\limits_{k = 1}^{K} {\sum\limits_{d = 1}^{{D_{ik} }} {r_{ikd} q_{ikd} } } } \le W$$
(12)
$$\sum\limits_{l = 1}^{L} {X_{il} } + V_{i} = T_{i} \quad \forall i$$
(13)
$$T_{i} = \sum\limits_{j = 1}^{J} {q_{ij} R_{j} } \quad \forall i$$
(14)
$$\sum\limits_{j = 1}^{J} {a_{j} P_{j} \le A}$$
(15)
$$e_{i} T_{i} \le P_{i} \quad \forall i$$
(16)
$$g_{il} X_{il} \le G_{il} y_{il} \quad \forall i,l$$
(17)
$$P_{j} = D_{j} \quad \forall j$$
(18)
$$\sum\limits_{i = 1}^{I} {X_{il} \le O_{i} T_{i} } \quad \forall i$$
(19)
$$V_{i} \le (1 - O_{i} )T_{i} \quad \forall i$$
(20)
$$R_{j} = H_{j} P_{j} \quad \forall j$$
(21)
$$\sum\limits_{l = 1}^{L} {\sum\limits_{i = 1}^{I} {y_{il} \le C} }$$
(22)
$$R_{j} \le My_{j} \quad \forall j$$
(23)
$$1 - e_{ik} \ge E_{i} \quad \forall i,k$$
(24)
$$\sum\limits_{i = 1}^{I} {V_{kpi} } I_{ikp} = e_{ik} \quad \forall i,k$$
(25)
$$\sum\limits_{n = 1}^{N} {U_{kin} } O_{nki} + e_{ik} = y_{ik} \quad \forall i,k$$
(26)
$$\sum\limits_{n = 1}^{N} {U_{kin} } O_{nzq} - \sum\limits_{m = 1}^{M} {V_{kim} I_{mzq} } \le 0\quad \forall k,\forall z(k \ne z),\forall i,\forall q(i \ne q)$$
(27)
$$U_{kin} \ge \varepsilon y_{ik} \quad \forall i,k,n$$
(28)
$$V_{kim} \ge \varepsilon y_{ik} \quad \forall i,k,m$$
(29)
$$U_{kin} O_{nki} \le y_{ik} \quad \forall i,k,n$$
(30)
$$\sum\limits_{k = 1}^{K} {y_{ik} } = N_{i} \quad \forall i$$
(31)
$$u^{\prime}_{ikd} = u_{ikd} - \varepsilon \quad \forall i,k,d$$
(32)
$$u_{ik0} = \varepsilon \quad \forall i,k$$
(33)
$$y_{il} ,y_{ik} ,y_{j} ,y_{ikd} \in \{ 0,1\} \quad \forall i,j,k,l,d$$
(34)
$$P_{j} ,R_{j} ,q_{ik} ,q_{ikd} ,e_{ik} ,T_{i} ,V_{i} ,X_{il} ,U_{kin} ,V_{kim} \ge 0\quad \forall i,j,k,l,d$$
(35)

Equation (6) guarantees that the amount of part i ordered from supplier k equals to total part i order in discount intervals offered by supplier k. Equations (7) and (8) show that the amount part i ordered from supplier k falls into discount interval offered by supplier k. Equation (9) states that in the case of selection supplier k for part i, order should be accomplished in only one of offered discount intervals. Equation (10) indicates the relationship between y ik and y ikd . Equation (11) guarantees that the number of produced parts equals to the total number of refurbished and purchased parts. Equation (12) indicates that costs of buying different parts for each selected supplier should not exceed the purchase budget available to the buyer. Equation (13) states that the disassembled parts equals to reusable and waste parts. Equation (14) indicates the relationship between parts and products. Equation (15) suggests that the amount of product manufacturing should be less than or equal to maximum production capacity. Equation (16) states that the amount of resources applied in part i for disassembly should be less than or equal to maximum capacity of disassembly site of part i. Equation (17) indicates that the applied resources for part i to be disassembled in set-up site l should be less than or equal to maximum capacity of refurbishing site l for part i. Equation (18) shows that the number of manufactured products should be equal to demand. Equations (19) and (20) indicate the optimal percentage of reusable and waste parts. Equation (21) implies the constraint of maximum percentage of returned parts. Equation (22) shows that the number of set-up refurbishing sites should be less than and/or equal to maximum number of launchable refurbishing sites. Equation (23) guarantees that if there is j returned production, disassembly site for production j is to be set up. Constraint (24) indicates that per each part those suppliers are selected who have the minimum efficiency required by that part. Equation (25) guarantees that the harmonized total input of each decision-making units (a combination of suppliers and parts) equals to variable zero and one. This equation should be considered in all decision-making units. Equation (26) implies the amount of inefficiency for harmonized total output of each decision-making unit, as well. This equation should be considered in all decision-making units. Equation (27) indicates that the harmonized total output should be less than its correspondent harmonized total input. Equations (28) and (29) indicate that input and output weights should be a non-negative value. Constraint (30) guarantees that the harmonized output for each decision making unit, as well as for each output type is less than and/or equal to 1. Equation (31) indicates the maximum number of selected suppliers per each part. Equations (32) and (33) show the quantity constraints for discount intervals; and Eqs. (34) and (35) indicate the sign limitation of decision-making variables.

Solution approach

It is obvious that the above mentioned objective functions are in conflict with each other; and optimization according to a certain objective function in a certain time, leads to deviation from optimal solutions of other objective functions. Therefore, to optimize all four objective functions mentioned above, a method is required through which all objectives are optimized simultaneously (Miettinen 1999). In such circumstances, the global criteria method works toward finding an agreement between all objectives, so that it minimizes the total relative deviance of all objectives from its optimal values (z i *). This section aims to change a multi-objective function into a single-objective function changing the objective functions of the main model in different intervals. Thus, to avoid the effect of these changes on the results, the global criteria method is used as a normalization method. Consequently, using global criteria method, the final objective function is expressed as Eq. (36):

$$\begin{aligned} {\text{Min}}\,Z & = w_{1} \times \frac{{z_{1}^{*} - \left[ {\sum\limits_{j = 1}^{J} {P_{j} } (S_{j} - C_{j} ) - \sum\limits_{i = 1}^{I} {\sum\limits_{k = 1}^{K} {\sum\limits_{d = 1}^{{D_{ik} }} {r_{ikd} q_{ikd} } } } - \sum\limits_{i = 1}^{I} {f_{i} T_{i} } - \sum\limits_{i = 1}^{I} {\sum\limits_{l = 1}^{L} {O_{il} X_{il} } } - \sum\limits_{i = 1}^{I} {h_{i} } V_{i} - \sum\limits_{l - 1}^{I} {\sum\limits_{l = 1}^{L} {P_{il} y_{il} } } - \sum\limits_{j = 1}^{J} {d_{j} } y_{j} } \right]}}{{z_{1}^{*} }} \\ & \quad + w_{2} \times \frac{{\left[ {\sum\limits_{i = 1}^{I} {\sum\limits_{k = 1}^{K} {S_{ik} q_{ik} } } } \right] - z_{2}^{*} }}{{z_{2}^{*} }} + w_{3} \times \frac{{\left[ {\sum\limits_{i = 1}^{I} {\sum\limits_{k = 1}^{K} {H_{ik} q_{ik} } } } \right] - z_{3}^{*} }}{{z_{3}^{*} }} + w_{4} \times \frac{{z_{4}^{*} - \left[ {\sum\limits_{i = 1}^{I} {\prod\limits_{k = 1}^{K} {\left( {(1 - e_{ik} ) - E_{i} } \right)} } } \right]}}{{z_{4}^{*} }} \\ \end{aligned}$$
(36)

As shown in Eq. (36), to consider decision maker’s idea, different weights may be given to the objective functions; so that w i is ith objective functions’ weight according to decision maker’s idea and equation ∑  4 i=1 w i  = 1 is established. Using this approach, if management gave the function a larger weight, in the state of simultaneous optimization, the result would be closer to the interested function’s optimal solution. In Eq. (36), first, the optimal amount of each objective function (z i *) is calculated independently considering all constraints of problem, and a new function is created as expressed in the equation.

Analysis of the results

In this section, an illustrative example is considered to validate the proposed model. The followings are assumed: there are five candidate suppliers for five parts required by the manufacturer in a CLSC. The manufacturer is going to select at the most three efficient suppliers according to managerial criteria; so that the maximum capacity of manufacturing factory and the available budget are, respectively, 200,000 and 750,000 monetary unit. Further, it is assumed that the maximum number of refurbishing sites is five sites; the maximum percentage of reusable parts and maximum percentage of returned products are equal to 0.5. Other data needed for CLSC optimization are presented in Tables 2, 3, 4, 5 and 6 according to Amin and Zhang (2012). Moreover, needed data on discount intervals and prices suggested by suppliers are simulated and shown in Table 7.

Table 2 Refurbishing sites’ parameters
Full size table
Table 3 Product’s parameters
Full size table
Table 4 Amount of part i used in each j product unit (q ij )
Full size table
Table 5 Part’s parameters
Full size table
Table 6 Parameters of suppliers and manufactured parts
Full size table
Table 7 Quantity discount intervals
Full size table

Moreover, for efficiency evaluation, an input and two outputs were assigned to each candidate supplier, as well as per each part. In the example, product transportation cost was defined as input I 1ki (minimum of which is desirable) while product safety and green packaging was defined as outputs O 1ki and O 2ki (maximum of which is desirable). Values of these criteria are provided in Table 8.

Table 8 Input and output values for each decision making unit
Full size table

In the first step, independent optimization of objective functions was performed using Lingo 14.0 software. Values for objective functions are highlighted in Table 9. These values were used as input for global criteria method so that all four functions were optimized simultaneously. Now, assuming that the decision maker has different ideas about weighting the four functions, global criteria method was performed. New values of the four functions in different weight status are presented in Table 9.

Table 9 Independent and simultaneous optimization of objective functions for different weight sets
Full size table

The last four columns of Table 9 show the objective functions’ independent optimization. Considering objective functions’ values during the simultaneous optimization for each weight set, it can be found that these values get away from their independent values, i.e., 368,102, 3114.58, 3758.375, and 0.09355841. The reason is in simultaneous optimization that indicates the effect of each objective function on CLSC optimization, supplier selection, and order allocation to suppliers in a competitive environment. Figures 2, 3 and 4 show efficiency function performance compared with other functions in a competitive environment. It should be noted that the horizontal graph of each three graphs indicates the efficiency function’s value for each different weight set in a competitive environment with ascending arrangement. According to Fig. 2, it can be found that the high efficiency function values mean lower organization profit. It is natural due this fact that, considering the criteria, highly efficient suppliers require more costs to be paid behalf of the organization leading to a lower profit. Figure 3 shows the efficiency objective function compared to defective rate. Considering the objective function of defective rate is minimization type, low values of defective rate lie in the beginning section of graph along with low efficiency values. That means the considered criteria are in conflict with defective rate and that indicate the importance of considering efficiency function. Moreover, in Fig. 4, except results S03, S11, and S13, other results lie in an identical interval. In this regard, it cannot be concluded that there is an especial relationship between efficiency function and delivery delay rate. Of course, these analyses are special to the example examined in this study while different analysis types are possible for different data. In the following, the amounts of allocated order to suppliers per each part in independent and simultaneous optimization are shown in Table 10.

Fig. 2
figure 2

Checking simultaneous performance of total profit and efficiency functions in different weight sets

Full size image
Fig. 3
figure 3

Checking simultaneous performance of defective rate and efficiency functions in different weight sets

Full size image
Fig. 4
figure 4

Checking simultaneous performance of delivery delay rate and efficiency functions in different weight sets

Full size image
Table 10 The amount of allocated order to suppliers in independent and simultaneous optimization of objective functions
Full size table

Comparing the amount of allocated orders in objective function’s independent and simultaneous optimization, it can be concluded that all functions are effective in supplier selection and order allocation processes, and the manufacturer (buyer)-suppliers coordination is fulfilled efficiently according to manufacturer quantity discount policy. Considering the applied approach, it can be claimed that giving more importance and weight to a certain function moves the resulted answer toward that function’s optimal value. More analysis on the findings indicates that those suppliers with acceptable supply chain’s profit maximization, as well as acceptable efficiency, defective rate, and delivery delay are selected. Indeed, Table 10 shows that function’s simultaneous optimization causes an effect on each function’s independent results leading to changes in items such as number of selected suppliers per each part, list of suppliers per each part, amount of allocated orders to selected suppliers per each part, and order discount interval selection. Other results obtained from simultaneous function optimization in a CLSC are presented in Table 11.

Table 11 Other results from simultaneous optimization of objective functions
Full size table

Reviewing Tables 10 and 11, it can be claimed that amounts of parts ordered from suppliers, amount of waste and disassembly parts, as well as amounts of production and returned items during decision making period are determined in such a way that the current costs are minimized, while model limitations such as the number of maximum supplier selection per each part, maximum level of suppliers’ discount interval (supplier’s capacity), buyer’s budget, and other constraints are not violated in a competitive environment. Furthermore, Table 11 states that considering the presence of returned items, disassembly sites are settled for all products to maximize chain’s profit. Also, refurbishing sites 1, 2, and 4 are settled for refurbishing products so that part troubleshooting is done with the minimum site number avoiding extra set-up costs.

Conclusion

During recent years, reverse logistic and CLSC have been taken more serious due to increased environmental concerns, stronger laws, as well as its excessive trading profit. In addition, supplier selection and optimal order allocation are the most important process in a close-looped supply chain. So that in the real world, in the competitive environment, suppliers provide incentives to the buyer such as discount and guarantee of production parts efficiency. The main objective of this study was to develop a model for designing a CLSC considering efficiency in competitive environments, as well as external suppliers’ quantity discount policies. In other words, the aim of this study is adding both efficiency and competition concepts to dimensions of supplier selection problem in the CLSC. Therefore, an integrated model was proposed using multi-objective programming based on DEA–Nash bargaining game to cover the circumstances. This model was consisted four objectives including total profit, defective rate, delivery delay rate, and efficiency that then were put together into one objective using global criteria method. In addition to supplier selection, the proposed model adopts decisions related to refurbishing and disassembly site set-up, as well as part and product amounts in existing in closed-loop network’s ties including manufacturer and sites for disassembly, refurbishing, and disposal. So that, in a CLSC, to produce its productions, the manufacturer purchases its needed parts from external efficient suppliers and/or set-up refurbishing sites. The proposed model can be used in industries such as household electrical appliances, accessories and electronic components, automobile parts and similar cases. The results of simulated example show that increasing efficiency objective function is synonymous with decreasing organization (buyer) profit, because buyer pays more prices for selling parts from efficient suppliers. The results demonstrated that the criteria considered in the evaluation of suppliers’ efficiency are in conflict with the defective rate. It is specified the importance of taking the efficiency objective function. This study is expandable considering uncertainty of other model’s certain parameters or fuzzy demand. More expandable issues resulted from this study including simultaneous competition between manufacturers and suppliers, as well as studying the pricing process between them may be considered in future researches.