Abstract
Robust supplier selection problem, in a scenario-based approach has been proposed, when the demand and exchange rates are subject to uncertainties. First, a deterministic multi-objective mixed integer linear programming is developed; then, the robust counterpart of the proposed mixed integer linear programming is presented using the recent extension in robust optimization theory. We discuss decision variables, respectively, by a two-stage stochastic planning model, a robust stochastic optimization planning model which integrates worst case scenario in modeling approach and finally by equivalent deterministic planning model. The experimental study is carried out to compare the performances of the three models. Robust model resulted in remarkable cost saving and it illustrated that to cope with such uncertainties, we should consider them in advance in our planning. In our case study different supplier were selected due to this uncertainties and since supplier selection is a strategic decision, it is crucial to consider these uncertainties in planning approach.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Supplier selection is a strategic decision that determines the long viability of a company, particularly when purchasing costs represents a significant portion of the operating costs. The supplier selection is considered as a crucial part in achieving the objectives of an effective supply chain (Ng 2008). The decisions related to the supplier selection problem in the relevant literature are mainly related to which supplier to select and how much to order from each supplier in each period and over the planning horizon. Some researchers outlined and classified the significant risks associated with global outsourcing (Christopher et al. 2011; Sawik 2011).
One of the significant risks of global purchasing is the risk of uncertain changes in the currency exchange rates that affects the total supply chain cost. If the buyer does not consider these changes, selection and purchasing decisions will be suboptimal. It seems necessary that global supplier selection models consider exchange rates fluctuations to cope with challenges that purchasing managers are facing in global environments. The literature seems to be sparse on analytical approaches involving the currency fluctuation uncertainty in the supplier selection process. It should be noted that it is one of our underlying principles in this research paper. We model the currency fluctuation through a scenario-based approach. The motivation of this modeling will be presented in detail in “Literature review” and “Overall comment and problem statement”.
The remainder of this paper is organized as follows. “Literature review” presents a literature review on existing suppliers’ selection models, and variety of risks associated with the selection of suppliers. In particular, emphasis was placed on currency fluctuation risk and discounts. “Overall comment and problem statement” is dedicated to problem statement. “Problem formulation” addresses the mathematical formulation for the problem under study. In “Solution method” a solution method has been provided. In “Numerical study”, the computational experiments are presented. “Conclusions” argues the concluding remarks and future research direction.
Literature review
Many analytical techniques have been used to address the supplier’s selection problem. Ghodsypour and O’Brien (1998) integrated an analytical hierarchy process with a linear programing model to cope with both tangible and intangible factors in supplier selection problem. Thus, their objective function was total value of purchasing.
Ghodsypour and O’Brien (2001) developed a mixed integer non-liner programing model to solve a multiple sourcing problem. It takes into account the total cost of logistics, including net price, storage, and transportation and ordering costs in which the buyer has limitation on budget, quality, and service. For this purpose, they proposed an algorithm to solve the problem.
An innovative literature review has been done on supplier selection problem by De Boer et al. (2001). They classified this problem according to the supplier’s selection stage.
Wadhwa and Ravindran (2007) broadly clustered the related literature by the method used in modeling the program into three clusters including: single or multi-objective mathematical programming methods, and game theoretic methods. For a detailed review of these three clusters, we kindly refer the reader to (Wadhwa and Ravindran 2007).
Other researchers have addressed risk uncertainty or sourcing risk through quantitative models. A two-stage stochastic model has been introduced by Xu and Nozick (2009) in which they considered different disruption scenarios. One of the scenarios specified the severity of the production capability lost at each supplier’s site in each time period. In this work, the researchers integrated the transportation model selection with the supplier selection. However, their model ignored price discounts, inventory costs, exchange rate fluctuations. Their objective function was to minimize the expected cost over the planning horizon.
Hammami et al. (2012) focused on low cost supplier issue with the uncertainty of delivery lead times from supplier sites to buyer’s sites and emphasized the impact of the safety stock at the buyer’s site while ignoring the price discount and exchange rate uncertainty of their model.
Amid et al. (2009) presented a fuzzy multi-objective model to deal with the supplier selection problem. In their research suppliers offered price breaks as a function of order quantity. Their three objective functions were (a) minimizing the net cost, (b) minimizing the net rejected items, and (c) minimizing the net late deliveries.
Hammami et al. (2014), proposed a stochastic model for supplier selection problem which considers price discount and inventory decisions for different scenarios.
Mazdeh et al. (2015) investigated the problem of supplier selection and lot-sizing in two cases with and without discount. Given the np-harded origin of the problem, the researchers developed a heuristic algorithm to solve the problem. Azadnia et al. (2015) integrated sustainable supplier selection with lot-sizing decision in multi-period multi-product situation.
Overall comment and problem statement
Given the fact that supplier selection problem is a strategic decision, it is difficult to be changed or modified in a short period of time. Hence, these decisions should be made based on parameters fluctuations. Despite the important role of parameter fluctuations, the currency fluctuation risk addressed in our approach has not been fully explored yet. Moreover, relatively few studies, if any, have developed effective models for supplier selection problem addressing simultaneously the sourcing uncertainties and the price discounts. In addition, a DEA model is applied for measuring suppliers’ ranking, these rankings have been later used in our multi-objective model. To the best of our knowledge, there is no study in literature addressing robust optimization in this context. Stage of work is shown in Fig. 1.
Problem statement
The supplier selection problem is typically considered for long term, ranging from one to three years. The long lasting nature of strategic decisions requires to have a robust planning for every possible scenario. In this research, we developed a multi-objective supplier selection model that integrates the exchange rate fluctuation uncertainties with price discount while explicitly considering transportation and inventory costs. Then, the robust optimization is used in our modeling approach which is regarded as the best method in overtaking the uncertainties.
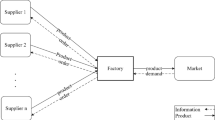
Our company is concerned with purchasing a product from heterogeneous suppliers over the planning horizon. The total amounts to be allocated to each supplier must be decided. Similarly, agreements must also be established. The set of suppliers are denoted by i. The total quantity bought from supplier i over the planning horizon is denoted by Q i based on which discounts are offered. A given supplier (i) offers discounts in N i intervals and a set of threshold quantities \(A_{i}^{n}\). The quantity \(A_{i}^{n}\) is the lower limit on the total purchased quantity bought from supplier i over the planning horizon. If \(A_{i}^{n} \le Q_{i} < A_{i}^{n + 1}\), then the unit price offered by supplier i on all purchased units is \(Pr_{i}^{n}\). Clearly, the larger n is, the smaller \(Pr_{i}^{n}\) will be, for each supplier i, the quantity \(A_{i}^{1}\) of the first discount interval is equal to the null value.
Since payment currencies of different suppliers differ, all prices are expressed in the currency of the parent company. Changes in the currency exchange rates are very difficult to predict in the long-term period. The difficulty economists have faced in finding an empirically successful exchange rate theory is well documented (Taylor 1995).
In this research to predict currency exchange rate fluctuations, different exchange rate scenarios on a quarterly basis are elaborated, some of which are published by financial organizations. Therefore, they are used in the current modeling approach.
We formulated the problem under study as a scenario-based stochastic model to address currency fluctuation. On the other hand, to cope with these uncertainties, we used a recent extension in robust optimization theory.
According to the time periods of the available currency fluctuation forecasts, the planning horizon has been divided into t period \(\left( {t \in \left\{ {1 \ldots T} \right\}} \right)\). For instance, if exchange rate scenarios are on a quarterly basis, then a period t would be a quarter. The set of all possible scenarios is denoted by \(\varOmega\). The exchange rate from the currency of supplier i to the standard currency in period t under scenario s is denoted by \(\alpha_{i}^{{t{\text{s}}}}\). The quantity \(p_{\text{s}}\) is the occurrence probability of each scenario s. The purchasing price depends on the order placement period while for a given scenario when exchange rate is attractive, buyer may order large quantities. We let \(q_{i}^{{t{\text{s}}}}\) represent the quantity ordered from supplier i in period t under scenario s. Ordering larger quantity may result in inventory issues which should be taken into account. \({\text{Inventory}}^{{t{\text{s}}}}\) denotes the inventory level at the beginning of period t under scenario s. At first, the efficiency of each supplier is evaluated using the DEA model. Then, the efficiency results are used in the second objective function. The first objective function was to minimize the total purchasing cost over the planning horizon while the second objective function is to maximize the rank of suppliers. In the first objective function, total cost is the sum of the supplier management, the purchasing price, the transportation cost, and the inventory cost. The supplier management cost is related to cost of doing business with suppliers and it occurs once the supplier is selected. By doing business with low-cost suppliers, management cost would be substantial and some hard work might be required to keep in line the low-cost suppliers. Quantity discounts were considered in the purchasing price. The transportation cost depended on the locations of suppliers, and finally average inventory level in each period is used to calculate the inventory cost for buyer. At the end, robust counterpart of deterministic problem was developed and the results were compared. The numerical example was obtained from STAM SANAT Company which is a large producer in automobile parts, spare part industry, and one of the Iran khodro’s suppliers. This company sources from multiple local and global suppliers, which is shown in Table 1. It is notable that this company is one of IRAN KHODRO’s suppliers; hence, it is under remarkably large competition and has to satisfy the demand of their customer with the best quality and in a timely manner.
Problem formulation
We developed a mixed integer scenario-based stochastic programing model for our supplier selection problem. First stage decisions (must be made immediately) included which suppliers to select and the total quantity to purchase from each supplier over the planning horizon. The second stage variables are the quantity ordered each period and inventory level. These variables are associated to each scenario and depend on first-stage variables.
Notations
First stage variable
-
\(Y_{i}\): Binary integer variables, \(Y_{i} = 1\) if supplier i was selected, 0 otherwise.
-
\(Q_{i}\): Total amount ordered from supplier i over the planning horizon.
-
\(e_{i}^{n}\): Binary integer variables, \(e_{i}^{n} = 1\) if the quantity purchased from supplier.
Second-stage variable
-
\(q_{i}^{{t{\text{s}}}}\): Quantity ordered from supplier i in period t under scenarios \({\text{s}}\).
-
\({\text{Inventory}}^{{t{\text{s}}}}\): Inventory level at the beginning of period t under scenario \({\text{s}}\).
Cost factors
-
\(Pr_{i}^{n}\): Supplier i’s Unit purchasing price in the currency of the supplier associated with its discount interval.
-
\({\text{TC}}_{i}\): Unit transportation cost from supplier i.
-
\(h^{t}\): Unit inventory holding cost over period t.
-
\({\text{MC}}_{i}\): Supplier i’s management cost.
-
\(D^{t}\): Demand in period t.
-
\(A_{i }^{n}\): Lower limit on the business volume of supplier i that corresponds to the discount interval n \(\left( {0 = A_{i}^{1} ,\forall i \in I} \right)\).
-
\(L_{i}^{t}\): Capacity of supplier i in period t.
-
\(\alpha_{i}^{{t{\text{s}}}}\): Exchange rate from the currency of supplier i to the standard currency.
-
\(p_{\text{s}}\): Probability of scenario \({\text{s}}\).
Objective functions
The objective function (1) minimized total cost z expressed in currency of reference. This cost was the sum of the supplier management cost, purchasing cost, and the inventory cost. All cost factors are expressed in the currency of reference except purchasing price.
Once the supplier is selected \((Y_{i} = 1)\), we have management cost. The quantity \(\mathop \sum \nolimits_{i \in I} {\text{MC}}_{i} Y_{i}\) is the total management cost for all selected suppliers. The unit purchasing price based on supplier i’s discount interval is \(\mathop \sum \nolimits_{n = 1}^{n = N} e_{i}^{n} Pr_{i}^{n}\). Under scenario \({\text{s}}\), the purchasing price is associated with the quantity \(q_{i}^{{t{\text{s}}}}\) in the currency of supplier i is \(\left( {\sum\nolimits_{n = 1}^{n = N} {e_{i}^{n} } Pr_{i}^{n} } \right)q_{i}^{t}\). It becomes \(\alpha_{i}^{t} \left( {\sum\nolimits_{n = 1}^{n = N} {e_{i}^{n} } Pr_{i}^{n} } \right)q_{i}^{t}\) in the currency of reference. Hence, the total purchasing price becomes \(\sum\nolimits_{i \in I} {\sum\nolimits_{t = 1}^{t = T} {\alpha_{i}^{t} } } \left( {\sum\nolimits_{n = 1}^{n = N} {e_{i}^{n} } Pr_{i}^{n} } \right)q_{i}^{t}\).
The transportation cost of the quantity \(q_{i}^{{t{\text{s}}}}\) from supplier i in period t under scenario s is \(q_{i}^{t} {\text{TC}}_{i}\). Inventory cost over the planning horizon is \(\sum\nolimits_{t = 1}^{t = T} {h^{t} } {\text{Invenotory}}^{t}\).
To linearize the objective function, new non-negative variables \(x_{i}^{tn}\), such as \(x_{i}^{tn} = e_{i}^{n} q_{i}^{t}\), are defined. Next, the objective function (1) is replaced with the new linear function (2), where \(x_{i}^{tn}\) is used instead of \(e_{i}^{n} q_{i}^{{t{\text{s}}}}\). We added constraints (3) and (4) to guarantee that \(x_{i}^{tn} = e_{i}^{n} q_{i}^{t}\) for all i, t, w, n. The parameter Ψ designated a sufficiently big number. Indeed, if \(e_{i}^{n} = 0\) then \(x_{i}^{{t{\text{n}}}} = 0\) according to constraint (4). If \(e_{i}^{n} = 1\) then the combination of constraints (3) and (5) ensures that \(x_{i}^{{t{\text{n}}}} = q_{i}^{t}\). Thus, \(x_{i}^{{t{\text{n}}}} = e_{i}^{n} q_{i}^{t}\) in all cases.
Efficiency of supplier (i) in the second objective function is \(\theta_{i}\) and second objective function is equal to the total value of suppliers, constraint (6)
Constraints
The second-stage decisions might vary from one scenario to another but have to be in line with the first-stage decisions. According to constraint (7), the total quantity purchased from supplier i \(\sum\nolimits_{t = 1}^{t = T} {q_{i}^{t} }\) must be equal to the total quantity allocated to supplier (i) \((Q_{i} )\).
If supplier i is selected \((Y_{i} = 1)\), then the quantity ordered from supplier i in period t \(\left( {\sum\nolimits_{t = 1}^{t = T} {q_{i}^{t} } } \right)\) must satisfy supplier i’s capacity in the same period (\(L_{i}^{t}\)). Otherwise (i.e., supplier i is not selected and (\(Y_{i} = 0\)), the quantity ordered from supplier i must take the null value. This is guaranteed by constraint (8).
To obtain the price associated with the discount interval n from supplier i, the total purchased quantity \((Q_{i} )\) must satisfy \(A_{i}^{n} \le Q_{i} < A_{i}^{n + 1}\). Note that for the first discount interval n = 1, the parameter \(A_{i}^{n} = 0,\quad \forall i \in I\). Only one discount interval could be selected for each supplier \((i)\). Since the purchasing cost in the objective function is minimized, the model tries to get the most profitable discount interval. Therefore, discount constraints are formulated as follows:
According to Constraints (11), in period t, the sum of the stock at the beginning of period t and the total quantity received in period t is equal to the sum of the stock at the beginning of period t + 1 and the demand of period t. The inventory level at the beginning of the planning horizon is null as given in Constraint (12). No inventories are kept at the end of the last period. In the last period, the inventory constraints could be formulated as given in Constraint (13).
Finally, we include the constraints on the domain of variables.
Solution method
The proposed model is actually a multi-objective stochastic mixed integer linear programing. To solve this model, a two-phased approach was proposed. In the first phase, we solved the multi-objective problem using lexicographic method. However, in the second phase, to cope with uncertainty, we adopted (Aghezzaf et al. 2010) method for the developed robust counterpart.
Coping with multiple objective
Several methods have been developed in the literature to deal with the multi-objective model. Among them, lexicographic method has been used in this study. With the lexicographic method, the objective functions were arranged according to their importance. Then, the following optimization problem was solved one at a time:
Here, \(i\) represents a function’s position in the preferred sequence, and \(F_{j} (x_{j}^{*} )\) represents the optimum of the \(j{\text{th}}\) objective function, found in the \(j{\text{th}}\) iteration (Stadler 1988).
To solve the multi-objective problem in our model, lexicographic method was applied which optimized second objective function while maintaining optimality of the first objective. Meanwhile, DM determined the weighting factor (B). We avoided using analytical methods to determine the weighting factor. However, multi-criteria decision-making techniques such as analytic hierarchy process (AHP) could be used to precisely determine the weighting factor.
We called objective function (6) under (3)–(5) and (7)–(19) constraints here after model (A) and by solving model (A), we obtained \(Z_{2}^{*}\) using it as Constraint (20) in model (B).
Model (A):
St.
Model (B):
St.
We called the above formulation here after model (B), where the objective function is (2) under (3)–(5) and (7)–(20) constraints.
Coping with uncertainty
\({\text{Min}}\; z_{1}\) was obtained by separately solving model (B). \({\text{Min}}\; z_{1}\) for each scenario is called \(({\text{Z}}_{\text{s}}^{*} )\).We adopted the method suggested by Aghezzaf et al. (2010) for the developed robust counterpart. It simultaneously minimized the expected value of objective function as well as the worst case scenario. However, the weighting factor between the worst case and expected value was given by DM as shown below:
\(Z_{\text{s}}^{*}\) is the optimal objective function value for each scenario. The corresponding value was considered as a given input parameter in model (R). As a result, by applying (21), robust counterpart would be:
Model (R)
where the total expected purchasing price is obtained by \(\mathop \sum \limits_{i \in I} \mathop \sum \nolimits_{t = 1}^{t = T} \mathop \sum \nolimits_{s \in \varOmega } p_{\text{s}} \alpha_{i}^{{t{\text{s}}}} \left( {\mathop \sum \nolimits_{n = 1}^{n = N} e_{i}^{n} Pr_{i}^{n} } \right)q_{i}^{{t{\text{s}}}}\). The total expected transportation cost is \(\mathop \sum \nolimits_{i \in I} \mathop \sum \nolimits_{t = 1}^{t = T} \mathop \sum \nolimits_{s \in \varOmega } p_{\text{s}} q_{i}^{{t{\text{s}}}} {\text{TC}}_{i}\) and total expected inventory cost is \(\mathop \sum \nolimits_{t = 1}^{t = T} \mathop \sum \nolimits_{s \in \varOmega } p_{\text{s}} h^{t} {\text{Inventory}}^{{t{\text{s}}}}\). The same linearization was used as mentioned before for (1).
Model (R):
Min (22)
St.
Numerical study
In this section, the models were primarily solved with nominal data according to Tables 1, 2 and 3.
Value of stochastic programing
The value of the stochastic solution (VSS) was used in order to illustrate the importance of applying exchange rate uncertainty in supplier selection problem.VSS measures the expected cost saving from stochastic model rather than its deterministic counterpart.
In our case, VSS equals the value of optimal objective function in deterministic solution subtracted by the value of optimal objective function in stochastic solution.
We considered 3 forecasts for exchange rates for each supplier over the planning horizon.
DMC: is the model in which there is only one scenario (the average value) in each period.
DMF: the model considered fluctuation in three different scenarios in each period with their prospective probabilities. This model is multi-period and multi-dynamic.
For example, considering Table 4, the exchange rate for supplier France in quarter 1 in DMC model would be (3560 + 3580 + 3600 + 3990)/4 = 3682.
On the other hand, the exchange rate for supplier France in quarter 1 in DMF model would be 3550 × 0.4 + 3500 × 0.3 + 3700 × 0.3 = 3580.
Through taking into account the exchange rate fluctuations in our modeling approach, the saving results were suggested in Table 5. We can simply conclude that this modeling approach is more convenient as it is more similar with real world problems and in our case problem, it resulted in 5% cost saving.
We suggest different scenarios according to the probability associated with the different forecasts.
Stochastic and deterministic solutions
Comparing stochastic and deterministic decision variables (Fig. 2) demonstrated that purchasing quantity is different in various models. Both stochastic and robust models result in cost saving since they decide to purchase in the best possible period in advance. The best possible purchase is due to considering exchange rate fluctuation and avoiding higher exchange rates. However, robust model revealed to be more convenient than stochastic model. This might be due to the fact that the robust model incorporates worst case scenario in modeling approach. As a matter of fact, in the absence of worst case scenario, we might face losing demand and higher exchange rates. Finally, this amount of saving is the result of solving these challenges.
The French supplier was selected in the deterministic and stochastic models. However, it was not selected in robust model. Since supplier selection is a strategic decision which might be impossible to change in short terms, it is important to be prepared for even worst case possible scenario. Therefore, the robust optimization method is needed in this content.
Figure 3 illustrates that the total expected cost in robust programing is considerably lower than the deterministic for nominal data.
To assess the desirability and robustness of the solutions obtained by the proposed models under nominal data, 3 random realizations were generated and then, the performance of the obtained solutions was tested under each realization. We produced each realization by generating a random number uniformly between the two extreme points of the corresponding interval. Afterwards, the solutions obtained by the models under nominal data would be replaced in a linear programing model as follow:
\({\text{Inventory}}^{1} = 0,\)
In this linear programming model, (error1) − (error11) are the only decision variables that determine the violation of Robust programing under random realization. The average of objective function value under random realizations was used as performance measures to evaluate the proposed model. The results of these experiments were reported in Fig. 4.
The impact of exchange rate fluctuations on purchased quantity is being illustrated in Fig. 5.
Conclusions
In the present study, a multi-objective mixed integer programing model and its robust counterpart was developed. The buyer sources a product from an international network of diverse suppliers. Prices were offered based on suppliers’ local currencies which were subject to uncertainty over time. In addition, suppliers offered discounts.
An industrial case study was used to demonstrate the performance and applicability of the proposed model. Numerical studies suggested that industry practitioner or leaders could apply this model to their problem to save money and have robust contracts with the best possible suppliers. It was indicated that in the presence of exchange rate fluctuations decision variables were different. It illustrated that to cope with such uncertainties, we should consider them in advance in our planning. In our case study, different suppliers were selected due to these uncertainties and since supplier selection is a strategic decision, it is crucial to consider these uncertainties in planning approach. This would help purchasing manager to save money and time by selecting the best suppliers. With robust optimization method we prepared ourselves for even worst case scenario in both demand and exchange rates, thereby, the decisions were made according to these circumstances. Therefore, the purchasing manager could be ascertain that they would not lose demands even in worst case scenario. At the same time, the supplier manager will be assured to save remarkable amount of money. For future research, it would be important to incorporate other uncertainty parameters and develop efficient heuristic approach that explores and uses the specific characteristics of our model.
Abbreviations
- DEA:
-
Data envelopment analyses
- DMU:
-
Decision making unit
- CNY:
-
China, Yuan Renminbi
- Toman:
-
Iranian Toman
References
Aghezzaf E-H, Sitompul C, Najid NM (2010) Models for robust tactical planning in multi-stage production systems with uncertain demands. Comput Oper Res 37(5):880–889
Amid A, Ghodsypour S, O’Brien C (2009) A weighted additive fuzzy multiobjective model for the supplier selection problem under price breaks in a supply chain. Int J Prod Econ 121(2):323–332
Azadnia AH, Saman MZM, Wong KY (2015) Sustainable supplier selection and order lot-sizing: an integrated multi-objective decision-making process. Int J Prod Res 53(2):383–408
Christopher M et al (2011) Approaches to managing global sourcing risk. Supply Chain Manag Int J 16(2):67–81
De Boer L, Labro E, Morlacchi P (2001) A review of methods supporting supplier selection. Eur J Purch Supply Manag 7(2):75–89
Ghodsypour SH, O’Brien C (2001) The total cost of logistics in supplier selection, under conditions of multiple sourcing, multiple criteria and capacity constraint. Int J Prod Econ 73(1):15–27
Ghodsypour SH, O’Brien C (1998) A decision support system for supplier selection using an integrated analytic hierarchy process and linear programming. Int J Prod Econ 56:199–212
Hammami R, Frein Y, Hadj-Alouane AB (2012) An international supplier selection model with inventory and transportation management decisions. Flex Serv Manuf J 24(1):4–27
Hammami R, Temponi C, Frein Y (2014) A scenario-based stochastic model for supplier selection in global context with multiple buyers, currency fluctuation uncertainties, and price discounts. Eur J Oper Res 233(1):159–170
Mazdeh MM, Emadikhiav M, Parsa I (2015) A heuristic to solve the dynamic lot sizing problem with supplier selection and quantity discounts. Comput Ind Eng 85:33–43
Ng WL (2008) An efficient and simple model for multiple criteria supplier selection problem. Eur J Oper Res 186(3):1059–1067
Sawik T (2011) Selection of supply portfolio under disruption risks. Omega 39(2):194–208
Stadler W (1988) Fundamentals of multicriteria optimization. In: Stadler W (ed) Multicriteria optimization in engineering and in the sciences. Plenum Press, New York, pp 1–25
Taylor MP (1995) The economics of exchange rates. J Econ Lit 33(1):13–47
Wadhwa V, Ravindran AR (2007) Vendor selection in outsourcing. Comput Oper Res 34(12):3725–3737
Xu N, Nozick L (2009) Modeling supplier selection and the use of option contracts for global supply chain design. Comput Oper Res 36(10):2786–2800
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Zarindast, A., Seyed Hosseini, S.M. & Pishvaee, M.S. A robust multi-objective global supplier selection model under currency fluctuation and price discount. J Ind Eng Int 13, 161–169 (2017). https://doi.org/10.1007/s40092-016-0177-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40092-016-0177-3