Redundancy allocation problem for k-out-of-n systems with a choice of redundancy strategies

Abstract

To increase the reliability of a specific system, using redundant components is a common method which is called redundancy allocation problem (RAP). Some of the RAP studies have focused on k-out-of-n systems. However, all of these studies assumed predetermined active or standby strategies for each subsystem. In this paper, for the first time, we propose a k-out-of-n system with a choice of redundancy strategies. Therefore, a k-out-of-n series–parallel system is considered when the redundancy strategy can be chosen for each subsystem. In other words, in the proposed model, the redundancy strategy is considered as an additional decision variable and an exact method based on integer programming is used to obtain the optimal solution of the problem. As the optimization of RAP belongs to the NP-hard class of problems, a modified version of genetic algorithm (GA) is also developed. The exact method and the proposed GA are implemented on a well-known test problem and the results demonstrate the efficiency of the new approach compared with the previous studies.

Introduction

Reliability optimization is one of the most important goals in high-tech industries. Redundancy allocation problems (RAP) are an efficient approach for improving system reliability that generally involves the selection of components type and number of redundant components to maximize system reliability under certain constraints. Chern (1992) proved that RAP belongs to the NP-hard class of optimization problems. In general, the redundancy allocation problem formulation has been presented for various systems with different structures and solved by numerous optimization approaches, such as dynamic programming, integer programming, and different meta-heuristic algorithms (Kuo and Prasad 2000; Tillman et al. 1977). Traditionally, there are two general strategies for using redundant components in system. These strategies are called active and standby strategies. Fyffe et al. (1968) formulated the RAP with the active strategy for all subsystems and used a dynamic programming algorithm to solve the problem. Coit (2001) proposed a new formulation for the cold-standby strategy with imperfect switching. An assumption that commonly made in the literature is that the type of redundancy strategy for each subsystem is predetermined and that either the active or the standby strategy may be used for each subsystem. However, Coit (2003) proposed a new formulation of the redundancy allocation problem with a choice of redundancy strategies for each subsystem. He added the type of redundancy strategy as an additional decision variable to the model and used integer programming to solve the problem. He obtained better results when the redundancy strategy could be chosen for each subsystem compared with approaches that consider predetermined strategies. After Coit’s study, several studies considered a system with a choice of strategies. Tavakkoli-Moghaddam et al. (2008), used a genetic algorithm (GA) to solve the same problem. Then, Safari and Tavakkoli-Moghaddam (2010) used a Memetic algorithm for an RAP problem with a choice of strategies. Recently, Chambari et al. (2012) and Safari (2012) extended this model by adding the overall system cost as the second objective and converted the single objective optimization (SOO) problem to a multi-objective optimization (MOO) one. The application of RAP problems with choice of redundancy strategies in these researches shows the advantageous of selecting the best redundancy strategy for each subsystem.

In addition, many studies have been done in the field of k-out-n systems. Wu and Chen (1994), proposed an algorithm for computing the reliability of a weighted k-out-of-n system. Coit and Smith (1996), and used a genetic algorithm to solve a RAP problem in a series–parallel k-out-of-n system with a multiple component choice and an active redundancy strategy. Coit and Liu (2000), considered the redundancy allocation problem in k-out-of-n systems when either the active or the cold-standby redundancy could be used, although it was assumed that the redundancy strategy (i.e., active or cold-standby) for each subsystem was predetermined. A consecutive k-out-of-n system is considered in Cui and Xie (2005). In this research, formulas are derived to calculate the k-out-of-n system reliabilities for both linear and circular cases. Tian and Zuo (2006) applied a GA for the reliability evaluation of a multi-state k-out-of-n system and Li and Zuo (2008) discussed multi-state, weighted k-out-of-n systems. In most of these studies, k is considered to be a fixed and predetermined parameter. However, Sooktip et al. (2011) considered k as a decision variable in the design process. Zhao and Cui (2010) proposed a finite Markov chain imbedding (FMCI) approach for generalized multi-state k-out-of-n systems. Chang et al. (2013) proposed a new method for calculating the reliability of a complex k-out-of-n system and the reliability model is designed based on expandable reliability block diagram. None of these studies in terms of k-out-of-n systems include the choice of strategy in system. Therefore, in this paper, a k-out-of-n system is considered when the redundancy strategy is a decision variable. To solve the proposed model, an exact method based on integer programming is developed to obtain the optimal solution. Besides, a modified GA is extended to solve the model and the results are compared with the previous studies in the literature.

Recently, a lot of new studies have also been devoted to RAPs which lead to significant results. Nematian (2007) considered a special redundancy allocation problem with fuzzy variables. Sardar Donighi and Khanmohammadi (2011) presented a new model which the reliability of components is as fuzzy set. Taghizadeh and Hafezi (2012) investigated the reliability evaluation of available relationships in supply chain which is suitable for computing reliability of supply chain for organizations. Abouei Ardakan and Zeinal Hamadani (2014b) and Ardakan et al. (2015) proposed a new redundancy strategy called mixed strategy which uses both active and cold-standby strategies in one subsystem simultaneously. Abouei Ardakan et al. (2016) extended the mixed strategy for reliability–redundancy allocation problem (RAP). These new studies show that mixed strategy in more powerful than active and standby strategies and leads to higher reliability values. In most of studies in terms of allocation of redundant components, it is assumed that the components are either non-repairable or repairable. Newly some researches considered both repairable and non-repairable components in one subsystem simultaneously (Zoulfaghari et al. 2014, Zoulfaghari et al. 2015a, b). Dolatshahi-Zand and Khalili-Damghani (2015) and (Khalili-Damghani et al. 2013a) considered a multi-objective RAP problem and proposed a multi-objective particle swarm optimization (MOPSO) method to solve it. Khalili-Damghani et al. (2013b) and Khalili-Damghani and Amiri (2012) also proposed an efficient ε-constraint method for solving multi-objective redundancy allocation problems. Then, a data envelopment analysis model is used to prune the non-dominated solutions. Srinivasa Rao and Naikan (2014) combined the Markov approach with system dynamics simulation approach to study the reliability of a repairable system with standby strategy.

As it is clear from the literature, numerous researches have been done in terms of redundancy allocation problem. Some of these studies considered the k-out-of-n systems. However, none of these studies include the choice of strategy in a k-out-of-n system and considered only active or standby strategy in their models. Therefore, in this paper, a k-out-of-n system is considered when the redundancy strategy is a decision variable and we have both active and standby strategies in the model. To solve the proposed model, an exact method based on integer programming is developed to obtain the optimal solution. Besides, a modified GA is extended to solve the model and the results are compared with the previous studies in the literature. The remainder of the paper is organized as follows. In the second section, we describe the system structure and the assumptions of the problem. Third section explains how to compute system reliability in a k-out-of-n system. In the fourth section, the choice of redundancy strategies is described in more detail. Fifth section presents the modeling of the problem and the exact solution for solving the model. In the sixth section, the design of our genetic algorithm is described. Seventh section considers a well-known benchmark problem and the experimental results to demonstrate the efficiency of the proposed methodology. Finally, conclusions are presented in eighth section.

Problem description

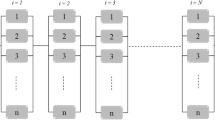
In this paper, a non-repairable k-out-of-n system with a choice of redundancy strategies is considered. In a k-out-of-n system, a subsystem operates correctly if at least k out of its n parallel components are operating. A typical structure of such a system is shown in Fig. 1. Since we want to solve the problem by an exact method, we have to consider special design restrictions in practice. Indeed, the model proposed in this study is an extension on Coit (2003) when the strategy adopted for each subsystem is not predetermined, but it is considered as a decision variable to be determined by the model. The assumptions and parameters are almost the same as Coit (2003), namely the type of failure time distribution and no component mixing once a component selection has been made. There are different component choices with different levels of cost, reliability, and weight, as well as other characteristics. Moreover, the redundant components for each subsystem are selected from the same type. The cold-standby strategy is considered with an imperfect switching and an exponential distribution for time-to-failures of components. Thus, the problem involves the simultaneous selection of component type, redundancy level, and the best redundancy strategy for each subsystem to maximize system reliability subject to budget and weight constraints. The assumptions of the model and the notations for a system with S subsystems are mentioned in the following section.

Fig. 1

Series–parallel system with k-out-of-n subsystems

Assumptions

• The components can be in either of two possible states (namely, a good state or a bad state).

• There are multiple component choices for each subsystem, while one of them should be selected for placing in subsystem.

• The component attributes, such as reliability, weight, and cost, are known and deterministic.

• Failures of components are statistically independent from each other and do not damage the system.

• The types of components used in each subsystem are the same.

• Subsystems with the cold-standby redundancy have an imperfect switching.

• Components and thereby the system are non-repairable.

• Components’ time-to-failures follow an exponential distribution.

Notations

i :

Index for subsystem

j :

Index for component type

m _i :

Number of available component choices for subsystem i

n _i :

Number of components in subsystem i

n:

$= (n_{1} ,n_{2} , \ldots ,n_{s} ),\,\,n_{i} \le n_{\rm{max} ,i} \;\forall i$

z _i :

Type of component selected for subsystem i, z _i  ∊ {1, 2,…,m _i }

z:

= (z ₁, z ₂,…,z _s )

n _max,i :

Maximum number of components allowed in each subsystem

s :

Number of subsystems

t :

Mission time

k _i :

Minimum number of operating components required per subsystem

w _ij :

Weight of component j used for subsystem i

c _ij :

Cost of component j used for subsystem i

C :

Cost constraint limit

W :

Weight constraint limit

λ _ij :

Exponential distribution parameter for failure rate of component j used in subsystem i

ρ _i (t):

Failure-detection/switching reliability at time t for scenario 1

ρ _i :

Failure-detection/switching reliability at time t for scenario 2

r _ij (t):

Reliability of component j used in subsystem i at time t

A :

Set of subsystems with active redundancy

S :

Set of subsystems with cold-standby redundancy

N :

Set of subsystems which can use active or cold-standby redundancy

R(t, z, n):

Overall reliability of system reliability at time t based on vectors z and n

$\tilde{R}\left( {t,z,n} \right)$ :

Approximation of R(t, z, n)

System reliability for k-out-of-n subsystems

As already mentioned, the objective function of the RAP problem is maximizing system reliability under cost and weight constraints, and is generally formulated as follows:

Problem P1

$$\begin{aligned} &\hbox{max} \,R\left( {t,z,n} \right) \\ &{\text{s}} . {\text{t}} . \\& \sum\limits_{i = 1}^{s} {c_{{iz_{i} }} } n_{i} \le C,\quad \quad n_{i} \in \left\{ {k_{i} ,k_{i + 1} ,k_{i + 2} , \ldots ,n_{{\rm{max}} ,i} } \right\}, \\ &\sum\limits_{i = 1}^{s} {w_{{iz_{i} }} } n_{i} \le W,\quad \;\;z_{i} \in \left\{ {1,2, \ldots ,m_{i} } \right\} \\ \end{aligned}$$

As we consider a system with a choice of redundancy strategies, the objective function consists of the reliability of k-out-of-n system with active and standby strategy. The reliability of a k-out-of-n system with the active redundancy can be determined using the binominal techniques. The formulation for computing this reliability is as follows:

$$R_{{_{i} }} (t) = \sum\limits_{{l = k_{i} }}^{{n_{i} }} {\left( {\begin{array}{*{20}c} {n_{i} } \\ l \\ \end{array} } \right)(} r_{ij} (t))^{l} (1 - r_{ij} (t))^{{n_{i} - l}}$$

(1)

where r _i,j represents the reliability of component j used for subsystem i. Since the component time-to-failure distribution is exponential, r _i,j is calculated as follows:

$$r_{ij} \left( t \right) = \exp \left( { - \lambda_{ij} t} \right).$$

(2)

Considering the reliability of cold-standby systems with switching failures is more realistic and important. Coit (2001) described two scenarios for imperfect switching in a cold-standby system. In the first scenario, switching hardware or software controls the system performance continually and activates the redundancy component when a failure occurs in the active component. In the second scenario, failure is only possible when the switch is required, and the probability of success at any time the switch is required is a constant value ρ _i . More details can be found in Coit (2001). Failure-detection/switching reliabilities for the two scenarios are determined by:

Scenarios 1: continuous detection and switching

$$R_{i} (t) = r_{{i,z_{i} }} (t) + \sum\limits_{x = 1}^{{n_{i} - 1}} {\int\limits_{0}^{t} {\rho_{i} (u)\,r_{{i,z_{i} }} (t - u)\,f_{{i,z_{i} }}^{(x)} (u)} } \,{\rm d}u$$

(3)

Scenarios 2: switch activation only in response to a failure

$$R_{i} (t) = r_{{i,z_{i} }} (t) + \sum\limits_{x = 1}^{{n_{i} - 1}} {\rho_{i}^{x} \int\limits_{0}^{t} \, } r_{{i,z_{i} }} (t - u)\,f_{{i,z_{i} }}^{(x)} (u)\,{\rm d}u$$

(4)

In these equations, ρ _i (t) and ρ _i are the failure-detection/switching reliabilities at time t for scenarios 1 and 2, respectively; $r_{{i,z_{i} }} (t)$ is the reliability of component j used for subsystem i at time t and $f_{{i,z_{i} }}^{(x)} (u)$ is the pdf for the xth failure of component j used for subsystem i, i.e., sum of x i.i.d component failure times. This paper investigates continuous detection and switching (scenario 1).

The reliability of a k-out-of-n system with the cold-standby redundancy is the probability that there are strictly less than or equal to n _i  − k _i failures observed until time t. Thus, if the component time-to-failure is exponential, then Eq. (5) can be represented by considering the occurrences of subsystem failures as a homogeneous Poisson process prior to the n _i  − k _i failures. In this case, the subsystem failure process is considered as a Poisson process at a rate of λ _ij k _i . Therefore,

$$\int\limits_{0}^{t} {r_{{i,z_{i} }} (t - u)f_{{i,z_{i} }}^{(x)} (u)} \,{\rm d}u = \frac{{e^{{ - \lambda_{{i,z_{i} }} k_{i} t}} (\lambda_{{i,z_{i} }} k_{i} t)^{x} }}{x!}$$

(5)

In addition, an approximation of the overall system reliability will be as follows:

$$\begin{aligned} \tilde{R}(t,z,n) &= \prod\limits_{i \in A} {\,\sum\limits_{{l = k_{i} }}^{{n_{i} }} {\,\left( {\begin{array}{*{20}c} {n_{i} } \\ l \\ \end{array} } \right)(\exp ( - } \lambda_{{i,z_{i} }} t))^{l} (1 - \exp \,( - \lambda_{{i,z_{i} }} t))^{{n_{i} - l}} } \\ & \quad \times \prod\limits_{i \in S} {\exp ( - \lambda_{{i,z_{i} }} k_{i} t)} + \rho_{i} (t)\exp \,( - \lambda_{{i,z_{i} }} k_{i} t)\\ & \quad\quad\quad\quad\quad\quad\times \sum\limits_{l = 0}^{{n_{i} - k_{i} }} {\frac{{(\lambda_{{i,z_{i} }} k_{i} t)^{l} }}{l!}} \end{aligned}$$

(6)

As mentioned in Coit (2001), it is difficult to determine a closed form for equations similar to Eq. (3). Therefore, an estimation for lower bound of Eq. (3) is determined in the equation above, because ρ _i (t) ≤ ρ _i (u) for all u ≤ t .

Choice of redundancy strategies

As previously mentioned, when the redundancy strategy for subsystems is not predetermined, the best strategy should be selected among the standby and the active redundancies by comparing their reliabilities. Coit (2003) explained the relationship between the reliabilities of cold-standby and active redundancies for an individual subsystem. When there is a perfect switching and the cold-standby switching is not exposed to operating stresses, the cold-standby strategy is always preferable to the active one. With imperfect switching, for component j with special characteristics (switching reliability, time-to-failure distribution), there is a maximum redundancy level, $n_{ij}^{{\prime }}$, where the reliability of the standby strategy is greater or equal to that of the active strategy. In other words, if the number of redundant components used in subsystem i is less than or equal to the maximum level ($n_{i} \le n_{ij}^{\prime }$), the cold-standby outperforms the active strategy; otherwise, the active strategy will have a better performance for all larger values of $n_{i} > n_{ij}^{\prime }$ (as shown in Fig. 2).

Fig. 2

Comparison of active and standby redundancies

To validate this conclusion, assume that the reliability of a component is 0.7408 and that of the switching for standby components is 0.99. Now suppose that the system includes a certain number of components in parallel. The following figure illustrates the reliability of the system for different values of n _i with the standby or active strategy.

Clearly, $n_{ij}^{{\prime }}$, in this example, is equal to four. As previously mentioned, with the cold-standby strategy, we expect reliability to reduce with increasing number of redundant components and this is due to the increased requirements of imperfect switching.

Exact solution methodology

For obtaining optimal solution of the proposed model, an integer programming-based method is presented. The bases of this approach were proposed by Misra and Sharma (1973). It is based on transforming the problem by taking the logarithm of Eq. (6) to develop an equivalent problem. The solution methodology is described as the following five steps:

• 1. First, we define y _ijp as the new zero–one decision variables as follows:

  $$y_{ijp} = \left\{ \begin{array}{ll}1,&\quad p{\text{ numbers of component type }}j \\&\quad {\text{ will place in subsystem }}i \\ 0,&\quad {\text{otherwise}} \end{array} \right.$$

• 2. Determine sets of A, S, and C based on the requirements of system design and identify the set each subsystem belongs to. If a subsystem belongs to set C, but its switching detection is perfect, transfer this subsystem from set C to set S.

• 3. Compute the value of $n_{ij}^{{\prime }}$ for all $i \in c$ and $j = 1, \ldots ,m_{i}$. $n_{ij}^{{\prime }}$ demonstrating the maximum level where the standby redundancy still has a higher reliability than the active one.

  $$\begin{aligned} n_{ij}^{\prime } &= \sup \left\{ {n_{ij} ;} \right.\exp ( - \lambda_{{i,z_{i} }} k_{i} t) + \rho_{i} (t)\exp ( - \lambda_{{i,z_{i} }} k_{i} t)\\ &\quad\times\sum\limits_{l = 0}^{{n_{i} - k_{i} }} {\frac{{(\lambda_{{i,sz_{i} }} k_{i} t)^{l} }}{l!}} \\ & > \sum\limits_{{l = k_{i} }}^{{n_{i} }} {\left( {\begin{array}{*{20}c} {n_{i} } \\ l \\ \end{array} } \right)(\exp ( - } \lambda_{{i,z_{i} }} t))^{l} (1 - \exp ( - \lambda_{{i,z_{i} }} t))^{{n_{i} - l}} \end{aligned}$$

• 4. Compute $\alpha_{ijp}$, $\beta_{ijp}$, and $\gamma_{ijp}$ as problem parameters,

  $$\begin{aligned} \alpha_{ijp} &= c_{ij} p \quad for \quad 1 \le i \le s,\quad1 \le j \le m_{i} ,\quad 1 \le p \le n_{\rm{max} ,i} \\ \beta_{ijp} &= w_{ij} p \quad for \quad1 \le i \le s, \quad 1 \le j \le m_{i} , \quad 1 \le p \le n_{\rm{max} ,i} \end{aligned}$$

  $for{\text{ i}} \in A$

  $$\gamma _{{ijp}} \left\{ {\begin{array}{*{20}c} { - \lambda _{{ij}} k_{i} t} & {p = k_{i} {\mkern 1mu} } \\ {\ln \left( {\sum\limits_{{l = k_{i} }}^{{n_{i} }} {\left( {\begin{array}{*{20}c} {n_{i} } \\ l \\ \end{array} } \right)} \left( {\exp \left( { - \lambda _{{ij}} t} \right)} \right)^{l} \left( {1 - \exp \left( {\lambda _{{ij}} t} \right)} \right)^{{n_{i} - l}} } \right)} & {k_{i} p \le n_{{{\text{max}},i}} } \\ \end{array} } \right.$$

  $for{\text{ i}} \in S$

  $$\gamma_{ijp} \left\{ \begin{array} {ll} - \lambda_{ij} k_{i} t & \quad {{ p = k}}_{i} \\ - \lambda_{ij} k_{i} t + \ln \left( {\sum\limits_{l = 0}^{{n_{i} - k_{i} }} {\frac{{\left( {\lambda_{ij} k_{i} t} \right)^{l} }}{l}} } \right) & \quad {{k}}_{i} {{ < p}} \le n_{\hbox{max} ,i} \\ \end{array} \right.$$

  $for{\text{ i}} \in C$

  $$\, \gamma_{ijp} = \, \left\{ \begin{array}{ll} - \lambda_{ij} k_{i} t & \quad {p = k}_{i} \\ - \lambda_{ij} k_{i} t + \ln \left( {\sum\limits_{l = 0}^{{n_{i} - k_{i} }} {\frac{{\left( {\lambda_{ij} k_{i} t} \right)^{l} }}{l!}} } \right) & \quad {{ k}}_{i} {{ < p}} \le n^{\prime}_{ij} \, \\ \ln \left( {\sum\limits_{{l = k_{i} }}^{{n_{i} }} {\left( \begin{aligned} n_{i} \\ l \\ \end{aligned} \right)\left( {\exp \left( { - \lambda_{ij} t} \right)} \right)^{l} \left( {1 - \exp \left( {\lambda_{ij} t} \right)} \right)^{{n_{i} - l}} } } \right) & \quad n^{\prime}_{ij} {{ < p}} \le n_{\hbox{max} ,i} \, \\ \end{array} \right.$$

• 5. Problem P2 is the linear form of problem P1 and belongs to the zero–one integer programming problems. The following problem can be solved by any convenient branch-and-bound or cutting plane algorithm.

Problem P2

$$\hbox{max} \sum\limits_{i = 1}^{s} {\sum\limits_{j = 1}^{{m_{i} }} {\sum\limits_{p = k}^{{n_{max,i} }} {\gamma_{ijp} y_{ijp} } } }$$

s.t.

$$\begin{aligned} \sum\limits_{i = 1}^{s} {\sum\limits_{j = 1}^{{m_{i} }} {\sum\limits_{p = k}^{{n_{max,i} }} {\alpha_{ijp} y_{ijp} } } \le c} \,\,\,\,\,\,\,\,\,\, \\ \sum\limits_{i = 1}^{s} {\sum\limits_{j = 1}^{{m_{i} }} {\sum\limits_{p = k}^{{n_{max,i} }} {\beta_{ijp} y_{ijp} } } \le w} \,\,\,\,\,\,\,\,\,\, \\ \sum\limits_{j = 1}^{{m_{i} }} {\sum\limits_{p = k}^{{n_{max,i} }} {y_{ijp} } = 1} \,\,\,\,\,\,\,\,\,\, \\ y_{ijp} \in \{ 0,1\} . \end{aligned}$$

Obtain the optimal solution of the above model. The results show that S numbers (subsystem index) of variable y _ijp are equal to one in the optimal solution and that the remainder is equal to zero. Therefore, the system structure will be as follows:

$$\begin{aligned} &{\text{ for y}}_{ijp} = 1, \\ &\left\{ \begin{aligned} & {\text{if \quad i}} \in A, \, p{\text{ numbers of component }}j{\text{ will place in}} \\ &\quad {\text{ subsystem }}i{\text{ with active redundancy}} \\ &{\text{if \quad i}} \in S, \, p{\text{ numbers of component }}j{\text{ will place in}} \\ &\quad {\text{ subsystem }} i{\text{ with standby redundancy }} \\ &{\text{if \quad i}} \in N{\text{ and }}p \le {\text{n}}_{ij}^{{\prime }} , \, p{\text{ numbers of component }}j{\text{ will}} \\ &\quad {\text{ place in subsystem }}i{\text{ with standby redundancy}} \\ & {\text{if \quad i}} \in N{\text{ and }}p > {\text{n}}_{ij}^{{\prime }} , \, p{\text{ numbers of component }}j{\text{ will}} \\ &\quad {\text{ place in subsystem }}i{\text{ with active redundancy}} . { } \\ \end{aligned} \right. \\ \end{aligned}$$

It should be noted that in a k-out-of-n subsystem with p components in parallel and a cold-standby strategy, there are k _i active components in the active state and p − k _i components in the cold-standby state.

Using this solution method for a large-scale problem will increase the number of variables to a too large set, so that the exact method would not be useful in this situation and it is hard to obtain optimal solution. It may be necessary to use other approaches for very large problems. Therefore, in addition to the existing solution, a genetic algorithm has been used to solve this model in the numerical example section. First, the structure of an appropriate genetic algorithm for this model is described in the following section.

Genetic algorithm implementation

Genetic algorithm (GA) is a well-known stochastic search method and belongs to the larger class of evolutionary algorithms (EA) which solve optimization problems using techniques inspired by natural selection in biological evolution. It was first popularized by Holland. It has successfully been applied to solve different system reliability optimization problems. The GA is described by the following features:

• 1. Solutions encoding

• 2. Generation of an initial population

• 3. Selection of parent solutions for breeding

• 4. Crossover operator

• 5. Mutation operator

• 6. Combine the offspring and former population and culling of the best solutions

• 7. Repeat steps 3 through 6 until termination criteria is satisfied.

Solution encoding

For this problem, each possible solution is a collection of redundancy strategies, type of selected components, and number of components in parallel for each subsystem. The solution encoding (chromosome) is presented as a 3 × s matrix, where s denotes the number of subsystems. The first, second, and third rows of this matrix represent the number of components, type of selected component, and the selected redundancy strategy for the subsystems, respectively. Figure 3 presents an example of encoding solution for this problem with s = 14. This figure demonstrates a solution, in which the first subsystem (s = 1) uses active redundancy with two components of the second type in parallel, while the last subsystem uses standby redundancy strategy with three components of the fourth type in parallel.

Fig. 3

Chromosome representation (solution encoding)

Initial population

At first, the minimum appreciate population size should be selected in accordance to problem size. For a given population size (p), the initial population is generated by selecting p chromosomes randomly. To produce each solution of the current population, s integers between k _i and n _max were randomly selected to represent the number of components in parallel (n _i ) for each subsystem. Types of components for each subsystem were randomly selected from among the m _i available components. Then, redundancy strategy (active or standby) is selected for each subsystem.

Crossover

Parents are selected from existing population at random in each iteration, then the proposed crossover operator is applied and two offspring will be generated from each two selected parents. Four crossover operators are applied to generate offspring from parents, namely, single-point crossover, double-point crossover, max–min crossover, and uniform crossover. In the double-point crossover, two points along the parent chromosomes are selected randomly, all the genes between the two points are swapped between the parent chromosomes, and then, two new offspring are produced (Fig. 4). In the max–min crossover, the subsystems with the highest and lowest reliabilities of parents are specified and all the genes of each selected subsystem are exchanged with genes of the same subsystem in the other parent (Fig. 5). The uniform crossover operator is a powerful crossover, because it enables to random recombination of different genes in parents. So, by considering mixing ratio of 0.5, offspring genes are selected from the first or from the second parent randomly.

Fig. 4

Double-point crossover operator

Fig. 5

Max–min crossover operator

Mutation

After the crossover operation, mutation is performed to maintain the diversity of solution space and to avoid getting stuck at a local optimum. Two mutation operators are employed, namely, simple mutation and max–min mutation. In the simple mutation with rate of p _M , for each candidate solution, a random value is selected for each gene and the gene value is altered if the random value is smaller than the mutation rate. The max–min mutation operator was developed by Tavakkoli-Moghaddam et al. (2008). In a system with several subsystems, the subsystem with the minimum reliability has a bad effect in reliability of overall system. Therefore, max–min mutation operator selects subsystems with the highest reliability and the lowest reliability among the all subsystems and then mutates the gene values of each selected subsystem randomly. A typical max–min mutation is shown in Fig. 6.

Fig. 6

Max–min mutation operator

Fitness function

To define the fitness function, a penalty approach is used for the proposed genetic algorithm to penalize infeasible solutions and to reduce their fitness values in proportion to their degrees of constraint violation. In other words, a value proportional to the constraints violation is added to the objective function as a dynamic penalty function, which results in adding a relatively large amount of penalty to the objective functions, if one solution violates a constraint. This penalty provides the feasibility of the final solution while keeping the efficient search through the infeasible region. It is important to search through the infeasible space of the problem, because it leads to reach appropriate diversity for the proposed GA and good feasible solutions can most efficiently be reached by breeding between a feasible and an infeasible solution.

Stopping criteria

The termination criterion for the proposed GA is a preselected number of generations.

Illustrative example

The example employed in this study is adopted from the example provided by Fyffe et al. (1968). The system consists of 14 subsystems with (t = 100) for mission time, (C = 130) for system cost constraint, (W = 170) for system weight constraint, (n _max = 6) for maximum number of allowed components in each subsystem, and three or four component choices for each subsystem. Our specific example is, however, different from Fyffe’s in a number of ways, namely, the redundancy strategy (active or standby) is considered to be selected for each subsystem and the exponential distribution is chosen for time-to-failure of components. Failure detection for the standby redundancy follows scenario 1 and the reliability of a switching (at 100 h) is 0.99 for each subsystem. k _i  = 1 was considered in the original example by Fyffe et al. (1968), whereas its values in the present example are randomly selected for each subsystem. It should be emphasized that the results are highly dependent on k _i values; so the results would be fundamentally different as a result of changes in k _i . In addition, it has been assumed that all the subsystems pertain to set C. The data are presented in Table 1.

Table 1 Component data for the illustrative example

Exact solution

Initially, exact solution methodology is used to solve the example. To find the optimal solution, the model can be solved by any standard algorithm for zero–one integer programming. The results are presented in Table 2. The optimal solution yields reliability equal to 0.4505 for the system. This solution has also been compared with those for two other problems. In the first problem, only the active redundancy is considered. In the second problem, redundancy strategy (i.e., active or standby) is predetermined for each subsystem. This problem is in accordance with the example solved in Coit and Liu (2000), but the exponential distribution is used instead of Erlang distribution for time-to-failure of components. The exponential distribution parameters are chosen, so that the components have the same reliability as in the original example (for t = 100) and our answer is quite equal to the result obtained in Coit and Liu (2000). The numerical results indicate that the choice of strategies led to a higher reliability compared with the other approaches.

Table 2 Example results

The performance of the proposed approach is evaluated by implementing on 33 test problems provided by Tavakkoli-Moghaddam et al. (2008). In this case, the value of cost constraint is fixed (130), while the weight constraint is varied from 159 to 191. Table 3 presents a comparison between the best results obtained by solving 33 problems in this paper and that reported in Coit and Liu (2000). In Table 3, as the weight constraint gradually increases, the optimal solution (best reliability) improves. Furthermore, maximum possible improvement (MPI) index is also used to measure the significance of the improvements made using the choice of strategies as compared with the previous best-known strategies. This index, which has been used in many previous studies, including Yeh and Hsieh (2011), Wu et al. (2011) and Abouei Ardakan and Zeinal Hamadani (2014a), is given by:

Table 3 Computational results between the proposed approach and Coit and Liu (2000) for the 33 test problems

$${\text{MPI}}(\% ) = [R_{s} ({\text{New}}\,{\text{Approach}}) - R_{s} ({\text{Other}})]/[1 - R_{s} ({\text{Other}})].$$

(7)

Here, R _s (NewApproach) represents the best system reliability obtained by the proposed approach and R _s (Other) represents the best system reliability obtained by any other method reported in the literature. Table 3 indicates that the choice of strategies used for the redundant components led to the improvements in the reliability levels of all the 33 benchmark problems compared to method which considered predetermined strategies. Therefore, this study provides better computational results than Coit and Liu (2000). Figure 7 presents the MPI index in all test problems.

Fig. 7

Maximum possible improvement (MPI) index values

Genetic algorithm

From the 33 test problems, seven problems are selected and the GA with penalty function which is discussed in “Genetic algorithm implementation” section is implemented on them. Because of the stochastic nature of GA, ten runs are performed for each problem and each run is terminated after 100 generations. The best and the worst solution amongst them are reported in Table 4. In all problems which are shown in Table 4, maximum reliability produced by the proposed GA is the same as optimal solution obtained in the previous section and it shows the good performance of our GA approach. In the primary instances with lower reliability, the improvement is small, but in the next instances, the improvement becomes larger. However, in high-reliability applications, even very small improvement in the reliability is often difficult to obtain. In all problems, we obtain system reliability higher than the previously studies.

Table 4 Computational results of GA performance over ten trials for 33 test problems

Conclusion

This paper investigated the redundancy allocation problem for a k-out-of-n system with a choice of redundancy strategies. In contrast to the existing approaches that often consider a predetermined strategy for each subsystem, we considered both active and standby strategies and developed a model to select the best strategy for each subsystem. The choice of redundancy strategies is more realistic and will be more successful for implementing. To solve the proposed model, we developed an exact method to obtain the optimal solution of the problem. The main advantage of this methodology is that a complex non-linear problem is reduced to an equivalent simple problem in the form of an integer-linear programming. Furthermore, a modified version of GA is developed to solve the problem is large size or other tough situation. To evaluate the efficiency of the proposed strategy, a well-known benchmark problem was considered. The results demonstrate considerable improvements in the reliability using the new approach. For future studies, one can focus on developing a bi-objective model to optimize this problem. In this model, one redundancy strategy is used for each subsystem. Another interesting extension may be the case where both active and standby strategies are simultaneously used in the subsystems. Furthermore, because RAPs belong to NP-hard problems for which it is not easy to obtain optimal solutions, researchers can test other meta-heuristic approaches for this problem.