Optimization of two-stage production/inventory systems under order base stock policy with advance demand information

Abstract

It is important to share demand information among the members in supply chains. In recent years, production and inventory systems with advance demand information (ADI) have been discussed, where advance demand information means the information of demand which the decision maker obtains before the corresponding actual demand arrives. Appropriate production and inventory control using demand information leads to the decrease of inventory and backlog costs. For a single stage system, the optimal base stock and release lead time have been discussed in the literature. In practical production systems the manufacturing system has multiple processes. The multiple stage production and inventory system with ADI, however, has been analyzed by simulation or assuming exponential processing time. That is, their theoretical analysis and optimization of release lead time and base stock level have little been obtained because of its difficulty. In this paper, theoretical analysis of a two-stage production inventory system with advance demand information is developed, where the processing time is assumed deterministic and identical; demand arrival process is Poisson, and an order base stock policy is adopted. Using the analytical results, optimal release lead time and optimal base stock levels for minimizing the average cost on the holding and backlog costs are explicitly derived.

Introduction

In production systems, the amount of items produced at each period and work-in-processes or finished products must be controlled appropriately. Many studies on control of production and inventory systems have been developed. In most of the studies, the demand for products is assumed to happen at the arrival of demand information.

In recent years, production and inventory systems with advance demand information have been discussed. Here, advance demand information (ADI) means the information of demand which the decision maker obtains before the corresponding actual demand arrives. Appropriate production and inventory control using ADI from downstream to the upstream makes the decrease of amount of products in inventory and backlogs.

It is important to share demand information among the members in supply chains. In many automakers, a car is produced after the demand happens. On the other hand, in recently developed internet retails, products are delivered later after demand is received. Therefore, the time lag exists between item requirement and its delivery to the customer. Efficient use of this time lag leads to the appropriate production and inventory control.

In a single stage production and inventory system, the effect of ADI has been developed in the literature. Milgrom and Roberts (1988) consider a single period random demand model and show the optimal level of investment of ADI. Hariharan and Zipkin (1995) discuss the supplier model with continuous review order base stock policy and Poisson arrivals of orders. Here, the order base stock policy means that the inventory position is kept in the system by replenishment order based on the advance demand information. In Karaesmen et al. (2003), processing times are assumed to follow a general distribution, and an approximate scheme for generalization of Buzacott and Shanthikumar (1993, 1994) is proposed. Karaesmen et al. (2004) develop the value of advance demand information for M/G/1 or M/M/1 make-to-stock queue with constant demand lead time. Bernstein and Decroix (2015) examine the impact of different types of advance demand information, volume information and mix information in a multiproduct system. They find that mix and volume information are complements.

In a single stage system, the optimality of base stock policy, optimal base stock levels, and optimal demand lead time have also been discussed. Gallego and Özer (2001) consider a single stage inventory system with exogenous demand, under periodic review and stochastic finite demand lead time, and when replenishing time is greater than the maximum of possible demand lead time, it is proven that the order base stock policy is optimal. Buzacott and Shanthikumar (1993, 1994) discuss the continuous review of one stage production inventory system with deterministic lead time and finite capacity, where the processing times have an exponential distribution. They show that in this system, optimal demand lead time and costs decreases in the number of base stocks.

Liberopoulos (2008) considers a single stage production and inventory system under an order base stock policy and continuous review, and analyzes the tradeoff between demand lead time and optimal numbers of base stocks theoretically. The optimal integer-value base stock level minimizing the average cost is developed and it is shown that increasing demand lead time leads to the decrease of the optimal number of base stocks. In particular, tradeoffs have been developed in detail for cases that the replenishment process is represented as M/D/1, M/M/1 and M/D/∞ queues. Gayon et al. (2009) consider a production inventory system with imperfect advance demand information with Poisson arrivals, exponential lead times and multiple classes, and show a state dependent base stock policy is optimal. Yokozawa and Nakade (2012) consider a M/D/1 base stock system with advance demand information, and the relationship between release lead time and demand lead time is discussed theoretically. Karaesmen (2013) discusses the value of advanced demand information in a single stage system with multiple customers. Assuming that each of customers has normal distributed demand, he gives the optimal order quantity for the system with and without ADI under inventory sharing and no inventory sharing. He also discusses them under capacitated supply with and without inventory and capacity sharing.

In practical production systems, the manufacturing system has multiple processes. The multiple stage production and inventory system with ADI, however, has been analyzed either by simulation or by assuming exponential processing time. Karaesmen et al. (2003) and Liberopoulos and Tsikis (2003) propose a framework for production policies with advance demand information for multistage production inventory system, although they do not derive the optimal base stock level. Liberopoulos and Koukoumialos (2005) investigate a two-stage production and inventory system with ADI. They assume the processing time to be exponentially distributed, and use simulation to evaluate control parameters and derive the optimal values numerically. Claudio and Krishnamurthy (2009) investigate multistage system with ADI under Kanban control with simulation. The benefit of integrating advance demand information with Kanban is obtained in many cases by numerical experiments.

Thus, several researches on multistage production and inventory systems has been developed, but the result is only obtained by simulation, or assuming the exponential distributed processing time, which is not observed in practice. That is, there seems no literature on the theoretical analysis and optimization on multistage production and inventory system because of its complexity. In this paper, theoretical analysis of two-stage production inventory system with advance demand information is developed under a framework on the two-stage model given in Karaesmen et al. (2003). In our model, the processing time is assumed deterministic and identical, demand arrival process is Poisson and an order base stock policy is adapted. Deterministic processing time is more acceptable in practice compared with exponential distribution. The base stock level and release lead time for each process are decision variables, and we want to derive optimal values to minimize average cost on inventory and backlog cost. If the system is fully developed, then it hardly has errors for processing, and thus the processing time is deterministic. A base stock order policy is easily installed in the production and inventory system because the policy is easily established by sending information on withdraw of each finished item to all upstream stations. Through theoretical analysis, explicit expressions on optimal release lead time and optimal base stock levels are obtained for each demand lead time.

The organization of this paper is as follows. In “Model”, the production and inventory system is described, and a relationship between finishing times of processes in both processes is discussed. In “Optimal base stock level”, optimal amounts of base stocks are investigated for given release lead time. In “Optimal release lead time of process 2”, optimal release lead time of process 2 is developed, and in “Optimal release lead time of process 1”, optimal release lead time of process 1 is discussed, and thus pairs of optimal base stock levels and optimal release lead time are derived for given demand lead time. “Optimal release lead time and optimal base stock level” summarizes results of “Optimal release lead time of process 1” and gives optimal base stock levels and release lead time explicitly, and theoretically, for each demand lead time, which is listed in Table 5. “Numerical experiments”, the relationship between the optimal average cost and demand lead time, is demonstrated through a few numerical examples.

Model

Model description

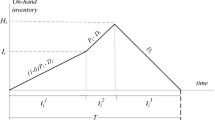
The two-stage production and inventory model with a single product is considered under continuous time review. Figure 1 shows the model.

Fig. 1

Two-stage production and inventory system with order base stock policy

Advance demand information arrives at the system in a Poisson process with arrival rate $\lambda.$ Each information requires one product T periods later. This time T is called demand lead time. The information cannot be declined after the demand information arrives.

Processes 1 and 2 follow the order base stock policy. The amounts of base stocks are defined as $S_{ 2}^{ 1}$ and $S_{2}$, respectively, which take values of nonnegative integers and $S_{2}^{1} \ge S_{2}$. The difference $S_{1} = S_{2}^{1} - S_{2}$, which is also a nonnegative integer, is called the amount of base stock of process 1 in the following of this paper.

Replenishment order for process 1 is made at $t_{0}$ periods $(0 \le t_{0} \le T)$ after the demand information arrival, and thus this order is done $L_{1} ({=T - t_{0}})$ periods before arrival of its requirement for product. There are assumed to be enough materials before process 1, and one part is entered immediately when the replenishment order is made. $L_{1}$ is called release lead time of process 1, and this replenishment order is called ‘order 1’. When the processing is completed at process 1, then the item is placed in an inventory space of work-in-process. After $t_{0} + t_{1}$ periods from the arrival of advance demand, that is, $L_{2} ({=T - t_{0} - t_{1}})$ periods before the arrival of requirement for product, replenishment order at process 2 is made, where $0 \le t_{1} \le T - t_{0}$, and $L_{2}$ is called release lead time of process 2. If there is no work-in-process, then the order waits for the finishing of process, and if there is a work-in-process, then it is taken and the replenishment order for process 2 is made. We call this replenishment order “order 2”. When the process for an item is finished in process 2 it is placed in an inventory space of finished items. At $T$ periods later from demand information arrival, the actual demand for finished item arrives. Thus, the k-th demand information in turn causes the k-th order 1, the k-th demand for work-in-process, the k-th order 2 and the k-th demand for a finished item. Processing time at each process is constant $d$, and thus the process 1 is modeled as an M/D/1 queue. Arrival rate of demand is given by $\lambda$, where $0 < \lambda < 1/d$. Let $\rho = \lambda d$. Holding costs are incurred for work-in-process after process 1 and before process 2, and finished items, whose cost rates are given by $h_{1}$ and $h_{2}$, respectively. It is assumed that 0 $\le h_{1} \le h_{2}$. Note that if $h_{1} > h_{2}$, then processed item in process 1 should be delivered to process 2 immediately, and thus, optimal release lead time of process 1 become the same as that of process 2, which is similar with a single stage production system with processing time $2d$ [this is also discussed in Karaesmen et al. (2003)]. The backlog cost is also incurred for demand for finished items, whose cost rate is given by $b({> 0})$.

We give notations defined above in the following.

$h_{1}$: holding cost rate per unit time per unit work-in-process, $h_{2}$: holding cost rate per unit time per unit finished item, $0 \le h_{1} \le h_{2}$, $b:$ backlog cost rate per unit time per unit backlog, $b > 0$, $d$: process time at process 1 and at process 2, $\lambda$: arrival rate of demand, 0 $< \lambda < 1/d, \rho = \lambda d,$ $T$: demand lead time, $t_{0}$: the delay of the replenish order at process 1 from the arrival of demand information, $t_{1}$: the time interval between the replenish orders at processes 1 and 2 for each demand, $L_{1}$: release lead time at process 1, $L_{1} = T - t_{0}$, $L_{2}$: release lead time at process 2, $L_{2} = T - t_{0} - t_{1}$, $S_{1}$: the number of base stocks at process 1, $S_{2}$: the number of base stocks at process 2.

We also define the notations in the following.

$a(k)$: the k-th arrival epoch of demand information, $r_{1} (k)$: the k-th occurrence time of order 1, $r_{2} (k):$ the k-th occurrence time of order 2, $b_{1} (k)$: the starting time of process induced by the k-th order at process 1, $b_{2} (k)$: the starting time of process induced by the k-th order at process 2, $W(k)$: the k-th sojourn time at process 1, which is the time interval from the occurrence of the k-th order 1 to the completion of the k-th processing at process 1,

$$ E(k) = W(0) - a(k). $$

The problem is to derive explicit expressions on optimal release lead time $L_{1}$ and $L_{2}$, and amount of base stocks $S_{1}, S_{2},$ for minimizing the average cost per unit time. The expression on the average cost is discussed in “Average cost”.

Preliminary results

Before investigation on optimal release lead time and base stock level, the preliminary results on this model are discussed in this section.

The k-th “order 1” is caused by the k-th advance demand information at time $a(k) + t_{0}$, that is, $r_{1} (k) = a(k) + t_{0}$. At epoch $a(k) + t_{0} + t_{1}$, the k-th arrival of work-in-process at process 2 is induced by the demand information. Since the order base stock policy is adopted, the corresponding item is processed at process 1 by the $k - S_{1}$-th order. This means that if $a(k) + t_{0} + t_{1} < b_{1} ({k - S_{1}}) + d$, the order 2 is postponed until $b_{1} ({k - S_{1}}) + d$, and if $a(k) + t_{0} + t_{1} \ge b_{1} ({k - S_{1}}) + d$, then the order 2 occurs immediately.

Since process time $d$ is the same for process 1 and process 2, the finishing time of process at process 2 is $t_{1}$ periods later from the finishing time of processing at process 1 when either $S_{1} > 0$ or {$S_{1} = 0$ and $t_{1} \ge d$} holds, and $d$ periods later when $S_{1} = 0$ and $t_{1} < d$. Thus, the starting time of processing at process 2 $b_{2} (k)$ is given by

$$ b_{2} (k) = b_{1} (k) + z({t_{1}, S_{1}}) $$

where

$$ z(t_{1} , S_{1} ) = \left\{ {\begin{array}{ll} {t_{1} } &\quad {S_{1} > 0, \;{\text{or}}\; S_{1} = 0,\; t_{1} \ge \,d} \\ d &\quad {S_{1} = 0, \;t_{1} <\,\, d} \\ \end{array} } \right.. $$

(1)

The arrival epoch of the zeroth demand information is set as 0, thus $a(0) = 0$. Since the demand arrives in a Poisson process with rate $\lambda$, it follows that

$$ P({a(k) \le x}) = 1 - \mathop \sum \limits_{j = 0}^{k - 1} \frac{{({\lambda x})^{j}}}{j!}e^{- \lambda x} \quad x > 0, {k} = 1,2, \ldots $$

(2)

In a steady state, the limiting distribution of $W(k)$ follows a waiting time distribution of M/D/1 queue $P({W \le x})$, where $W$ is a waiting time in a steady state in a M/D/1 queue. This is well-known and given as follows (Erlang 1909).

$$ \begin{aligned} & P(W \le x) = (1 - \rho )\sum\limits_{k = 0}^{m} {\frac{{\{ - \lambda (x - (k + 1)d)\}^{k} }}{k!}} e^{\lambda (x - (k + 1)d)} \quad (m + 1)d \le x < (m + 2)d, m \ge 0, \hfill \\ &P(W \le x) = 0,\quad x < d \end{aligned} $$

(3)

Then we have the following proposition.

Proposition 1

For ${P}({W \le x} )$, the waiting time distribution of M/D/1 queue, it follows that

$$ \int\limits_{T - d}^{T} P (W > x){\text{d}}x = \left\{ { \begin{array}{*{20}l} {\frac{1}{\lambda }P(W > T)} \hfill & {T \ge d,} \hfill \\ d \hfill & {T < d} \hfill \\ \end{array} } \right.. $$

The proofs of propositions in this paper are given in Appendices.

From Liberopoulos (2008), $P({E(k ) > x} )$ is given for $x \ge 0$

$$ P({E(k ) \le x} ) = P({W \le x + kd} ) \quad k = 0, 1, 2 \ldots $$

(4)

Using Laplace transform of the sojourn time distribution of M/D/1 queue, we have the following proposition.

Proposition 2

For $x < 0$, we have

$$ \begin{array}{*{20}c} {P({E(0 ) \le x} ) = P({W \le x} ) = 0, } & { } \\ \end{array} $$

$$ P({E(k ) \le x} ) = ({1 - \rho} )\mathop \sum \limits_{n = 0}^{k - 1} \frac{{\{{- \lambda ({x + nd} )} \}^{k - 1 - n}}}{{({k - 1 - n} )!}}e^{{\lambda ({x + nd} )}} \quad k = 1, 2, 3, \ldots $$

In particular, for $- d \le x < 0$

$$\begin{aligned} P(E(k) \le x) & = (1 - \rho )\frac{{( - \lambda x)^{{k - 1}} }}{{(k - 1)!}}e^{{\lambda x}} \\ & \quad + P(W \le x + kd)\quad k = 1,2,3 \ldots \\ \end{aligned}$$

(5)

Note that $P({E(k ) \le x} )$ is continuous in x for $k = 1, 2, 3, \ldots$, whereas $P({E(0 ) \le x} )$ is continuous except $x = d$. From Eqs. (4) and (5), the relationship between $E({k + 1} )$ and $E(k )$ is obtained.

Corollary 1

$$ P({E({k + 1} ) \le x} ) = P({E(k ) \le x + d} ) x \ge 0,\quad k = 0, 1, 2, \ldots $$

(6)

$$ P({E({k + 1} ) \le x} ) = ({1 - \rho} )\frac{{({- \lambda x} )^{k}}}{k!}e^{\lambda x} + P({E(k ) \le x + d} ) \ge P({E(k ) \le x + d} ) - d \le x < 0,\quad k = 0, 1, 2, \ldots. $$

(7)

Average cost

We derive the average cost which is the sum of the average holding cost and backlog cost. The holding cost for the k-th work-in-process is incurred from the k-th completion of processing at process 1, $b_{1} (k ) + d$, to the $k + S_{1}$-th finishing time of processing at process 2, $b_{2} ({k + S_{1}} ) + d$. Thus, by (1) the average cost is given by

$$ \lambda h_{1} \left\{{\frac{{S_{1}}}{\lambda} + z({t_{1}, S_{1}} )} \right \} = h_{1} \{{S_{1} + \lambda z({t_{1}, S_{1}} )} \}. $$

Next, the holding cost for finished products and the backlog cost are considered. These costs for the $S_{2}$-th demand are determined by the difference between the $S_{2}$-th demand arrival epoch, $a({S_{2}} ) + T,$ and the finishing epoch of the zeroth process at process 2, $b_{2} (0 ) + d = b_{1} (0 ) + d + z({S_{1}, t_{1}} ) = t_{0} + W(0 ) + z({S_{1}, t_{1}} )$ in steady state, which is $\{{a({S_{2}} ) + T} \} - \{{b_{2} (0 ) + d} \} = \{{L_{1} - z({S_{1}, t_{1}} )} \} - E({S_{2}} )$. Thus, a sum of the average holding cost for finished items and the average backlog cost is given by

$$ \begin{aligned} & \lambda h_{2} {\mathbf{E}}[{ \hbox{max} }(\{ L_{1} - z(S_{1} , t_{1} )\} - E(S_{2} ), 0)] + \lambda b{\mathbf{E}}[{ \hbox{max} }(E(S_{2} ) - \{ L_{1} - z(S_{1} , t_{1} )\} , 0)] \\ & \quad = \lambda (h_{2} + b ){\mathbf{E}}[{ \hbox{max} }(E(S_{2} ) - \{ L_{1} - z(S_{1} , t_{1} )\} , 0)] - \lambda h_{2} {\mathbf{E}}[E(S_{2} )] + \lambda h_{2} \{ L_{1} - z(S_{1} , t_{1} )\} \\ & \quad = \lambda (h_{2} + b )\int\limits_{{L_{1} - z(t_{1} , S_{1} )}}^{\infty } {P(E(S_{2} ) > x){\text{d}}x - \lambda h_{2} {\mathbf{E}}[E(S_{2} )] + \lambda h_{2} \{ L_{1} - z(S_{1} , t_{1} )\} ,} \\ \end{aligned} $$

where E[X] means the expectation of X. When the release lead time of process 1 is $L_{1} = T - t_{0}$, the release lead time of process 2 is $L_{2} = L_{1} - t_{1} = T - t_{0} - t_{1}$, the amount of base stocks at process 1 is $S_{1}$, and the amount of base stocks at process 2 is $S_{2}$, the average cost, which is denoted by $C({L_{1}, t_{1}, S_{1}, S_{2}} )$, is given by

$$ \begin{aligned} C(L_{1} , t_{1} , S_{1} , S_{2} ) & = h_{1} \{ S_{1} + \lambda z(t_{1} , S_{1} )\} - \lambda h_{2} {\mathbf{E}}[E(S_{2} ) ] + \lambda h_{2} \{ L_{1} - z(t_{1} , S_{1} )\} \\ & \quad + \lambda (h_{2} + b )\int\limits_{{L_{1} - z(t_{1} , S_{1} )}}^{\infty } P (E(S_{2} ) > x){\text{d}}x, \\ \end{aligned} $$

(8)

where ${\mathbf{E}}[{E({S_{2}} ) } ] = {\mathbf{E}}[{ W(0 ) - a({S_{2}} )} ] = \frac{{d({2 - \rho} )}}{{2({1 - \rho} )}} - \frac{{S_{2}}}{\lambda}.$

In the following, the optimal release lead time and optimal base stock levels minimizing (8) are developed. Here, we use parameter $t_{1}$ instead of $L_{2}$, owing to easier analysis and discussion.

Optimal base stock level

We derive an optimal base stock level of process 2 $S_{2}^{*} (L_{1}, t_{1}, S_{1})$ when parameters $L_{1}, t_{1} \,{\text{and}}\,S_{1}$ are given.

Proposition 3

For given $L_{1}, t_{1}\,and\,S_{1},$ the optimal amount of base stocks at process 2 is given by

$$ S_{2}^{*} (L_{1} , t_{1} , S_{1} ) = \begin{array}{*{20}c} {\arg { \hbox{min} }} \\ {S_{2} :S_{2} = 0, 1, 2 \ldots } \\ \end{array} \left\{ {P(E(S_{2} + 1) > L_{1} - z(t_{1} , S_{1} )) \le \frac{{h_{2} }}{{h_{2} + b }}} \right\}. $$

(9)

Here we define additional notations.

$$ T_{k} = \begin{array}{*{20}c} {\arg { \hbox{min} }} \\ { x} \\ \end{array} \left\{ {P(E(k) > x) \le \frac{{h_{2} }}{{h_{2} + b }}} \right\}, \quad k = 0, \;1,\, 2 \ldots, $$

(10)

$$ \bar{S}(L_{1} ) = \begin{array}{*{20}c} {\arg { \hbox{min} }} \\ {S_{2} :S_{2} = 0, \;1,\; 2 \ldots } \\ \end{array} \left\{ {P(E(S_{2} + 1) > L_{1} - d) \le \frac{{h_{2} }}{{h_{2} + b }}} \right\}, $$

(11)

$$ \hat{S}_{0} = \begin{array}{*{20}c} {\arg { \hbox{min} }} \\ {S_{2} :S_{2} = 0, 1, 2 \ldots } \\ \end{array} \left\{ {P(E(S_{2} + 1) > 0) \le \frac{{h_{2} }}{{h_{2} + b }}} \right\}. $$

(12)

From Liberopoulos (2008), we have

$$ T_{k} = T_{k + 1} + d \quad k = 0, 1, \ldots,\quad \hat{S}_{0} - 1 $$

(13)

and by (7) it follows that

$$ T_{{\hat{S}_{0}}} \ge T_{{\hat{S}_{0} + 1}} + d, $$

(14)

which leads to $T_{0} \ge d, 0 < T_{{\hat{S}_{0}}} \le d, T_{{\hat{S}_{0} + 1}} \le 0$.

From Eqs. (10) to (14) and the result of Corollary 1, the relationship between $P({E(k ) \le x} )$ and $T_{k}$ are given in Fig. 2. In this figure, the dotted line on the left hand side is obtained by moving the line $P({W \le x} )$ in parallel along the x-axis by $- kd, {\text{for }}k = \hat{S}_{0} - 2, \hat{S}_{0} - 1, \hat{S}_{0}, \hat{S}_{0} + 1$. From Corollary 1, the distribution function ${\text{P}}(E(k ) \le x)$ is obtained by moving $P({W \le x} )$ in parallel by $kd$ when $x \ge 0$, but in the range $x < 0$, it is greater than the value obtained by the similar movement. From (13), the difference between $T_{k}$ and $T_{k + 1}$ is $d$ for all $k = 0, 1, \ldots, \hat{S}_{0} - 1, {\text{but }}$ by (14), the difference between $T_{{\hat{S}_{0}}}$ and $T_{{\hat{S}_{0} + 1}}$ is no less than $d$.

Fig. 2

Relationship between $P ({E (k ) \le x} )$ and ${\text{T}}_{\text{k}}$

When $S_{1} > 0$ or ($S_{1} = 0$ and $t_{1} \ge d$), by Proposition 3

$$ S_{2}^{*} (L_{1} , t_{1} , S_{1} ) = \begin{array}{*{20}c} {\arg { \hbox{min} }} \\ {S_{2} :S_{2} = 0, 1, 2 \ldots } \\ \end{array} \left\{ {P(E(S_{2} + 1) > L_{1} - t_{1} ) \le \frac{{h_{2} }}{{h_{2} + b }}} \right\} $$

Thus, if $T_{S + 1} \le L_{2} = L_{1} - t_{1} < T_{S}$ then $S_{2}^{*} (L_{1}, t_{1}, S_{1} ) = S$, and if $T_{0} \le L_{2}\, \, {\text{then}} \, \, S_{2}^{*} (L_{1}, t_{1}, S_{1} ) = 0$.

When $S_{1} = 0$ and $t_{1} < d$, we have

$$ S_{2}^{*} (L_{1} , t_{1} , S_{1} ) = \bar{S}(L_{1} ) = \begin{array}{*{20}c} {\arg { \hbox{min} }} \\ {S_{2} :S_{2} = 0, 1, 2 \ldots } \\ \end{array} \left\{ {P(E(S_{2} + 1) > L_{1} - d) \le \frac{{h_{2} }}{{h_{2} + b }}} \right\} $$

That is, if $T_{S + 1} + d \le L_{1} < T_{S} + d$ then $S_{2}^{*} (L_{1}, t_{1}, S_{1} ) = \bar{S}({L_{1}} ) = S$, and if $T_{0} + d \le L_{1}$ then $S_{2}^{*} = \bar{S}({L_{1}} ) = 0$. By (13) and (14), if $L_{1} < T_{{\hat{S}_{0} + 1}} + d$ then $S_{2}^{*} (L_{1}, t_{1}, S_{1} ) = \bar{S}({L_{1}} ) = \hat{S}_{0} + 1$, if $T_{{\hat{S}_{0} + 1}} + d \le L_{1} < T_{{\hat{S}_{0} - 1}}$ then $S_{2}^{*} (L_{1}, t_{1}, S_{1} ) = \hat{S}_{0}$, if $T_{S} \le L_{1} < T_{S - 1}, S = 1, \ldots, \hat{S}_{0} - 1$ then $S_{2}^{*} (L_{1}, t_{1}, S_{1} ) = S$, and if $T_{0} \le L_{1}$ then $S_{2}^{*} (L_{1}, t_{1}, S_{1} ) = \bar{S}({L_{1}} ) = 0$.

Figure 3 shows that the optimal base stock level of process 2 for the cases (a) $S_{1} > 0$ and (b) $S_{1} = 0$, for given $L_{1}$ and $t_{1}$, where the vertical axis is $t_{1}$ and the horizon axis is $L_{1}$, and slanted lines show $L_{2} = 0$ and $L_{2} = T_{k}$ for $k = 0, 1, \ldots, \hat{S}_{0}$. In case (a) that $S_{1} > 0$, if the pair $({L_{1}, t_{1}} )$ is placed in the region between the two lines $L_{2} = T_{S + 1}$ and $L_{2} = T_{S}$, then the optimal amount of base stocks in process 2 is $S$. Similarly, in case (b) that $S_{1} = 0$, if $({L_{1}, t_{1}} )$ is in the region between lines $L_{2} = T_{S + 1}$ and $L_{2} = T_{S}$ and $t_{1} \ge d$, or in the region between $L_{1} = T_{S}$ and $L_{1} = T_{S - 1}$ and $t_{1} < d$, then optimal base stock level of process 2 is $S$.

Fig. 3

${\text{Optimal base stock level }}S_{2}^{*} (L_{1}, t_{1}, S_{1})$

Next, we derive the optimal amount of base stocks of process 1 when $L_{1}$ and $t_{1}$ are given. In the following, $S_{2}^{*} ({L_{1}, t_{1}, S_{1}} )$ is simply written by $S_{2}^{*}.$

When $S_{1} > 0$, if $T_{S + 1} \le L_{2} < T_{S}$ then $S_{2}^{*} = S$, and if $T_{0} \le L_{2}$ then $S_{2}^{*} = 0$, thus $S_{2}^{*}$ does not depend on $S_{1}$. Thus, when $S_{1} > 0,$ by (1) and (8)

$$ \begin{aligned} C(L_{1} , t_{1} , S_{1} , S_{2}^{*} ) & = h_{1} (S_{1} + \lambda t_{1} ) - \lambda h_{2} {\mathbf{E}}[E(S_{2}^{*} ) ] \\ & \quad + \lambda h_{2} L_{2} + \lambda (h_{2} + b )\int\limits_{{L_{2} }}^{\infty } P (E(S_{2}^{*} ) > x)\text{d}x, \\ \end{aligned} $$

which implies $C({L_{1}, t_{1}, S_{1}, S_{2}^{*}} ) - C({L_{1}, t_{1}, S_{1} + 1, S_{2}^{*}} ) = - h_{1} \le 0,$ and thus $C({L_{1}, t_{1}, 1, S_{2}^{*}} ) \le C({L_{1}, t_{1}, 2, S_{2}^{*}} ) \le C({L_{1}, t_{1}, 3, S_{2}^{*}} ), \ldots$, where the equality holds only when $h_{1} = 0$. This means that the optimal base stock level of process 1, $S_{1}^{*} (L_{1}, t_{1}$), is 1 or 0. If $t_{1} \ge d$, in the same way it holds that $C({L_{1}, t_{1}, 0, S_{2}^{*}} ) \le C({L_{1}, t_{1}, 1, S_{2}^{*}} )$. From the above discussion, when $t_{1} \ge d$, the optimal amount of base stocks of process 1 becomes 0, and when $t_{1} < d$, the optimal amount of base stocks is 1 or 0. Note that when $h_{1} = 0$, the smallest $S_{1}$ which minimizes the average cost is set as $S_{1}^{*}$($L_{1}, t_{1}$).

Figure 4 shows the candidate of optimal base stock levels $(S_{1}^{*}$($L_{1}, t_{1}$), $S_{2}^{*} ({L_{1}, t_{1})} )$. ${\text{where }} S_{2}^{*} (L_{1}, t_{1})$ is $S_{2}^{*} ({L_{1}, t_{1}, S_{1}^{*} ({L_{1}, t_{1}} )} ).$ When $t_{1} \ge d$, optimal base stock level of process 1 is 0, and so if the pair $({L_{1}, t_{1}} )$ is placed in the region between lines $L_{2} = T_{S + 1}$ and $L_{2} = T_{S}$, then a pair of base stock levels of processes 1 and 2, $(S_{1}^{*}$($L_{1}, t_{1}$), $S_{2}^{*}$($L_{1}, t_{1}$)), is $({0, S} )$. ${\text{When }}t_{1} < d$, the optimal base stock level $S_{1}^{*}$ is 1 or 0. By superimposing cases (a) and cases (b) of Fig. 3, Fig. 4 is obtained. For example, if $(L_{1}, t_{1})$ is placed between lines $L_{2} = T_{S + 1}$ and $L_{1} = T_{S}$, then the candidates for optimal base stocks $(S_{1}^{*}$($L_{1}, t_{1}$), $S_{2}^{*}$($L_{1}, t_{1}$)) are $({1, S} )$ and $({0, S + 1} )$. Thus, when $t_{1} < d$, by comparing these two pairs optimal base stock levels can be obtained.

Fig. 4

Candidates for optimal base stoke levels for given ${\text{L}}_{1} \, {\text{and}} \,{\text{t}}_{1}$

Optimal release lead time of process 2

For given $L_{1}$ we derive optimal release lead time $L_{2},$ which is equivalent to derive optimal $t_{1}$, which is denoted by $t_{1}^{*} (L_{1})$.

From discussion of “Optimal base stock level”, if $t_{1} \ge d$ then optimal base stock level of process 1 is $0$, and if $t_{1} < d$ then there are two possible cases on the optimal base stock levels. ${\text{In the following}}, {\text{for given }}L_{1}, {\text{the case}}\, \,t_{1} \ge d$ is considered in “The case that ${t}_{1} \ge {d}$ ”, the case $0 \le t_{1} < d$ and $S_{1} = 0$ is considered in “The case that $0 \le { t}_{1} < d$ and ${S}_{1} = 0$ ”, and the case $0 \le t_{1} < d$ and $S_{1} = 1$ is considered in “The case that $0 \le { t}_{1} < {d}$ and ${S}_{1} = 1$ ”. Using obtained results there, optimal $t_{1}$ is derived in “Optimal ${t}_{1}$ for Given ${L}_{1}$ ”, and in “Optimal ${t}_{1}^{{*}}, {S}_{1}^{{*}}, {S}_{2}^{{*}}$ ” the results are summarized.

The case that ${t}_{1} \ge {d}$

“Optimal base stock level” shows that $S_{1}^{*} (L_{1}, t_{1}) = 0$, and

$$ S_{2}^{*} (L_{1} , t_{1} ) = \begin{array}{*{20}c} {\arg { \hbox{min} }} \\ {S_{2} :S_{2} = 0, 1, 2 \ldots } \\ \end{array} \left\{ {P(E(S_{2} + 1) > L_{1} - t_{1} = L_{2} ) \le \frac{{h_{2} }}{{h_{2} + b }}} \right\}, $$

If $T_{S + 1} \le L_{2} < T_{S}$ then $S_{2}^{*} (L_{1}, t_{1}) = S$, and if $T_{0} \le L_{2}$ then $S_{2}^{*} (L_{1}, t_{1}) = 0$. Here, we define

$$ \tilde{T} = \begin{array}{*{20}c} {\arg { \hbox{min} }} \\ x \\ \end{array} \left\{ {P(W > x) \le \frac{{h_{2} - h_{1} }}{{h_{2} + b }}} \right\}. $$

(15)

Note that $h_{1} \ge 0$ implies $\tilde{T} \ge T_{0}$.

Proposition 4

(a) If $d \le L_{1} < T_{0}$, then average cost $C({L_{1}, t_{1}, S_{1}^{*} (L_{1}, t_{1}), S_{2}^{*} (L_{1}, t_{1})} )$ is increasing in $t_{1 }$ where $t_{1} \ge d$.

(b) If $T_{0} \le L_{1} < \tilde{T} + d$, then the average cost is increasing in $t_{1}$ where $t_{1} \ge d$.

(c) If $\tilde{T} + d \le L_{1}$, then the average cost is decreasing in $t_{1}$ where $d \le t_{1} \le L_{1} - \tilde{T}$, and increasing in $t_{1}$ where $t_{1} > L_{1} - \tilde{T}$.

From Proposition 4, if $d \le L_{1} < \tilde{T} + d$, then $t_{1}^{*} = d$ in the region that $t_{1} \ge d$, and thus $L_{2}^{*} = L_{1} - d, S_{1}^{*} = 0$, and

$$ S_{2}^{*} = \begin{array}{*{20}c} {\arg { \hbox{min} }} \\ {S_{2} :S_{2} = 0, 1, 2 \ldots } \\ \end{array} \left\{ {P(E(S_{2} + 1) > L_{1} - d) \le \frac{{h_{2} }}{{h_{2} + b }}} \right\} = \bar{S}(L_{1} ) $$

If $L_{1} \ge \tilde{T} + d$, then $t_{1}^{*} = L_{1} - \tilde{T}$, in the region that $t_{1} \ge d$, and thus $L_{2}^{*} = \tilde{T}, S_{1}^{*} = 0$, and since $\tilde{T} \ge T_{0}$ it follows that

$$ S_{2}^{*} = \begin{array}{*{20}c} {\arg { \hbox{min} }} \\ {S_{2} :S_{2} = 0, 1, 2 \ldots } \\ \end{array} \left\{ {P(E(S_{2} + 1) > \tilde{T}) \le \frac{{h_{2} }}{{h_{2} + b }}} \right\} = 0. $$

The case that $0 \le { t}_{1} < d$ and ${S}_{1} = 0$

From the result of “Optimal base stock level”,

$$ S_{2}^{*} = \bar{S}(L_{1} ) = \begin{array}{*{20}c} {\arg { \hbox{min} }} \\ {S_{2} :S_{2} = 0, 1, 2 \ldots } \\ \end{array} \left\{ {P(E(S_{2} + 1) > L_{1} - d) \le \frac{{h_{2} }}{{h_{2} + b }},} \right\} $$

which is independent on $t_{1}.$ From (8) when $S_{1} = 0$

$$ \begin{aligned} C(L_{1} , t_{1} , S_{1} , S_{2}^{*} ) & = \lambda dh_{1} - \lambda h_{2} {\mathbf{E}}[E(S_{2}^{*} ) ] + \lambda h_{2} (L_{1} - d) \\ & \quad + \lambda (h_{2} + b )\int\limits_{{L_{1} - d}}^{\infty } P (E(S_{2}^{*} ) > x){\text{d}}x, \\ \end{aligned} $$

and thus when $S_{1} = 0, C({L_{1}, t_{1}, S_{1}, S_{2}^{*}} ) = C({L_{1}, t_{1}, 0, \bar{S}({L_{1}} )} )$ is constant in $t_{1}$ when $0 \le t_{1} < d$.

The case that $0 \le { t}_{1} < {d}$ and ${S}_{1} = 1$

From the result of “Optimal base stock level”,

$$ S_{2}^{*} = \begin{array}{*{20}c} {\arg { \hbox{min} }} \\ {S_{2} :S_{2} = 0, 1, 2 \ldots } \\ \end{array} \left\{ {P(E(S_{2} + 1) > L_{1} - t_{1} = L_{2} ) \le \frac{{h_{2} }}{{h_{2} + b }}} \right\}. $$

If $T_{S + 1} \le L_{2} < T_{S}, S_{2}^{*} = S$ and $T_{0} \le L_{2}$ then $S_{2}^{*} = 0$.

Proposition 5

(a) When $0 \le L_{1} < T_{0}$, $S_{1} = 1$, $C({L_{1}, t_{1}, 1, S_{2}^{*}} )$ is increasing in $t_{1}$ where $0 \le t_{1} < d$.

(b) When $T_{0} \le L_{1}, S_{1} = 1$, if $T_{0} \le L_{1} < \tilde{T}$, then $C({L_{1}, t_{1}, 1, S_{2}^{*}} )$ is increasing in $t_{1}$ where $0 \le t_{1} < d.$ If $\tilde{T} \le L_{1} < \tilde{T} + d$ then $C({L_{1}, t_{1}, 1, S_{2}^{*}} )$ is decreasing in $t_{1}$ where $0 \le t_{1} < L_{1} - \tilde{T}$ and increasing in $t_{1}$ where $L_{1} - \tilde{T} \le t_{1} < d$. If $\tilde{T} + d \le L_{1}$, $C({L_{1}, t_{1}, 1, S_{2}^{*}} )$ is decreasing in $t_{1}$ where $0 \le t_{1} < d$.

Proposition 5 shows that when $S_{1} = 1$ in the region that $0 \le t_{1} < d$ the followings hold.

If $0 \le L_{1} < \tilde{T}$, then $t_{1}^{*} = 0$, $L_{2}^{*} = L_{1}$, and

$$ S_{2}^{*} = \begin{array}{*{20}c} {\arg { \hbox{min} }} \\ {S_{2} :S_{2} = 0, 1, 2 \ldots } \\ \end{array} \left\{ {P(E(S_{2} + 1) > L_{1} ) \le \frac{{h_{2} }}{{h_{2} + b }}} \right\} = \left\{ {\begin{array}{*{20}l} {\bar{S}(L_{1} ) - 1} \hfill & {\bar{S}(L_{1} ) \ge 1,} \hfill \\ 0 \hfill & {\bar{S}(L_{1} ) = 0} \hfill \\ \end{array} } \right.. $$

If $\tilde{T} \le L_{1} < \tilde{T} + d$, then $t_{1}^{*} = L_{1} - \tilde{T}$, $L_{2}^{*} = \tilde{T}$, and

$$ S_{2}^{*} = \begin{array}{*{20}c} {\arg { \hbox{min} }} \\ {S_{2} :S_{2} = 0, 1, 2 \ldots } \\ \end{array} \left\{ {P(E(S_{2} + 1) > \tilde{T}) \le \frac{{h_{2} }}{{h_{2} + b }}} \right\}0. $$

If $L_{1} \ge \tilde{T} + d$, then $t_{1}^{*} = d$, $L_{2}^{*} = L_{1} - d({\ge \tilde{T} \ge T_{0}} )$, and

$$ S_{2}^{*} = \begin{array}{*{20}c} {\arg { \hbox{min} }} \\ {S_{2} :S_{2} = 0, 1, 2 \ldots } \\ \end{array} \left\{ {P(E(S_{2} + 1) > L_{1} - d) \le \frac{{h_{2} }}{{h_{2} + b }}} \right\} = 0. $$

Optimal ${t}_{1}$ for given ${L}_{1}$

Based on the results in “Optimal base stock level” and in “The case that ${t}_{1} \ge {d}$ ” to “The case that $0 \le { t}_{1} < {d}$ and ${S}_{1} = 1$ ”, the five cases are considered to derive optimal $t_{1}$ for given $L_{1}$.

The case that $L_{1} < T_{{\hat{S}_{0} + 1}} + d$ or $T_{{\hat{S}_{0}}} \le L_{1} < T_{0}$

From results in “The case that ${t}_{1} \ge {d}$ ” and “The case that $0 \le { t}_{1} < d$ and ${S}_{1} = 0$ ”, when $S_{1} = 0$, $C({L_{1}, 0, 0, \bar{S}({L_{1}} )} )$ is minimal cost, where $\bar{S}({L_{1}} ) \ge 1, z({t_{1}, S_{1}} ) = d$. From “The case that $0 \le { t}_{1} < {d}$ and ${S}_{1} = 1$ ”, when $S_{1} = 1$, $C({L_{1}, 0, 1, \bar{S}({L_{1}} ) - 1} )$ is minimal and $z({t_{1}, S_{1}} ) = t_{1} = 0.$ By (8)

$$ \begin{aligned} & C(L_{1} , 0, 0,\bar{S}(L_{1} )) - C(L_{1} , 0, 1,\bar{S}(L_{1} ) - 1) = (h_{2} - h_{1} )(1 - \rho ) \\ & \quad + \lambda (h_{2} + b )\int\limits_{{L_{1} - d}}^{\infty } {\{ P(E(\bar{S}(L_{1} )) > x) - P(E(\bar{S}(L_{1} ) - 1) > x + d)\} } {\text{d}}x \\ \end{aligned} $$

and by (6)

$\int\nolimits_{a}^{\infty } {\{ P(E(\bar{S}(L_{1} )) > x) - P(E(\bar{S}(L_{1} ) - 1) > x + d)\} } {\text{d}}x = 0$ for all $a \ge 0$.

If $L_{1} \ge d,$ then $C({L_{1}, 0, 0, \bar{S}({L_{1}} )} ) - C({L_{1}, 0, 1, \bar{S}({L_{1}} ) - 1} ) \ge 0$.

If $L_{1} < d,$ (2) and (7) imply that

$$ \begin{aligned} & \int\limits_{{L_{1} - d}}^{0} {\{ P(E(\bar{S}(L_{1} )) > x) - P(E(\bar{S}(L_{1} ) - 1) > x + d)\} {\text{d}}x = - (1 - \rho )} \int\limits_{{L_{1} - d}}^{0} {\frac{{( - \lambda x)^{{S(L_{1} ) - 1}} }}{{(\bar{S}(L_{1} ) - 1)!}}} e^{\lambda x} {\text{d}}x \\ & \quad = - (1 - \rho )\frac{1}{\lambda }P(a(\bar{S}(L_{1} )) \le - (L_{1} - d)) \\ \end{aligned} $$

and

$$ \begin{aligned} & C(L_{1} , 0, 0, \bar{S}(L_{1} )) - C(L_{1} , 0, 1, \bar{S}(L_{1} ) - 1) = (h_{2} - h_{1} )(1 - \rho ) \\ & - (h_{2} + b )(1 - \rho )P(a(\bar{S}(L_{1} )) \le - (L_{1} - d)). \\ \end{aligned} $$

When $L_{1} < d$, $L_{1}$ satisfying $C({L_{1}, 0, 0, S} ) = C({L_{1}, 0, 1, S - 1} )$ is set as $\hat{L}(S )$. Thus, $\hat{L}(S )$ satisfies

$$ P({a(S ) \le - ({\hat{L}(S ) - d} )} ) = \frac{{h_{2} - h_{1}}}{{h_{2} + b}}. $$

Note that $\hat{L}(S ) \le d$.

In summary, when $d \le L_{1} < T_{0}$, the optimal cost is $C({L_{1}, 0, 1, \bar{S}({L_{1}} ) - 1} )$. When $L_{1} < T_{{\hat{S}_{0} + 1}} + d$ or $T_{{\hat{S}_{0}}} \le L_{1} < d$, then if $L_{1} \ge \hat{L} ({\bar{S} ({L_{1}} )} )$ the optimal cost is $C ({L_{1}, 0, 1, \bar{S} ({L_{1}} ) - 1} )$, whereas if $L_{1} < \hat{L} ({\bar{S} ({L_{1}} )} )$ then the optimal cost is $C ({L_{1}, 0, 0, \bar{S} ({L_{1}} )} )$.

The case that $T_{{\hat{S}_{0} + 1}} + d \le L_{1} < T_{{\hat{S}_{0}}}$

From the result in “The case that ${t}_{1} \geq {d}$" and ${S}_{1} = 0$ ”, when $S_{1} = 0$, $C ({L_{1}, 0, 0, \hat{S}_{0}} )$ is the minimal cost, whereas from “The case that $0 \le {t}_{1} < {d}$ and ${S}_{1} = 1$ ”, when $S_{1} = 1$, the minimal cost is $C ({L_{1}, 0, 1, \hat{S}_{0}} )$. By (8), we have

$$ \begin{aligned} C(L_{1} , 0, 0, \hat{S}_{0} ) - C(L_{1} , 0, 1,\hat{S}_{0} ) & = - h_{1} - \rho (h_{2} - h_{1} ) \\ & \quad + \lambda (h_{2} + b )\int\limits_{{L_{1} - d}}^{{L_{1} }} P (E(\hat{S}_{0} ) > x){\text{d}}x. \\ \end{aligned} $$

When $\rho \le \frac{{h_{1}}}{{h_{1} + b }}$, since $\mathop \int \nolimits_{{L_{1} - d}}^{{L_{1}}} P ({E ({\hat{S}_{0}} ) > x} ){\text{d}}x \le d$ it follows that $C ({L_{1}, 0, 0,\hat{S}_{0}} ) - C ({L_{1}, 0, 1, \hat{S}_{0}} ) \le 0$, and thus the optimal cost becomes $C ({L_{1}, 0, 0, \hat{S}_{0}} ).$

When $\rho > \frac{{h_{1}}}{{h_{1} + b }}$, let $\bar{L} (S )$ denote $L_{1}$ satisfying $C ({L_{1}, 0, 0, S} ) = C ({L_{1}, 0, 1, S} )$, and thus

$$ \int\limits_{{\bar{L}(S) - d}}^{{\bar{L}(S)}} P (E(S) > x){\text{d}}x = \frac{1}{\lambda }\frac{{h_{1} }}{{h_{2} + b }} + d\frac{{h_{2} - h_{1} }}{{h_{2} + b }}. $$

When $T_{{\hat{S}_{0} + 1}} + d \le L_{1} < T_{{\hat{S}_{0}}}$, if $L_{1} \ge \bar{L} ({\hat{S}_{0}} )$ then the optimal cost is $C ({L_{1}, 0, 0, \hat{S}_{0}} )$, whereas if $L_{1} < \bar{L} ({\hat{S}_{0}} )$ then it follows that $C ({L_{1}, 0, 1, \hat{S}_{0}} )$ is the minimal cost.

The case that $T_{0} \le L_{1} < \tilde{T}$

From “The case that ${t}_{1} \ge {d}$ ” and “The case that $0 \le { t}_{1} < d$ and ${S}_{1} = 0$ ”, when $S_{1} = 0, C ({L_{1}, 0, 0, 0} )$ is the optimal cost, whereas from “The case that $0 \le {t}_{1} < {d}$ and ${S}_{1} = 1$ ”, when $S_{1} = 1,$ the minimal cost is $C ({L_{1}, 0, 1, 0} )$. By (8),

$$ C(L_{1} , 0, 0, 0) - C(L_{1} , 0, 1, 0) = - h_{1} - \rho (h_{2} - h_{1} ) + \lambda (h_{2} + b )\int\limits_{{L_{1} - d}}^{{L_{1} }} P (W > x){\text{d}}x. $$

When $\rho \le \frac{{h_{1}}}{{h_{1} + b }}$, $C ({L_{1}, 0, 0, 0} ) - C ({L_{1}, 0, 1, 0} ) \le 0$ and the minimal cost is $C ({L_{1}, 0, 0, 0} )$.

When $\rho > \frac{{h_{1}}}{{h_{1} + b }}$, let $\bar{L} (0 )$ denote $L_{1}$ satisfying $C ({L_{1}, 0, 0, 0} ) = C ({L_{1}, 0, 1, 0} )$, and thus

$$ \int\limits_{{\bar{L}(0) - d}}^{{\bar{L}(0)}} P (W > x){\text{d}}x = \frac{1}{\lambda }\frac{{h_{1} }}{{h_{2} + b }} + d\frac{{h_{2} - h_{1} }}{{h_{2} + b }}, $$

where $\bar{L} (0 ) > d$. Then when $T_{0} \le L_{1} < \tilde{T},$ if $L_{1} \ge \bar{L} (0 )$, then $C ({L_{1}, 0, 0, 0} )$ is the minimal cost, and if $L_{1} < \bar{L} (0 )$ the optima cost becomes $C ({L_{1}, 0, 1, 0} )$.

The case that $\tilde{T} \le L_{1} < \tilde{T} + d$

From “The case that ${t}_{1} \ge {d}$ ” and “The case that $0 \leq {t}_{1} < {d}$ and ${S}_{1} = 0$ ”, when $S_{1} = 0, C ({L_{1}, 0, 0, 0} )$ is the minimal cost, and from “The case that $0 \le { t}_{1} < {d}$ and ${S}_{1} = 1$ ”, when $S_{1} = 1, C ({L_{1}, L_{1} - \tilde{T}, 1, 0} )$ is the optimal cost. By (8),

$$ C(L_{1} , 0, 0, 0) - C(L_{1} , L_{1} - \tilde{T}, 1, 0) = - h_{1} - \lambda (d - L_{1} + \tilde{T})(h_{2} - h_{1} ) + \lambda (h_{2} + b )\int\limits_{{L_{1} - d}}^{{\tilde{T}}} P (W > x){\text{d}}x. $$

Let $\tilde{L}$ denote $L_{1}$ satisfying $C ({L_{1}, 0, 0, 0} ) = C ({L_{1}, L_{1} - \tilde{T}, 1, 0} )$, and thus

$$ \int\limits_{{\tilde{L} - d}}^{{\tilde{T}}} P (W > x){\text{d}}x = \frac{1}{\lambda }\frac{{h_{1} }}{{h_{2} + b}} + (\tilde{T} - \tilde{L} + d)\frac{{h_{2} - h_{1} }}{{h_{2} + b}}, $$

where $\tilde{L} \le \tilde{T} + d$. When $\tilde{T} \le L_{1} < \tilde{T} + d$, if $L_{1} \ge \tilde{L}$ the optimal cost is $C ({L_{1}, 0, 0, 0} ),$ and if $L_{1} < \tilde{L}$, thus the optimal cost is $C ({L_{1}, L_{1} - \tilde{T}, 1, 0} )$.

The case that $\tilde{T} + d \le L_{1}$

From “The case that ${t}_{1} \ge {d}$ ” and “The case that ${t}_{1} \ge {d}$ and ${S}_{1} = 0$ ”, when $S_{1} = 0$, $C ({L_{1}, L_{1} - \tilde{T}, 0, 0} )$ is the minimal cost, and from “The case that $0 \le { t}_{1} < {d}$ and ${S}_{1} = 1$ ”, when $S_{1} = 1, C ({L_{1}, d, 1, 0} )$ is the minimal cost. By (8),

$$ \begin{aligned} C(L_{1} , L_{1} - \tilde{T}, 0, 0) - C(L_{1} , d, 1, 0) & = - h_{1} - \lambda (L_{1} - d - \tilde{T})(h_{2} - h_{1} ) \\ & \quad + \lambda (h_{2} + b )\int\limits_{{\tilde{T}}}^{{L_{1} - d}} P (W > x){\text{d}}x, \\ \end{aligned} $$

and by (15) it holds that

$$ \int\limits_{{\tilde{T}}}^{{L_{1} - d}} P (W > x){\text{d}}x < \frac{{h_{2} - h_{1} }}{{h_{2} + b }}(L_{1} - d - \tilde{T}). $$

Thus, $C ({L_{1}, L_{1} - \tilde{T}, 0, 0} ) - C ({L_{1}, d, 1, 0} ) < 0$ and the optimal cost is $C ({L_{1}, L_{1} - \tilde{T}, 0, 0} )$.

Optimal ${t}_{1}^{{*}}, {S}_{1}^{{*}}, {S}_{2}^{{*}}$

Notations defined in this section are summarized in the following.

$$ \tilde{T} = \begin{array}{*{20}c} {\arg { \hbox{min} }} \\ x \\ \end{array} \left\{ {P(W > x) \le \frac{{h_{2} - h_{1} }}{{h_{2} + b }}} \right\}, $$

$$ P ({a (S ) \le - ({\hat{L} (S ) - d} )} ) = \frac{{h_{2} - h_{1}}}{{h_{2} + b}}, $$

(16)

$$ \int\limits_{{\bar{L}(S) - d}}^{{\bar{L}(S)}} P (E(S) > x){\text{d}}x = \frac{1}{\lambda }\frac{{h_{1} }}{{h_{2} + b }} + d\frac{{h_{2} - h_{1} }}{{h_{2} + b }}, $$

(17)

$$ \int\limits_{{\tilde{L} - d}}^{{\tilde{T}}} P (W > x){\text{d}}x = \frac{1}{\lambda }\frac{{h_{1} }}{{h_{2} + b}} + (\tilde{T} - \tilde{L} + d)\frac{{h_{2} - h_{1} }}{{h_{2} + b}}, \tilde{L} \le \tilde{T} + d. $$

(18)

Note that $\bar{L} (S )$ exists only when $\rho > \frac{{h_{1}}}{{h_{1} + b }}$, and it is assumed $\tilde{L} \le \tilde{T} + d$. Since $\hat{L} (S ) \le d,$ when $d \le L_{1} < T_{0}$ it is satisfied that $L_{1} \ge \hat{L} (S )$. It is noted that $\tilde{T} \ge T_{0}$.

When $\rho \le \frac{{h_{1}}}{{h_{1} + b }}$, it follows that $\rho \le \frac{{h_{2}}}{{h_{2} + b }}$ by assumption $h_{2} \ge h_{1},$ and hence by Eqs. (10) and (12), it follows that $T_{0} = d$, $T_{1} \le 0$ and $\hat{S}_{0} = 0$. The following proposition holds on $\hat{L} (1 )$.

Proposition 6

When $\rho \le \frac{{h_{1}}}{{h_{1} + b }}$, it is satisfied that $\hat{L} (1 ) \ge T_{1} + d$ and $\tilde{L} \le \tilde{T}$.

As summary of this section, Table 1 shows optimal $t_{1}$ and base stock levels for given $L_{1}$, where a...b means that all x in [a, b] are optimal.

Table 1 Optimal $t_{1}^{*}, S_{1}^{*}, S_{2}^{*}$ for given $L_{1}$

Optimal release lead time of process 1

Optimal release lead time of process 1 is considered. In “Optimal release lead time when ${T} \ge {T}_{0}$ and ${\rho}> \frac{{{h}_{1}}}{{{h}_{1} + {b }}}$ ”, the case that $T \ge T_{0}$ and $\rho > \frac{{h_{1}}}{{h_{1} + b }}$ is considered, and in “Optimal release lead time when ${T} \ge {T}_{0}$ and ${\rho}\le \frac{{{h}_{1}}}{{{h}_{1} + {b }}}$ ”, the case $T \ge T_{0}$ and $\rho \le \frac{{h_{1}}}{{h_{1} + b }}$ is discussed.

For open intervals on $L_{1}$ where $t_{1}^{*}, S_{1}^{*}, S_{2}^{*}$ are not changed, by (8)

$$ \frac{{{\text{d}}C(L_{1} , t_{1}^{*} , S_{1}^{*} , S_{2}^{*} )}}{{{\text{d}}L_{1} }} = \lambda h_{2} - \lambda (h_{2} + b )P(E(S_{2}^{*} ) > L_{1} - z(t_{1}^{*} , S_{1}^{*} )), $$

and thus from the definition of $T_{0}$, when $L_{1} < T_{0} + z ({t_{1}^{*}, S_{1}^{*}} ),$ $\frac{{{\text{d}}C(L_{1} , t_{1}^{*} , S_{1}^{*} , S_{2}^{*} )}}{{{\text{d}}L_{1} }} < 0$, whereas when $L_{1} \ge T_{0} + z ({t_{1}^{*}, S_{1}^{*}} ),$ $\frac{{{\text{d}}C(L_{1} , t_{1}^{*} , S_{1}^{*} , S_{2}^{*} )}}{{{\text{d}}L_{1} }} < 0.$ When $0 \le L_{1} < T_{0}$, $C ({L_{1}, t_{1}^{*}, S_{1}^{*}, S_{2}^{*}} )$ is decreasing in $L_{1}$, and thus when $T \le T_{0}$ optimal release lead time is $L_{1}^{*} = T$.

Optimal release lead time when ${T} \ge {T}_{0}$ and ${\rho}> \frac{{{h}_{1}}}{{{h}_{1} + {b }}}$

We have the following relationships among $\bar{L} (0 )$, $\tilde{L}$, $\tilde{T}$ and $T_{0} + d$.

Proposition 7

(a) When $\rho > \frac{{h_{1}}}{{h_{1} + b }},$ if $h_{1} < h_{2}$, then $T_{0} < \bar{L} (0 ) < T_{0} + d$, and if $h_{1} = h_{2}$, then $T_{0} = \bar{L} (0 ) < T_{0} + d$.

(b) When $\rho > \frac{{h_{1}}}{{h_{1} + b }}$, if $\tilde{L} < \tilde{T}$, then $\bar{L} (0 ) < \tilde{L} < \tilde{T}$, if $\tilde{T} < \tilde{L}$, then $\tilde{T} < \bar{L} (0 ) < \tilde{L}$, and if $\tilde{L} = \tilde{T}$, then $\bar{L} (0 ) = \tilde{L} = \tilde{T}$.

(c) When $\tilde{T} < \tilde{L}$, $\tilde{L} < T_{0} + d$ is satisfied.

First, we consider the case $\tilde{L} < \tilde{T}$. From Proposition 7, it holds that $T_{0} \le \bar{L} (0 ) < \tilde{L} < \tilde{T}$. By (a) of Table 1, in the case that $L_{1} \ge T_{0}$ and $\tilde{L} < \tilde{T},$ optimal $t_{1}$ and optimal base stock levels are given in Table 2. When $T_{0} \le L_{1} < \tilde{T}$ and $L_{1} < \bar{L} (0 )$, it holds that $T_{0} + z ({t_{1}^{*}, S_{1}^{*}} ) = T_{0} \le L_{1}$, and thus $C ({L_{1}, t_{1}^{*}, S_{1}^{*}, S_{2}^{*}} )$ is increasing in $L_{1}$. When $T_{0} \le L_{1} < \tilde{T}$ and $L_{1} \ge \bar{L} (0 )$, it follows that $T_{0} + z ({t_{1}^{*}, S_{1}^{*}} ) = T_{0} + d$, and thus in the case that $T_{0} \le L_{1} < T_{0} + d$, $C ({L_{1}, t_{1}^{*}, S_{1}^{*}, S_{2}^{*}} )$ is decreasing in $L_{1}$. When $T_{0} + d \le L_{1}$, $C ({L_{1}, t_{1}^{*}, S_{1}^{*}, S_{2}^{*}} )$ is increasing in $L_{1}$. When $\tilde{T} \le L_{1} < \tilde{T} + d$, it follows that $T_{0} + z ({t_{1}^{*}, S_{1}^{*}} ) = T_{0} + d$, and in the case that $L_{1} < T_{0} + d$, $C ({L_{1}, t_{1}^{*}, S_{1}^{*}, S_{2}^{*}} )$ is decreasing in $L_{1}$. When $T_{0} + d \le L_{1} \le \tilde{T} + d$, $C ({L_{1}, t_{1}^{*}, S_{1}^{*}, S_{2}^{*}} )$ is increasing in $L_{1}$. When $\tilde{T} + d < L_{1}$, $T_{0} + z ({t_{1}^{*}, S_{1}^{*}} ) = T_{0} + L_{1} - \tilde{T} \le L_{1}$ and $C ({L_{1}, t_{1}^{*}, S_{1}^{*}, S_{2}^{*}} )$ is increasing in $L_{1}$.

Table 2 $t_{1}^{*}$, $S_{1}^{*}$, $S_{2}^{*}$ when $\rho > \frac{{h_{1}}}{{h_{1} + b }}, L_{1} \ge T_{0}$ and $\tilde{L} < \tilde{T}$

Since $T_{0} \le \tilde{T}, T_{0} \le \bar{L} (0 ) < T_{0} + d$ and $\bar{L} (0 ) < \tilde{L} < \tilde{T}$, we consider two cases that (1) $T_{0} + d \le \tilde{T}$ and (2) $\tilde{T} < T_{0} + d$. Figure 5 shows the relationship between average expected cost and $L_{1}$, where symbols + and − show that the average cost increases and decreases in $L_{1},$ respectively, and the circles show the local minimum.

Fig. 5

Relationships between average cost and $L_{1}$ when $\rho > \frac{{h_{1}}}{{h_{1} + b }}, L_{1} \ge T_{0}, \tilde{L} \ge \tilde{T}$

When $h_{1} < h_{2}$, $T_{0} < \bar{L} (0 )$ and there are two local minimum, and thus optimal cost $C ({T_{0}, 0, 1, 0} )$ for $L_{1} = T_{0}$ is compared with $C ({T_{0} + d, 0, 0, 0} )$ for $L_{1} = T_{0} + d$, and then

$$ C(T_{0} , 0, 1, 0) - C(T_{0} + d, 0, 0, 0) = (1 - \lambda d)h_{1} \ge 0, $$

which means that $C ({T_{0} + d, 0, 0, 0} )$ is optimal cost.

Here let $T$ satisfying $C ({T_{0}, 0, 1, 0} ) = C ({T, 0, 0, 0} )$ be denoted by $T^{\prime} ({\le T_{0} + d} )$, thus $T^{\prime} ({T_{0} < T^{\prime} \le T_{0} + d} )$ satisfies

$$ \int\limits_{{T^{\prime } - d}}^{{T_{0} }} P (W > x){\text{d}}x = \left( {\frac{1}{\lambda } - d} \right)\frac{{h_{1} }}{{h_{2} + b }} + (T_{0} - T^{\prime } + d)\frac{{h_{2} }}{{h_{2} + b }}. $$

When $h_{1} = h_{2}$, it holds that $T_{0} = \bar{L} (0 ),$ and thus the minimal cost is $C ({T_{0} + d, 0, 0, 0} )$. From above discussion, optimal release lead time of process 1, $L_{1}^{*}$ is $T_{0}$ when $T_{0} \le T < T^{\prime}$, $T$ when $T^{\prime} \le T < T_{0} + d$ and $T_{0} + d$ when $T_{0} + d \le T$.

Next, we consider the case that $\tilde{L} \ge \tilde{T}$. From Proposition 7, when $\tilde{L} > \tilde{T}$ it holds that $T_{0} \le \tilde{T} < \bar{L} (0 ) < \tilde{L} < T_{0} + d \le \tilde{T} + d$, and when $\tilde{L} = \tilde{T}$ it follows that $T_{0} \le \tilde{T} = \tilde{L} = \bar{L} (0 ) < T_{0} + d \le \tilde{T} + d$. From (a) of Table 1, when $L_{1} \ge T_{0}$ and $\tilde{L} \ge \tilde{T},$ optimal $t_{1}$ and base stock level are given in Table 3. In the same way of the previous case, by considering increase and decrease of $C ({L_{1}, t_{1}^{*}, S_{1}^{*}, S_{2}^{*}} )$, it has two local minimum when $L_{1} = T_{0}$ and $L_{1} = T_{0} + d$. Since $C ({T_{0}, 0, 1, 0} ) \ge C ({T_{0} + d, 0, 0, 0} )$, $C ({T_{0} + d, 0, 0, 0} )$ attains minimal cost.

Table 3 $t_{1}^{*}, S_{1}^{*}, S_{2}^{*} {\text{when }}\rho > \frac{{h_{1}}}{{h_{1} + b }}, L_{1} \ge T_{0}$ and $\tilde{L} \ge \tilde{T}$

Let $T$ satisfying $C ({T_{0}, 0, 1, 0} ) = C ({T, 0, 0, 0} )$ be denoted by $T^{\prime} ({T_{0} < T^{\prime} \le T_{0} + d} )$. Then optimal release lead time $L_{1}^{*}$ is $T_{0}$ when $T_{0} \le T < T^{\prime}$, $T$ when $T^{\prime} \le T < T_{0} + d$ and $T_{0} + d$ when $T_{0} + d \le T$.

Optimal release lead time when ${T} \ge {T}_{0}$ and ${\rho}\le \frac{{{h}_{1}}}{{{h}_{1} + {b }}}$

From (b) of Table 1, when $L_{1} \ge T_{0}$ optimal $t_{1}$ and optimal inventory levels are given in Table 4. Note that when $T_{0} \le L_{1} < \tilde{T}$ it holds that $T_{0} + z ({t_{1}^{*}, S_{1}^{*}} ) = T_{0} + d$, and thus when $T_{0} \le L_{1} < T_{0} + d,$ $C ({L_{1}, t_{1}^{*}, S_{1}^{*}, S_{2}^{*}} )$ is decreasing in $L_{1}$. When $T_{0} + d \le L_{1}$, $C ({L_{1}, t_{1}^{*}, S_{1}^{*}, S_{2}^{*}} )$ is increasing in $L_{1}$. When $\tilde{T} \le L_{1} < \tilde{T} + d$, $T_{0} + z ({t_{1}^{*}, S_{1}^{*}} ) = T_{0} + d$, and thus when $L_{1} < T_{0} + d C ({L_{1}, t_{1}^{*}, S_{1}^{*}, S_{2}^{*}} )$ is decreasing in $L_{1}$, and when $T_{0} + d \le L_{1} \le \tilde{T} + d C ({L_{1}, t_{1}^{*}, S_{1}^{*}, S_{2}^{*}} )$ is increasing in $L_{1}$. When $\tilde{T} + d < L_{1}$, $T_{0} + z ({t_{1}^{*}, S_{1}^{*}} ) = T_{0} + L_{1} - \tilde{T} \le L_{1}$, and $C ({L_{1}, t_{1}^{*}, S_{1}^{*}, S_{2}^{*}} )$ is increasing in $L_{1}$.

Table 4 ${t}_{1}^{{*}}, { S}_{1}^{{*}}, { S}_{2}^{{*}}$ when ${\rho}\le \frac{{{h}_{1}}}{{{h}_{1} + {b }}}$ and ${L}_{1} \ge {T}_{0}$

Optimal release lead time and optimal base stock level

From Table 1 and discussion in “Optimal release lead time when ${T} \ge {T}_{0}$ and ${\rho}> \frac{{{h}_{1}}}{{{h}_{1} + {b }}}$ ” and “Optimal release lead time when ${T} \ge {T}_{0}$ and ${\rho}\le \frac{{{h}_{1}}}{{{h}_{1} + {b }}}$ ”, optimal release lead time and optimal base stock levels are given in Table 5.

Table 5 Optimal release lead time and optimal base stock level

As demand lead time is shorter, the optimal base stock level of process 2 is higher. It is because more finished items are needed for preventing the system from backlogs.

The optimal base stock level of process 1 is less than 2. It is because that by (1), if the inventory level of process 1 is positive, then the starting epoch for processing an item in process 2 ordered by demand information is $t_{1}$ periods later from the start time for process 1 ordered by the same order.

If the optimal base stock level of process 1 is one, then optimal $t_{1}$ is 0, which means the optimal release lead time of process 1 is the same as process 2. Then by (1), processes 1 and 2 start process items at the same time.

If the optimal base stock level of process 1 is 0, then the average cost is identical when $t_{1}$ is changed from 0 to $d$. Note that if $t_{1}$ is no more than $d$, then after finishing process 1 the process for the same item is immediately started in process 2 by the same advance demand information. That means that both processes 1 and 2 proceed in the same way as $t_{1}$ increases when the base stock of process 1 is 0.

(a) $\rho > \frac{{h_{1}}}{{h_{1} + b }}$

When demand lead time is in $(d, T_{0})$ , then optimal base stock level is 1. If demand lead time is less than $d$, then there are two cases that the optimal base stock level is 0 or 1.

When demand lead time is in $(T_{k},T_{k + 1})$ $({k = 1, 2, \ldots \widehat{S}_{0} - 1} ),$ the sum of optimal base stock levels of processes 1 and 2 becomes $k$. For T < d, this value decreases from $\widehat{S}_{0} + 1$ to $\widehat{S}_{0}$ when demand lead time exceeds one of $T_{{\widehat{S}_{0} + 1}} + d, \overline{L} ({\widehat{S}_{0}} )$ or $T_{{\widehat{S}_{0}}}$, which depends on parameters.

When demand lead time is in ($T_{0}, T^{\prime}),$ optimal release lead time of process 1 becomes $T_{0}$, which means that when demand information arrives an order is not made immediately, and at $T_{0}$ periods before the corresponding demand arrives, orders 1 and 2 are made at the same time. Since the optimal base stock of process 2 is 0 and the immediate order leads to more finished items, by delaying the orders, inventory cost for finished item can be reduced.

When demand lead time is in $(T^{\prime}$, $T_{0} + d),$ optimal base stocks of both processes are zero and it is optimal that the order 1 is done immediately when demand information arrives and the item which the corresponding demand receives is processed at processes 1 and 2 sequentially.

When demand lead time is more than $T_{0} + d$, it is optimal that the order 1 is done $T_{0} + d$ periods before the actual demand arrives, and the corresponding item is processed at processes 1 and 2 sequentially.

If demand lead time can be set arbitrarily, then demand lead time should be no less than $T_{0} + d$, because under optimal parameters for given demand lead time the average cost decreases in the demand lead time.

(b) $\rho \le \frac{{h_{1}}}{{h_{1} + b }}$

This case happens when the arrival rate is small or backlog cost is small. In this case, we need not have items in inventory, and thus the sum of numbers of optimal base stocks is one or zero. The optimal number of base stocks in process 1 is always zero, and when demand lead time exceeds $T_{1} + d$ the optimal number of base stocks in process 2 also becomes zero. That is, processing of processes 1 and 2 ordered by the same demand information were done continuously and if demand lead time is greater than $T_{1} + d,$ the same order receives this item, and otherwise its next demand order receives it. When demand lead time can be set longer, the corresponding order is set 2d periods before the corresponding actual demand arrives and then an item is processed in processes 1 and 2 continuously, by which this actual demand is satisfied.

(c) $h_{1} = h_{2}$

By (15) it holds $L_{1} < \tilde{T}$. When $d \le L_{1} < T_{0}$, by the result in “The case that $L_{1} < T_{{\hat{S}_{0} + 1}} + d$ or $T_{{\hat{S}_{0}}} \le L_{1} < T_{0}$ ” both $C ({L_{1}, 0, 0, \overline{S} ({L_{1}} )} )$ and $C ({L_{1}, 0, 1, \overline{S} ({L_{1}} ) - 1} )$ are the optimal average costs. By (16), it follows that $\widehat{L} ({\overline{S} ({L_{1}} )} ) = d$. By Proposition 3, (10) and (17), when $\rho > \frac{{h_{1}}}{{h_{1} + b }} , \overline{L} (0 ) = T_{0}.$

Only when $T_{{\widehat{S}_{0} + 1}} + d \le T < T_{{\widehat{S}_{0}}}$ and $T < \overline{L} ({\widehat{S}_{0}} ),$ the optimal base stock level in process 1 is 1, and otherwise it is 1 or 0.

Numerical experiments

By numerical experiments, we discuss the properties of optimal release lead time and optimal numbers of base stocks. The computation is done on a computer with Intel^® Core™ i7-2600 CPU 3.40 GHz and 8.00 GB RAM, and the program is coded with C language and compiled with Intel^® C++ Compiler. $T_{k}, \widehat{S}_{0}, T^{\prime}, \widehat{L} (S )$ and $\overline{L} (S )$ are computed numerically, and using Table 5 optimal release lead time and optimal base stock levels are computed.

Parameters are given in Table 6. Among these cases parameters are the same except arrival rates. $\frac{{h_{1}}}{{h_{1} + b }} \cong 0.130$, and in first two cases it holds $\rho > \frac{{h_{1}}}{{h_{1} + b }}$, and in the case 3 $\rho \le \frac{{h_{1}}}{{h_{1} + b }}.$ The values of $\widehat{S}_{0}, \widehat{L} ({\widehat{S}_{0}} ), \overline{L} ({\widehat{S}_{0}} ), \widehat{L} ({\widehat{S}_{0} + 1} )$ are given in Table 7. By Table 5, the optimal release lead time and optimal base stock levels are given in Table 8.

Table 6 Parameter sets

Table 7 $\widehat{S}_{0}, \widehat{L} ({\widehat{S}_{0}} ), \overline{L} ({\widehat{S}_{0}} ), \widehat{L} ({\widehat{S}_{0} + 1} )$ for each case

Table 8 Optimal release lead time and base stock levels

In case 1, if demand lead time is no more than 3.442 optimal base stock of process 1 is 1, and otherwise it becomes 0. In case 2, when demand lead time is from 0.000 to 0.198 or from 0.821 to 0.893, the optimal base stock level of process 1 is 0, and in case 3 it is 0 for any demand lead time.

The average cost under these optimal release lead time and optimal base stock levels for each case are illustrated in Fig. 6, where the horizon axis is demand lead time and the vertical axis is an optimal average cost.

Fig. 6

Average cost

In the interval of demand lead time where optimal base stocks are the same, the average cost is convex or linear. In case 1, in the interval (3.323, 3.442) or (4.323, $\infty$), optimal release lead time of process is constant. This is found in the interval (1.821, 1.897) for case 2, and (2.00, $\infty$) for case 3. In case 2, when demand lead time is around 1, the optimal base stock is the same but the average cost decreases in the different ways. From 0.893 to 1, $S_{1}^{*} = 1\, \, {\text{and}}\, \, S_{2}^{*} = 0$ and in this interval it holds $\frac{{\partial C ({L_{1}, t_{1}, S_{1}, S_{2}} )}}{{\partial L_{1}}} = - \lambda b$, which leads to the linear average cost in this interval.

Concluding remarks

In this paper, a two-stage production and inventory system with advance demand information is considered under base stock order policy and deterministic process time. The base stock levels and release lead time for each process are decision variables, and the objective is to derive optimal values on the decision variables to minimize the average cost on inventory and backlog costs. Through theoretical analysis, optimal base stock levels and optimal release lead time at each process are explicitly derived in Table 5.

Release lead time of process 1 is shorter than the demand lead time when the latter is long to decrease excess inventory. Optimal release lead time of process 2 is the same as that of process 1, that is, it is optimal to order processes at the same time. Note that when the optimal base stock level of process 1 is zero, there is an optimal positive interval for release lead time of process 2. When demand lead time can be long enough, then it is optimal to have no base stocks and wait for several time and process an item at processes 1 and 2 continuously. Optimal base stock level of process 1 is 1 or 0, which depends on demand lead time. As demand lead time is longer, the sum of optimal base stocks at processes 1 and 2 is smaller. In particular, when parameters satisfy $\rho \le h_{1}/ ({h_{1} + b} )$, optimal base stock level of process 1 is zero and it is optimal to process an item at processes 1 and 2 continuously.

Further research is left when the process times are different among the processes, they are stochastic, or when the number of processes is more than 2.

Appendices

Appendices

A. Proof of Proposition 1

When $({m + 1} )d \le T < ({m + 2} )d, m \ge 1$, by (3) and

$$ \int {x^{m} e^{\lambda x} {\text{d}}x = - \frac{m!}{{( - \lambda )^{m + 1} }}e^{\lambda x} \sum\limits_{k = 0}^{m} {\frac{{( - \lambda )^{k} }}{k!}} x^{k} + C} $$

we have

$$ \begin{aligned} \int\limits_{T - d}^{T} P (W \le x){\text{d}}x \, & = \int\limits_{T - d}^{(m + 1)d} P (W \le x){\text{d}}x + \int\limits_{(m + 1)d}^{T} P (W \le x){\text{d}}x \\ & = (1 - \rho )\sum\limits_{k = 0}^{m - 1} {\frac{{( - \lambda )^{k} }}{k!}} \int\limits_{T - (k + 2)d}^{T - (k + 1)d} {x^{k} } e^{\lambda x} {\text{d}}x + (1 - \rho )\frac{{( - \lambda )^{m} }}{m!}\int\limits_{0}^{T - (m + 1)d} {x^{m} } e^{\lambda x} {\text{d}}x \\ & = - (1 - \rho )\frac{1}{\lambda } + (1 - \rho )\frac{1}{\lambda }\sum\limits_{k = 0}^{m} {e^{{\lambda \{ T - (k + 1)d\} }} } \frac{{( - \lambda )^{k} }}{k!}\{ T - (k + 1)d\}^{k} \\ & = - (1 - \rho )\frac{1}{\lambda } + \frac{1}{\lambda }P(W \le T) = - \frac{1}{\lambda }P(W > T) + d. \\ \end{aligned}$$

Thus,

$$ \int\limits_{T - d}^{T} P (W > x){\text{d}}x = d - \int\limits_{T - d}^{T} P (W \le x){\text{d}}x = \frac{1}{\lambda }P(W > T). $$

When $d \le T < 2d$

$$ \begin{aligned} \int\limits_{T - d}^{T} P (W \le x){\text{d}}x\, & = \int\limits_{T - d}^{d} P (W \le x){\text{d}}x + \int\limits_{d}^{T} P (W \le x){\text{d}}x \\ & = (1 - \rho )\left\{ {\frac{1}{\lambda }e^{\lambda (T - d)} - \frac{1}{\lambda }} \right\} = - \frac{1}{\lambda }P(W > T) + d, \\ \end{aligned} $$

which implies $\mathop \int \nolimits_{T - d}^{T} P ({W > x} ){\text{d}}x = \frac{1}{\lambda}P ({W > T} ).$

When $T < d$, $\int_{T - d}^{T} P (W \le x){\text{d}}x = 0$ and $\int_{T - d}^{T} P (W > x){\text{d}}x = d - \int_{T - d}^{T} P (W \le x){\text{d}}x = d.$ Thus, we have,

$$ \int\limits_{T - d}^{T} P (W > x){\text{d}}x = \left\{ {\begin{array}{*{20}l} {\frac{1}{\lambda }P(W > T)} \hfill & {T \ge d,} \hfill \\ d \hfill & {T < d} \hfill \\ \end{array} } \right.. $$

B. Proof of Proposition 2

We derive $P ({E (k ) > x} ), {\text{for }}x < 0$ in steady state. When $k = 0$

$$ P ({E (k ) > x} ) = P ({E (0 ) > x} ) = P ({W > x} ) = 1 - P ({W \le x} ) $$

For $k = 1, 2, 3 \ldots$

$$ \begin{aligned} P(E(k) > x) & = P(W - a(k) > x) = \int\limits_{0}^{\infty } P (W > x + y)\frac{{{\text{d}}P(a(k) \le y)}}{{{\text{d}}y}}{\text{d}}y \\ & = \frac{{\lambda^{k} }}{(k - 1)!}\int\limits_{0}^{ - x} P (W > x + y)y^{k - 1} e^{ - \lambda y} {\text{d}}y + \frac{{\lambda^{k} }}{(k - 1)!}\int\limits_{ - x}^{\infty } P (W > x + y)y^{k - 1} e^{ - \lambda y} {\text{d}}y \\ & = \frac{{\lambda^{k} }}{(k - 1)!}\int\limits_{0}^{ - x} {y^{k - 1} } e^{ - \lambda y} {\text{d}}y + \frac{{\lambda^{k} }}{(k - 1)!}\int\limits_{0}^{\infty } P (W > u)(u - x)^{k - 1} e^{ - \lambda (u - x)} {\text{d}}u \\ & = 1 - e^{\lambda x} \sum\limits_{j = 0}^{k - 1} {\frac{{\lambda^{j} }}{j!}} ( - x)^{j} + \lambda^{k} e^{\lambda x} \sum\limits_{j = 0}^{k - 1} {\frac{{( - x)^{k - 1 - j} }}{j!(k - 1 - j)!}} \int\limits_{0}^{\infty } P (W > u)e^{ - \lambda u} u^{j} {\text{d}}u. \\ \end{aligned} $$

Here we derive $\int_{0}^{\infty } P (W > u)e^{ - \lambda u} u^{j} {\text{d}}u$. Define $f(u) = P(W > u) \;{\text{and}}\;f^{*} (u) = \, {\mathcal{L}}\{ f(u)\} = \int\nolimits_{0}^{\infty } {P(W > u)e^{ - su} {\text{d}}u}$. Since $\int\nolimits_{0}^{\infty } {e^{ - su} } u^{n} f(u){\text{d}}u = ( - 1)^{n} f^{*(n)} (s)$

$$ \int\limits_{0}^{\infty } P (W > u)e^{ - \lambda u} u^{j} {\text{d}}u = ( - 1)^{j} f^{*(j)} (\lambda ). $$

Therefore,

$$ \begin{aligned} f^{*} (s) & = \int\limits_{0}^{\infty } P (W > u)e^{ - su} {\text{d}}u = \int\limits_{0}^{\infty } {\{ 1 - P(W \le u)\} } e^{ - su} {\text{d}}u \\ & = \frac{1}{s} - \frac{1}{s}\int\limits_{0}^{\infty } {e^{ - su} } {\text{d}}P(W \le u). \\ \end{aligned} $$

The Laplace transform of sojourn time distribution in M/D/1 is set as $W^{*} (s) = \int_{0}^{\infty } {e^{ - su} } {\text{d}}P(W \le u)$, and then $f^{*} (s ) = \frac{1}{s} - \frac{1}{s}W^{*} (s )$, which implies $sf^{*} (s ) = 1 - W^{*} (s ).$

By differentiating $s$ $f^{*} (s) + sf^{*(1)} (s) = - W^{*(1)} (s),$ and thus $f^{*}{ (1)} (s ) = - \frac{1}{s}W^{*}{ (1 )} (s ) - \frac{1}{s}f^{*} (s ).$ By deriving the j-th derivative of f(s) and substituting $\lambda$ to $s$

$$ \begin{aligned} f^{*} (\lambda ) & = \frac{1}{\lambda } - \frac{1}{\lambda }W^{*} (\lambda ),f^{*(j)} (\lambda ) = \sum\limits_{m = 1}^{j} {\frac{j!}{{( - \lambda )^{j + 1 - m} m!}}} W^{*(m)} (\lambda ) \\ & \quad + \frac{j!}{{( - \lambda )^{j} }}f^{*} (\lambda ),\quad j = 1, 2, 3, \ldots \\ \end{aligned} $$

It is well-known that

$$ W^{*} (s ) = \frac{{ ({1 - \rho} )se^{- sd}}}{{s - \lambda + \lambda e^{- sd}}}. $$

To obtain $f^{{*}{ (j )}} (\lambda )$, $W^{{*}{ (m )}} (\lambda ), {\text{for }}m = 1, 2, 3 \ldots$, is discussed in the following.

Let $h (s ) = ({1 - \rho} )se^{- sd}, g (s ) = s - \lambda + \lambda e^{- sd}$. Then $W^{*} (s ) = \frac{h (s )}{g (s )}$. By differentiating $h (s ) = g(s)W^{*} (s )$ and substituting $\lambda$

$$ \begin{aligned} W^{*(j)} (\lambda ) & = - \left( {\begin{array}{*{20}c} j \\ 0 \\ \end{array} } \right)\frac{{g^{(j)} (\lambda )}}{g(\lambda )}W^{*} (\lambda ) - \sum\limits_{k = 1}^{j - 1} {\left( {\begin{array}{*{20}c} j \\ k \\ \end{array} } \right)\frac{{g^{(j - k)} (\lambda )}}{g(\lambda )}W^{*(k)} (\lambda )} \\ & \quad+ \frac{{h^{(j)} (\lambda )}}{g(\lambda )}, \quad j = 1, 2, 3 \ldots \\ \end{aligned} $$

Here, we have

$$ \frac{h(\lambda )}{g(\lambda )} = (1 - \rho ),\frac{{h^{(j)} (\lambda )}}{g(\lambda )} = \frac{{(1 - \rho )( - d)^{j - 1} (j - \lambda d)}}{\lambda }, \quad j = 1, 2, 3 \ldots $$

$$ \frac{{g^{(1)} (\lambda )}}{g(\lambda )} = \frac{{e^{\lambda d} }}{\lambda } - d,\frac{{g^{(j)} (\lambda )}}{g(\lambda )} = ( - d)^{j} , \quad j = 2, 3, 4 \ldots $$

Therefore,

$$ W^{*} (\lambda ) = ({1 - \rho} ),W^{* (1 )} (\lambda ) = - \frac{1}{\lambda} ({1 - \rho} ) ({e^{\lambda d} - 1} ) $$

$$ W^{*(j)} (\lambda ) = \frac{{j(1 - \rho )( - d)^{j - 1} }}{\lambda } - \sum\limits_{m = 1}^{j - 1} {\left( {\begin{array}{*{20}c} j \\ m \\ \end{array} } \right)} ( - d)^{j - m} W^{*(m)} (\lambda ) - \left( {\begin{array}{*{20}c} j \\ {j - 1} \\ \end{array} } \right)\frac{1}{\lambda }e^{\lambda d} W^{*(j - 1)} (\lambda )\quad j = 2, 3, 4 \ldots $$

Now, we show

$$ \begin{aligned} & W^{*(j)} (\lambda ) = ( - 1)^{j} \frac{j!}{{\lambda^{j} }}(1 - \rho )e^{j\lambda d} + ( - 1)^{j} \frac{j!}{{\lambda^{j} }}(1 - \rho ) \\ & \sum\limits_{n = 1}^{j - 1} {\frac{{( - n\lambda d)^{j - n - 1} }}{(j - n - 1)!}} e^{n\lambda d} \left\{ {\frac{( - n\lambda d)}{(j - n)} - 1} \right\}\quad {\kern 1pt} j = 2, 3, 4 \ldots \\ \end{aligned} $$

(A.1)

For $j = 2$

$$ \begin{aligned} W^{*(2)} (\lambda ) & = \frac{{2(1 - \rho )( - d)^{1} }}{\lambda } - \left( {\begin{array}{*{20}c} 2 \\ 1 \\ \end{array} } \right)\frac{1}{\lambda }\{ e^{\lambda d} + ( - \lambda d)\} W^{*(1)} (\lambda ) \\ & = \frac{2}{{\lambda^{2} }}(1 - \rho )e^{2\lambda d} + \frac{2}{{\lambda^{2} }}(1 - \rho )e^{\lambda d} \{ ( - \lambda d) - 1\} \\ \end{aligned} $$

Thus, (A.1) holds for $j = 2$. Assume that (A.1) holds for $j = 2, 3, \ldots, k$. For $j = k + 1$,

$$ \begin{aligned} W^{*(k + 1)} (\lambda ) &= \frac{{(k + 1)(1 - \rho )( - d)^{k} }}{\lambda } - \sum\limits_{m = 1}^{k - 1} {\left( {\begin{array}{*{20}c} {k + 1} \\ m \\ \end{array} } \right)} ( - d)^{k + 1 - m} W^{*(m)} (\lambda ) \\ & \quad - \left( {\begin{array}{*{20}c} {k + 1} \\ k \\ \end{array} } \right)\frac{1}{\lambda }\{ e^{\lambda d} + ( - \lambda d)\} W^{*(k)} (\lambda ) = ( - 1)^{k + 1} \frac{(k + 1)!}{{\lambda^{k + 1} }}(1 - \rho ) \times B \\ \end{aligned} $$

where

$$ \begin{aligned} B & = ( - \lambda d)^{k} e^{\lambda d} \left\{ {\frac{1}{{k!( - 1)^{k + 1} }} - \sum\limits_{m = 2}^{k} {\frac{1}{{(k + 1 - m)!(m - 1)!( - 1)^{k + 1 - m} }}} } \right\} + ( - \lambda d)^{k - 1} e^{\lambda d} \sum\limits_{m = 2}^{k} {\frac{1}{{(k + 1 - m)!(m - 2)!( - 1)^{k + 1 - m} }}} \\ & \quad + \sum\limits_{n = 2}^{k - 1} {( - \lambda d)^{k - n} } e^{n\lambda d} \left\{ {\sum\limits_{m = n + 1}^{k} {\frac{{n^{m - n - 1} }}{{(k + 1 - m)!(m - n - 1)!( - 1)^{k + 1 - m} }} - \frac{{(n - 1)^{k - n} }}{(k - n)!}} } \right\} \\ & \quad + k( - \lambda d)e^{k\lambda d} - e^{k\lambda d} + e^{(k + 1)\lambda d} + \sum\limits_{n = 2}^{k - 1} {( - \lambda d)^{k + 1 - n} } e^{n\lambda d} \\ & \;\left\{ { - \frac{1}{{(k + 1 - n)!( - 1)^{k + 1 - n} }} - \sum\limits_{m = n + 1}^{k} {\frac{{n^{m - n} }}{{(k + 1 - m)!(m - n)!( - 1)^{k + 1 - m} }}} .. + \frac{{(n - 1)^{k - n + 1} }}{(k - n + 1)!}} \right\}. \\ \end{aligned} $$

Here, by developing $({1 - 1} )^{k}, ({1 - 1} )^{k - 1}, ({n - 1} )^{k - n + 1}, ({n - 1} )^{k - n}$ it follows that

$$ \frac{1}{{k!( - 1)^{k + 1} }} - \sum\limits_{m = 2}^{k} {\frac{1}{{(k + 1 - m)!(m - 1)!( - 1)^{k + 1 - m} }}} = \frac{1}{k!},\quad k \ge 2 $$

$$ \sum\limits_{m = 0}^{k - 2} {\frac{1}{{(k - m - 1)!m!( - 1)^{k - m - 1} }}} = - \frac{1}{(k - 1)!}, \quad k \ge 2 $$

$$ \begin{aligned} & - \frac{1}{{(k + 1 - n)!( - 1)^{k + 1 - n} }} - \sum\limits_{m = n + 1}^{k} {\frac{{n^{m - n} }}{{(k + 1 - m)!(m - n)!( - 1)^{k + 1 - m} }}} \\ & + \frac{{(n - 1)^{k - n + 1} }}{(k - n + 1)!} = \frac{{n^{k - n + 1} }}{(k - n + 1)!},\quad k \ge n + 1 \\ \end{aligned} $$

$$ \sum\limits_{m = n + 1}^{k} {\frac{{n^{m - n - 1} }}{{(k + 1 - m)!(m - n - 1)!( - 1)^{k + 1 - m} }}} - \frac{{(n - 1)^{k - n} }}{(k - n)!} = - \frac{{n^{k - n} }}{(k - n)!},\quad k \ge n + 1 $$

Thus,

$$ \begin{aligned} W^{*(k + 1)} (\lambda ) & = ( - 1)^{k + 1} \frac{(k + 1)!}{{\lambda^{k + 1} }}(1 - \rho )e^{(k + 1)\lambda d} + ( - 1)^{k + 1} \frac{(k + 1)!}{{\lambda^{k + 1} }} \\ & (1 - \rho )\sum\limits_{n = 1}^{k + 1 - 1} {\frac{{( - n\lambda d)^{k + 1 - n - 1} }}{(k + 1 - n - 1)!}} e^{n\lambda d} \left\{ {\frac{( - n\lambda d)}{(k + 1 - n)} - 1} \right\} \\ \end{aligned} $$

That is, (A.1) holds for $j = k + 1$. By induction it is proven that (A.1) holds.

Since

$$ f^{*} (\lambda ) = \frac{1}{\lambda} - \frac{1}{\lambda}W^{*} (\lambda ) = \frac{1}{\lambda} - \frac{1}{\lambda} ({1 - \rho} ) = d $$

$$ f^{*(j)} (\lambda ) = \sum\limits_{m = 1}^{j} {\frac{j!}{{( - \lambda )^{j + 1 - m} m!}}} W^{*(m)} (\lambda ) + \frac{j!}{{( - \lambda )^{j} }}f^{*} (\lambda ),\quad j = 1, 2, 3, \ldots $$

we have

$$ f^{*(j)} (\lambda ) = \frac{j!}{{( - \lambda )^{j + 1} }}(1 - \rho )\left\{ {e^{j\lambda d} + \sum\limits_{n = 1}^{j - 1} {\frac{{( - n\lambda d)^{j - n} }}{(j - n)!}} e^{n\lambda d} } \right\} - \frac{j!}{{( - \lambda )^{j + 1} }}, \quad j = 1, 2, 3, \ldots $$

And thus

$$ \begin{aligned} \int\limits_{0}^{\infty } P (W > u)e^{ - \lambda u} {\text{d}}u & = f^{*} (\lambda ) = d,\int\limits_{0}^{\infty } P (W > u)e^{ - \lambda u} u^{j} {\text{d}}u \\ & = ( - 1)^{j} f^{*(j)} (\lambda ) = - \frac{j!}{{\lambda^{j + 1} }}(1 - \rho )\left\{ {e^{j\lambda d} + \sum\limits_{n = 1}^{j - 1} {\frac{{( - n\lambda d)^{j - n} }}{(j - n)!}} e^{n\lambda d} } \right\} \\ & \quad + \frac{j!}{{\lambda^{j + 1} }},\quad j = 1, 2, 3, \ldots \\ \end{aligned} $$

Here, we show

$$ P(E(k) > x) = 1 - e^{\lambda x} \sum\limits_{j = 0}^{k - 1} {\frac{{\lambda^{j} }}{j!}} ( - x)^{j} + \lambda^{k} e^{\lambda x} \sum\limits_{j = 0}^{k - 1} {\frac{{( - x)^{k - 1 - j} }}{j!(k - 1 - j)!}} \int\limits_{0}^{\infty } P (W > u)e^{ - \lambda u} u^{j} {\text{d}}u. $$

For $k = 1$

$$ P(E(1) > x) = 1 - e^{\lambda x} + \lambda e^{\lambda x} \int\limits_{0}^{\infty } P (W > u)e^{ - \lambda u} {\text{d}}u = 1 - (1 - \rho )e^{\lambda x}. $$

For $k \ge 2$

$$ \begin{aligned} P(E(k) > x) & = 1 - e^{\lambda x} \sum\limits_{j = 0}^{k - 1} {\frac{{\lambda^{j} }}{j!}} ( - x)^{j} + \lambda^{k} e^{\lambda x} \frac{{( - x)^{k - 1} }}{(k - 1)!} \\ & \quad + \lambda^{k} e^{\lambda x} \frac{{( - x)^{k - 2} }}{(k - 2)!}\left\{ { - \frac{1}{{\lambda^{2} }}(1 - \rho )e^{\lambda d} + \frac{1}{{\lambda^{2} }}} \right\} \\ & \quad + \lambda^{k} e^{\lambda x} \sum\limits_{j = 2}^{k - 1} {\frac{{( - x)^{k - 1 - j} }}{j!(k - 1 - j)!}} \left\{ { - \frac{j!}{{\lambda^{j + 1} }}(1 - \rho )\left\{ {e^{j\lambda d} + \sum\limits_{n = 1}^{j - 1} {\frac{{( - n\lambda d)^{j - n} }}{(j - n)!}} e^{n\lambda d} } \right\} + \frac{j!}{{\lambda^{j + 1} }}} \right\} \\ & = 1 - (1 - \rho )\frac{{( - \lambda x)^{k - 1} }}{(k - 1)!}e^{\lambda x} - (1 - \rho )\frac{{\{ - \lambda (x + d)\}^{k - 2} }}{(k - 2)!}e^{\lambda (x + d)} \\ & \quad - \sum\limits_{n = 2}^{k - 2} {(1 - \rho )} \frac{{\{ - \lambda (x + nd)\}^{k - 1 - n} }}{(k - 1 - n)!}e^{\lambda (x + nd)} - (1 - \rho )e^{\lambda (x + (k - 1)d)} \\ & = 1 - (1 - \rho )\frac{{( - \lambda x)^{k - 1} }}{(k - 1)!}e^{\lambda x} - (1 - \rho )\sum\limits_{n = 1}^{k - 1} {\frac{{\{ - \lambda (x + nd)\}^{k - 1 - n} }}{(k - 1 - n)!}} e^{\lambda (x + nd)} . \\ \end{aligned} $$

When $m = k - 2$, that is, when $- d \le x < 0$,

$$ P ({W \le x + kd} ) = ({1 - \rho} )\mathop \sum \limits_{n = 0}^{k - 2} \frac{{ \{{- \lambda ({x + kd - ({n + 1} )d} )} \}^{n}}}{n!}e^{{\lambda ({x + kd - ({n + 1} )d} )}}, $$

$$ P ({E (k ) > x} ) = 1 - ({1 - \rho} )\frac{{ ({- \lambda x} )^{k - 1}}}{{ ({k - 1} )!}}e^{\lambda x} - P ({W \le x + kd} ). $$

Therefore,

$$ \begin{array}{*{20}c} {P ({E (0 ) \le x} ) = P ({W \le x} ) = 0, } & { x < 0} \\ \end{array}, $$

$$ P ({E (k ) \le x} ) = ({1 - \rho} )\mathop \sum \limits_{n = 0}^{k - 1} \frac{{ \{{- \lambda ({x + nd} )} \}^{k - 1 - n}}}{{ ({k - 1 - n} )!}}e^{{\lambda ({x + nd} )}} x < 0,\quad k = 1, 2, 3\ldots $$

Comparing with $P ({W \le x} )$, we have

$$ P ({E (k ) \le x} ) = ({1 - \rho} )\frac{{ ({- \lambda x} )^{k - 1}}}{{ ({k - 1} )!}}e^{\lambda x} + P ({W \le x + kd} ), \quad - d \le x < 0,\quad k = 1, 2, 3 \ldots$$

C. Proof of Proposition 3

For given $L_{1}, t_{1}, S_{1}$, we derive optimal base stock level of process 2, $S_{2}^{*}$. From (8)

$$ \begin{aligned} C(L_{1} , t_{1} , S_{1} , S_{2} + 1) - C(L_{1} , t_{1} , S_{1} , S_{2} ) & = - \lambda h_{2} \{ E[E(S_{2} + 1)] - E[E(S_{2} ) ]\} \\ & \quad + \lambda (h_{2} + b )\int\limits_{{L_{1} - z(t_{1} , S_{1} )}}^{\infty } {\{ P(E(S_{2} + 1) > x) - P(E(S_{2} ) > x)\} } {\text{d}}x \\ & = h_{2} + \lambda (h_{2} + b )\int\limits_{{L_{1} - z(t_{1} , S_{1} )}}^{\infty } {\{ P(E(S_{2} + 1) > x) - P(E(S_{2} ) > x)\} } {\text{d}}x \\ \end{aligned} $$

Since

$$ \frac{{{\text{d}}P(a(k) \le y)}}{{{\text{d}}y}} = \frac{{\lambda^{k} y^{k - 1} }}{(k - 1)!}e^{ - \lambda y} ,\quad k = 1, 2, 3 \ldots, $$

$$ P(E(k) > x) = \int\limits_{0}^{\infty } P (W > x + y)\frac{{\lambda^{k} y^{k - 1} }}{(k - 1)!}e^{ - \lambda y} {\text{d}}y, \quad k = 1, 2, 3 \ldots , x \in {\mathbb{R}} $$

(A.2)

$$ P(E(0) > x) = P(W > x), x \in {\mathbb{R}} $$

For $S_{2} = 1, 2, 3 \ldots$ by (A.2)

$$ \begin{aligned} & \int\limits_{{L_{1} - z(t_{1} , S_{1} )}}^{\infty } {\{ P(E(S_{2} + 1) > x) - P(E(S_{2} ) > x)\} } {\text{d}}x \\ & \quad = \int\limits_{{L_{1} - z(t_{1} , S_{1} )}}^{\infty } {\int\limits_{0}^{\infty } P } (W > x + y)\left\{ {\frac{{\lambda^{{S_{2} + 1}} y^{{S_{2} }} }}{{S_{2} !}} - \frac{{\lambda^{{S_{2} }} y^{{S_{2} - 1}} }}{{(S_{2} - 1)!}}} \right\}e^{ - \lambda y} {\text{d}}y{\text{d}}x \\ & \quad = \int\limits_{0}^{\infty } {(\lambda y - S_{2} )} \frac{{\lambda^{{S_{2} }} y^{{S_{2} - 1}} }}{{S_{2} !}}e^{ - \lambda y} \int\limits_{{L_{1} - z(t_{1} , S_{1} )}}^{\infty } P (W > x + y){\text{d}}x{\text{d}}y \\ & \quad = - \int\limits_{0}^{\infty } {\frac{{\lambda^{{S_{2} }} y^{{S_{2} }} }}{{S_{2} !}}} e^{ - \lambda y} P(W > L_{1} - z(t_{1} , S_{1} ) + y){\text{d}}y \\ & \quad = - \frac{1}{\lambda }P(E(S_{2} + 1) > L_{1} - z(t_{1} ,S_{1} )). \\ \end{aligned} $$

For $S_{2} = 0$

$$ \begin{aligned} & \int\limits_{{L_{1} - z(t_{1} , S_{1} )}}^{\infty } {\{ P(E(S_{2} + 1) > x) - P(E(S_{2} ) > x)\} } {\text{d}}x \\ & \quad = \int\limits_{{L_{1} - z(t_{1} , S_{1} )}}^{\infty } {\{ P(E(1) > x) - P(W > x)\} } {\text{d}}x \\ & \quad = \int\limits_{{L_{1} - z(t_{1} , S_{1} )}}^{\infty } {\int\limits_{0}^{\infty } P } (W > x + y)\lambda e^{ - \lambda y} {\text{d}}y{\text{d}}x - \int\limits_{{L_{1} - z(t_{1} , S_{1} )}}^{\infty } P (W > x){\text{d}}x \\ & \quad = \int\limits_{0}^{\infty } \lambda e^{ - \lambda y} \int\limits_{{L_{1} - z(t_{1} , S_{1} )}}^{\infty } P (W > x + y){\text{d}}x{\text{d}}y - \int\limits_{{L_{1} - z(t_{1} , S_{1} )}}^{\infty } P (W > x){\text{d}}x \\ & \quad = - \int\limits_{0}^{\infty } {e^{ - \lambda y} } P(W > L_{1} - z(t_{1} , S_{1} ) + y){\text{d}}y \\ & \quad = - \frac{1}{\lambda }P(E(1) > L_{1} - z(t_{1} , S_{1} )). \\ \end{aligned} $$

Thus, we have

$$ C ({L_{1}, t_{1}, S_{1}, S_{2} + 1} ) - C ({L_{1}, t_{1}, S_{1}, S_{2}} ) = h_{2} - ({h_{2} + b } )P ({E ({S_{2} + 1} ) > L_{1} - z ({t_{1}, S_{1}} )} ), $$

and $P ({E ({S_{2} + 1} ) > L_{1} - z ({t_{1}, S_{1}} )} )$ is decreasing in $S_{2}$, and thus for given $L_{1}, t_{1}, S_{1}$

$$ S_{2}^{*} = \begin{array}{*{20}c} {\arg { \hbox{min} }} \\ {S_{2} :S_{2} = 0, 1, 2 \ldots } \\ \end{array} \left\{ {P(E(S_{2} + 1) > L_{1} - z(t_{1} , S_{1} )) \le \frac{{h_{2} }}{{h_{2} + b }}} \right\}. $$

D. Proof of Proposition 4

(a) When $T_{S} \le L_{1} < T_{S - 1}, S = 1, 2, \ldots, \widehat{S}_{0} - 1$, if $0 \le L_{2} < T_{{\hat{S}_{0}}}$ then $S_{2}^{*} = \widehat{S}_{0}$, if $T_{k + 1} \le L_{2} < T_{k}, k = S + 1, S + 2, \ldots, \widehat{S}_{0} - 1$ then $S_{2}^{*} = k$, and if $T_{S + 1} \le L_{2}$ then $S_{2}^{*} = S$. Since $L_{2} = L_{1} - t_{1}$, if, $L_{1} - T_{{\hat{S}_{0}}} < t_{1} \le L_{1}$ then $S_{2}^{*} = \widehat{S}_{0}$, if $L_{1} - T_{k} < t_{1} \le L_{1} - T_{k + 1}, k = S + 1, S + 2, \ldots, \widehat{S}_{0} - 1$ then $S_{2}^{*} = k$, and if $d \le t_{1} \le L_{1} - T_{S + 1}$ then $S_{2}^{*} = S$.

${\text{For each inside inteval of }}L_{1} - T_{{\hat{S}_{0}}} < t_{1} \le L_{1}, L_{1} - T_{k} < t_{1} \le L_{1} - T_{k + 1}, k = S + 1, S + 2, \ldots, \widehat{S}_{0} - 1, d \le t_{1} \le L_{1} - T_{S + 1}$, by (8)

$$ \begin{aligned} C(L_{1} , t_{1} , S_{1}^{*} , S_{2}^{*} ) & = \lambda h_{1} t_{1} - \lambda h_{2} E[E(S_{2}^{*} ) ] + \lambda h_{2} (L_{1} - t_{1} ) \\ & \quad + \lambda (h_{2} + b )\int\limits_{{L_{1} - t_{1} }}^{\infty } P (E(S_{2}^{*} ) > x){\text{d}}x \\ \end{aligned} $$

$$ \frac{{{\text{d}}C(L_{1} , t_{1} , S_{1}^{*} , S_{2}^{*} )}}{{{\text{d}}t_{1} }} = \lambda h_{1} - \lambda h_{2} + \lambda (h_{2} + b )P(E(S_{2}^{*} ) > L_{1} - t_{1} ), $$

and by (9), when $L_{2} < T_{0} , P ({E ({S_{2}^{*}} ) > L_{1} - t_{1} = L_{2}} ) > \frac{{h_{2}}}{{h_{2} + b }}$. Thus, we have

$$ \frac{{{\text{d}}C(L_{1} , t_{1} , S_{1}^{*} , S_{2}^{*} )}}{{{\text{d}}t_{1} }} > 0. $$

From discussion of “Optimal base stock level”,

$$ C ({L_{1}, L_{1} - T_{{\widehat{S}_{0} - 1}}, S_{1}^{*}, \widehat{S}_{0}} ) = C ({L_{1}, L_{1} - T_{{\widehat{S}_{0} - 1}}, S_{1}^{*}, \widehat{S}_{0} - 1} ), $$

$$ C(L_{1} , L_{1} - T_{k} , S_{1}^{*} , k) = C(L_{1} , t_{1} , S_{1}^{*} , k - 1),\quad k = S + 2, \ldots , \hat{S}_{0} - 1, $$

and

$$ C ({L_{1}, L_{1} - T_{S + 1}, S_{1}^{*}, S + 1} ) = C ({L_{1}, L_{1} - T_{S + 1}, S_{1}^{*}, S} ). $$

Thus, for $T_{S} \le L_{1} < T_{S - 1}, S = 1, 2, \ldots, \widehat{S}_{0} - 1,$ $C ({L_{1}, t_{1}, S_{1}^{*}, S_{2}^{*}} )$ is increasing in $t_{1 } {\text{for }}t_{1} \ge d$.

For $d \le L_{1} < T_{{\hat{S}_{0} - 1}}$, $S_{2}^{*} = \widehat{S}_{0}$, and in the same way by (8)

$$ \frac{{dC ({L_{1}, t_{1}, S_{1}^{*}, S_{2}^{*}} )}}{{dt_{1}}} > 0 $$

And thus, for $d \le L_{1} < T_{{\widehat{S}_{0} - 1}} C ({L_{1}, t_{1}, S_{1}^{*}, S_{2}^{*}} )$ is increasing in $t_{1}$ for $t_{1} \ge d$.

(b) When $T_{0} \le L_{1}$, if 0 $\le L_{2} < T_{{\widehat{S}_{0}}}$ then $S_{2}^{*} = \widehat{S}_{0}$, if $T_{k + 1} \le L_{2} < T_{k},\quad k = 1, 2, \ldots, \widehat{S}_{0} - 1$ then $S_{2}^{*} = k$ and if $T_{1} \le L_{2}$ then $S_{2}^{*} = 0$. Since $L_{2} = L_{1} - t_{1}$, if $L_{1} - T_{{\widehat{S}_{0}}} < t_{1} \le L_{1}$ then $S_{2}^{*} = \widehat{S}_{0}$, if $L_{1} - T_{k} < t_{1} \le L_{1} - T_{k + 1},\quad k = 1, 2, \ldots, \widehat{S}_{0} - 1$ then $S_{2}^{*} = k$, and if $d \le t_{1} \le L_{1} - T_{1}$ then $S_{2}^{*} = 0$.

In each inside interval of $L_{1} - T_{{\widehat{S}_{0}}} < t_{1} \le L_{1}, L_{1} - T_{k} < t_{1} \le L_{1} - T_{k + 1},\quad k = 1, 2, \ldots, \widehat{S}_{0} - 1, L_{1} - T_{0} \le t_{1} \le L_{1} - T_{1}$, in the same way of (a) by (8), we have

$$ \frac{{{\text{d}}C(L_{1} , t_{1} , S_{1}^{*} , S_{2}^{*} )}}{{{\text{d}}t_{1} }} > 0. $$

It follows that

$$ C ({L_{1}, L_{1} - T_{{\widehat{S}_{0}}}, S_{1}^{*}, \widehat{S}_{0}} ) = C ({L_{1}, L_{1} - T_{{\widehat{S}_{0}}}, S_{1}^{*}, \widehat{S}_{0} - 1}), $$

$$ C ({L_{1}, L_{1} - T_{k}, S_{1}^{*}, k} ) = C ({L_{1}, L_{1} - T_{k}, S_{1}^{*}, k - 1} ),\quad k = 2, 3, \ldots, \widehat{S}_{0} - 1. $$

$$ C ({L_{1}, L_{1} - T_{1}, S_{1}^{*}, 1} ) = C ({L_{1}, L_{1} - T_{1}, S_{1}^{*}, 0}). $$

When $d \le t_{1} \le L_{1} - T_{0}$ it follows that $S_{2}^{*} = 0$, and by (8)

$$ \begin{aligned} C(L_{1} , t_{1} , S_{1}^{*} , S_{2}^{*} ) & = \lambda h_{1} t_{1} - \lambda h_{2} E[W ] + \lambda h_{2} (L_{1} - t_{1} ) \\ & \quad + \lambda (h_{2} + b )\int\limits_{{L_{1} - t_{1} }}^{\infty } P (W > x){\text{d}}x, \\ \end{aligned} $$

$$ \frac{{{\text{d}}C(L_{1} , t_{1} , S_{1}^{*} , S_{2}^{*} )}}{{{\text{d}}t_{1} }} = \lambda h_{1} - \lambda h_{2} + \lambda (h_{2} + b )P(W > L_{1} - t_{1} = L_{2} ). $$

Since $t_{1} \le L_{1} - T_{0}$, $P ({W > L_{1} - t_{1} = L_{2}} ) \le \frac{{h_{2}}}{{h_{2} + b }}.$ Let

$$ \tilde{T} = \, \begin{array}{*{20}c} {\arg \hbox{min} } \\ x \\ \end{array} \left\{ {P(W > x) \le \frac{{h_{2} - h_{1} }}{{h_{2} + b }}} \right\}. $$

Here $\tilde{T} \ge T_{0}$. When $L_{2} < \tilde{T}$ that is $L_{1} - \tilde{T} < t_{1}$, then $P ({W > L_{2}} ) > \frac{{h_{2} - h_{1}}}{{h_{2} + b }},$ and thus $\frac{{{\text{d}}C(L_{1} , t_{1} , S_{1}^{*} , S_{2}^{*} )}}{{{\text{d}}t_{1} }} > 0$. When $\tilde{T} \le L_{2}$, that is $t_{1} \le L_{1} - \tilde{T}$, $P ({W > L_{2}} ) \le \frac{{h_{2} - h_{1}}}{{h_{2} + b }},$ and thus $\frac{{{\text{d}}C(L_{1} , t_{1} , S_{1}^{*} , S_{2}^{*} )}}{{{\text{d}}t_{1} }} \le 0$. When $T_{0} \le L_{1} < \tilde{T} + {\text{d}}C(L_{1} , t_{1} , S_{1}^{*} , S_{2}^{*})$ is increasing in $t_{1}$ for $\le t_{1}$ . When $T_{0} \le L_{1} < \tilde{T} + {\text{d}}C(L_{1} , t_{1} , S_{1}^{*} , S_{2}^{*} )$ is decreasing in $t_{1}$ for $d \le t_{1} \le L_{1} - \tilde{T}$ and is increasing for $t_{1} > L_{1} - \tilde{T}$.

E. Proof of Proposition 5

(a) When $T_{S + 1} \le L_{1} < T_{S}, S = 0, 1, \ldots, \widehat{S}_{0} - 1$, if $0 \le t_{1} \le L_{1} - T_{S + 1}$ then $S_{2}^{*} = S$ and if $L_{1} - T_{S + 1} < t_{1} \le d$ then $S_{2}^{*} = S + 1$.

For each interval of $0 \le t_{1} \le L_{1} - T_{S + 1}$ and $L_{1} - T_{S + 1} < t_{1} \le d$, by (8)

$$ \begin{aligned} C(L_{1} , t_{1} , 1, S_{2}^{*} ) & = h_{1} (1 + \lambda t_{1} ) - \lambda h_{2} E[E(S_{2}^{*} ) ] + \lambda h_{2} (L_{1} - t_{1} ) \\ & \quad + \lambda (h_{2} + b )\int\limits_{{L_{1} - t_{1} }}^{\infty } P (E(S_{2}^{*} ) > x){\text{d}}x \\ \end{aligned} $$

$$ \frac{{{\text{d}}C(L_{1} , t_{1} , 1, S_{2}^{*} )}}{{{\text{d}}t_{1} }} = \lambda h_{1} - \lambda h_{2} + \lambda (h_{2} + b )P(E(S_{2}^{*} ) > L_{1} - t_{1} ), $$

and from (9) if $L_{1} < T_{0 }$ then $P ({E ({S_{2}^{*}} ) > L_{1} - t_{1}} ) > \frac{{h_{2}}}{{h_{2} + b }}$, which leads to $\frac{{{\text{d}}C(L_{1} , t_{1} , 1, S_{2}^{*} )}}{{dt_{1} }} > 0.$ It also follows that $C ({L_{1}, L_{1} - T_{S + 1}, 1, S} )C ({L_{1}, L_{1} - T_{S + 1}, 1, S + 1} )$. Thus, if $T_{S + 1} \le L_{1} < T_{S}, S = 0, 1, \ldots, \widehat{S}_{0} - 1$, then $C ({L_{1}, t_{1}, 1, S_{2}^{*}} )$ is increasing in $t_{1}$ for $0 \le t_{1} < d$.

If $0 \le L_{1} < T_{{\hat{S}_{0}}}$, $S_{2}^{*} = \widehat{S}_{0}$, and in the same way as above by (8) it follows that $\frac{{{\text{d}}C(L_{1} , t_{1} , 1, S_{2}^{*} )}}{{{\text{d}}t_{1} }} > 0$. Thus, when $0 \le L_{1} < T_{{\widehat{S}_{0}}}$, $C ({L_{1}, t_{1}, 1, S_{2}^{*}} )$ is increasing in $t_{1}$ for $0 \le t_{1} < d$.

(b) When $T_{0} \le L_{1} S_{2}^{*} = 0$, and by (8)

$$ \begin{aligned} C(L_{1} , t_{1} , 1, S_{2}^{*} ) & = h_{1} (1 + \lambda t_{1} ) - \lambda h_{2} E[W ] + \lambda h_{2} (L_{1} - t_{1} ) \\ & \quad + \lambda (h_{2} + b )\int\limits_{{L_{1} - t_{1} }}^{\infty } P (W > x){\text{d}}x \\ \end{aligned} $$

$$ \frac{{{\text{d}}C(L_{1} , t_{1} , 1, S_{2}^{*} )}}{{{\text{d}}t_{1} }} = \lambda h_{1} - \lambda h_{2} + \lambda (h_{2} + b )P(W > L_{1} - t_{1} = L_{2}) $$

and $P ({W > L_{1} - t_{1}} ) \le \frac{{h_{2}}}{{h_{2} + b }}$. By (15), when $L_{2} < \tilde{T}$, that is when $L_{1} - \tilde{T} < t_{1}$, it follows that $P ({W > L_{2}} ) > \frac{{h_{2} - h_{1}}}{{h_{2} + b }}$, and thus $\frac{{{\text{d}}C(L_{1} , t_{1} , 1, S_{2}^{*} )}}{{{\text{d}}t_{1} }} > 0$ and when $\tilde{T} \le L_{2}$, it follows that $P ({W > L_{2}} ) \le \frac{{h_{2} - h_{1}}}{{h_{2} + b }}$, and thus $\frac{{{\text{d}}C(L_{1} , t_{1} , 1, S_{2}^{*} )}}{{{\text{d}}t_{1} }} \le 0.$

When $T_{0} \le L_{1} < \tilde{T}$, $C ({L_{1}, t_{1}, 1, S_{2}^{*}} )$ is increasing in $t_{1}$ for $0 \le t_{1} < d$. When $\tilde{T} \le L_{1} < \tilde{T} + d$, $C ({L_{1}, t_{1}, 1, S_{2}^{*}} )$ is decreasing in $t_{1} \,\,{\text{for}}\,\,0 \le t_{1} < L_{1} - \tilde{T}$, and is increasing for $L_{1} - \tilde{T} \le t_{1} < d$. When $\tilde{T} + d \le L_{1}$, $C ({L_{1}, t_{1}, 1, S_{2}^{*}} )$ is decreasing in $t_{1}$ for $0 \le t_{1} < d$.

F. Proof of Proposition 6

Under $\rho \le \frac{{h_{1}}}{{h_{1} + b }} \widehat{L} (1 )$ is compared with $T_{1} + d$.

It follows $T_{1} \le 0$ and $\widehat{S}_{0} = 0$, and from (2) and (16),

$$ P ({a (1 ) \le - ({\widehat{L} (1 ) - d} )} ) = 1 - e^{{\lambda ({\widehat{L} (1 ) - d} )}} = \frac{{h_{2} - h_{1}}}{{h_{2} + b}}, $$

which implies $e^{{\lambda ({\widehat{L} (1 ) - d} )}} = \frac{{h_{1} + b}}{{h_{2} + b}}.$ From Proposition 2 and (10), $P ({E (1 ) > T_{1}} ) = ({1 - \rho} )e^{{\lambda T_{1}}} = \frac{b}{{h_{2} + b }}$, which implies $e^{{\lambda T_{1}}} = \frac{1}{1 - \rho}\frac{b}{{h_{2} + b }}.$ Since $\rho \le \frac{{h_{1}}}{{h_{1} + b }}$, it holds that $\frac{1}{1 - \rho} \le \frac{{h_{1} + b}}{b }.$ Thus $e^{{\lambda T_{1}}} = \frac{1}{1 - \rho}\frac{b}{{h_{2} + b }} \le \frac{{h_{1} + b}}{{h_{2} + b }} = e^{{\lambda ({\widehat{L} (1 ) - d} )}},$ which means $T_{1} \le \widehat{L} (1 ) - d$.

Next, under $\rho \le \frac{{h_{1}}}{{h_{1} + b }} \tilde{T}$ is compared with $\tilde{L}$. From (18),

$$ \begin{aligned} \int\limits_{{\tilde{T} - d}}^{{\tilde{T}}} P (W > x){\text{d}}x \, & = \int\limits_{{\tilde{L} - d}}^{{\tilde{T}}} P (W > x){\text{d}}x + \int\limits_{{\tilde{T} - d}}^{{\tilde{L} - d}} P (W > x){\text{d}}x \\ & = \frac{1}{\lambda }\frac{{h_{1} }}{{h_{2} + b}} + d\frac{{h_{2} - h_{1} }}{{h_{2} + b}} + (\tilde{T} - \tilde{L})\frac{{h_{2} - h_{1} }}{{h_{2} + b}} + \int\limits_{{\tilde{T} - d}}^{{\tilde{L} - d}} P (W > x){\text{d}}x \\ & = \frac{1}{\lambda }\frac{{h_{1} }}{{h_{2} + b}} + d\frac{{h_{2} - h_{1} }}{{h_{2} + b}} \quad + \int\limits_{{\tilde{T} - d}}^{{\tilde{L} - d}} {\left\{ P(W > x) - \frac{{h_{2} - h_{1} }}{{h_{2} + b}}\right\} } {\text{d}}x. \\ \end{aligned} $$

Since $\int\nolimits_{{\tilde{T} - d}}^{{\tilde{T}}} P (W > x){\text{d}}x \le d$ and $\frac{1}{\lambda}\frac{{h_{1}}}{{h_{2} + b}} + d\frac{{h_{2} - h_{1}}}{{h_{2} + b}} \ge d$ under $\rho \le \frac{{h_{1}}}{{h_{1} + b }},$ it follows that

$$ \int\limits_{{\tilde{T} - d}}^{{\tilde{L} - d}} {\left\{ {P(W > x) - \frac{{h_{2} - h_{1} }}{{h_{2} + b}}} \right\}} {\text{d}}x \le 0, $$

Since $\tilde{L} - d < \tilde{T} {\text{and}} \tilde{T} - d < \tilde{T}$, by (15) $P ({W > \tilde{L} - d} ) > \frac{{h_{2} - h_{1}}}{{h_{2} + b}} {\text{and }}P ({W > \tilde{T} - d} ) > \frac{{h_{2} - h_{1}}}{{h_{2} + b}}$, and thus $\tilde{L} \le \tilde{T}$.

G. Proof of Proposition 7

(a) Under $\rho > \frac{{h_{1}}}{{h_{1} + b }} \;\; \overline{L} (0 )$ is compared with $T_{0}$. From (17),

$$ \int\limits_{{\bar{L}(0) - d}}^{{\bar{L}(0)}} P (W > x){\text{d}}x = \left( {\frac{1}{\lambda } - d} \right)\frac{{h_{1} }}{{h_{2} + b }} + d\frac{{h_{2} }}{{h_{2} + b }} \ge d\frac{{h_{2} }}{{h_{2} + b }} $$

and from (10)

$$ \int\limits_{{T_{0} }}^{{T_{0} + d}} P (W > x){\text{d}}x < {\text{d}}P(W > T_{0} ) \le d\frac{{h_{2} }}{{h_{2} + b }}. $$

Thus, $\overline{L} (0 ) < T_{0} + d$. Under $\rho > \frac{{h_{2}}}{{h_{2} + b }}$, by (10) and Proposition 1

$$ \int\limits_{{T_{0} - d}}^{{T_{0} }} P (W > x){\text{d}}x = \frac{1}{\lambda }P(W > T_{0} ) = \frac{1}{\lambda }\frac{{h_{2} }}{{h_{2} + b }} $$

When $h_{2} = h_{1}$ by (17)

$$ \int\limits_{{\bar{L}(0) - d}}^{{\bar{L}(0)}} P (W > x){\text{d}}x = \frac{1}{\lambda }\frac{{h_{2} }}{{h_{2} + b }} $$

and thus $\overline{L} (0 ) = T_{0}$. When $h_{2} > h_{1}$,

$$ \int\limits_{{\bar{L}(0) - d}}^{{\bar{L}(0)}} P (W > x){\text{d}}x < \frac{1}{\lambda }\frac{{h_{2} }}{{h_{2} + b }} $$

and thus $\overline{L} (0 ) > T_{0}$.

When $\frac{{h_{1}}}{{h_{1} + b }} < \rho \le \frac{{h_{2}}}{{h_{2} + b }}$, it follows that $T_{0} = d$, and $\overline{L} (0 ) > d$ implies that $\overline{L} (0 ) > T_{0}$.

Therefore, when $\rho > \frac{{h_{1}}}{{h_{1} + b }}$, if $h_{2} = h_{1} T_{0} = \overline{L} (0 ) < T_{0} + d$, and if $h_{2} > h_{1}$, $T_{0} < \overline{L} (0 ) < T_{0} + d.$

(b) Under $\rho > \frac{{h_{2}}}{{h_{2} + b }}$, $\tilde{T}, \tilde{L}$, and $\overline{L} (0 )$ are compared. Three cases, $\tilde{L} < \tilde{T}, \tilde{T} < \tilde{L}$ and $\tilde{T} = \tilde{L}$ are considered.

(i) $\tilde{L} < \tilde{T}$

By (17) and (18),

$$ \begin{aligned} \int\limits_{{\tilde{L} - d}}^{{\tilde{L}}} P (W > x){\text{d}}x& = \int\limits_{{\tilde{L} - d}}^{{\tilde{T}}} P (W > x){\text{d}}x - \int\limits_{{\tilde{L}}}^{{\tilde{T}}} P (W > x){\text{d}}x \\ & \quad = \int\limits_{{\bar{L}(0) - d}}^{{\bar{L}(0)}} P (W > x){\text{d}}x + (\tilde{T} - \tilde{L})\frac{{h_{2} - h_{1} }}{{h_{2} + b}} - \int\limits_{{\tilde{L}}}^{{\tilde{T}}} P (W > x){\text{d}}x. \\ \end{aligned} $$

Since by (15) $\mathop \int \nolimits_{{\tilde{L}}}^{{\tilde{T}}} P ({W > x} ){\text{d}}x > ({\tilde{T} - \tilde{L}} )\frac{{h_{2} - h_{1}}}{{h_{2} + b}}$, and

$$ \mathop \int \limits_{{\tilde{L} - d}}^{{\tilde{L}}} P ({W > x} ){\text{d}}x < \mathop \int \limits_{{\overline{L} (0 ) - d}}^{{\overline{L} (0 )}} P ({W > x} ){\text{d}}x. $$

Thus, $\overline{L} (0 ) < \tilde{L} < \tilde{T}$.

(ii) $\tilde{T} < \tilde{L}$

$$ \begin{aligned} \int\limits_{{\tilde{L} - d}}^{{\tilde{L}}} P (W > x){\text{d}}x & \quad= \int\limits_{{\tilde{L} - d}}^{{\tilde{T}}} P (W > x){\text{d}}x + \int\limits_{{\tilde{T}}}^{{\tilde{L}}} P (W > x){\text{d}}x \\ & \quad = \int\limits_{{\bar{L}(0) - d}}^{{\bar{L}(0)}} P (W > x){\text{d}}x \quad+ (\tilde{T} - \tilde{L})\frac{{h_{2} - h_{1} }}{{h_{2} + b}} + \int\limits_{{\tilde{T}}}^{{\tilde{L}}} P (W > x){\text{d}}x. \\ \end{aligned} $$

Since $\mathop \int \nolimits_{{\tilde{T}}}^{{\tilde{L}}} P ({W > x} ){\text{d}}x < ({\tilde{L} - \tilde{T}} )\frac{{h_{2} - h_{1}}}{{h_{2} + b}}$

$$ \int\limits_{{\tilde{L} - d}}^{{\tilde{L}}} P (W > x){\text{d}}x < \int\limits_{{\bar{L}(0) - d}}^{{\bar{L}(0)}} P (W > x){\text{d}}x $$

and thus $\overline{L} (0 ) < \tilde{L}$. $\overline{L} (0 )$ is compared with $\tilde{T}$ next. By (17) and (18)

$$ \begin{aligned} \int\limits_{{\tilde{T} - d}}^{{\tilde{T}}} P (W > x){\text{d}}x & \quad= \int\limits_{{\tilde{L} - d}}^{{\tilde{T}}} P (W > x){\text{d}}x + \int\limits_{{\tilde{T} - d}}^{{\tilde{L} - d}} P (W > x){\text{d}}x \\ & \quad = \int\limits_{{\bar{L}(0) - d}}^{{\bar{L}(0)}} P (W > x){\text{d}}x + (\tilde{T} - \tilde{L})\frac{{h_{2} - h_{1} }}{{h_{2} + b}} \quad + \int\limits_{{\tilde{T} - d}}^{{\tilde{L} - d}} P (W > x){\text{d}}x \\ \end{aligned} $$

From (15) and $\tilde{L} - d \le \tilde{T}$, it follows $\int_{{\tilde{T} - d}}^{{\tilde{L} - d}} P (W > x){\text{d}}x > (\tilde{L} - \tilde{T})\frac{{h_{2} - h_{1} }}{{h_{2} + b}}$, and thus

$$ \int\limits_{{\tilde{T} - d}}^{{\tilde{T}}} P (W > x){\text{d}}x > \int\limits_{{\bar{L}(0) - d}}^{{\bar{L}(0)}} P (W > x){\text{d}}x $$

Therefore $\tilde{T} < \overline{L} (0 ) < \tilde{L}$.

(iii) $\tilde{T} = \tilde{L}$

$$ \int\limits_{{\tilde{L} - d}}^{{\tilde{L}}} P (W > x){\text{d}}x = \int\limits_{{\tilde{L} - d}}^{{\tilde{T}}} P (W > x){\text{d}}x = \frac{1}{\lambda }\frac{{h_{1} }}{{h_{2} + b}} + (\tilde{T} - \tilde{L} + d)\frac{{h_{2} - h_{1} }}{{h_{2} + b}} $$

$$ \int\limits_{{\bar{L}(0) - d}}^{{\bar{L}(0)}} P (W > x){\text{d}}x = \frac{1}{\lambda }\frac{{h_{1} }}{{h_{2} + b }} + d\frac{{h_{2} - h_{1} }}{{h_{2} + b }} $$

$$ \int\limits_{{\tilde{L} - d}}^{{\tilde{L}}} P (W > x){\text{d}}x = \int\limits_{{\bar{L}(0) - d}}^{{\bar{L}(0)}} P (W > x){\text{d}}x $$

This implies $\overline{L} (0 ) = \tilde{L} = \tilde{T}$.

(c) When $\rho > \frac{{h_{2}}}{{h_{2} + b }}$ and $\tilde{T} < \tilde{L}$, $\tilde{L}$ is compared with $T_{0} + d$. By (18)

$$ \begin{aligned} & \int\limits_{{\tilde{L} - d}}^{{\tilde{T}}} P (W > x){\text{d}}x = \frac{1}{\lambda }\frac{{h_{1} }}{{h_{2} + b}} + \int\limits_{{\tilde{L} - d}}^{{\tilde{T}}} {\frac{{h_{2} - h_{1} }}{{h_{2} + b}}} {\text{d}}x, \\ & \int\limits_{{\tilde{L} - d}}^{{\tilde{T}}} {\left\{ {P(W > x) - \frac{{h_{2} - h_{1} }}{{h_{2} + b}}} \right\}} {\text{d}}x = \frac{1}{\lambda }\frac{{h_{1} }}{{h_{2} + b}}. \\ \end{aligned} $$

By (10) and (15),

$$ \int\limits_{{T_{0} }}^{{\tilde{T}}} {\left\{ {P(W > x) - \frac{{h_{2} - h_{1} }}{{h_{2} + b}}} \right\}} {\text{d}}x \le (\tilde{T} - T_{0} )\frac{{h_{1} }}{{h_{2} + b}}. $$

By (b), when $\tilde{T} < \tilde{L}$ it follows $\tilde{T} < \overline{L} (0 )$, and by (a), $\overline{L} (0 ) < T_{0} + d$, which implies that $\tilde{T} < T_{0} + d$, and thus $\tilde{T} - T_{0} < d < \frac{1}{\lambda}, ({\tilde{T} - T_{0}} )\frac{{h_{1}}}{{h_{2} + b}} < \frac{1}{\lambda}\frac{{h_{1}}}{{h_{2} + b}},$

$$ \int\limits_{{T_{0} }}^{{\tilde{T}}} {\left\{ {P(W > x) - \frac{{h_{2} - h_{1} }}{{h_{2} + b}}} \right\}} {\text{d}}x < \int\limits_{{\tilde{L} - d}}^{{\tilde{T}}} {\left\{ {P(W > x) - \frac{{h_{2} - h_{1} }}{{h_{2} + b}}} \right\}} {\text{d}}x. $$

Therefore when $\tilde{T} < \tilde{L}$ it holds that $\tilde{L} < T_{0} + d$.