Abstract
The present research aims at predicting the required activities for preventive maintenance in terms of equipment optimal cost and reliability. The research sample includes all offshore drilling equipment of FATH 59 Derrick Site affiliated with National Iranian Drilling Company. Regarding the method, the research uses a field methodology and in terms of its objectives, it is classified as an applied research. Some of the data are extracted from the documents available in the equipment and maintenance department of FATH 59 Derrick site, and other needed data are resulted from experts’ estimates through genetic algorithm method. The research result is provided as the prediction of downtimes, costs, and reliability in a predetermined time interval. The findings of the method are applicable for all manufacturing and non-manufacturing equipment.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
As the trade-off between the preventive maintenance costs and corrective maintenance requires different methods, the present research focuses on a schedule that cuts the costs and keeps the reliability at an acceptable level; the optimization of the task is undertaken through genetic algorithm.
A handful of researches have devoted to the preventive maintenance scheduling in the recent years, most of which are attempts for coordinating preventive maintenance scheduling with the production line (Moghaddam and Usher 2011; Fitouhi and Nourelfath 2012; Nourelfath and Chatelet 2012). In this respect, some researchers also focus on the optimization of preventive maintenance scheduling (Moradi et al. 2011; Nourelfath et al. 2012; Xiaojun et al. 2012). Munoz et al. (1997) are among the first researchers who proposed the genetic algorithm as an optimization tool for preventive maintenance scheduling (Lapa et al. 1999, 2000; Munoz et al. 1997) and then Lapa et al. (2006) used the genetic algorithm for the optimization of maintenance and inspection intervals in a new approach. Most of the schedules were originally developed for power plants but shortly after that the optimized scheduling was employed for mechanical components (Tsai et al. 2001) and then for production lines (Sortrakul et al. 2005). So far, it has not been used in the drilling industry.
Since machines depreciate over time, they need a new maintenance schedule. The main advantage of this method is revealed in providing updated schedule consistent with the system life cycle at a pre-determined time interval. The cost of maintenance for production or project-based equipment’s forms a substantial portion of the firm’s total cost. An in-time preventive maintenance would result in the reduction of unwanted downtimes and ultimately the total cost of maintenance. The maintenance schedule used by most firms is in accordance with the manufacturer’s instructions and standards, but the depreciation of the equipment loses the credibility of such instructions. In this way, the schedules should be updated continuously according to the equipment life cycle to keep them in an optimum condition. The proposed method aims at predicting the maintenance events using flexible intervals for a pre-determined period. It is expected that the implementation of this method results in predicting downtime, and also the PM department can fix the components before its failure.
In this approach, numerous parameters are used including maintenance probability, cost of each maintenance event, preventive maintenance cost, impact of maintenance on system reliability, maintenance errors probability, impact of reliability on optimization, etc. Some of these values are determined through software and others are decided upon by the operator. In the reliability model as well as the cost model, the computations are firstly undertaken for each component and then for the system as a whole.
Preventive maintenance
Business leaders who have significant investments in physical assets and equipment increasingly realize the strategic importance of maintenance, and so the maintenance cost is necessary expense in their operating budget. In other words, reliability has become a critical issue in capital-intensive operations. The maintenance and resource management can increase profit in two ways: (1) by decreasing running costs and (2) increasing capability. If the annual maintenance cost exceeds five percent of the asset value, the organization is probably faced to financial difficulties. The total maintenance cost depends on the quality of the equipment, the way it is used, the maintenance policy, and the business strategy. Maintenance activities are divided into two main categories: (1) corrective maintenance and (2) preventive maintenance (Duffuaa and Al-Sultan 1997). Corrective maintenances fireman maintenance is performed when the action is taken to restore the previous functionality. This type of maintenance is known as a reactive approach because the action is started when the unscheduled event happens (Khanlari et al. 2007). Preventive maintenance includes repair, replacement, and maintenance of equipment to avoid unexpected failure during use (Mann et al. 1995). Preventive maintenance is performed to keep the equipment in an appropriate operational condition and it is divided into (1) time-based and (2) condition-based maintenance.
Time-based maintenance is performed after fixed time-intervals to avoid failure during operation. Time-based maintenance results in a huge amount of costs for keeping the system in an acceptable reliability level because the majority of items should be replaced without taking their usefulness into consideration. Condition-based management is valuable for components which deteriorate rapidly with time (Eti et al. 2006). The objective of preventive maintenance is the minimization of the total cost of inspection, repair, and downtime (also known as lost production capacity or reduced product quality). In the fixed policies, PM activities are performing exactly pre-specified time intervals while in the conservative policies, whenever production and PM activities have overlap the production operation is postponed and PM activities are conducted first (Jolai et al. 2009).
In the preventive maintenance, feedback observations and functionality degradation are considered to achieve the following objectives:
-
To model the system lifetime and to quantify the degradation of functionality or failure probability,
-
To detect important variables involved in the functionality degradation process and to design maintenance events to eliminate ageing effect of equipment,
-
To determine the effect of maintenance activities on the system behavior,
-
To propose diagnosis and help in decision making,
-
To propose data extraction and sensibility analysis (Celeux et al. 2006).
Preventive maintenance involves a series of managerial, executioner, and technical activities to prevent components lifetime reduction and also to improve the availability and reliability of the system. Management takes the following decisions into account:
-
If/why maintenance is performed for equipment?
-
What is the average interval between component failures? When preventative maintenance is performed?
-
Which actions are required?/What actions are undertaken for equipment?
-
How the work is done?
-
Where the work is done?
-
How long the work takes? (Knezevic et al. 1997).
Genetic algorithm
The original principle of genetic algorithm was proposed by Holland (1975). After that, researchers used and developed the concept in numerous studies. Genetic algorithm pertains to the larger class of evolutionary algorithms (EA) which generate solutions of optimization problems using techniques derived by natural selection (Sadeghi et al. 2011). Genetic algorithm is one of the oldest meta heuristic algorithms that have received much attention by researchers worldwide (Sedighpour et al. 2011). In the genetic algorithms, the optimum solution is the winner of genetic play and every potential solution is a solution which its creation dependents on different parameters. The parameters are considered as genes of chromosomes that are assumed in a binary string. A genetic algorithm is especially suited for solving complex optimization problems. In general, a genetic algorithm consists of simultaneously evaluating multiple regions of the solution space during each iteration (Pourvaziri and Azimi 2014). In this algorithm, the superior algorithm is one that is closer to the optimum solution. In the studies using genetic algorithm, the chromosome populations were selected randomly. Genetic algorithm requires a population of potential solution of the give problem to be initialized. The initial population of individuals is randomly generated by a number of chromosomes (Karimi et al. 2011). The number of these populations differs according to the considered problem. In the related literature, some points are proposed about the choice of appropriate population numbers (Mann et al. 1997). The size of chromosome depends on the required precision in the problem. Decision variables do not have necessarily the same size of secondary string (Deb 1995).
In the genetic algorithm, new candidates for the solution are created by two mechanisms i.e. crossover and mutation. A number of the new created chromosomes may be not necessarily applicable, and so they need some corrections for more reliable application.
The crossover operation recombines the genes of two selected chromosomes to generate a new crossover child to be formed in the next generation. It aims to take the best features of each parent and mix the remaining features in forming the offspring (Asghari and Nezhadali 2014). If the new individuals that are called offsprings inherit good features from their parent, the chance of their survival will increase. The process is continued until the termination criterion is reached. Afterward, the best result is selected as the optimum solution. In the crossover operation, the mating of chromosomes is necessary for offspring production. There are various types of crossover operation including one-point crossover, two-point crossover, integrated crossover, cut and slice crossover, semi-integrated crossover, etc. In one-point crossover, two chromosomes are selected randomly from a single point and exchange the considered numbers which results in two other chromosomes. The original chromosomes are known as parents and the resulted chromosomes are called offspring. The crossover for parent chromosomes is indicated by \( P_{\text{c}} \) probability; it means that the crossover operation will happen with \( P_{\text{c}} \) probability. If the crossover does not happen, the chromosomes results will be mostly like the parents.
Mutation is the second mechanism in the genetic algorithm for seeking new solutions. In mutation, one gene is selected with a random number and is substituted in a limit of parameters (Gen 1997). Then a random number between (0 and 1) is created for each gene. If the random number is less than a pre-determined mutation probability, \( P_{\text{m}} \), mutation of gene will happen. In other words, mutation of another gene does not happen. After the creation of new chromosomes, they should be re-evaluated by crossover and mutation operators.
The last step in genetic algorithm method is answering the question that whether the founded solution by algorithm will meet user expectations. Termination criterion is a set of conditions according to which the expected correct solution is obtained. Different criteria used in the previous studies are as follows:
-
Termination of algorithm after a specified number of generations,
-
There is no optimization in objective function,
-
Reaching a specified value of objective function.
Goldberg (1989) enumerated some differences between genetic algorithm and other optimization methods as follows:
-
Genetic algorithm works with encoding parameters set instead of individual parameters,
-
Genetic algorithm starts its search from a set of points instead of a single point,
-
Genetic algorithm uses data from objective function instead of supportive or driving knowledge,
-
Genetic algorithm pursues the probable change rules instead of definite change (Goldberg 1989).
In solving a problem according to the genetic algorithm, we need:
-
A method which provides the solution in a pseudo-chromosome structure and starts its work with available population,
-
A function for estimating data fitness,
-
A set of genetic algorithm operators including selection, crossover, and mutation that are used for development or change of members’ genetic combination (Machani and Nourelfath 2012).
Methodology
Equipment in FATH 59 Derrick Site are divided into electrical and mechanic devices. There may be more than one devices of the same kind which are used interchangeably and others are working in parallel. For programming purpose, a sample was selected from each kind of equipment. MATLAB software was used for programming.
Data collection was based on the case study method using documents and interview with the net technicians.
In this section, some models are proposed for computation of reliability and cost. At first, the models are used for a single component and then for the system as a whole. The present research relies on Lapa’s theory (Lapa et al. 2000, 2006) according to a model proposed by Lewis (1996).
Reliability model
Let \( R\left( t \right) \) stand for reliability of a component with corrective maintenance potential and/or is subjected to preventive maintenance policy but it did not include any maintenance intervention event at a time t accordingly, i indicates the operating time or the time when the component is ready to start. Assume \( T_{m} \left( i \right) \) as the scheduled date for ith maintenance event of component m and \( T_{m} ({\text{ult}}) \) as the last received maintenance event at time t. Thus, \( {\text{ult}} \) reveals the number of maintenance events at time t. Equation (1) includes hypotheses in the traditional model:
Since we aimed at evaluating the influence of single component maintenance on entire of the operational system, we assumed that the considered component was out of operation during its maintenance time (outage time) \( \Delta_{m} \left( i \right) \). We also considered the probability p (unsatisfactory maintenance):
Equation (2) is not exactly the component’s reliability; it is sometimes a cumulative distribution function and is not able to change the values to smaller than those obtained previously. In this way, Eq. (2) represents the reliability during the operational and the non-operational states during the outage time.
The factor p (unsatisfactory maintenance probability) presents a new condition in which a maintenance event may not result in the system reliability or even may be detrimental. For evaluation purpose, the flexible interval method was used employing Eq. (2) for the times when the components are operating:
Given that the component’s reliability under aging effects can be shown by Weibull distribution, and with \( p \ll 1 \), and \( \left( {1 - p} \right)^{ult} \cong e^{ - pult} \), the following result is obtained:
where, \( m \) and \( \theta \) are aging factors and the component’s characteristic life.
Evaluation of total maintenance policy at system level
The above mentioned model (Eq. 4) shows the behavior of an individual component used for testing maintenance policy. The aim of it is to estimate the availability of multi-component systems. To estimate the system failure probability for each specified combination of component states (operating or testing), some global evaluation techniques including fault trees, minimum cut sets or Markovian chains should be employed to provide the reliability of the system as a whole,
where, x is the number of components of the system.
Cost model
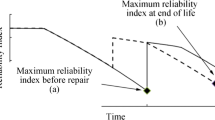
At first, a cost estimation model is created for a specified maintenance policy for a single component. Figure 1 shows the time axis for maintenance dates for a specific mission during \( T_{\text{mis}} \)
\( T_{m} \left( 0 \right) \) is the mission start date. At the last interval \( T_{m} ( {\text{ult}}) \to T_{\text{mis}} \), the potential cost of corrective maintenance is added, and in Eq. (6) the total cost with respect to single component is evaluated which undergoes preventive maintenance in time \( T_{m} \left( j \right) \), where, \( j = 1 \ldots {\text{ult}} \) and mission duration is \( T_{\text{mis}} \). To consider several aspects including repair and maintenance duration interval in the cost model, it is necessary to evaluate their compatibility with the reliability model (Eq. 5) which deals with such features.
More details about such relations between the two models along with the objective function definition are described in the following sections. It is necessary to mention that such relations are significant and the cost model considers the mission as a sum of shutdowns between the maintenance events. The impact of the shutdowns on the whole system is not considered. In system with X components, the total cost for the system operation is the sum of the total cost for each component; therefore, we obtain the following relation adding up X’s:
where, Q is component index and j is maintenance event index.
In general, modeling the optimization problem by genetic algorithms includes two basic views:
-
(a)
Definition of chromosome which is known as data structure for decoding the selected solutions, and
-
(b)
Providing an objective function for evaluating the selected solutions.
Chromosome structure
In this new problem, the chromosome should decode all the possible scheduling combinations for all the system components. Traditionally, the problem is a numerical optimization problem in which the test search or maintenance frequency is considered as the variable. Now, we need to know when and how a number of events should be performed for all the system components. In this approach, the time axis considers a 10-day interval along with a constant number of genes and string in the searching process for scheduling problems.
A fixed binary string was used based on the genetic algorithm paradigm. Each gene (chromosome sub-string) contains \( T_{\text{miss}} /10 \) bits and its decoding (chromosome) is such that 1 shows that the considered combination is working or ready to work and 0 indicates testing at pre-determined date (multiple of 10 days).
Figure 2 shows the chromosome and its decoding (phenotype) for each component or a vector whose elements are testing dates. The proposed chromosome may be customized to match time with different steps. The computational cost may be affected by the method, but its consideration is necessary. In this task, time steps of 10 days may be enough to reach the solution of the problem.
Membership function
The function for evaluating the determined chromosome (scheduling) is a weighted sum which includes the system reliability, all missions, computation of the impact of component outage, and total costs related to the considered maintenance policy. Equation (8) indicates the integrated impact of a specified maintenance policy on the system reliability:
Thus, the membership function is a linear combination between the function (Eq. 9) and total costs in relation to maintenance policy
where, \( W_{d} \) varies between 0 and 1, and \( W_{c} \) varies in a rage from 0 and \( 1/\left( {N\_COMP*MAX\_INT} \right) \), here, \( N\_COMP \) shows the number of components and \( MAX\_INT \) is the maximum number of maintenance events. The combination is necessary because the cost model is not compatible with the effect of component outage.
Data analysis
Input data
The electrical equipments of FATH 59 Derrich Site are as follows (Table 1):
The list of mechanical equipment is as follows (Table 2).
In the present research, the parameters used in equipment’s scheduling based on genetic algorithm adjustments are as follows.
-
The effect of reliability on optimization,
-
The effect of cost on optimization,
-
The possible maximum number of maintenance events,
-
Number of components,
-
Specifications of components,
-
Useful life of components,
-
The probability of faulty maintenance,
-
Scheduling time,
-
Cost of component maintenance,
-
Number of generations,
-
Number of population,
-
Crossover rate.
In this scheduling, the effects of reliability and costs are adjusted at 0.7 and 0.3, respectively. The probability of faulty maintenance is 0.1, and the time frame for scheduling includes 150 days in the future. The numbers of generations and population are, respectively 30 and 100. The crossover rate is 0.7 i.e. the future generation is determined by this value through selection and by 0.3 through mutation. Other parameters are based on condition and data from previous scheduling.
Due to the extent of the task, only the input data and scheduling results for one system i.e. “Main engine” are presented in this section.
Table 3 shows the input data for scheduling related to the main engine. The cost of preventive maintenance per component indicates the cost of each maintenance event for each component. The maximum number of maintenance events shows the prediction of maintenance events in the scheduling time. The number of components per system shows the components which are appropriate for maintenance. The component specification is the score of each component with respect to its robustness.
Results
Given the input data, the cost and reliability of preventive maintenance scheduling related to the main engine for future 150 days are obtained (Table 4). In addition, the final value with fitness function of 3411.2 is determined. The best fitness value—the smallest fitness value for all population individuals—along with the mean fitness values are depicted in Fig. 3. Finally, the prediction of downtimes during the scheduled period is reported in Table 5. The main advantage of this method is revealed in providing updated schedule consistent with the system life cycle at a pre-determined time interval. Other advantages of this model include: Presents stop forecast, cost and reliability simultaneously; Presents reliability in both operational and nonoperational conditions, it means that the piece will be considered at the time of repair out of operation; it’s very appropriate For planning preventative maintenance that belongs to repairable parts; according to failure history of each component, forecasts it’s future stops in flexible intervals at the lowest cost and most reliability.
Conclusion and recommendations
Based on the proposed model, the cost and reliability of each component are computed firstly by each component and secondly by the system as a whole. Then, the results are deployed in the objective function. The secondary data including the effects of reliability and cost on the optimization, cost of component maintenance and repair, faulty maintenance, etc. are determined and used as the input of MATLAB software. Some of the mentioned data are extracted from database of the net department, and other needed data are collected through interview with experts. It is worth mentioning that the scheduling procedure is only useful for components which are prone to maintenance.
The optimization method results in introducing new procedure for preventive maintenance activities using the flexible intervals technique. Given that the scheduling framework is for future 150 days, the results reveal that most of the failures happen in the first and third parts of the period. To reference the software results, the fitness function diagram is provided.
For better scheduling, future researchers can consider the following recommendations: records of the system failures date of system start up, engineers comments, reliability, hours of system operation per day, and number of off days. Additionally, this type of researches should be performed where very precise information about equipment’s available and active approach to preventive maintenance is followed.
References
Asghari M, Nezhadali S (2014) Fuzzy programming for parallel machines scheduling: minimizing weighted tardiness/earliness and flow time through genetic algorithm. J Optim Ind Eng 14:61–73
Celeux G, Corset F, Lannoy A, Ricard B (2006) Designing a Bayesian network for preventive maintenance form expert opinions in a rapid and reliable way. Reliab Eng Syst Saf 91:849–856
Deb K (1995) Optimization for engineering design: algorithms and examples. Prentice Hall, New Delhi
Duffuaa SO, Al-Sultan KS (1997) Mathematical programming approaches for the management of maintenance planning and scheduling. J Qual Maint Eng 3(3):163–176
Eti MC, Ogaji SOT, Probert SD (2006) Reducing the cost of preventive maintenance (PM) through adopting a proactive reliability-focused culture. Appl Energy 83:1235–1248
Fitouhi MC, Nourelfath M (2012) Integrating noncyclical preventive maintenance scheduling and production planning for a single machine. Int J Prod Econ 136(2):344–351
Gen M (1997) Genetic algorithm and engineering design. Wiley, New York
Goldberg D (1989) Genetic algorithms in search, optimization and machine learning. Addison-Wesley, Boston
Holland JH (1975) Adoption in neural and artificial systems. The University of Michigan Press, Ann Arbor
Jolai F, Zandieh M, Naderi B (2009) A memetic algorithm for hybrid flowshops with flexible machine availability constraints. J Ind Eng 3:59–64
Karimi A, Sharifi M, Chambari A (2011) Genetic algorithm and simulated annealing for redundancy allocation problem with cold-standby strategy. J Optim Ind Eng 8:65–72
Khanlari A, Mohamadi K, Sohrabi B (2007) Prioritizing equipments for preventive maintenance (PM) activities using fuzzy rules. Comput Ind Eng 54:169–184
Knezevic J, Papic L, Vasic B (1997) Sources of fuzziness in vehicle maintenance management. J Qual Maint Eng 3(4):281–288
Lapa CMF, Pereira CMNA, Mol ACA (1999) Aplicacao de algoritmos geneticos naotimizacao da polıtica de manutencoes preventivas de um sistema nuclear centradaem confabilidade. In: Proceedings of the 15th Brazilian congress of mechanical engineering (COBEM)
Lapa CMF, Pereira CMNA, Mol ACA (2000) Maximization of a nuclear system availability through maintenance scheduling optimization using a genetic algorithm. Nucl Eng Des 196(2):219–231
Lapa CMF, Pereira CMNA, Barros MPD (2006) A model for preventive maintenance planning by genetic algorithms based in cost and reliability. Eng Syst Saf 91(2):233–240
Lewis EE (1996) Introduction to reliability engineering. Wiley, New York
Machani M, Nourelfath MA (2012) Genetic algorithm for integrated production and preventive maintenance planning in multi-state systems. 8th international conference of modeling and simulation—mosim’10, pp 10–12, Hammamet, Tunisia
Mann L, Saxena A, Knapp GM (1995) Statistical-based or condition-based preventive maintenance. J Qual Maint Eng 1(1):46–59
Mann KF, Tang KS, Kwong S, Halang WA (1997) Genetic algorithms for control and signal processing. Springer, Londen
Moghaddam KS, Usher JS (2011) Preventive maintenance and replacement scheduling for repairable and maintainable systems using dynamic programming. Comput Ind Eng 60:654–665
Moradi E, FatemiGhomi SMT, Zandieh M (2011) Bi-objective optimization research on integrated fixed time interval preventive maintenance and production for scheduling flexible jobshop problem. Expert Syst Appl 38–6:7169–7178
Munoz A, Martorell S, Serradell V (1997) Genetic algorithms in optimizing surveillance and maintenance of components. Reliab Eng Syst 57(2):107–120
Nourelfath M, Chatelet E (2012) Integrating production, inventory and maintenance planning for a parallel system with dependent components. Reliab Eng Syst Saf 101:59–66
Nourelfath M, Chatelet E, Nahs N (2012) Joint redundancy and imperfect preventive maintenance optimization for series—parallel multi-state degraded systems. Reliab Eng Syst Saf 103:51–60
Pourvaziri H, Azimi P (2014) A tunned-parameter hybrid algorithm for dynamic facility layout problem with budget constraint using GA and SAA. J Optim Ind Eng 15:65–75
Sadeghi J, Sadeghi A, Saidi-Mehrabad M (2011) A parameter-tuned genetic algorithm for vendor managed inventory model for a case single-vendor single-retailer with multi-product and multi-constraint. J Optim Ind Eng 9:57–67
Sedighpour M, Yousefikhoshbakht M, Darani Nm (2011) An effective genetic algorithm for solving the multiple traveling salesman problem. J Optim Ind Eng 8:73–79
Sortrakul N, Nachtmann HL, Cassady CR (2005) Genetic algorithms for integrated preventive maintenance planning and production scheduling for a single machine. Comput Ind 56(2):161–168
Tsai YT, Wang KS, Teng HY (2001) Optimizing preventive maintenance for mechanical components using genetic algorithms. Reliab Eng Syst Saf 74(1):89–97
Xiaojun Z, Lu Z, Zi L (2012) Preventive maintenance optimization for a multi-component system under changing job shop schedule. Reliab Eng Syst Saf 101:14–20
Acknowledgments
We would like to thank the National Iranian Drilling Company and also thank the employees of the Maintenance Engineering Department and FATH 59 Derrick Site.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Javanmard, H., Koraeizadeh, A.aW. Optimizing the preventive maintenance scheduling by genetic algorithm based on cost and reliability in National Iranian Drilling Company. J Ind Eng Int 12, 509–516 (2016). https://doi.org/10.1007/s40092-016-0155-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40092-016-0155-9